Abstract
Research has demonstrated that when learning mechanics, students’ conceptions (SCs) improve gradually (1) and are often activated depending on problem features (2). The aim of this study is to combine these two research lines to investigate how different task characteristics affect the activation of SCs at different levels of sophistication. Data were collected from N = 356 students using a paper–pencil test in which conceptual and contextual task characteristics (CCTCs) are varied systematically across ordered multiple-choice items. Answer options were constructed according to the four levels of a force and motion learning progression. Results, obtained using quantitative methods (e.g., Rasch analysis and regression), demonstrate that the effects of CCTCs may differ at different levels of SCs. For the direction of problem, for example, activating the correct conception, assuming force proportional to acceleration, seems to be easier in tasks asking for the resulting motion. However, activating more appropriate conceptions regarding lower levels, e.g., assuming force proportional to velocity, compared to a rather undifferentiated understanding of force and motion, seems to be easier in tasks asking for the forces. Results of our study can be used for choosing tasks with specific CCTCs to support conceptual change along specific steps of a learning path.
1. Introduction
When students enter a science classroom, there is consensus in research that they have often established particular conceptions about the learning content from their prior experiences and education (e.g., [1,2,3,4]). These conceptions, often not matching the physics point of view, are tendencies or dispositions to solve a physics problem or to explain a specific phenomenon [3] and can be assumed as important starting points for further learning (e.g., [3,5]). With that in mind, learning should not be assumed to be a sudden shift from initial conceptions to scientific concepts. Rather, learning can be understood as a developmental process that occurs in interaction with the environment and as a process in which students’ conceptions (SCs) and their relationships improve gradually (e.g., [6,7,8,9]). Therefore, it is important to determine a learner’s current level of conceptual development and to provide instruction that matches this level to support individual progress (see the concept of the “zone of proximal development”; [10] (p. 86)). Research in science education stresses the importance of SCs and therefore the need to design adaptive instruction (e.g., [3,5,11,12]). As a consequence, SCs have been investigated extensively (see [13] for a collection of research on SCs). One area of focus is SCs regarding Newtonian mechanics (see overview in [14]), as this is a very challenging topic for students (e.g., as summarized in [7,14,15]). Research in this area has investigated and documented many SCs, particularly for the relationship between force and motion (e.g., as summarized in [16]), because this seems hard for students to understand correctly. Although many of these SCs are well documented, the development of adaptive instruction remains challenging. On the one hand, it is important to know how inappropriate conceptions can be graduated from a low level of understanding towards a higher level (e.g., as modeled in a “learning progression”, [17,18]). On the other hand, constructing adaptive instruction is challenged by the fact that SCs are variable and may be activated differently depending on the situation described in a task (e.g., [2,3,15,16,19,20,21] or as summarized in [1]; and many more). Research reported in this paper addresses the combination of both challenges by employing a learning progression perspective on conceptual change (see Section 1.1) to investigate how particular task characteristics relate to conceptions activated (see Section 1.2). The results can help to generate information on how tasks with specific characteristics should be used for adaptive instruction.
1.1. Theoretical Background and State of Research
1.1.1. Conceptual Change and Learning Progressions
Learners develop new conceptions based on their current conceptions, which is why this process is discussed in research as a “conceptual change” (CC; e.g., in [7,15,22]). CC research focuses on the question of “[…] how naive, nonscientific or “wrong” conceptions develop to become improved, scientific or “correct” concepts” [22] (p. 209). Such a change is needed, because non-scientific or commonsense knowledge is often associated with specific contexts, describing “what makes sense” [23] (p. 11) and students often “think[ing] as they do” [23] (p. 11). Scientific knowledge, on the other hand, is rather independent of context, relies on theoretical models that have been investigated and elaborated and results from an agreement between scientists [23]. Commonsense knowledge often does not match the scientific knowledge, which is why a change in SCs is important. Typically, SCs do not shift from being “wrong” to “right” all of a sudden, but rather develop in steps towards an adequate concept. CC is therefore often considered as a process in which conceptions develop rather than change suddenly (e.g., [6,7,8]). The idea of describing the development of SCs towards more appropriate science concepts is not new (see for example [24] summarizing research on the development of a scientific concept over “intermediate conceptions” (p. 131)) but has, more recently, gained more attention in research regarding the field of Learning Progressions (LPs). LPs are just like the conceptual change approach built on “the assumption that learning occurs in steps” [6] (p. 470), and arrange students’ conceptions at levels ranging from low (rather far from an adequate understanding) to high (adequate understanding) (e.g., [17]). The levels represent a hypothetical way in which students’ conceptions could evolve while students learn (e.g., [18,25]). It is important to note that two different meanings may be captured under the label of LPs. In addition to understanding LPs in the context of CC research, LPs can also be thought of as a content or teaching progression in instructional research (e.g., as summarized in [16]). Content or teaching progressions describe a sequence of appropriate conceptions in the order in which they should be taught in class or contain instructional aspects (e.g., [26,27]). In the study described in this paper, we understand LPs only as a model of development describing how SCs become more sophisticated while they learn (e.g., as in [6,16,28]).
For mechanics, a one-dimensional LP on force and motion is often mentioned (FMLP; [6,16]; an additional LP for Newton’s 3rd law is described in [28]). The FMLP distinguishes four levels of understanding (higher level = higher understanding) that can be summarized as follows (for more details see [6,16]):
- no clear distinction between force and motion (force = motion),
- force is proportional to motion (force~motion),
- force is proportional to velocity (force~velocity),
- force is proportional to acceleration (force~acceleration).
A distinctive feature of the FMLP is that it describes progress not only in students’ understanding of the relationship between force and motion but also in their understanding of each of these two components (see also Figure 5) individually [6].
LPs can be used for assessing SCs, for example, by using the LP levels as tiers for answer options in closed tasks (so-called ordered multiple-choice (OMC) items; [29]) or as categories for evaluating students’ responses in open-ended tasks (e.g., [16,29,30]). In terms of adaptive instruction, LPs can provide information on which concepts may be addressed early in the learning process (corresponding to SCs at lower levels) and which are more likely to be understood later (higher levels) (e.g., [17]). If, for instance, students cannot distinguish between force and motion, instruction may focus on this distinction rather than attempting to establish that force can point in a different direction than velocity (required for moving from level 3 to 4). For the FMLP in particular, the information offered in the LP can also help to decide whether more progress in one component (e.g., motion) may be needed before the relationship between the two components can be addressed to foster progress to the next level [6].
When using LPs, it is important to keep in mind that they only describe idealized ways (e.g., [25]) of how progress may occur. They can serve as a frame of reference to make sense of what students say and do and should not be used to assign a learner to a particular level. The same person may sometimes give an answer to a task that indicates one level of understanding and shortly afterwards an answer that may indicate a different level [6]. This variability indicates that it is also important to consider under which circumstances particular SCs are activated and whether students seem to demonstrate a more stable or a rather variable understanding. The former may allow designing instruction that challenges students to progress to the next level, the latter may indicate that students need more practice to stabilize at the levels they can reach under particular circumstances.
1.1.2. Variability of Students’ Conceptions
There is consensus in the literature that small changes of a situation or the description of a problem may lead to students activating different SCs even when identical physics concepts would be appropriate (e.g., [20,31,32] or as summarized in [1,8,9,15] and many more). This variability is explained differently regarding the debate of researchers describing students’ understanding either as “coherent” (e.g., [33,34]) or as rather “fragmented” (e.g., [20,31]) [35] (p. xv). Seeing SCs as a rather coherent construct, the variability of SCs may be due to the fact that students adapt to specific situations and activate specific elements of their coherent knowledge construct [8]. Other frameworks considering more fragmented mental entities (e.g., p-prims [31] or facets [20]), explain the variability by stating that these entities are activated depending on the specific situation. Regardless of the explanation, the fact that students activate different ideas in physically similar but superficially different situations is an important starting point for adapting to students’ needs [8].
1.2. Effects of Conceptual and Contextual Task Characteristics: Focus of the Study
In this study, the focus is on the characteristics of tasks in mechanics to explore the relationship between these characteristics and the activation of SCs. Within the range of potentially relevant task characteristics that can be derived from research (e.g., from [2,6,19,21,32,36,37,38,39,40,41,42] and more), we identify at least two different types of characteristics: conceptual and contextual task characteristics (CCTCs). With the notion of conceptual TCs, two different variations were subsumed. The first kind of variation refers to situations that are different in terms of their underlying concepts but have a high potential to be confused by learners because they cannot identify the conceptual difference. In particular, this may happen when a task asks to argue with forces acting on different bodies (focusing on Newton’s 3rd law) in contrast to situations in which forces acting on the same body have to be considered (Newton’s 1st/2nd law). Learners sometimes seem to treat the former like the latter (e.g., [4]). The second kind of variation refers to how a particular concept is approached. For instance, tasks may differ in the direction of problem, asking students to describe what happens with the velocity of a body if there is no net force acting on the body compared to having to decide whether or not a net force is present when a body moves at a constant velocity. Both tasks refer to the same concept (1st law), but differ in its approach (asking to conclude from force to motion vs. from motion to force). Contextual TCs are characterized by variations in surface characteristics of a situation. For instance, tasks in which students are asked to describe the forces acting on a body may vary with regard to the plane of motion, meaning whether the body is moving horizontally or vertically. Both tasks appear different on the surface but require the same concepts to be solved correctly.
Although existing research found some evidence for the effects of CCTCs, there is still a need for further studies. For example, research mostly investigates conceptual or contextual task characteristics (e.g., for conceptual characteristics the direction of the problem; e.g., [41]; or for contextual characteristics the plane of motion, e.g., [19,21,32,40]). Therefore, only little is known about the interaction of conceptual and contextual characteristics. Additionally, studies sometimes only focus on a particular conception (e.g., [39] for the impetus idea or [2] for the conception that heavy objects fall faster), which results in important information on the activation of SCs but there is still a need for systematic research on the combination of CCTCs concerning a wider range of conceptions. Results of previous studies regarding the influence of CCTCs sometimes also appeared only as secondary implicit findings of studies whose main objective was different, which is why tasks were not necessarily systematically designed to investigate the effect of task characteristics (e.g., Fazio and Battaglia [38] using cluster-analysis in the Force Concept Inventory (FCI) [43] to find patterns of students understanding in Newtonian mechanics). Additionally, task characteristics could be derived from theoretical considerations (e.g., suggesting the direction of problem as a possible trigger for students to answer tasks differently [6,16]). Therefore, a previous study [44] investigated systematically which CCTCs are likely to result in correct or incorrect solutions for tasks addressing all three of Newtons laws, but it remained unclear if the CCTCs may also affect inappropriate SCs of different levels of sophistication. In consequence, the study presented here uses the FMLP to investigate the effects of the combination of conceptual and contextual task characteristics on the activation of SCs at different levels of sophistication. However, LPs are not the only way to measure students’ understanding of varying adequacy. For example, Zhai and Li [45] used another approach to measure students understanding at different levels of sophistication. The increasing level of SCs is described by the number of correct fundamental ideas used to solve a task. This approach seemed very fruitful, but information about the type of ideas is missing, when solely looking at the number of fundamental ideas in an answer. Using the FMLP instead allows to directly attain information on the type of conceptions used, because each level represents specific SCs of an equal level of sophistication. The FMLP offers the opportunity to investigate SCs when TCs vary, even if SCs remain incorrect, but may demonstrate variations at lower levels. Therefore, the main research question guiding research reported in this paper is:
How does the variation of CCTCs affect the activation of SCs at different levels of understanding in mechanics?
2. Materials and Methods
2.1. Instrument
In order to explore the relationship between conceptual and contextual task characteristics (CCTCs) and the activation of SCs in Newtonian mechanics, an instrument was needed in which potentially relevant CCTCs are systematically varied across items. While existing instruments (e.g., the Force Concept Inventory (FCI), [43]; the Force and Motion Conceptual Evaluation (FMCE), [46]; tests regarding the EPSE-Project (Evidence-informed Practice in Science Education), [47,48] and a test based on the FMLP, [16]) typically include a few variations on some of these characteristics, none of the instruments known to the authors include a comprehensive and controlled variation of CCTCs while simultaneously allowing to assign a specific level of a LP to all answer options. Existing instruments often only use items with a dichotomous response structure (i.e., the answer to an item is either considered right or wrong), which limits the possibility to distinguish between different levels of students’ conceptual understanding and possible information gets lost [29]. To address these issues, a new instrument was needed. The goals for the development of this instrument were to vary potentially relevant CCTCs systematically and to implement OMC items representing a polytomous response structure. In the following section, the CCTCs varied in the instrument, the design of the items, the polytomous response structure, and how the items were distributed across test booklets are briefly described. Please note that the descriptions of the instrument and the data collected (Section 2.1 and Section 2.2) are partly similar to descriptions of the research reported in [44], as the database (instrument and sample) is the same. However, the descriptions in this study are enriched with more detailed descriptions of specific CCTCs and contain more examples of items and the implementation of the FMLP, which are essential for the current study.
2.1.1. Selection of Conceptual and Contextual Task Characteristics
The first step to identifying potentially relevant CCTCs was an analysis of a physics curriculum [49], multiple school- (e.g., [50,51]), and textbooks (e.g., [52,53,54]), as well as documented SCs (e.g., [6,14,16]). All these resources were used to reconstruct conceptual characteristics related to Newtonian mechanics. The focus is on Newton’s laws and, in particular, on concepts that address the relationship between force and motion in linear motion qualitatively (e.g., “a/no resulting net force means a/no change in motion” rather than “F = m × a”). Thereafter, existing test instruments (e.g., FCI, FMCE, EPSE-Tests, and FMLP-Test) related to these concepts were analyzed to identify and select contextual characteristics that potentially impact the activation of SCs when solving items related to these conceptions. Existing research (e.g., [2,6,19,21,32,40,41,42]) was also analyzed to provide support for the chosen CCTCs. For research reported in this paper, four major groups of task characteristics are distinguished (two conceptual and two contextual) that allow for extended comparisons (smaller subgroups of CCTCs varied in the instrument are detailed in [44]).
Based on the analytical procedures described above, two main potentially relevant conceptual task characteristics are:
- 1.
- The Newtonian law, that is, whether an item addresses the 1st or 2nd law (see Figure 1 for a pair of items differing in the addressed law).
 Figure 1. Comparison of items differing in the law addressed; (a) 1st law (item code: 1mf08, see Figure 6 for an explanation of item codes; context similar to [48]), (b) 2nd law (2mf08).
Figure 1. Comparison of items differing in the law addressed; (a) 1st law (item code: 1mf08, see Figure 6 for an explanation of item codes; context similar to [48]), (b) 2nd law (2mf08).
- 2.
- The direction of problem, that is, whether students have to reason from given forces to resulting motion (force → motion) or from given motion to acting forces (motion → force; see Figure 2 for a pair of items differing in the direction of problem).
 Figure 2. Comparison of items differing in the direction of problem; (a) motion → force (1mf09; based on [43,44]), (b) force → motion (1fm09; [44]).
Figure 2. Comparison of items differing in the direction of problem; (a) motion → force (1mf09; based on [43,44]), (b) force → motion (1fm09; [44]).
In addition to the two main conceptual task characteristics, two main contextual task characteristics were identified:
- 3.
- The plane of motion, describing if an item addresses either horizontal or vertical motion (see Figure 3 for a pair of items differing in the plane of motion).
 Figure 3. Comparison of items differing in the plane of motion; (a) horizontal (1mf06; context similar to [43,47]), (b) vertical (1mf09; based on [43,44]).
Figure 3. Comparison of items differing in the plane of motion; (a) horizontal (1mf06; context similar to [43,47]), (b) vertical (1mf09; based on [43,44]).
- 4.
- The type of object considered, describing if an item addresses either a non-living object or a person (see Figure 4 for a pair of items differing in the type of object considered).
 Figure 4. Comparison of items differing in the type of object considered; (a) non-living object (1mf11; answer options partly similar to [43]), (b) person (1mf12; answer options partly similar to [43]).
Figure 4. Comparison of items differing in the type of object considered; (a) non-living object (1mf11; answer options partly similar to [43]), (b) person (1mf12; answer options partly similar to [43]).
2.1.2. Development and Compilation of Items and Test Booklets
Wherever possible, items from existing instruments were employed that assessed students’ understanding of Newtonian mechanics. These items were modified according to the construction principles outlined below for our purposes. In addition, new items were developed to complement the existing item pool. To investigate the effect of the CCTCs in a controlled and systematic way, all items were constructed in a standardized way. The items were designed in accordance with guidelines for multiple-choice items (e.g., [55,56]). Each item begins with a presentation of the situation (everyday situation, one-dimensional) which is accompanied by an image and, if applicable, a statement regarding the boundary conditions (e.g., the instruction to ignore effects of air resistance or friction; see Figure 1, Figure 2, Figure 3 and Figure 4 for examples). The items consist of four answer options from which one must be ticked by the students. Items asked students to tick the “best” answer to engage students to think about the different answer options and to only tick one (e.g., [21,56]). It was ensured that responses to an item are similar in language and length to avoid other factors affecting the choice of a response. For the development of a polytomous response structure in which each response represents a different level of understanding, an ordered multiple-choice (OMC; [29]) format was used. OMC items provide more detailed information about SCs than normal multiple-choice items and at the same time maintain their advantages regarding efficiency [29] (p. 33). LPs can be used for the construction of OMC items by linking every response to a specific level of sophistication (e.g., [16]; see Figure 5 for an example). For the construction of the answer options, the four levels of understanding were employed that were described in the FMLP established by Alonzo and Steedle [16] and further unpacked by Alonzo and von Aufschnaiter [6]. Usually, each item provides answer options corresponding to all four levels of the FMLP. There are, however, some exceptions, as some items did not allow for a plausible answer option on the lowest level of understanding, while others could be entirely solved correctly with only a partial understanding of the underlying concept. For instance, for the item presented in Figure 5, no plausible answer on level 1 could be constructed. Therefore, some items offer only answer options on three or, very rarely, on two different levels. Consequently, two or three of the offered responses represent the same level of understanding. This is common for OMC items (e.g., [29,30]). Either way, all items have in common, that the correct option always corresponds to the highest level possible in the item. Figure 5 depicts an example demonstrating how levels correspond to answer options. In general, the order of answer options did not follow any particular order in levels, rather, the options were randomly ordered so that the highest level occurs at different positions.

Figure 5.
Example of an OMC item (1mf06; context similar to [43,47]) with three different levels of understanding according to the FMLP [6,16]. Level 1 is missing, as an answer on that level would not have been plausible for students, instead, level 3 appears twice.
Wherever possible, items were modified for which levels were already assigned to answer options from existing research [16]. Furthermore, items and responses were constructed that align with those for which assigned levels already exist (e.g., items from the FCI for which Neumann, Fulmer and Liang [57] have already assigned levels taken from the FMLP). Some items included in our test are completely new, so sometimes it was not possible to transfer assignments of levels from existing instruments. For these new items, 7 representative examples were chosen and discussed with Dr. Alicia C. Alonzo who is an expert in that field, to ensure that the corresponding answer options represent the intended FMLP levels. Consensus was reached on the levels of the responses which were then transferred to all other new items for which a “master” from existing research did not exist. Finally, the items were checked by Ph.D. students to, again, verify levels, to identify possible difficulties to understanding the items, and for the assignment of items to particular CCTCs. Items were revised according to the feedback given. It should be noted that a specific level may be assigned to specific answer options for different reasons because each level of the FMLP is described by more than one conception. For example, level 3 may be assigned because more than one force is acting on a body or because of an assumed proportionality between force and velocity. This should be taken into account when interpreting the results.
The construction process resulted in a pool of 72 OMC items. This allowed for a systematic and controlled variation of the CCTCs addressed, but the items one can answer in a survey is restrained by cognitive fatigue and/or test motivation. Therefore, we used a booklet design (e.g., [58]) so that all items of the item pool were distributed among four test booklets. Each booklet contains 31 OMC items. Nine of these items were identical in all the booklets (so-called ‘anchors’ or ‘anchor items’; e.g., [58,59,60]) to enable the linking of the booklets. The remaining 22 items were presented only in one or two of the four booklets. It was taken care that the CCTCs are distributed as similarly as possible across all booklets. In addition, 5 items on more general mechanics understanding (e.g., about concepts of velocity, acceleration, and circular motion; included in all booklets) and 28 open-ended items matching specific OMC items (4 items in all booklets (anchors), 6 additional items in each booklet) were employed. These items are not described in more detail as they are used to investigate research questions beyond the scope of this paper (e.g., regarding the relationship between answers to open-ended and closed formats). However, they need to be taken into account when considering the total test duration. The open-ended items are located in front of the OMC items and students were not allowed to go back to avoid an influence of previous items on the one hand and revision of previous answers on the other hand (e.g., [30]). Additionally, items where students have to infer the forces from the motion given are located before items where the resulting motion should be described.
In a pilot study, one booklet was used with N = 17 physics pre-service teachers at the end of their university education to detect potential problems with the instrument (e.g., understanding of the items and time constraints). As a result, minor changes were made regarding the items or their order in the booklet. The other three booklets were then revised accordingly.
2.2. Data Collection
For data collection (also described in [44]), the booklets were handed out to three different student groups. The first group consists of N = 85 undergraduate students with physics as a major subject (pmaj; mainly B.Sc. in physics and technology for space travel applications, B.Sc. in physics, pre-service high school physics teachers, B.Sc. in advanced materials and B.Sc. in maths). The second group consists of N = 114 undergraduate students with physics as a minor subject (pmin; mainly B.Sc. in nutritional sciences, B.Sc. in environmental management, B.Sc. in agricultural sciences and B.Sc. in biology). The third group consists of N = 157 high school students (hss) of three German high schools (~16 years in grade levels E2/Q1). Data were collected separately for each cohort (pmaj, pmin, and hss) in 2019. The booklets were assigned to the students randomly and testing took about 60 min with no strict time limit for completing the test. To gather information about students’ conceptions after instruction, the test was handed out to the groups after mechanics has been covered, either in high school (for hss) or after mechanics lectures in university (for pmaj and pmin).
2.3. Data Analysis
2.3.1. Step 1: Data Entry and Rasch Modeling of Raw Scores
For every response chosen, the corresponding level of the FMLP was assigned. If students did not give an answer or ticked more than one response, although only one was required, the corresponding item was coded as missing, since no particular level could be assigned. In addition to some items not having responses on all levels of understanding by design (“structural zeroes”; [60]), it was also observed that in some items a specific response (resp. level of either the highest or lowest category in the item) was never selected. Because such “sampling zeroes” [60] impart the analysis and the comparability of the items, a single dummy person was added to the sample who selected the missing responses [60].
After data entry, the raw scores were used to estimate a Partial Credit Rasch model. A Rasch model was used because it allows for variable item difficulties and describes a psychologically plausible relationship between students’ ability and the probability to solve an item of a specific difficulty (e.g., [59,60,61]). Furthermore, Rasch measurement techniques allowed us to link the four test booklets while retaining the same metric for all students and items, respectively, and to conduct a detailed investigation of instrument functioning [59]. The Partial Credit Model was chosen as it also allows each item to have its own response structure [60,62]. This is necessary to address the fact that not all items provide responses on all levels of understanding and to investigate the impact of CCTCs, as it cannot be assumed that the increase in ability, necessary to move from one level to another, is the same for all items. For instance, an item with CCTC combination A and an item with CCTC combination B may both offer responses on all four levels of understanding (1–4). However, achieving level 3 may just be slightly more difficult than achieving level 2 for item A, but considerably more difficult for item B.
Since the items in our test covered all three Newtonian laws, the first step of the Rasch analysis was to investigate whether the items define a single trait or multiple latent traits. To that end, five different Rasch models were estimated using the R packages TAM [63] and CDM [64]:
- Model 1: All items are assumed to define one single trait.
- Model 2a: Items on Newton’s 1st and 2nd law define one trait, items on Newton’s 3rd law another.
- Model 2b: Items on Newton’s 1st and 3rd law define one trait, items on Newton’s 2nd law another.
- Model 2c: Items on Newton’s 1st law define one trait, items on Newton’s 2nd and 3rd law another.
- Model 3: Items on Newton’s 1st, 2nd, and 3rd law define three separate traits.
Based on common recommendations for model fit comparisons, the final deviance and the Bayesian Information Criterion (BIC) were used as indicators for model fit. The lower the deviance and respectively the BIC, the better the model fits the data (e.g., [28,61]).
The model fit parameters presented in Table 1 show that Model 3 and Model 2a fit the data considerably better than all other models. Furthermore, while Model 3 fits slightly better with regard to the final deviance than Model 2a (∆Deviance = 13.07, df = 3, χ2 = 13.07, p = 0.004), Model 2a fits slightly better with regard to BIC (∆BIC = 4.54). Based on these results, the analysis was continued with Model 2a, since this model is not only simpler but also plausible, since Newton’s 1st law represents a special case of Newton’s 2nd law, and thus is conceptually more closely related to the 2nd law than the 1st and the 2nd law are to the 3rd. Additionally, studies have shown that sometimes students treat these two laws as rather undifferentiated (e.g., as described in [38]). Therefore, for the research reported here, the following steps focused exclusively on the 54 items that address Newton’s 1st and 2nd law.

Table 1.
Comparison of different models regarding Newton’s laws (Npars: Number of estimated parameters; BIC: Bayesian Information Criterion).
2.3.2. Step 2: Investigation of Instrument Functioning
Following the initial model estimation of a Partial Credit Rasch Model with the 54 items regarding Newton’s 1st and 2nd law, a Rasch analysis was conducted to analyze the functioning of the instrument and the quality of measurement using Winsteps Version 4.4.4. [60]. The analysis showed that the items are internally consistent and can be precisely located on the latent variable (model item reliability = 0.97, model person reliability = 0.90, comparable to Cronbachs Alpha; [59,60]). Furthermore, applying common ranges for item fit (0.5 < Infit/Outfit MNSQ < 2.0; −1.9 < Outfit ZSTD < 1.9; ZSTD was only considered when MNSQ-values were outside the range; [59]) revealed that the data fits the Partial Credit Rasch Model. A total of 53 items were found to be well within these ranges (0.63 < Infit MNSQ < 1.31; 0.62 < Outfit MNSQ < 1.98), while one item exhibited considerable outfit (Outfit MNSQ = 5.10; Outfit ZSTD = 8.04). After a close examination of the misfitting item, it was decided to keep the item in the analyses regardless of its fit values because no plausible issues regarding the content of the item could be identified and because the misfit was most likely caused by only a few persons who answered this item very unexpectedly. Lastly, the Principal Component Analysis suggested that the items define a single latent variable (Eigenvalue < 3; [60]). Overall, the Rasch analysis suggests good instrument functioning and demonstrates that item and person measures can be computed using a Partial Credit Model.
2.3.3. Step 3: Estimation of Item Difficulty
In a Rasch model, the probability of responding to an item on a specific level is modeled as a function of the difference between a person’s ability and the difficulty of the item [59]. A Partial Credit Rasch Model provides an overall measure for item difficulty as well as measures for the difficulty of the individual levels (represented by so-called thresholds; [60]). For our analysis of the relationship between CCTCs and item difficulty, the overall item difficulty as well as the Thurstonian thresholds as estimates for the difficulty of individual levels were used. The item difficulties mark the point at which answer options on the lowest and highest level have the same probability [60]. The thresholds mark the point at which the probability of choosing an answer option at a specific level or higher is equal to the probability of choosing an answer option at any lower level ([60]; see Figure 6 for examples).
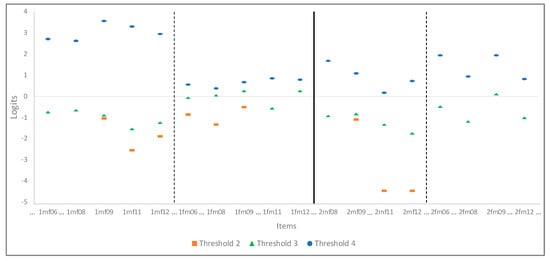
Figure 6.
Graphical illustration of the Thurstonian thresholds for exemplary items. Note: Item codes (e.g., 1mf06) were build according the following scheme: Newton’s law–direction of problem–item label. (…): Items blended out for better readability.
The three Thurstonian thresholds 2, 3, and 4 can be described as:
- 2: the probability of choosing an answer on level 2 or higher is equal to the probability of choosing an answer on level 1.
- 3: the probability of choosing an answer on level 3 or higher is equal to the probability of choosing an answer on a lower level (i.e., 2 or 1).
- 4: the probability of choosing an answer on level 4 is equal to the probability of choosing an answer on a lower level (i.e., 3, 2, or 1).
For instance, threshold 3 for item 1mf06 has a difficulty measure of −0.80 (see Figure 6), which means that a person with an ability measure of −0.80 solves this item with a probability of 50% at level 3 or higher. Threshold 4 has a difficulty measure of 2.66, so a person with this ability measure will solve this item with a probability of 50% on level 4, and therefore with the correct answer. For comparison, threshold 3 for item 1fm09 has a difficulty measure of 0.19, indicating that the person with an ability measure of −0.80 has a smaller chance than 50% to solve this item on level 3. The higher the difficulty measure of a threshold, the more difficult it is for a person with a given ability to solve the item on the respective level or above. Therefore, an analysis of the difficulty measures of the thresholds (see Step 4) provides insights into the extent to which the individual CCTCs affect the choice of a particular level of understanding. Please note, that not every threshold exists for every item and sometimes not only the highest or lowest but also a middle level was not included in the answer options. For instance, an item could consist only of answer options on levels 1, 2, and 4, missing level 3, or on 1, 3, and 4, missing level 2. In the first case, values for threshold 2 and 4 and in the latter, values for threshold 3 and 4 were calculated.
2.3.4. Step 4: Investigating Effects of CCTCs Using Multiple Regression
To investigate the impact of different CCTCs on item difficulty, four regression analyses [65] were conducted using SPSS Version 28. The first analysis used the overall item difficulty as the dependent variable, while the following three analyses used the Thurstonian thresholds of the three individual levels (2, 3, and 4) as dependent variables. In all regression models, the CCTCs were used as independent variables (predictors). Furthermore, all models included one or two control variables that represent the number of different levels that occur in an item as additional predictors, because as a result of the definition of the overall item difficulty [60] the type of available levels may have an impact on the difficulty estimates (e.g., higher difficulty when a task contains more higher levels), and, thus needs to be controlled in the regression. A hierarchical regression was used [65], implementing the control variables in the first step. In the second step, the conceptual characteristics were added, as it is assumed that these have a greater influence than the contextual characteristics [44]. In the third step, the contextual task characteristics were included in the model. Before each regression analyses, the relevant prerequisites [65] were checked. Nearly all of the assumptions were met. Only the assumption of homoscedasticity seemed to be violated for the analysis regarding thresholds 2 and 3. A violation “[…] invalidates [the] confidence intervals and significance tests […]” [66] (p. 387), but model parameters stay valid [66]. For the regression regarding threshold 2, this does not seem to be a great problem, because only one predictor seemed to have a significant influence on the difficulty measure. This influence is very important (great B-value, highly significant), so there seems to be no problem due to heteroscedasticity here. For the regression regarding threshold 3, heteroscedasticity was detected for the analysis in general, but a specific predictor causing it could not be detected when analyzing the partial plots for each predictor, as suggested in [66].
3. Results
The first regression analysis focused on the effect of CCTCs on the overall item difficulty (Table 2). The number of available response levels already explains 52.0% (49.9% for the adjusted R2) of the variance in item difficulties (Table 2, Model 1), since mostly lower levels are missing in tasks consisting of fewer available response levels. This is in line with the theoretical considerations regarding the definition of the overall item difficulty in a Partial Credit Rasch Model. Including the conceptual task characteristics in the model (Model 2) further increases the amount of variance explained significantly. In particular, the item difficulty is higher for Newton’s 1st rather than for the 2nd law. Note that all tables use descriptions, such as A_B for the CCTCs. If the values in the tables according to a TC are negative, this means that items with the characteristic B are easier than items with the characteristic A (in terms of the item difficulty). For the threshold regressions, this means that for items with the characteristic B the difficulty measures are lower than for items with the characteristic A. If the values in the tables are positive, it is the other way around. Further, adding the contextual task characteristics into the model (Model 3) increases the variance explained by approximately 4% (2% for the adjusted R2). This change in R2 is non-significant and none of the contextual characteristics has a significant effect on item difficulty.

Table 2.
Hierarchical multiple regression results regarding the impact of CCTCs on item difficulty.
Three additional regression analyses were conducted to assess the impact of the CCTCs on the difficulty of reaching each individual level of the FMLP in an item (Table 3, Table 4 and Table 5). These analyses followed the same procedure as the initial analysis but used the Thurstonian thresholds between the FMLP levels as the dependent variable instead of the overall item difficulty.

Table 3.
Hierarchical multiple regression results regarding the impact of CCTCs on the level 2 threshold of the FMLP.

Table 4.
Hierarchical multiple regression results regarding the impact of CCTCs on the level 3 threshold of the FMLP.

Table 5.
Hierarchical multiple regression results regarding the impact of CCTCs on the level 4 threshold of the FMLP.
For threshold 2, the regression analysis focused on the effect of CCTCs on the difficulty of answering an item on level 2 or higher (Table 3). Only 4% (1% for the adjusted R2) of the variance in the threshold difficulty measures is explained by the control variable (L4_L3 in Table 3, if an item contained answers on 3 or 4 different levels of sophistication). Including the conceptual task characteristics in the model (Model 2) significantly increases the amount of variance explained to 46.8% (41.1% for the adjusted R2). The probability of answering an item on a level 2 or higher is higher if the items ask for the resulting forces than for the resulting motion, so choosing an answer on level 2 or above is easier for items asking for the resulting forces. Adding the contextual task characteristics in the model (Model 3) increases the variance explained by approximately 4% (0% for the adjusted R2). This increase is non-significant and none of the contextual characteristics has a significant effect on the difficulty measures of threshold 2.
For threshold 3 (Table 4), nearly zero variance in the difficulty measures is explained by the control variable. Including the conceptual task characteristics in the model (Model 2) significantly increases the amount of variance explained to 25.0% (19.3% for the adjusted R2). The probability of answering an item on a level 3 or higher is significantly higher if the items address Newton’s 2nd law and ask for the resulting forces acting on an object. Adding the contextual task characteristics in the model (Model 3) increases the variance explained by additional 20.5% (18.9% for the adjusted R2). This increase is significant and the contextual TC plane of motion has a significant effect on the difficulty measures for threshold 3. The probability of answering an item on level 3 or higher is significantly higher for items addressing vertical motion. The type of object considered has no significant effect.
The last regression analysis focused on the effect of CCTCs on the difficulty of answering an item on level 4 (threshold 4; Table 5). Only 0.60% (3.8% for the adjusted R2) of the variance in the difficulty measures is explained by the control variables. Including the conceptual task characteristics in the model (Model 2) significantly increases the amount of variance explained to 29.6% (23.0% for the adjusted R2). The probability of answering an item on level 4, which is correct, is significantly higher if the items ask for the resulting motion of an object when the forces are described. Adding the contextual task characteristics in the model (Model 3) increases the variance explained by 4.0% (0.8% for the adjusted R2). This change in R2 is non-significant and the contextual TCs have no significant effect on the difficulty measures for threshold 4.
4. Discussion
In this section, the results of the hierarchical regression analyses are summarized and discussed along the CCTCs. Afterwards, all results are elaborated from an overarching perspective to discuss the combination of CCTCs and the value added through a differentiated analysis looking at SCs at different levels of sophistication rather than solely focusing on item difficulties. Before interpreting and discussing the results, it is important to note that the study has focused on four main characteristics with items typically offering more than these four (for example the cause of motion, i.e., whether an object is initially pushed and then released or pushed with a constant force). These variations were controlled too (see [44]), but it was not possible that all items consist of all characteristics, so not every characteristic is represented by the same number of items. This should not significantly affect the results but should be considered if the results are to be generalized. Since our sample sizes were rather small [66], expanding sample sizes therefore not only add to a more reliable regression model but also may result in more nuanced results when assessing other variations in addition to or as mediators for the four groups reported in this paper.
4.1. Effects of Newton’s Laws (Conceptual)
Looking at the impact of the law addressed by the items, the results consistently show that solving items addressing Newton’s 2nd law is easier than for Newton’s 1st law. This result is particularly evident for threshold 3: answering an item on level 3 or higher is easier and thus more likely in items addressing the 2nd law. Comparing these results with existing research reveals a rather unclear picture at first. While a study [44], which used the same instrument and data but scored the items dichotomously, could not detect any differences between Newton’s laws, others found exactly the opposite correlation (e.g., [67]). We assume that particular variations play an important additional role in Newton’s 1st law, e.g., is the body at rest or does it move with a constant velocity that is not zero (e.g., as compared in [44])? Furthermore, it has to be taken into account that for any situation with a body at rest, a level 3 answer would already be correct (no velocity, no force), even though the idea of net force might be missing. Heuer and Wilhelm [67], for example, found the effect that tasks of the FMCE where an object is moving with constant velocity (1st law) were solved better than tasks where the object is slowing down (2nd law), while we compared tasks concerning objects with constant velocity with tasks where objects were slowing down or speeding up. If the set of items used in different tests show different numbers of particular combinations resulting in different effects, differences in results would be reasonable. Here, it would be important to further explore which CCTCs may be the reasons for students’ difficulties regarding Newton’s 1st or 2nd law.
4.2. Effects of the Direction of Problem (Conceptual)
The direction of the problem has the greatest effect on the prediction of the dependent variables. However, this only holds true for the prediction of the thresholds (2: mf < fm, β = 0.697 ***; 3: mf < fm, β = 0.381 **; and 4: mf > fm, β = −0.541 ***). There is no significant contribution to the prediction of the overall item difficulties. This seems plausible because of the very interesting result, that the difficulty measures for thresholds 2 and 3 are higher when items are asking for the resulting motion, while the difficulty measures for threshold 4 are higher when items are asking for the forces acting. Although regarding the relative directions of force and velocity, Rosenblatt and Heckler [41] found an effect of the direction of problem on answers representing a partially correct understanding of the relationship between force and velocity. The results in our study regarding thresholds 2 and 3 in comparison to 4, which may cancel each other out, are likely the reason for the missing effect of the direction of the problem on the overall item difficulty. The lower probability for choosing answers on level 2 or 3 regarding items asking for the resulting motion in contrast to choosing answers on these levels when items ask for the forces acting, implies that in these items (fm) it seems to be harder for students to pick an answer representing a conception which assumes that force is at least proportional to motion or velocity. A higher difficulty measure for threshold 4 regarding items asking for the forces when the motion is described (mf) implies that for these kinds of items, it may be harder for students to pick an answer representing the correct conception that force is proportional to acceleration. Similar results, describing items to be easier when the motion should be inferred from the acting forces, are documented in earlier studies (e.g., for Newtons 1st law in [44]). In 2022, Weber [68] was also able to show that students preferred to reason about the resulting motion from the forces acting. Additionally, this direction of argumentation also tended to lead to more correct discussions. A possible reason might be that, on the one hand, looking at items regarding the 1st law, it seems to be easier for students to activate the conception that when no forces are acting on a moving object, its motion will not be changed (e.g., [6]). On the other hand, if a motion with constant velocity is described, students often use the conception that a resulting net force in the direction of motion is acting on the object (e.g., [16]). This matches research describing these kinds of conceptions as a result of everyday experiences, for example, while riding a bike and having to constantly exert a force to move forward (e.g., [69]). Furthermore, forces are not visible to students which may make it easier for them to pick the right answer when reasoning about a motion and not about the forces acting. In a broader sense, our results described above also fit with studies describing that students’ answers vary when predicting the motion of an object (e.g., predicting its velocity, and drawing or choosing the path of an object) in contrast to explaining the motion (e.g., describing the factors influencing the motion (e.g., the forces acting); e.g., [36,39]). A possible reason might also be that students can use their experience for predicting a motion but not necessarily for an explanation (e.g., [36]).
4.3. Effects of the Plane of Motion (Contextual)
In the literature, several studies indicate an effect of the plane of motion (e.g., [19,21,32,40,42,44]). Therefore, it is no big surprise that looking at the study reported here, the plane of motion does seem to have an effect on the activation of students’ conceptions in contributing to the prediction of the difficulty measure for threshold 3 (h > v, β = −0.463 ***). However, there is no significant contribution to the prediction of the item difficulty or the difficulty measures for threshold 2 or 4. Conceptions assumed with an understanding on level 3 describe that force is proportional to velocity and/or that more than one force can act on an object. Especially, these two conceptions may be a reason why choosing answers on this level seem to be harder for horizontal than for vertical motion. This also matches findings from previous research, describing students sometimes only reasoning about gravity or a motion force and not about reaction forces (e.g., [38]). Additionally, in our study for items regarding horizontal motion, not only the horizontal but also the vertical forces should be taken into consideration, at least when reasoning about the forces acting on an object (see for example Figure 3). For vertical motion, only vertical forces played a role. It might be harder for students to think about forces in two dimensions, since for horizontal motion, the vertical forces acting lie transversely to the direction of motion.
4.4. Effects of the Type of Object (Contextual)
In contrast to the other TCs, the type of object does not contribute to any of the dependent variables, therefore, at least at first sight, it does not seem to affect the activation of SCs, no matter the level of sophistication. Comparing this to other studies, there are mixed results. An earlier study, for example, also did not find any differences regarding the nature of an object, when comparing the solution probabilities of dichotomous coded items using the same data set [44]. Other studies found students reasoning about the nature of the object in specific items, for example, using incorrect reasoning for a ball rather than for a person [32] or assuming personal experience as a possible reason for the influence of the type of object considered [21]. In conclusion, there are maybe some other TCs, such as personal experience or the type of motion (e.g., if an object was initially pushed), that influence the activation of SCs in combination with the type of object.
4.5. General Results
Comparing the effects of conceptual and contextual task characteristics, the results of the hierarchical regression analyses indicate that conceptual TCs contribute much more to the prediction of the overall item difficulty and threshold difficulty measures. All in all, there are more significant effects for Newton’s law and the direction of the problem than for the plane of motion and the type of object. When looking at the parameters of the regression, the conceptual TCs explain more variance than the contextual TCs. This result adds to existing studies (e.g., [44]) which assume that conceptual characteristics have a greater effect on the activation of SCs.
Another interesting finding is the value added through a differentiated analysis looking at SCs at different levels of sophistication rather than solely on the overall item difficulties or a dichotomous analysis of items. One result is that most effects are visible regarding threshold 3. This is the only dependent variable where conceptual and contextual TCs contribute to the prediction of the threshold. SCs associated with a level 3 understanding are therefore of great interest, since they seem to be susceptible to specific TCs. Looking only at the overall item difficulty, CCTCs in general do not explain much of the total variance (only adding 11.1% adding the ΔR2s of Model 2 and 3; and 7.9% for the adjusted R2) to the total variance explained). In contrast, CCTCs that were included in the regression model additionally explained 46.3% (40.0% for the adjusted R2) of the total variance regarding threshold 2 and 45.5% (38.5% for the adjusted R2) for threshold 3. For threshold 4, 33.0% (27.6% for the adjusted R2) of the total variance could be explained. This is an indicator to focus more on a differentiated analysis. These insights would probably not have been visible when only looking at items scored dichotomously because therein inappropriate SCs would have been bundled together as “incorrect” and effects within these conceptions would have gone unseen.
5. Conclusions
The overall goal of this study was to enrich already existing research with more detailed information on how specific CCTCs have an effect on the activation of SCs to foster conceptual change. In the described approach to design a test instrument with reference to a learning progression, it was acknowledged that SCs can vary in their degree of adequacy and that conceptual development is a rather gradual process and not a sudden shift from an incorrect to a correct concept (e.g., [6,7,8]). Though this has been debated over years within conceptual change research, assessing SCs has only more recently started to employ the idea of learning progressions for the design of test instruments (e.g., [6,16,28,30]). The results gained with such a test in Newtonian mechanics demonstrate that these kinds of tests can offer more information on students’ understanding compared to solely focusing on the overarching item difficulties or a dichotomous scoring of items (e.g., as in [44]) taking into account that some effects of CCTCs were only visible because SCs were investigated here at different levels of sophistication (e.g., for the plane of motion or the contradictory effects for the direction of problem regarding different levels of sophistication).
Knowing about the effects of CCTCs on SCs at different levels is not only important in terms of better understanding the activation of SCs depending on task characteristics, but also to develop instruction that is tailored to students’ learning process. Comparing conceptual and contextual TCs, the regression analyses showed that especially the conceptual characteristics, first and foremost the direction of problem, have a great impact on all threshold difficulty measures. For adaptive instruction, this may result in the idea that tasks asking for the forces acting on an object may be used when learners tend to activate conceptions on rather low levels of the learning progression and should master the step to a more appropriate conception. For mastering the step to the correct conception, maybe tasks asking for the resulting motion should be considered since here it seems easier for students to activate the correct conception in comparison to tasks asking for the forces acting. Subsequently, both types of tasks may be contrasted as pairs (e.g., [2,44,70]) to show and practice the conceptual equivalence of both directions. The fact that conceptual as well as contextual TCs have a great impact, especially on the threshold regarding the third level of the LP (assuming force proportional to velocity or the acceptance that more than one force can act simultaneously on a body; [6]), may indicate that these conceptions are especially prone to situational changes. For instruction, this may help to use tasks in a targeted manner to foster conceptual change.
Given that at this point, only a rather small set of TCs with two conceptual and two contextual TCs were analyzed regarding their effects on the activation of SCs at different levels of sophistication, it would be interesting to investigate which TCs may also contribute to the explanation of variance (e.g., the cause of motion, if an object was initially pushed or moved with a constant force acting on it). This would require greater, but maybe also more focused sets of tasks in order to have a big enough sample size for regression analyses. For instance, more exploration would be helpful to understand better which CCTCs are the reasons for Newton’s 1st law becoming more difficult than the 2nd law or if the type of object considered affects SCs for specific groups of tasks (e.g., if students have more or less personal experience with specific situations).
Author Contributions
Conceptualization, A.M.J., A.V. and C.v.A.; methods, A.M.J. and A.V.; validation, A.M.J., A.V. and C.v.A.; formal analysis, A.M.J.; investigation, A.M.J.; data curation, A.M.J.; writing—original draft preparation, A.M.J., A.V. and C.v.A.; writing—review and editing, A.M.J., A.V. and C.v.A.; visualization, A.M.J.; supervision, C.v.A. and A.V. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Ethical review and approval were waived for this study due to federal data protection regulations. Participation was completely voluntary and informed consent was obtained from all participating students, and by their parents if they were underaged (<18 years old) prior to data collection. Participants were informed that a withdrawal of their consent was possible without any personal disadvantage. No identifiable personal data were collected. The study was carried out in accordance with the ethical policy of the ethics committee of the department 6 (psychology and sports) at the Justus Liebig University Giessen [71].
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
Data are available upon request from the authors. A booklet of the test instrument (originally in German but also translated into English) is available upon request from Claudia von Aufschnaiter.
Acknowledgments
We would like to thank Alicia C. Alonzo for the very helpful discussion about levels of the FMLP assigned to the answer options. In addition, we would like to thank all students who participated in this study as well as the Ph.D. students who were very helpful in revising the tasks.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bao, L.; Redish, E.F. Educational Assessment and Underlying Models of Cognition. In The Scholarship of Teaching and Learning in Higher Education: The Contributions of Research Universities; Becker, W.E., Andrews, M.L., Eds.; Indiana University Press: Bloomington, IN, USA, 2004; pp. 221–264. [Google Scholar]
- Ferreira, A.; Lemmer, M.; Gunstone, R. Alternative conceptions: Turning adversity into advantage. Res. Sci. Educ. 2019, 49, 657–678. [Google Scholar] [CrossRef]
- Schecker, H.; Duit, R. Schülervorstellungen und Physiklernen [Students’ conceptions and physics learning]. In Schülervorstellungen und Physikunterricht; Ein Lehrbuch für Studium, Referendariat und Unterrichtspraxis [Students’ Conceptions and Physics Learning. A Textbook for Studies, Teacher Training and Practice]; Schecker, H., Wilhelm, T., Hopf, M., Duit, R., Eds.; Springer Spektrum: Berlin, Germany, 2018; pp. 1–21. [Google Scholar] [CrossRef]
- Terry, J.; Jones, G.; Hurford, W. Children’s conceptual understanding of forces and equilibrium. Phys. Educ. 1985, 20, 162–165. [Google Scholar] [CrossRef]
- Ausubel, D.P. Educational Psychology: A Cognitive View; Holt, Rinehart and Winston: New York, NY, USA, 1968. [Google Scholar]
- Alonzo, A.C.; von Aufschnaiter, C. Moving beyond misconceptions: Learning progressions as a lens for seeing progress in student thinking. Phys. Teach. 2018, 56, 470–473. [Google Scholar] [CrossRef]
- DiSessa, A.A. A History of Conceptual Change Research: Threads and Fault Lines. In The Cambridge Handbook of the Learning Sciences, 2nd ed.; Sawyer, R., Ed.; Cambridge University Press: Cambridge, UK, 2014; pp. 88–108. [Google Scholar] [CrossRef]
- Hopf, M.; Wilhelm, T. Conceptual Change—Entwicklung physikalischer Vorstellungen [Conceptual Change—development of physics conceptions]. In Schülervorstellungen und Physikunterricht; Ein Lehrbuch für Studium, Referendariat und Unterrichtspraxis [Students’ Conceptions and Physics Learning. A Textbook for Studies, Teacher Training and Practice; Schecker, H., Wilhelm, T., Hopf, M., Duit, R., Eds.; Springer Spektrum: Berlin, Germany, 2018; pp. 23–38. [Google Scholar] [CrossRef]
- Niedderer, H.; Schecker, H. Towards an Explicit Description of Cognitive Systems for Research in Physics Learning. In Research in Physics Learning. Theoretical Issues and Empirical Studies; Duit, R., Goldberg, F., Niedderer, H., Eds.; IPN: Kiel, Germany, 1992; pp. 74–98. [Google Scholar]
- Vygotsky, L.S. Mind in Society; Cole, M., John-Steiner, V., Scribner, S., Souberman, E., Eds.; Harvard University Press: Cambridge, MA, USA; London, UK, 1978. [Google Scholar]
- Duit, R.; Treagust, D.F. Learning in Science—From Behaviourism towards Social Constructivism and Beyond. In International Handbook of Science Education; Fraser, B.J., Tobin, K.G., Eds.; Kluwer: Dordrecht, The Netherlands, 1998; Volume 2, pp. 3–25. [Google Scholar]
- National Research Council. How People Learn: Brain, Mind, Experience, and School, Expanded Edition; The National Academies Press: Washington, DC, USA, 2000. [Google Scholar] [CrossRef]
- Duit, R.; Bibliography—STCSE. Students’ and Teachers’ Conceptions and Science Education. 2009. Available online: https://archiv.ipn.uni-kiel.de/stcse/ (accessed on 6 March 2023).
- Schecker, H.; Wilhelm, T. Schülervorstellungen in der Mechanik [Students’ conceptions in mechanics]. In Schülervorstellungen und Physikunterricht, Ein Lehrbuch für Studium, Referendariat und Unterrichtspraxis [Students’ Conceptions and Physics Learning. A Textbook for Studies, Teacher Training and Practice]; Schecker, H., Wilhelm, T., Hopf, M., Duit, R., Eds.; Springer Spektrum: Berlin, Germany, 2018; pp. 63–88. [Google Scholar] [CrossRef]
- Brown, D.E.; Hammer, D. Conceptual Change in Physics. In International Handbook of Research on Conceptual Change; Vosniadou, S., Ed.; Routledge: New York, NY, USA, 2008; pp. 127–154. [Google Scholar]
- Alonzo, A.C.; Steedle, J.T. Developing and assessing a force and motion learning progression. Sci. Educ. 2009, 93, 389–421. [Google Scholar] [CrossRef]
- Alonzo, A.C. Learning progressions: Significant promise, significant change. Z. für Erzieh. 2012, 15, 95–109. [Google Scholar] [CrossRef]
- National Research Council. Taking Science to School: Learning and Teaching Science in Grades K-8; The National Academies Press: Washington, DC, USA, 2007. [Google Scholar] [CrossRef]
- Lemmer, M. Nature, cause and effect of students’ intuitive conceptions regarding changes in velocity. Int. J. Sci. Educ. 2013, 35, 239–261. [Google Scholar] [CrossRef]
- Minstrell, J. Facets of Students’ Knowledge and Relevant Instruction. In Research in Physics Learning. Theoretical Issues and Empirical Studies; Duit, R., Goldberg, F., Niedderer, H., Eds.; IPN: Kiel, Germany, 1992; pp. 110–128. [Google Scholar]
- Palmer, D. The effect of context on students’ reasoning about forces. Int. J. Sci. Educ. 1997, 19, 681–696. [Google Scholar] [CrossRef]
- von Aufschnaiter, C.; Rogge, C. Conceptual change in learning. In Encyclopedia of Science Education; Gunstone, R., Ed.; Springer: Dordrecht, The Netherlands, 2015; pp. 209–218. [Google Scholar] [CrossRef]
- Ogborn, J. Science and Commonsense. In Connecting Research in Physics Education with Teacher Education—Volume 2; Vicentini, M., Sassi, E., Eds.; International Commission of Physics Education: Singapore, 2008; Available online: https://web.phys.ksu.edu/icpe/Publications/teach2/Ogborn.pdf (accessed on 12 April 2023).
- Niedderer, H. Überblick über Lernstudien in der Physik [Overview of learning studies in physics]. In Lernen in den Naturwissenschaften [Learning in science]; Duit, R., von Rhöneck, C., Eds.; IPN: Kiel, Germany, 1996; pp. 119–144. [Google Scholar]
- National Assessment Governing Board. Science Framework for the 2009 National Assessment of Educational Progress. 2008. Available online: https://files.eric.ed.gov/fulltext/ED502955.pdf (accessed on 7 March 2023).
- Krajik, J.S. The Importance, Cautions and Future of Learning Progression Research. In Learning Progressions in Science. Current Challenges and Future Directions; Alonzo, A.C., Gotwals, A.W., Eds.; SensePublishers: Rotterdam, The Netherlands, 2012; pp. 27–36. [Google Scholar] [CrossRef]
- Popham, W.J. The lowdown on learning progressions. Educ. Leadersh. 2007, 64, 83–84. [Google Scholar]
- Fulmer, G.W.; Neumann, I.; Liang, L.L.; Neumann, K. Empirical Validation of a Learning Progression for Newton’s Third Law Using Items from the Force Concept Inventory [Paper presentation]. In Proceedings of the Annual Meeting of the National Association for Research in Science Teaching (NARST), Rio Grande, Puerto Rico, 6–9 April 2013. [Google Scholar]
- Briggs, D.C.; Alonzo, A.C.; Schwab, C.; Wilson, M. Diagnostic assessment with ordered multiple-choice items. Educ. Assess. 2006, 11, 33–63. [Google Scholar] [CrossRef]
- Hadenfeldt, J.C.; Bernholt, S.; Liu, X.; Neumann, K.; Parchmann, I. Using ordered multiple-choice items to assess students’ understanding of the structure and composition of matter. J. Chem. Educ. 2013, 90, 1602–1608. [Google Scholar] [CrossRef]
- DiSessa, A.A. Knowledge in Pieces. In Constructivism in the Computer Age; Forman, G., Pufall, P.B., Eds.; Lawrence Erlbaum Publishers: Mahwah, NJ, USA, 1988; pp. 49–70. [Google Scholar]
- Palmer, D. How consistently do students use their alternative conceptions? Res. Sci. Educ. 1993, 23, 228–235. [Google Scholar] [CrossRef]
- Vosniadou, S.; Vamvakoussi, X.; Skopeliti, I. The Framework Theory Approach to the Problem of Conceptual Change. In International Handbook of Research on Conceptual Change; Vosniadou, S., Ed.; Routledge, Taylor and Francis: New York, NY, USA; London, UK, 2008; pp. 3–34. [Google Scholar]
- Vosniadou, S. Refraiming the Classical Approach to Conceptual Change: Preconceptions, Misconceptions and Synthetic Models. In Second International Handbook of Science Education; Fraser, B., Tobin, K., McRobbie, C.J., Eds.; Springer: Dordrecht, The Netherlands, 2012; Volume 2, pp. 119–130. [Google Scholar] [CrossRef]
- Vosniadou, S. Conceptual Change Research: An Introduction. In International Handbook of Research on Conceptual Change; Vosniadou, S., Ed.; Routledge, Taylor and Francis: New York, NY, USA; London, UK, 2008; pp. xiii–xxviii. [Google Scholar]
- Anderson, T.; Tolmie, A.; Howe, C.; Mayes, T.; Mackenzie, M. Mental Models of Motion? In Models in the Mind. Theory, Perspective & Application; Rogers, Y., Rutherford, A., Bibby, P.A., Eds.; Academic Press: London, UK, 1992; pp. 57–71. [Google Scholar]
- Bao, L.; Hogg, K.; Zollman, D. Model analysis of fine structures of student models: An example with Newton’s third law. Am. J. Phys. 2002, 70, 766–778. [Google Scholar] [CrossRef]
- Fazio, C.; Battaglia, O.R. Conceptual Understanding of Newtonian Mechanics Through Cluster Analysis of FCI Student Answers. Int. J. Sci. Math. Educ. 2019, 17, 1497–1517. [Google Scholar] [CrossRef]
- Liu, X.; MacIsaac, D. An investigation of factors affecting the degree of naïve impetus theory application. J. Sci. Educ. Technol. 2005, 14, 101–116. [Google Scholar] [CrossRef]
- Palmer, D. The effect of the direction of motion on students’ conceptions of forces. Res. Sci. Educ. 1994, 24, 253–260. [Google Scholar] [CrossRef]
- Rosenblatt, R.; Heckler, A.F. Systematic study of student understanding of the relationships between the directions of force, velocity, and acceleration in one dimension. Phys. Rev. Spec. Top. Phys. Educ. Res. 2011, 7, 020112. [Google Scholar] [CrossRef]
- Twigger, D.; Byard, M.; Driver, R.; Draper, S.; Hartley, R.; Hennessy, S.; Mohamed, R.; O’Malley, C.; O’Shea, T.; Scanlon, E. The conception of force and motion of students aged between 10 and 15 years: An interview study designed to guide instruction. Int. J. Sci. Educ. 1994, 16, 215–229. [Google Scholar] [CrossRef]
- Hestenes, D.; Wells, M.; Swackhamer, G. Force concept inventory. Phys. Teach. 1992, 30, 141–158. [Google Scholar] [CrossRef]
- Just, A.M.; von Aufschnaiter, C.; Vorholzer, A. Effects of conceptual and contextual task characteristics on students’ activation of mechanics conceptions. Eur. J. Phys. 2021, 42, 025702. [Google Scholar] [CrossRef]
- Zhai, X.; Li, M. Validating a partial-credit scoring approach for multiple-choice science items: An application of fundamental ideas in science. Int. J. Sci. Educ. 2021, 43, 1640–1666. [Google Scholar] [CrossRef]
- Thornton, R.K.; Sokoloff, D.R. Assessing student learning of Newton’s laws: The force and motion conceptual evaluation and the evaluation of active learning laboratory and lecture curricula. Am. J. Phys. 1998, 66, 338–352. [Google Scholar] [CrossRef]
- Millar, R. Diagnosing Pupils’ Understanding. Forces and Motion 1: Identifying Forces. Evidence-Informed Practice in Science Education (EPSE) Project Diagnostic Question Set; University of York Science Education Group: York, UK, 2003. [Google Scholar]
- Millar, R. Diagnosing Pupils’ Understanding. Forces and Motion 2: The Link between Force and Motion. Evidence-Informed Practice in Science Education (EPSE) Project Diagnostic Question Set; University of York Science Education Group: York, UK, 2003. [Google Scholar]
- Hessisches Kultusministerium 2016 Kerncurriculum Gymnasiale Oberstufe Physik. Available online: https://kultusministerium.hessen.de/sites/default/files/media/kcgo-ph.pdf (accessed on 27 May 2020).
- Blüggel, L.; Hegemann, A.; Schmidt, M. Impulse Physik (Oberstufe); [Impulse Physics (Senior Level)]; Ernst Klett Verlag: Stuttgart, Germany; Leipzig, Germany, 2016. [Google Scholar]
- Grehn, J.; Krause, J. Metzler Physik [Metzler Physiscs], 4th ed.; Schroedel: Braunschweig, Germany, 2007. [Google Scholar]
- Demtröder, W. Experimentalphysik 1 (Mechanik und Wärme) [Experimental Physics 1 (Mechanics and Heat)], 8th ed.; Springer: Berlin, Germany, 2018. [Google Scholar]
- Giancoli, D.C. Physik (Lehr- und Übungsbuch) [Physics (Text- and Workbook)], 3rd ed.; Pearson Studium: München, Germany; Boston, MA, USA, 2010. [Google Scholar]
- Tipler, P.A.; Mosca, G. Physik (Für Wissenschaftler und Ingenieure) [Physics (for Scientists and Engineers)], 6th ed.; Wagner, J., Ed.; Springer: Berlin, Germany, 2015. [Google Scholar]
- Haladyna, T.M.; Downing, S.M.; Rodriguez, M.C. A review of multiple-choice item-writing guidelines for classroom assessment. Appl. Meas. Educ. 2002, 15, 309–330. [Google Scholar] [CrossRef]
- Tamir, P. Multiple choice items: How to gain the most out of them. Biochem. Educ. 1991, 19, 188–192. [Google Scholar] [CrossRef]
- Neumann, I.; Fulmer, G.W.; Liang, L.L. Analyzing the FCI based on a force and motion learning progression. Sci. Educ. Rev. Lett. 2013, 2013, 8–14. [Google Scholar]
- Frey, A.; Hartig, J.; Rupp, A.A. An NCME instructional module on booklet designs in largescale assessments of student achievement: Theory and practice. Educ. Meas. 2009, 28, 39–53. [Google Scholar] [CrossRef]
- Boone, W.J.; Staver, J.R.; Yale, M.S. Rasch Analysis in the Human Sciences; Springer: Dordrecht, The Netherlands; Heidelberg, Germany; New York, NY, USA; London, UK, 2014. [Google Scholar] [CrossRef]
- Linacre, J.M. A User’s Guide to Winsteps® Ministep Rasch-Model Computer Programs: Program Manual 5.2.3. Available online: https://www.winsteps.com/winman/ (accessed on 13 March 2023).
- Rost, J. Lehrbuch Testtheorie, Testkonstruktion [Textbook Test Theory, Test Construction], 1st ed.; Verlag Hans Huber: Bern, Switzerland, 2004. [Google Scholar]
- Boone, W.J.; Staver, J.R. Advances in Rasch Analyses in the Human Sciences; Springer: Cham, Switzerland, 2020. [Google Scholar]
- Robitzsch, A.; Kiefer, T.; Wu, M. Package ‘TAM’. Available online: https://cran.r-project.org/web/packages/TAM/TAM.pdf (accessed on 14 March 2022).
- Robitzsch, A.; Kiefer, T.; George, A.C.; Uenlue, A. Package CDM. Available online: https://cran.r-project.org/web/packages/CDM/CDM.pdf (accessed on 14 March 2023).
- Field, A. Discovering Statistics Using SPSS, 3rd ed.; Sage Publications Ltd.: London, UK, 2009. [Google Scholar]
- Field, A. Discovering Statistics Using SPSS, 5th ed.; Sage Publications Ltd.: London, UK, 2018. [Google Scholar]
- Heuer, D.; Wilhelm, T. Aristoteles siegt immer noch über Newton. Unzulängliches Dynamikverstehen in Klasse 11 [Aristotle still triumphs over Newton. Inadequate understanding of dynamics in grade 11]. Math. und Nat. Unterr. 1997, 50, 280–285. [Google Scholar]
- Weber, J. Mathematische Modellbildung und Videoanalyse zum Lernen der Newtonschen Dynamik im Vergleich; [Comparison of Mathematical Modeling and Video Analysis for Learning Newtonian Dynamics]; Logos Verlag Berlin: Berlin, Germany, 2022. [Google Scholar] [CrossRef]
- von Aufschnaiter, C.; Rogge, C. Misconceptions or missing conceptions? Eurasia J. Math. Sci. Tech. Educ. 2010, 6, 3–18. [Google Scholar] [CrossRef]
- Redish, E.F. Changing Student Ways of Knowing: What Should our Students Learn in a Physics Class? Invited talk presented at the conference World View on Physics Education 2005: Focusing on Change, Delhi, India, 21–26 August 2005. Available online: http://physics.umd.edu/perg/papers/redish/IndiaPlen.pdf (accessed on 15 November 2020).
- Berufsverband Deutscher Psychologinnen und Psychologen & Deutsche Gesellschaft für Psychologie. Berufsethische Richtlinien des Berufsverbandes Deutscher Psychologinnen e.V. [Professional Ethical Guidelines of the Professional Association of German Psychologists e.V.]. 2016. Available online: https://uni-giessen.de/fbz/fb06/psychologie/ethikkommission/downloads-intern/ethischerichtlinien (accessed on 14 March 2023).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).