Distinguishing between Grit, Persistence, and Perseverance for Learning Mathematics with Understanding

Abstract

Learning mathematics with understanding involves productively struggling to make connections between different mathematical ideas. Such productive struggle is associated with three primary constructs: grit, persistence, and perseverance. Each of these constructs has a distinct definition, background, and implied utility in mathematics education research. However, these constructs are often colloquially conceptualized as synonyms, leading to a misconception of what can be learned through the lens of each construct. The purpose of this paper is to carefully examine the literature on grit, persistence, and perseverance and to review and distinguish the ways in which these constructs offer insights into learning mathematics with understanding.

1. Introduction

Learning mathematics with understanding focuses on conceptual understanding, that is, the connections learners make among mathematical facts, procedures, and ideas [1,2]. In contrast to procedural skills, such as executing rehearsed mnemonic devices or memorized algorithms to solve problems, conceptual understanding is developed as mental connections become richer and more widespread [3]. In the context of problem solving, a key process that supports the development of conceptual understanding is productive struggle. The purpose of this paper is to carefully examine constructs that are commonly associated with such struggle, namely grit, persistence, and perseverance, and to review and distinguish the ways in which these constructs offer insights into learning mathematics with understanding. The idea of struggle has long been recognized as key to learning mathematics with understanding [4,5,6], and Hiebert and colleagues [7] conceptualized productive struggle as grappling with key mathematical ideas that are within reach but not yet well formed. It is in this process of productively struggling to overcome mathematical obstacles that learners begin to make their own mathematical meanings and build their conceptual understanding [8,9,10,11]. Yet, developing conceptual understanding by incorporating productive struggle can be a challenge for both teachers and students. Teachers must provide their students with opportunities to wrestle with challenging mathematics, and students must be willing to carry out the wrestling amid frustration or difficulties.

Wrestling with mathematical ideas while managing frustration, however, can be grueling for students. Some students may prefer to avoid engaging in struggling to solve challenging tasks. As Schoenfeld [12] posits, students may come to believe that “if you can’t solve a problem in a short amount of time, you should simply give up” (p. 159). This mindset may limit students’ opportunities to learn and explains the recent emphasis on developing productive student dispositions toward mathematics concept learning in guiding texts such as the National Research Council’s (NRC) Adding it Up [13], the Common Core State Standards for Mathematics (CCSSM) [14], and the National Council for Teachers of Mathematics’ (NCTM) Principles to Actions [15]. The NRC defines a productive disposition as a “habitual inclination to see mathematics as sensible, useful, and worthwhile, coupled with a belief in diligence and one’s own efficacy” [13] (p. 116).

The focus on developing a productive disposition toward struggling with mathematical ideas and connections represents a nationwide mathematics education investment in supporting students to stay engaged with difficult mathematics content. A key feature of such engagement is the continuation of effort, despite challenges and setbacks, to encourage deeper mathematics learning. This commitment is evident in the first Standard for Mathematical Practice in the CCSSM [14], “[students should] make sense of problems and persevere in solving them” (p. 6). As such, dispositional factors such as grit, persistence, and perseverance have entered into the discourse about mathematics learning, both among researchers and practitioners. These terms are being used, sometimes synonymously, to refer to the ideas of sticking with it or never giving up in the context of students working with challenging mathematics.

In addition to informing teaching practice, researchers have focused empirical studies on investigating grit, persistence, and perseverance in the context of mathematics learning. Research on learning mathematics with understanding should be seeking to uncover the nuanced ways learners use both cognitive and non-cognitive skills to make meaning of important mathematical ideas [16]. Research emphasizing dispositional constructs such as grit, persistence, and perseverance provides insight into students’ engagement with mathematics learning, and these factors contain both cognitive and non-cognitive components. In the context of working on a challenging mathematical task, when learners enact a productive disposition, they are aware of obstacles that they encounter when solving problems, develop ideas about their options for navigating these obstacles, and also exercise a willingness or desire to keep trying despite inevitable setbacks. Hence, research incorporating the perspectives of grit, persistence, and perseverance is particularly important because they address the resilience and self-regulation that is necessary to withstand the frustration and uncertainty of productive struggle and to continue moving forward toward meaning-making. Therefore, with such dispositional factors as potential sources of support for productive struggle, and with productive struggle as a key process by which learning mathematics is supported, it is valuable to investigate constructs such as grit, persistence, and perseverance to understand students’ experiences while learning mathematics.

A fine-grained analysis of scholarship focused on these dispositional constructs unveils ample distinctions between grit, persistence, and perseverance. These constructs’ respective definitions, operationalizations, usage in research, and potential for uncovering insights into how students learn mathematics have distinct differences. These distinctions are important to make in order to help researchers select and define the particular construct best suited to investigate their particular phenomenon of interest. Accordingly, this paper elaborates upon the ways in which grit, persistence, and perseverance have been defined and operationalized in research on mathematics learning.

Specifically, in the context of research on mathematics learning, the questions that guided the analysis of the constructs were:

• How are grit, persistence, and perseverance defined?
• How are grit, persistence, and perseverance operationalized?
• How are grit, persistence, and perseverance associated, or not, with learning mathematics?
• What are the similarities and differences between grit, persistence, and perseverance?

In the following sections, each construct will be depicted separately before they are compared and contrasted. First, the methods that guided this review of literature are explained. Next, a review of how grit, persistence, and perseverance are all uniquely defined, the ways that the constructs are each typically measured, and then present findings associated with learning (with an emphasis on learning mathematics, if applicable), as well as critique of how each construct fits into the growing call for research on learning mathematics with understanding, will be presented. Then, grit, persistence, and perseverance will all be considered in relation to one another, making explicit the differences between each dispositional construct. This review will show how each construct affords different insights into mathematics learning at various grain sizes. This review will end by advocating for researchers to purposefully select and define constructs to reflect their phenomenon of interest, and it will argue that examining students’ perseverance with challenging mathematics, compared to studying grit or persistence, better informs the research community about how students navigate obstacles to learn mathematics with understanding.

2. Methods

To facilitate a quality and rigorous review, the author of this review began by searching for relevant papers. First, useful databases in education to which the author had access were identified. These included Education Source, ERIC (EBSCOhost), ERIC (ProQuest), Educator’s Reference Complete, PsycINFO, and Google Scholar. Across all databases, the author used search criteria that included keywords such as the nouns “grit”, “persistence”, and “perseverance”, as well as other forms of those keywords, including adjectives such as “gritty”, “persistent”, and “perseverant” and verbs such as “persist” and “persevere.” To widen the search, and to ensure the search was not omitting literature that did not draw on those exact terms but was still relevant to grit, persistence, and perseverance, the author also searched keywords such as “engagement”, “motivation”, “goals”, “achievement”, “problem solving”, “resilience”, “setbacks”, “discouragements”, and “uncertainty.” The search criteria also included a wide timeframe (from 1900 to present day) because many of these constructs have historical roots in education literature. Only literature that was available in English was considered because the author of this review is only fluent in English; this admittedly is a limitation of this review because there may exist literature written in other languages that could inform a review of these constructs. Future research should consider conducting a multilingual literature search.

After removing any duplicate papers from the review list, the author of this review read each paper’s title and abstract to help ensure all papers were relevant to the constructs of grit, persistence, or perseverance in the context of education. There were rare instances of papers from irrelevant fields that mistakenly made it to the review list, such as a paper focused on the persistent use of evidence-based pharmacotherapy in heart failure. All such papers were removed from the review list.

For the papers that remained on the review list, the author of this review read each of them in full. If a paper that was read included a citation to a source relevant to the goals of the literature review that was not already on the review list, that paper was added to the review list and read in full. In total, the literature review search provided 141 papers that met the inclusion criteria (see the Reference list, excluding reference 46, for the citations of these papers). As these papers were read, the author of this review took detailed notes about how each paper informed one or many of the questions that guided the analysis of grit, persistence, and perseverance. The author made notes about if and how each paper defined or drew on a definition of one of these constructs, if and how a construct was operationalized, if and how a construct had been associated with learning (with an emphasis on learning mathematics), and if and how constructs have been compared or contrasted, either explicitly or implicitly. A spreadsheet was used to store these notes, and different functions of the spreadsheet were used to help facilitate synthesis across papers. Such synthesis directly informed how each of the questions that guided the analysis of these constructs was answered.

3. Grit

To achieve goals of learning mathematics for understanding, the trait of grit epitomizes hard work and a steadfast will to never give up. First introduced by Duckworth [17], grit is “[continuance of effort] (Duckworth et al. [18] used “perseverance” here, but to avoid confusion between constructs, I will use “continuance of effort”, a phrase Duckworth and colleagues suggested is synonymous with their perspective of perseverance) and passion for specific, high goals, sustained over years” (p. 73). Grit was originally introduced and studied to help explain differences in achievement across all domains between people of similar intelligence and resources. The concept of grit was hypothesized by Duckworth, Peterson, Matthews, and Kelly [18] to be just as important as talent when explaining why individuals were successful in achieving their long-term goals. Framing grit as an individual’s “sustained commitment to their ambitions” (p. 1088), Duckworth and colleagues [18] believed such relentless hard work, over time, could propel someone into the upper echelons of achievement, perhaps before a more-gifted but less-gritty peer.

A key feature of this non-cognitive construct is the nature of the long-term goal toward which an individual is striving. For example, grit can help explain a student achieving goals such as earning a college degree in mathematics or scoring highly on an Advanced Placement calculus exam. Such achievements require years of preparation, dedication, and strenuous hard work, maintaining both interest and effort despite distractions, failure, adversity, and plateaus in progress [18]. Duckworth and colleagues [18] allude to grit metaphorically via a long-distance runner: “The gritty individual approaches achievement as a marathon; their advantage is stamina. Whereas disappointment or boredom signals to others that it is time to change trajectory and cut losses, the gritty individual stays the course” (p. 1088). Most runners would agree, finishing a 26.2-m race is indeed a long-term goal. Moreover, numerous challenges emerge during the hours spent running—physical pain, mental anguish, and other competitors who appear faster and stronger. It takes grit to keep running despite these challenges. It is no different for the mathematics student with a passion to learn. Learning mathematics with understanding is a marathon that requires stamina. There will always be setbacks and challenges, such as making mistakes, struggling to understand a concept, and peers who appear to be smarter and progressing faster, but the gritty individual stays the course.

3.1. Measures/Operationalization of Grit

The operationalization of grit considers both the long-term consistency of interests and long-term continuance of effort. Because the grit construct is meant to describe a personality trait, Duckworth and colleagues [18] developed a 27-item Likert survey asking participants to discern the degree to which a particular statement described how they tend to pursue long-term goals. The research team generated one scale to assess continuance of effort that “tapped the ability to sustain effort in the face of adversity” (p. 1090). The team generated another scale to assess consistency of interests, that is, to reveal the motivation behind such sustained effort. Motivators such as “subjective interest, [being] afraid of change, compliant with the expectations of others, or unaware of alternative options” (p. 1090) were included. After several rounds of correlation analysis, internal reliability analysis, efficiency analysis, and exploratory factor analysis, Duckworth et al. [18] retained 12 of the 27 original items to construct the two-factor grit scale (Grit-O) (see

Table 1. Grit scale (Grit-O) items [18].

Factors and Grit Scale 1 Items
Consistency of Interests	Continuance of Effort
I often set a goal but later choose to pursue a different one. 2	I have achieved a goal that took years of work.
New ideas and new projects sometimes distract me from previous ones. 2	I have overcome setbacks to conquer an important challenge.
I become interested in new pursuits every few months. 2	I finish whatever I begin.
My interests change from year to year. 2	Setbacks don’t discourage me.
I have been obsessed with a certain idea or project for a short time but later lost interest. 2	I am a hard worker.
I have difficulty maintaining my focus on projects that take more than a few months to complete. 2	I am diligent.

¹ Participants rated items on a 5-point scale from 1 = “not at all like me” to 5 = “very much like me”. ² Item was reverse scored.

for items).

The grit scale (Grit-O) theorized grit as a compound trait comprising stamina in dimensions of interest and effort but had room for improvement regarding predictive validity and efficiency [19]. Across six studies, Duckworth and Quinn [19] employed item analysis, confirmatory factor analysis, validity analysis, and stability analysis to validate a more efficient measure of grit, the short grit scale (Grit-S). Grit-S retained “the 2-factor structure of the original grit scale (Grit-O) with four fewer items and improved psychometric properties” [19] (p. 166) (see

Table 2. Short grit scale (Grit-S) items [19].

Factors and Grit Scale 1 Items
Consistency of Interests	Continuance of Effort
I often set a goal but later choose to pursue a different one. 2	I finish whatever I begin.
New ideas and new projects sometimes distract me from previous ones. 2	Setbacks don’t discourage me.
I have been obsessed with a certain idea or project for a short time but later lost interest. 2	I am a hard worker.
I have difficulty maintaining my focus on projects that take more than a few months to complete. 2	I am diligent.

¹ Participants rated items on a 5-point scale from 1 = “not at all like me” to 5 = “very much like me”. ² Item was reverse scored.

for the retained items in Grit-S). Used to measure grit for pursuing long-term goals across fields and domains, including goals of mathematical understanding and meaning-making, Grit-S is considered the most valid self-reporting measure of its kind today.

3.2. Associations between Grit and Learning

Research on grit has suggested several positive outcomes relative to long-term student learning and achievement. During initial research validating the construct, grit predicted educational attainment and retention in scholarly programs, grade-point average (GPA), and competitive academic achievement for subjects of different ages and contexts, including adult volunteers (ages 25–65+), West Point cadets (ages 18–22), and Scripps National Spelling Bee contestants (ages 7–15) [17,18]. Among large samples of adults, grit predicted higher education levels and traits supportive of achievement motivation, including conscientiousness, agreeableness, extraversion, and openness to experience [18,20]. Such findings suggest that the willingness and stamina to stick with long-term goals over time make possible the achievement of higher educational degrees and accolades.

Duckworth and colleagues [18] also found that undergraduate students’ GPAs were positively associated with grit scores. However, students with high GPAs and high grit scores tended to have lower SAT scores than their peers with lower evidence of grit. These correlational data suggest that perhaps grit can supplement ability, supporting academic achievement. In other words, among relatively intelligent individuals, those who may be less bright than their peers can compensate by working harder with more determination [21]. These contentions were additionally supported by data that showed the importance of grit in extracurricular accomplishment. Duckworth et al. [18] found that grittier children competing in the Scripps National Spelling Bee more diligently prepared and performed better than their less gritty peers.

Upon validation of the grit scale [18,19], research has continued to show grit as a determinant of student achievement [22,23,24,25,26,27], teacher retention and effectiveness [28,29], and general life successes [30,31]. Working with a large sample of eighth-grade public school students, West and colleagues [26] determined a positive, significant relationship between grit and mathematics test-score gains. These findings suggest non-cognitive skills such as grit may play a key role in academic performance in mathematics.

Teachers may also benefit from being gritty. As a result of two longitudinal studies of novice teachers in low-income districts, including teachers of mathematics at primary and secondary levels, Robertson-Kraft and Duckworth [29] found:

Teachers in their first and second year in the classroom who had demonstrated higher levels of grit [via Grit-S] in their pursuits prior to entering teaching were more likely to remain in the classroom for the school year and, among those who stayed, to make academic gains with their students. (p. 17)

Coupled with similar results demonstrating how teachers reporting higher grit celebrate greater academic gains from their students [28], these findings suggest that students’ long-term understandings may be affected by their teachers’ grit in addition to their own.

In the context of pursuing long-term goals, measures of grit have generally correlated with measures of achievement. Grit has predicted various educational successes from the perspective of both the student and the teacher. In all, the research base on grit supports Duckworth’s [17] original hypothesis that grit is a powerful forecaster of achievements that necessitate continuous effort and decided interest over extended periods of time.

3.3. Critiques of Grit Relative to Learning Mathematicsc with Understanding

Although grit has been predictive of long-term achievements, it is met with some criticism for lacking insights for the processes of learning mathematics with understanding. Much of the research base on grit suggests that gritty students work hard and feel determined, but there is little evidence of specific connections to understanding mathematics over time. Few grit studies have focused on relationships with mathematics at all, and those that have only considered broad-strokes achievements, such as SAT scores (see [18]), standardized state tests (see [26]), or passing one’s mathematics courses to help graduate high school (see [25]). Prior evidence that grit supports a person’s capability with achieving high scores on a mathematics exam or passing a mathematics class simply demonstrates that a gritty individual has achieved these things but fails to explain how grit helps individuals actually learn mathematics with understanding, primarily by making their own connections between important mathematical ideas [32].

Other related criticisms of grit research have concentrated on the outcomes in structured versus unstructured learning environments [33,34,35,36,37,38,39]. In their synthesis of how new research can boost student engagement, Headden and McKay [36] set forth the general critique that grit may help explain how individuals achieve in proceduralized settings focused on routine, but the relationships between grit and creative work are far less apparent. As part of a study on the relationships between undergraduates’ non-cognitive traits and creative problem solving, Grohman [34] found that grit did not predict creative achievement or ingenuity. Similarly, Ivcevic and Bracket [38] found that grit was unrelated to several measures of high schoolers’ success and posited that grit did not help explain how students regulate their behavior during emotion-laden situations, such as sticking with it during particularly challenging moments of academic work. These findings suggest that grit may forecast success in predictable situations with solution pathways or procedures to follow, but grit may not explain the intricacies of navigating uncertain situations requiring exploration, such as making progress on a challenging mathematical task for which a solution path is not known.

Duckworth et al.’s [18] conceptualization of grit clearly recognizes the salience of “the amount of energy one invests in a particular task at a given moment in time … [and] the consistency of one’s long-term goals and the stamina with which one pursues those goals” (p. 1098). Items in Grit-O and Grit-S, such as “I am diligent”, “Setbacks don’t discourage me”, and “I often set a goal but later choose to pursue a different one”, appear to measure what they are intended to measure but offer little insight into what and how someone may have learned in a given moment in time.

Also unclear is the nature of obstacles obstructing a long-term achievement. Not knowing the ways in which an individual was challenged during their time spent pursuing a goal clouds the issue of whether or not achieving such a goal implies grit, by default. In this way, measuring a person’s high score on the grit scale may just be measuring achievement of a long-term goal in general, not necessarily a struggle over years despite setbacks and frustrations at key moments in time. This is not to say that achieving a summative goal cannot be difficult: certainly, a consistency of interest and effort over a long period of time is useful for success toward almost any accomplishment. But without knowing the details of the ways in which an individual was challenged, it is difficult to know what a high grit score reveals about a person other than that they achieved a long-term goal.

Although grit has been shown to coincide with several types of summative achievements and is often celebrated as a key predictor for successful learning in general, the construct has been criticized for lacking insights into the process by which rich mathematical meanings are developed. Grit does not explain the details of key moments in time when an individual was challenged and pushed to the brink of giving up, nor does it explain any creative insights that may have been developed. Learning mathematics with understanding requires many moments of approaching and grappling with unfamiliar challenges to create meaning [9], yet the key mechanisms of how a gritty individual navigates such obstacles in the moment, propelling them forward toward success in the long term, are unclear. It is in those details that help explain how an individual becomes gritty, and how they incrementally learn mathematics with understanding. Therefore, to better learn about those key moments, researchers should consider engagement and experiences toward more short-term goals, within those trying moments when individuals encounter specific obstacles. The next section will detail a related construct, persistence, which shifts the analytic focus to such in-the-moment engagement.

4. Persistence

During challenging moments along the pathway toward mathematical meaning-making, the construct of persistence portrays when a person refuses to quit when faced with setbacks. Peterson and Seligman [40] define persistence as “voluntary continuation of a goal-directed action in spite of obstacles, difficulties, or discouragement” (p. 229). The concept of persistence describes steadfast, in-the-moment effort in the face of challenge—refusing to quit by continuing one’s particular effort before the task is accomplished. Scholars posit persistence does not alone guarantee accomplishment, but accomplishment is often unattainable without it [41,42,43,44].

Contrary to grit, the construct of persistence includes the nature of the short-term goal toward which an individual is working [40]. Although the conceptualization of persistence primarily concerns short-term goals, consistent persistence on short-term goals can accumulate and develop into long-term achievements [45]. In this way, the construct of persistence can be considered through the perspective of long- and short-term endeavors, with a general emphasis on the short-term.

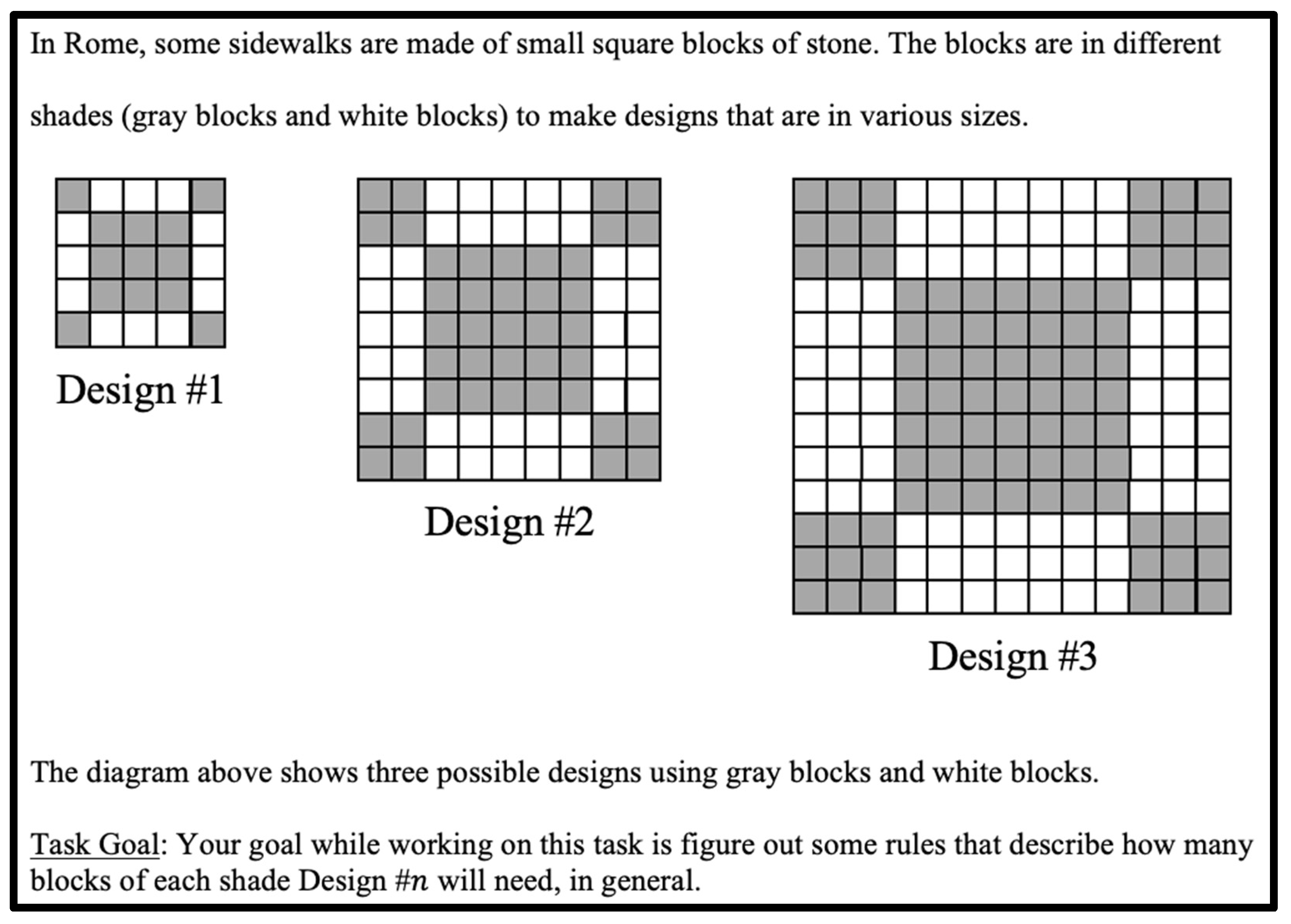
Trying to solve a challenging mathematical task is an example of a short-term goal in which an individual could be engaged. Consider the task Sidewalk Stones in Figure 1 [46]. To persist in achieving the goal of Sidewalk Stones, an individual must (a) be met with an obstacle of some kind and (b) endure and attempt to overcome such an obstacle. In these ways, persistence embodies self-regulation through tenacity. With the goal of solving the problem in mind, regulating one’s own behavior underlies the dichotomous battle between continuing engagement and giving up [47].

Assuming the individual did not immediately know how to solve Sidewalk Stones from the outset, they may begin working on the task by looking for patterns between the different designs of square stones. Using this problem-solving heuristic, the individual may be counting the different shaded stones and noting common characteristics, variations, or differences amongst Design #1, Design #2, and Design #3. If the individual has not yet generalized the relationship between the different sidewalk stones after a concerted first effort, the essence of persistence is embodied in the ways they respond to these struggles—by staying the course and continuing effort using their chosen plan of attack. The individual simply starts over, spending effort looking again for similarities and differences between the different designs of squares, hoping to come upon a generalizable pattern that had eluded them previously. This steadfast insistence and dedication to their problem-solving strategy describes an individual persisting in the moment toward a short-term goal of developing mathematical understanding.

4.1. Measures/Operationalization of Persistence

Persistence measures have taken the form of self-reports of a tendency to continue effort as well as observations of such engaged behavior. A number of questionnaires include a persistence scale or subscale to help discern an individual’s propensity for sustaining involvement and expending effort while facing obstacles [45,48,49,50,51,52,53]. In an effort to synthesize past measures of persistence, Constantin, Holman, and Hojbota [45] developed and validated a three-dimensional, 13-item model dividing the construct based on the proximity of desired ends: short-term pursuits, long-term pursuits, and recurrence of unattained pursuits (see

Table 3. Persistence scale items [45].

Dimensions and Persistence Scale 1 Items
Short-term Pursuits
I have a good capacity to focus on daily tasks.
Once I decide to do something, I am like a bulldog: I don’t give up until I reach the goal.
I continue a difficult task even when the others have already given up on it.
The more difficult a task is, the more determined I am to finish it.
Long-term Pursuits
I remain motivated even in activities that spread on several months.
Long term purposes motivate me to surmount day to day difficulties.
I purposefully pursue the achievement of the projects that I believe in.
I keep on investing time and effort in ideas and projects that require years of work and patience.
Recurrence of Unattained Pursuits
I often come up with new ideas on an older problem or project.
From time to time I imagine ways to use opportunities that I have given up.
Even though it doesn’t matter anymore, I keep thinking of personal aims that I had to give up.
I often find myself thinking about older initiatives that I had abandoned.

¹ Participants rated items on a 5-point scale from 1 = “in a very low degree” to 5 = “in a very high degree”.

for items). Items addressing short-term pursuits aim to apprehend an individual’s “ability to remain focused on the goals at hand and to prolong effort in the face of boredom, fatigue or stress” (p. 102). Because short-term pursuits can amass and be directed toward more distal goals, items addressing long-term pursuits aim to assess one’s “ability to remain committed to resource-consuming, higher-order goals that require prolonged investment, despite failures or short-term hedonic costs” (p. 103). Lastly, items addressing the recurrence of unattained pursuits aim to assess “the tendency to continue the pursuit of past, unaccomplished goals” (p. 104), in part to help discern an individual’s willingness to spend long-term effort in response to short-term failure.

Perhaps the most common measures of persistence involve observations of engaged behaviors toward short-term goals. Framed in the experimental tradition of assessing endurance to discomfort and self-control [54], persistence has often been operationalized as the amount of time spent on difficult tasks [43,55,56,57,58,59,60,61,62,63,64,65,66]. Outside of strict time calculations, persistence on challenging tasks has been dichotomously measured by asking the individual if they would like to stop or continue working after a certain amount of time [67,68,69]. Additionally, persistence has been operationalized without any time component at all. Instead, the number of subtasks attempted or completed within a task [44,55] or the number of rounds exploring a task has served as a persistence assessment [70,71]. In all, each of these measures of persistence emphasizes whether or not an individual stays engaged with a task, not the ways in which a person is engaging.

4.2. Associations between Persistence and Learning

Relatively little research has focused on the primary purpose of gaining insight into persistence, yet numerous studies have found associations between persistence and short-term learning [72]. Often measured as a result of a different variable in which researchers were more interested, persistence coexists with several outcomes facilitative of in-the-moment learning. For instance, there is much evidence of a symbiotic relationship between persistence and self-efficacy in the context of students engaging in learning activities of various structures [41,42,43,44,55,65,70,73,74,75]. Bandura and Schunk [55] explored the effects of encouraged goal structures in an elementary-age self-directed mathematics learning environment. They found that children persisted more and perceived greater self-efficacy on more complex subtraction tasks when adhering to short-term, proximal goals compared to more long-term, distal goals or no goals at all. Specifically, children were asked to work independently across seven sessions on a 42-page series of subtraction tasks of increasing difficulty. The researchers encouraged children in the proximal goal group to complete about six pages of tasks per session. Children in the distal group were encouraged to complete all 42 pages by the end of the seventh session, and children in the control group were not given any goal suggestions. Under proximal goals, children attempted more subtraction tasks, spent more time on more challenging subtraction tasks, and judged themselves as more competent than all other groups. The authors suggest, at least in part, that students found it easier to persist toward manageable investments of time and energy toward short-term goals. Such persistence, then, often resulted in making mathematical progress and thus greater perceptions of self-efficacy.

Additionally, Niemivirta and Tapola [70] found evidence of a dynamic relationship between persistence and self-efficacy. Working with 100 ninth-grade students, participants in small groups worked on a task intended to induce complex mathematical problem solving. While working, student self-efficacy was assessed three times. Niemivirta and Topola [70] found an increasing overall trend of self-efficacy, suggesting students’ self-efficacy became stronger as they continued to engage with the task. They concluded that subsequent changes in self-efficacy appeared to be a function of the students’ unfolding task-specific experiences and overall persistence.

Much research also points to ties between persistence and students’ affective experiences relative to work on challenging tasks [67,68,69,76,77,78,79,80,81,82,83,84,85,86,87,88]. For instance, Tulis and Fulmer [69] found that persistence was related to both positive-activating and negative-activating emotions. Working with 141 seventh-grade students, participants were asked to individually engage with a challenging mathematics task. Participants described the current state of their general affect and emotions three times during engagement: at the outset, after 1 min and 30 s, and after 3 min. Also, after 5 min had passed, participants were provided with the option to stop or continue working on the task, and if students wished to continue, they were told they could stop at any point thereafter. Tulis and Fulmer [69] found the decision to continue working to be positively related to both enjoyment, a positive-activating emotion, and anxiety, a negative-activating emotion. The authors concluded that “activating emotions, regardless of whether these emotions are positive or negative, can support students’ decision to persist” (p. 43).

Another example of research examining the relationship between persistence and affect includes Mukhoiyaroh, Atmoko, and Hanurawan’s [89] investigation of inquiry-based learning and students’ learning persistence. Measuring persistence with Constantin et al.’s [45] validated scale, Mukhoiyaroh et al. [89] found a significant effect of inquiry-based pedagogy in an eighth-grade class integrating science, technology, engineering, and mathematics (STEM) on student self-reports of persistence and emotional commitments to academic learning compared to a more traditional teaching style in an analogous class. The authors concluded that students’ learning within a STEM environment conducive for autonomy can influence persistence and emotional regulation during engagement with learning tasks. This is likely because such freedoms encourage genuine exploration and authentic interest in the inquiry process.

Although they rarely have been directly studied, the benefits of persistence are widely recognized relative to short-term, and ultimately accumulating to long-term, learning. Studies involving persistence generally connect steadfast continuations of effort to more positive learning outcomes. Peterson and Seligman [40] synthesize three chief conclusions applicable to learning mathematics with understanding within research including persistence as a measure. First, persistence may enhance an individual’s emotional enjoyment of subsequent success. Enduring the difficulty of continuing effort in the face of learning challenging mathematics might make the eventual achievement more satisfying, thereby developing a level of interest and pleasure in productive struggle. Second, persistence may improve one’s skills and resourcefulness. Overcoming new mathematical obstacles inevitably requires developing new approaches and new ways to solve problems. In this way, those who persist learn new ways to persist, which may be applicable to future meaning-making scenarios. Thus, persistence tends to produce further persistence. Lastly, and arguably most importantly, persistence is necessary to accomplish almost all difficult learning goals. The very nature of learning mathematics with understanding requires persistence because the process is filled with obstacles with which to wrestle. Peterson and Seligman [40] posit:

Persistence increases one’s chances of attaining difficult goals. Relatively few major undertakings are marked by a steady stream of progress and positive feedback. Setbacks and problems are typically encountered, and these can be discouraging, but if the person gives up, [they] will not reach those goals. Persistence is thus often necessary if success is to be achieved. (p. 238)

Quitting at the first sign of struggle essentially assures failure, while willingness to continue one’s effort and withstand the discomfort of struggle prolongs the opportunity to learn. Therefore, in a domain where struggle is inevitable, such as learning mathematics with understanding, persistence is a valuable tool.

Research incorporating persistence has yielded several general findings supportive of educational gains. Rarely studied directly, persistence has been shown to correlate with in-the-moment factors such as self-efficacy, enjoyment, and anxiety—all of which have been shown to facilitate short-term mathematics achievements in certain contexts. Because learning mathematics requires wrestling with difficult ideas that are not immediately apparent [9], the research involving persistence implies a consistent relationship between staying engaged despite challenges and making mathematical progress.

4.3. Critiques of Persistence Relative to Learning Mathematicsc with Understanding

Persistence is generally celebrated as a key component of learning, yet studying persistence to better understand the meaning-making process in mathematics still has its shortcomings. Most notably, research incorporating persistence has yielded relatively few insights about how people who persist are spending their time while persisting. This is a function of the method by which the construct is measured. Peterson and Seligman [40] warn that “simply measuring how long someone works at a task does not adequately capture the essence of [persistence] because continuing to perform something that is fun or rewarding does not require one to endure and overcome setbacks” (pp. 229–230). In this way, counting the minutes spent working on a challenging mathematical task reveals very little about the obstacles encountered during engagement, if they encountered any obstacles at all, or how an individual navigated such obstacles to persist toward a solution. Yet, time on task remains arguably the most widely used measure of persistence.

Persistence, by definition, encapsulates one’s effort “in spite of obstacles, difficulties, or discouragement” [40] (p. 229), but, similar to grit, one is left guessing about the degree to which an individual was challenged or discouraged. Although tasks in research involving persistence were designed to warrant difficulty, most analyses are not at a fine enough grain size to reveal the nature of challenges nor the individuals’ specific learning gains while overcoming such assumed challenges. In this way, once again similar to grit, an individual achieving their short-term goal of solving a theoretically challenging mathematics problem may mean, by default, that they persisted. This is despite the fact it is unclear the degree to which the individual was challenged and the specifics of the mathematical meanings developed through the student’s time on task.

Other critiques of a time-on-task operationalization of persistence concern the different rates and purposes by which students work. In their study of motivation and learning in a complex system, Vollmeyer, Rollett, and Rheinberg [90] found that counting the minutes spent working on a task was an unreliable predictor of achievement on that task. Undergraduate participants were tasked with solving a mathematical system in the context of biochemistry, relating three input and three output variables. Researchers found the time spent exploring different aspects of the system to be very inconsistent and did not correlate with the performance measures of the task. For example, spending more time exploring a relationship between certain input and output variables did not lead to more knowledge about the system. Some participants performed highly after relatively short amounts of time, while others worked much longer and achieved less. Vollmeyer, Rollett, and Rheinberg [90] concluded that time on task was not a reliable measure of persistence in this context because learners could have different reasons to spend more or less time on the task (e.g., a learner who wants to discover the system’s structure right now, as opposed to a learner who does not give a full effort and starts daydreaming or pseudo-engaging).

To remove time from the measurement method, Vollmeyer and Rheinberg [71] used the number of rounds of exploration of the complex system as a measure of persistence in a related follow-up study. Researching the effect of persistence as a mediator of motivation on problem solving, Vollmeyer and Rheinberg [71] found that undergraduate participants who persisted through more rounds exploring the task actually performed worse than less persistent individuals. The authors speculate prior knowledge differences as a possible explanation to these findings. Still, such results echo the overall wonderment about how those who persist are spending their time while persisting.

The construct of persistence captures steadfast, in-the-moment effort toward a challenging task. Any effort, let alone consistent sustained effort, is certainly useful when striving to make connections between student engagement and student achievement. Assuming an individual is giving their best effort, the more time spent and the more willing one is to engage with a challenge, the more opportunities one has to learn from that challenge. However, incorporating a persistence lens when analyzing student engagement during challenges omits key features of learning mathematics with understanding. Specifically, it is unclear how persisting learners overcome setbacks in the moment to develop the meanings behind the mathematics, that is, to uncover relationships between the mathematical ideas present [32]. Also, observing whether or not an individual gives up on a task does not discern if they encountered an obstacle. In this manner, the mechanisms within wrestling with an obstacle are unexplained by persistence analysis. Simply refusing to give up does not guarantee successful learning. Counting the time spent on a task or assessing the willingness to sustain effort on a task does not unpack the actual engagement with unfamiliar challenges that is so crucial for meaning-making in mathematics. For researchers to better understand how students learn mathematics with understanding, a more fine-grained analysis of how students spend their time engaging is necessary. Perseverance, a related dispositional construct that more closely considers the learner’s perspective around challenge and struggle, is unpacked next.

5. Perseverance

As inevitable obstacles are approached during the process of learning mathematics with understanding, perseverance describes in-the-moment tenacity towards accomplishing a goal while also accounting for the malleability to alter a strategy when necessary. Different from the individual factors of grit and persistence, perseverance has been conceptualized both from individual and collective perceptions. From the individual perspective, DiNapoli and Miller [91] define the construct of perseverance as “initiating and sustaining, and re-initiating and re-sustaining, in-the-moment productive struggle in the face of one or more obstacles, setbacks, or discouragements” (page). In contrast, Sengupta-Irving and Agarwal [92] define perseverance as a collective enterprise, as “peers engaging together in productive struggle with effort over time” (p. 116). The authors use the term “collective” [92] (p. 115) to account for both (a) the aggregation of peers’ individual productive struggle and (b) the group’s efforts to productively struggle in a collaborative sense.

In the context of working on a challenging mathematical task, both definitions reject the idea that whenever children solve a problem they have, by default, persevered. Instead, perseverance requires an effortful response to the initial obstacle of a non-routine task and altered efforts in response to any setbacks or difficulties that may arise in the work that follows. It is making explicit the nature of the challenges at hand that separates perseverance, in part, from persistence and grit. Individuals or groups that try to persevere past a mathematical obstacle are not guaranteed success but are equipped with more resources to approach the learning opportunity than those giving up on the mathematical task.

Similar to persistence and contrary to grit, the concept of perseverance concerns working toward a short-term goal with the recognition that a consistent tendency to persevere, over time, can accumulate and develop into long-term pursuits. During mathematical problem solving, it is the emphasis on the flexibility to change a strategy upon setbacks, or “amending one’s plan of attack” [93] (p. 5), that distinguishes perseverance from persistence. In this way, perseverance has been discussed as “productive persistence, defined as tenacity plus effective strategy [use]” [94] (p. 451), because an individual or group may need to employ different plans to make progress on a problem if their first plan was unsuccessful. At the core of perseverance is the intersection of self-regulatory and metacognitive skills: regulating oneself to not only continue engagement in the face of challenge but to notice progress or the lack thereof and decide to change course when necessary [47,95,96,97,98,99].

Gresalfi and Barnes [100] suggest how mathematical or consequential justification can inform a decision to continue to persevere and change course. Achieving mathematical awareness through effort, that is, using made mathematical connections (i.e., “this plan is not working because the slope of my function is incorrect”) to justify taking a different approach, demonstrates the productive relationship of perseverance and mathematical meaning-making. In contrast, achieving consequential awareness through effort, that is, using consequences (i.e., “this plan is not working because I’m not getting the right answer”) to justify a decision to change course, showcases a less mathematically productive outcome.

Again, consider solving the Sidewalk Stones task (see Figure 1) as an example of a short-term goal in which an individual or group could be interested. To persevere in achieving the task goal, one must individually or collectively (a) be met with an initial obstacle of some kind, (b) endure and make a diligent initial attempt to overcome such an obstacle, and (c) if the prior attempt is unsuccessful, recognize this setback and endure and change solution strategies to make a diligent additional attempt(s) to overcome such an obstacle. Assuming Sidewalk Stones is a non-routine task for an individual or group, not immediately knowing how to proceed to discern the block rules constitutes the first obstacle toward which they can persevere. To persevere, an individual or group must make an effort to begin working toward the task goal, perhaps by counting the different shaded stones and noting similarities and differences amongst the provided designs. If the problem is not solved via this initial attempt, an individual or group must recognize this difficulty and alter their plan to continue their engagement, perhaps by drawing a larger sidewalk design, Design #4, to help them discern a relationship between the different blocks and the size of the design. This process of initiating, sustaining, and altering effort toward a short-term task goal can continue indefinitely, ideally until mathematical progress is made or the problem is solved, and describes perseverance from both an individual and group perspective.

5.1. Measures/Operationalization of Perseverance

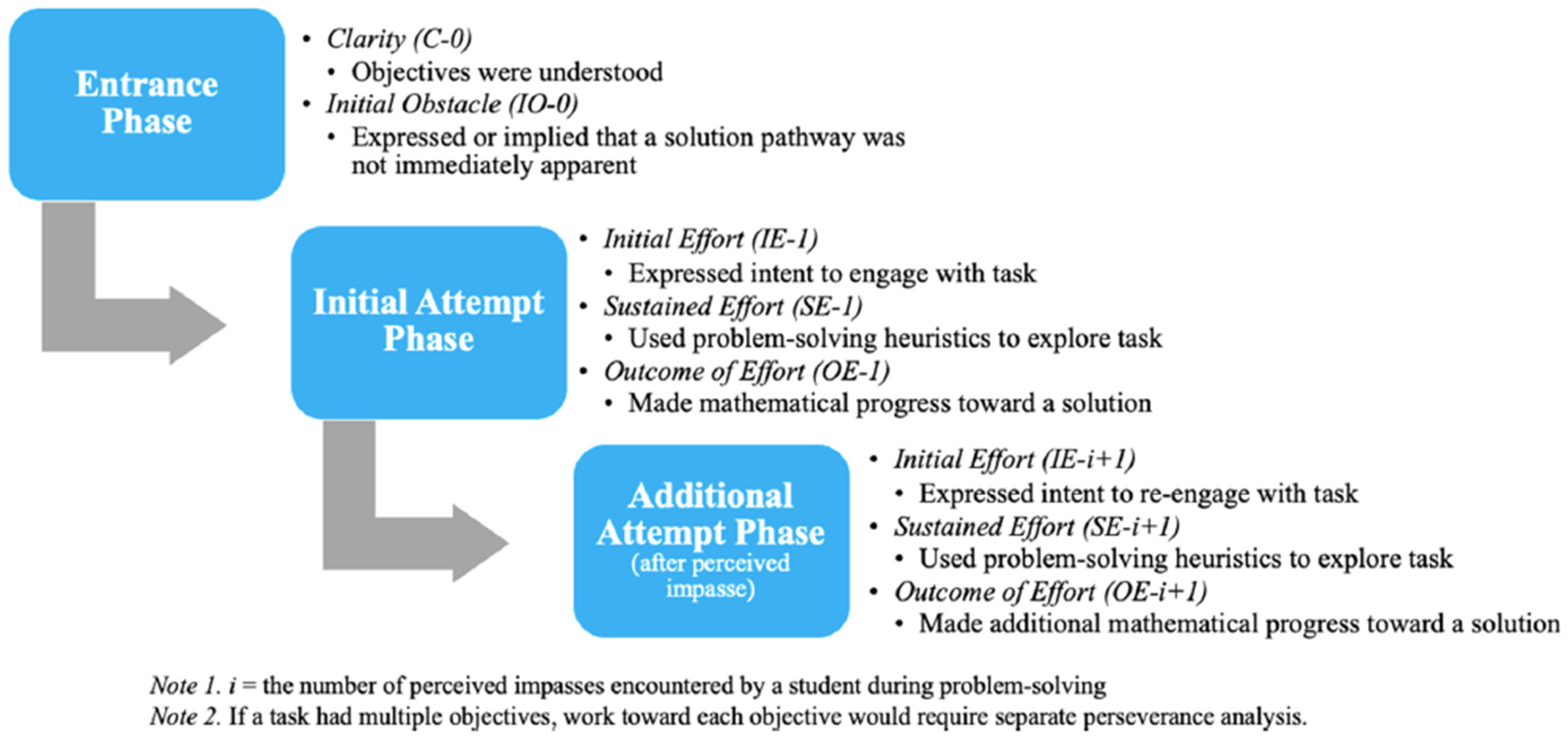
Perseverance measures are a fine-grained account of an individual or group’s engagement with a challenging task, particularly focused on identifying when obstacles surfaced and how such obstacles were navigated [11,91,92,101,102,103,104]. In the context of an individual student working on a non-routine mathematical task, DiNapoli and Miller [91] operationalized perseverance using a three-phase engagement framework: the Entrance Phase, the Initial Attempt Phase, and the Additional Attempt Phase (see Figure 2). The structure of the framework was developed using an inductive approach, emerging from the following data sources: observation, in-the-moment interview as the student thought aloud, and video reflection interview as the student reviewed clips of their own engagement. The framework was designed to capture perspectives of the concept of perseverance [93,94,101,104], problem-solving actions and the different manifestations of productive struggle [6,9,11,97,105,106,107], monitoring and self-regulation [97,108], and making and recognizing mathematical progress [100,109]. Substantially capturing the student point of view during engagement with tasks, coding decisions, or whether or not certain engagement constituted evidence of perseverance largely depended on student cues from in-the-moment thinking aloud and video reflection interviews. For instance, evidence of mathematical progress consisted of the student themselves affirming, describing, and/or defending their point of view that they better understood the mathematical context embedded in a task after their effort(s).

While initially reading the task, the Entrance Phase captured whether the student understood the entirety of what the task was asking (clarity component) and if the student immediately knew how to solve the problem (initial obstacle component). Essentially, this phase established the appropriateness of a task for perseverance analysis with a particular individual. An ideal outcome in the Entrance Phase was a student affirming the task made sense and was within their perceived realm of capability, yet they did not immediately know a procedure by which to solve it. In this case, the task was deemed as appropriate for perseverance measurement, and participants entered into the next phase of engagement.

The Initial Attempt Phase examined whether and how the student initiated and sustained their effort and the outcome of such effort as they worked toward solving all parts of the problem. Since the student did not immediately know a solution pathway, evidence of perseverance included deciding to engage with the task at all (initial effort component). If the student decided to pursue solving the problem, evidence of perseverance included using a problem-solving strategy to diligently explore the uncertain nature of the mathematical situation (sustained effort component). In this context, a problem-solving strategy was defined as using one or more heuristics, in conjunction, to work toward a solution. As a result of these diligent efforts, evidence of perseverance included making mathematical progress toward better understanding the mathematical relationships or solving the problem outright (outcome of effort component).

In the event the student did not solve the problem after making an initial attempt, the Additional Attempt Phase aimed to measure if and how the student amended their original problem-solving plan and the outcome of such efforts as they worked to overcome any setbacks and toward solving all parts of the problem. To enter this phase (marking the end of an initial attempt and the beginning of a second attempt), the student must first be stuck, that is, they perceived to have exhausted all options immediately stemming from their first plan of attack and are unsure of how to keep moving forward toward finding a solution. At this point, evidence of perseverance included deciding to re-engage with the task using a different strategy—one that was not used during the initial attempt (initial effort component). Assuming the student decided to pursue solving the problem with a new plan of attack, additional evidence of perseverance included diligently exploring the mathematical situation with the new strategy (sustained effort component) and making new progress toward better understanding the mathematics involved in the task or solving the problem outright (outcome of effort component). Depending on the number of times a student amends their original problem-solving plan, or the logistical constraints of scheduling time for students to work, a student could continue working in the Additional Attempt Phase, making third attempts, fourth attempts, and so on.

In sum, DiNapoli and Miller’s [91] three-phase engagement framework measures a student’s in-the-moment perseverance by first determining in the Entrance Phase if the task with which the student is working necessitates perseverance. The components within the Initial and Additional Attempt Phases then detail the evidence of perseverance at specific moments during problem solving with a challenging mathematical task. It is important to note that DiNapoli and Miller’s [91] perseverance framework prizes how students spend their time—spending effort to grapple with important mathematical ideas and making mathematical progress—not time on task or necessarily obtaining correct answers. This focus encourages a mathematics-as-activity perspective, in which doing mathematics constitutes the process of thinking mathematically, while simultaneously wrestling with inherent obstacles toward the goal of better understanding a mathematical structure embedded in a task or situation [98].

In the context of a group of students collectively working on a challenging mathematical task in a classroom setting, Sengupta-Irving and Agarwal [92] studied a group’s perseverance by focusing on interactions that may have evidenced productive struggle. The goal of their analysis was to better “demarcate the boundaries of perseverance as collective enterprise” (p. 124). Such perseverance was evidenced by students modeling or representing ideas to their peers, considering others’ explanations, or monitoring their own problem solving while wrestling with important mathematical ideas that were just beyond reach. The research team video recorded and observed groups of four students working collaboratively on a challenging mathematical task. They systematically chronicled when a struggle emerged, what led to the struggle, and details of the talk and activity that preceded and followed each episode of struggle. As such, the discursive, in-the-moment indicators of potential productive struggle in this collaborative context were:

• Conflict in declared solution or strategy.
• Declaration of uncertainty about solution or strategy.
• Declaration of inelegant or inefficient strategy.
• Clarification of task expectations or features.
• Seeking expert support [from teacher] (p. 122).

In addition to identifying indicators of potential productive struggle, Sengupta-Irving and Agarwal’s [92] perseverance framework specified five outcomes of collective engagement immediately after an opportunity for productive struggle emerged:

• Problem solving but not persevering because of agreement on incorrect answer.
• Problem solving but not persevering because solution is immediately obvious.
• Perseverance in problem solving but not as collective enterprise.
• Perseverance in problem solving as collective enterprise (brief).
• Perseverance in problem solving as collective enterprise (extended) (p. 124).

In this way, the authors identified relationships between particular indicators and subsequent perseverance to detail perseverance as collective enterprise in this context. Viewing perseverance as a collective construct “capitalizes on [the] opportunity to build stronger and more supportive classroom communities—communities that will prove themselves unbreakable in the midst of great struggle” [92] (p. 134). Thus, this perspective encourages the design of learning environments that bring students together to productively struggle with unformulated mathematical ideas that collective effort will bring within reach. It remains to be seen the specific ways in which developing such collective perseverance with challenging mathematics, with students working collaboratively, may influence the development of individual perseverance, with the same students working individually [101].

5.2. Associations between Perseverance and Learning

Studies specific to perseverance endorsing conceptualizations that focus on in-the-moment engagement around obstacles, although relatively few, have made deep connections to students learning mathematics with understanding. By studying how students navigate the challenging moments during mathematical work when a formulated idea is just out of reach, research on perseverance reveals the dynamics of how children overcome setbacks to make their own connections between important mathematical ideas [11,91,92,101,102,103]. Further, such research has borne great insights into how teachers can support students in their meaning-making process.

From the individual learning perspective, DiNapoli [102] found that students who reported holding generally positive motivations may not know what it means to persevere to accomplish their goal of understanding mathematics. In this study, the researcher explored the relationship between 11 ninth-grade students’ self-reported achievement goals and their subsequent perseverance on a mathematical task with which they were unfamiliar yet interested. Via a problem-solving interview, the researcher discerned the goal(s) toward which each student worked and measured perseverant actions using the three-phase framework in Figure 2. Results showed that students may have the best intentions to persevere and develop their own mathematical understandings in the face of a challenge but hold a distorted view of what counts as productive effort.

In this study, students shared how satisfied they felt from their effort, even though they only worked for mere seconds on a challenging problem. The same students shared how their teachers consistently encouraged approaching challenges and not giving up, suggesting students may be interpreting this message in a binary way: you can either try or not try, there is no in-between. Students may exert minimum effort to check-the-box of perseverance and feel proud of their work but not make real progress. This inquiry into student perseverance suggests that teachers should be more explicit about what counts as perseverance and help children realize the difference between minimal and meaningful effort in the learning process.

Studying student perseverance over a series of several challenging mathematical tasks, DiNapoli and Miller [91] found that ninth graders persevered more on tasks embedded with prompts to promote conceptual thinking and demonstrated an improvement in quality of perseverance over time compared to their work on similar tasks without such scaffolds. Using problem-solving interview and video retrospection interview methodologies, the researchers worked in-depth with 30 students as they worked and thought aloud on a challenging task. Then, the research facilitated a discussion with each individual participant about how they experienced the specific moments when perseverance was necessary while together watching a video of their engagement immediately thereafter. Over a five-week period, each participant worked on five analogous mathematical tasks for which they had demonstrated prerequisite knowledge. Each student worked on one task per week in a random order. Three of the tasks were embedded with scaffolds designed to activate prior knowledge and/or support planning a solution pathway, both methods of conceptualizing a mathematical situation while maintaining cognitive demand [110]; two of the tasks had no scaffolds.

Using the three-phase perseverance framework (see Figure 2), results showed that these ninth-grade students’ perseverance was supported by these scaffolds, but the type of scaffold did not seem to matter. The most prevalent difference in demonstrated perseverance between tasks with and without scaffolds occurred in the Additional Attempt Phase. After making an initial attempt at solving a task and reporting they were unsure how to continue, the quality of students’ perseverance in their additional attempt was significantly better while working on scaffolded tasks compared to non-scaffolded tasks. After engaging with the scaffolds, students were more often amending their original plan of attack, deeply exploring the task with a new set of exploratory heuristics, and making additional mathematical progress as a result of their additional efforts. On the non-scaffolded tasks, students were much more likely to give up earlier and opt out of making an additional attempt altogether. From the participant point of view, several students cited their initial conceptualization work as the primary reason for their higher-quality perseverance on the scaffolded tasks. By initially making explicit the important mathematical ideas and the connections between them, participants found such work helpful after making a mistake, even when they were at their most frustrated, because they could more easily reconsider their original mathematical conceptualization, make some adjustments in their thinking, and try something new. Without such conceptualizations written down, many participants cited disorganization and frustration as reasons for giving up after encountering a setback.

Additionally, participants’ perseverance improved in quality over time, more so across their work on scaffolded tasks than on non-scaffolded tasks. While reflecting on their experiences, participants reported they believed they were getting better at making progress on these challenging tasks. Many cited the phenomenon of momentum, or a drive to finish what they had started, as responsible for their improvement. Others cited more cognitive gains, reporting they found it easier to design plans of attack, both for their first and additional attempts, the more opportunities they had to practice their perseverant engagement. Since participants had a significantly easier time initiating first and additional efforts on tasks with scaffolds, this research suggests that giving students a formal space to think and record their ideas can encourage subsequent perseverance in ways that will facilitate making meaningful mathematical connections.

From the collective learning perspective, Sengupta-Irving and Agarwal [92] aimed to describe what collective perseverance looked like, and they found that the most perseverant groups of students were working in a collaborative zone of proximal development, that is, these students were grappling with the mathematics at similar levels of struggle, while also being able to awaken possible mathematical connections in one another through collaboration. The researchers observed 16 fifth-grade students engage with six challenging tasks, working in groups of four, over the course of six days. By identifying in-the-moment indicators of potential productive struggle and examining the perseverance (or lack thereof) demonstrated by a group immediately afterwards, Sengupta-Irving and Agarwal [92] found that peer dynamics both constrained and advanced children in persevering.

During work on one task, a group of two boys and two girls (this use of gendered language is to stay consistent with the language used by the original authors [92]) had trouble working together. The boys were overcritical of the girls’ initial solution strategy because they thought it was inefficient. This critique seemed to rupture the good will necessary for persevering together. The children decided to continue working in smaller groups of two, sacrificing the opportunity to learn from more diverse perspectives in problem solving to gain a deeper understanding of the mathematics. The researchers determined that only the girls in this group were engaged in real productive struggle, because the boys seemed to never encounter a true obstacle. Thus, at the level of the entire group, the students failed to evidence perseverance as collective enterprise.

During work on another task, a different group of two boys and two girls demonstrated a productive collaboration. The children worked at times in smaller groups of two and then together in one group of four to persevere past several obstacles during problem solving. The group of girls initiated effort with a visual representation strategy, while the group of boys began with a numeric strategy. Several times during their work, the group convened as a collective to share how they were thinking about solving the problem from their own points of view. It is through these collective efforts that each group member advanced their understanding of the mathematical situation and was able to progress with their work in meaningful ways. Ultimately, the group of boys and the group of girls both productively struggled and solved the task in different ways. This group demonstrated perseverance as collective enterprise in their willingness to share their struggles and learn from one another.

In sum, Sengupta-Irving and Agarwal [92] stressed the importance of teachers creating learning environments with norms that sustain collective perseverance. Such norms include shared student accountability, student-driven inquiry, and, most importantly, grouping students by a collaborative zone of proximal development. This research points to substantial learning gains to be had through collective perseverance but only if each member of the collective has similar opportunities for productive struggle.

Although rather uncommon, research on perseverance has made progress describing challenging moments for learners during work with mathematical tasks. Unlike grit and persistence, constructs that have primarily been studied as a related outcome with achievement, perseverance has been studied directly to reveal the ways in which students initiate, sustain, re-initiate, and re-sustain productive struggle within the learning process. As a result of such work, perseverance has operationalized from the individual and collective perspective and has been implemented in empirical work to uncover resources—such as conceptual thinking scaffolds and collaborative discourse—supportive of productive struggle with challenging mathematics.

5.3. Critiques of Perseverance Relative to Learning Mathematicsc with Understanding

There is general consensus that perseverance is vital for learning mathematics because struggling with important mathematical ideas while recovering from setbacks is fundamental for the sense making process [9]. Yet, critiques exist regarding the explicit relationship between student perseverance and conceptual development. While studies on perseverance (e.g., [91,92,103]) uncover resources learners can leverage to further propel their perseverance with a mathematical challenge, the specific learning gains are often unclear. In these studies, the main focus of research is the perseverance itself, not necessarily the resulting mathematical gains. Although an important factor of operationalizing perseverance in the moment is making mathematical progress, the details of such progress are not well defined. For instance, DiNapoli and Miller [91] account for making mathematical progress primarily from the student point of view, that is, if the student believes they better understand the mathematical situation as a result of their engagement, they made mathematical progress. The student perspective is certainly valued in research on perseverance, but more emphasis on specifically how students are constructing and clarifying the relationships between mathematical ideas is warranted in future research.

Also, the way perseverance has been studied has been critiqued. For instance, Sengupta-Irving and Agarwal [92] contend that perseverance should be investigated from a collaborative, not individual, point of view. They argue that framing perseverance as a collective enterprise offers a vantage point from which to consider how children collaborate around challenging mathematics. This assertion derives from the well-known relationship between group dynamics and mathematical learning and problem solving, namely that peer collaboration can encourage making connections between important mathematical ideas [97,98,111,112,113]. In practice, encouraging collective perseverance can help build more equitable and effective learning communities [103,114,115,116], help teachers create and sustain opportunities for groups of children to persevere [117], and build understanding of how the context might constrain its emergence [108]. The authors [92] insist that “the problem with an individual perspective on perseverance is that it presumes the child is the cause of success/failure (i.e., they lack perseverance) without considering what role the context plays in supporting or constraining their efforts” (p. 117).

One note about Sengupta-Irving and Agarwal’s [92] critique of the individual perspective is that it is rooted in research on persistence, not perseverance. Sengupta-Irving and Agarwal [92] reference works from the mid-twentieth century (e.g., [118,119,120,121,122,123,124]) to paint an “empirical history of the construct” (p. 117) and to describe “how perseverance has typically been studied” (p. 117). However, these studies all focused on the notion of persistence, not perseverance, by operationalizing effort through time on task. Studies such as these over-simplify the idea of spending time to grapple with a challenge because their measures do not consider how that time was spent.

Researching perseverance from the individual perspective does not discount what can be learned from the collective perspective but instead tries to better understand what states of engagement are enacted by a person when wrestling with a mathematical challenge. Such states are not inert traits of these individuals but a collection of in-the-moment mindsets, motives, and actions potentially living within all persons that can be brought to the surface in certain contexts [125]. This point of view is rooted in the fundamentals of mathematics learning, as explained in Adding It Up [13], in which the National Research Council posits that mathematically proficient children develop a productive disposition and a respect for perseverance:

Productive disposition refers to the tendency to see sense in mathematics, to perceive it as both useful and worthwhile, to believe that steady effort in learning mathematics pays off, and to see oneself as an effective learner and doer of mathematics. If students are to develop conceptual understanding, procedural fluency, strategic competence, and adaptive reasoning abilities, they must believe that mathematics is understandable, not arbitrary; that, with diligent effort, it can be learned and used; and that they are capable of figuring it out. Developing a productive disposition requires frequent opportunities to make sense of mathematics, to recognize the benefits of perseverance, and to experience the rewards of sense making in mathematics. [13] (p. 131)

The individual perspective should always be considered in context, however. The individual’s prior experiences, interest level, achievement goals, self-efficacy, and other motivators all play a role in one’s willingness to persevere in a given situation [93]. The structure of a mathematical task and the level of challenge are also important contextual variables to recognize in this work [126].

In all, both perspectives, the individual and collective, offer fruitful lenses through which to study perseverance. The individual point of view reveals the inner mechanisms of how a student can manage to struggle to make sense of mathematics, even after a setback or discouragement. The collective point of view reveals the ways in which a community of learners can approach, sustain, and make progress upon a mathematical challenge, even after a conflict in a solution or strategy. This outlook is echoed in NCTM’s Principles to Actions [15], asserting that mathematics instruction should consider perseverance from both standpoints. They affirm “effective teaching of mathematics consistently provides students, individually and collectively, with opportunities and supports to engage in productive struggle as they grapple with mathematical ideas and relationships” (p. 48). Extending this notion to include making multiple attempts to grapple with mathematical ideas and relationships, even after a mistake or setback, encapsulates the importance of teachers providing students with opportunities to persevere.

6. Toward a Distinction of Constructs

Grit, persistence, and perseverance are three dispositional factors that embody the principle of continuing effort in the face of a challenge. The process of learning mathematics for understanding is full of challenges because one must wrestle with ideas that are not immediately apparent to help make sense of them. From an analytical perspective, each construct reveals something different about a student’s engagement with mathematics. On the surface, grit, persistence, and perseverance all describe the idea of sticking with it, a “stamina” [18] (p. 1098) of sorts while navigating obstacles during pursuits of learning mathematics. Yet, each construct explains the details of such stamina at varying grain sizes. Therefore, it is important to make explicit the distinctions between grit, persistence, and perseverance and how they can be used in the context of research on learning mathematics for understanding. The primary differences between the constructs are the focused timeframe and the details revealed about how one spends their time while engaged with challenging mathematics (see

Table 4. Distinctions between grit, persistence, and perseverance.

Construct	Definition	Primary Measure	Timescale	Grain Size of Analysis
Grit	The [continuance of effort] and passion for specific, high goals, sustained over years [17] (p. 73).	Questionnaire: Grit-S scale—Consistency of Interests and [Continuation] of Effort (factors) [19].	Long-term, a tendency over time.	Determines if students’ self-reports of focused hard work and summative mathematical achievements are associated.
Persistence	The voluntary continuation of a goal-directed action in spite of obstacles, difficulties, or discouragement [40] (p. 229).	Observed engagement: the amount of time spent working on a difficult task.	Short-term, in the moment.	Quantifies for how long a student engaged with a mathematical challenge, suggesting more opportunities to learn emerge from more time spent on task.
Perseverance	Initiating and sustaining, and re-initiating and re-sustaining, in-the-moment productive struggle in the face of one or more obstacles, setbacks, or discouragements [91] (page).	Observed engagement: Three-Phase Perseverance Framework—Initial Effort, Sustained Effort, Outcome of Effort (components) [91].	Short-term, in the moment.	Describes student engagement with a mathematical challenge, the ways in which effort was initiated and sustained before and after setbacks, and the apparent mathematical progress made.

).

Grit, persistence, and perseverance differ in terms of the timeframe concerning their nature. Grit describes stamina across challenges toward a long-term goal, while persistence and perseverance depict stamina within effort toward a short-term goal. For persistence and perseverance, such short-term goals are often solving challenging mathematical tasks. Students must persist or persevere despite setbacks to begin to develop an understanding about the mathematics embedded in a task; all of this stamina occurs in the moment while grappling with obstacles in the problem. For this reason, persistence and perseverance are framed not as a character trait but as a state of engagement in those trying moments (At times, persistence has been framed as a measure via questionnaire of one’s tendency to not give up on a task (e.g., [45]), which implies a trait of one’s character. However, persistence has most often been measured via time on task in the moment, which implies a state of engagement, not a characteristic. Therefore, persistence is considered here as a time-on-task measure.). Grit, on the other hand, implies a consistency of effort toward a summative achievement, such as earning a mathematics degree. This measure concerns the tendency of a person to continue to work toward a long-term goal; thus, grit is framed as a trait of one’s character. These types of achievement are presumably a result of the accumulation of in-the-moment persistence or perseverance with formative achievements. Both achievements, solving a challenging mathematical task or earning a mathematics degree, imply effort was spent toward developing one’s mathematical understanding, but the dispositional factors at play are operating within different timeframes.

While pursuing a goal related to learning mathematics with understanding, grit, persistence, and perseverance all reveal something different about how one maintains one’s stamina. Grit and persistence describe the generic action of staying the course, while perseverance digs deeper into the specific actions one takes to continue effort despite obstacles and disappointments. Questionnaires such as the Grit-S Scale [19] aim to discern whether or not an individual is tenacious in their work to achieve their goal in spite of challenges. Similarly, time-on-task measures of persistence imply the level of tenacity exerted in the moment. Thus, studying mathematics learning via grit and persistence affords information about if an individual decided to stay the course in a particular timeframe but not how. Although affirmative responses to Grit-S [19], for example, suggest an individual is consistent, over time, with their efforts in the face of challenge, such reports do not detail how those efforts were maintained. It is apparent the gritty individual leveraged their stamina to reach the finish line (i.e., earned a math degree), but it is not clear how exactly they overcame the many obstacles to arriving there. Likewise, the more time spent working on a challenging task, for instance, demonstrates a stamina and an in-the-moment commitment to not give up. Yet, it is the details of how this time was spent that are missing. It is clear this individual persisted in their efforts to stay engaged with the task, but it is unclear what exactly they did to overcome obstacles and make mathematical progress despite setbacks, if they did at all.

Perseverance, on the other hand, affords more insights into how effort was spent while maintaining stamina during challenging moments with mathematics. For instance, the three-phase perseverance framework [91] first accounts for whether the task necessitated perseverance and, if so, secondly captures the student’s problem-solving strategies used to continue engagement, overcome obstacles and make progress, and, most importantly, thirdly make an additional attempt to stay engaged with the task if an initial attempt was unsuccessful. Because learning mathematics with understanding can involve multiple obstacles, it is likely one must tenaciously and flexibly try several different strategies to make progress toward solving a problem.

Separately, these self-regulatory facets of tenacity and flexibility can be limited in the context of learning mathematics. A student can demonstrate tenacity with a persistent stubbornness to never give up but make little progress toward their goal if the plan is flawed. Conversely, one can have multiple productive ideas for how to solve a challenging task for which a solution pathway is unknown, but without thorough and diligent exploration of those strategies, they will never know which strategy works well and which strategy does not. In this case, making mathematical progress is unlikely. These two facets necessitate and complement one another to help describe in-the-moment perseverance. Thus, in addition to determining if a student was engaged with a mathematical task that was indeed challenging, measures of perseverance seek to depict the quality of such engagement by considering the specific actions students take when solving challenging problems, flexibility to amend one’s plan, and overall productivity of effort in the context of learning mathematics.

Therefore, studies including grit, persistence, or perseverance tell us something different about students learning mathematics with understanding. Learning mathematics with understanding requires ample opportunities for students to productively struggle with challenging content to discover and describe relationships between mathematical ideas at play. Research on learning mathematics with understanding is constantly looking for ways different learners navigate obstacles successfully and how they continue to propel themselves forward, despite struggles and setbacks. Although studies of grit and persistence have been tied to mathematical achievements in general—such as gritty students scoring highly on the SATs (see [18]) or persistent students celebrating increased perceptions of confidence with mathematical problem solving (see [70])—little evidence exists that using these constructs as an analytical tool reveals much about the process of meaning-making in mathematics. Self-reports of grit depict a general willingness to maintain focus and effort toward a goal, but nothing is revealed about what a student carries out during uncertain moments when obstacles present themselves. Observed persistence depicts continued engagement with a task, but nothing is revealed about the quality of that engagement. Researchers simply know a student reported as gritty or was observed to be on-task, yet they do not know the details of how the presumed hard work was carried out. Learning to be gritty or persistent certainly would have its academic advantages, but the lack of details provided by these constructs makes it difficult to extract ideas for how to help develop grit or persistence in students. Instead, social-psychological interventions (e.g., teaching growth mindset and malleable intelligence theory, [127]) are often tasked with trying to develop such non-cognitive factors in students. Without specific empirical data for how students became gritty or managed to persist with a mathematical challenge, these interventions can be ill-received and ineffective because they offer no concrete strategies for students to practice in order to help generate long-lasting effects [128].

Perseverance, conversely, has been operationalized in ways to provide such empirical data as students traverse in-the-moment mathematical obstacles. Thus, perseverance can be operationalized through an analytic framework that details the ways in which students productively struggle and incrementally make connections between important mathematical ideas. Studies of perseverance can inform researchers of specific conditions that encourage perseverance in specific ways, such as the finding that prompting students to make a list of potentially relevant mathematical ideas prior to working on a mathematical task can encourage them to amend their original problem-solving plan (if it was unsuccessful) and try a different heuristic to make progress (see [91]). Further, discussing key decision-making moments with participants themselves can offer a valuable perspective from which to interpret findings, such as learning that students felt more invested in a task after making a list of mathematical ideas. As a result, it was easier for them to explore uncertain terrain as a result of such an investment (see [91]). These types of results are helpful for researchers in this context because they reveal exactly what students are carrying out while wrestling with mathematical ideas and offer practical suggestions about how one might overcome in-the-moment mathematical obstacles.

It is important to note that studying perseverance is not as simple as providing students with a mathematical task and expecting them to productively struggle. No person is always perseverant. Perseverance is not a character trait; it is a state of engagement idiosyncratic in nature [92]. Perseverance with a challenging task is influenced by a variety of environmental factors, including interest level [129,130], goals for engagement [102,131], prerequisite knowledge [132,133], self-efficacy [134,135], uncertainty affect [136,137], and the structure of the task itself [91,102,103,126,138,139]. Thus, examining student perseverance requires careful planning and consideration of the situational variables at play. In fact, if even one variable is incompatible with a student in a particular situation, a reasonable response to a challenge task may be to not persevere (see [140]). Every student perseveres, or does not persevere, in different ways for different reasons, so research on perseverance should describe explicitly the conditions under which any study was conducted and what was gleaned about learning mathematics in that specific context.

It is also important to note that grit and persistence may be easier to measure than perseverance. The ways several perseverance methodologies have been described in this paper (e.g., [91,92]) are arguably more laborious than measuring a general disposition via survey (i.e., grit) or measuring time spent working on a challenging task (i.e., persistence). Methods for measuring perseverance are closely aligned with making sense of the productive struggle aspect of the learning process, which is useful for studying learning mathematics with understanding [1,2] but can also be complex to measure. This suggests a research design tradeoff of sorts: studying the learning process through a perseverance lens may require complex and laborious methodologies, while studying constructs not directly related to the learning process (i.e., grit or persistence) may require less effortful methodologies.

Researchers should carefully select and define constructs to reflect their phenomenon of interest. As it stands, grit, persistence, and perseverance are often used interchangeably, which leads to a misconception of what can be learned through the lens of each construct. For example, in studies of grit, Duckworth and colleagues consistently refer to “perseverance”, but in a long-term, less nuanced sense than what is argued in this paper. Christensen and Knezek [141] discuss measures of “perseverance” in their study on motivation and study habits, yet they use grit questionnaires to do so. Marshall [142] aimed to depict “perseverance” in an algebra class, yet largely relied on time-on-task calculations, or persistence, to describe the extent of student effort. In the context of learning mathematics, studies of grit and persistence are equipped to draw conclusions far different, and far less detailed, than studies of perseverance. Future research could consider adding a perseverance lens to studies of grit or persistence. In these potential studies, findings related to perseverance could add explanatory power to findings related to grit or persistence, which could help connect grit or persistence more closely to learning mathematics with understanding. Still, these constructs deserve distinction to clarify what an investigation is studying and how it is relevant to understanding mathematics and mathematics education in general.

7. Conclusions

Grit, persistence, and perseverance are distinct, dispositional factors that afford different insights into how students learn mathematics with understanding. Although each construct refers generally to not giving up in the face of a challenge, perseverance digs far more deeply into how students spend their time navigating mathematical obstacles than grit or persistence. For the purposes of research on meaning-making in mathematics, studying how students persevere with challenging problems can reveal the ways in which they overcome setbacks and make their own mathematical connections in the moment—revelations that can pragmatically inform teachers for how to set up mathematical activities and encourage students to necessitate and nurture such practices. This is not to say that research incorporating grit and persistence is not useful in mathematics education. Grit research can establish associations between accomplishments and consistency of interest and effort, which can posit the construct as a predictor of general mathematical achievements in the long term. Research incorporating persistence can efficiently describe the time a student spent engaging with a challenge and thus the opportunity they had to learn from that challenge. Yet, in the context of learning more about how students learn mathematics with understanding, examining students’ perseverance with challenging tasks has the most potential to bear the most fruitful and fine-grained insights.