Abstract
The awareness that many problems in our society are interdisciplinary in nature and require the integration of multiple STEM (Science, Technology, Engineering, Mathematics) concepts to solve them has given rise to a new instructional approach, called “integrated STEM education”. Integrated STEM education aims to remove the barriers from the STEM fields and has the potential to increase students’ interest and motivation for learning, as well as to lead to improved achievement. It is important to assess the effectiveness of educational STEM initiatives in terms of students’ integrating ability, but to date, no such instruments are available. This study provides a definition of “integrating ability” and establishes a framework for understanding its components. Based on this definition and framework, a multiple-choice instrument for testing integrated physics and mathematics in the ninth grade (IPM9) was developed and validated. The definition and framework for integrating ability and the construction guidelines for an integrated test, can be used by researchers to assess students’ ability to integrate STEM subjects.
1. Introduction
Growing concerns about students’ achievement in and motivation for science, technology, engineering and mathematics (STEM) has led to much attention being paid to STEM education. To face the challenges of the current knowledge-based society in a growing global economy, high-quality educational STEM programs are necessary [1,2]. The awareness that many problems in our ever-changing society are interdisciplinary in nature and require the integration of multiple STEM concepts to solve them has given rise to a new instructional approach called the “integrated STEM education” [3,4,5].
1.1. Integrated STEM Education
According to Sanders [6] (2009, p. 21), integrated STEM is “an approach that explores teaching and learning between/among any two or more of the STEM subject areas, and/or between a STEM subject and one or more other school subjects”. We conceptualize integrated STEM education as tasks that require students to use knowledge and skills from multiple disciplines, adopting an interdisciplinary approach [7]. In the literature, the metaphor of chicken noodle soup versus tomato soup is often used to illuminate the difference between a multidisciplinary approach and an interdisciplinary approach [8]. The chicken noodle soup represents multidisciplinary integration. All ingredients are separately recognizable and maintain their identity in the larger soup of integration. However, the tomato soup, which represents the interdisciplinary integration, is a mixture of blurry ingredients. When we translate this into integrated STEM education, we could argue that a multidisciplinary approach starts from subject-based content and skills, from which students form connections between the subjects that were addressed in different classes [3]. An interdisciplinary approach in integrated STEM education would start from a (mixed) problem that requires the understanding of content and skills of multiple subjects. Hence, the starting point in multidisciplinarity is content and skills, where the starting point in interdisciplinarity is the problem.
In this paper, we approach integrated STEM education as an interdisciplinary construct. Accordingly, integrated STEM education is defined as problem-based education that aims to merge the content fields of the different STEM areas into a single curricular project. This project emphasizes concepts and their application from across the four disciplines [9]. The removal of the barriers between these disciplines demands an educational approach in which students participate in engineering design and research. The adoption of integrated STEM education in secondary education is promising; by integrating science, technology, engineering and mathematics, students gain a deeper conceptual understanding and learn to recognize the relevance of the subjects in relation to each other and to real-world problems [10]. Thus, integrated STEM education has the potential to increase students’ interest in STEM learning [11], as well as to lead to improved achievement [10].
1.2. Evaluating Integrated STEM Education
Despite the promising effects of integrated STEM education and the development of various programs (e.g., [4,12]), less attention has been given to a sound way to evaluate the degree to which students are able to handle interdisciplinary problems by using concepts from different STEM areas. One likely reason for this gap in the literature is that assessing integrated ability in an interdisciplinary STEM context is not straightforward [13]. Existing studies that investigate the effectiveness of integrated STEM (e.g., [10,14,15]) often fail to provide a clear definition of the measured construct. Moreover, little explanation of the integrated nature of the test questions is given. Some researchers do report the use of integrated questions in their studies, but do not include a definition of integrating ability. Depelteau et al. [14], for example, examined the effects of “Symbiosis”, a biology-math integrated curriculum. They developed a concept test, consisting of 33 items that were identified as either “predominantly math”, “predominantly biology”, or as “truly integrated conceptually”. However, no information was given about what exactly constitutes a “truly integrated” question. Kiray and Kaptan [15] investigated the effects of an integrated science and mathematics program on the achievements of eighth-grade students. A multiple-choice test consisting of 30 questions in three categories (“only science”, “integrated science/math” and “overall”) was created. In this study as well, no details about the nature of the integrated questions were provided. The lack of conceptual clarity in previous studies indicates the need for a thorough definition and conceptualization of students’ ability to integrate. Thus, the integrated STEM literature is in need of a clear definition and conceptualization of integrating abilities.
As well as a clear definition of integrating ability, an instrument to assess integrating ability is also needed. Douglas et al. [16] have described the possibilities of assessment practices when it comes to making inferences about learners’ STEM-related competences and their ability to make connections between different STEM subjects. To make claims about the effectiveness of integrated STEM approaches, students’ ability to make connections between the different STEM subjects should be tested with integrated questions. In integrated questions, the content knowledge or application of at least two STEM domains should be utilized to solve the given question. For instance, one should apply the concept of a force (physics) and a vector (mathematics) to obtain a solution. Note that many physics application questions are often integrated questions as they require both physics and mathematics. However, in a true integrated question, both elements are intentionally included, and the student needs to understand both the physical and the mathematical concept to solve the problem. The ability to integrate both concepts in the given context is what eventually constitutes the integrating ability.
Effectiveness studies regarding integrated STEM education have focused mainly on students’ achievement in separate subjects (e.g., [17]), but research into the impact on students’ ability to make connections between disciplines is scarce [7,11]. One of the main challenges is the design of an assessment instrument that covers the integration of the numerous concepts and skills inherent to STEM. To our current knowledge, no validated instrument has been developed that specifically assesses the ability to integrate STEM.
To summarize, the ability to integrate across STEM disciplines has not yet been captured by a clear definition. Moreover, no assessment instrument exists that specifically covers integration ability. The current study aims at developing a theoretically supported and empirically validated instrument to measure students’ ability to solve integrated physics and mathematics problems, thus providing a first step towards fully assessing the effectiveness of integrated STEM instructional approaches (i.e., not only assessing separate STEM contents, but also assessing the ability to integrate STEM contents). To do so, we provide a definition and a framework for integrating ability. Based on this conceptualization, we then present the development and validation of an instrument to contribute to research in STEM education.
1.3. “Integrating Ability”: Definition and Framework
We define integrating ability as the ability to purposefully combine recently acquired knowledge and skills from two or more distinct STEM disciplines to solve a problem in a familiar context that necessitates this very combination to solve it. In this study, “recently” covers the time frame of the ongoing school year and refers to the integration of new learning content (and not already-acquired knowledge and skills) through its application in other disciplines. A “familiar context” is a context that has been addressed during classroom activities. The knowledge and skills mentioned in the definition are those that are typically attributed to discipline-specific curricula but share cross-disciplinarily related underlying concepts.
The ability to solve integrated problems, however, cannot merely be defined as finding the correct solution to integrated problems. To illustrate this issue, we use a metaphor of constructing a wall with building blocks. There are two types of building blocks: high-quality ones which are perfectly rectangular, and ill-shaped ones. Besides the quality of the building blocks, the skill of the builder is also crucial to construct a stable wall: expert builders can arrange the bricks perfectly, while less competent builders cannot. Giving the builders access to the two types of building blocks can result in four different possible outcomes for the wall, as represented in Figure 1: (1) a well-structured wall with good-quality bricks, (2) a well-structured wall with ill-shaped bricks, (3) a badly-structured wall with good-quality bricks and (4) a badly-structured wall with ill-shaped bricks.
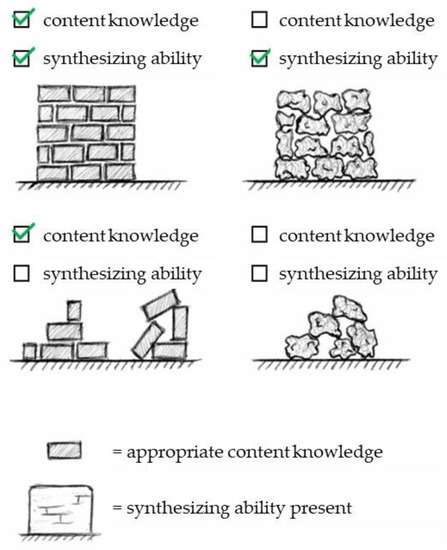
Figure 1.
Constructing a wall with building blocks as a metaphor for integrating ability: four situations.
The ability to build a well-structured wall represents synthesizing ability (i.e., the ability to select and combine STEM concepts) and the good-quality building blocks represent the appropriate content knowledge. Integrating ability combines these two notions in order to correctly solve an integrated problem. In Table 1, the four possible situations are displayed. The presence of synthesizing ability (Table 1, Situation 2) is a condition for integrating ability (Table 1, Situation 1), i.e., employing the present synthesizing ability by making use of the appropriate content knowledge. Theoretically, it is possible for the synthesizing ability to be present, but the appropriate content knowledge not to be present, which would lead to an incorrect answer. We assume that all participants who answer the question correctly find themselves in Situation 1, except where a fortunate guess was made. If we wanted to measure synthesizing ability separately from content knowledge, (a) additional discipline-specific questions that evaluate the presence of the appropriate content knowledge would need to precede the integrated questions, and (b) with the integrated questions, the appropriate content knowledge would need to be provided. Thus, the present instrument only measures integrating ability without making separate statements about synthesizing ability.

Table 1.
Combinations of integrated ability presence and content knowledge appropriateness.
In this study, we focus on students’ integrating ability for physics and mathematics. In Table 2, an example can be found of an integrated physics–math problem, applied to the four possible situations.

Table 2.
Example of an integrated physics–mathematics problem, applied to the four possible situations.
Given the importance of integrated STEM education, and given the need to assess educational initiatives regarding this integrated approach, good instruments to evaluate the effectiveness of these initiatives are necessary. Students’ ability to integrate STEM concepts is one important outcome in the evaluation of educational initiatives regarding integrated STEM. This section has provided a definition and a framework for integrating ability. In the next section, the development of a multiple-choice instrument for integrated physics and mathematics for the ninth grade will be presented.
2. Method
2.1. Developing the Instrument
The goal of the study presented here is to capture students’ integrating ability. The developed multiple-choice test targets students in Grade 9. Consequently, the test is referred to as the Integrated Physics and Mathematics Test for Grade 9, abbreviated “IPM9”. Based on our definition of integrating ability, the integrated content test was developed following the standards for educational and psychological testing [18]. The development process had six different steps, which were based on the standards for educational and psychological testing of the American Psychological Association (APA [18]).
- (1)
- Establishing the test format;
- (2)
- Listing the physics and mathematics concepts that have been introduced in the ongoing school year;
- (3)
- Identifying cross-disciplinary links between these concepts;
- (4)
- Developing draft items that cover these links;
- (5)
- Having experts review these draft items;
- (6)
- Implementing the experts’ feedback.
The IPM9 was developed by a multidisciplinary team consisting of engineers, physicists, educational researchers and pedagogical advisors. Step (1) was performed by a researcher with a background in educational research, who also executed the validation of the instrument, and Steps (2)–(4) and (6) were performed by four researchers with backgrounds in engineering or physics. Step (5) was performed by experts in content and test design. As a first step, the choice for a multiple-choice format was made, in response to the large number of participants. The second step involved listing all the new learning content in physics and mathematics covered during the targeted grade, as can be seen in Table 3.

Table 3.
List of new concepts regarding physics and mathematics.
Once the concepts were listed, the third step was to identify links between these concepts in order to construct integrated items. In the fourth step, 17 questions that combined a physics concept (left column in Table 3) with a mathematical concept (right column in Table 3) were developed. During the fifth step, the drafted items were handed to experts (engineers, physicists and educational advisors). These experts verified the formulation of the items as well as the content validity. The items had to be formulated in an unambiguous way to prevent any misunderstandings or misinterpretations. The difficulty level of the items was also monitored by the experts. The feedback of the experts was implemented in a new version of the items, which was the sixth and final step in the development of the item battery and resulted in an item battery of 16 questions.
In Figure 2, an example of an integrated physics and mathematics item can be found. This item is situated in the domain of mechanics, a context that is familiar to students, since it has been regularly addressed in classroom problems throughout the ongoing school year. To solve the problem, students should determine the resulting force on the tractor, taking into account the nature of forces. They therefore have to apply mathematical ideas concerning vector addition. As illustrated by this solving strategy, students need to combine concepts from both physics and mathematics in an effective manner, hence giving evidence of integrating ability.
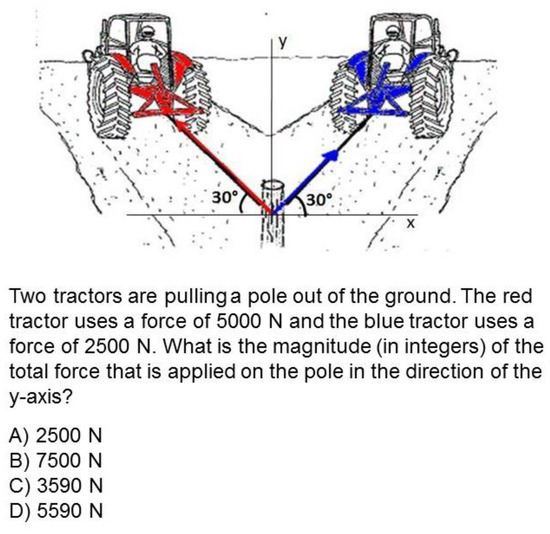
Figure 2.
Example of an integrated physics–math item: the integration of force, vector and cosine.
2.2. Validation of the Instrument
2.2.1. Participants
To validate the developed IPM9 items, a study was conducted among 988 Flemish students (age: M = 13.85, SD = 0.55; gender ratio: boys:girls = 1.56). All participants were in a curriculum with an emphasis on science, technology and mathematics, and attended classes in 42 different schools. All were part of the STEM@School project [4].
2.2.2. Procedure
Before the actual administration, a pilot study was conducted with a smaller group of 372 students in order to investigate the psychometric qualities of the 16 developed items, which resulted in an item battery of 14 remaining questions. Two items were excluded due to insufficient discrimination capability (discrimination value < 0.15). The pilot study was also necessary to ensure the online test functioned well technically, and the questions were understandable.
In the current study, the 14 items of the IPM9 were administered to 988 ninth graders between the beginning and the end of May 2016 (=one month before the end of the ninth grade). The items of the IPM9 were part of an overarching STEM test, concerning several STEM fields. In this overarching test, all taught physics, mathematics, technology and research competences were addressed.
Students completed the online tests in their schools during normal school hours. Eight out of the 14 multiple choice questions were randomly presented to each student, as the IPM9 had to fit into the provided time frame of the overarching STEM test. Students were informed that only one out of the four alternatives was correct. Students could use and integrate their prior content knowledge to solve the problem, as all knowledge and skills were recently acquired during classroom activities. While students could principally utilize all knowledge and skills (including long-acquired knowledge and skills), the questions were designed in such a way that they specifically required more recently acquired knowledge and skills (i.e., acquired in the time frame of the ongoing school year). A paper copy with a list of formulae was provided to the students. The list contained the basic formulae that were needed to solve some of the questions (e.g., the formula to calculate the circumference of a circle) but not relevant to the assessed integrating ability. However, students were not informed where given basic formulae should be utilized. The goal of the list of formulae was to make sure that content knowledge about formulae would not prevent students from giving the right answer. In other words, students still needed to be able to select and integrate the right content knowledge (i.e., synthesizing ability) in order to give the right answer. Students and their parents were provided with information about the aim of the study and with a passive informed consent procedure, approved by an institutional ethical committee, which accorded with the Belgian law on clinical trials.
2.2.3. Analysis of Instrument Validity
Item response theory (IRT) was used to investigate the psychometric qualities of the IPM9, using latent trait models under IRT. The ltm-package of R-4.2.2 (open source software for statistical computing) was used, which is fit for an analysis of multivariate dichotomous data [19]. Item characteristics (i.e., difficulty and discrimination) were analyzed using IRT, with the probability of item responses being regressed on the latent trait “integrating ability”. Items with a discrimination value below 0.15 were removed from the item battery, and IRT was reperformed with the remaining items. After IRT analysis, the reduced version of the item battery was evaluated by the item developers to guarantee the content validity of the scale.
IRT-based models are widely used in psychometric research for the assessment of educational abilities [20]. In IRT, the underlying trait is often referred to as the Greek letter theta (θ), with a mean of zero and a standard deviation of one. In the current validation study, θ is conceptualized as “integrating ability”. The difficulty of an item is the ability required to guarantee a 50% probability of answering the item correctly. Only participants with a high degree of “integrating ability” will be able to answer the difficult items, which implies they will only be answered correctly by a few individuals. Conversely, items with lower difficulty values are likely to be answered correctly by participants with lower ability as well, and thus answered correctly by many participants. Item discrimination, on the other hand, is an index of an item’s capability to differentiate between students in different positions on the latent “integrating ability”. This implies that persons with low ability have a smaller chance of correctly responding than persons of higher ability and vice versa. Items with a high discrimination value are better indicators of “integrating ability” than items with a smaller discrimination value.
Various IRT models exist with different assumptions and parameters. The Rasch model is the most parsimonious IRT model for dichotomous items, and assumes all items have a discrimination index of 1 logit, which is the slope of the item characteristic curve (ICC). A less strict IRT model is the one-parameter logistic model (1-PL model), where the discrimination index can have a value other than 1, and where all items have equivalent discriminations. Within the two-parameter logistic model (2-PL model), all items that fit the model can have different discrimination indices. The three-parameter logistic model (3-PL) includes an item guessing parameter. The model with the best fit for the data was identified by analysis of variance (ANOVA). Once the most suitable model had been selected, the precision of each integrated item was calculated, and the test information function (which presents the degree of precision at different values of “integrating ability”) was requested.
With regard to external validity, convergent validity and discriminant validity were investigated with theoretically related concepts (i.e., physics application and mathematics application) and theoretically unrelated concepts (i.e., technological concepts), respectively.
3. Results
In this study, analysis of variance (ANOVA) showed that the 2-PL model had the best fit for the data. Estimators of the relative quality of the different measurement models can be found in Table 4. After inspection of the infit values (which were close to zero) and outfit values (which were close to one), we concluded that all items fitted well in the chosen model. In Table 5, the discrimination value (α) and difficulty (β) of each item is presented. Five items were omitted due to low discrimination values.

Table 4.
Akaike Information Criterion (AIC), Bayesian Information Criterion (BIC) and Log-Likelihood values for the Rasch model, 1-PL model, 2-PL model and 3-PL model.

Table 5.
RT item parameter estimates for the IPM9: remaining item battery.
The discrimination values for all the nine remaining items were above 0.15 (min. = 0.18, max. = 17.91), which indicated that all items were able to differentiate between students with divergent integrating ability. The discrimination value of Item 3 (α = 17.91) was remarkably high, which positively affected the mean discrimination index of the nine integrating ability items (M = 2.30, SD = 5.52). Difficulty varied between β = −0.92 and β = 5.60, with Item 1 as least difficult and Item 13 as most difficult, respectively.
The precision of the IPM9 can be evaluated by the item information functions that are calculated from the parameters displayed in Table 4. The test information function is the sum of the item information functions and can be found in Figure 3.
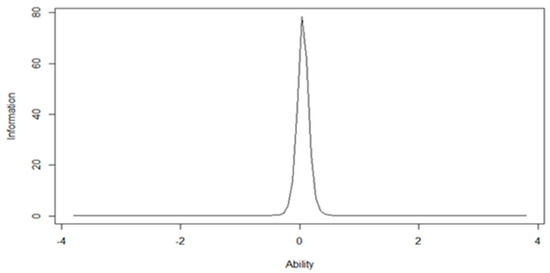
Figure 3.
Test information function by level of integrating ability (θ).
The test information function shows a sharp peak around θ = 0, due to the high discrimination value of Item 3, which has a difficulty of 0.06. This means that the IPM9 is very informative for students with a medium integrating ability.
The content validity of the remaining nine items was assessed by the developers who had constructed the initial items of the IPM9. More specifically, the items needed to cover all the new mathematics and physics learning content of the last school year. The remaining items were still able to cover the definition and the aim of the integrated physics and mathematics test. These results indicate that the IPM9 is a valid test of integrating ability with discriminating items of varying difficulty.
External validity was investigated by comparing the IPM scores of students with scores on physics, mathematics and technological concepts. As physics and mathematics concepts are necessary to solve integrated questions (i.e., the presence of the appropriate content knowledge) but are not sufficient to correctly answer an integrated question, we would expect a weak positive correlation between these outcomes. The ability to answer questions with regard to technological concepts, on the other hand, should be unrelated to integrating ability. Hence, we expect no significant correlation between those constructs. As Table 6 shows, a significant but moderate convergence between the IPM on the one hand and the physics application and mathematics application on the other hand was found. This illustrates that integrating ability is a qualitative different construct than the application of physics or mathematics. No significant correlation with technological concepts was present. Thus, we can conclude that the IPM exhibits satisfactory external validity.

Table 6.
Correlations between IPM, physics application, mathematics application and technological concepts.
4. Discussion
With the increased interest in integrated STEM education, the need has arisen to evaluate students’ abilities relating to integration. This paper provides a first step towards evaluating students’ integrating ability. To accommodate the lack of a definition in the literature, we formulated integrating ability as the ability to purposefully combine recently acquired knowledge and skills from two or more distinct STEM disciplines to correctly solve a problem in a familiar context that necessitates this very combination to solve it. A framework for understanding integrating ability and its components (i.e., synthesizing ability and content knowledge) was also established. As synthesizing ability is difficult to grasp without explicitly providing the necessary content knowledge, we focused on the assessment of integrating ability.
Based on this definition and framework, we developed and validated an evaluation instrument for ninth-grade students. After several steps in the development process, this resulted in the IPM9: an instrument of nine multiple choice items with satisfactory psychometric properties (all items had a satisfactory discrimination value).
4.1. Applications
The definition and framework can be used by researchers and practitioners to develop new instruments regarding the ability to integrate STEM subjects. Since the differences between concepts such as integrating ability, synthesizing ability and content knowledge are clarified, this framework can be beneficial when it comes to making considered conceptual choices. In addition, this conceptual separation reveals which components should be incorporated into a test. For instance, when a researcher aims to capture all the separate components of integrating ability, the test should include discipline-specific content knowledge questions, as well as synthesizing ability questions (which are integrated questions where the appropriate content knowledge is provided). The definition and framework of integrating ability in STEM provide clarity in making decisions regarding the assessment of educational STEM initiatives. Moreover, this definition and framework has the potential to be applicable in a wider context than that of STEM. This approach to integrating ability could also be useful in relation to other subjects.
As for the integration of STEM content, our results indicate that this approach can be used to develop an instrument to test integrating ability regarding physics and mathematics. In this study, this approach resulted in the IPM9, which is a valid and reliable instrument for assessing integrated physics and mathematics for students in the ninth grade. Note that the specific learning goals which are incorporated into the IPM9 are determined by context-dependent STEM curricula. Nevertheless, the IPM9 and its designing process are widely applicable. First, the IPM9 could be useful in a research context that is similar to the one in this study to evaluate educational initiatives regarding integrated STEM. For instance, this test instrument could benefit research that examines differences between STEM learning programs (e.g., traditional disciplinary curriculum versus cross-disciplinary integrated curriculum), such as STEM@School [4]. Second, the theoretical approach and the development process of this test are universally applicable, and the developed framework can be used for constructing similar test instruments for integrating ability in all STEM disciplines and for a broad range of ages.
It should be noted that this instrument is designed to be used as a research instrument, not as an instrument to be adopted in an assessment context in class.
4.2. Limitations and Directions for Future Research
An important characteristic of the IPM9 is its potential to assess integrating ability. We focused on integrating ability (which is the combination of synthesizing ability and content knowledge) since the assessment of synthesizing ability alone is difficult without providing the necessary content knowledge. As a result, in this study, no statements about synthesizing ability could be made. Future studies aiming to distinguish between the different components of integrating ability would need to incorporate separate content knowledge questions. It could be argued that it is difficult to guarantee the presence of integrating ability without explicitly testing content knowledge. However, no correct answer could be obtained without having the appropriate content knowledge (as content knowledge is part of integrating ability); consequently, a correct answer to a question regarding integrating ability implicitly indicates the presence of appropriate content knowledge.
The exception in which a correct answer is given to an integrating ability question without having the appropriate content knowledge is that of a fortunate guess in a multiple-choice test. However, several measures were taken to outweigh the impact of guessing on the test results. First, distractor items were constructed so that the right answer was intuitively not more plausible than the wrong answer. Second, the answer alternatives were presented in a random order to each participant individually. Thus, we eliminated the tendency of item constructors to “hide” the right answer in option C, which could unintentionally nudge guessers to choose this option more often [21]. Third, we also examined whether a three-parameter logistic model (i.e., with an item guessing parameter) better fitted the data, which was not the case. Hence, a more parsimonious model was selected.
A second point of critique relates to the multiple-choice format of the test items, which can essentially only answer the questions, “How many students pass or fail?” and “Which incorrect responses are chosen most?”. It cannot easily answer the question, “Why do students pass or fail?”. Future research could therefore extend this test with student interviews, and request that students to follow a “think aloud” protocol, to gain further insight into how students solve integrated questions.
Finally, it should be apparent that the IPM9 is a suitable test to evaluate the ability to solve integrated physics and mathematics questions, but that it is only one possible instrument to test integrating ability, and therefore not the gold standard for measuring integrating ability in all possible contexts. Researchers should bear in mind that the IPM9 was tested in a specific country, and targeted concepts that were incorporated into the national curricula. In addition, the IPM9 only incorporates physics and mathematics; it does not include any other STEM subjects. Nonetheless, this study provides a definition, a framework and a test construction guideline on which researchers can rely when developing a test to evaluate the integrating ability of students.
5. Conclusions
This study has demonstrated the need for an instrument that can assess the integrating ability of students in STEM subjects. A definition of integrating ability was provided, as well as a theoretical framework. In addition, a test was constructed and validated to determine the integrating ability of students in the ninth grade regarding physics and mathematics. Despite some shortcomings, we believe that the contributions of this framework and instrument could benefit both future research and the evaluation of STEM education initiatives.
Author Contributions
Conceptualization, H.D.L., S.C. and J.D.M.; methodology, H.D.L.; validation, H.D.L., M.D.C. and W.D.; formal analysis, H.D.L.; item construction, S.C., J.D.M., L.G. and L.T.; data curation, H.D.L.; writing—original draft preparation, H.D.L., S.C. and J.D.M.; writing—review and editing, H.D.L.; visualization, J.D.M.; supervision, M.D.C., W.D., F.D., H.K., J.B.-d.P. and P.V.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Agency for Innovation by Science and Technology (IWT).
Institutional Review Board Statement
The study was conducted in accordance with the Declaration of Helsinki, and approved by the Ethics Committee of University of Antwerp and KU Leuven.
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
The data are not publicly available due to privacy and ethical reasons.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Committee on Prospering in the Global Economy of the 21st Century. Rising Above the Gathering Storm; The National Academies Press: Washington, DC, USA, 2007. [Google Scholar]
- World Economic Forum. The Future of Jobs Report 2020; World Economic Forum: Geneva, Switzerland, 2020. [Google Scholar]
- Wang, H.H.; Moore, T.J.; Roehrig, G.H.; Park, M.S. STEM integration: Teacher perceptions and practice. J. Pre-Coll. Eng. Educ. Res. 2011, 1, 1–13. [Google Scholar]
- Knipprath, H.; Thibaut, L.; Buyse, M.P.; Ceuppens, S.; De Loof, H.; De Meester, J.; Goovaerts, L.; Struyf, A.; Boeve-De Pauw, J.; Depaepe, F.; et al. STEM education in Flanders: How STEM@ school aims to foster STEM literacy and a positive attitude towards STEM. IEEE Instrum. Meas. Mag. 2018, 21, 36–40. [Google Scholar] [CrossRef]
- Spikic, S.; Van Passel, W.; Deprez, H.; De Meester, J. Measuring and Activating iSTEM Key Principles among Student Teachers in STEM. Educ. Sci. 2022, 13, 12. [Google Scholar] [CrossRef]
- Sanders, M.E. STEM, STEM education, STEMmania. Technol. Teach. 2008, 68, 20–26. [Google Scholar]
- National Academy of Engineering and National Research Council. STEM Integration in K-12 Education: Status, Prospects and an Agenda for Research; The National Academies Press: Washington, DC, USA, 2014. [Google Scholar] [CrossRef]
- Lederman, N.G.; Niess, M.L. Integrated, interdisciplinary, or thematic instruction? Is this a question or is it questionable semantics? Sch. Sci. Math. 1997, 97, 57–58. [Google Scholar] [CrossRef]
- Roehrig, G.H.; Moore, T.J.; Wang, H.-H.; Park, M.S. Is Adding the E Enough? Investigating the Impact of K-12 Engineering Standards on the Implementation of STEM Integration. Sch. Sci. Math. 2012, 112, 31–44. [Google Scholar] [CrossRef]
- De Loof, H.; Boeve-de Pauw, J.; Van Petegem, P. Integrated STEM education: The effects of a long-term intervention on students’ cognitive performance. Eur. J. STEM Educ.-[Sl] 2022, 7, 1–17. [Google Scholar] [CrossRef] [PubMed]
- De Loof, H.; Boeve-de Pauw, J.; Van Petegem, P. Engaging Students with Integrated STEM Education: A Happy Marriage or a Failed Engagement? Int. J. Sci. Math. Educ. 2022, 20, 1291–1313. [Google Scholar] [CrossRef]
- Aldemir, T.; Davidesco, I.; Kelly, S.M.; Glaser, N.; Kyle, A.M.; Montrosse-Moorhead, B.; Lane, K. Investigating Students’ Learning Experiences in a Neural Engineering Integrated STEM High School Curriculum. Educ. Sci. 2022, 12, 705. [Google Scholar] [CrossRef]
- Becker, K.; Park, K. Effects of integrative approaches among science, technology, engineering, and mathematics (STEM) subjects on students’ learning: A preliminary meta-analysis. J. STEM Educ. 2011, 12, 23–37. [Google Scholar]
- Depelteau, A.M.; Joplin, K.H.; Govett, A.; Miller, H.A.; Seier, E. SYMBIOSIS: Development, implementation and assessment of a model curriculum across biology and mathematics at the introductory level. CBE-Life Sci. Educ. 2010, 9, 342–347. [Google Scholar] [CrossRef] [PubMed]
- Kiray, S.A.; Kaptan, F. The Effectiveness of an Integrated Science and Mathematics Programme: Science-Centred Mathematics-Assisted Integration. Soc. Educ. Stud. 2012, 4, 943–956. [Google Scholar]
- Douglas, K.A.; Gane, B.D.; Neumann, K.; Pellegrino, J.W. Contemporary methods of assessing integrated STEM competencies. In Handbook of Research on STEM Education; Routledge: London, UK, 2020; pp. 234–254. [Google Scholar]
- Turpin, T.J. A Study of the Effects of an Integrated, Activity-Based Science Curriculum on Student Achievement, Science Process Skills and Science Attitudes. Ph.D. Thesis, University of Louisiana, Monroe, LA, USA, 2000. [Google Scholar]
- Eignor, D.R. The standards for educational and psychological testing. In Handbook of Testing and Assessment in Psychology, Volume 1: Test Theory and Testing and Assessment in Industrial and Organizational Psychology; Geisinger, K.F., Bracken, B.A., Carlon, J.F., Hansen, J.-I.C., Kuncel, N.R., Reise, S.P., Rodriguez, M.C., Eds.; American Psychological Association: Washington, DC, USA, 2013; pp. 245–250. [Google Scholar]
- Rizopoulos, D. ltm: An R package for latent variable modeling and item response theory analyses. J. Stat. Softw. 2006, 17, 1–25. [Google Scholar] [CrossRef]
- Crocker, L.; Algina, J. Introduction to Classical and Modern Test Theory; Harcourt Brace Jovanovich: Orlando, FL, USA, 1991. [Google Scholar]
- Obinne, A.D.E. Using IRT in Determining Test Item Prone to Guessing. World J. Educ. 2012, 2, 91–95. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).