1. Introduction
Motivation is a driving force of human achievement. It has been shown to positively influence academic performance, study strategies, and the mental health of students [
1]. If students are stripped of motivation, i.e., if a student obtains the exam key, there is no extrinsic reward to put the time and effort into studying the material. The expectancy value theorem is a psychological model that suggests that an individual’s motivation is affected by the expectation of success at a task and the value that the individual assigns to the outcome [
2].
College is academically challenging, even for the most gifted high school students with strong GPAs, experience in advanced placement (AP) classes, and high American College Test (ACT)/Scholastic Aptitude Test (SAT) scores. Transitioning from high school to university is often met with gaps between students’ expectations and the realities of university life [
3]. The expectancy value theorem comes into play when students believe that their prior experience and study habits are sufficient enough that extra preparation will have no effect on the outcome of their grades [
4]. When this case arises, students’ motivation is depreciated, and grade outcomes are poor [
5].
However, often, failure needs to occur before success can begin. Psychologist K. Anders Ericsson identified the importance of deliberate practice focused on specific elements to lead to expertise. To achieve success after failure, deliberate reflection through investigating and evaluating the root of the failure is needed to affect our future actions [
6]. For example, students who did not achieve their desired grade on an exam reflect on their study habits so that further assessments in the course fulfill their target grade. Without deliberate reflection, students performing poorly would continue their low performance, in turn reducing their motivation to succeed. Often, when students’ motivation drops alongside poor performance, class drop rates skyrocket and students are quick to switch their college plans [
7].
Reflection is not only an important tool used by students but is a must for educators. Research in the field of engineering education has shown that deliberate reflection by educators raises students’ performance [
8]. Using reflection on a departmental level suggests that education with extensive faculty engagement in tune with student’s educational demands raises performance across the department’s curriculum [
9]. Without deliberate reflection, educators with poor performing students will see the trend continue [
10]. This further inhibits student success in future courses by taking away the necessary knowledge needed to perform well [
11]. It is important that we, as educators, identify weaknesses in our course and take the necessary time to revisit the topics that students are struggling with, which can only occur if we take time to deliberately reflect.
The following article focusses on an observational analysis of college freshman who have taken an entry level mechanical engineering course, titled mechanical engineering problem solving with computer application. The research question of interest in this analysis was how the impact of an early learning assessment effects student motivation. The students in the course were tested on introductory static and mechanic topics in exams that will be referenced as the static body and mechanics of materials exams, respectively. They were assigned assessments during the semester that utilized these topics to write programs that computed forces and stresses using GUIs. It is hypothesized that students were motivated to achieve their desired grade outcome due to the poor performance results of the first exam.
2. Materials and Methods
The observational analysis featured data analysis taken following the computer application to mechanics exam. The analysis featured students in the mechanical engineering problem solving with computer application course, which was dominated by male students, accounting for 90% of the class profile. The analysis was restricted to students taking their first mechanical engineering course. A total of 60 students’ data were included in the study. This pool of students was gathered from two in person class sections, either from three 52 minute or two 75 minute class meeting schedules. Students who dropped the course through the university registrar had their scores removed from the pool of data. The data from the class were compiled following course completion and identifying factors, such as age, gender, etc., were removed from the pool of variables prior to analysis. The data encompassed two exams and five learning assessments. The students were taught topic material during lectures and assigned homework following the topic conclusion. The lectures involved introducing equations alongside engineering application examples. In class assignments were given to students in groups as problem solving exercises. The homework was assigned to students for practice, which is important for the growth of their engineering problem solving skills. There was no preview exam or concluding exam to measure the students’ growth.
The first exam tested the students’ ability to solve static body forces by using moments and free body diagrams. The students were provided schematics that detailed the angles and forces applied to the bodies. They were asked to compute the reaction forces at the supports, as well as the resultant forces with the direction. To solve the problem, students were to sum forces, take moments, and apply applicable trigonometric identities, such as the law of cosines or the law of sines. The information tested in the static body exam covered the topics that should have been covered in high school physics and trigonometry, as well as new static body material. The time allocated to the students was 50 min to solve three problems.
The second exam in the mechanical engineering problem solving with computer application course tested the new mechanics of material topics, such as the factor of safety and shear and tensile stresses. Similar to the static body exam, the mechanical systems had forces applied to a static body and tested the students’ knowledge of material stress equations and factors of safety. The problems required the students to understand the effect of how the applied force effects the resultant force on specific supports. It also made use of free body diagrams and the taking of moments at key points, which had been previously covered in the static body exam. The mechanics exam builds off the statics exam by requiring a baseline of knowledge of the material, but also requires knowledge of new mechanics of materials topics taught during the lecture. The approach to the exams was similar. Students who understood how to approach an engineering problem in the first exam would have similar success in the second mechanics of material exam. The mechanics of materials exam was taken in a 50 min period with three problems, congruent to the setup of the first statics exam.
The engineering approach assessment assigned to the students tested their knowledge of static bodies and the mechanics of materials, a continuation of the material assessed in the exams. This project was an assessment of the students’ ability to approach multi-faceted engineering problems and extrapolate conclusions based on computational results. The assessment asked the students to create four designs with respect to their factor of safety in worst-case loading conditions of a bridge repair system. They were given a set of material and loading requirements and tasked with computing the tensile stress and factors of safety of the cables of their bridge repair system designs. Following their computations, they were asked to analyze their results and give their recommendation on which design should be utilized.
Throughout the course, the students utilized Matlab to solve the computer application assessments. The GUI assessment was used to introduce the power of computer applications to engineering. The students were assessed on their understanding of the ways to implement a GUI to execute functions. The students were presented with a scenario of a truck with forces applied against the vehicle as it remained in equilibrium. They were asked to use their knowledge of introductory physics and statics to find the resultant force of a vehicle when force is applied to the truck engine. This involved summing forces in the x and y directions to yield a resultant force. The engineering application was then modeled by the students through writing a Matlab script that would output the trucks’ resultant force when the user is prompted by a GUI that asks for the drag, mass, and force of wind on the truck.
The control structure assessment introduced control statements and plots to the students. They were tasked with asking the user for inputs of a linear equation and outputting the x-intercept. In order to complete the task, the students depended on their knowledge of basic algebra while integrating step wise control statements to identify the x-intercept. The project assessed the students’ understanding of for loops and the generation of plots. The nested function assessment required a similar mathematical background, this time integrating a quadratic equation to find the roots. The students used menus to input the user’s values of the quadratic equation and outputted the plot and data. Correct scripts involved writing if statements in combination with while loops, for loops, and plots. The nested function assessment tested the students’ ability to implement if statements to their prior knowledge of while loops and GUIs.
Finally, the computer application to mechanics assessment solved for the stress, strain, and material response based on the user inputs and its units. The assignment required students to create functions that would solve for the stress, strain, and response, which would then be called the main function. The students relied on their mechanics of material knowledge to achieve the correct responses. They also had to create separate control statements pending the user’s unit input. This assignment was the final testament of the students’ knowledge of Matlab and the mechanics of materials. A summary of the exams and assessments is included in
Table 1.
The observational analysis of the course focused on the assignments that were directly related to the static and mechanics of material principals. The highlighted assignments that were analyzed from the effect of the static body exam scores were the mechanics of materials exam, engineering approach, GUI, control structures, nested functions, and the computer application of mechanics assessment. Assessments for learning are important as it gauges students’ academic standing and progress [
12,
13]. Students who did poorly in the static body exam, grades under the required passing score (%60), were tracked in the assignments to compile data to present evidence for the study. The data were then analyzed to see if there had been any effect on student performance.
3. Results and Discussion
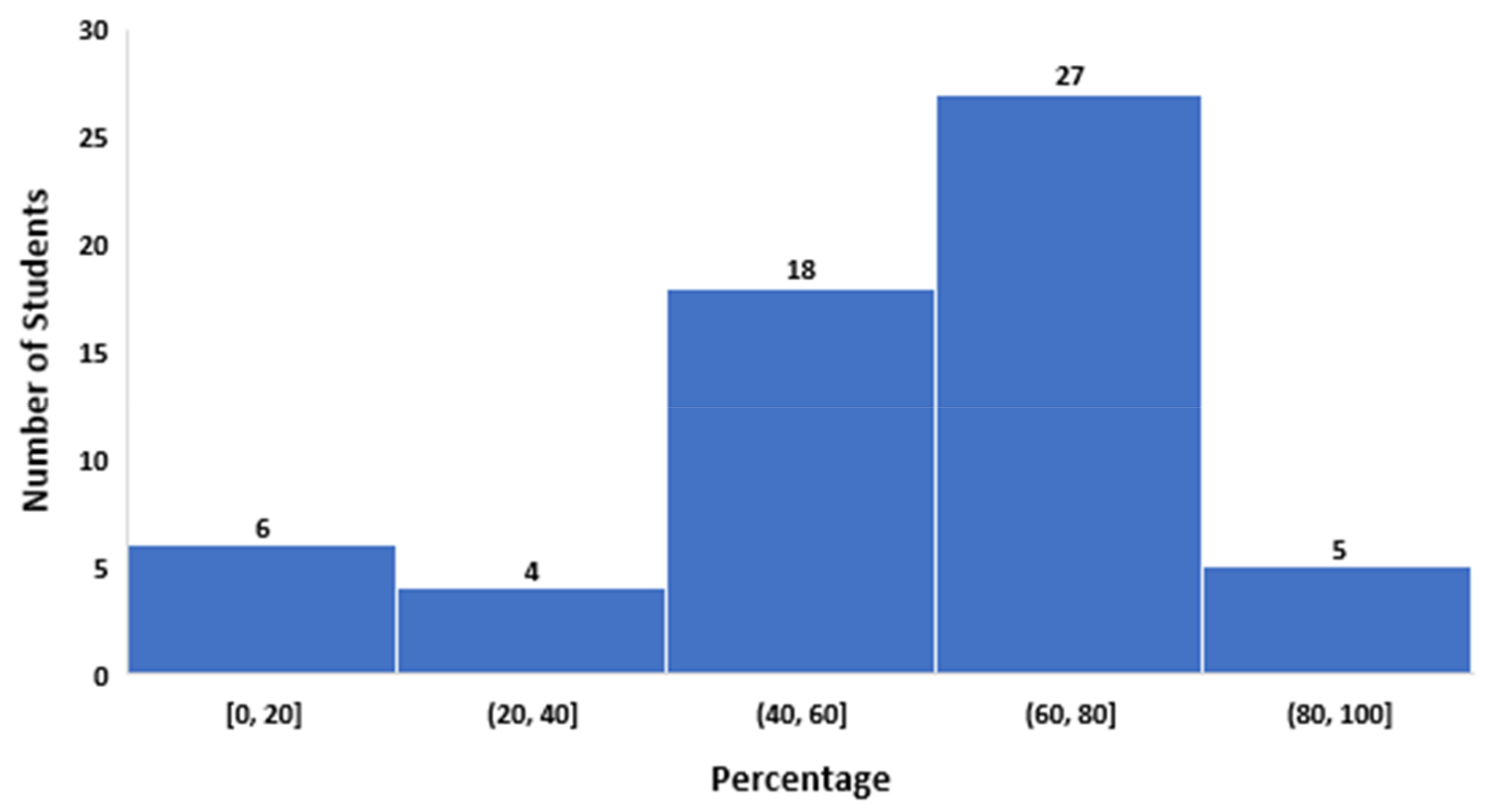
The fall of 2022 mechanical engineering problem solving with computer application course focused on preparing students for future static and mechanic courses that are a part of the core engineering curriculum at Iowa State University. The first exam taken by the students focused on introductory static material, showed disappointing results, with the average of the exam falling below passing at 58.075%. A breakdown of the statics exam scores is shown below, in
Figure 1.
The troubling statistics display that a majority of the class did not receive a passing grade. It can be concluded from these results that the students were not prepared to take their first mechanical engineering exam, as the average was not enough to pass.
Table 2, below, details the grade breakdown of the exam, showing that 28 out of the 60 students did not pass the exam.
Table 2 notes that nearly half the students in the course (46.6%) failed the first exam and only 5% were able to achieve the grade mark of an A. The data shown were enough of a cause to begin an observation study, detailing the remaining assessment and exam scores. The students were placed in 20% increment grade bands to track their results for the remainder of the course. The highlighted assignments, which focused on preparing students for future engineering coursework, were detailed above and analyzed in comparison to the first exam taken in the course. The results of the remaining coursework dramatically increased. The average of the second mechanics of materials exam showed great progress in student preparation and performance.
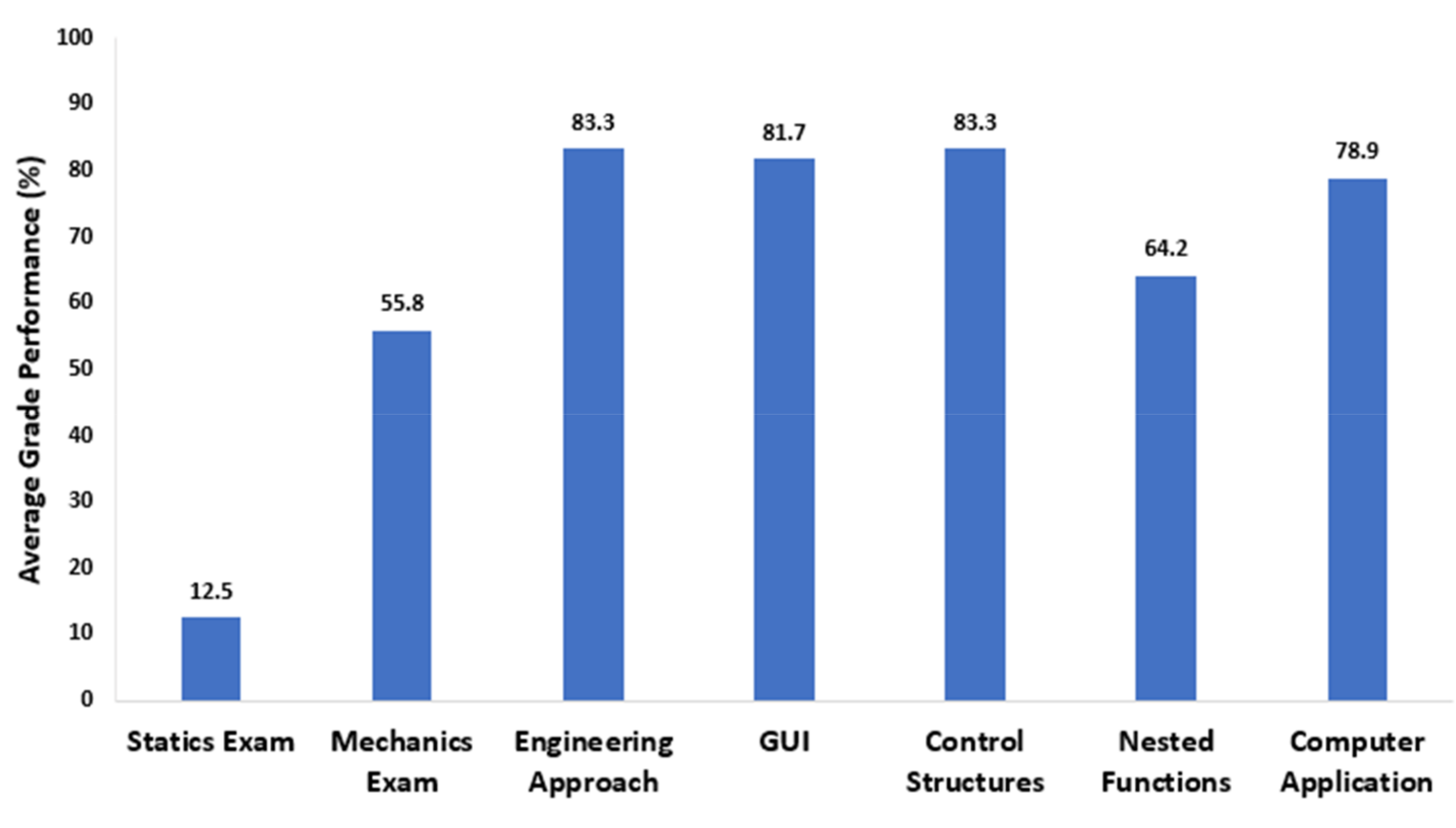
Figure 2, below, details the grade improvement in students who received a score between 0 and 20 percent.
Figure 2 shows a clear increase in the average academic performance for the 0 to 20 grade band following the first statics exam. The results show that the students who received a grade between 0 to 20 percent on the first statics exam increased their second exam score by, on average, 43.333%, however, still averaging an exam grade that does not pass the course. The remaining assessments also increased significantly, with all following assessments reaching higher than a passing grade. This suggests that the first statics exam significantly increased the student performance. The next grade band from the first statics exam, between 21 and 40 percent, is tracked and detailed in
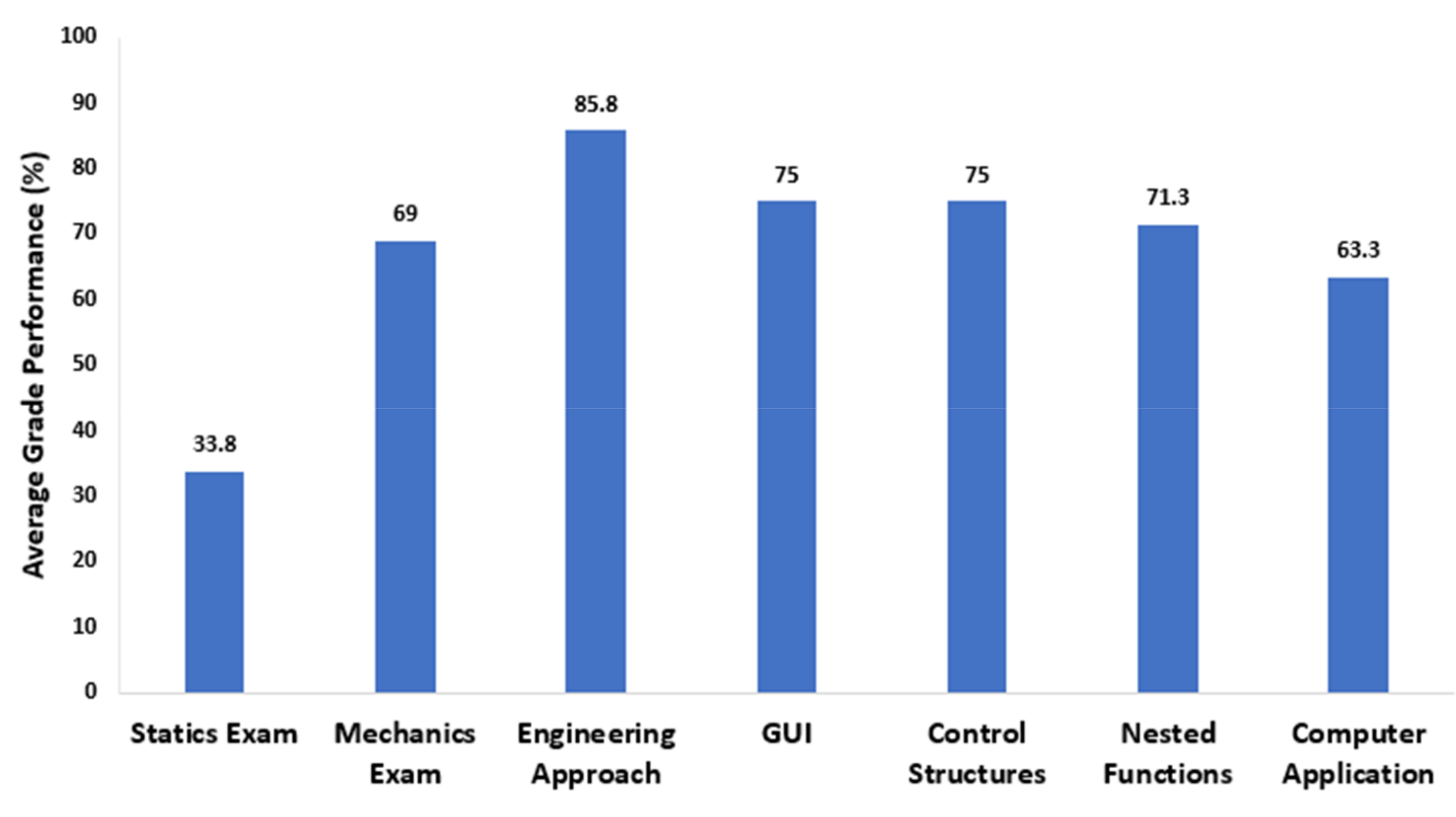
Figure 3.
The results from this band are similar to the previous figure, with noted increases in the second mechanics exam yielding positive grade increases. The increase, on average, was 35.25% for the second mechanics exam. The assessment grades also improved; however, the averages were skewed by a student in the band not completing the final assessments, the nested functions and computer application. This hinders the data in supporting the hypothesis; however, it can still be seen that a significant increase occurred in the performance from the first statics exam. It can be concluded from
Figure 3 that the student performance rose following the first statics exam. The next and final grade band that did not receive a passing score from the first statics exam, between 41 and 60 percent, is tracked and detailed in
Figure 4.
A similar story is detailed in
Figure 4. The students who received a failing grade in the range between 40 and 60 percent increased their remaining curriculum focused grades significantly, with a rise of 30.0555%, on average, for the second mechanics exam. The results of the assessments also showed improved growth. The assessments increased to an average of 92.64% for the grade bands’ remaining scores, peaking with an impressive 100% for the engineering approach assessment. This signifies clear growth in academic performance following the first statics exam.
Overall, the students did significantly better in the rest of the course when faced with failing grades in the first statics exam. The second mechanics exam results were higher across the board, with the average in the second exam being nearly 1.5 times higher than the first statics exam, at 82.74% for the class and 74.7% for the students who did not pass the first exam. The score and grade distribution of the exam is broken down in
Figure 5 and
Table 3.
The results in
Table 3 show that only 8.33% of the students failed the second mechanics exam, a drop from the noted 46.7% fail rate of the first statics exam. The number of students receiving an A on the exams also increased dramatically. The first static exam reported that only 5% of students achieved the grade mark A, whereas the second mechanics exam had 43.3% of students achieving this mark. Without motivation from a poor performance, the grades on the first exam were the result of students not allocating proper preparation time to the course. The students were likely unwilling to put in the necessary time to achieve a successful grade because the class work taught students the topics needed to problem solve, but not the problem-solving ability needed to be a successful engineer. The class work and lectures prior to the first statics exam allowed the students to bounce ideas off one another, but did not task them with applying what they had learned in an independent exam environment. As the material was introductory, the students were likely not concerned with developing engineering problem solving skills, resulting in the poor performance on the first statics exam. Exam preparation was essential in building the students’ engineering problem solving skills. Practicing more problems before the exams grew students’ ability to independently work through complicated topics, further developing their engineering mindset. The increases found following the first statics exam were indicative of the dedication that the students had put into preparing for the second mechanics exam. The students with a continued poor performance likely had not mastered the topics of the second exam, an indicator that either they had not put in a sufficient amount of practice or that they were uninterested in achieving success in the course, a barrier that cannot be removed from prior failure in the first statics exam. The students were willing to put in more effort following a poor performance to achieve their desired grade outcome. The results of this exam were accompanied by an increase in student engagement with the teaching assistant. To this end, the students began coming to office hours only after the first exam was taken. In preparation for the second mechanics exam, students came to him asking for extra practice material, for which he supplied textbook problems to study from. The students’ attendance also increased when the assessments drew near. The students began routinely attending his office hours asking for help with Matlab, specifically inquiring about the upcoming assessment and the knowledge needed to perform well. During these hours, he was able to revisit prior topics that students had struggled with, such as the creation of nested functions. With this in mind, the uptick in exam scores and student engagement supports the hypothesis that the students were alarmed by the first exam scores and took the course more seriously; however, it is of importance to address the confounding variables. Students entering Iowa State Universities mechanical engineering department are placed into learning communities to gain familiarity with students that they will be taking classes with until graduation. These communities often become a vital source for students’ academic improvement as they group students with the same professors and class. Students use these communities to form study groups, which can be highly correlated to growth in academic performance [
14,
15]. This community meets once a week, and by the time the second exam was taken, the students were likely to be more comfortable reaching out to one another outside of the class setting. This can support the hypothesis that the first statics exam startled the students into improving their preparation, but it also disrupts a clear connection between the static exams’ effect on the students’ performance as building relationships helps students succeed, regardless of in the outcome of the first exam. If students did not adjust well within their communities prior to the exam, the learning community variable has no effect on their performance on future exams or assessments. The second confounding variable is that the material in the remaining assessments and exams did not build off the first statics exam, but introduced other engineering topics. Statics and mechanics are closely related; however, students can perform well in mechanics with a baseline knowledge of statics. In the second mechanics exam, the students needed to rely on basic concepts, such as summing forces to find a resultant, but they did not need to master the material from the first exam to do well [
16]. The assessments tell a similar story; the students needed to have the underlying knowledge from the first statics exam, but the assessments were focused on computer applications and were graded as such. This variable is important to consider; however, even though the topics were different, if the students learned how to think and approach an engineering problem in one topic, they should have been able to approach the rest of the course work similarly. This negates the significance of the material being different, but the variable is needed to be addressed for a full picture of the class performance. The final confounding variables that need to be addressed is that the students and the professor adapted to the course. Many students’ previous experience from high school is that the teaching environment is a place to acquire facts and skills; however, in college, the environment switches and requires students to take responsibility for thinking through and applying what they have learned [
17,
18]. This tends to be difficult for college freshman, but as the course continued and students grew their relationships in their communities, their learning style adjusted and their performance in exams rose. The poor performance on the first exam was a catalysis for students that were looking to succeed. The performance indicated to students that more time would need to be dedicated to mastering the topics of the course, not just relying on examples from lectures. The increased time developed the students’ engineering problem solving skills. which explains the increase in the grade performances on the remaining exams and assessments. The professor also adjusted the course to benefit the students’ learning. Following the first statics exam, the professor analyzed the results and took time to discuss the material that they would like to spend more time on. The class spent the next week of lectures following the first statics exam reviewing the material to ensure that they were prepared for the upcoming material. This review involved fielding questions from students on prior material and executing example problems to clear up confusion. Questions regarding the best ways to prepare for the upcoming exams were answered by the professor, with detailed feedback on what students have found beneficial in the past. They were instructed to review the prior lecture examples, as well as the outlined problems from the textbook to develop their engineering problem solving skills. Understanding what students needed help with resolved the gaps in their knowledge following the first exam, which promoted their success in the future material.
4. Conclusions
The results of the class support the hypothesis that students were motivated to achieve their desired grade outcome due to their poor performance results following the first exam. The students who received a grade between 0 to 20 on the first statics exam significantly improved in the second mechanics of materials exam, by an average of 43.333%. This theme continued for the students who received a score between 20 to 40, improving, on average, by 35.25%. Finally, this theme is seen in the grade band ranging between 40 and 60, improving with an average increase of 30.055%. The assessment scores increased across the class, with an average of 91.095%, with each grade band increasing their score from the first statics exam. The increase in the scores point towards the hypothesis that students were motivated to significantly improve their performance; however, the confounding variables must be considered for a full picture.
The variables that effected the students’ performance focused on both outside and in-class changes. The students in the learning community had the benefit of their classmates for exam and assessment preparation. They were able to reach out to others for support, helping them improve their academic performance. The material being slightly different also influenced the scores. The students could improve their scores in the remaining material without mastering the topics of the first statics exam. Although the material did not directly build on the statics exam, if students learned how to think and approach an engineering problem in the first topic, they were able to approach the rest of the course work with success, thus negating the effect of the material switch. Finally, adapting the course to fit the needs of all may have been critical to the success in the rest of the course. Students entering college are often taught facts and skills without the need to take responsibility for thinking through and applying their knowledge. As the semester continued, the students and the professor were able to adjust their ways of learning and teaching to make the semester as successful as possible for each party. This entailed analyzing the strengths and weakness of the classes’ performance on the first exam by the professor and applying extra time to improve the students’ learning. It also involved students taking responsibility for their learning. Overall, the confounding variables were determined to not affect our hypothesis. The students growing their relationships and using them to study is a result of the urgency imposed by poor performance and can be correlated to rejuvenated motivation following the first exam. The material being slightly different, but having the same approach in each assessment, nullifies the material being a variable that influences the improved academic performance. Finally, student and professor adaptation was concluded to be a byproduct of the poor initial performance. The disappointing grades from the first statics exam caused both the educators and students to change their behaviors, leading to more dedication to the course. This variable would not have been introduced without the alarming results of the first exam and can be tied to the improvement in both the students and professor’s motivation to succeed. The study could be improved to negate the confounding variables. To isolate the variable tested in our hypothesis, it is difficult to analyze the effect without having an entrance and exit exam. Previous studies that have investigated student performance used standardized exams to structure their observational analysis [
19]. Including exams that can be compared to each other allowed for better repeatability and concise conclusions. In future studies, having an introductory and concluding exam that assesses the students’ prior and subsequent knowledge would allow us to draw a clearer correlation of the academic progress in regard to the first statics exam performance. This study could also be improved by asking students who did poorly on the first exam to highlight the factors that influenced their performance for the rest of the semester. Finally, having a future study that focuses on the academic growth of a unified topic would reject any potential influence of the material on improving exam and assessment performance.
Ultimately, the poor performance on the first statics exam set the tone for the course. The students realized that they needed to approach the class more seriously if they wanted to achieve their desired grade. Following the first statics exam, the scores dramatically increased on the remaining exams and assessments. Attendance to office hours also increased, with students asking for extra preparation material, showing that they were motivated to prepare for the upcoming assessments. With the combination of the internal and external factors, the students dedicated more effort to achieve success. As the grades increased dramatically, the hypothesis that students were motivated to achieve their desired grade due to a reality check in the first statics exam is accepted.