Helping Students Become Proficient Problem Solvers Part II: An Example from Waves
Abstract
1. Introduction
2. Methodology
2.1. Participants
2.2. Interventions Used in This Study
2.3. Problem Used, Correct Solution, and Grading Criteria
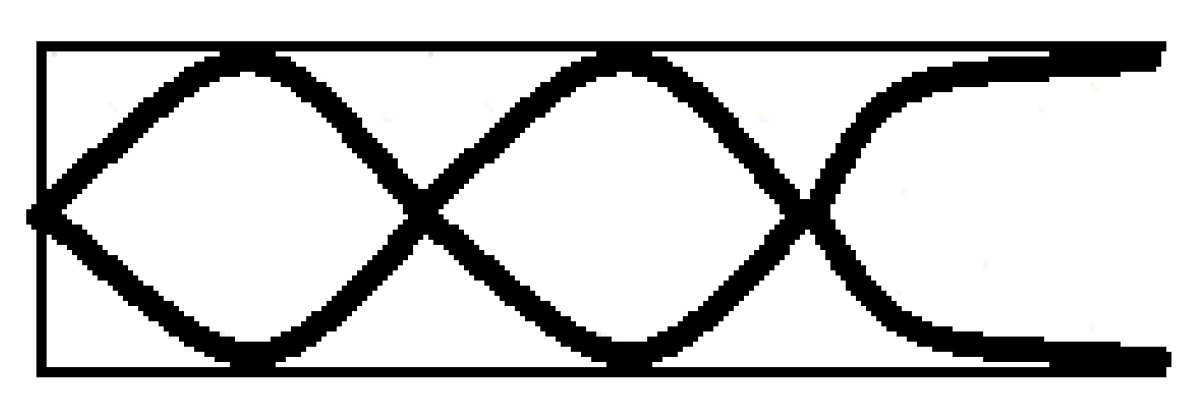
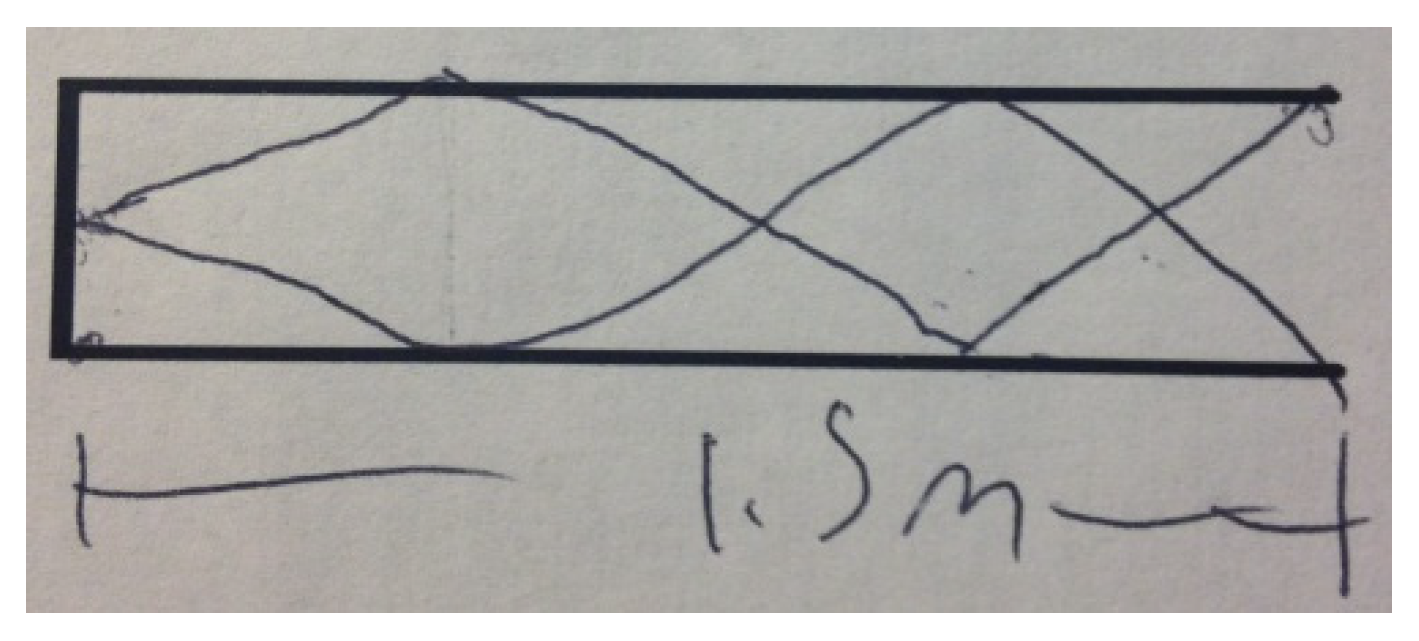
- Quiz problem: “A tube with air is open at only one end and has a length of 1.5 m. This tube sustains a standing wave at its third harmonic. What is the distance between a node and the adjacent antinode?”. We note that students in the DO group were provided with a diagram of an empty tube in addition to this problem statement. Students in the PO intervention were explicitly asked to draw a diagram after the above problem statement, and students in the comparison group (NS) only saw the problem statement.
- Midterm problem: The midterm exam problem was identical to the quiz problem except that the tube was open at both ends instead of just one end. All students received the problem statement only. No diagram or prompt to draw a diagram was included.
2.4. Research Questions
3. Results
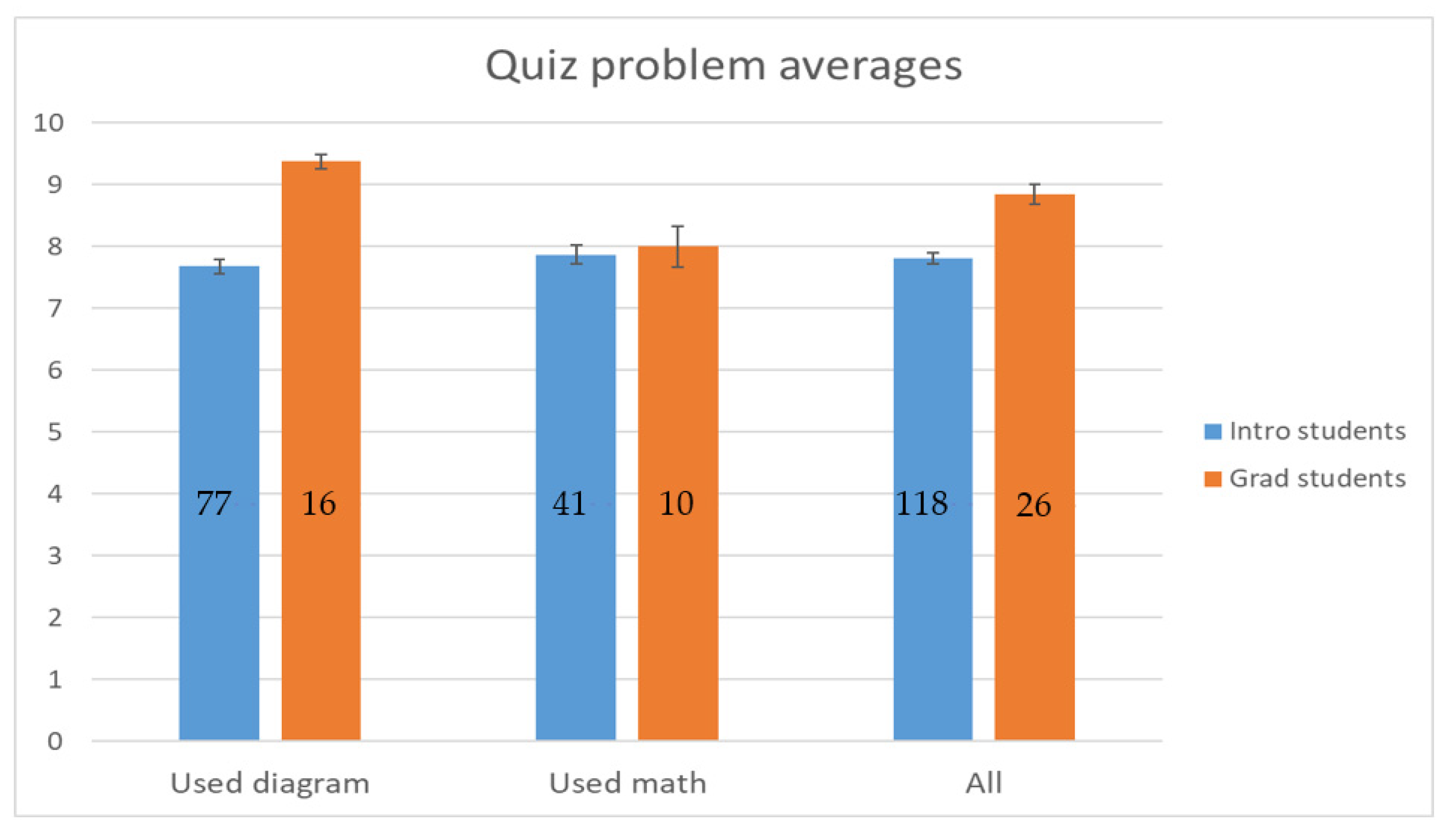
3.1. RQ1: How Do Introductory Students Compare to Graduate Students (Ph.D. Students in Their First Year) in Their Problem-Solving Performance?
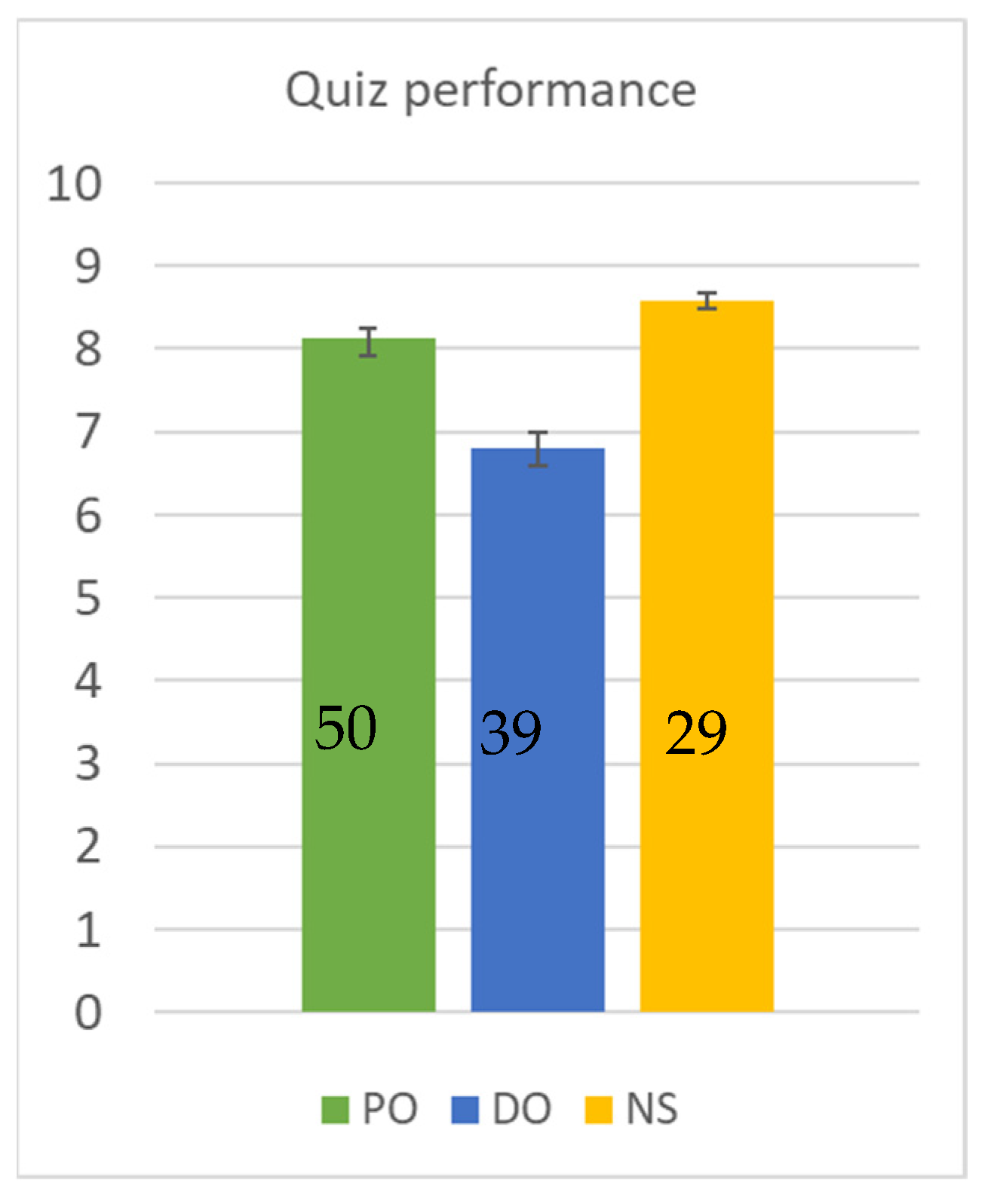
3.2. RQ2: How Do the Different Interventions Impact Students’ Problem-Solving Performance?
3.3. RQ3: How Does Drawing a Diagram Impact Students’ Problem-Solving Performance?
3.4. RQ4: How Facile Are Students at Using the Mathematical Approach to Solve the Problem? What Are Some Common Difficulties Students Exhibit When Using the Mathematical Approach?
3.5. RQ5: What Are Some Common Difficulties with Students’ Use of Diagrams to Solve These Problems?
3.6. Other Findings from Interviews
4. Summary and Discussion
5. Acknowledgements
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Heller, J.; Reif, F. Prescribing effective human problem-solving processes: Problem description in physics. Cogn. Instruct. 1984, 1, 177–216. [Google Scholar] [CrossRef]
- Larkin, J.; Simon, H. Why a diagram is (sometimes) worth ten thousand words. Cogn. Sci. 1987, 11, 65–99. [Google Scholar] [CrossRef]
- Van Heuvelen, A. Overview, case study physics. Am. J. Phys. 1991, 59, 898–907. [Google Scholar] [CrossRef]
- Reif, F. Millikan lecture 1994: Understanding and teaching important scientific thought processes. Am. J. Phys. 1994, 63, 17–32. [Google Scholar] [CrossRef]
- Zhang, J. The nature of external representations in problem solving. Cogn. Sci. 1997, 21, 179–217. [Google Scholar] [CrossRef]
- van Someren, M. Learning with Multiple Representations; Elsevier Science: New York, NY, USA, 1998. [Google Scholar]
- Singh, C. Assessing student expertise in introductory physics with isomorphic problems, Part I: Performance on a non-intuitive problem pair from introductory physics. Phys. Rev. ST-PER 2008, 4, 010104. [Google Scholar]
- Lin, S.-Y.; Maries, A.; Singh, C. Student difficulties in translating between mathematical and graphical representations in introductory physics. AIP Conf. Proc. 2013, 1513, 250. [Google Scholar]
- Dunbar, K. Problem Solving. In A Companion to Cognitive Science; Bechtel, W., Graham, G., Eds.; Blackwell Publishing: Malden, MA, USA, 2017; pp. 289–298. [Google Scholar]
- Maries, A.; Singh, C. Do students benefit from drawing productive diagrams themselves while solving introductory physics problems? The case of two electrostatics problems. Eur. J. Phys. 2018, 39, 015703. [Google Scholar] [CrossRef]
- Bajracharya, R.; Emigh, P.J.; Manogue, C.A. Students’ strategies for solving a multirepresentational partial derivative problem in thermodynamics. Phys. Rev. PER 2019, 15, 020124. [Google Scholar] [CrossRef]
- Morphew, J.; Gladding, G.E.; Mestre, J.P. Effect of presentation style and problem-solving attempts on metacognition and learning from solution videos. Phys. Rev. PER 2020, 16, 010104. [Google Scholar] [CrossRef]
- Burkholder, E.; Miles, J.K.; Layden, T.J.; Wang, K.D.; Fritz, A.V.; Wieman, C.E. Template for teaching and assessment of problem solving in introductory physics. Phys. Rev. PER 2020, 16, 010123. [Google Scholar] [CrossRef]
- Price, A.; Kim, C.J.; Burkholder, E.W.; Fritz, A.V.; Wieman, C.E. A detailed characterization of the expert problem-solving process in science and engineering: Guidance for teaching and assessment. CBE-Life Sci. Educ. 2021, 20, ar43. [Google Scholar] [CrossRef]
- Conceição, T.; Baptista, M.; Ponte, J.P. Lesson Study as a Means to Change Secondary Preservice Physics Teachers’ Practice in the Use of Multiple Representations in Teaching. Sci. Educ. 2021, 11, 791. [Google Scholar] [CrossRef]
- Ibrahim, B.; Ding, L. Sequential and simultaneous synthesis problem solving: A comparison of students’ gaze transitions. Phys. Rev. PER 2021, 17, 010126. [Google Scholar] [CrossRef]
- Vignal, M.; Wilcox, B. Investigating unprompted and prompted diagrams generated by physics majors during problem solving. Phys. Rev. PER 2022, 18, 010104. [Google Scholar] [CrossRef]
- Koenig, K.; Maries, A.; Teese, R.; Chabot, M. Promoting problem solving through interactive video-enhanced tutorials. Phys. Teach. 2022, 60, 331–334. [Google Scholar] [CrossRef]
- Reinhard, A.; Felleson, A.; Turner, P.C.; Green, M. Assessing the impact of metacognitive postreflection exercises on problem-solving skillfulness. Phys. Rev. PER 2022, 18, 010109. [Google Scholar] [CrossRef]
- Testa, I.; Catena, D. High School Students’ Performances in Transitions between Different Representations of Linear Relationships in Mathematics and Physics. Sci. Educ. 2022, 12, 776. [Google Scholar] [CrossRef]
- Kirstein, J.; Nordmeier, V. Multimedia representation of experiments in physics. Eur. J. Phys. 2007, 28, S115–S126. [Google Scholar] [CrossRef]
- Coletta, V.P.; Phillips, J.A. Developing Thinking & Problem Solving Skills in Introductory Mechanics. AIP Conf. Proc. 2010, 1289, 13–16. [Google Scholar]
- Clement, J. Observed methods for generating analogies in scientific problem solving. Cogn. Sci. 1998, 12, 563–586. [Google Scholar] [CrossRef]
- DeMul, F.; Batlle, C.M.; DeBruijn, I.; Rinzema, K. How to encourage university students to solve physics problems requiring mathematical skills: The ‘adventurous problem solving’ approach. Eur. J. Phys. 2003, 25, 51–61. [Google Scholar]
- Marušić, M.; Erceg, N.; Sliško, J. Partially specified physics problems: University students’ attitudes and performance. Eur. J. Phys. 2011, 32, 711–722. [Google Scholar] [CrossRef]
- Bolton, J.; Ross, S. Developing students’ physics problem-solving skills. Phys. Educ. 1997, 32, 176–185. [Google Scholar] [CrossRef]
- Mashood, K.; Singh, V. Large-scale studies on the transferability of general problem-solving skills and the pedagogic potential of physics. Phys. Educ. 2013, 48, 629–635. [Google Scholar] [CrossRef]
- Van Heuvelen, A.; Zou, X. Multiple representations of work-energy processes. Am. J. Phys. 2001, 69, 184–194. [Google Scholar] [CrossRef]
- Lesh, R.; Post, T.; Behr, M. Representations and translating between representations in mathematics learning and problem solving. In Problems of Representations in the Teaching and Learning of Mathematics; Janvier, C., Ed.; Lawrence Erlbaum Associates: Hillsdale, NJ, USA, 1987; p. 33. [Google Scholar]
- Meltzer, D. Relation between students’ problem solving performance and representational mode. Am. J. Phys. 2005, 73, 463–478. [Google Scholar] [CrossRef]
- Ibrahim, B.; Rebello, N.S. Representational Task Formats and problem solving strategies in kinematics and work. Phys. Rev. ST-PER 2012, 8, 010126. [Google Scholar] [CrossRef]
- Larkin, J. Skilled problem solving in physics: A hierarchical planning approach. J. Struct. Learn. 1980, 6, 121–130. [Google Scholar]
- Harper, K. Student problem-solving behaviors. Phys. Teach. 2006, 44, 250–251. [Google Scholar] [CrossRef]
- McDermott, L.; Rosenquist, M.L.; van Zee, E. Student difficulties in connecting graphs and physics: Examples from kinematics. Am. J. Phys. 1987, 55, 503–513. [Google Scholar] [CrossRef]
- Mason, A.; Singh, C. Helping students learn effective problem solving strategies by reflecting with peers. Am. J. Phys. 2010, 78, 748–754. [Google Scholar] [CrossRef]
- Court, J.E. Free-body diagrams. Phys. Teach. 1993, 31, 104–108. [Google Scholar] [CrossRef]
- Rosengrant, D.; Van Heuvelen, A.; Etkina, E. Free-body diagrams-Necessary or sufficient. AIP Conf. Proc. 2005, 790, 177–200. [Google Scholar]
- Mazens, K. Conceptual change in physics: Naïve representations of sounds in 6- to 10-year old children. In Proceedings of the EARLI Conference, Athens, Greece, 25–31 August 1997; pp. 1–9. [Google Scholar]
- Mazens, K.; Lautrey, J. Conceptual change in physics: Children’s naïve representations of sound. Cogn. Dev. 2003, 18, 159–176. [Google Scholar] [CrossRef]
- Eshach, H.; Schwartz, J. Sound Stuff? Naïve materialism in middle-school students’ conceptions of sound. Int. J. Sci. Educ. 2007, 28, 733–764. [Google Scholar] [CrossRef]
- Boyes, E.; Stanisstreet, M. Development of pupils’ ideas about seeing and hearing–The path of light and sound. Res. Sci. Technol. Educ. 1991, 9, 223–251. [Google Scholar] [CrossRef]
- Houle, M.E.; Barnett, G.M. Students’ Conceptions of Sound Waves Resulting from the Enactment of a New Technology-Enhanced Inquiry-Based Curriculum on Urban Bird Communication. J. Sci. Educ. Technol. 2008, 17, 242–251. [Google Scholar] [CrossRef]
- Katsarova, K.; Raykova, Z. An opportunity to study mechanical waves by the use of inquiry methods. AIP Conf. Proc. 2021, 2075, 180019. [Google Scholar]
- Linder, C.J.; Erickson, G.L. A study of tertiary physics students’ conceptualizations of sound. Int. J. Sci. Educ. 1989, 11, 491–501. [Google Scholar] [CrossRef]
- Linder, C.J. University physics students’ conceptualizations of factors affecting the speed of sound propagation. Int. J. Sci. Educ. 1993, 15, 655–662. [Google Scholar] [CrossRef]
- Rhoads, T.R.; Roedel, R.J. The wave concept inventory–A cognitive instrument based on Bloom’s taxonomy. In Proceedings of the 28th Annual Frontiers in Education Conference, Tempe Mission Palms Hotel, Tempe, AZ, USA, 4–7 November 1999. [Google Scholar]
- Tumanggor, A.M.R.; Supahar; Kuswanto, H.; Ringo, E.S. Using four-tier diagnostic test instruments to detect physics teacher candidates’ misconceptions: Case of mechanical wave concepts. J. Phys. Conf. Ser. 2020, 1440, 012059. [Google Scholar] [CrossRef]
- Reiner, M.; Slotta, J.D.; Chi, M.T.H.; Resnick, L.B. Naïve physics reasoning: A commitment to substance-based conceptions. Cogn. Instruct. 2000, 18, 1–34. [Google Scholar] [CrossRef]
- Volfson, A.; Eshach, H.; Ben-Abu, Y. Preliminary development of a simple statistical tool for estimating mental model states from a diagnostic test. Phys. Rev. Phys. Educ. Res. 2021, 17, 023105. [Google Scholar] [CrossRef]
- Wittmann, M.; Steinberg, R.N.; Redish, E.F. Understanding and affecting student reasoning about sound waves. Int. J. Sci. Educ. 2003, 25, 991–1013. [Google Scholar] [CrossRef]
- Wittmann, M.; Steinberg, R.N.; Redish, E.F. Making sense of how students make sense of mechanical waves. Phys. Teach. 1999, 37, 15–16. [Google Scholar] [CrossRef]
- Hrepic, Z.; Zollman, D.; Rebello, N.S. Identifying students’ mental models of sound propagation: The role of conceptual blending in understanding conceptual change. Phys. Rev. ST-PER 2010, 6, 020114. [Google Scholar] [CrossRef]
- Wittman, M. Making Sense of How Students Come to an Understanding of Physics: An Example from Mechanical Waves. Ph.D. Thesis, University of Maryland, College Park, MD, USA, December 1998. [Google Scholar]
- Tongchai, A.; Sharma, M.D.; Johnston, I.D.; Arayathanitkul, K.; Soankwam, C. Developing, evaluating and demonstrating the use of a conceptual survey of mechanical waves. Int. J. Sci. Educ. 2009, 31, 2437. [Google Scholar] [CrossRef]
- Tongchai, A.; Sharma, M.D.; Johnston, I.D.; Arayathanitkul, K.; Soankwam, C. Consistency of students’ conceptions of wave propagation: Findings from a conceptual survey in mechanical waves. Phys. Rev. ST-PER 2011, 7, 020101. [Google Scholar] [CrossRef]
- Frank, B.W.; Kanim, S.E.; Gomez, L.S. Accounting for variability in student responses to motion questions. Phys. Rev. ST-PER 2008, 4, 020102. [Google Scholar] [CrossRef]
- Clough, E.E.; Driver, R. A study of consistency in the use of students’ conceptual frameworks across different task contexts. Sci. Educ. 1986, 70, 473–496. [Google Scholar] [CrossRef]
- Palmer, D. How consistently do students use their alternative conceptions? Res. Sci. Educ. 1993, 23, 228–235. [Google Scholar] [CrossRef]
- Finegold, M.; Gortsky, P. Students’ concepts of force as related to physical systems: A search for consistency. Int. J. Sci. Educ. 1991, 13, 97–113. [Google Scholar] [CrossRef]
- Watson, J.R.; Prieto, T.; Dillon, J.S. Consistency of students’ explanations about combustion. Sci. Educ. 1997, 81, 425–443. [Google Scholar] [CrossRef]
- Kryjevskaia, M.; Stetzer, M.R.; Heron, P. Student difficulties measuring distances in terms of wavelength: Lack of basic skills or failure to transfer? Phys. Rev. ST-PER 2013, 9, 010106. [Google Scholar] [CrossRef]
- Singh, C. Assessing student expertise in introductory physics with isomorphic problems, Part II: Examining the effect of some potential factors on problem solving and transfer. Phys. Rev. ST-PER 2008, 4, 010105. [Google Scholar]
- Glass, G.V.; Hopkins, K.D. Statistical Methods in Education & Psychology; Allyn & Bacon: Boston, MA, USA, 1996. [Google Scholar]
- Maries, A.; Singh, C. Case of two electrostatics problems: Can providing a diagram adversely impact introductory physics students’ problem solving performance? Phys. Rev. PER 2018, 14, 010114. [Google Scholar] [CrossRef]
- Heckler, A.F. Some consequences of prompting novice physics students to construct force diagrams. Int. J. Sci. Educ. 2010, 32, 1829. [Google Scholar] [CrossRef]
- Chen, Z.; Demirci, N.; Choi, Y.-J.; Pritchard, D.E. To draw or not to draw? Examining the necessity of problem diagrams using massive open online course experiments. Phys. Rev. ST-PER 2017, 13, 010110. [Google Scholar] [CrossRef]
- Redish, E.F. Using math in physics: Overview. Am. J. Phys. 2021, 59, 314. [Google Scholar] [CrossRef]
- Tuminaro, J.; Redish, E.F. Understanding students poor performance on mathematical problem solving in physics. J. AIP Conf. Proc. 2004, 720, 11. [Google Scholar]
- Redish, E.F. Problem solving and the use of math in physics courses. In Proceedings of the World View on Physics Education Conference, Delhi, India, 21–26 August 2005. [Google Scholar]
- Sweller, J. Cognitive load during problem solving: Effects on learning. Cogn. Sci. 1988, 12, 257–285. [Google Scholar] [CrossRef]
- National Research Council. Knowing What Students Know: The Science and Design of Educational Assessment. Committee on the Foundations of Assessment; Pellegrino, J.W., Chudowsky, N., Glaser, R., Eds.; National Academy Press: Washington, DC, USA, 2001. [Google Scholar]


| Correct Ideas | ||
| Section 1 | Used equation provided | 1 p |
| Section 2 | Chose or | 1 p |
| Section 3 | Wrote | 3 p |
| Section 4 | Solved for correctly | 2 p |
| Section 5 | Calculated distance between node and antinode by dividing by 4 | 2 p |
| Section 6 | Correct unit for answer | 1 p |
| Incorrect Ideas | ||
| Section 1 | Used incorrect equation | −1 p |
| Section 2 | Chose value for n other than 3 or 5 | −1 p |
| Section 3 | 3.1 Did not write | −3 p |
| 3.2 Tried to write down , but made a mistake (i.e., wrote something like ) | −2 p | |
| Section 4 | 4.1 Did not solve for | −2 p |
| 4.2 Used a value for other than that for sound wave | −1 p | |
| 4.3 Made an error and obtained incorrect | −1 p | |
| 4.4 Unclear how was calculated or other error | −1 p | |
| Section 5 | Did not divide λ by 4 to obtain the answer or did not obtain an answer | −2 p |
| Section 6 | Incorrect units | −1 p |
| Correct Ideas | ||
| Section 1 | Drew a diagram of the correct standing wave | 4 p |
| Section 2 | Used diagram correctly to obtain the answer | 5 p |
| Section 3 | Correct units for answer | 1 p |
| Incorrect Ideas | ||
| Section 1 | 1.1 Diagram is a sinusoidal wave that does not clearly indicate locations of nodes and antinodes | −1 p |
| 1.2 Diagram has either two nodes or two antinodes at the endpoints | −2 p | |
| 1.3 Diagram does not represent the third or fifth harmonic * (if endpoints are a node and an antinode) | −1 p | |
| 1.4 Diagram does not represent the third harmonic ** (if endpoints are both nodes or both antinodes) | −1 p | |
| Section 2 | 2.1 Answer found is not the distance between a node and an antinode, nor the distance between two nodes (based on student’s diagram) | −4 p |
| 2.2 Used diagram correctly, but found the distance between two nodes | −2 p | |
| 2.3 Unclear how answer was obtained or other error | −1 p | |
| Section 3 | Incorrect units | −1 p |
| Quiz | PO-DO | DO-NS | PO-NS |
|---|---|---|---|
| 0.016 | <0.001 | 0.414 |
| Quiz | |
| 1. Solved correctly for λ (algebraically, i.e., without plugging in a value for v) | 48% |
| 2. Did not solve correctly for λ or did not solve at all | 10% |
| 3. Solved for λ by plugging in a numerical value for v | 41% |
| Midterm | |
| 1. Solved correctly for λ (algebraically, i.e., without plugging in a v) | 36% |
| 2. Did not solve correctly for λ or did not solve at all | 8% |
| 3. Solved for λ by plugging in a numerical value for v | 55% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maries, A.; Singh, C. Helping Students Become Proficient Problem Solvers Part II: An Example from Waves. Educ. Sci. 2023, 13, 138. https://doi.org/10.3390/educsci13020138
Maries A, Singh C. Helping Students Become Proficient Problem Solvers Part II: An Example from Waves. Education Sciences. 2023; 13(2):138. https://doi.org/10.3390/educsci13020138
Chicago/Turabian StyleMaries, Alexandru, and Chandralekha Singh. 2023. "Helping Students Become Proficient Problem Solvers Part II: An Example from Waves" Education Sciences 13, no. 2: 138. https://doi.org/10.3390/educsci13020138
APA StyleMaries, A., & Singh, C. (2023). Helping Students Become Proficient Problem Solvers Part II: An Example from Waves. Education Sciences, 13(2), 138. https://doi.org/10.3390/educsci13020138





