Correlation between High School Students’ Computational Thinking and Their Performance in STEM and Language Courses
Abstract
:1. Introduction
2. Theoretical Perspectives
2.1. Computational Thinking and STEM Courses
2.2. Computational Thinking and Language Courses
2.3. CT Assessment Tool
2.4. Research Objectives
- Is our research tool adequate for estimating students’ CT levels?
- Is there a correlation between students’ CT levels and their performance in STEM and language courses?
- Is there a detectable correlation between students’ CT levels and their choice of field of study?
3. Method
3.1. Settings and Participants
3.2. Research Tool for Assessing CT Skills
3.3. The Strategy of Data Analysis
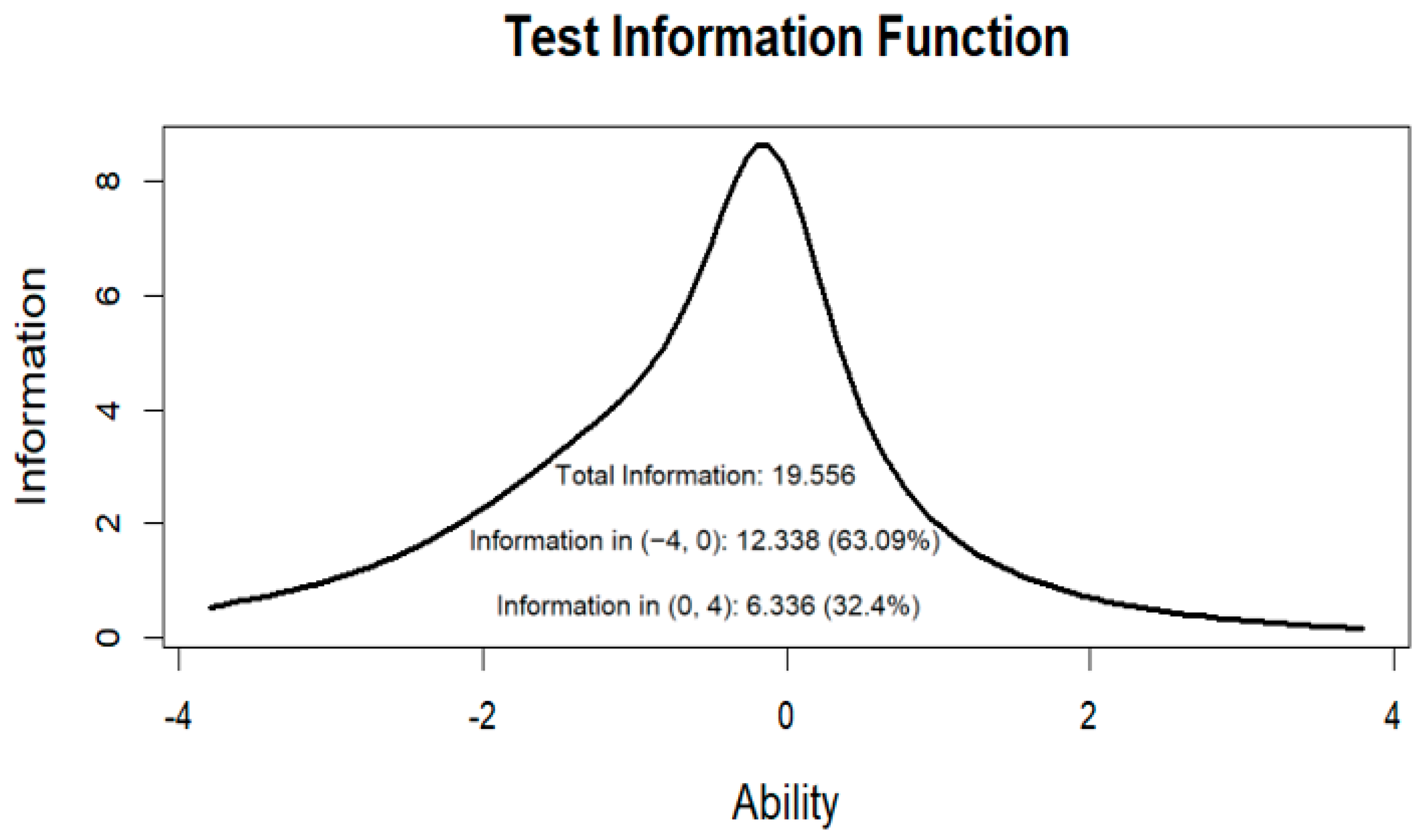
4. Results
5. Discussion
6. Limitations and Implications
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A




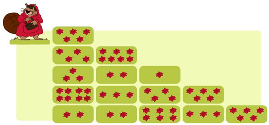

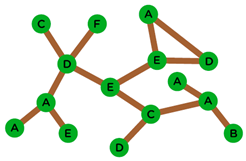
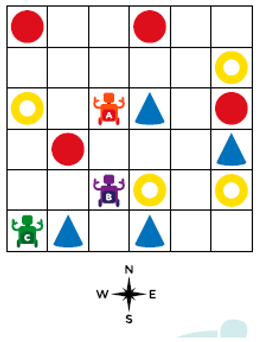
- Alice is sitting directly opposite David.
- Henry is sitting between Greta and Eugene.
- Franny is not next to Alice or David.
- There is one person between Greta and Claire.
- Eugene is sitting immediately to David’s left.



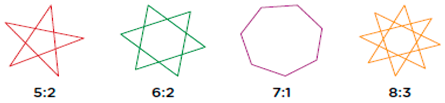
- Some points on the star.
- A number indicating if a line from a point is drawn to the nearest point (1), the second closest point (the number 2), etc.

References
- Arastoopour, G.I.; Dabholkar, S.; Bain, C.; Woods, P.; Hall, K.; Swanson, H.; Horn, M.; Wilensky, U. Modeling and measuring high school students’ computational thinking practices in science. J. Sci. Educ. Technol. 2020, 29, 137–161. [Google Scholar] [CrossRef]
- Barr, V.; Stephenson, C. Bringing computational thinking to K-12: What is Involved and what is the role of the computer science education community? ACM Inroads 2011, 2, 48–54. [Google Scholar] [CrossRef]
- Brief, R.R.; Ly, J.; Ion, B.A. A Framework for K-12 Science Education: Practices, Crosscutting Concepts, and Core Ideas; National Academies Press, National Research Council US: Washington, DC, USA, 2012. [Google Scholar]
- Cutumisu, M.; Adams, C.; Lu, C. A scoping review of empirical research on recent computational thinking assessments. J. Sci. Educ. Technol. 2019, 28, 651–676. [Google Scholar] [CrossRef]
- González, M.R. Computational thinking test: Design guidelines and content validation. In Proceedings of the EDULEARN15 Conference, Barcelona, Spain, 6–8 July 2015; pp. 2436–2444. [Google Scholar]
- Grover, S.; Pea, R. Computational thinking in K-12: A review of the state of the field. Educ. Res. 2013, 42, 38–43. [Google Scholar] [CrossRef]
- Gouws, L.A.; Bradshaw, K.; Wentworth, P. Computational thinking in educational activities: An evaluation of the educational game light-bot. In Proceedings of the 18th ACM Conference on Innovation and Technology in Computer Science Education, Canterbury, UK, 1–3 July 2013; pp. 10–15. [Google Scholar]
- National Research Council US. Report of a Workshop on the Scope and Nature of Computational Thinking; National Academies Press: Washington, DC, USA, 2010.
- National Research Council US. Report of a Workshop on the Pedagogical Aspects of Computational Thinking; National Academies Press: Washington, DC, USA, 2011.
- National Research Council US. Next Generation Science Standards: For States, by States. 2013. Available online: https://nap.nationalacademies.org/catalog/18290/next-generation-science-standards-for-states-by-states/ (accessed on 20 July 2022).
- Wang, C.; Shen, J.; Chao, J. Integrating computational thinking in stem education: A literature review. Int. J. Sci. Math. Educ. 2021, 20, 1949–1972. [Google Scholar] [CrossRef]
- Weintrop, D.; Beheshti, E.; Horn, M.; Orton, K.; Jona, K.; Trouille, L.; Wilensky, U. Defining computational thinking for mathematics and science classrooms. J. Sci. Educ. Technol. 2016, 2, 127–147. [Google Scholar] [CrossRef]
- Werner, L.; Denner, J.; Campe, S.; Kawamoto, D.C. The fairy performance assessment: Measuring computational thinking in middle school. In Proceedings of the 43rd ACM Technical Symposium on Computer Science Education, Raleigh, NC, USA, 29 February–3 March 2012; pp. 215–220. [Google Scholar]
- Wing, J.M. Computational thinking. Commun. ACM 2006, 49, 33–35. [Google Scholar] [CrossRef]
- Bower, M.; Wood, L.N.; Lai, J.W.; Highfield, K.; Veal, J.; Howe, C.; Lister, R.; Mason, R. Improving the computational thinking pedagogical capabilities of schoolteachers. Aust. J. Teach. Educ. 2017, 42, 53–72. [Google Scholar] [CrossRef]
- Heintz, F.; Mannila, L.; Färnqvist, T. A review of models for introducing computational thinking, computer science and computing in K-12 education. In Proceedings of the 2016 IEEE Frontiers in Education Conference (FIE), Erie, PA, USA, 12–15 October 2016; pp. 1–9. [Google Scholar]
- Hsu, Y.C.; Irie, N.R.; Ching, Y.H. Computational thinking educational policy initiatives (CTEPI) across the globe. TechTrends 2019, 63, 260–270. [Google Scholar] [CrossRef]
- Kafai, Y.B.; Proctor, C. A Revaluation of Computational Thinking in K-12 Education: Moving Toward Computational Literacies. Educ. Res. 2022, 51, 146–151. [Google Scholar] [CrossRef]
- Lockwood, J.; Mooney, A. Computational thinking in education: Where does it fit? A systematic literary review. arXiv 2017, arXiv:1703.07659. [Google Scholar] [CrossRef]
- Mannila, L.; Dagiene, V.; Demo, B.; Grgurina, N.; Mirolo, C.; Rolandsson, L.; Settle, A. Computational thinking in K-9 education. In Proceedings of the Working Group Reports of 2014 on Innovation & Technology in Computer Science Education Conference, Uppsala, Sweden, 23–25 June 2014; pp. 1–29. [Google Scholar]
- Mohaghegh, M.; McCauley, M. Computational Thinking: The Skill Set of the 21st Century. Int. J. Comput. Sci. Inf. Technol. 2016, 7, 1524–1530. [Google Scholar]
- Nordby, S.K.; Bjerke, A.H.; Mifsud, L. Computational thinking in the primary mathematics classroom: A systematic review. Digit. Exp. Math. Educ. 2022, 8, 27–49. [Google Scholar] [CrossRef]
- Settle, A.; Franke, B.; Hansen, R.; Spaltro, F.; Jurisson, C.; Rennert-May, C.; Wildeman, B. Infusing computational thinking into the middle- and high-school curriculum. In Proceedings of the 17th ACM Annual Conference on Innovation and Technology in Computer Science Education, Haifa, Israel, 3–5 July 2012; pp. 22–27. [Google Scholar]
- Voogt, J.; Fisser, P.; Good, J.; Mishra, P.; Yadav, A. Computational thinking in compulsory education: Towards an agenda for research and practice. Educ. Inf. Technol. 2015, 20, 715–728. [Google Scholar] [CrossRef]
- Yadav, A.; Hong, H.; Stephenson, C. Computational thinking for all: Pedagogical approaches to embedding 21st century problem solving in K-12 classrooms. TechTrends 2016, 60, 565–568. [Google Scholar] [CrossRef]
- Yadav, A.; Good, J.; Voogt, J.; Fisser, P. Computational thinking as an emerging competence domain. In Competence-Based Vocational and Professional Education; Springer: Cham, Switzerland, 2017; pp. 1051–1067. [Google Scholar] [CrossRef]
- Papert, S. Mindstorms: Children, Computers, and Powerful Ideas; Basic Books: New York, NY, USA, 1980. [Google Scholar]
- Çoban, E.; Korkmaz, Ö. An alternative approach for measuring computational thinking: Performance-based platform. Think. Ski. Creat. 2021, 42, 100929. [Google Scholar] [CrossRef]
- García-Peñalvo, F.J.; Cruz-Benito, J. Computational thinking in pre-university education. In Proceedings of the Fourth International Conference on Technological Ecosystems for Enhancing Multiculturality, Salamanca, Spain, 2–4 November 2016; pp. 13–17. [Google Scholar]
- Gouws, L.A.; Bradshaw, K.; Wentworth, P. First year student performance in a test for computational thinking. In Proceedings of the South African Institute for Computer Scientists and Information Technologists Conference, East London, South Africa, 7–9 October 2013; pp. 271–277. [Google Scholar]
- Korkmaz, Ö.; Xuemei, B.A.İ. Adapting computational thinking scale (CTS) for Chinese high school students and their thinking scale skills level. Particip. Educ. Res. 2019, 6, 10–26. [Google Scholar] [CrossRef]
- Shute, V.J.; Sun, C.; Asbell-Clarke, J. Demystifying computational thinking. Educ. Res. Rev. 2017, 22, 142–158. [Google Scholar] [CrossRef]
- Poulakis, E.; Politis, P. Computational thinking assessment: Literature review. In Research on E-Learning and ICT in Education; Tsiatsos, T., Demetriadis, S., Mikropoulos, A., Dagdilelis, V., Eds.; Springer Nature: Berlin, Germany, 2021; pp. 111–128. [Google Scholar] [CrossRef]
- Tang, X.; Yin, Y.; Lin, Q.; Hadad, R.; Zhai, X. Assessing computational thinking: A systematic review of empirical studies. Comp. Educ. 2020, 148, 103798. [Google Scholar] [CrossRef]
- Weintrop, D.; Beheshti, E.; Horn, M.S.; Orton, K.; Trouille, L.; Jona, K.; Wilensky, U. Interactive assessment tools for computational thinking in high school STEM classrooms. In Proceedings of the International Conference on Intelligent Technologies for Interactive Entertainment, Chicago, IL, USA, 9–11 July 2014; pp. 22–25. [Google Scholar]
- Wing, J.M. Computational Thinking Benefits Society. In 40th Anniversary Blog of Social Issues in Computing; DiMarco, J., Ed.; Academic Press: New York, NY, USA, 2014; Volume 2014, Available online: http://socialissues.cs.toronto.edu/index.html%3Fp=279.html (accessed on 28 March 2023).
- Brennan, K.; Resnick, M. New frameworks for studying and assessing the development of computational thinking. In Proceedings of the 2012 Annual American Educational Research Association Meeting, Vancouver, BC, Canada, 13–17 April 2012; p. 25. [Google Scholar]
- Denner, J.; Werner, L.; Ortiz, E. Computer games created by middle school girls: Can they be used to measure understanding of computer science concepts? Comp. Educ. 2012, 58, 240–249. [Google Scholar] [CrossRef]
- Barr, D.; Harrison, J.; Conery, L. Computational thinking: A digital age skill for everyone. Learn. Lead. Technol. 2011, 38, 20–23. [Google Scholar]
- Selby, C.; Woollard, J. Computational Thinking: The Developing Definition; University of Southampton, e-prints: Southampton, UK, 2013. [Google Scholar]
- Yadav, A.; Mayfield, C.; Zhou, N.; Hambrusch, S.; Korb, J.T. Computational thinking in elementary and secondary teacher education. ACM Trans. Comput. Educ. 2014, 14, 1–16. [Google Scholar] [CrossRef]
- Siekmann, G. What is STEM? The Need for Unpacking its Definitions and Applications; National Centre for Vocational Education Research (NCVER): Adelaide, Australia, 2016. [Google Scholar]
- Institute of Educational Policy (IEP). Primary and Secondary Education Programs of Studies. Available online: http://iep.edu.gr/el/nea-programmata-spoudon-arxiki-selida (accessed on 20 July 2022).
- Aho, A.V. Computation and computational thinking. Comp. J. 2012, 55, 832–835. [Google Scholar] [CrossRef]
- CSTA Standards Task Force. [Interim] CSTA K-12 Computer Science Standards; CSTA: New York, NY, USA, 2016. [Google Scholar]
- Google. Exploring Computational Thinking. Available online: https://edu.google.com/resources/programs/exploring-computational-thinking/ (accessed on 20 July 2022).
- Theodoropoulou, I.; Lavidas, K.; Komis, V. Results and prospects from the utilization of Educational Robotics in Greek Schools. Technol. Knowl. Learn. 2021, 28, 225–240. [Google Scholar] [CrossRef]
- Blum, W.; Ferri, R.B. Mathematical modelling: Can it be taught and learnt? J. Math. Modell. Appl. 2009, 1, 45–58. [Google Scholar]
- Gravemeijer, K.; Doorman, M. Context problems in realistic mathematics education: A calculus course as an example. Educ. Stud. Math. 1999, 39, 111–129. [Google Scholar] [CrossRef]
- Hiebert, J.; Carpenter, T.P.; Fennema, E.; Fuson, K.; Human, P.; Murray, H.; Olivier, A.; Wearne, D. Problem solving as a basis for reform in curriculum and instruction: The case of mathematics. Educ. Res. 1996, 25, 12–21. [Google Scholar] [CrossRef]
- Hu, C. Computational thinking: What it might mean and what we might do about it. In Proceedings of the 16th Annual Joint Conference on Innovation and Technology in Computer Science Education, Darmstadt, Germany, 27–29 June 2011; pp. 223–227. [Google Scholar]
- Kallia, M.; van Borkulo, S.P.; Drijvers, P.; Barendsen, E.; Tolboom, J. Characterizing computational thinking in mathematics education: A literature-informed Delphi study. Res. Math. Educ. 2021, 23, 159–187. [Google Scholar] [CrossRef]
- Lockwood, E.; DeJarnette, A.F.; Asay, A.; Thomas, M. Algorithmic Thinking: An Initial Characterization of Computational Thinking in Mathematics. In Proceedings of the Annual Meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education, Tucson, AZ, USA, 3–6 November 2016. [Google Scholar]
- Polya, G. How to Solve it: A New Aspect of Mathematical Method; Princeton University Press: Princeton, NJ, USA, 2004; Volume 85. [Google Scholar]
- Gilbert, J.K. Models and modelling: Routes to more authentic science education. Int. J. Sci. Math. Educ. 2004, 2, 115–130. [Google Scholar] [CrossRef]
- Larkin, J.H.; McDermott, J.; Simon, D.P.; Simon, H.A. Models of competence in solving physics problems. Cogn. Sci. 1980, 4, 317–345. [Google Scholar] [CrossRef]
- Orban, C.M.; Teeling-Smith, R.M. Computational thinking in introductory physics. Phys. Teach. 2020, 58, 247–251. [Google Scholar] [CrossRef]
- Reif, F.; Heller, J.I. Knowledge structure and problem solving in physics. Educ. Psychol. 1982, 17, 102–127. [Google Scholar] [CrossRef]
- Heller, J.I.; Reif, F. Prescribing effective human problem-solving processes: Problem description in physics. Cognit. Instr. 1984, 1, 177–216. [Google Scholar] [CrossRef]
- Sengupta, P.; Dickes, A.; Farris, A. Toward a phenomenology of computational thinking in STEM education. Comput. Think. STEM Discip. 2018, 49–72. [Google Scholar] [CrossRef]
- ISTE; CSTA. Operational Definition of Computational Thinking for K-12 Education. 2011. Available online: https://cdn.iste.org/www-root/Computational_Thinking_Operational_Definition_ISTE.pdf?_ga=2.26204856.423629428.1680452395-598677210.1667674549 (accessed on 20 July 2022).
- Lu, J.J.; Fletcher, G.H. Thinking about computational thinking. In Proceedings of the 40th ACM Technical Symposium on Computer Science Education, Chattanooga, TN, USA, 4–7 March 2009; pp. 260–264. [Google Scholar]
- Parsazadeh, N.; Cheng, P.Y.; Wu, T.T.; Huang, Y.M. Integrating computational thinking concept into digital storytelling to improve learners’ motivation and performance. J. Educ. Comput. Res. 2021, 59, 470–495. [Google Scholar] [CrossRef]
- Nesiba, N.; Pontelli, E.; Staley, T. DISSECT: Exploring the relationship between computational thinking and English literature in K-12 curricula. In Proceedings of the 2015 IEEE Frontiers in Education Conference (FIE), El Paso, TX, USA, 21–24 October 2015; pp. 1–8. [Google Scholar]
- Rottenhofer, M.; Sabitzer, B.; Rankin, T. Developing Computational Thinking skills through modeling in language lessons. Open Educ. Stud. 2021, 3, 17–25. [Google Scholar] [CrossRef]
- Sabitzer, B.; Demarle-Meusel, H.; Jarnig, M. Computational thinking through modeling in language lessons. In Proceedings of the 2018 IEEE Global Engineering Education Conference (EDUCON), Santa Cruz de Tenerife, Spain, 17–20 April 2018; pp. 1913–1919. [Google Scholar]
- De Paula, B.H.; Burn, A.; Noss, R.; Valente, J.A. Playing Beowulf: Bridging computational thinking, arts and literature through game-making. Int. J. Child Comput. Interact. 2018, 16, 39–46. [Google Scholar] [CrossRef]
- López, A.R.; García-Peñalvo, F.J. Relationship of knowledge to learn in programming methodology and evaluation of computational thinking. In Proceedings of the Fourth International Conference on Technological Ecosystems for Enhancing Multiculturality, Salamanca, Spain, 2–4 November 2016; pp. 73–77. [Google Scholar]
- Román-González, M.; Moreno-León, J.; Robles, G. Combining assessment tools for a comprehensive evaluation of computational thinking interventions. In Computational Thinking Education; Springer: Singapore, 2019; pp. 79–98. [Google Scholar]
- Kalelioğlu, F.; Gulbahar, Y.; Kukul, V. A framework for computational thinking based on a systematic research review. Baltic J. Modern Comput. 2016, 4, 583–596. [Google Scholar]
- Calcagni, A.; Lonati, V.; Malchiodi, D.; Monga, M.; Morpurgo, A. Promoting computational thinking skills: Would you use this Bebras task? In Proceedings of the International Conference on Informatics in Schools: Situation, Evolution, and Perspectives, Helsinki, Finland, 13–15 November 2017; pp. 102–113. [Google Scholar]
- Dagienė, V.; Futschek, G. Bebras international contest on informatics and computer literacy: Criteria for good tasks. In Proceedings of the International Conference on Informatics in Secondary Schools-Evolution and Perspectives, Lausanne, Switzerland, 23–25 October 2008; pp. 19–30. [Google Scholar]
- Grover, S. The 5th ‘C’ of 21st Century Skills? Try Computational Thinking (Not Coding). 2018. Available online: https://www.edsurge.com/news/2018-02-25-the-5th-c-of-21st-century-skills-try-computational-thinking-not-coding (accessed on 28 March 2023).
- Li, Y.; Schoenfeld, A.H.; di Sessa, A.A.; Graesser, A.C.; Benson, L.C.; English, L.D.; Duschl, R.A. Computational thinking is more about thinking than computing. J. STEM Educ. Res. 2020, 3, 1–18. [Google Scholar] [CrossRef]
- Zhang, N.; Biswas, G. Defining and assessing students’ computational thinking in a learning by modeling environment. In Computational Thinking Education; Springer: Singapore, 2019; pp. 203–221. [Google Scholar]
- Aslan, U.; La Grassa, N.; Horn, M.; Wilensky, U. Putting the taxonomy into practice: Investigating students’ learning of chemistry with integrated computational thinking activities. In Proceedings of the American Education Research Association Annual Meeting (AERA), Virtual, 17–21 April 2020. [Google Scholar]
- Lapawi, N.; Husnin, H. The effect of computational thinking module on achievement in science on all thinking modules on achievement in science. Sci. Educ. Int. 2020, 31, 164–171. [Google Scholar] [CrossRef]
- Chongo, S.; Osman, K.; Nayan, N.A. Impact of the Plugged-In and Unplugged Chemistry Computational Thinking Modules on Achievement in Chemistry. EURASIA J. Math. Sci. Technol. Educ. 2021, 17, 1–21. [Google Scholar] [CrossRef]
- Weller, D.P.; Bott, T.E.; Caballero, M.D.; Irving, P.W. Development and illustration of a framework for computational thinking practices in introductory physics. Phys. Rev. Phys. Educ. Res. 2022, 18, 020106. [Google Scholar] [CrossRef]
- Britton, J. Language and Learning; Penguin Books: London, UK, 1970. [Google Scholar]
- Polat, E.; Hopcan, S.; Kucuk, S.; Sisman, B. A comprehensive assessment of secondary school students’ computational thinking skills. Br. J. Educ. Technol. 2021, 52, 1965–1980. [Google Scholar] [CrossRef]
- Sun, L.; Hu, L.; Yang, W.; Zhou, D.; Wang, X. STEM learning attitude predicts computational thinking skills among primary school students. J. Comput. Assist. Learn. 2021, 37, 346–358. [Google Scholar] [CrossRef]
- Sun, L.; Hu, L.; Zhou, D. The bidirectional predictions between primary school students’ STEM and language academic achievements and computational thinking: The moderating role of gender. Think. Ski. Creat. 2022, 44, 101043. [Google Scholar] [CrossRef]
- Chongo, S.; Osman, K.; Nayan, N.A. Level of Computational Thinking Skills among Secondary Science Student: Variation across Gender and Mathematics Achievement. Sci. Educ. Int. 2020, 31, 159–163. [Google Scholar] [CrossRef]
- Hava, K.; Koyunlu Ünlü, Z. Investigation of the relationship between middle school students’ computational thinking skills and their STEM career interest and attitudes toward inquiry. J. Sci. Educ. Technol. 2021, 30, 484–495. [Google Scholar] [CrossRef]
- Lei, H.; Chiu, M.M.; Li, F.; Wang, X.; Geng, Y.J. Computational thinking and academic achievement: A meta-analysis among students. Child. Youth Serv. Rev. 2020, 118, 105439. [Google Scholar] [CrossRef]
- Creswell, J.W. Educational Research: Planning, Conducting, and Evaluating Quantitative; Prentice Hall: Upper Saddle River, NJ, USA, 2002. [Google Scholar]
- Lavidas, K.; Petropoulou, A.; Papadakis, S.; Apostolou, Z.; Komis, V.; Jimoyiannis, A.; Gialamas, V. Factors Affecting Response Rates of The Web Survey with Teachers. Computers 2022, 11, 127. [Google Scholar] [CrossRef]
- Baker, F.B.; Kim, S.H. The Basics of Item Response Theory Using R; Springer: New York, NY, USA, 2017; pp. 17–34. [Google Scholar]
- De Ayala, R.J. The Theory and Practice of Item Response Theory; Guilford Publications: New York, NY, USA, 2013. [Google Scholar]
- Tsigilis, N. Examining Instruments’ Psychometric Properties within the Item Response Theory Framework: From Theory to Practice. Hell. J. Psychol. 2019, 16, 335–376. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2018; Available online: https://www.R-project.org/ (accessed on 10 May 2022).
- Rizopoulos, D. LTM: An R package for latent variable modeling and item response analysis. J. Stat. Softw. 2006, 17, 1–25. [Google Scholar] [CrossRef]
- Revelle, W. Psych: Procedures for Personality and Psychological Research (Version 1.8.4) (Computer Software); Northwestern University: Evanston, IL, USA, 2018. [Google Scholar]
- Field, A. Discovering Statistics Using IBM SPSS Statistics, 5th ed.; SAGE: Washington, DC, USA, 2018. [Google Scholar]
- Beheshti, E. Computational thinking in practice: How STEM professionals use CT in their work. In Proceedings of the American Education Research Association Annual Meeting, San Francisco, CA, USA, 27 April–1 May 2017. [Google Scholar]
- Childs, P.E.; Markic, S.; Ryan, M.C. The role of Language in the teaching and learning of chemistry. In Chemistry Education: Best Practices, Opportunities and Trends; García-Martínez, J., Serrano-Torregrosa, E., Eds.; Wiley: Hoboken, NJ, USA, 2015; pp. 421–446. [Google Scholar] [CrossRef]

| Computational Thinking (Related to Computer Science) | |
|---|---|
| Bar and Stephenson (2011) [2] | Grover and Pea (2013) [6] |
| Data collection | Abstractions and pattern generalizations |
| Data representation and analysis | Systematic processing of information |
| Abstraction | Symbol systems and representations |
| Analysis and model validation | Algorithmic notions of flow of control |
| Automation | Structured problem decomposition (modularizing) |
| Testing and verification | Iterative, recursive, and parallel thinking |
| Algorithms and procedures | Conditional logic |
| Problem decomposition | Efficiency and performance constraints |
| Control structures | Debugging and systematic error detection |
| Parallelization | |
| Simulation | |
| Computational Thinking (Related to Computer Science and STEM) | ||
|---|---|---|
| Yadav et al. (2014) [41] | ISTE and CSTA (2011) [61] | Weintrop et al. (2016) [12] |
| Problem identification and decomposition | Formulating problems in a way that enables us to use a computer and other tools to help solve them | Data practices |
| Abstraction | Logically organizing and analyzing data | Modelling and simulation practices |
| Logical thinking | Representing data through abstractions, such as models and simulations | Problem-solving practices |
| Algorithms | Automating solutions through algorithmic thinking (a series of ordered steps) | System thinking practices |
| Debugging | Identifying, analyzing, and implementing possible solutions to achieve the most efficient and effective combination of steps and resources | |
| Generalizing and transferring the problem-solving process to a wide variety of problems | ||
| Log-Likelihood | x2 | Δx2 | Δdf | p-Value | |
|---|---|---|---|---|---|
| 1PL | −622.48 | 1244.96 | |||
| 2PL | −605.35 | 1210.70 | 34.26 | 14 | 0.002 |
| 3PL | −598.02 | 1196.04 | 14.66 | 14 | 0.402 |
| Parameters | Fit Indices of Every Element | |||
|---|---|---|---|---|
| Elements | Difficulty | Distinction | x2 | Pr (>x2) |
| q1 | 1.266 | 0.324 | 4.0136 | 0.9208 |
| q2 | −0.426 | 1.114 | 6.4867 | 0.6337 |
| q3 | −1.030 | 0.605 | 6.0765 | 0.6436 |
| q4 | −0.136 | 1.269 | 5.5186 | 0.8515 |
| q5 | −3.020 | 0.705 | 9.9105 | 0.2772 |
| q6 | −0.707 | 0.750 | 5.6962 | 0.7426 |
| q7 | −1.245 | 2.033 | 8.0635 | 0.3168 |
| q8 | −2.208 | 1.238 | 7.3209 | 0.4653 |
| q9 | 1.047 | 0.773 | 7.2294 | 0.6436 |
| q10 | −1.200 | 1.290 | 8.1537 | 0.5149 |
| q11 | 0.162 | 0.952 | 9.5822 | 0.3663 |
| q12 | −0.122 | 4.272 | 5.3639 | 0.495 |
| q13 | −0.486 | 2.250 | 9.2992 | 0.2673 |
| q14 | 0.166 | 2.018 | 10.1331 | 0.3564 |
| 95% Confidence Interval | |||||
|---|---|---|---|---|---|
| Ν | r | Lower CI | Upper CI | ||
| 2PL_scores | Mathematics | 51 | 0.270 | 0.045 | 0.500 |
| Physics | 33 | 0.514 | 0.208 | 0.729 | |
| Informatics | 32 | −0.046 | −0.389 | 0.307 | |
| Biology | 13 | 0.806 | 0.459 | 0.940 | |
| Greek Language | 80 | 0.272 | 0.056 | 0.464 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bounou, A.; Lavidas, K.; Komis, V.; Papadakis, S.; Manoli, P. Correlation between High School Students’ Computational Thinking and Their Performance in STEM and Language Courses. Educ. Sci. 2023, 13, 1101. https://doi.org/10.3390/educsci13111101
Bounou A, Lavidas K, Komis V, Papadakis S, Manoli P. Correlation between High School Students’ Computational Thinking and Their Performance in STEM and Language Courses. Education Sciences. 2023; 13(11):1101. https://doi.org/10.3390/educsci13111101
Chicago/Turabian StyleBounou, Aikaterini, Konstantinos Lavidas, Vassilis Komis, Stamatis Papadakis, and Polyxeni Manoli. 2023. "Correlation between High School Students’ Computational Thinking and Their Performance in STEM and Language Courses" Education Sciences 13, no. 11: 1101. https://doi.org/10.3390/educsci13111101
APA StyleBounou, A., Lavidas, K., Komis, V., Papadakis, S., & Manoli, P. (2023). Correlation between High School Students’ Computational Thinking and Their Performance in STEM and Language Courses. Education Sciences, 13(11), 1101. https://doi.org/10.3390/educsci13111101








