Creating the Conditions for Geographic Conceptual Development in Post-Primary Students through Collaborative Guided Inquiry

Abstract

This paper explores the potential for a collaborative guided inquiry task to stimulate geographic thinking using core geographic concepts of ‘location’, ‘distance and direction’, ‘scale’, ‘symbols’, ‘relative location’ and ‘slope and topography.’ The guided inquiry began with a visit to a park, with students then applying geographic thinking to redesign the park in a way that optimised utility for various user groups. The data generated included student work samples and video recordings of student groups as they worked through the task. The results show that the task design facilitated a deeper understanding of geographic concepts, including spatial relationships, connections and interactions. Furthermore, the collaborative nature of the task prompted students to use skills of explaining, negotiating and justifying their decisions. A critical feature of this analysis is the role that the teacher has in providing specialised guidance to support geographic thinking based on the needs of each group. The study highlights the value of practical, real-world experiences in geography education to learn, discuss and explore geographic concepts, enabling development of critical thinking, reasoning and problem-solving skills.

1. Introduction

Geography is an everyday life skill that enables students to develop a deep knowledge and understanding of why the world is the way it is and the interconnections between people, places and environments over place and time. An essential skill in the study of geography is describing and explaining spatial distributions of phenomena, which involves and promotes spatial thinking [1]. Spatial thinking is frequently defined as the knowledge, skills and habits of mind relating to use of spatial concepts, tools of spatial representation and processes of spatial reasoning to conceptualize and solve problems [2]. Spatial thinking as a cognitive skill that can be formally taught and extends to practical applications in everyday contexts is well established [2]. Some, such as Gryl and Jekel [3], Gordon et al. [4], Kim and Bednarz [5] and Bednarz [6], argue that developing critical spatial thinking skills is essential for young people to be active citizens in the digital age. Geographic thinking requires the application of spatial thinking within a geospatial reference frame, using geospatial relational thinking to look at interactions and relations between natural and human systems [7] and applying this reasoning to everyday problem solving [8]. Geography educators seek to enhance student geographic thinking by teaching students about spatial representations, to understand spatial patterns, to reason spatially, to think about human–nature interactions and construct theories enabling them to understand the world [8]. By engaging in geographic inquiry, where students pose geographic questions then collect, organise and analyse information to answer and critically reflect on those questions, students learn to make informed decisions regarding the consequences of stability and change in human–nature interactions [6].

Although geospatial technologies are pervasive and increasingly embedded in mainstream culture [9], spatial thinking is not mastered automatically, effortlessly or universally by all individuals and groups [1]. Children are quick to develop relative cognition of perspective, location and size, yet knowledge and understanding of symbol representation, co-ordinates and scale, which underpin mapping, have to be taught [10]. Geography education scholars have long demonstrated that making maps helps children learn spatial concepts such as pattern, scale, relative location, and orientation [11]. Map users must understand declarative spatial knowledge such as measurement, spatial representations and procedural spatial skills. Without instruction, neither children nor adults can exploit the full representational and spatial meaning maps offer [1]. Liben [1] argues that many teachers focus on the importance of map elements in map creation but rarely address the relationship between a mapped space and a larger frame of reference such as magnetic north or a regional landmark, leading children to solve future mapping exercises without linking a map with referential reality.

Geographic fieldwork and inquiry is an active, practical way for children to learn about relationships between maps and the real world [10]. As Schlemper et al. [12] note, providing students with opportunities to be spatial thinkers at the local scale prepares them to apply those skills to more complex, larger scale challenges. However, students will gain most from a fieldwork experience where they are carefully supported by their teacher in linking map representations to the real world. For instance, Kastens and Liben [13] found that children had greater difficulty connecting a map to the observed landscape than in understanding the map, and found the process of identifying, gathering and combining relevant information from the environment complex. As Catling [10] and Robertson et al. [14] highlight, children differ in the way and level to which they have developed local mental maps based on their experiences in exploring and navigating the world. When children follow a designated point-to-point route, they may not observe the space they pass through or the relative location of places within this space, so they are not developing cognitive maps of places [14]. Differences between students in terms of their experiences, capabilities and interests will affect the degree of challenge that a shared geographic experience presents to learners [15].

Geographic concepts consist of key knowledge and generalisations that help us make sense of the world and are essential for developing spatial thinking. The core geographic concepts, as described by Robertson, Maude and Kriewaldt [14], defined for the purposes of this research project include: ‘location’, ‘distance and direction’, ‘scale’, ‘symbols’, ‘relative location’ and ‘slope and topography.’ Developing an understanding of each concept is foundational to spatial thinking and fostering capacity to use them concurrently is ultimately the goal to promote spatial thinking. A key skill in demonstrating understanding of geographic concepts is the ability to explore, interpret and communicate the relationships and connections they have [16]. This is particularly necessary for decision-making when working on a real-life problem that has been structured as a collaborative inquiry-based task.

This paper reports on an investigation situated within a study examining how secondary student geographic conceptual knowledge develops whilst undertaking geographic inquiry, and the nature of teacher–student interactions during inquiry learning. Students and teachers were filmed while engaged in an inquiry-based learning design task that required posing questions, making decisions, synthesising and analysing information and critically thinking about geographic knowledge [17]. Previous analyses focused on teacher actions and teacher–student interactions during the between desks instruction stages of inquiry learning [17,18].

This current investigation examines how engaging in a collaborative inquiry-based task contributed to student geographic conceptual understanding by analysing student references to and use of geographic concepts in their discussions and the work they produced. Specifically, how can a rich geographic task be used to prompt, develop and elicit student spatial concepts and spatial thinking?

2. Materials and Methods

This qualitative study draws on the filmed actions and dialogue of a teacher and students undertaking a collaborative problem-based inquiry task in a secondary school geography classroom. This research was approved by the Ethics Committee of the University of Melbourne [1648192.1] and conducted according to these ethical requirements. As described in Kriewaldt, Robertson, Ziebell, Di Biase and Clarke [17], the class comprised twenty-two year nine students aged fourteen to fifteen years old from a government secondary school located in inner northern metropolitan Melbourne, Australia. Their teacher had over twenty years of experience in teaching geography and humanities subjects. At the time of data collection, the school’s Index of Community Socio-Educational Advantage profile indicated that students come from, on average, advantaged socio-educational backgrounds. Student academic performance was higher than average in relation to benchmark testing scores across Australian schools.

The task, developed by the teacher, involved students redesigning a local inner-city park whilst addressing five specified parameters and three optional parameters. At the time, the park was undergoing a planned redevelopment including controversial measures to dissuade skateboarders from congregating at the site. The specified core parameters were: (1) including accessibility for people with disability, (2) reflecting and respecting the indigenous Wurundjeri culture, (3) incorporating sustainability, (4) including commercial activity, and (5) offering something for a wide range of users. In addition, students could choose to (1) reflect the park’s proximity to the University of Melbourne, (2) reflect the area’s multicultural history, and/or (3) use for public events. Each group of students were asked to develop their ideas into a scaled design on a map, which they then orally presented and justified to the class. During these presentations, the other students assessed each design’s success in addressing the criteria, reflecting on their own designs and efforts in the process.

This task combines content, geographic thinking and skills with careful pedagogical choices to foster student conceptual development and spatial thinking (Figure 1). Applying the Jo and Bednarz Spatial Thinking Taxonomy [19], this task required students to engage in spatial thinking at lower through to higher levels because students will use spatial concepts that range from primitives (location) through to complex spatial (scale, gradient), use maps as the tool of representation, and use processes of reasoning covering input (listing, observing, selecting), processing (categorising, comparing, contrasting) and output (creating, designing, judging) cognitive functions. The task embeds geographic concepts both explicitly, as the production of a scaled map directs students to consider scale and symbols, and implicitly through the specified core parameters. For example, ‘commerce’ and ‘appealing to wide range of users’ leads students to consider relative location within the site and wider neighbourhood, ‘accessibility’ leads to consideration of people’s movement through the site given slope and topography, while aspects of ‘sustainability’, such as the siting of solar panels or vegetable gardens to maximise sunlight exposure, may trigger consideration of direction.

The students were introduced to the task during their usual humanities class. The teacher used explicit teaching about characteristics of open space, definitions of the five parameters, and examples of the parameters as observed in other Melbourne parks, then the students brainstormed and discussed possible ideas to address the parameters. This was followed by a full day dedicated to the task, with learning taking place outside of their school setting. In Session 1, the students visited the park to observe site characteristics, while the teacher drew their attention to specific design features. Students could take photographs and note specific features during the site visit. Sessions 2–4 were conducted at the University of Melbourne, where students worked on the design task collaboratively in assigned groups of up to four students. Each table group had access to two iPads to assist with research, tape measures and stationery items. The primary focus of Session 2 was on ‘Brainstorming and Research.’ Groups were provided with an A4 1:400 scale map of the existing park layout and an A3 gridded brainstorm sheet to guide their thinking. Session 3 was dedicated to creating a ‘Detailed Design’, which involved negotiating priorities and incorporating ideas onto an A2 blank 1:250 scale plan of the park, where all existing features except for most trees were removed. These blank plans did not contain a north arrow. Session 4 was focused on finalising their designs and planning their final four-minute presentation to the whole class. During the presentations students justified how they had addressed the criteria.

At the beginning of each session, the teacher outlined what students were expected to do and then systematically circulated among the table groups, monitoring global progress on the task and providing targeted and differentiated support to groups [17]. At approximately twenty to thirty minute intervals during each session, the teacher used short periods of explicit teaching to the whole class to reinforce geographic concepts such as scale, refocus student attention or highlight possible approaches to the task [17]. The students spent about 80% of each session working independently in their groups without teacher presence.

This study focuses on the data generated in Sessions 2–4 conducted at the University of Melbourne’s Science of Learning Research Centre Classroom Laboratory. The laboratory is equipped with ten unobtrusive video cameras and microphones mounted on the ceiling, which recorded student table groups activities and discussions, as well as the teacher’s movements and interactions with each group. Researchers took observation notes while watching the lesson from an adjacent room separated by a one-way mirror, and any student work samples produced during the lesson were digitised.

In this paper, the five groups are referred to as 9A, 9B, 9C, 9D and 9E, with the students within a group referred to as A1, A2, A3 and A4, etc. Video footage and transcriptions for each table group captured all dialogue, gestures and work produced over the three sessions. The transcripts were coded using NVivo and analysed both quantitatively and qualitatively to identify which core geographic concepts (location, distance and direction, scale, symbols, relative location, and slope and topography) were used by groups, and any other evidence of spatial reasoning used by students while justifying their design decisions during group discussions and presentations.

3. Results

3.1. Approach to Design Task

The groups approached the design process in two ways: Groups 9A and 9D developed scaled versions of the items on their brainstormed list and then arranged them within the park boundaries, whereas groups 9B, 9C and 9E thought about the overall design of the park, how it would be used by visitors and how it fitted into its surroundings. All students adopted the convention that any space left blank on the 1:250 map was grassed lawn, with all groups expressing some concerns about the white space in their draft designs, except for group 9B who did not discuss it all. While Groups A, D and E positioned additional items to fill perceived blank space, when C2 suggested doing this the others in 9C resisted, with C4 claiming ‘Empty space is good!’, C3 pointing out that ‘people can just sit around, have picnics’, C1 agreeing that ‘it should be just open space’ and C4 concluding that ‘people just sit there to have picnics and stuff, we don’t have to fill up every space.’ The teacher supported them, telling C2 that: ‘Spots with grass, you saw there were a few spaces like that in the university and they were empty when we walked past because it was 9 o’clock in the morning, but on any given day they’re crowded. Those spaces are used!’.

This process of negotiation and reasoning to reach a mutually agreed solution was a feature of the collaborative guided inquiry. The final group designs are shown in Figure 2.

3.2. Overall Use of the Concepts

Across the total video footage covering Sessions 2–4 and the group presentations, there were 356 instances where the focal geographic concepts were used by students. The most evident concepts were ‘relative location’ (27% of instances), ‘scale’ (21%), ‘slope and topography’ (20%), ‘location’ (19%), ‘symbols’ (12%), and the least evident was ‘distance and direction’, with only one instance recorded. Overall, groups 9B and 9E referred to the concepts most frequently, responsible for 24% and 30%, respectively, of all instances, which was almost double the references to the concepts made by groups 9A and 9C. Group 9E made more than 30% of the references to ‘location’ and ‘relative location’ while 9B made more than 30% of references for ‘symbols’ and ‘slope and topography’ (Figure 3). Together, 9E and 9B accounted for 60% of the instances for ‘slope and topography’, ‘relative location’ and ‘symbols’. Group 9A was the sole group that mentioned ‘distance and direction’.

Figure 4 and Figure 5 show the differences in the frequency to which various concepts were used across the full day in comparison to the final presentation. For example, ‘scale’ was one of the most-used concepts by most groups across the full day, as students discussed and decided on the final size of items in their scaled design, yet during the presentations, scale was dealt with implicitly by most and only briefly referred to by A3 from 9A and E1 from 9E, with A3 stating ‘Our paths, they look pretty small here but they’re going to be 2.5 m wide’ and E1 explaining that ‘We added a lot of extra things that you can’t really see because they’re pretty small’. During the presentations, the most-used concept for all groups was ‘location’, as students pointed out the location of items on their plan. This was followed by ‘relative location’, where they linked the location of items to that of other features on their plan. Four of the groups referred to the concepts of ‘slope and topography’ during their presentation. It is important to note that these data do not make a judgement about the quality or sophistication of the references to the concepts. They show the frequency of references throughout the day.

3.3. Use of Specific Concepts: Location, Distance and Direction, and Relative Location

It is not surprising that all groups referred to the location of items on their plans as they described design features during their presentations. Most instances where students referred to location during the sessions occurred while they read or looked for details on the 1:400 map, and later when cross-referencing between the 1:400 and 1:250 maps. The concepts of distance and direction were not discussed by the groups, nor did students refer to cardinal directions during their discussions or presentations, except for one student from group 9A who referred to the western entrance of the park during the presentation. This conforms with Kastens and Liben [13], who reported that, when mapping, children tended to use topological and projective spatial concepts rather than Euclidean concepts such as distance and direction, but the finding may also have arisen from the supplied maps not including a north orientation, which Liben [1] notes is common in many school-based mapping tasks.

Relative location is a geographic concept with explanatory power [20] that helps students to understand and explain why phenomena occur where they do. There were two levels of ‘relative location’ evident during group discussions: some focused solely on the relative location of items within the park, others considered the park’s relative location within the surrounding area.

Most discussions around relative location of items within the park related to the playground. For example, students discussed placing drinking taps near the playground (9C, 9E), the pros and cons of having a dog park near the playground (9A) and placing food or beverage enterprises near the playground (see

Table 1. Student approaches to relative location of playground and food.

Group	Suggestion	Suggested by
9A	‘If we do a playground, we could have a little barbeque place, a little revenue, that and the playground could go well together.’	A2
9D	‘The playground should be next to the café.’	D4
	‘Yep, so parents can watch their kids while they order.’	D2
9B	‘The café could be near the playground for like the mums.’	B2
	Later:
	‘You can get the coffee near the tram stop, then go to the playground.’	B2
	‘We’re going to create more money putting it near the tram stop.’	B4
9C	‘Yeah, so like from here to this corner here (shows with hands) is like just food, basically, and seating. This space over here is for fun and kids.’	C2

). Other ideas for within-park relative location involved positioning items near or under trees for shade, including benches and tables (9A, 9D, 9C, 9E), the playground (9B, 9E) and food trucks (9A and 9C); placing a greenhouse near the café that would use the produce (9C), and placing a shade canopy that captured rainwater over seating near the fountain that would use the water (9C). Another aspect of relative location concerned the positioning of items along or near paths. For example, 9D put garden beds and benches along the paths and during their presentations, A2 mentioned that ‘solar powered lights are around the paths’, and B2 highlighted the ‘benches for the elderly and anyone who needs to sit down along the paths and by the playground’. Group 9E considered the relative location of features such as drinking taps, bicycle facilities, benches and other items with varying consistency. For example, E2 repeatedly advised that ‘drinking taps and bike stuff should go along the paths’, but when E4 sought initial suggestions about where to put tables on the draft plan, E2 said to ‘just scatter them around the place’ and E1 agreed, suggesting E4 place them in ‘any spot that looks empty’. After the teacher intervened and prompted the group to consider the potential drawbacks of randomly dotting tables in space, 9E considered likely users, views and potential preferences for sun and shade when positioning their benches and tables.

The site’s proximity to a nearby university was flagged to students as important by its inclusion as an optional parameter. Some groups focused solely on university students visiting the park as part of daily routines, with their designs including services that would provide student discounts, employment opportunities or spaces for studying, such as A2 suggesting ‘We can give students a discount for food trucks, coffee. Stuff like that’, B4 proposing to ‘get the med students to help out when someone is injured, do their final exams as a practical at the park!’ and D3 explaining ‘we’ve left plenty of empty space and tables for students to utilise for study and socialising during breaks or lunch’. Some groups also considered how students living locally might require recreational or other facilities. This point was also raised by the teacher with some groups when circulating amongst tables, particularly when discussing the demand for sports facilities or the potential inclusion of dog parks.

Students also considered other aspects of the surrounding area when planning their designs. When contemplating potential commerce ideas, B2 argued that: ‘There’s a bunch of other restaurants around, so why would you go to a food truck? I mean we have to compete with the rest of the area, like that street nearby is really full of restaurants. But there’s not many cafes, it’s mostly restaurants, so the coffee thing could be okay’.

Some students had registered the eastern edge trams as a factor to consider when positioning artwork, such as when B4 suggested ‘You could put a statue near the tram because everyone’s going to see it when they go past’ and E3 stated ‘I think somewhere where when you pass on the tram you can see it’. Some students wanted to improve connectivity with the tram stop, such as 9E proposing to install solar panels on the roof or B4 recommending ‘maybe have a little path going to the tram or whatever’, while others preferred to site items at a distance from the tram, such as B2’s assessment of a proposed playground position ‘I think it’s a pretty good spot. It’s further away from like that (points at tram stop)’ or A1’s ‘Nah, don’t put the food trucks there right next to the tram’. The proximity of bike racks to surrounding streets was considered by some groups, such as D2 stating, ‘Maybe have like bike racks, maybe near the street?’, E2 asking ‘Wouldn’t you have just like a row of bike racks up here because that’s where people usually leave them?’ and E4 adding ‘and one at the bottom maybe, near the entrance’.

3.4. Use of Specific Concepts: Scale

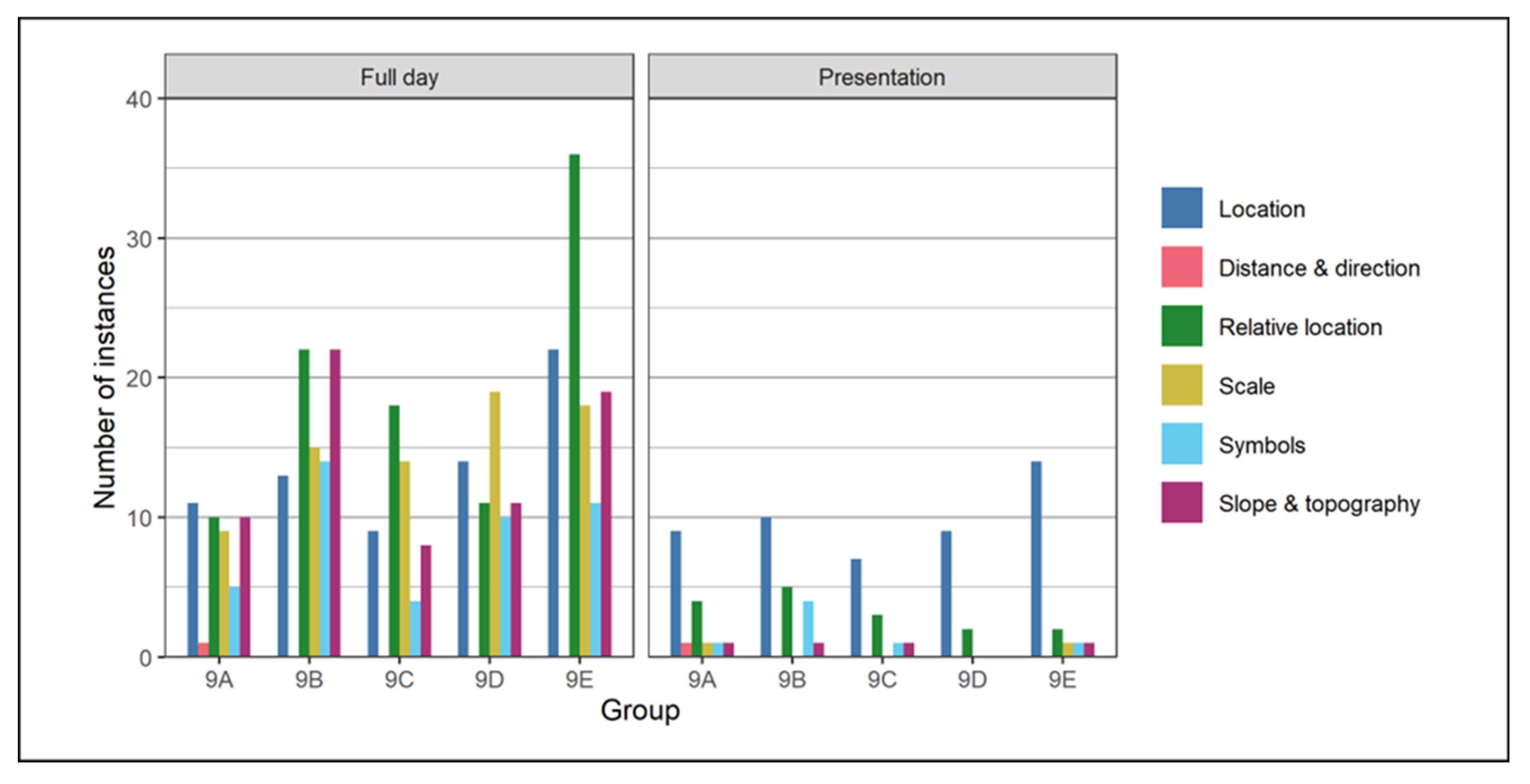
‘Scale’ was one of the most evident geographic concepts used during the day (Figure 4 and Figure 5) due to the inherent task requirement of producing a scaled design. For some students, the challenge was in visualising the desirable or necessary size for an item, rather than applying the set scale. When group 9E considered what size to make their playground, they initially started with a five-centimetre × five-centimetre square but E3 was concerned, stating, ‘The playground is way too big’, so E2 pointed out ‘Look how small it is relative to the rest of the park! The playground can be that big!’ and E1 added, ‘Think about it, if we’re going to have wheelchair stuff it’s going to take up more room’. A little later, E3 told the teacher that ‘It’s going to be twelve [metres] by twelve [metres], we decided the kids deserved a very big playground!’, with E2 adding that ‘It’s not that big but it’s way bigger than the one there now’. The teacher asked the group to consider the size of another playground near their school and how that compared with the size of the room they were in, stating ‘It would be wider than this room, wouldn’t it? Like even maybe double, or triple? So about twenty metres. So like E2 said, twelve by twelve is not exceptionally big for a playground, you know, you’ve got the space’. This is a typical student–teacher interaction demonstrating how the teacher guided students in estimating and visualising the size of the features they were designing while circulating amongst the groups. The teacher also encouraged use of a tape measure to check distances when required and reassured students that the park was larger than they may have felt during the site visit, stating, ‘It is genuinely 100 m across by 125 m wide, I double checked this using Google Earth!’ The student dialogue shows that many still did not understand how large a twelve-metre by twelve-metre item was, which is an important consideration in future iterations of the task and could be addressed during the field visit to the site. Getting students to physically measure items at the field site using a tape measure would assist them in understanding the actual dimensions of features they considered small or large, which assists with mentally reconciling sizes during the design stage.

Students used a variety of resources to determine the scaled dimensions of features on their plan. This included internet research, such as when D2 investigated the standard dimensions of a basketball court (twenty-eight × fifteen metres). Some adopted the dimensions of existing layout items by measuring off the 1:400 scale map and then calculating the equivalent distance for the 1:250 scale plan. For example, when 9D considered what path width to use, D2 pointed at the 1:400 map and said, ‘The paths on here are pretty good’, so then D3 stated: ‘I want to see how wide the path is here, so we can copy, it’s about half a centimetre, so that means, ah, two metres, about two metres wide, okay. So this needs to be, ah, a bit less than a centimetre’.

Some discussed possible sizing before checking what those proposed dimensions looked like using a tape measure, particularly for items such as path widths and bench sizing. This dialogue between members of 9A is typical of this approach:

A2—Two and a half metres is still a pretty wide path!

A4—It’s like (physically shows a metre on one side and a metre on the other).

A2—You could grab a tape measure and actually see how big it is.

A4—Yes. (pulls out tape to the distance). This is two and a half metres!

A3—Oh wow.

A4—That is a wide path!

Some compared their proposed dimensions relative to the classroom width, with students from 9F measuring the room width and the teacher then sharing that important information with the rest of the class. When A4 proposed making a 20 m by 20 m greenhouse, A2 responded that ‘I think that might be a bit big, because if this room is nine metres by nine metres, that’s like double-sized, is it a reasonable thing to do that?’ Similarly, the students in 9C used the room width as a gauge for their proposed greenhouse dimensions:

C4—So should that just be five by five metres? That’s like half this room, square. That’s pretty big.

C3—Yeah maybe five is too big.

C2—What about that side, that’s nine. (Gets up and looks for the tape measure).

C4—Or we could have five by two point five. Wait, C2, go back to like there. (points to where wants C2 to stand). Five by two and a half, like that?

C4 points at corner of room and then across, with C2 being the diagonally opposite corner of the rectangle.

C2—Yeah, I think that’s enough.

Once groups had decided on the actual size for items, they calculated the scaled size using technology (calculator applications on iPad or their own phones) or as a mental calculation. As the dimensions for most items were decided by the students, the groups were quite amenable to adjusting dimensions further for ease of calculation and drafting. Many groups rounded item dimensions to a multiple of 2.5 m to align with the 1:250 scale. For example, B2 originally proposed a 22 m by 9 m dog park, but in explaining this to B1 self-adjusted the nine metres: ‘Let’s just do ten metres ‘cos it’s easier! So that is four centimetres’. When B1 queried why the other dimension was twenty-two, B2 replied that ‘I dunno [don’t know], because that’s how much I could fit in it, you know?’, to which B1 advised ‘Do twenty, so then it’s easy and you don’t have to do maths to work it out’. Thus, the final dog park dimensions on the plan were 8.0 cm by 4.0 cm, rather than 8.8 × 3.6 cm as B2 initially intended. Similarly, when 9C were scaling an item across from the 1:400 map, C4 stated that ‘on this it is two centimetres, which is eight metres in real life, and eight metres in real life is 3.2 cm on that’. When C2 checked with C4 before drawing a 1.0 cm by 3.2 cm rectangle on the plan, C4 exclaimed, ‘Wait, just make it like four centimetres, so it’s like ten metres long. We could just have a huge space, just say four by four so it’s ten by ten metres, and we’ll have some sort of water design fountain in there’.

Although students considered the scale of items in their design and the relative location of items, they did not specify distances between items and many groups tended to position items to have symmetrical white space surrounding them. For example, when D4 decided that ‘The playground should be next to the café’, in the scaled design the café was located five metres off the path and five metres away from the playground space (Figure 2). Similarly, all groups included paths with features to improve accessibility and most included wheelchair accessible playground equipment in order to meet the accessibility criteria, yet only groups 9C and 9E created additional paths to access the proposed playground or other attractions within their design (Figure 2), with the other groups’ playgrounds situated about 5 m away from the nearest path.

3.5. Use of Specific Concepts: Symbols

There were two aspects to student use of symbols: first, the students’ interpretation of symbols on the provided 1:400 and 1:250 scaled plans, and their use of symbols in preparing their own designs (

Table 2. Students’ use of symbols in their designs.

Group	Approach Used
9A	Labelled cut coloured paper shapes and labelled drawn features.
9B	Labelled cut coloured paper shapes for main items, coloured symbols for smaller items with key on side.
9C	Drafted design with dimensions, symbols for smaller items, used colour to represent the set parameters.
9D	Labelled cut coloured paper shapes for main items, coloured symbols copied from 1:400 map for smaller items (e.g., ‘The bins and stuff are marked like that’), with key on separate sheet.
9E	Hand-drawn labelled shapes, coloured symbols for smaller items with key on side.

). During the brainstorming and research session, if students were unclear about how to interpret the 1:400 site map, they tended not to seek assistance from the teacher, usually drawing on other resources such as digital maps, digital images or their digital photos taken during the site visit instead. When developing their own designs for the park on the 1:250 plan, students were more likely to seek help from the teacher in interpreting unknown symbols and features. For example, B2 stated that ‘I don’t even know what these things are, all these tiny little things on the side, I don’t know what they are’ then asked the teacher directly ‘Is that the edge of the park?’, which the teacher initially confirmed, with B2 then querying ‘I thought this sort of thing was’ whilst pointing at a different spot. The teacher then clarified that one edge was the boundary while the other markings indicated car parking spaces.

A key interpretive element for students to grasp about the provided 1:250 scaled plans was the depiction of trees, which were shown with a large circle representing the full canopy and a very small central circle representing the position of the trunk. Students had to reconcile this representation with their earlier experiences of the trees as three-dimensional objects during the field visit, and then understand what this meant for their design when drawing any items that might be positioned between trees or located under tree canopies. The teacher did not explicitly teach this to the class, but on occasion with individual groups, the teacher referred to the depiction, for example, when discussing the scale of trees by explaining that the canopy and foliage of a tree could be twelve metres across while the trunk was much less. At least one student in each group successfully interpreted the depiction and then advised the others how to deal with it. For example, when 9D were developing their path design, D3 showed D4 that ‘All of these tiny ones are tree stumps, so just weave, I guess’ with D4 responding that ‘Oh, I was drawing around the trees! I’ll go in between them’.

The groups differed in the extent to which they adopted symbols within their designs (Table 2). Many used symbols to represent smaller items such as bins, drinking taps, benches and bike stations, but not all included a key on their plan to explain what the symbols represented. Group 9E were the only group to check how their design looked from across the room prior to the presentation, with E1 realising ‘You can’t really see all the little things’. Consequently, during the presentation E1 explicitly described the symbol as well as where items were, for example: ‘We’ve labelled benches with little yellow spots’.

4. Discussion and Conclusions

The present study aimed to investigate how a rich geographic task can be used to prompt, develop and elicit student spatial concepts and spatial thinking, in the context of one year 9 class with an experienced teacher. The teacher’s prior knowledge and capability was well established in this case, and may serve as inspiration to some. Considering that, this case suggests that the role of teacher expertise in influencing learning outcomes is significant [21]. This study points to three elements that together can develop students’ spatial thinking. These were the rich design of the task, contingent guidance by the teacher and simulated real-world processes of design.

First, by design, students could not complete the collaborative problem-based inquiry task without applying spatial concepts. Spatial concepts comprise the ‘grammar’ used by students in describing and justifying their designs for a public space. As shown in the results, students foregrounded various concepts as they worked through the task, with some concepts, such as location and scale, more evident than others, such as direction and distance. Differing sophistication in the use of some concepts, such as relative location, occurred among student groups. Students used coding, decoding and recoding skills as they worked with the different representations of the physical space (field visit, provided 1:400 site map, blank 1:250 map), regularly drawing on digital resources such as Google maps, their own photos and other publicly available site images to inform them as moved from one representation to the next. Bolstering use of direction could have been achieved by asking students to consult a compass or compass application on their phone during the site visit, and by ensuring north was clearly delineated in all maps provided to students. Likewise, whilst on site asking the students to measure aspects of the site may have boosted their use and understanding of distance.

Second, contingent guidance and prompting by the teacher during interactions with groups fostered a deeper understanding of the concepts by students. In designing the task, the teacher anticipated that scale might be a tripping point for students, so adopted a three-prong teaching strategy comprising of targeted short bursts of whole class explicit teaching, provision of supporting resources such as tape measures, and systematically engaging in discussions about the size of potential design items and how that was represented on the scaled plan with each group whilst circulating around the classroom. In contrast, the teacher gave students agency in deciding how to use symbols on their designs and provided minimal guidance other than reminding groups that their design needed to be clear, colourful and ‘stand out’ when viewed from across the room during the presentation. Most groups chose to follow geographic conventions by adopting symbols for smaller items and including a key on their design.

Third, a challenge in developing understanding of spatial concepts is that exercises that systematically teach concepts in isolation can seem of no immediate relevance to the students’ lives and thus may be unengaging. This task invited the use of spatial concepts in concert, simulating the processes that teams such as urban planners and landscape designers might undertake to redesign a park. A key feature of the task design was the visit to the park site, which provided a sense of real-world connection to the geographic concepts students would be addressing. The direct student engagement with the physical site enabled them to get a sense of space, with the redesign task being critical in creating the conditions that would prompt geographic thinking. Students’ experience of the physical environment supported the more abstract task of imagining and creating a space that maximised utility and significance for those who could use it. The use of a sophisticated task design, limited direct instruction, prompting and contingent guidance together enabled students to use and strengthen their use of concepts together. This task simulated real-world processes of design.

This study found that a rich geographic task was a useful way to develop students’ spatial concepts and spatial thinking and, as Metoyer and Bednarz argue [22], created conditions that fostered their geographic thinking. However, while the sophisticated features of the task design in terms of geographic content, geographic thinking and reasoning were essential, the contingent support and guidance of the teacher was equally critical to its success. We acknowledge that replicating this study with less experienced teachers may yield different results. Implications of this current study is that rich real-world tasks should be included in school education as they not only promote spatial thinking, but also foster students’ capacity to think geographically by drawing on a suite of geographic concepts to form and assess generalisations and link to theories.