Teacher Beliefs and Perspectives of Practice: Impacts of Online Professional Learning
Abstract
1. Introduction
2. Interrelating Teachers’ Beliefs, Practice, and Orientations
2.1. Teachers’ Beliefs: Young Children, Mathematics, and Teaching and Learning
2.2. Teaching Math to Young Children: Online Professional Learning
3. The Current Study
4. Materials and Methods
4.1. Course Context
4.2. Participants
4.3. Data Sources
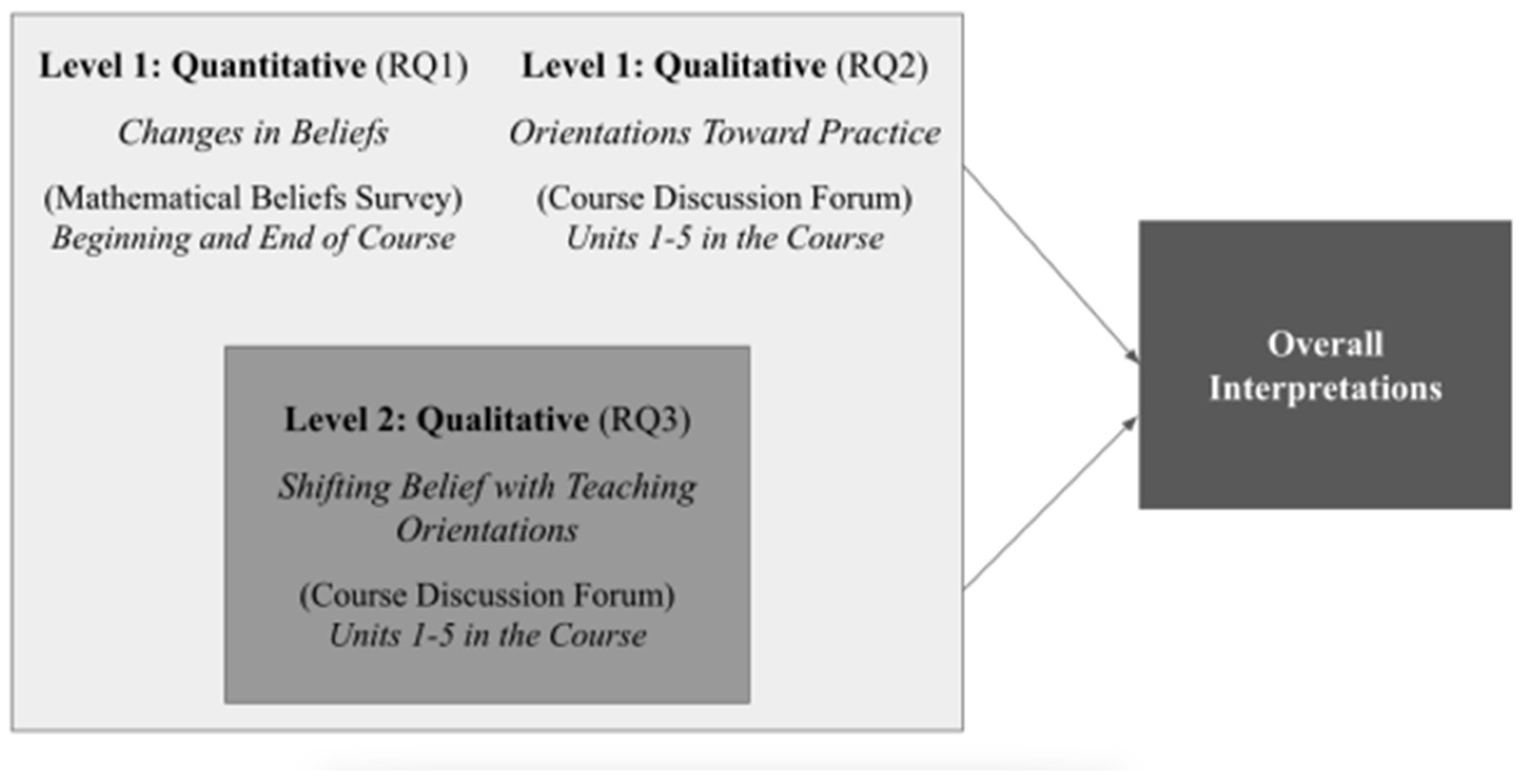
4.4. Study Design and Analysis
4.5. Level-One Quantitative Analysis
4.6. Level-One Qualitative Analyses
4.7. Level-Two Qualitative Analyses
5. Results
6. Level-One Quantitative Differences in Participant Beliefs after Online Professional Learning
7. Level-One Qualitative Results
Overall Themes
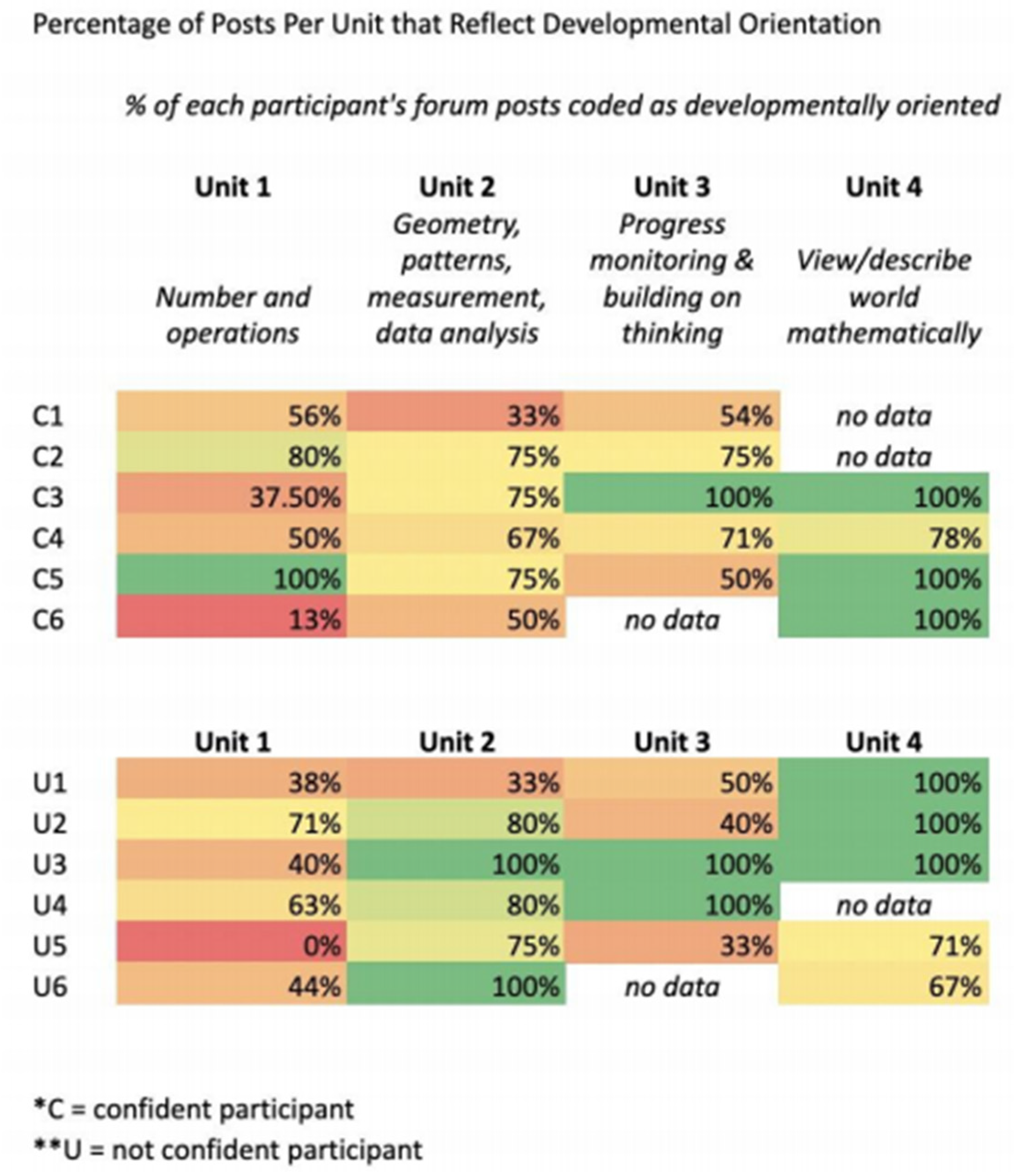
8. Level-Two Qualitative Results
Close Analysis of Participant Comfort and Interaction with Themes
9. Overall Interpretation
10. Discussion
11. Bolstering Teachers’ Beliefs about Mathematics and Developmentally Based Mathematics Teaching
12. Expanding Positive Effects of Online Professional Learning to Bolster Other Beliefs
13. Limitations and Future Research
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- National Research Council. Adding It Up: Helping Children Learn Mathematics; The National Academies Press: Washington, DC, USA, 2001. [Google Scholar]
- Jordan, N.C.; Kaplan, D.; Ramineni, C.; Locuniak, M.N. Early math matters: Kindergarten number competence and later mathematics outcomes. Dev. Psychol. 2009, 45, 850–867. [Google Scholar] [CrossRef] [PubMed]
- Raudenbush, S.W. The Brown legacy and the O’Connor challenge: Transforming schools in the images of children’s potential. Educ. Res. 2009, 38, 169–180. [Google Scholar] [CrossRef]
- National Mathematics Advisory Panel. Foundations for Success: The Final Report of the National Mathematics Advisory Panel; U.S. Department of Education: Washington, DC, USA, 2008. [Google Scholar]
- Opper, I.M. Teachers Matter: Understanding Teachers’ Impact on Student Achievement; RAND Corporation: Santa Monica, CA, USA, 2019. [Google Scholar]
- National Association for the Education of Young Children (NAEYC) and National Council for Teachers of Mathematics (NCTM). Early Childhood Mathematics: Promoting Good Beginnings; Joint Position Statement; National Association for the Education of Young Children: Washington, DC, USA, 2010. [Google Scholar]
- Clements, D.H.; Sarama, J. Mathematics in early childhood. In Contemporary Perspectives on Mathematics in Early Childhood Education; Saracho, O.N., Spodek, B., Eds.; Information Age Publishing: Charlotte, NC, USA, 2008; pp. 67–94. [Google Scholar]
- Clements, D.H.; Sarama, J. Early childhood mathematics intervention. Science 2011, 333, 968–970. [Google Scholar] [CrossRef] [PubMed]
- Frye, D.; Baroody, A.J.; Burchinal, M.; Carver, S.M.; Jordan, N.C.; McDowell, J. Teaching Math to Young Children: A Practice Guide; National Center for Education Evaluation and Regional Assistance (NCEE), Institute of Education Sciences, U.S. Department of Education: Washington, DC, USA, 2013. [Google Scholar]
- Sarama, J.; Clements, D.H.; Baroody, A.J.; Kutaka, T.S.; Chernyavskiy, P.; Shi, J.; Cong, M. Testing a theoretical assumption of a learning-trajectories approach in teaching length measurement to kindergartners. AERA Open 2021, 7, 1–15. [Google Scholar] [CrossRef]
- Platas, L.M. The Mathematical Development Beliefs Survey: Validity and reliability of a measure of preschool teachers’ beliefs about the learning and teaching of early mathematics. J. Early Child. Res. 2014, 13, 295–310. [Google Scholar] [CrossRef]
- Pajares, M. Teachers’ beliefs and educational research: Cleaning up a messy construct. Rev. Educ. Res. 1992, 62, 307–332. [Google Scholar] [CrossRef]
- Vartuli, S. How early childhood teacher beliefs vary across grade level. Early Child. Res. Q. 1999, 14, 489–514. [Google Scholar] [CrossRef]
- Fives, H.; Gill, M.G. International Handbook of Research on Teachers’ Beliefs; Routledge: London, UK, 2015. [Google Scholar]
- Chen, C.S. Reflections on learning how to teach mathematics: The initial training of kindergarten teachers. Creat. Educ. 2015, 6, 1328–1335. [Google Scholar] [CrossRef]
- Richardson, V. Preservice teachers’ beliefs. In Teacher Beliefs and Classroom Performance: The Impact of Teacher Education (Advances in Teacher Education); Raths, J., McAninch, A.C., Eds.; Information Age Publishing: Charlotte, NC, USA, 2003; pp. 1–22. [Google Scholar]
- Leatham, K.R. Viewing mathematics teachers’ beliefs as sensible systems. J. Math. Teach. Educ. 2006, 9, 91–102. [Google Scholar] [CrossRef]
- Schoenfeld, A.H. How We Think: A Theory of Goal-Oriented Decision Making and its Educational Applications; Routledge: New York, NY, USA, 2011. [Google Scholar]
- Potari, D.; Georgiadou–Kabouridis, B. A primary teacher’s mathematics teaching: The development of beliefs and practice in different “supportive” contexts. J. Math. Teach. Educ. 2009, 12, 7–25. [Google Scholar] [CrossRef]
- Kutaka, T.S.; Ren, L.; Smith, W.M.; Beattie, H.L.; Edwards, C.P.; Green, J.L.; Lewis, W.J. Examining change in K-3 teachers’ mathematical knowledge, attitudes, and beliefs: The case of primary math. J. Math. Teach. Educ. 2018, 21, 147–177. [Google Scholar] [CrossRef]
- Wilkins, J.L. The relationship among elementary teachers’ content knowledge, attitudes, beliefs, and practices. J. Math. Teach. Educ. 2008, 11, 139–164. [Google Scholar] [CrossRef]
- Stockero, S.L.; Leatham, K.R.; Ochieng, M.A.; Van Zoest, L.R.; Peterson, B.E. Teachers’ orientations toward using student mathematical thinking as a resource during whole-class discussion. J. Math. Teach. Educ. 2020, 23, 237–267. [Google Scholar] [CrossRef]
- Pilitsis, V.; Duncan, R.G. Changes in belief orientations of preservice teachers and their relation to inquiry activities. J. Sci. Teach. Educ. 2012, 23, 909–936. [Google Scholar] [CrossRef]
- Ginsburg, H.; Hyson, M.; Woods, T.A. Preparing Early Childhood Educators to Teach Math: Professional Development That Works; Brookes Publishing: Baltimore, MD, USA, 2014. [Google Scholar]
- Claessens, A.; Engel, M. How important is where you start? Early mathematics knowledge and later school success. Teach. Coll. Rec. 2013, 115, 1–29. [Google Scholar] [CrossRef]
- Duncan, G.J.; Dowsett, C.J.; Claessens, A.; Magnuson, K.A.; Huston, A.C.; Klebanov, P.K.; Pagani, L.S.; Feinstein, L.; Engel, M.; Brooks-Gunn, J.; et al. School readiness and later achievement. Dev. Psychol. 2007, 43, 1428–1446. [Google Scholar] [CrossRef]
- Ginsburg, H.P.; Kaplan, R.G.; Cannon, J.; Cordero, M.I.; Eisenband, J.G.; Galanter, M.; Morgenlander, M. Helping early childhood educators to teach mathematics. In Critical Issues in Early Childhood Professional Development; Zaslow, M., Martinez-Beck, I., Eds.; Paul H Brookes Publishing: Baltimore, MD, USA, 2006; pp. 171–202. [Google Scholar]
- Lee, J.S.; Ginsburg, H.P. What is appropriate mathematics education for four-year-olds? J. Early Child. Res. 2007, 5, 2–31. [Google Scholar] [CrossRef]
- LeFevre, J.; Sowinski, C.; Osana, H.P.; Skwarchuk, S.; Manay, Q.N. Who’s Counting? Numeracy and Literacy Practices of Early Learning and Child Care Practitioners; Canadian Council on Learning: Ottowa, ON, Canada, 2009. [Google Scholar]
- Elkind, D. The Hurried Child: Growing Up Too Fast Too Soon; Da Capo Press: Cambridge, MA, USA, 2007. [Google Scholar]
- Institute of Medicine and National Research Council. From Neurons to Neighborhoods: The Science of Early Childhood Development; The National Academies Press: Washington, DC, USA, 2000. [Google Scholar]
- Morris, P.; Millenky, M.; Raver, C.; Jones, S.M. Does a preschool social and emotional learning intervention pay off for classroom instruction and children′s behavior and academic skills? Evidence from the Foundations of Learning project. Early Educ. Dev. 2013, 24, 1020–1042. [Google Scholar] [CrossRef]
- Bandura, A. Self-efficacy: Toward a unifying theory of behavioral change. Psychol. Rev. 1977, 84, 191. [Google Scholar] [CrossRef] [PubMed]
- Bandura, A. The explanatory and predictive scope of self-efficacy theory. J. Soc. Clin. Psychol. 1986, 4, 359–373. [Google Scholar] [CrossRef]
- Bandura, A. Self-Efficacy: The Exercise of Control; W. H. Freeman and Company: New York, NY, USA, 1997. [Google Scholar]
- Nurlu, Ö. Investigation of teachers’ mathematics teaching self-efficacy. Int. Electron. J. Elem. Educ. 2015, 8, 21–40. [Google Scholar]
- Buczynski, S.; Hansen, C. Impact of professional development on teacher practice: Uncovering connections. Teach. Teach. Educ. 2010, 26, 599–607. [Google Scholar] [CrossRef]
- Creswell, J.W.; Clark, V.P.L. Designing and Conducting Mixed Methods Research, 3rd ed.; SAGE Publications, Inc.: Thousand Oaks, CA, USA, 2017. [Google Scholar]
- Cohen, J. Statistical Power Analysis for the Behavioral Sciences, 2nd ed.; Lawrence Erlbaum Associates, Inc.: Mahwah, NJ, USA, 1988. [Google Scholar]
- Miles, M.B.; Huberman, M.A.; Saldana, J. Qualitative Data Analysis: A Methods Sourcebook, 4th ed.; SAGE Publications, Inc: Thousand Oaks, CA, USA, 2019. [Google Scholar]
- Miles, M.B.; Huberman, A.M. Qualitative Data Analysis: An Expanded Sourcebook; Sage Publications, Inc: Thousand Oaks, CA, USA, 1994. [Google Scholar]
- Leech, N.L.; Onwuegbuzie, A.J. An array of qualitative data analysis tools: A call for data analysis triangulation. Sch. Psychol. Q. 2007, 22, 557–584. [Google Scholar] [CrossRef]
- Karatas, I.; Guven, B.; Öztürk, Y.; Arslan, S.; Gürsoy, K. Investigation of pre-school teachers’ beliefs about mathematics education in terms of their experience and structure of their education. EURASIA J. Math. Sci. and Technol. Educ. 2017, 13. [Google Scholar] [CrossRef]
- National Research Council. Mathematics Learning in Early Childhood: Paths toward Excellence and Equity; The National Academies Press: Washington, DC, USA, 2009. [Google Scholar]
- Sheridan, K.M.; Banzer, D.; Pradzinski, A.; Wen, X. Early math professional development: Meeting the challenge through online learning. Early Child. Educ. J. 2019, 48, 223–231. [Google Scholar] [CrossRef]
- Heyder, A.; Weidinger, A.F.; Cimpian, A.; Steinmayr, R. Teachers’ belief that math requires innate ability predicts lower intrinsic motivation among low-achieving students. Learn. and Instr. 2020, 65. [Google Scholar] [CrossRef]
- Burns, A. Teacher beliefs and their influence on classroom practice. Prospect 1992, 7, 56–66. [Google Scholar]
| Unit | Focus & Concepts | Aims | Sample Activities |
|---|---|---|---|
| 1 | Teaching Number and Operations Using a Developmental Progression
|
|
|
| 2 | Teaching Geometry, Patterns, Measurement, and Data Analysis Using a Developmental Progression
|
|
|
| 3 | Using Progress Monitoring and Building on Student Thinking
|
|
|
| 4 | Teach Children to View and Describe their World Mathematically
|
|
|
| 5 | Dedicate Time to Teaching Math and Integrating Math Instruction Throughout the School Day
|
|
|
| Identified Role | Experience Level in Early Mathematics Education | Grade Level Specification | |||
|---|---|---|---|---|---|
| Classroom Teachers | 62 | No Experience | 9 | Pre-K | 7 |
| Curriculum & Instruction | 7 | Less Than 2 Years | 11 | Kindergarten | 1 |
| Special Education | 12 | 2–5 Years | 19 | Elementary | 5 |
| School Admin & Support Staff | 3 | 6–15 Years | 41 | Middle and/or High School | 5 |
| Teacher Prep | 3 | 16+ Years | 17 | Post-Secondary | 0 |
| Other (e.g., parent, non-education profession) | 10 | Not Provided | 19 | ||
| Subscale | Sample Statements |
|---|---|
| Classroom locus of generation of mathematics knowledge | In preschool children construct mathematical knowledge Teachers should show preschoolers the correct way |
| Age appropriateness of mathematics as a school subject | Math is a worthwhile and necessary subject for preschoolers Very few preschoolers are ready for math |
| Teacher confidence with classroom support of mathematical development | I am unsure how to support math development for young children Math would be easy for me to incorporate into preschool curricula |
| Survey Subscale | Mean Raw Score | SD | df | t | p | Cohen’s d 1 |
| Pre Overall | 101.67 | 10.64 | 96 | 7.714 | <0.001 | 0.78 |
| Post Overall | 107.73 | 7.70 | ||||
| Pre Locus | 34.07 | 6.74 | 96 | 1.590 | 0.115 | 0.16 |
| Post Locus | 34.87 | 5.99 | ||||
| Pre Age | 29.64 | 2.98 | 96 | 1.906 | 0.060 | 0.19 |
| Post Age | 30.26 | 2.36 | ||||
| Pre Confidence | 37.96 | 7.29 | 96 | 7.600 | <0.001 | 0.77 |
| Post Confidence | 42.61 | 5.57 |
| Theme | Description | Corresponding codes |
|---|---|---|
| Orientation to Teaching-Exposure | A clear focus in a discussion string on children’s exposure to math skills, vocabulary, or interaction with skills with cognitive features, such as attention or behavior. | *Behavior; *attention; *ability to remember; * ability; *ability with vocabulary; *cognition. |
| Orientation to Teaching-Development | A clear focus in a discussion string on children’s development of mathematical ideas or understandings, or interaction with prior knowledge or stages of knowledge. | *Access;*Prior knowledge; *Concepts; *Stages; *Grow; *Connect,*Progressions |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hunt, J.; Duarte, A.; Miller, B.; Bentley, B.; Albrecht, L.; Kruse, L. Teacher Beliefs and Perspectives of Practice: Impacts of Online Professional Learning. Educ. Sci. 2023, 13, 68. https://doi.org/10.3390/educsci13010068
Hunt J, Duarte A, Miller B, Bentley B, Albrecht L, Kruse L. Teacher Beliefs and Perspectives of Practice: Impacts of Online Professional Learning. Education Sciences. 2023; 13(1):68. https://doi.org/10.3390/educsci13010068
Chicago/Turabian StyleHunt, Jessica, Alejandra Duarte, Brittany Miller, Brianna Bentley, Laura Albrecht, and Lance Kruse. 2023. "Teacher Beliefs and Perspectives of Practice: Impacts of Online Professional Learning" Education Sciences 13, no. 1: 68. https://doi.org/10.3390/educsci13010068
APA StyleHunt, J., Duarte, A., Miller, B., Bentley, B., Albrecht, L., & Kruse, L. (2023). Teacher Beliefs and Perspectives of Practice: Impacts of Online Professional Learning. Education Sciences, 13(1), 68. https://doi.org/10.3390/educsci13010068






