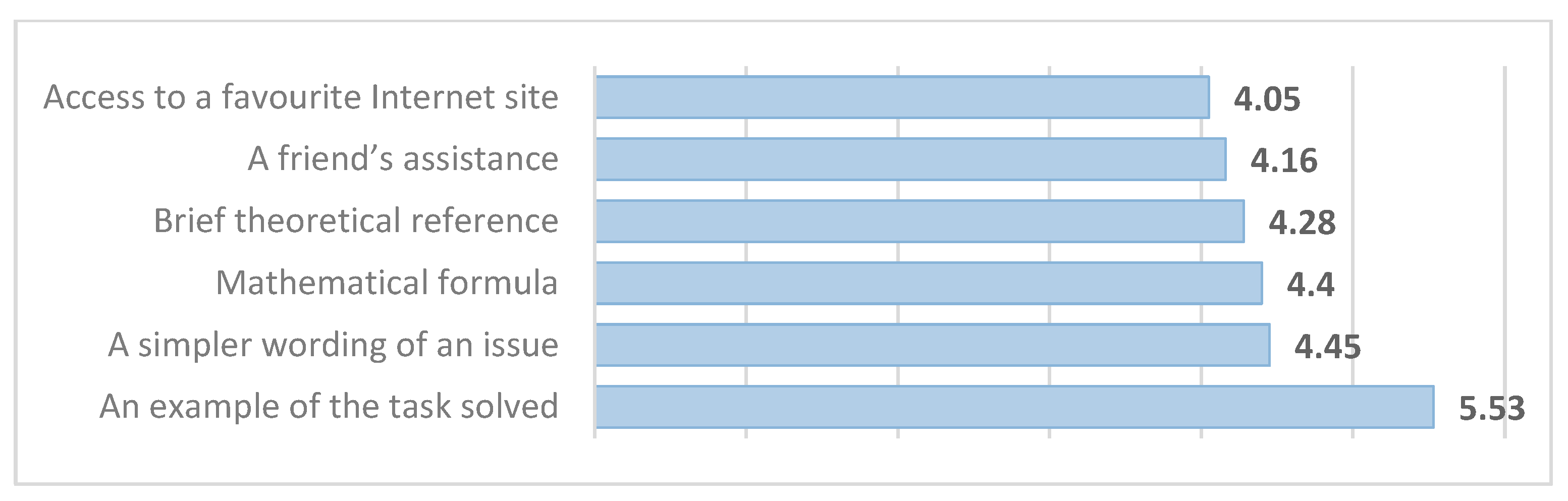Technologies for Teaching Mathematics in a Multilingual Digital Environment

Abstract

The article considers the expansion of digital technologies and their impact on training modern specialists. The increase in the volume of information, students’ requests for interdisciplinary practice-oriented training, and the involuntary transition to online learning during the COVID-19 pandemic encouraged changes in the ways educational information is presented. The multilingual approach, enhanced by digitalization, also contributes to these transformations. The purpose of this study is to develop a methodology aimed at improving the perception and understanding of mathematics. The experience of combining digital training in mathematics, multilingual technologies and scaffolding is considered. Scaffolding is implemented in a digital environment and is extended by the reverse scaffolding approach, when the educational material first appears without prompts, and then the prompts are given from complex to simple. Based on the idea of presenting information in various ways, a test was created on the Moodle LMS platform. The surveys showed that the current generation of students prefers educational information based on visualization and supporting symbolic signs. When presenting new material and generating training tests, the teacher should refer to inter-subject multilingualism, reinforcing it with a professional context. Digital implementation of scaffolding proved to be especially in demand during the transition to online learning.

1. Introduction

The rapid development of digital and manufacturing technologies and significant changes in financial and banking spheres affect the training programs of modern specialists. Programs and curricula are changing. The introduction of new disciplines into the program, as a rule, is accompanied by a reduction in the training hours of those already existing. This also applies to the basic disciplines, which include mathematics, the number of hours devoted to the study of which is regularly reduced. At the same time, the number of didactic units does not change and even grows due to the increasing requirements for interdisciplinary and professional training. Final knowledge is evaluated in the language of competencies, which implies the free use of knowledge of various disciplines to solve multifactorial tasks. Students’ expectations are also in tune with this goal, being focused, today, on a wide range of training.

The total transition to e-learning during the COVID-19 pandemic had a dramatic impact on the educational process and its transformation. Digital technologies proved to be of paramount importance for teaching students during quarantine. School and university teachers had to instantly master them, be it as supporters or opponents of digitalization in education.

Pedagogical approaches are changing due to new types of tasks, but the educational literature on basic disciplines is barely modified. Students are usually offered traditional math textbooks designed for different study hours, with different requirements, and for a different generation of students.

This contradiction can be resolved by developing new approaches to delivering and presenting educational information. In this case, the peculiarities of perception by modern students come to the fore. Modern students are characterized by their rapid perception of information, clip thinking and multitasking.

Educators working in different fields of higher education refer to the above debatable matters quite often. In [1] the difference in mental codes is discussed, as well as the fundamental non-linearity in the perception of the world. Psychologists note that, as a result of the spread of the Internet and digital technologies, there is a decrease in the ability of today’s youth to memorize information and they experience difficulty in reading long texts [2].

The traditional systems of transmitting systematized scientific and professional information, and the explanatory–illustrative type of education, are not very efficient today and should not be used to the usual extent.

At this point, the phenomenon of specialty sublanguages should be considered. This research is conducted within the context of mathematical disciplines, which in turn have subvarieties. The sublanguage of mathematics is characterized by the simplified structure of the language, which is thus more amenable to automatic processing; this is especially relevant to teaching mathematics with its metasubject character. It is common knowledge that mathematics is the lingua franca for a host of academic disciplines, such as information technologies, modeling economic processes, statistics, econometrics and others. The vocabulary of the sublanguage of mathematics is restricted and highly specialized.

It is difficult to distinguish in practice between the variety of genre, or LSP (languages for special purposes), or even code-switching, as here we find many similarities.

A talented teacher always tries to use different genres of the specialty sublanguage to explain difficult material, depending on the time available, the level of students’ preparedness and expediency.

In teaching mathematics, the sublanguage of mathematics is used. Moreover, different styles of discourse are used: academic learning style, academic scientific style, academic slang, symbolic notation (mathematical formulas, quantifiers, etc.), interdisciplinary terms derived from professions and IT, as well as structural and logical schemes.

The authors consider that this diversity of sublanguages (we call it intra-subject multilingualism) can be used to improve the quality of education in modern conditions. The purpose of our research is to develop a methodology for using multilingual opportunities in order to improve the perception and understanding of mathematical theory.

In addition to the contradictions mentioned above, we single out several additional factors confirming the relevance of the goal:

• Widespread introduction of digitalization in the educational environment;
• Use of blended forms of education;
• More frequent transitions to remote format (sometimes sudden, due to the pandemic);
• Student demands for dynamism in the learning process and regular change of activities;
• Development of inclusive approaches to the education of students with physical disabilities and health impairments.

In regard to the last point, it should be noted that the specificity of health impairment refers to a variety of health problems that dictate the need for special educational services. Some students have no restrictions on what they can do and learn, while others are extremely limited in their activities and require intensive educational help. This is the point at which scaffolding can be applied.

To achieve the above goals, the following objectives were set:

(1)

To analyze methods of the digital teaching of mathematical theory;

(2)

To study and systematize traditional and interdisciplinary multilingual technologies;

(3)

To consider the possibilities of scaffolding technology for organizing educational information;

(4)

To identify experimentally the most effective ways of presenting an educational topic for twenty-first century students;

(5)

To outline prospects for improving the presentation of mathematical theory.

The authors have vast experience in teaching at the university and observing students for many years, which made it possible to formulate the following hypothesis: the current generation of students needs special forms of presenting educational information, which should be maximally structured, based on visualization and supporting symbolic signs.

2. Literature Review

The literature review presented below is structured in the following areas:

(1)

The new system of educational resources created in connection with the development of digital technologies and due to forced global transition to distance learning (COVID-19);

(2)

The multilingual approach to the educational process;

(3)

Scaffolding technology as a means of presenting educational content.

Today, a new system of digital educational resources and tools is being created. Digital technologies make it possible to find new formats of educational materials, develop pedagogical technologies, modernize the process of interaction between the teacher and students, implement individual trajectories and much more.

The above issues receive wide coverage in publications on related matters. Namely, the paper [3] deals with the digital educational environment as a specially organized and updated resource for organizing a self-sufficient personalized learning system. A detailed overview of the methodological and instrumental features of e-learning is presented in [4,5,6]. Even before the pandemic, educationalists [7] admitted that, due to rapid digitalization, innovation evolved all the time and it had already changed educational processes tremendously. Among major innovations were listed digital platforms, online corpora, mobile learning, online authentic materials, communicating with people online, online CPD and the global staffroom. The COVID-19 enhanced the trend and advanced it further.

Due to COVID-19 and a series of lockdowns, the education sector faced many challenges. The pandemic called for a new model of learning, becoming “tech-savvy” and, first and foremost, mastering Information and Communications Technology (ICT). At present the pedagogical communities have adopted ICT, and have accumulated sufficient experience to come to certain conclusions. When quarantine—with its forced turn to online learning—is over, we face the fact that ICT has obtained a new dimension and become part and parcel of the teaching–learning process. Questions of how teaching and learning can be developed after the pandemic arise: whether we should return to digital reality or whether digital education should be further deepened, are discussed in [8,9,10,11]. Science, technology, engineering and math (STEM) subjects underwent remarkable change due to advances in educational technology, and such advances are gradually changing their focus further. Institutions providing higher education are developing more engaging curricula for integrated learning, with a variety of software, as well as applications for remote communication. Educationalists admit that the most rational choice for universities are learning management systems (LMS), among which the Moodle LMS rightfully occupies a leading position [12,13]. Moodle is very popular all over the world, and is currently used to develop and implement e-learning courses and organize knowledge testing. Educators around the world appreciated this platform’s capabilities, both in the emergency transition to distance mode, and in the blended learning mode. Extensive methodological experience was accumulated in the creation of various tests. In a detailed up-to-date review of trends in the use of Moodle in education [14], it was shown that the platform effectively increases academic performance, student satisfaction and student engagement. A better study of the use of Moodle is required, in particular, the study of the teacher point of view. Further research is also needed on the use of Moodle in non-STEM and non-academic disciplines. Further application of ICT in the educational process offers several features that contribute to the advantages of this format. The authors support the point of view in [15] that the most evident are, firstly, a protocol of the student’s activity, which is created in the student’s personal account, where the so-called “learning events” (in LMS terminology) are recorded. With the help of these records, it is easy to track not only the effectiveness of an individual student, but also how systematically they worked, whether they completed all the tasks on time and with what effort they achieved the required score. Secondly, the electronic format for presenting the results of written assignments allows for automatic processing of the examination or test achievement statement.

Another advantage provided by ICT is the diversity of options for teacher assessment of student work; options include sending feedback to students for familiarization and work on errors, as well as ways of discussing their answers. In [16] the possibilities of Moodle as an online assessment tool for mathematical disciplines are described. Summative assessment of student progress and control of the gained knowledge are very important tasks in the educational process. It is common knowledge that, in addition to the control tests, training tests ought to be created [17].

The author of [18] draws the conclusion that most teachers take the right attitude towards, and have positive perceptions of, the meaningful use of ICT. It is evident that participants use different types of technology not only to enhance learning, but also to create an interactive atmosphere in the classroom. The authors of [19] admit that teachers in the twenty-first-century classroom are expected to facilitate student learning and create productive classroom environments and should be proactive in tailoring their teaching methods to the motivation of their students.

New opportunities are opening up for the creation of educational materials. For our research, the topic of effective, modern ways to present information for students was of interest. Accordingly, we decided to explore and use the potential of multilingual and bilingual approaches.

Polylingualism or multilingualism, being a multiple-aspect issue, may be considered either in the natural or in the educational environment. In the educational environment, numerous academic disciplines require dual-language instruction (most often it refers to teaching international students or teaching academic disciplines in English, as a component of English Medium Instruction). However, some disciplines, mostly of mathematical cycle, IT or Economics, combine sub-languages of their specialty with international terms in English, Latin, Greek and several other languages. The key areas in this sphere refer to academic didactic bilingualism/trilingualism; insufficient language skills; and triglossia/trilingualism, consisting of the native language, the first and the second foreign languages [20].

A number of works pertaining to the subject of multilingualism draw the conclusion that there is a lack of complex system-oriented on how to apply the basic principles of multilingualism in content and language integrated learning to methodological, psychological, pedagogical and methodical concepts.

Surveys presented by [21] coincide, to a certain extent, with the results of our investigation. The respondents to the survey in question associated multilingualism, firstly, with the ability of a person to use several languages; secondly, with the alternative use of several languages; and thirdly and fourthly—with similar values—referred to the coexistence of several languages within a social group and the coexistence of several communities in a given geographical area, respectively. The authors also found the intention to promote multilingualism in the didactic and extracurricular activities relevant and inferred that education is a form of dissemination of multilingualism.

We support the idea of several educators who conclude that mathematics is not as language dependent as other disciplines. Many English language learners excel in mathematics because, on the one hand, it is a “universal language”, but on the other hand, it abounds in international mathematical terms in English, consists mostly of signs and symbols and is carefully and purposefully designed. It is one and the same all over the world, though the people of different countries convert it into their particular spoken language. Mathematics supplies a language for the treatment of the qualitative problems of various sciences. Linguists call the language of instruction an educational and scientific substyle [22], stating that its characteristic features are a smaller number of terms and a larger number of examples.

It should be noted that, some time ago, such switching between languages within the same discipline was considered unprofessional. A similar situation was observed when teaching foreign languages (bilingualism and multilingualism were not welcomed by the academic community). Today, the use of several languages in presenting the learning material shows good results and contributes to the formation of an inter-disciplinary approach among students. Applying content and language-integrated learning, we base training for mathematics on the professional context, as part of the study of mathematics. We necessarily discuss how this can be calculated using various programs (Excel, R), while switching to the IT language. We developed and used a glossary of economics terms that combines an economics definition, an international (English) name, a symbolic description, a mathematical formula and calculation codes in R [23].

One of the ways to encourage students towards effective cognitive activity is scaffolding, “scaffolding theory” or the creation of a design of educational activity, which, with the assistance of a teacher, makes it easier for a student to assimilate educational material and helps to move them from the simple to the complex. It is a well-known fact that the methodological basis of the scaffolding technology is the theory of the zone of proximal development (ZPD), developed by the Russian psychologist L.S. Vygotsky. The research of this scientist is still in demand by teachers and psychologists. Thus, in the publication of [24], the concept of ZPD is expanded by including within it the active role of the child in the process of not only acquiring knowledge, but also realizing it [25]. Vygotsky’s thesis was further developed in the theory of scaffolding [26].

3. Materials and Methods

The research methodology consisted of mostly empirical methods, including observation and comparison, as well as analysis of modern scientific works of domestic and foreign authorship. Other research methods involve pedagogical design, pretests and posttests, test analysis and questionnaire surveys. The results from all the methods were then discussed and conclusions drawn.

3.1. Intra-Disciplinary Multilingualism

An important stage of the learning process is the initial presentation and further explanation of new material. The teacher selects a learning/teaching methodology, taking into account the learning objectives, students’ background knowledge and progress, and the time allotted by the curriculum. Mathematics allows us to describe and investigate quantitative, structural, stochastic dependencies and processes. The scientific sublanguage of mathematics penetrates into many fields of activity, and admittedly, is widely used in the field of finance and economics. An important task, today, is not only to convey to the student the knowledge embedded in the program, but also to form self-education skills, e.g., the ability to independently analyze scientific literature.

The language of mathematics with its terminology, logic, abstraction and symbolism should be understandable to the would-be graduate. However, education cannot be built only in academic language. In addition to special terms, any scientific language characterizes accuracy, brevity and the absence of personal and emotional coloring. Summing up such a strict formulation involves the use of other language codes. It is useful to begin the introduction of any concept by defining its expediency and necessity, thereby answering the favorite question of modern students: “Why?”. This may be required within the academic discipline or even professional context.

The use of the contextual approach in higher education confirmed its effectiveness. Its author, A. A. Verbitsky, believes that it is impossible to form students’ transferable skills for professional activity within a different framework of purpose, form and content to that of educational activity. Therefore, it is necessary to “impose the assimilation of theoretical and other knowledge by students on the “canvas” of the professional, and in [the] general practical, activity they are assimilating” [27]. The universality of the approach lies in the possibility of its use in teaching any discipline within higher education. The authors make extensive use of the professional context when teaching English for special purposes and mathematics [28].

Turning to the essence of the material studied, teachers, as a rule, resort to the simplification of scientific language, replacing terms with more understandable words and, if possible, making use of visualization in the form of graphs and structures.

Under the condition of reducing teaching hours, the language of teacher’s explanation tends to become descriptive, everyday and emotionally colored. It can be attributed more to the popular than to the scientific language style.

The definition or theorem is then formulated in the academic scientific language style and students are offered a symbolic notation of the same material.

For example, introducing the concept of the limit of sequence, the teacher expands on the marginal values in economics; discusses the meaning of the Russian word “пpeдeл” (Eng. limit); considers a graphic illustration; speaks about the “concentration” of points, their falling into a certain neighborhood, regardless of the number of the member of the sequence; and only after that is a strict definition given, which is then duplicated by an entry in the language of mathematical symbols:

$$\underset{n\to \infty }{\lim }{y}_n=a\iff \forall \epsilon >0 \exists n_0\in N: \forall n\ge n_0\Rightarrow |y_n-a|<\epsilon$$

In teaching mathematics, the sublanguage of mathematics is used alongside the language of structural and logical schemes. Moreover, different styles of discourse are applied: academic learning style, academic scientific style, academic slang, symbolic notation (mathematical formulas, quantifiers, etc.), as well as interdisciplinary terms derived from the professions and IT.

The use of mathematical slang is of particular interest. Slang is regarded as very informal and is typically restricted to a particular context. However, it gives the speech a novelty effect and makes it emotional, as words, phrases and expressions with a specific meaning are, nevertheless, understood by the interlocutors. For the authors of [29], slang replaces an academic synonym and can serve as a bridge or a barrier. This is done for further elaboration of the material in a descriptive style with a more emotional coloring or to express a certain emotional attitude.

Obviously, the definitions formulated in the academic scientific substyle and the language of mathematical symbols have the highest degree of abstractness and are the most difficult for students. Moreover, despite the fact that classroom hours are constantly decreasing, such introduction of definitions should be preceded by the step-by-step anticipation, where each step requires a particular sublanguage in a particular sequence:

(1)

The introduction of the topic is carried out using the academic scientific style of presentation in the sublanguage of mathematics;

(2)

In the next stage, working out the material is carried out and the language of mathematical symbols (sign–symbol language) is used;

(3)

The material is then repeated in a simplified language, in a descriptive style, and an academic learning style is applied, with mathematical slang being used if emotional coloring is required;

(4)

In the final stage, the sublanguage of mathematics is used in the context of the direction of student training and is supplemented by the sublanguage of the specialty. In this stage, the most frequently used technology is case analysis (Figure 1).

The conditions of the educational process impose changes on the presentation of educational information. It is necessary to take into account the reduction in the time allotted to the discipline, the addition of professional context and the peculiarities of perception by modern students. During the experiment and the survey, it was decided to investigate which forms of presentation of educational information are more understandable and preferable to students, in order to focus attention on such forms in the future.

3.2. Experiment Design

To achieve the research goal, an experiment was conducted using scaffolding technologies in reverse, the strategy of which was supplemented with elements of multilingualism, namely, the use of several discipline-specific sublanguages. Based on the idea of presenting mathematical information in various ways, an electronic test was designed and created on the Moodle LMS platform.

The test was conducted with first-year bachelor students at the Financial University studying Economics. A cohort of 159 students from the Faculty of Finance participated in the experiment.

The active part of the experiment consisted of three components: pretest, posttest and questionnaire, with the same group of respondents taking part in all three stages.

The purpose of the pretest was to identify the most effective ways of presenting a mathematical theory. For testing, we chose a topic on linear algebra, which until that moment, had not been studied either in a lecture, or at a seminar on mathematics.

The test items contained an explanation of the theory in various ways.

The posttest was offered to the same students after studying the relevant topic. The order of tasks and questions of the test didn’t change essentially. The purpose of the second stage of the experiment was to identify the progress of students’ academic achievements after the teacher explained the topic.

The content of the test was the material of Linear Algebra, on the topic of Operators and Quadratic Forms, and consisted of three questions on the:

• Definition of operators;
• Definition of quadratic forms;
• Compilation of a quadratic form matrix.

In the search for educational digital resources that not only check the student’s academic achievements, but also encourage the study of theory, as well as independent progress in solving educational problems, we focused on interactive test tasks. As an instrumental basis for the test, the task type “Interactive with several attempts” was, therefore, chosen. It allows several attempts at doing one task, while the student can use the clues embedded in the test. All tasks in the compiled test were created in the Formulas plugin and were of generating type. Moreover, along with the general wording of the task, each student received an individual unique option, which differed in numerical data.

When analyzing the results of the first two stages of the experiment for each question, we built the distribution of points received by students in percent, i.e., studied quantitative variables.

The third stage of the experiment was an anonymous survey of the same respondents, in order to receive feedback and analyze the effectiveness of the methodology of using multilingual opportunities to improve the perception and understanding of mathematical theory. The students were asked to prioritize the answer options by assigning them the appropriate scores. These variables can be considered qualitative or, more precisely, ordinal qualitative in nature.

4. Results

To identify the most effective ways for teachers to present educational information to modern students, and aimed at the study of new material rather than at the control of knowledge and training, a test “Operators and Quadratic Forms” was arranged.

Moodle was chosen as the platform for creating and implementing the test, offering a wide range of tools that open up new educational opportunities when creating control and measuring materials. For our study, it was important to present educational information in different ways.

Examples of various ways of presenting mathematical information within the framework of an intra-subject multilingual approach are shown in

Table 1. Multilingual approach to the formulations of a didactic unit on the example of a quadratic form definition.

Language	Definition
Academic scientific style with mathematical symbols (Mathematical text)	Quadratic form on $R^n$ is called a transformation $\Phi :R^n\to R$, which we can write in matrix notation as $\Phi (\overline{x})=X^T·A·X={\displaystyle \sum _{i=1}^n{\displaystyle \sum _{k=1}^n{a}_{ik}{x}_i{x}_k}}$, $\forall \overline{x}(x_1,x_2,\dots ,x_n)\in R^n$, in which $A=(a_{ik})$ is the symmetric matrix $(a_{ki}=a_{ik})$, and $X=\left(\begin{array}{c}{x}_1\\ x_2\\ ⋮\\ x_n\end{array}\right)$ is the column vector $\overline{x}$ form
Mathematical descriptive text (Description)	Quadratic form$\Phi (x_1,\dots ,x_n)$ is the expression in which all cross-product term $\overline{x}(x_1,\dots ,x_n)$ coordinates occur to the second power
Structural schedule with mathematical symbols (Schedule)	Quadratic form on $R^3$ would typically be expressed as $\begin{array}{c}\Phi (x_1,x_2,x_3)=\hfill \\ \hfill =\underset{only second power}{\underbrace{a_{11}{x_1}^2+a_{22}{x_2}^2+a_{33}{x_3}^2+2a_{12}{x}_1{x}_2+2a_{13}{x}_1{x}_3+2a_{23}{x}_2{x}_3}}\end{array}$
Mathematical example (Example)	$\Phi (x_1,x_2,x_3)=3{x_1}^2-8x_1{x}_2+4x_1{x}_3+2{x_2}^2-7x_2{x}_3-{x_3}^2$

.

In Moodle, an interactive question permitting several attempts means that, after an incorrect answer, there is an opportunity to use hints prepared in advance by the teacher. Each of the three tasks in our test contained a theoretical background and three answer attempts. The presentation of the theory in the main task, and in prompts, was represented by various styles and sublanguages of mathematics, examples of which are shown in Table 1. The maximum score for a correct answer without a prompt was 0.3 points. Each subsequent attempt reduced the maximum score by 0.1.

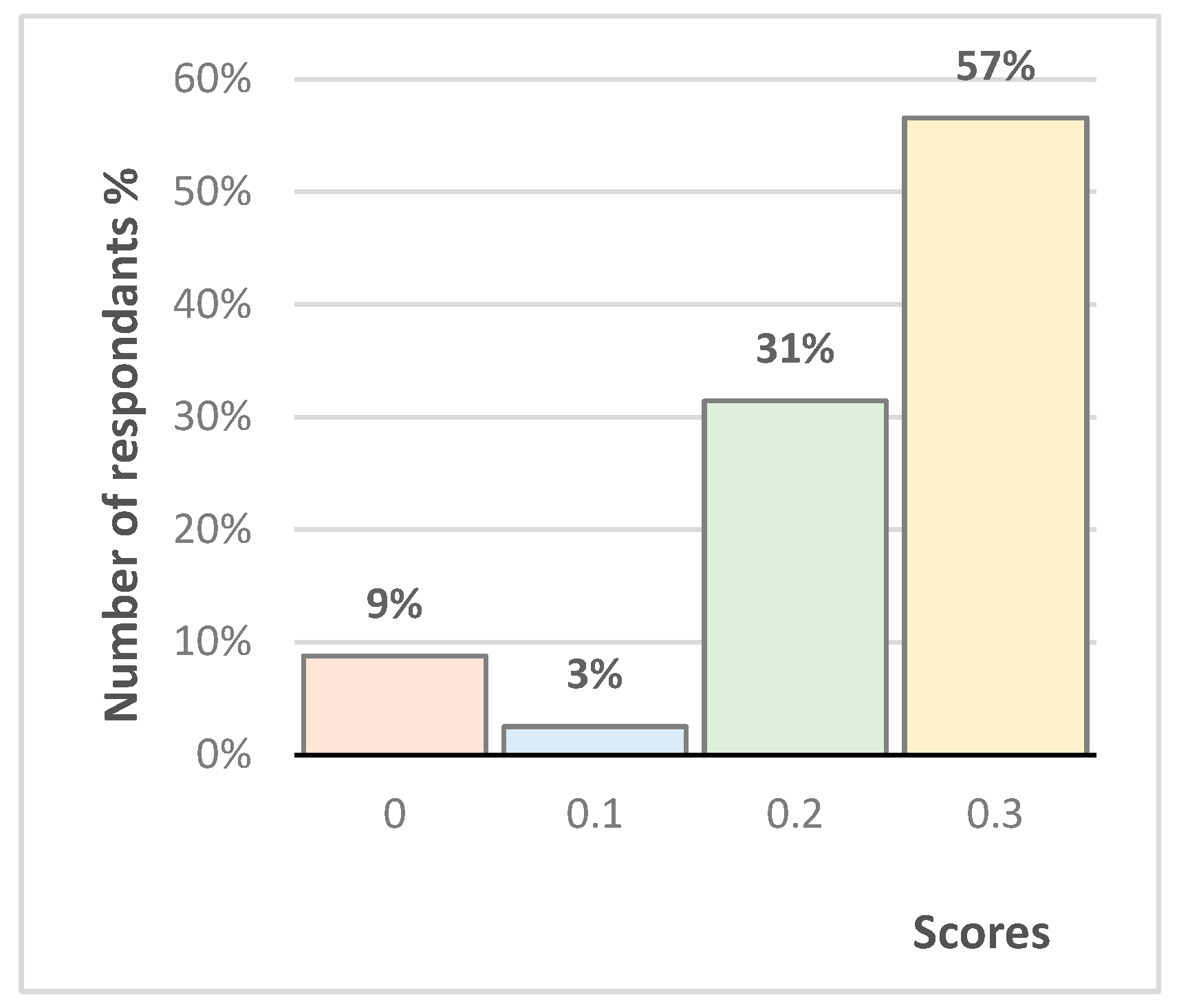
The first task concerned the definition of the operator. Its formulation was descriptive; the first clue gave a symbolic representation of the operator and the second clue contained an example. The distribution of answers to the first question is shown in Figure 2. Here and below, 0.3 points were awarded for an answer not using a clue, 0.2 points for using the first clue and 0.1 points for using both clues (Figure 2). As can be seen from the diagram, half of the students coped with the task without using a clue, only after reading the explanatory text. Another 37% answered correctly using a symbolic clue.

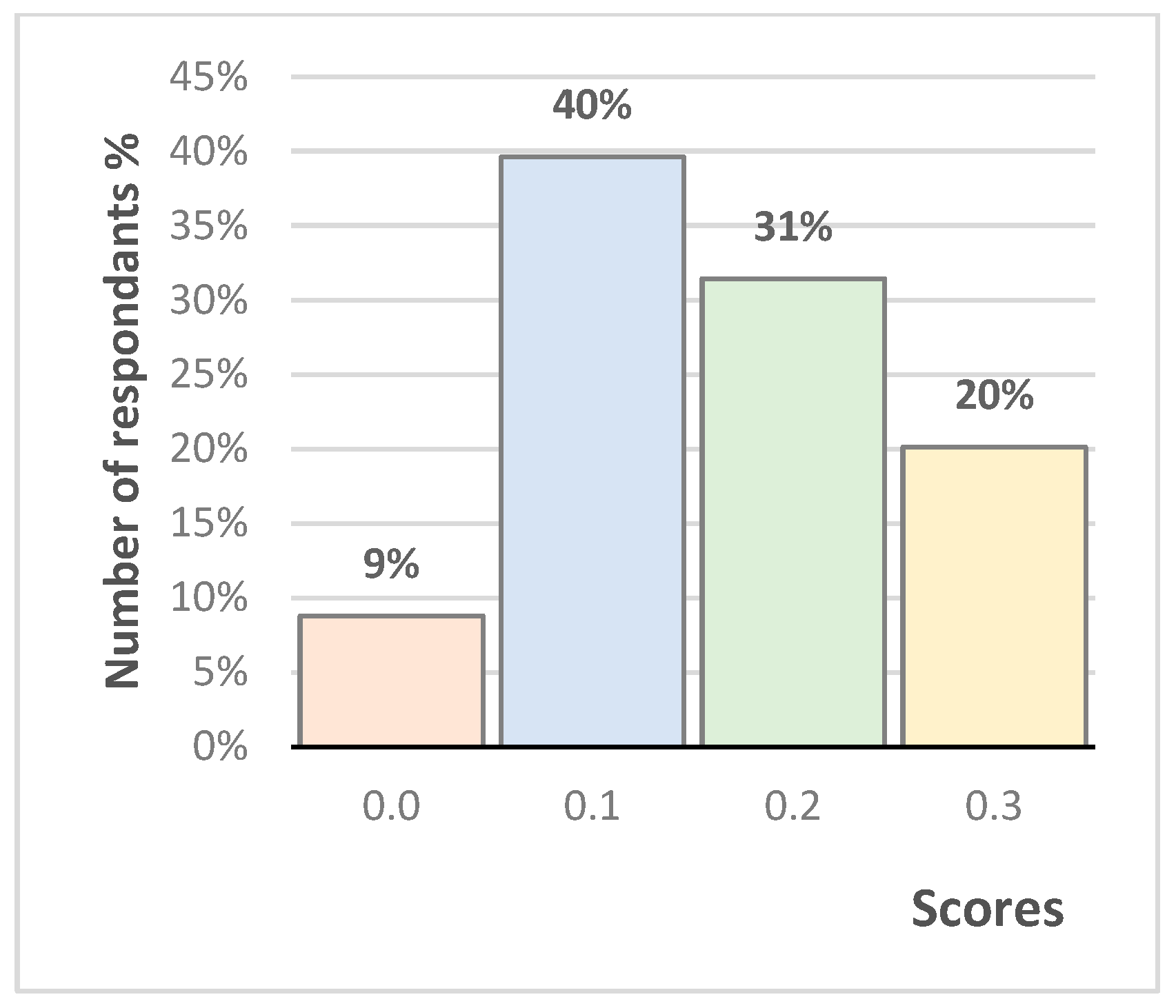
The second task with the definition of the quadratic form was formulated in a more complex mathematical language; the first clue contained a symbolic notation and the second clue contained an example. Figure 3 shows a diagram of the answers to the second task. Note that only 33% of respondents coped with the task without a clue, since the classical definition taken from the textbook was understood by students who had sufficient skills to work with a scientific text. However, the number of students who found the answer after being acquainted with the symbolic designation was quite large.

The third task on the distribution of styles duplicated the second (Figure 4) and concerned the compilation of a matrix of quadratic shape.

To study the effectiveness of students perception of mathematical information, a summary diagram was compiled for all tasks (Figure 5). Here, the data from all three tasks were calculated. The number of correct answers were assigned to tasks or clues formulated in the mathematical text, with the help of mathematical symbolism, descriptive language, or with an illustration of an example. The most successful presentation form for students (namely, 76% of correct answers) were tasks written with the help of mathematical symbols and presented in the form of a visual block diagram.

It is evident that the best result was for tasks and hints formulated in the language of mathematical symbols; this shows that it is necessary to strengthen the symbolic and structural–logical presentation of educational material. At the same time, the analysis of the summary diagram allows us to conclude that all the described methods (languages) of presenting information are in demand by students. Therefore, despite the reduction in training hours, teachers should not reject any of them.

The interactive mode of the task, incorporating several attempts and presented above, can be used to familiarize students with mathematical definitions and properties, i.e., as a drill but not verification tests. The clue system can be implemented as a scaffolding support when scaffolding technology is applied.

Furthermore, in our case, the well-known technique was expanded by the so-called “flipped” scaffolding, when a new concept was initially given without specially organized propaedeutics. Further hints were formulated from more complex to simpler. This approach is a good motivating platform for the most competent students, who always try to complete the task without using the clues. Orientation to such students, and appropriate tasks for them, must be present in the teacher’s arsenal. Independent acquaintance with definitions and formulations contributes to the formation of skills, thereby enabling students to work with scientific literature, autonomously.

The use of clues also makes it possible to activate the work of students for whom mathematics is far from being easy. After studying the clues, they are more likely to complete the task.

On concluding the test, the task completion rate is calculated; this refers to the percentage of tasks that users were able to successfully complete. This metric is measured at the end of the test.

The conducted test on new educational topics showed the interest of students during the lecture and practical training. The test, repeated with the same tasks after studying the material, showed good results.

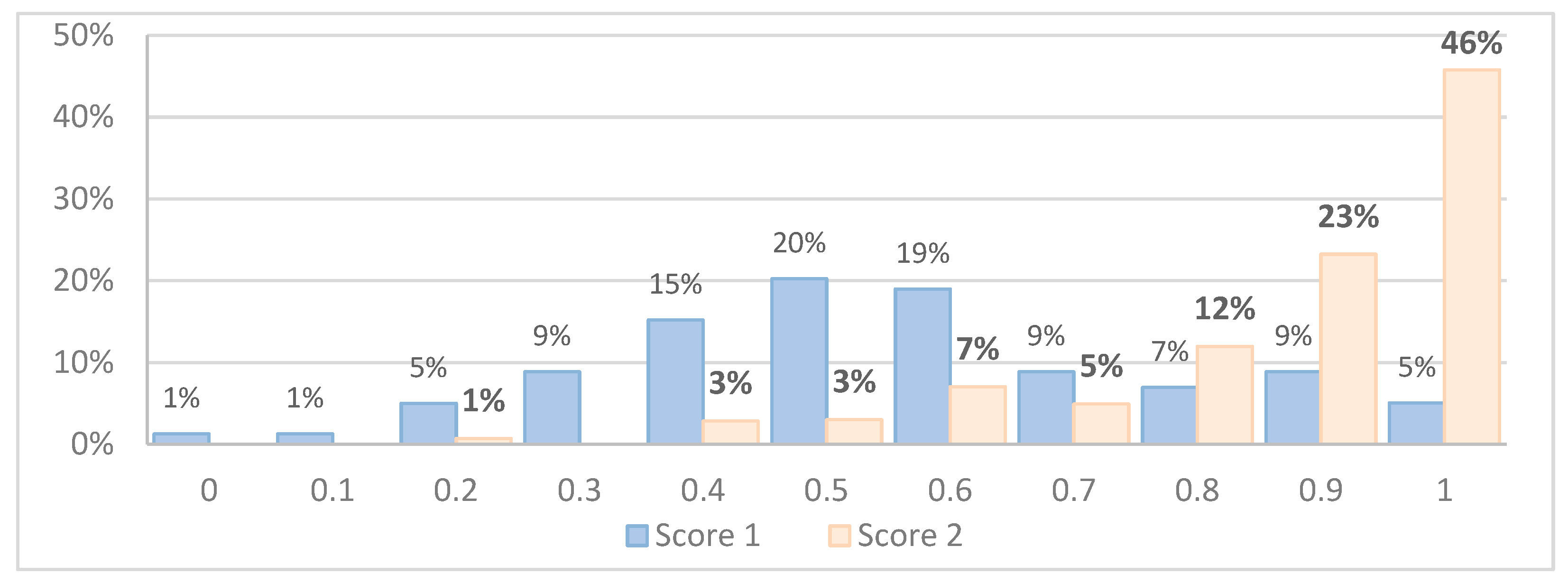
We do not provide statistics for the posttest for each task separately, but Figure 6 shows the distribution of points for the entire test before studying (Score 1) and after studying the material in class (Score 2). Note that in the first case, 5% of students carried out all the three tasks without prompting, and in the second case this number increased to 46%.

The experience of conducting a test with clues showed the interest of students in this type of educational activity. Strong students were motivated to respond without using clues, and weak students had the opportunity to complete the task after learning the clues. The results of the second test, conducted after teacher’s explanations, show the importance of face-to-face transfer of knowledge and personal communication with students.

5. Discussion

The results obtained in this research show that students perceive the language of symbols and structural–logical schemes more effectively. Having the extensive experience of dealing with iconic information of various kinds in a digital environment, they prefer concise, rigidly structured information. In this regard, the task of presenting educational information in this form arises. Visual conceptualization, based on the tools of visual thinking, comes to the fore [1]. The authors formulate the didactic principles of such visual conceptualization in regard to the educational text:

• Presenting structured semantic blocks to students;
• Embedding these blocks into a single whole, thereby motivating students to deploy condensed information;
• Modeling situations for using knowledge in practice, “here and now”.

The latter is especially relevant for modern students. The need to design and use new visual didactic tools to improve learning technologies is discussed in the study [30]. The presentation of educational information in the form of multidimensional logical–semantic models of visual–didactic regulators is proposed. Their content component is presented in natural language, and their logical component is presented in the graphic language. The keywords are located along the coordinate axes on the basis of the greatest semantic proximity; between the nodes of neighboring coordinates, there is an associative link and a semantically coherent system of keywords. Unfortunately, this paper does not provide data on the experience of using such regulators in the educational process.

Modern digital resources provide powerful support for the implementation of new forms to present educational information. Such resources allow the design of interactive electronic educational materials based on the concept of cognitive visualization [31]. Cognitive visualization allows instructors to shift the focus from the illustrative function in teaching to the development of cognitive abilities, such as abstract and critical thinking.

The academic success of university students depends on the pedagogical experience and emotional flexibility of instructors and lecturers who are capable of creating a positive educational environment for the transfer of complex theoretical content of the lectures and workshops [32].

The individualization of the learning process is promoted by the creation of didactic materials that take into account various types of cognitive processes (perception, memory, thinking). Digital tools make it possible to present material in various forms. For theoretical material, therefore, a video lecture, the text of a lecture, a presentation, a structural and logical diagram [33] are all appropriate.

In addition to the test, in order to obtain feedback and analyze the effectiveness of the methodology for using multilingual opportunities to improve the perception and understanding of mathematical theory, a survey of first-year students of the Faculty of Finance was organized. The survey involved 132 students who completed a pretest and a posttest. The results of the survey can be seen in Figure 7 and Figure 8.

Students were asked two questions about the forms and methods of presenting new theoretical material in mathematics. They ranked the suggested answer options from 1 to 6 according to their preferences. For each position in the answers, the mean was calculated, which made it possible to determine the priorities in the students’ preferences.

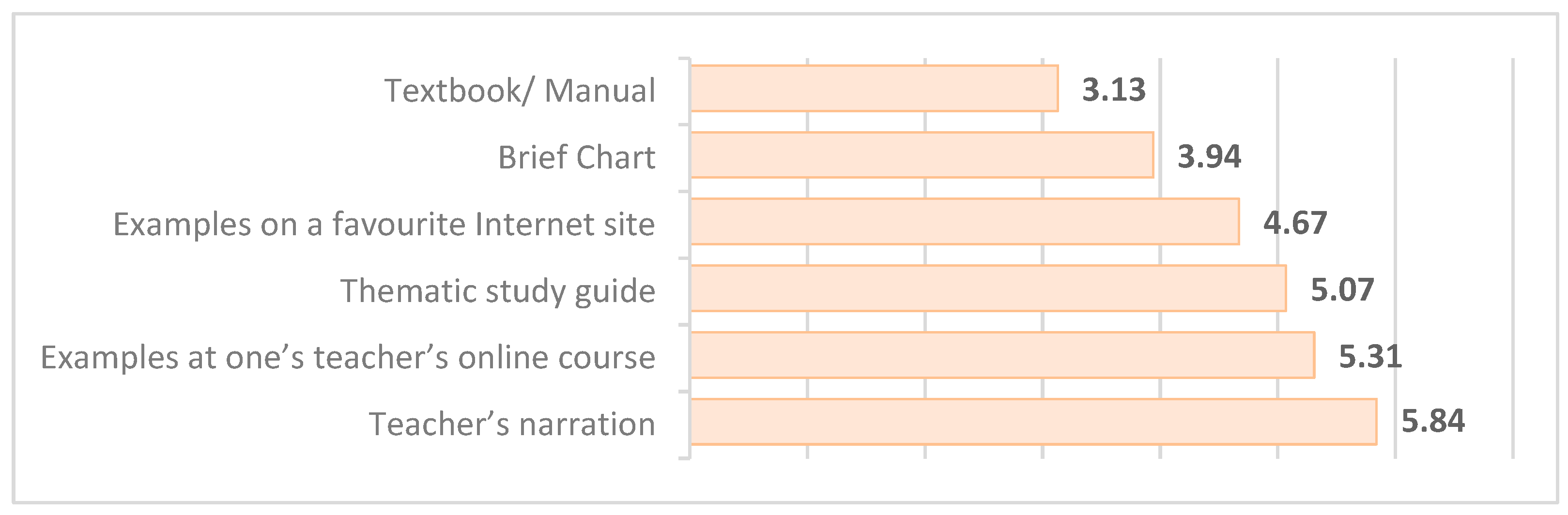
The first question concerned the form of presenting the new material (Figure 7). The largest number of students selected the teacher’s explanation. This opinion is especially important since the students surveyed had quite a vast experience of forced distance learning during the pandemic. This suggests that the total transition to online learning is not supported by students. At the same time, digital technologies today can provide significant qualitative support to the educational process. Our students rated the analyzed examples second in terms of the forms of presentation of educational material in their teacher’s electronic training course. The reference to the teacher was made by the students themselves, since throughout the year we regularly posted interactive examples in our courses with solutions and theoretical references in the form of structural and logical diagrams. The creation of such digital materials is an important task for the teacher, and the fact that the students put the classical textbook in the last place in popularity confirmed this.

The second question concerned the form of presenting information (Figure 8). Here, the majority of students preferred the analyzed example. This, once again, emphasizes the significance of obtaining information “here and now” for modern students and the emphasis on its practical application. Further, the answers differed slightly, but it is still noteworthy that many students are ready to delve into the essence of the formulas, which is important not only for understanding the subject, but also for the development of abstract thinking.

The survey results confirm previous studies [7,9,10,11]. Students do not want to relinquish face-to-face communication with a teacher in favor of remote communication. At the same time, they are ready to actively use modern digital resources enhanced by structural visualization, which is consistent with the works [19,31,32]. The priority of students in relation to examples of problem solving shows their clear orientation towards the practical use of the acquired knowledge, which corresponds to [30]. The use of this orientation in students allows the contextual approach [23,28]. The low demand for classical textbooks confirms the conclusions of psychologists [2] about the reluctance of students to read long texts. This once again confirms the importance of creating new educational resources that are compactly structured and practice oriented. In particular, for mathematics, a more active use of the language of formulas in the presentation of new material has broad prospects.

6. Conclusions

The conducted research allows us to draw several conclusions regarding the presentation of mathematical information to modern students.

• When explaining new material and developing learning tests for Mathematics, it is advisable for the teacher to turn to multilingual intra-subject opportunities. Explanations in a popular descriptive language, examples, classical scientific and mathematical symbols, and even slang, allow students to better understand the considered material while, simultaneously, developing logic and abstract thinking. A mandatory foundation for explaining a new topic should be a professional context. Elements of interdisciplinary multilingualism strengthen the teaching of mathematics and make it meaningful for students. In our case, the teacher should navigate in economic terms, their English names and commands of programming languages in order to make the necessary calculations on a computer.
• The study clearly confirms the hypothesis that present-day students need educational information to be presented in special forms; these should be maximally structured and based on visualization and supporting symbolic signs. It is especially important to create brief visual structural diagrams for students, and if possible, that these are kept together with the main theoretical material of the topic given in its concise form (e.g., on not more than one page) and based on the symbolic language of mathematics.
• In our opinion, the expanded technology of scaffolding has great potential, i.e., “flipped scaffolding”, when the educational material first appears without clues, and then the clues appear from complex to simple. This approach allows instructors and lecturers to stimulate strong students and encourage the others to make use of fewer clues.
• Educational activity with higher education students should not completely switch to a remote format.
• The results of tests and questionnaires confirm the high importance of the full-time educational process and personal communication between the teacher and students. At the same time, a teacher can, and should, widely use the possibilities of digital technologies both for organizing communication, training and testing, and also for presenting educational information.
• The experience of the pandemic demonstrated that instructors and lecturers must be prepared to provide quality education even when the transition to online learning is forced. To do this, it is necessary to provide students with modern digital educational resources and tools. In particular, the development of generated tasks in the Moodle LMS provides ample opportunities for the study of mathematics. In addition, a significant proportion of students with special health needs are constantly in need of additional electronic manuals with interactive elements and step-by-step analyses for problem solving. The developing inclusive education has shown a lack of such materials.

Of particular interest, in our opinion, is the fact that a significant number of students prefer the explanation of mathematical theory in the language of symbols. This trend has not been previously noted in pedagogical research and awaits further study.