Abstract
The paper is written as a reflection on the author’s online teaching of a graduate elementary mathematics content and methods course through the asynchronous modality. The need for developing skills in posing problems that integrate non-technological and technological problem-solving strategies is emphasized. Such problems are considered agency of design-based mathematics education. The importance of revealing hidden mathematical ideas stemming from teacher candidates’ willingness to explore self-posed problems within the forum components of the course is discussed. Using these hidden ideas, the paper demonstrates connectivity among different mathematical concepts including historical connections. Teacher candidates’ reflections on the course have been included and reviewed.
1. Introduction
The concept of the technology-immune/technology-enabled (TITE) problem was introduced in [1] as an extension of the Type I vs. Type II technology applications framework [2]. Technology application of the former type deals with tasks characterized by what is often called scripted instruction [3], a didactic approach grounded in drill and practice emphasizing the primality of procedural skills [4,5]. An application of the latter type deals with using technology as a conceptual tool in support of design-based learning [6,7] emphasizing pedagogy of reflective inquiry [8,9]. Nowadays, in order to sustain educational gains from the Type I vs. Type II technology applications framework in the context of mathematics, teacher candidates have to be proficient in designing tasks that are still cognitively challenging despite (or perhaps because of) commonly available digital power of symbolic computations and graphic constructions. This is where a TITE concept comes into play. A TITE mathematical problem cannot be automatically solved by software, yet the role of technology in solving the problem remains critical. TITE problem solving may include the use of multiple software tools in support of a single mathematical task. In many cases, using different tools—numeric, symbolic, graphic—not only provides support in solving a problem but also motivates one’s deep thinking about experimentally obtained results that can lead to formulating a new problem. Even if an experiment begins with using technology in an intuitive way [10] and experimental results are unintended, the emergence of deep thinking about them, enabling the intuitive to give way to the conceptual, serves as a testament to design-based learning focusing on creative, theory-oriented thinking.
Educational computing in mathematics elevates interplay between experiment and theory to a higher cognitive level and it may be supported by an electronic spreadsheet and Wolfram Alpha—a computational knowledge engine (https://www.wolframalpha.com accessed on 19 May 2022) often used as mutually complimentary tools [11]. If problem-solving activities are scripted and expected to be memorized, their non-dialogic structure does not allow for epistemically oriented activities, through which learners of mathematics can practice the idea of using different problem-solving techniques leading to the same answer. In doing so, they can design their own problem-solving techniques and, in the true spirit of a student-centered classroom [12], pose their own mathematical problems to solve. At the same time, an epistemic development always has a pragmatic component in the sense of memorizing arithmetical facts through interacting with numbers under the umbrella of inquiry into the relationships that the numbers form.
Design-based (or problem-based) approaches to education emerged in the 1990s from the fields associated with engineering design [13,14] towards developing the science of education by taking advantage of new technologies and by investigating how different designs of learning environments affect teaching and learning in the technological paradigm [15]. Whereas the ideas of design education, especially at the pre-college level, had major influence on teaching science [16], quite a few researchers and practitioners of mathematical education described educational innovations of the subject matter from the perspectives of design-based teaching and learning [17,18,19,20]. Due to the rapid advent of technology, both digital and tactile, in the K-12 mathematical classroom, the design of technology-rich environments for the teaching and learning of mathematics focused on the importance of inquiry into the appropriate use of the modern-day tools by future teachers of mathematics, including those intended to teach the subject matter at the elementary level. With this in mind, the main objective of this paper is to contribute to the conception of design-based education from a mathematics teacher education perspective, emphasizing the use of technology in the context of asynchronous education. More specifically, the author’s goal is to demonstrate how the concept of TITE problem solving and posing may become an agency of design approaches to the teaching of mathematics to elementary teacher candidates within mathematics education courses, which, despite a number of negative affordances of teaching such courses using the Internet [21], have been increasingly taught online around the world.
An important aspect of an asynchronous course is the use of a discussion forum designed by the course instructor to structure and motivate students’ engagement and peer interaction, as well as (ideally) to maximize their learning. Although discussion forums have been mostly associated with asynchronous courses [22,23,24,25], the forums can also be integrated with blended educational courses [26,27] and be a part of synchronous and face-to-face learning modalities [28,29]. Whereas the author’s experience in the design of computational learning environments emphasizing the TITE concept includes traditional and synchronous mathematics teacher education courses, experience with designing and managing a discussion forum enriched (as will be shown below) by digital and virtual tools is the most recent one being limited to the asynchronous educational modality.
Design thinking in mathematics education, among other things, includes the appreciation of technological advances, critical thinking, and learning from mistakes. This kind of thinking was demonstrated by an elementary teacher candidate, one of the author’s students in a mathematics content and methods course (asynchronous enrollment of some 20 students), who believes that “Wolfram Alpha is a great tool for students to be able to manipulate and receive actual feedback immediately. This feedback helps students gain independence in their learning with trial and error. Some students need to be able to make these errors and correct them without feeling like a failure, among others. Wolfram Alpha really helps individuals learn how to problem solve and use complex critical thinking skills. I had never heard of Wolfram Alpha before this course and now I cannot wait to provide my students with another tool to help them gain confidence in their mathematical and critical thinking skills.” Design-based learning activities of posing and solving mathematical problems supported by modern-day digital tools motivate students’ interest in “evidence of proof, the recognition of new phenomena, their reproduction and utilization, [and thereby] undoubtedly place it [mathematics] among the experimental sciences” [30] (pp. 73–74). This, in turn, by acquiring new information through critical reflection when one, by “looking at the past … can more wisely build the future” [31] (p. 80), makes it possible for transformative learning [7] to take place through a continuous reflection on a solved problem through the (potentially) never-ending cycle “solve–reflect–pose.” That is, problem solving and posing can be seen as an iterative learning process integrating conceptual and procedural knowledge [32].
Nowadays, especially within an online asynchronous mathematics education course, the cycle “solve–reflect–pose” can be enhanced procedurally through the use of a variety of virtual environments, both physical and digital, for sharing problems as responses to prompts initiated by the instructor within the forum component of the course. While the “solve–reflect–pose” cycle is a typical technique used by professional mathematicians, one way to pursue it in an asynchronous mathematics teacher education course with a contribution of a “more knowledgeable” instructor is through the process of student-to-student interaction within the forum. By experiencing reciprocity in posing problems, teacher candidates can learn that one of the main difficulties involved in this process is finding the right balance between the challenge and the frustration, sentiments commonly associated with solving problems. David Hilbert, in the keynote address to the 1900 International Congress of Mathematicians, advised the audience, “a mathematical problem should be difficult … yet not completely inaccessible” [33] (p. 438). This advice also sends a message to educators in general, who, more recently, were reminded that “subject matter has an instrumental value as a means of promoting discovery” [34] (p. 362). As will be shown in this paper, mathematical discovery can be initiated by a student by reflecting on their solution to a problem posed by the instructor and being willing to explore mathematics beyond the information given [35]. It is the prompt contribution of the instructor to emerging creative discovery by a student that makes it possible for the TITE concept to serve as agency for design-based mathematics education.
2. Materials and Methods
Two types of materials have been used by the author when working on this paper. The first type includes teaching and learning mathematics standards from the United States and Canada.
These include Common Core States Standards [36]—the major educational documents in the US at the time of writing this paper, recommendations for teacher educators by the Conference Board of the Mathematical Sciences [37]—an umbrella organization of 19 professional societies in the US concerned, in particular, with mathematics teacher education, Standards for Preparing Teachers of Mathematics by the Association of Mathematics Teacher Educators [38], and mathematics curriculum materials for grades 1–8 by the Ontario Ministry of Education in Canada [39]. The university where the author prepares elementary teacher candidates to teach mathematics is located in upstate New York in close proximity to the province of Ontario, and many of the author’s students are Canadians pursuing their master’s degrees in education. This diversity of students suggests the importance of aligning mathematics education courses with North American perspectives on the teaching and learning of elementary mathematics. Whereas there exist multiple arguments toward more context-based and authentic mathematics curricula, it appears that regardless of the direction one takes in the teaching of mathematics, the importance of design-based education with an emphasis on alternative perspectives and integrative thinking, when students “check their answers to problems using a different method … understand the approaches of others … and identify correspondence between different approaches” [36] (p. 6) thereby enabling teachers “to give full attention to alternative possibilities” [8] (p. 30), is not debatable.
The second type of materials is technological (both digital and physical). The materials include computational knowledge engine Wolfram Alpha, an electronic spreadsheet, and a variety of virtual manipulatives. North American standards uniformly call for the teaching of multiple solution strategies in solving a single problem, for solving problems using technology, for encouraging students to ask questions while expecting teachers not to reject a challenge coming from students’ questions, to make mathematical connections through multiple representations, and to pose new problems. The paper is supported by solicited reflections by teacher candidates in which they describe their mostly novel experience using digital tools when working on the course assignments and willingness to use their transformative learning of technology in their own classroom as well as with their own children.
There are two types of data (the data shared includes the description of one candidate’s contribution to the forum (Section 4) that serves as the crux of the discussion in the subsequent sections of the paper and five (selected out of about 100) technology-related comments by the teacher candidates (Introduction—one comment, Section 8—two comments, Conclusion—two comments)) shared in this paper: an elementary teacher candidate’s epistemically rich serendipitous contribution to the discussion forum and several didactically pragmatic representative reflections by future elementary teachers regarding the use of technology in the teaching and learning of mathematics. In general, the latter type was collected, using two major instruments, over a few semesters of teaching asynchronously. Firstly, the candidates’ contributions to the forum that were motivated in part by prompts—a series of questions posed by the author for each week (out of 14 total)—were analyzed to structure a discussion on a specific topic (e.g., Conceptual Shortcuts, Friendly Face of Mathematics, Wolfram Alpha, Informal Geometry). Secondly, solicited comments by teacher candidates in response to open-ended questions included in the final exam were analyzed (e.g., Why do elementary teacher candidates need to possess “deep understanding” of mathematics?). The use of different instruments serves as evidence of triangulation [40] in qualitative data collection from solicited and non-solicited sources. This triangulation perspective makes it possible to avoid seeing the author’s reflections on the course design through the lens of such reflections, as mentioned by Artigue in [41] (p. 314), being “necessarily subjective” because they are balanced by teacher candidates’ reflective thinking. The data analysis indicates the candidates’ appreciation of the need for deep mathematical knowledge as the pivot of the modern-day pedagogy of multiple, technology-enhanced, solution strategies by means of which one can make schoolchildren interested in the subject matter [37,38].
Methods specific for mathematics education used in this paper include computer-based mathematics education, standards-based mathematics, and problem solving and posing. Activities described and analyzed in the paper are aimed at developing in the candidates conceptual understanding of mathematics [37] and may be characterized as action learning. The concept of action learning was introduced in [42,43] in the context of business education and problem solving. The genesis of the idea of action learning can be traced back to the writings of John Dewey, who emphasized the importance of educational activities that include “the development of artistic capacity of any kind, of special scientific ability, of effective citizenship, as well as professional and business occupations” [44] (p. 307). It is scientific ability and professional mindset that allow one, in true congruence with the principals of action learning [42], to develop through reflective questioning, either self- or peer-initiated, a deeper insight into the initial solution to an important problem.
In mathematics education the concept of action learning is understood as learning through students’ work on a real problem followed by true reflection on this work under the guidance of their professor, leading to posing and solving new problems applicable to reality and seeing learning as the primary goal of the action [45]. From an educational perspective, a mathematical problem may be considered real if it is important for a deeper understanding of the subject matter and provides multiple opportunities for action learning by taking action and reflecting on the results [42] in order to navigate through the web of classic ideas, the appeal of which is due to their connectivity that unexpectedly eases their perceived complexity. Max Wertheimer, one of the founders of Gestalt psychology, argued that for many children “it makes a big difference whether or not there is some real sense in putting the problem at all” [46] (p. 273) so that reflecting on a real-life problem as “simple” as putting cookies or candies on plates is likely to be appealing to them. In general, reflection is the main mechanism of metacognitive development, something that Flavell [47] defined as “one’s knowledge concerning one’s own cognitive processes and products or anything related to them” (p. 232). In most cases, reflection, or “inquiry about inquiry” [48] (p. 215), has to be supported by a “more knowledgeable other” [49], because, as noted in [50], without being cognitive in a field, one may not be metacognitive in the field. Finally, metacognitive development is critical for acquiring mathematical skills of “integrative thinking and problem solving” [39] (p. 30) when using “previously established results in constructing arguments” [36] (p. 6).
3. A TITE Problem: An Example
As an example of a TITE problem, consider
Problem 1.
Let the general term of a numeric sequence be defined as half the product of two consecutive natural numbers. From this sequence, every other term beginning from the first one is removed. This procedure is applied to the sequence three times. Using a spreadsheet, generate the resulting sequence and find its term of rank 100. Determine the rank of this term in the original sequence.
Discussion.
According to the definition, the terms of the sequence are
One can use a spreadsheet (Figure 1) to generate more terms of this sequence: 1, 3, 6, 10, 15, 21, 28, 36, 45, 55, and apply the elimination procedure for the first time to get 3, 10, 21, 36, 55, …—terms of even rank. A TI part of the problem is to “express regularity in repeated reasoning” [36] (p. 8) by describing algebraically the general term of the last sequence. One can see that
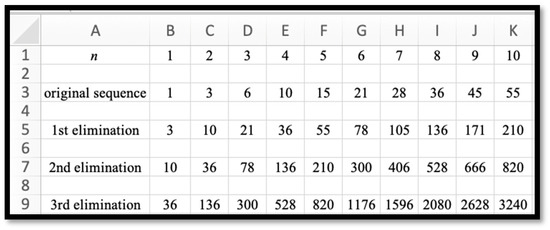
Figure 1.
Spreadsheet modeling of the elimination problem.
Once again, using a spreadsheet, one can check to see that the TI part works and apply the elimination procedure to the last sequence to get 10, 36, 78, 136, 210, … . A TI part of the problem is to describe the general term of the last sequence. One can see that
Finally, one can use a spreadsheet to check that the TI part works and apply the elimination procedure to the last sequence to get 36, 136, 300, 528, … . One can see that
Therefore, . Because any number in the original sequence and its subsequences is half the product of two consecutive integers, the representation implies that 800 is its rank in the original sequence . One can see that the problem needs a spreadsheet (a TE part) in order to generate sequences subjected to the process of elimination and as a verification of the correctness of algebraic generalization (a TI part) needed to “extend previous understanding of arithmetic to algebraic expressions” [36] (p. 43).
Furthermore, one can use Wolfram Alpha to verify the correctness of algebraic generalizations within a TI part of problem solving. As shown in Figure 2, entering “36, 136, 300, 528, …,” the first four integers that survived the third elimination, into the input box of Wolfram Alpha not only confirms the algebraic formula but also generates the number 320,400 as part of a numeric table into which the results of the third elimination were arranged. As Hans Freudenthal, one of the leading mathematics educators of the second part of the 20th century, put it, “It is independency of new experiments that enhances credibility … [for] repeating does not create new evidence, which in fact is successfully aspired to by independent experiments” [51] (pp. 193–194). Indeed, using different computational tools in support of the TE parts of problem solving enhances credibility of its TI parts and, by developing self-confidence in intellectual growth of the modern-day inquirer, contributes to the fulfilment of the transformative learning of mathematics. Put another way, just as the use of different theoretical approaches to a problem enhances the validity of the final result, the use of more than one digital instrument in solving a TITE problem provides evidence of triangulation [40] of mathematical reasoning using technology.
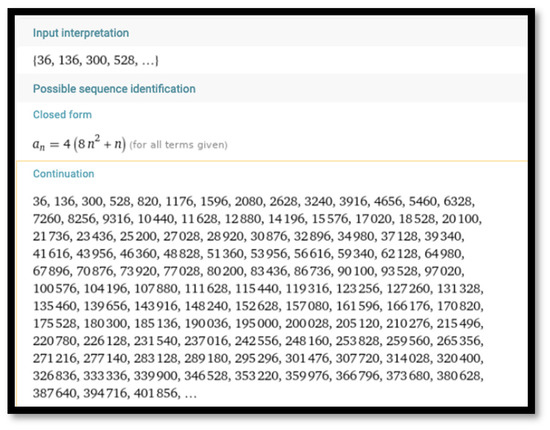
Figure 2.
Wolfram Alpha provides closed form and continuation using just four numbers.
4. Reflecting on an Unexpected Exploration by an Elementary Teacher Candidate
According to Common Core State Standards, already at the kindergarten level students are expected to “use basic shapes to construct more complex shapes” [36] (p. 9). With this expectation for young children in mind, elementary teacher candidates, enrolled in a master’s-level mathematics education course taught online through the asynchronous modality, were offered the following hands-on task.
Problem 2.
Construct a 4-by-4 square using 16 (multicolored) counters. Then rearrange the counters to build an isosceles triangle. Write an equality describing such rearrangement.
Discussion.
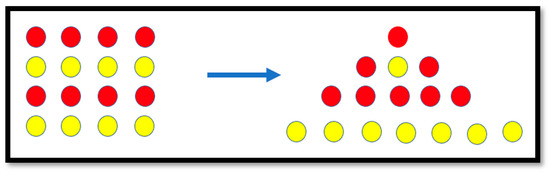
The goal of the task was for teacher candidates to experimentally “discover” a property of squares being the sums of consecutive odd numbers stating from one (Figure 3), the general form of which is
This property can already be observed within the multiplication table by interpreting gnomons (something that, according to Heron of Alexandria, a Greek mathematician and engineer of the 1st century A.D., when added to or removed from a shape, yields a similar formation) as images of odd numbers. Didactically, just as the teaching of writing can “be arranged by shifting the child’s activity from drawing things [the first-order symbols] to drawing speech [the second-order symbols]” [49] (p. 115), the mathematical ideas can be taught to young children (and their future teachers alike) as transition from tasks involving concrete objects (the first-order symbols) to describing the images constructed through culturally accepted mathematical notation (the second-order symbols). Indeed, the above formula belongs to the most basic relations of elementary number theory, something that at the pre-school age was noticed (perhaps playing with children’s blocks) by A. N. Kolmogorov, one of the major contributors to mathematics in the 20th century, who considered the formula his first mathematical discovery [52]. The importance of using this task with elementary teacher candidates is in its historical and socio-cultural significance, connection to basic concepts and structures of primary school mathematics (including odd numbers and the multiplication table), and direct accentuation of tactile learning (encouraged by educational psychology) as the critical instrument of mathematical education.

Figure 3.
An experimental approach to the relation
One teacher candidate, clearly demonstrating design thinking in mathematics education as a means of “seeking the release of human potentialities” [53] and “desire to go on learning” [54] (p. 49), decided to experiment with other rearrangements. In the words of Canadian mathematics educators, “when problem solving is … relevant to students’ experiences and derived from their own problem posing, it furthers their understanding of mathematics and develops their math agency” [39] (p. 75). To this end, the candidate tried to construct through trial and error an equilateral trapezoid out of 16 counters (each row of which has one more counter than the previous row). When this construction did not work (see explanation in Section 6 below), he noticed that if the first row of counters forming the square is removed, then, out of the remaining counters (forming a rectangle), such a trapezoid can be constructed (Figure 4). In terms of the second-order symbols, this was described as
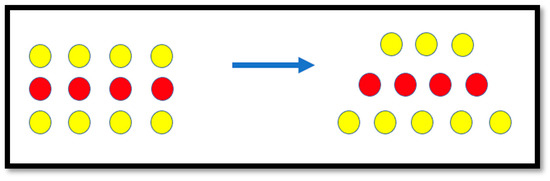
Figure 4.
Rearranging a rectangle into an isosceles trapezoid.
The candidate went even further and, out of 12 counters forming an isosceles trapezoid, constructed an isosceles triangle and two self-embedded regular pentagons (Figure 5). Although these might be seen as out of mainstream constructions, they were not entirely accidental: Out of 12 counters used by the candidate, four counters were red and eight counters were yellow. This, as the candidate explained, prompted the construction of all the three shapes. In terms of action learning [43], one can say that the candidate, by seeing the original task, due to its concreteness and tactile nature, as a real problem, took action and reflected on the results.
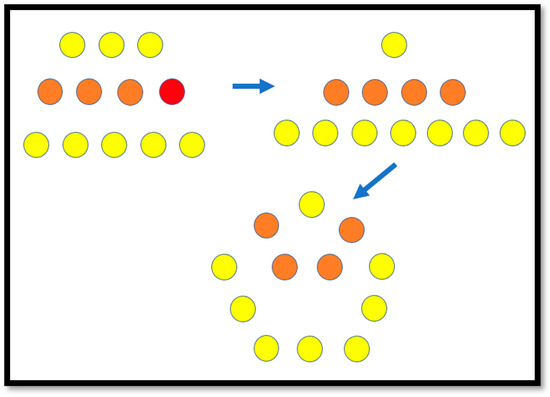
Figure 5.
Another experiment: from trapezoid to triangle to pentagon.
The author envisioned that, while being unable to ask questions in person, students still could (and should) be curious (and thus their possible curiosity has to be addressed through the online course management system where the instructor can leave reflections on the candidate’s responses to prompts):
- Is there something special behind the constructions of isosceles trapezoids, isosceles triangles, and self-embedded regular pentagons?
- Does the number of rows in an isosceles trapezoid (each row of which has one more counter than the previous row) have to be the same as in an isosceles triangle (the difference between the number of counters in each row is the same) in order for the latter to be constructed?
- Can more than one isosceles trapezoid be constructed out of an isosceles triangle?
- Can any isosceles trapezoid be rearranged to have self-embedded regular pentagons?
- Is there a square that can be rearranged into an isosceles trapezoid?
- Is there a square that can be rearranged into an equilateral triangle (each row of which has one more counter than the previous row)?
- Is there a square that can be rearranged into self-embedded regular pentagons?
Note that the above questions and their order can be interpreted through lens of the didactic cycle “solve–reflect–pose” [32]. In fact, it was due to the candidate’s self-engagement in action learning that such questions came to light. That is, the more information the mind has processed, the more intricate it formulates new inquiries into related situations. Below, the seven questions will be addressed through those lenses.
5. A TITE Problem Stemming from the Teacher Candidate’s Exploration
Interesting mathematics is hidden behind the seven questions stemming from reflections on experimental constructions by a teacher candidate, and it required intervention of the “more knowledgeable other” [49]. As a result of experimentation motivated by Problem 2, a new problem was formulated and discussed online.
Problem 3.
In Figure 5, the number of rows in the (isosceles) trapezoid is the same as the number of rows in the (isosceles) triangle. Do these numbers always have to be the same in order for the latter shape to be constructed from the former shape?
Discussion.
As emphasized by the Association of Mathematics Teacher Educators, sometimes mathematics teachers, when facing students whose thinking is different from what is expected, “may inadvertently seek to remedy those differences rather than seeing them as strength and resources upon which to build” [38] (p. 22). Therefore, it was the author’s didactic responsibility to reflect on the three constructions; in other words, to initiate “inquiry about inquiry” [29] (p. 215). Indeed, behind the shapes constructed by the teacher candidate was hidden mathematics curriculum [55], which, by representing “biologically secondary information … requires direct, explicit instruction” [56] (p. 121). The authors of [56] gave just one example of biologically secondary knowledge in mathematics—the base-ten system. Referring to even such basic mathematical knowledge as being “biologically secondary” indicates that, in general, although the subject matter of mathematics does emphasize many components of design thinking, including propensity for experimentation, acceptance of ambiguity, open mindedness, and critical questioning, a mathematical classroom does require the presence of a competent instructor capable of recognizing the presence of deep mathematical ideas behind students’ initial experimentation that, once revealed through TITE problem solving, have great potential to give way to their transformative learning.
Numerically, the first two constructions shown in Figure 5 can be described through the relationship
3 + 4 + 5 = 1 + 4 + 7.
A significant aspect of the first construction, in terms of the first-order symbols, is that each row of the image of an isosceles trapezoid has one more counter than the previous row. In terms of the second-order symbols, we have a sum of consecutive natural numbers that can be referred to as a trapezoidal number [57]. A significant aspect of the second construction, in terms of the first-order symbols, is that each row of the image of an isosceles triangle has three more counters than the previous row. In terms of the second-order symbols, we have a sum of arithmetic series with the difference three.
To answer the question posed by Problem 3, one has to move from particular (numeric) to general (algebraic) in order to provide a TE component of the problem through the development of its TI component. In general, a trapezoid with k rows, the top row of which has m counters, needs a total of
counters in order to be constructed. Likewise, a triangle with n rows, in which each row includes three more counters than the previous row, needs counters in order to be constructed. Using Wolfram Alpha (a TE part of the problem), one can solve the equation in positive integers (developed as a TI part of the problem), enabling one to see whether the equality k = n is necessary for a trapezoid and the corresponding triangle with the same number of rows. As shown in Figure 6, the bottom row of the table generated by Wolfram Alpha displays the case This case gives a negative answer to the question of Problem 3. Furthermore, as shown in Figure 7, two trapezoids can be constructed out of 35 counters; one trapezoid, 35 = 5 + 6 + 7 + 8 + 9, with five rows, and another trapezoid with seven rows, 35 = 2 + 3 + 4 + 5 + 6 + 7 + 8. Put another way, trapezoidal representations of numbers may not be unique.
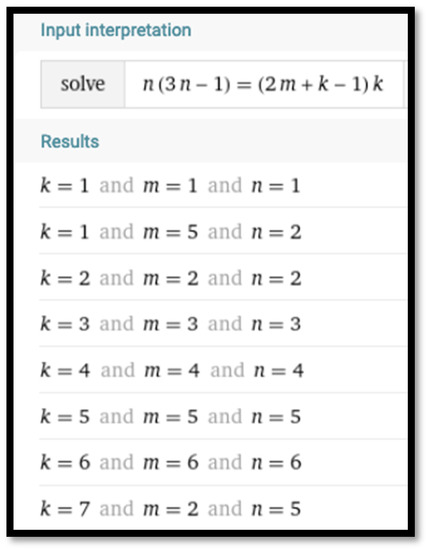
Figure 6.
A counterexample shown by Wolfram Alpha.
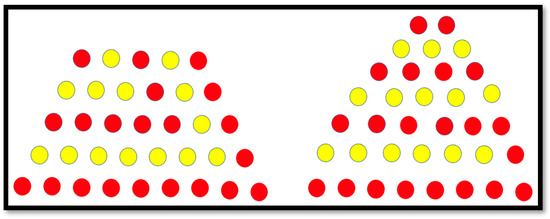
Figure 7.
Counterexample as metacognition: from Wolfram Alpha to counters.
Moreover, the former trapezoid, as shown in the left-hand side of Figure 7, can be rearranged into an isosceles triangle, 35 = 1 + 4 + 7 + 10 + 13 (1 red counter followed by 4 yellow counters followed by 7 red counters followed by 10 yellow counters followed by 13 red counters), with five rows as well. In other words, there exists an isosceles triangle out of which more than one isosceles trapezoid can be constructed. This gives a positive answer to Question 3 from the above list.
6. Explaining Why the Candidate Could Not Construct a Trapezoid Using 16 Counters
Whereas out of 12 counters only one isosceles trapezoid can be constructed, out of 35 counters one can construct even more than two isosceles trapezoids. Indeed, 35 = 17 + 18 yields a new trapezoid with two rows. Formally (a TI part of the discussion), as it follows from Equation (1), the equation shows that 70 can be factored in two factors in three ways: , and each factorization defines an isosceles trapezoid: the first one with two rows, the second one with five rows, and the third one with seven rows. At the same time, the equation immediately implies whence . Although 24 has also three factorizations, the first and the third ones yield, respectively, the relations 2m = 11 and 2m = 3, not solvable over integer m. Only when k = 3 do we have m = 3—the case found experimentally by the teacher candidate (Figure 4). This number theory explanation makes it possible to clarify why the teacher candidate failed to construct a trapezoid out of 16 counters. Indeed, the only factorizations for the double of 16 are those with both even factors, , none of which yield an integer value of counters for the first row. In particular, because powers of two may not be represented as a product of two factors of different parity, trapezoidal numbers may not be powers of two. At the same time (answering Question 5 from the above list), a square of side length 3 can be rearranged into an isosceles trapezoid in two ways. This fact can be explained theoretically and practically. Factorization yields and the first factors, 2 and 3, point at the trapezoids with two and three rows, respectively. Those trapezoids can be confirmed practically as 9 = 4 + 5 = 2 + 3 + 4.
7. Integrating TITE Problems and the History of Mathematics
The history of mathematics provides learners with interesting mathematical ideas and is worth to “be woven into existing mathematics courses” [37] (p. 61). Mathematically speaking, Question 6 from the above list asks for the existence of squares among triangular numbers. This is a classic number theory problem that spans from the time of Diophantus (3rd century) to that of Euler (18th century). The smallest such square and equilateral triangle (an image of a triangular number) can be constructed out of 36 counters. Indeed, Other cases can be provided by entering into the input box of Wolfram Alpha the command “solve over the positive integers n(n+1)=2m^2.” Such use of the tool is of the TITE type, as constructing the last equation requires knowledge of mathematics, something that in the case m = 6 can be verified through a hands-on experiment. Such interplay of theory and experiment is a distinctive characteristic of design-based mathematics education. The next case, m = 35, is way beyond hands-on confirmation (to deal with 1225 counters). Leonhard Euler, the father of all modern mathematics, proved the existence of an infinite number of triangular squares [58]. Although Wolfram Alpha does not prove this statement, its computational power “immensely extends the possibilities of behavior by making the results of the work of geniuses available to everyone” [59].
The history of mathematics preserves examples of using numeric tables as tools of advancing computational ideas. Ahmes, an ancient (ca. 1500 B.C.) Egyptian scribe, often considered the first mathematician because he was the first one to save and present mathematical results in a written form, is credited with developing a table, representing fractions of the form 2/n as a sum of distinct unit fractions. Michael Stifel, a 16th-century German monk and mathematician, used a table, known as Stifel’s triangle [60], to recursively compute binomial coefficients. In the 17th century, Blaise Pascal, one of the founders of probability theory, came across his famous triangle by recording sample spaces of experiments of tossing coins from where one can determine chances of having a certain result of an experiment [61]. In the 18th century, Élie de Joncourt, a Dutch minister of church and mathematics teacher, used the fact that within a numeric table comprised of triangular numbers, the sum of two consecutive triangular numbers is the square of the rank of the larger number, to compute squares and square roots [62]. As mentioned in [63] (p. 324), with reference to the rise and ubiquity of electronic spreadsheets in industry and education, “the two-dimensional table would arise spontaneously in any civilization where a writing surface was used.”
8. From Self-Embedded Pentagons to the Addition Table
The teacher candidate’s construction of self-embedded regular pentagons was accidental, and it can be described as collateral creativity [64]—an unintended but favorable and often accidental educative outcome of one’s technology-enhanced learning experience. In order to explain the success of this experiment, geometry has to be connected to arithmetic (or, better, to theoretical arithmetic known as number theory). Problems of number theory have their origin in ancient, ca. 1000 B.C., China [65], where geometric images (first-order symbols) were described through relationships among numbers (second-order symbols). As shown in Figure 5, the construction of the pentagon was guided by the sum 1 + 4 + 7. The last three addends can be selected from the natural number sequence using skip counting by twos or by eliminating pairs of numbers (similar to how it was done in Problem 1): Start with 1 and skip the pairs (2, 3), (5, 6), and so on. Then the partial sums surviving the elimination can be associated with a pentagon and thus called pentagonal numbers. As was shown above, the n-th partial sum of numbers surviving step-by-step elimination of pairs (skip counting by twos), , represents half the product of two integers of different parity (otherwise, might not be divisible by two), out of which an isosceles trapezoid can be constructed, sometimes in more than one way.
In order to answer whether a square can be rearranged into self-embedded regular pentagons (Question 7 from the above list), one has to solve the equation , something that can be done by Wolfram Alpha. It turns out that the smallest pair of integers satisfying the last equation is n = 81, m = 99; that is, the smallest square would consist of 992 counters, the rearrangement of which into self-embedded pentagons would be guided by the sum . The next pair is n = 7921, m = 9701. This shows that answering Question 7 is indeed a TITE problem not solvable through hands-on experimentation with counters. At the same time, the problem was motivated by the teacher candidate’s delight in “collateral learning [something that] may be and often is much more important than the spelling lesson or lesson in geography or history … [forming] desire to go on learning” [8] (p. 49).
An unexpected connection of the product to the addition table is worth mentioning: The sums of numbers in the gnomons of the table (Figure 8) are twice pentagonal numbers, as the sum of numbers in the gnomon of rank n is equal to the product. In particular, the recognition of connection between pentagonal numbers and an addition table makes it possible to find the sum of all numbers in the addition table as follows:
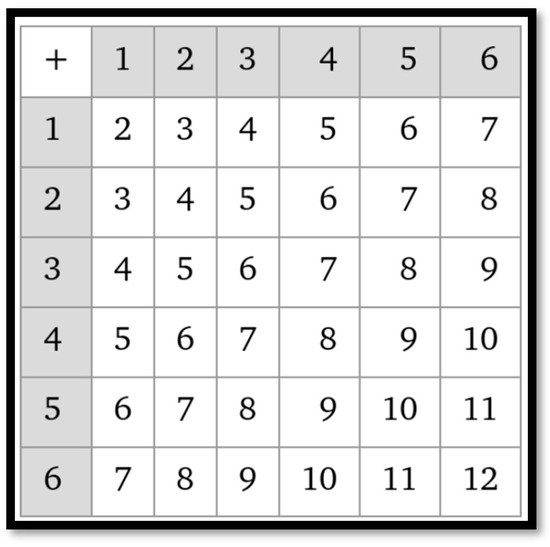
Figure 8.
An addition table generated by Wolfram Alpha.
However, as shown in Figure 9, the above symbolic computations can be outsourced to Wolfram Alpha by typing in its input box “sum of k(3k-1) for k from 1 to n.” As Langtangen and Tveito put it, “Much of the current focus on algebraically challenging, lengthy, error prone paper and pencil work can be significantly reduced. The reason for such an evolution is that the computer is simply much better than humans on any theoretically phrased well-defined repetitive operation” [66] (pp. 811–812). This quote emphasizes the educational importance of the TITE concept for the teaching of mathematics, as more and more traditionally conceptual problems can be solved almost at the push of a button with minimal skills in designing a programming code needed for machine-based symbolic computations.

Figure 9.
Symbolic computations carried out by Wolfram Alpha.
Note that explorations with an addition table offer many conceptually rich TITE problem-solving activities. Such activities can incorporate developing different ways of finding the sum of all numbers in the table. Those ways include adding numbers by rows, adding numbers along bottom-left/top-right or top-left/bottom-right diagonals, and adding numbers located in the diagonals equidistant from the bottom-left/top-right diagonal. The activities provide teacher candidates with experience in solving a problem in more than one way so that each new way may be considered posing a new problem to solve. All of this describes metacognitive development and using TITE problems as agency of design-based learning. As mentioned by an elementary teacher candidate, “I think it is important to teach students multiple strategies to solve problems and let them choose the one that works best for them or the one that applies the best to the specific question they are working with. When students are given multiple strategies for solving problems, they can take ownership of their math and find success with the strategy that works best for them. They learn that not all strategies work in every situation, so they apply the one that works the best for their skill set and ability”.
Similarly, recognizing a clear-cut distinction between yesterday’s learning experience and today’s expectations for an elementary mathematics teacher, another teacher candidate admitted, “I think my experience solving math problems in more than one way really began only when I started working in education. As a student myself, my experience was that math was black and white- this is the formula and this is the answer and this is the strategy. Now we teach our students to show their work and often several strategies are used to solve the problem and it results in the same answer. Also, the use of manipulatives, paper and pencil, mental math, technology etc. are all tools in solving mathematical problems”.
As was mentioned above at the conclusion of Section 3, solving a mathematical problem in more than one way; that is, by using multiple TITE perspectives (supported by multiple digital tools) on how the problem can be solved, provides evidence of the triangulation [40] of problem solving carried out collectively (students supervised by the teacher) under collateral [8] and action [42] learning umbrellas.
9. Conclusions
Four major points described in this paper can be singled out to serve as concluding remarks. The first point is the importance of technology-immune/technology-enabled problems for modern-day mathematics teacher education. With the increasing computational power—numeric, symbolic, graphic—of technology in solving mathematical problems, teaching the subject matter by integrating conceptual ideas and procedural techniques becomes more and more pedagogically challenging. This integration may include using technology in answering conceptual questions that can result from students’ experimentation with concrete materials. That is, as shown in the diagram of Figure 10 (which reflects a specific episode described in this paper), a TITE problem may be formulated by the instructor in order to clarify mathematically the result(s) of a hands-on experiment shared by a teacher candidate within the forum as a response to a specific prompt. In that way, the student-motivated TITE problem and its solution posted by the instructor on the forum in a “non-invasive” (or minimally invasive [67]) mode aim at augmenting mathematical knowledge of teacher candidates and serve as agency of new design-based mathematics education activities. The descriptive nature of this paper follows the path of reflective writings in mathematics education that underscore the “pivotal role of reflections in mathematising and didactising” [68] (p. 163) and demonstrate how learners think “through reflection on the epistemological and ontological status of mathematical constructs” [69] (p. 2). Furthermore, from an educational psychology perspective, the author’s descriptive reflection on a forum-related episode shows a transition “from just being able to do something to thinking about the doing of that thing … by reconstructing on a higher level what existed on a lower level … so that when one reflects onto a higher level, it is incumbent upon one to enrich it with new elements” [70] (p. 225). All things considered, the author’s intent was to demonstrate how one can make a transition from knowing mathematics to using this knowledge in recognizing in a teacher candidate’s contribution to the discussion forum an unwitting problem posing, then sharing this recognition in detail within the forum, and, finally, writing about the whole thing using the TITE framework. In particular, digitally solving Equation (1), which equated the number of counters used in constructing a trapezoid and a triangle, yielded an unexpected counterexample showing the epistemic deficiency of an experiment as a means of generalization on the one hand, and the source of metacognition on the other hand. In addition, the diagram of Figure 10 shows that the resolution of a TITE problem becomes a springboard for posing new problems when action learning [42,43,45] and design thinking [6,7] are used as instruments of metacognitive development [47,48] geared towards the initiation of the “solve–reflect–pose” cognitive cycle [32].
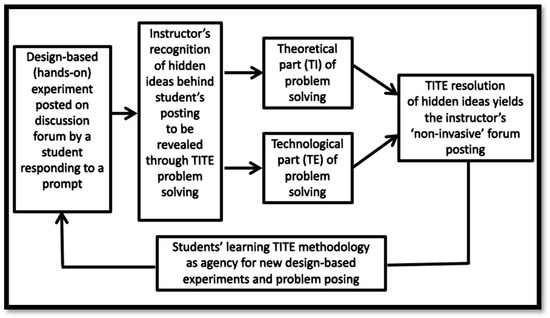
Figure 10.
A TITE problem-solving framework.
The second point deals with a unique opportunity to enrich an asynchronous mathematics education course by means of the instructor’s reflections on teacher candidates’ creative responses to the prompts that structure the forum component of the course. This enrichment is at least three-fold. First, teacher candidates learn that the ontology of elementary mathematics is full of hidden ideas that could be recognized by their future students requesting further elaboration and clarification. Having experience with revealing such ideas both mathematically and technologically is important for developing deep understanding of the subject matter [37,38]. Second, teacher candidates can read the instructor’s “non-invasive” responses to a contribution by one of their peers at the time of their own choice and convenience, something that is not possible in the face-to-face teaching modality [71]. Third, it might be tempting for the candidates to try to contribute to the forum in like manner to see whether their design thinking could also touch upon new hidden ideas.
The third point embraces the first two points, and it concerns the issue of the importance of mathematical knowledge for teaching [72,73,74], especially, as the author strongly believes, when an online course is offered through the asynchronous modality. Whereas an asynchronous course, unlike a synchronous course, is not recorded, everything that happens within the former course remains online and students may revisit the shell of the course at any time during the semester. That is why the omnipresent contribution of the instructor to the forum and their responses to students’ answers to the prompts is pedagogically important—as is well known, teachers teach similarly to how they were taught [75,76,77]. The author’s experience with teaching an asynchronous course provides evidence that some teacher candidates may demonstrate a number of interesting ideas that are presented through an experiment using virtual manipulatives. In this paper, one such experiment was shared when a teacher candidate unintentionally touched upon several hidden ideas including trapezoidal numbers and self-embedded regular pentagons. This is where mathematical knowledge for teaching becomes very important, because recognition of a hidden idea behind the candidate’s initial experimentation, some parts of which were successful and some were not, required from the author to elaborate on this idea to explain, using TITE framework, why some experiments were successful and some were not. In particular, explaining mathematically the reason for the failure of an experiment demonstrated that not every problem in mathematics has a solution. This elaboration remains a part of the course serving as an online appendix to any traditional course materials, including a textbook.
Finally, the fourth major point described in the paper deals with the issue of teaching and learning to use technology throughout the course. The course participants, through their comments (collected by the author, as mentioned in Section 2, by analyzing about 100 responses to the final exam questionnaire and the discussion forum prompts), provided evidence that transformative learning of technology-enabled pedagogy, when new information affects earlier developed knowledge and skills, took place. Regarding the use of Wolfram Alpha in the course, a teacher candidate acknowledged, “Prior to taking this course, I had little experience using Wolfram Alpha except when trying to independently research areas of difficulty during high school (particularly when studying trigonometry and entry-level calculus). I initially found it somewhat difficult to navigate, although I believe this was due to my already limited understanding of the content I was learning. However, its use throughout this course has opened my eyes to the versatility of this tool!”.
An aspect worthy of mention of asynchronous graduate teacher education deals with a possible increase in the exchange of knowledge within a nuclear family when non-traditional students, motivated to advance their education by the apparent convenience of online programs, spend more time at home. This aspect is reflected in a comment by a teacher candidate regarding the use of spreadsheets in the course: “It is crucial that students know how to use technology in the classroom so they can utilize it as an adult also. Our son uses spreadsheets to manage his money. When we helped our son create a spreadsheet that does his calculations for him, it changed how he looks at his money. He can now create and modify his spreadsheet to fit his needs as well as help others. This also shows why it is important to use technology in the classroom. Students do not want to solve problems using paper and pencil anymore. With that said, the students must show they understand the concepts too, not just the answer on a piece of paper”.
Elementary teacher candidates’ appreciation of versatility of the modern-day digital tools inside (as well as outside) the context of school mathematics, with expectations of incorporating TITE problem solving and posing as agency of design-based mathematical education, is a testament that the author’s pedagogical efforts in demonstrating that procedural competence in the subject matter and its conceptual understanding go hand in hand do bear fruit. Possible suggestions for practitioners of asynchronous mathematics teaching that can be drawn from this paper may embrace paying attention to the value of “non-invasive” uplifting of teacher candidates’ mathematical knowledge through discussion forums, recognizing the importance of such knowledge for teaching in the technological paradigm, using the TITE didactics as appropriate, being sensitive and open to students’ ideas, and taking notice of the potential educative effect of enrolling in online courses on the knowledge base of family members. As online pedagogy becomes more and more common around the world, other experiences of design-based mathematics education courses of different teaching modalities will come to light.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Conflicts of Interest
The author declares no conflict of interest.
References
- Abramovich, S. Revisiting mathematical problem solving and posing in the digital era: Toward pedagogically sound uses of modern technology. Int. J. Math. Educ. Sci. Technol. 2014, 45, 1034–1052. [Google Scholar] [CrossRef]
- Maddux, C.D. Educational microcomputing: The need for research. Comput. Sch. 1984, 1, 35–41. [Google Scholar] [CrossRef]
- Beatty, B. The dilemma of scripted instruction: Comparing teacher autonomy, fidelity, and resistance in the Froebelian kindergarten, Montessori, direct instruction, and success for all. Teach. Coll. Rec. 2011, 113, 395–430. [Google Scholar] [CrossRef]
- Thorndike, E.L. The Psychology of Arithmetic; MacMillan: New York, NY, USA, 1922. [Google Scholar]
- Michalowicz, K.D.; Howard, A.C. Pedagogy in text: An analysis of mathematics texts from the nineteenth century. In A History of School Mathematics; Stanic, G.M.A., Kilpatrick, J., Eds.; National Council of Teachers of Mathematics: Reston, VA, USA, 2003; Volume 1, pp. 77–109. [Google Scholar]
- Geitz, G.; de Geus, J. Design-based education, sustainable teaching, and learning. Cogent Educ. 2019, 6, 1647919. [Google Scholar] [CrossRef]
- Avsec, S. Design thinking to enhance transformative learning. Glob. J. Eng. Educ. 2021, 23, 169–175. [Google Scholar]
- Dewey, J. How We Think; D.C. Heath and Company: New York, NY, USA, 1933. [Google Scholar]
- Piaget, J. Comments on mathematics education. In Developments in Mathematics Education: Proceedings of the Second International Congress on Mathematical Education; Howson, G., Ed.; Cambridge University Press: Cambridge, UK, 1973; pp. 79–87. [Google Scholar]
- Bryant, P. Making Education Better: Implementing Pedagogical Change through Technology in a Modern Institution. In Higher Education in the Digital Age. Moving Academia Online; Zorn, A., Haywood, J., Glachant, J.-M., Eds.; Edward Elgar Publishing: Cheltenham, UK, 2018; pp. 1–16. [Google Scholar]
- Abramovich, S. Exploring Mathematics with Integrated Spreadsheets in Teacher Education; World Scientific: Singapore, 2016. [Google Scholar]
- Jones, L. The Student-Centered Classroom; Cambridge University Press: New York, NY, USA, 2007. [Google Scholar]
- Dixon, J.R. The state of education. Mech. Eng. CIME 1991, 113, 64. [Google Scholar]
- Perrenet, J.C.; Bouhuijs, P.A.J.; Smits, J.G.M.M. The suitability of problem-based learning for engineering education: Theory and practice. Teach. High. Educ. 2000, 5, 345–358. [Google Scholar] [CrossRef]
- Collins, A. Toward a design science of education. In New Directions in Educational Technology; NATO ASI Series; Scanlon, E., O’Shea, T., Eds.; Springer: Berlin, Germany, 1992; Volume 96, pp. 15–22. [Google Scholar]
- Fortus, D.; Krajcik, J.; Dershimer, R.C.; Marx, R.W.; Mamlok-Naaman, R. Design-based science and real-world problem-solving. Int. J. Sci. Educ. 2005, 27, 855–879. [Google Scholar] [CrossRef]
- Wittmann, E. Mathematics education as a design science. In Mathematics Education as a Research Domain: A Search for Identity; Sierpinska, A., Kilpatrick, J., Eds.; Kluwer: Dordrecht, The Netherlands, 1998; pp. 87–103. [Google Scholar]
- Artigue, M. Perspectives on design research: The case of didactical engineering. In Approaches to Qualitative Research in Mathematics Education: Examples of Methodology and Methods; Bikner-Ahsbahs, A., Knipping, C., Presmeg, N., Eds.; Springer: New York, NY, USA, 2015; pp. 467–496. [Google Scholar]
- Confrey, J. Leading a design-based research team using agile methodologies to build learner-centered software. In Designing, Conducting, and Publishing Quality Research in Mathematics Education; Leatham, K.R., Ed.; Springer: Cham, Switzerland, 2019; pp. 123–142. [Google Scholar]
- Fowler, S.; Cutting, C.; Fiedler, S.H.; Leonard, S.N. Design-based research in mathematics education: Trends, challenges and potential. Math. Educ. Res. J. 2022. [Google Scholar] [CrossRef]
- Huang, D.; Manouchehri, A. Online mathematics teacher education in the US: A status report. Contemp. Issues Technol. Teach. Educ. 2019, 19, 171–194. [Google Scholar]
- Markel, S.L. The use of forums in education courses. Online J. Dist. Learn. Admin. 2001, 4, 1–11. [Google Scholar]
- Andresen, M.A. Asynchronous discussion forums: Success factors, outcomes, assessments, and limitations. Educ. Technol. Soc. 2009, 12, 249–257. [Google Scholar]
- Nandi, D.; Hamilton, M.; Harland, J. Evaluating the quality of interaction in asynchronous discussion forums in fully online courses. Distance Educ. 2012, 33, 5–30. [Google Scholar] [CrossRef]
- de Lima, D.P.; Gerosa, M.A.; Conte, T.U.; de MNetto, J.F. What to expect, and how to improve online discussion forums: The instructors’ perspective. J. Internet Serv. Appl. 2019, 10, 1–15. [Google Scholar] [CrossRef]
- Alzahrani, M.G. The effect of using online discussion forums on students’ learning. Turkish Online J. Educ. Technol. 2017, 16, 164–176. [Google Scholar]
- Olivier, B.H. The impact of contact sessions and discussion forums on the academic performance of open distance learning students. Int. Rev. Res. Open Distr. Learn. 2016, 17, 75–88. [Google Scholar] [CrossRef]
- Conde, M.A.; García, F.; Rodríguez-Conde, M.J.; Alier, M.; García-Holgado, A. Perceived openness of Learning Management Systems by students and teachers in education and technology courses. Comp. Hum. Behav. 2014, 31, 517–526. [Google Scholar] [CrossRef]
- Tibi, M.H. Computer science students’ attitudes towards the use of structured and unstructured discussion forums in online courses. Online Learn. 2018, 22, 93–106. [Google Scholar] [CrossRef]
- Montessori, M.; Frederick, A. Spontaneous Activity in Education; Frederick A. Stokes Publishers: New York, NY, USA, 1917. [Google Scholar]
- Freire, P. Pedagogy of the Oppressed; Continuum: New York, NY, USA, 2003. [Google Scholar]
- Rittle-Johnson, B.; Siegler, R.S.; Alibali, M.W. Developing conceptual understanding and procedural skill in mathematics: An iterative process. J. Educ. Psych. 2001, 93, 346–362. [Google Scholar] [CrossRef]
- Hilbert, D. Mathematical problems (Lecture delivered before the International Congress of Mathematicians at Paris in 1990). Bull. Am. Math. Soc. 1902, 8, 437–479. [Google Scholar] [CrossRef]
- McEvan, H.; Bull, B. The pedagogic nature of subject matter knowledge. Am. Educ. Res. J. 1991, 28, 316–334. [Google Scholar]
- Bruner, J.S. Beyond the Information Given; Norton: New York, NY, USA, 1973. [Google Scholar]
- Common Core State Standards. Common Core Standards Initiative: Preparing America’s Students for College and Career. 2010. Available online: http://www.corestandards.org (accessed on 19 May 2022).
- Conference Board of the Mathematical Sciences. The Mathematical Education of Teachers II; The Mathematical Association of America: Washington, DC, USA, 2012. [Google Scholar]
- Association of Mathematics Teacher Educators. Standards for Preparing Teachers of Mathematics. 2017. Available online: https://amte.net/standards (accessed on 19 May 2022).
- Ontario Ministry of Education. The Ontario Curriculum, Grades 1–8, Mathematics (2020). Available online: http://www.edu.gov.on.ca (accessed on 19 May 2022).
- Cohen, L.; Manion, L.; Morrison, K. Research Methods in Education, 8th ed.; Routledge: London, UK, 2017. [Google Scholar]
- Thompson, P.W.; Artigue, M.; Töner, G.; de Shalit, E. Reflections on Collaboration Between Mathematics and Mathematics Education. In Mathematics & Mathematics Education: Searching for Common Ground; Fried, M.N., Dreyfus, T., Eds.; Springer: New York, NY, USA, 2014; pp. 314–333. [Google Scholar]
- Revans, R.W. Action Learning: New Techniques for Management; Blond & Briggs: London, UK, 1980. [Google Scholar]
- Revans, R.W. The Origin and Growth of Action Learning; Chartwell-Bratt: Bromley, UK, 1982. [Google Scholar]
- Dewey, J. Democracy and Education; The Free Press: New York, NY, USA, 1916. [Google Scholar]
- Abramovich, S.; Grinshpan, A.Z.; Milligan, D.L. Teaching mathematics through concept motivation and action learning. Educ. Res. Int. 2019, 2019, 3745406. [Google Scholar] [CrossRef]
- Wertheimer, M. Productive Thinking; Harper & Brothers: New York, NY, USA, 1959. [Google Scholar]
- Flavell, J.H. Metacognitive aspects of problem solving. In The Nature of Intelligence; Resnick, L., Ed.; Lawrence Erlbaum: Hillsdale, NJ, USA, 1976; pp. 231–236. [Google Scholar]
- White, B.; Frederiksen, J. A theoretical framework and approach for fostering metacognition. Educ. Psych. 2005, 40, 211–223. [Google Scholar] [CrossRef]
- Vygotsky, L.S. Mind in Society; Harvard University Press: Cambridge, MA, USA, 1978. [Google Scholar]
- Campione, J.C.; Brown, A.L.; Connell, M.L. Metacognition: On the importance of understanding what you are doing. In Teaching and Assessing Mathematical Problem Solving; Charles, R.I., Silver, E., Eds.; National Council of Teachers of Mathematics: Reston, VA, USA, 1989; Volume 3, pp. 93–114. [Google Scholar]
- Freudenthal, H. Weeding and Sowing; Kluwer: Dordrecht, The Netherlands, 1978. [Google Scholar]
- Tikhomirov, V.M.A.N. Kolmogorov. In Wolf Prize in Mathematics; Chern, S.S., Hirzebruch, F., Eds.; World Scientific: Singapore, 2001; Volume 2, pp. 119–164. [Google Scholar]
- Montessori, M. Education for a New World; Kalakshetra: Madras, India, 1946. [Google Scholar]
- Dewey, J. Experience and Education; MacMillan: New York, NY, USA, 1938. [Google Scholar]
- Abramovich, S. Hidden curriculum of mathematics teacher education: An example. PRIMUS 2009, 19, 39–56. [Google Scholar] [CrossRef]
- Sweller, J.; Kitschner, P.A.; Clark, R.E. Why minimally guided teaching techniques do not work: A reply to commentaries. Educ. Psych. 2007, 42, 115–121. [Google Scholar] [CrossRef]
- Pólya, G. Mathematical Discovery: On Understanding, Learning, and Teaching Problem Solving; John Wiley & Sons: New York, NY, USA, 1965; Volume 2. [Google Scholar]
- Dickson, L.E. History of the Theory of Numbers. Diophantine Analysis; Dover: New York, NY, USA, 2005; Volume 2. [Google Scholar]
- Vygotsky, L.S. The Instrumental Method in Psychology (Talk Given in 1930 at the Krupskaya Academy of Communist Education). Lev Vygotsky Archive. 1930. Available online: https://www.marxists.org/archive/vygotsky/works/1930/instrumental.htm (accessed on 19 May 2022).
- Coolidge, J.L. The story of binomial theorem. Am. Math. Month. 1949, 56, 147–157. [Google Scholar] [CrossRef]
- Kline, M. Mathematics for the Non-Mathematician; Dover: New York, NY, USA, 1985. [Google Scholar]
- Roegel, D. A Reconstruction of Joncourt’s Table of Triangular Numbers (1762). Technical Report. Nancy, France: Lorraine Laboratory of IT Research and Its Applications. A Reconstruction of: Élie de Joncourt. De Natura et Præclaro Usu Simplicissimæ Speciei Numerorum Trigonalium. Husson: The Hague, The Netherlands. 1762. Available online: http://locomat.loria.fr (accessed on 19 May 2022).
- Campbell-Kelly, M. The rise and rise of the spreadsheet. In The History of Mathematical Tables: From Sumer to Spreadsheets; Campbell-Kelly, M., Croarken, M., Flood, R., Robson, E., Eds.; Oxford University Press: New York, NY, USA, 2003; pp. 323–347. [Google Scholar]
- Abramovich, S.; Freiman, V. Collateral creativity and technology. In Newsletter of the International Group for Mathematical Creativity and Giftedness; Slavic, M., Ed.; Mathematical Creativity and Giftedness Group: Norman, OK, USA, 2021; Volume 17, pp. 29–35. [Google Scholar]
- Beiler, A.H. Recreations in the Theory of Numbers: The Queen of Mathematics Entertains; Dover: New York, NY, USA, 1964. [Google Scholar]
- Langtangen, H.P.; Tveito, A. How should we prepare the students of science and technology for a life in the computer age? In Mathematics Unlimited—2001 and Beyond; Engquist, B., Schmid, W., Eds.; Springer: New York, NY, USA, 2001; pp. 809–825. [Google Scholar]
- Mitra, S.; Rana, V. Children and the Internet: Experiments with minimally invasive education in India. Br. J. Educ. Technol. 2001, 32, 221–232. [Google Scholar] [CrossRef]
- Zolcower, B.; Bressan, A.M.; Perez, S.; Gallego, M.F. From the bottom up—Reinventing realistic mathematics education in Southern Argentina. In International Reflection in the Netherlands Didactics of Mathematics: Vision on and Experiences with Realistic Mathematics Education; Van den Heuvel-Panhuizen, M., Ed.; Springer: Cham, Switzerland, 2020; pp. 133–166. [Google Scholar]
- Sfard, A. On the dual nature of mathematical conceptions: Reflections on processes and objects as different sides of the same coin. Educ. Stud. Math. 1991, 22, 1–36. [Google Scholar] [CrossRef]
- Piaget, J. Creativity. In Learning Theory of Piaget and Inhelder; Gallagher, J.M., Reid, D.K., Eds.; Brook/Cole: Monterey, CA, USA, 1981; pp. 221–229. [Google Scholar]
- Clay, E.; Silverman, J.; Fischer, D.J. Unpacking online asynchronous collaboration in mathematics teacher education. ZDM Math. Educ. 2012, 44, 761–773. [Google Scholar] [CrossRef]
- Schoenfeld, A.H. Models of the teaching process. J. Math. Behav. 2000, 18, 243–261. [Google Scholar] [CrossRef]
- Ball, D.; Thames, M.H.; Phelps, G. Content knowledge for teaching: What makes it special? J. Teach. Educ. 2008, 59, 389–404. [Google Scholar] [CrossRef]
- Masingila, J.O.; Olanoff, D.; Kimani, P.M. Mathematical knowledge for teaching teachers: Knowledge used and developed by mathematics teacher educators in learning to teach via problem solving. J. Math. Teach. Educ. 2018, 21, 429–450. [Google Scholar] [CrossRef]
- Lortie, D.C. Schoolteacher: A Sociological Study; University of Chicago Press: Chicago, IL, USA, 1975. [Google Scholar]
- Sexton, S.S. Voices echoing the past: I decided to do teaching because of the teacher that I had. Thirteen female secondary entry-level teacher candidates teaching not only what but also how they were taught. Aust. J. Teach. Educ. 2007, 32, 63–75. [Google Scholar] [CrossRef][Green Version]
- Oleson, A.; Hora, M.T. Teaching the way they were taught? Revisiting the sources of teaching knowledge and the role of prior experience in shaping faculty teaching practices. High. Educ. 2014, 68, 24–45. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).