Abstract
This study examines instructional reasoning in an approximation of practice that simulates a teacher sitting down after class to examine students’ written work. The participants were prompted to attend to, interpret, and decide how to respond to student thinking contained in a piece of written work. Our purpose was to capture the additional cognitive work that teachers engage in. Using qualitative content analysis, we identified the most frequent types of instructional reasoning used by expert teachers just prior to engaging in a responsive deciding action about how to respond. We used the results of our analysis to present three illustrative cases of responsive instructional reasoning.
1. Introduction
Effective mathematics instruction involves teachers engaging with and taking up student ideas and then deciding how to respond in ways that develop that thinking [1,2,3,4]. There are various constructs used by mathematics educators to refer to teaching that centers student thinking, including cognitively guided instruction [5], formative assessment focused on disciplinary thinking [6], professional noticing of children’s mathematical thinking [7], and responsive teaching [2,8,9]. While these practices are nuanced, they all require a dynamic interplay between students and teachers that is difficult to facilitate even for expert teachers [8,10].
In this study, we draw on research related to professional noticing of children’s mathematical thinking [7] and responsive teaching [2,8,9] to create and study teachers engaged in a practice space that simulates a teacher sitting down after class is over to examine students’ written work. To prepare for their participation in this practice space, the teachers were asked to bring pieces of written work from their classrooms. They were then prompted to attend to, interpret, and decide how to respond to the student thinking contained in the piece of written work. When asked to do this, teachers first attended to and interpreted student thinking directly on the piece of written work; they often then made sense of the student thinking by reasoning in ways removed from the written work and prior to deciding how to respond. Our purpose was to capture this additional cognitive work, referred to by Dyer and Sherin [2] as instructional reasoning, that involves the ways teachers interpret what they notice about student thinking that are instructionally relevant. We were particularly interested in the ways that teachers reasoned about student thinking just prior to deciding how to respond in ways that align with responsive teaching practices. Therefore, we seek to answer the following research question: What types of instructional reasoning support responsive teaching practices as a teacher examines student written work?
2. Literature Review
2.1. Teacher Cognition: Pedagogical and Instructional Reasoning
Teacher cognition is complex. It involves the processes teachers work through as they make instructional decisions. This invisible cognitive work is often referred to as pedagogical reasoning. Loughlin et al. [11] described pedagogical reasoning as “the thinking that underpins informed professional practice” (p. 4). According to Loughlin et al. [12], understanding how pedagogical reasoning develops and the way it influences practice is critical for teacher development. Building on the concept of pedagogical reasoning, Dyer and Sherin [2] introduce the term instructional reasoning to describe the additional thinking that goes beyond describing what a student said or did, to making interpretations of student mathematical thinking that “…help teachers make sense of student thinking in ways that are instructionally-relevant” (p. 70). For example, teachers may connect student thinking to broad disciplinary thinking [13], synthesize and compare across interpretations of student thinking [14], hypothesize links between classroom experiences and interpretations of student thinking, or consider individual student characteristics [15]. While many of the ways that teachers might engage in instructional reasoning are known, more research is needed on how teachers engage in instructional reasoning in ways that align with responsive teaching.
2.2. Responsive Teaching
Responsive teaching is grounded in a sociocultural theory in which learning is viewed as an active process situated in authentic activities and discourses of communities of practice [16,17,18]. It is both a teaching stance and a practice enacted in classroom settings in which teachers recognize the importance of using the substance of student thinking to guide instructional decisions [19]. To engage in this kind of learning, teachers must view students as active learners with prior knowledge developed in and outside the classroom and draw on that knowledge to develop student ideas. For example, responsive teachers ask questions in a way that draws out student emergent ideas and helps students connect and build off each other’s ideas during classroom instruction [18] or encourages students to provide alternative explanations of natural phenomena [20].
Dyer and Sherin [2] identified three responsive teaching practices during classroom discussions that involve: (1) a substantive probe of student ideas; (2) an invitation for student comment; and (3) a teacher uptake of student ideas. To characterize the instructional reasoning that led to responsive teaching practices, Dyer and Sherin [2] identified video clips of whole class instruction that captured these practices. Then, they analyzed the video clips alongside the interview transcripts to identify the instructional reasoning just prior to an instance of responsive teaching. Dyer and Sherin [2] were able to identify three types of instructional reasoning that lead to responsive teaching. These involve a teacher (a) connecting specific moments of student thinking across different points in time and situated student thinking in relation to two or more students; (b) considering the relationship between student thinking and the structure of a mathematical task; and (c) developing tests of student thinking. In this study, we identified instructional reasoning that leads to responsive teaching practices in a different context. Rather than using teacher-selected video clips, we used teacher-selected pieces of student work. In addition, we drew on literature related to the design of approximations of practices in which responsive teaching practices can be rehearsed in a setting of reduced complexity [8,21,22].
2.3. Modeling Responsive Teaching
To capture how expert teachers make instructional decisions that are responsive to student thinking, there is a growing movement toward practice-based teacher education. Practice-based teacher education is a form of teacher education that focuses using scaffolded experiences to prepare teachers to enact high-quality instruction [10,23,24]. One approach to practice-based teacher education includes the design and facilitation of approximations of practice [25].
There are numerous studies that have examined the affordances of approximations of practice that include teachers reviewing video of their own teaching [21] and coached classroom discussions [26]. These studies can be organized into two categories, the first of which are studies that explore the teachers learning a set of instructional moves and responses that center student thinking and work to press on student thinking. For example, researchers have identified discussion moves that work to elicit student thinking and provide concrete exemplars for teachers to adapt and use during mathematics instruction [14]. These studies help educators to conceptualize and enact responsive teaching practices.
The second category of studies that examine approximations of practice involve teacher educators shifting their focus from a set of behaviors or actions to a focus on the teacher as an instructional decision maker who can leverage core practices that keep learner thinking central to teaching and learning [8,10,26,27]. One finding from these studies involves the idea that because teaching is dynamic, practice spaces should not be scripted, allowing educators to have time and space to examine learner thinking and to respond and act spontaneously [8,25,28]. A second characteristic involves the idea that approximations of practice should be authentic in terms of its setting (i.e., using video of an actual classroom), its artifacts (i.e., the use of student work), or in the nature of the activity (i.e., writing specific questions to ask students) [8]. These characteristics of effective approximations of practice helped to conceptualize the approximation of practice used in this study, which was designed to engage participants in professional noticing of children’s mathematical thinking.
2.4. Professional Noticing of Children’s Mathematical Thinking
Professional noticing of children’s mathematical thinking, hereafter referred to as professional noticing, involves three skills: (1) attending to children’s strategies, (2) interpreting children’s understanding, and (3) deciding how to respond based on children’s understanding [7]. According to prior research, professional noticing skills do not happen in isolation; they are interrelated and often cyclical [7]. Research exploring the interrelated nature of professional noticing skills often consider attending and interpreting together and explore the relationship of these two skills with the skill of deciding how to respond [7,29,30]. For example, Monson et al. [30] discovered that after participation in a learning module designed to support prospective teachers in attending to student strategies and deciding how to respond they not only showed growth in deciding how to respond but also showed gains in attending and interpreting.
Researchers also suggest that there are components embedded within professional noticing skills. For example, Luna and Selmer [31] examined the skill of deciding how to respond and identified the components of time, focus, and action. In this study, we examine expert teacher instructional reasoning when their deciding actions and purposes align with responsive teaching practices. We engage participants in an approximation of practice that involves three expert teachers in the professional noticing of student written work outside the active classroom.
3. Methods
3.1. Approximation of Practice
The approximation of practice used in this study (see Figure 1) involves participants teaching a typical math lesson (A), choosing pieces of written work from that teaching event (B), then participating in a semi-structured interview (C–F). The semi-structured interview includes the questions: (1) How would you describe your students’ work? (2) What does that tell you about your students’ thinking? (3) How do you make sense of/interpret what you have noticed? (4) How did you respond to this student? (5) Can you explain your thinking regarding your decision about how to respond? These questions were used to prompt the participants to engage in professional noticing and served to make their instructional reasoning explicit. Instructional reasoning occurred at two points in this space, first, when the participants interpreted what they noticed about student thinking on the written work, and second, when they shared their purposes for a deciding action. This latter type of instructional reasoning is used as a method to identify and verify whether participant decisions about how to respond demonstrated responsive teaching practices. The instructional reasoning that occurred as participants interpreted student thinking not directly shown on the written work is the focus of the current study.
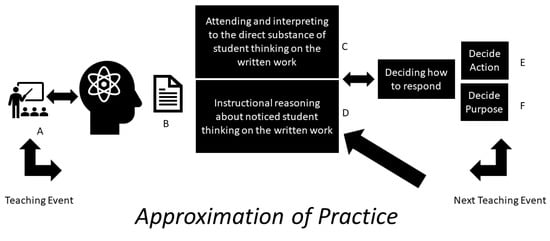
Figure 1.
Approximation of practice space (A–F).
3.2. Study Context
The three participants for this study all worked at Hill Elementary, a public school located in a suburban, ethnically diverse neighborhood in a medium-sized city in the Southern Appalachian region of the United States. Over 650 students attend the school and 43% of the students qualify for free or reduced-price lunch, and 33% of the students identified as a minority. At Hill Elementary school, 65% of the students scored at or above the proficient level for mathematics, well above the state and county average. Hill Elementary is part of a professional development school partnership with a research university and faculty in a college of education that is focused on identifying best practices for teaching science and mathematics. The participants for this project were chosen because they were active in professional development leadership initiatives. Two of the participants had previously participated in research projects that specifically focused on professional noticing of student thinking.
Ingrid has five years of teaching experience in a fifth-grade classroom. She earned her national board certification as a Middle Childhood Generalist and an Elementary Mathematics Specialist Certification. As part of her National Board Certification, she engaged students in math conversations and had students self-assess, peer-assess, and teacher-assess the accuracy of their mathematical language and thinking. Ingrid also participated in several partnerships activities that involved video clubs to support the professional noticing of students’ mathematical thinking.
Kendall has seven years of teaching experience in a fourth-grade classroom. She is a certified elementary and general science (grades 5–9) teacher and earned a Master of Arts in Instructional Design and Technology. At the time of the project, Kendall was working on her Elementary Mathematics Specialist certification and National Board Certification. Kendall also participated in partnership activities that involved a workshop on noticing student thinking in the context of an integrated science and mathematics garden-based learning project.
Hannah is a certified k–6th grade elementary teacher with additional certifications in English as a second language and gifted education (K-12). At the time of the project, she was obtaining a mentoring certification and was mentoring prospective teachers. Hannah also participated in several university and school partnership projects that involved noticing student thinking in the context of an integrated science and mathematics garden-based project. Ingrid, Kendall, and Hannah were considered teacher leaders because they all had five or more years of teaching experience and were active participants in a professional development school partnership. They all co-authored presentations and/or articles with university faculty focused on improving the teaching and learning of math and science in their school context [32].
3.3. Data Sources
The data set for this study involved the participants’ engagement with the approximation of practice across four cycles and consisted of 12 interview transcripts and 37 pieces of student written work. We coded the transcripts by identifying and separating out evidence of each professional noticing skill identified as attending, interpreting, and deciding. Next, we coded each attending and interpreting segment as either written work or not written work. A segment was coded as written work if the participant was attending to or interpreting student thinking directly on the piece of learning work. If the participant was attending to or interpreting student thinking not observable on the written work, the segment was coded as not written work. We separated the not written work segments, focusing on the written work segments. We conducted a preliminary analysis focused on the written work segments to confirm that the participants had noticed the important mathematical elements in 36 out of 37 pieces of written work, a prerequisite to teaching responsively [9]. Across the remaining 36 pieces of written work, participants shared 59 deciding actions and related shared purposes, hereafter referred to as deciding sequences. Each deciding sequence was identified as responsive based on whether the given action aligned with a responsive teaching practice and whether the shared purpose was rooted in the idea of picking up and pursuing student thinking [2,9]. This resulted in the identification of 35 responsive deciding sequences. Each of these deciding sequences contained an identified responsive deciding action and a related purpose. The four responsive deciding actions are displayed in Table 1.

Table 1.
Responsive deciding actions.
The four deciding purposes (see Table 2) identified as responsive were that the teacher wants: to test student understanding, to understand additional student thinking, the student to make mathematical connections, and the student to address a conceptual error.

Table 2.
Responsive deciding purposes.
Each of these 35 deciding sequences were identified as responsive in the context of this study. It is important to note that the deciding sequences were not enacted in a live classroom setting. Next, for each of the 35 identified responsive deciding sequences, we returned to the transcripts and combined the chunks of transcript coded as not written work. We then separated the transcripts each time the participants shifted in their instructional reasoning focus; hereafter referred to as an instructional reasoning turn. For example, a participant might start out by reasoning about their students’ thinking using big mathematical ideas (e.g., this student understands the properties of quadrilaterals) and then shift to reasoning about the source of a student’s understanding (e.g., learned this in a previous classroom lesson). Across the four cycles, we examined 36 pieces of written work and identified 35 responsive deciding sequences and 85 instructional reasoning turns (see Table 3).

Table 3.
Instructional reasoning turns.
3.4. Instructional Reasoning Coding Scheme
To develop the codes for the instructional reasoning turns, we conducted a qualitative content analysis using “theme” as the unit of analysis [33]. For example, we noticed that our participants were comparing students’ strategies with each other and then generalizing about what needed to be addressed in the next lesson [2]. At other times, our participants connected what they had noticed about student thinking to the source of that thinking, such as a previous lesson [15,34]. At other times, our participants considered the relationships between the curriculum and the development of students’ ideas [35]. The final coding scheme (see Table 4) resulted in the following codes in which a teacher (1) uses previous classroom experiences to reason about student thinking, (2) considers the relation between student thinking and the structure of a mathematical task [2], (3) situates a student’s idea in relation to two or more other students’ ideas, (4) considers student characteristics, and (5) situates student thinking in relation to mathematics according to (a) conceptual understanding, (b) procedural understanding, and (c) content standards.

Table 4.
Instructional reasoning codes.
The researchers first coded separately and then met to discuss and modify the emerging codes. Once the final codes were developed, the researchers coded the remaining data independently, met and discussed differences, and modified the codes until a 100% consensus across all data points was achieved.
4. Results
4.1. Instructional Reasoning
The participants engaged four times in the approximation of practice, which resulted in 35 responsive deciding sequences and 85 instructional reasoning turns prior to the 35 responsive deciding sequences. Table 5 shows the frequency of each type of instructional reasoning that occurred during the four cycles.

Table 5.
Instructional reasoning results.
Our results show that the most frequent type of instructional reasoning involved teachers situating student thinking in relation to mathematics with a focus on conceptual understanding (20 instances). The second most common type of instructional reasoning involved teachers using previous classroom experiences to reason about student thinking (18 instances), followed by situating the individual students’ thinking in relation to two or more other student ideas (16 instances) and considering the relationship between student thinking and the structure of a mathematical task (14 instances).
4.2. Responsive Deciding Sequences
Recall that these 85 instructional reasoning turns occurred prior to the participants’ sharing of a deciding sequence identified as responsive. The most common of these deciding sequences involved a participant sharing the deciding action of the teacher asking the student to work on a new task because the teacher wanted the student to make mathematical connections (nine instances). The second most common deciding sequence involved the deciding action of the teacher asking the student to elaborate on and/or clarify their thinking for the purpose of testing student understanding (eight instances). The third most common deciding sequence (seven instances) involved the deciding action of asking a student to elaborate on and/or clarify their thinking for the purpose of having the student make mathematical connections. The frequency of all the deciding sequences, including the three most common, and the associated number of instructional turns are shared in Table 6.

Table 6.
Deciding actions and instructional reasoning.
We used the common deciding sequences in Table 6, starting with the most common decide sequence, to serve as illustrative cases of responsive instructional reasoning.
4.2.1. Case 1: A Teacher Asks a Student to Work on a New Task for the Purpose of Having the Student Make Mathematical Connections
Across the three participants, there were nine instances of asking a student to work on a new task because the teacher wanted the student to make mathematical connections. Prior to these deciding sequences, the participants engaged in 23 instructional reasoning turns (see Table 7).

Table 7.
Case 1: Instructional reasoning turns.
To illustrate this case, we present an example from Kendall’s third cycle in the approximation of practice. Kendall began her engagement in the practice space by examining a piece of written work that involved students identifying angles on the playground (see Figure 2). Kendall stated, “I think that she’s got a very good handle on all of them” (finding angles on the playground) and highlighted that a student identified the monkey bars as an example of an acute angle, an affirmation that the chosen task was effective in helping Kendall determine the student’s understanding of angles.

Figure 2.
Piece of student work (Cycle 3, Kendall).
Kendall then considered the relation between student thinking and the structure of the mathematical task, explaining that it might be beneficial to give the students a task in which the students first choose an angle and then determine the measurement of the other angles without using a protractor. She explains: “I might have them choose a specific angle and find the measurement for that one using a protractor and then try to figure out what all of the rest would be without using the protractor (Transcript 3K)”. Kendall continues to engage in instructional reasoning by situating student thinking in relation to the mathematical content standards:
“I would also like to connect to our next standard, with shapes and how she has an acute angle for the monkey bars ……so what type of shape would that be so taking what you know about this and translating it into our next standard (Transcript 3K)”.
Kendall then shifted her instructional reasoning back to considering the relation between the mathematics of student thinking and the structure of a mathematical task: “I think maybe another thing that I could have them do is to disconnect it from school, have them look at their home for these shapes (Transcript 3K)”. Then, Kendall decided that she was going to have the student work on a new task involved finding angles and shapes at home, for the purpose of having students connect what they know about angles to shapes found in their houses. This deciding sequence was coded as the teacher asking the student to work on a new task for the purpose of having the student make mathematical connections.
4.2.2. Case 2: A Teacher Asks the Student to Elaborate on and/or Clarify Their Thinking for the Purpose of Testing Student Understanding
Across the three participants, there were eight instances of a teacher asking students to elaborate on and/or clarify their thinking in order to test student understanding. Prior to sharing these deciding sequences, the participants engaged in 24 instructional reasoning turns (see Table 8).

Table 8.
Case 2: Instructional reasoning turns.
To illustrate Case 2, we present an example from Ingrid’s third cycle in the approximation of practice as she examined a piece of student written work that involved the following problem: Stella bought an aquarium with a rectangular base that measures 18 inches wide by 14 inches long and a height of 10 inches. One fish needs 40 cubic inches of space in the aquarium. What is the volume of the aquarium? How many fish can live in the aquarium and how do you know?
The student thinking shown in Figure 3 involved a student-constructed strategy for finding the volume.

Figure 3.
Piece of student work (Cycle 3, Ingrid).
Ingrid began by describing and interpreting the procedures and operations the student used to solve the problem: “I can see that she was able to multiply 14 by 8 got 112 and then 112 by 10 so she was able to find her volume and knew it was 1120 (Transcript 3I)”. Notice how she interpreted the procedures and operations the student used to solve the word problem and provided evidence of the student’s conceptual and procedural understanding for finding volume:
“I think that she grasps what math goes into solving this problem…that you need to multiply to find the volume and that she needed to take that amount of volume and divide it up to find out how many fish needed to go in it. So overall she understands the process and the operations behind what fit with the scenario (Transcript 3I)”.
This transcript excerpts provide evidence of two different, but often related, types of instructional reasoning, both involving mathematics. The first is that the instructional reasoning focuses on a student’s procedural understanding, which was one of the least used types of instructional reasoning by our participates (three total instances). For example, notice how Ingrid focused on detailing the accuracy of the processes and operations the student used to solve the problem. For example, she explained: “she needed to take that amount of volume and divide it to find out how many fish needed to go in it, so she understood the process …. the operations behind what fit with the scenario (Transcript 3I)”. This type of instructional reasoning differs from instructional reasoning that situates student thinking in relation to students’ conceptual understanding, which was the most often used type of instructional reasoning (20 total instances). Ingrid engaged in this instructional reasoning just prior to the deciding action of asking a student to elaborate on and/or clarify their thinking for the purpose of testing student understanding. Ingrid explained: “I would have her further explain her thinking about the problem to make sure she grasped the overall idea of the problem and the way to solve it (Transcript 3I)”.
4.2.3. Case 3: A Teacher Asks the Student to Elaborate on and/or Clarify Their Thinking for the Purpose of Having the Student Make Mathematical Connections
Across the three participants, there were seven instances of the deciding sequence involving the deciding action of the teacher asking students to elaborate on and/or clarify their thinking for the purpose of having the student make mathematical connections. Prior to sharing this deciding sequence, the participants engaged in 17 instructional reasoning turns (see Table 9).

Table 9.
Case 3: Instructional reasoning turns.
To illustrate this case, we present an example from Hannah’s third cycle in the approximation of practice when she examined a piece of written work that involved a student finding the volume of a cube and explaining their solution (see Figure 4).

Figure 4.
Piece of student work (Cycle 3, Hannah).
As with the other pieces of written work, Hannah began her engagement in the approximation of practice by noticing the student thinking on the piece of written work, stating: “The shape is four blocks up and across and four blocks back, so she didn’t necessarily use the mathematical term but definitely she has an understanding of up, across, and back, and that’s where she is getting her measurements (Transcript H3)”. Hannah continued to instructionally reason by situating individual student thinking in relation to two or more other student ideas (16 total instances), “so I felt like her description there was very fifth grade student like, and it fit perfectly with what we were doing (Transcript H3)”. Hannah’s instructional reasoning about her students’ thinking in relation to others is important as teachers need to focus simultaneously on individual students and on the entire class. Hannah also instructionally reasoned using previous classroom experiences that the student had perhaps drawn on to find a solution to the current problem:
“We practiced these types of problems, I gave them graph paper, I used this great really neat interactive volume site where you can like put layers up and then click the sides…so we spent I mean a whole day just on that and figuring out ok the length the width and the height and then practiced multiplying them together (Transcript H3)”.
Shifting her noticing back to the student, Hannah stated that she would respond to this student by asking the student “to add to her answers for the purpose of having the student use more formal mathematical vocabulary and to connect her written explanation more clearly to the figure and her use of units, and then connect what she wrote to the actual shape”. This response was coded as the teacher asking the student to elaborate on and/or clarify their thinking so that the student can make mathematical connections.
5. Discussion
5.1. Instructional Reasoning
Our data analysis helped us to identify and distinguish between two types of instructional reasoning. The first type of instructional reasoning is novel and involves a teacher’s purpose for a deciding action. By capturing a teacher’s purpose for a deciding action, we prompted additional instructional reasoning which, in turn, provided additional evidence of responsive teaching. For example, a deciding purpose that involved a teacher wanting a student to make mathematical connections is focused on student thinking, in contrast to a teacher whose purpose is for a student not to make a procedural error. We suggest that this type of instructional reasoning is empirically important as it could be used in future research on responsive teaching to identify and understand teachers’ intentions behind teaching practices that appear responsive.
The second type of instructional reasoning involves the instructional reasoning that occurs just prior to engaging in a responsive deciding action. Like Dyer and Sherin [2], we found that our participants engaged in this type of instructional reasoning when considering the relation between student thinking and the structure of a mathematical task and when they situated student thinking in relation to two or more students. However, our findings characterize additional types of instructional reasoning that include a teacher (1) using previous classroom experiences to reason about student thinking, (2) considering student characteristics, and (3) situating student thinking in relation to the mathematics by focusing on (a) conceptual understanding, (b) procedural understanding, and/or (c) content standards.
The ways that teachers instructionally reasoned about student thinking prior to engaging in a responsive deciding sequence was clearly connected to the kinds of work these teachers conducted in their classrooms. To support this claim, we revisit the cases to demonstrate how instructional reasoning by expert teachers enhances the work they do in their classrooms.
5.1.1. Case 1: A Teacher Asks a Student to Work on a New Task for the Purpose of Having the Student Make Mathematical Connections
In Case 1, recall that Kendall began by examining a piece of student work that involved students identifying angles on the playground. Prior to asking students to work on a new task, she engaged in instructional reasoning that involved considering the relation between student thinking and the structure of a mathematical task. For example, she thought about how a future task involving her students using a protractor in a real-world context would develop her students’ understanding of angels as well address critical content standards, because “…students can only learn what they have the opportunity to think about, student thinking is bounded by the tasks they are assigned” [36] (p. 606). Choosing and/or designing the right task to frame student thinking and connect these tasks to content standards requires strong pedagogical knowledge and the ability to attend deeply to student thinking as they reason about future task structures. Additionally, this type of instructional reasoning results in tasks that draw out student thinking, which in turn enhances responsive teaching practices. This suggests that teachers would benefit from professional learning experiences that center task structures and mathematical content standards to develop responsive teaching practices.
5.1.2. Case 2: A Teacher Asks the Student to Elaborate on and/or Clarify Their Thinking for the Purpose of Testing Student Understanding
In Case 2, Ingrid examined a piece of student written work that involved a student-constructed strategy for finding volume (see Figure 3). Ingrid’s instructional reasoning focused on connecting student thinking to disciplinary ideas [7]. It is not surprising that our participants (teacher leaders) primarily reasoned about conceptual mathematical understanding over procedural understanding or the content standards (20 times vs. 3 times vs. 6 times, respectively). This finding suggests that teacher leaders are intentional about developing students’ conceptual mathematical understanding and focus on substantive rather than surface-level understanding of students’ ideas [6]. This finding also suggests that approximations of practice should be designed to provide novice teachers with opportunities to practice connecting students’ mathematical thinking to broader mathematical ideas and standards.
5.1.3. Case 3: A Teacher Asks the Student to Elaborate on and/or Clarify Their Thinking for the Purpose of Making Mathematical Connections
In Case 3, Hannah discussed a piece of student written work that involved a student finding the volume of a cube (see Figure 4). In this deciding sequence, Hannah engaged in the deciding action of asking the student to elaborate on and/or clarify their thinking for the purpose of having the student make mathematical connections. Hannah first situated her students’ thinking in relation to other fifth-grade students. This type of instructional reasoning suggests that responsive teachers should unpack and hold on to the substance of individual students’ thinking in ways that are connected to patterns of thinking in groups of students in connection to a whole class. This finding suggest that approximations of practice should be designed to help prospective teachers develop efficient ways of attending to the breadth and substantive details of an individual student’s thinking while connecting that thinking to groups of students within a whole class.
Hannah also connected her students’ thinking by reasoning about a previous class experience. We, like others, find the idea of teachers referencing specific moments from classroom teaching events notable as it suggests that responsive teacher thinking and reasoning is situated in the context in which that thinking appeared [2]. Therefore, as teachers reason about the source of students’ knowledge, they might be recalling and synthesizing several past classroom learning experiences, suggesting that their ability to easily reference and make sense of these specific moments may be a necessary condition for teaching responsively. These findings support the idea that approximations of practice should be implemented in ways that provide prospective teachers with the time and space to develop the practice of recalling specific moments of classroom learning in connection with student thinking [8,25].
6. Conclusions
This study confirms and expands our understandings about how teachers engage in instructional reasoning in ways that have pedagogical value and empirical implications for teacher education. Our research distinguished between two types of instructional reasoning. The first focused on teachers’ purposes for their deciding actions. This type of instructional reasoning is empirically important because it provides additional evidence of the often-hidden instructional reasoning that supports responsive teaching practices. The second type of instructional reasoning focused on the ways participants made sense of the student thinking noticed in pieces of written work. The second type of instructional reasoning was illustrated through three cases that captured the different ways expert teachers instructionally reasoned about students’ thinking prior to engaging in a responsive deciding sequence. These findings demonstrate the importance of capturing responsive teaching practices taking place in and out of active classroom settings. In doing so, teacher educators can design approximations of practices to develop prospective teachers’ professional noticing skills and ways of instructional reasoning that support responsive teaching practices. The authors acknowledge that the small sample size involving three teachers from the same school setting means that there are limitations to the generalizability of the findings. Future research should include a larger sample size of teachers from diverse school settings to confirm and/or identify the various ways mathematics teachers reason about student mathematical thinking.
Author Contributions
Conceptualization, D.L. and S.S.; methodology, D.L. and S.S.; software, D.L. and S.S.; validation, D.L. and S.S.; formal analysis, D.L. and S.S.; investigation, D.L. and S.S.; resources, D.L. and S.S.; data curation, D.L. and S.S.; writing—original draft preparation, D.L. and S.S.; writing—review and editing, D.L. and S.S.; visualization, D.L. and S.S.; supervision, D.L. and S.S.; project administration, D.L. and S.S.; funding acquisition, D.L. and S.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
The study was conducted in accordance with and approved by the Institutional Review Board (or Ethics Committee) of West Virginia University, IRB Code: 1602999970. Date of Approval: 2 November 2016.
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ball, D.L. With an eye on the mathematical horizon: Dilemmas of teaching elementary school mathematics. Elem. Sch. J. 1996, 93, 373–397. [Google Scholar] [CrossRef]
- Dyer, E.B.; Sherin, M.G. Instructional reasoning about interpretations of student thinking that supports responsive teaching in secondary mathematics. ZDM—Int. J. Math. Educ. 2016, 48, 69–82. [Google Scholar] [CrossRef]
- Franke, M.L.; Kazemi, E. Learning to teach mathematics: Focus on student thinking. Theory Pract. 2001, 40, 102–109. [Google Scholar] [CrossRef]
- Jacobs, V.R.; Spangler, D.A. Research on core practices in K-12 mathematics teaching. In Compendium for Research in Mathematics Education; Cai, J., Ed.; NCTM: Reston, VI, USA, 2017; pp. 766–792. [Google Scholar]
- Carpenter, T.P.; Fennema, E.; Franke, M.L. Cognitively guided instruction: A knowledge base for reform in primary mathematics instruction. Elem. Sch. J. 1996, 97, 3–20. [Google Scholar] [CrossRef]
- Coffey, J.E.; Hammer, D.; Levin, D.M.; Grant, T. The missing disciplinary substance of formative assessment. J. Res. Sci. Teach. 2011, 48, 1109–1136. [Google Scholar] [CrossRef]
- Jacobs, V.R.; Lamb, L.L.; Philipp, R.A. Professional noticing of children’s mathematical thinking. Math. Educ. Res. J. 2010, 41, 169–202. [Google Scholar] [CrossRef]
- Kavanagh, S.S.; Metz, M.; Hauser, M.; Fogo, B.; Taylor, M.W.; Carlson, J. Practicing responsiveness: Using approximations of teaching to develop teachers’ responsiveness to students’ ideas. J. Teach. Educ. 2020, 71, 94–107. [Google Scholar] [CrossRef]
- Richards, J.; Robertson, A.D. A review of the research on responsive teaching in science and mathematics. In Responsive Teaching in Science and Mathematics; Robertson, A.D., Scherr, R., Hammer, D., Eds.; Routledge: London, UK, 2015; pp. 54–73. [Google Scholar] [CrossRef]
- McDonald, M.; Kazemi, E.; Kavanagh, S.S. Core practices and pedagogies of teacher education: A call for a common language and collective activity. J. Teach. Educ. 2013, 64, 378–386. [Google Scholar] [CrossRef]
- Loughran, J. Pedagogical reasoning: The foundation of the professional knowledge of teaching. Teach. Teach. 2019, 25, 523–535. [Google Scholar] [CrossRef]
- Loughran, J.; Keast, S.; Cooper, R. Pedagogical reasoning in teacher education. In International Handbook of Teacher Education; Loughran, J., Hamilton, M.L., Eds.; Springer Science and Business Media: Cham, Switzerland, 2016; pp. 387–421. [Google Scholar]
- Crespo, S. Seeing more than right and wrong answers: Prospective teachers’ interpretations of students’ mathematical work. J. Math. Teach. Educ. 2000, 3, 155–181. [Google Scholar] [CrossRef]
- Stein, M.K.; Engle, R.A.; Smith, M.S.; Hughes, E.K. Orchestrating productive mathematical discussions: Five practices for helping teachers move beyond show and tell. Math. Think. Learn. 2008, 10, 313–340. [Google Scholar] [CrossRef]
- Selmer, S.; Lampen, E.; Lindstrom, D.L. Pre-service teachers engaged in noticing aspects of learner written work. S. Afr. J. Educ. 2021, 41, 1–9. [Google Scholar] [CrossRef]
- Gee, J.P. Literacy, discourse, and linguistics. J. Educ. 1989, 171, 5–25. [Google Scholar] [CrossRef]
- Lave, J.; Wenger, E. Situated Learning: Legitimate Peripheral Participation; Cambridge University Press: Cambridge, UK, 1991. [Google Scholar]
- Moje, E.B. Doing and teaching disciplinary literacy with adolescent learners: A social and cultural enterprise. Harv. Educ. Rev. 2015, 85, 254–278. [Google Scholar] [CrossRef]
- Hammer, D.; Goldberg, F.; Fargason, S. Responsive teaching and the beginnings of energy in a third-grade classroom. Rev. Sci. Math. ICT Educ. 2012, 6, 51–72. [Google Scholar] [CrossRef]
- Lineback, J.E. The redirection: An indicator of how teachers respond to student thinking. J. Learn. Sci. 2015, 24, 419–460. [Google Scholar] [CrossRef]
- Lampert, M.; Franke, M.L.; Kazemi, E.; Ghousseini, H.; Turrou, A.C.; Beasley, H.; Cunard, A.; Crowe, K. Keeping it complex: Using rehearsals to support novice teacher learning of ambitious teaching. J. Teach. Educ. 2013, 64, 226–243. [Google Scholar] [CrossRef]
- Schutz, K.; Danielson, K.; Cohen, J. Approximations in English language arts: Scaffolding a shared teaching practice. Teach. Teach. Educ. 2019, 81, 100–111. [Google Scholar] [CrossRef]
- Ball, D.L.; Forzani, F.M. The work of teaching and the challenge for teacher education. J. Teach. Educ. 2009, 60, 497–511. [Google Scholar] [CrossRef]
- Grossman, P.; Kavanagh, S.S.; Dean, C.P. The turn to practice in teacher education: An introduction to the work of the core practice consortium. In Teaching Core Practices in Teacher Education; Grossman, P., Ed.; Harvard Education Press: Cambridge, MA, USA, 2018; pp. 1–14. [Google Scholar]
- Grossman, P.; Hammerness, K.; McDonald, M. Redefining teaching, re-imagining teacher education. Teach. Teach.: Theory Pract. 2009, 15, 273–289. [Google Scholar] [CrossRef]
- Kazemi, E.; Ghousseini, H.; Cunard, A.; Turrou, A.C. Getting inside rehearsals: Insights from teacher educators to support work on complex practice. J. Teach. Educ. 2016, 67, 18–31. [Google Scholar] [CrossRef]
- Tyminski, A.M.; Zambak, V.S.; Drake, C.; Land, T.J. Using representations, decomposition, and approximations of practices to support prospective elementary mathematics teachers’ practice of organizing discussions. J. Math. Teach. Educ. 2014, 17, 463–487. [Google Scholar] [CrossRef]
- Cohen, D.K.; Raudenbush, S.W.; Ball, D.L. Resources, instruction, and research. Educ Eval Policy Anal. 2003, 25, 119–142. [Google Scholar] [CrossRef]
- Fisher, M.H.; Thomas, J.; Schack, E.O.; Jong, C.; Tassell, J. Noticing numeracy now! Examining changes in preservice teachers’ noticing, knowledge, and attitudes. Math. Educ. Res. J. 2018, 30, 209–232. [Google Scholar] [CrossRef]
- Monson, D.; Krupa, E.; Lesseig, K.; Casey, S. Developing secondary prospective teachers’ ability to respond to student work. J. Math. Teach. Educ. 2018, 23, 209–232. [Google Scholar] [CrossRef]
- Luna, M.; Selmer, S. Examining the responding component of teacher noticing: A case of one teacher’s pedagogical responses to students’ thinking in classroom artifacts. J. Teach. Educ. 2021, 72, 579–593. [Google Scholar] [CrossRef]
- Rummel, S.; Rye, J.; Selmer, S.; Luna, M. Action research to integrate science with mathematics through Garden-Based Learning at the elementary school level. J. Adv. Educ. Res. 2017, 2, 199–211. [Google Scholar]
- Miles, M.B.; Huberman, A.M. Qualitative Data Analysis: An Expanded Sourcebook; Sage Publications: Thousand Oaks, CA, USA, 1994. [Google Scholar]
- Luna, M.J.; Sherin, M.G. Using a video club design to promote teacher attention to students’ ideas in science. Teach. Teach. Educ. 2017, 66, 282–294. [Google Scholar] [CrossRef]
- Ball, D.L.; Thames, M.H.; Phelps, G. Content knowledge for teaching: What makes it special? J. Teach. Educ. 2008, 59, 389–407. [Google Scholar] [CrossRef] [Green Version]
- Tekkumru-Kisa, M.; Stein, M.K.; Doyle, W. Theory and research on tasks revisited: Task as a context for students’ thinking in the era of ambitious reforms in mathematics and science. Educ. Res. 2020, 49, 606–617. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).