Similarities in Procedures Used to Solve Mathematical Problems and Video Games
Abstract
1. Introduction
Mathematical competence is the ability to use mathematical knowledge in a cross-cutting manner in mathematical and non-mathematical situations and contexts. Mathematical competence goes beyond procedural knowledge; it is manifested in the use of conceptual knowledge in different practical situations.(pp. 116–117)
1.1. Problem-Solving
1.2. Video Games for Problem-Solving
1.3. Research Questions and Objectives
2. Materials and Methods
2.1. Population and Sample
2.2. Method
2.3. Instruments
2.4. Data Analysis
3. Results and Discussion
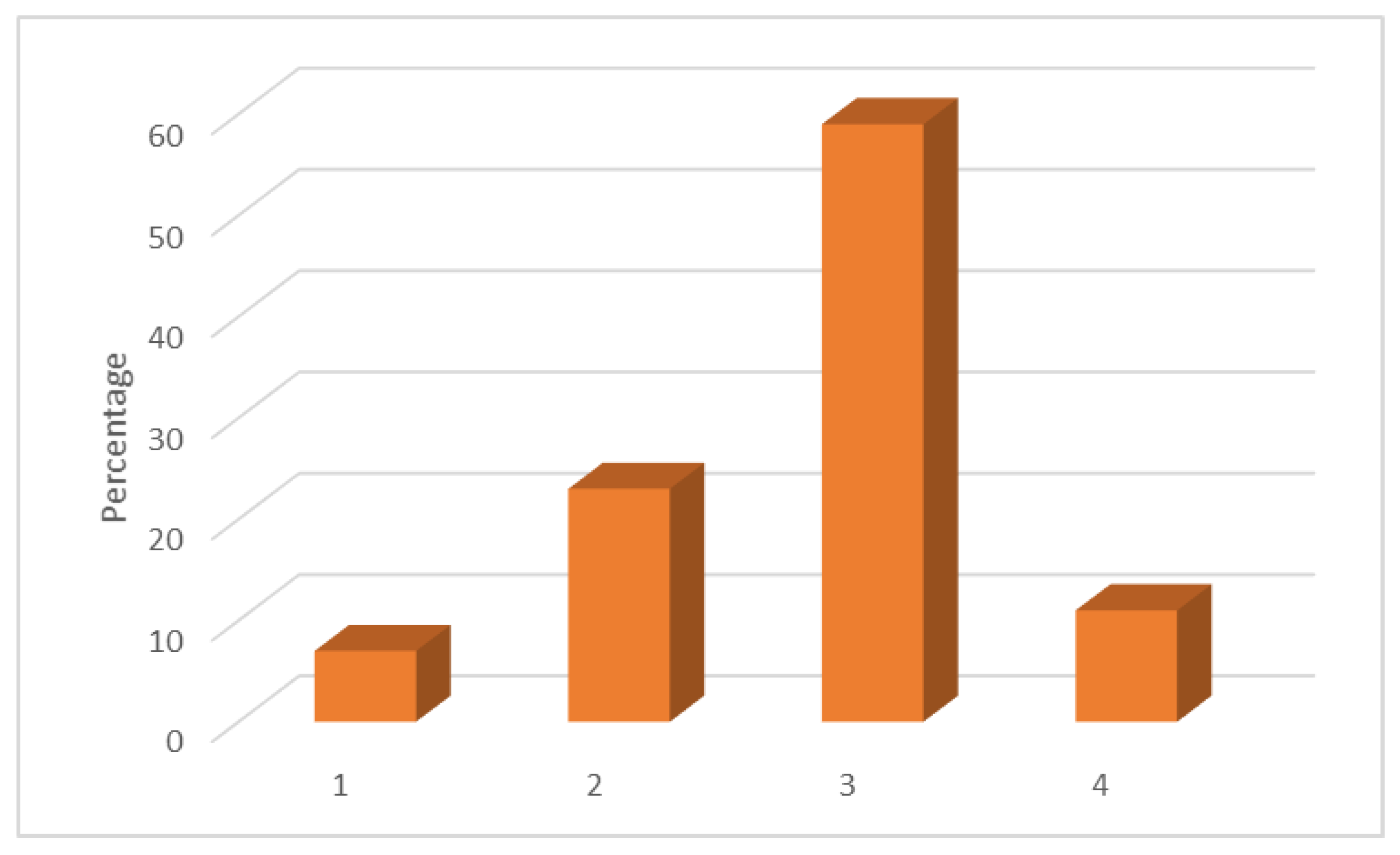
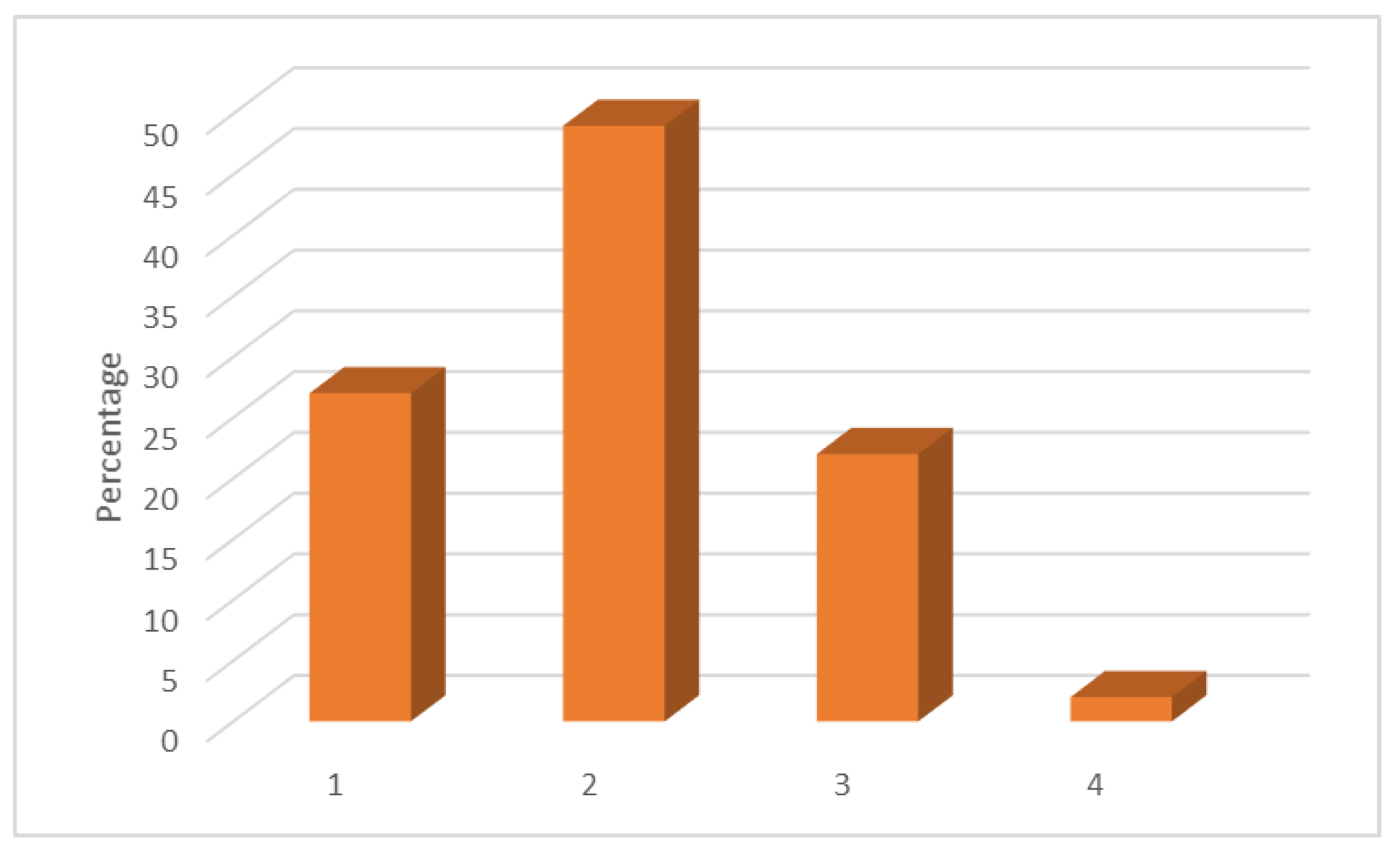
3.1. J11-Type Player. Player Who Does Not Need External Help to Pass a Level
3.2. J21-Type Player. Player Who Is Stuck but Passes the Level without External Help
3.3. J31-Type Player. Player Who Gets Stuck on a Level and Does Not Continue
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- McGonigal, J. Reality Is Broken: Why Games Make Us Better and How They Can Change the World; Penguin: Sidney, Australia, 2011. [Google Scholar]
- Revuelta, F.I.; Guerra, J. ¿Qué aprendo con videojuegos? Una perspectiva de meta-aprendizaje del videojugador. Rev. Educ. Distancia 2012, 33, 1–25. [Google Scholar]
- Gorgorió, N.; Albarracín, L. Mathematical knowledge prior to the Initial Education of Teachers: The need for and specification of a test for their evaluation. In Research on the Mathematics Teacher: Training, Classroom Practice, Knowledge and Professional Competence; University of Salamanca: Salamanca, Spain, 2019; pp. 111–132. [Google Scholar]
- Beserra, V.; Nussbaum, M.; Oteo, M. On-Task and Off-Task Behavior in the Classroom: A Study on Mathematics Learning With Educational Video Games. J. Educ. Comput. Res. 2019, 56, 1361–1383. [Google Scholar] [CrossRef]
- Moore-Russo, D.; Diletti, J.; Strzelec, J.; Reeb, C.; Schillace, J.; Martin, A.; Arabeyyat, T.; Prabucki, K.; Scanlon, S. A study of how Angry Birds has been used in Mathematics Education. Digit. Exp. Math. Educ. 2015, 1, 107–132. [Google Scholar] [CrossRef]
- Tokac, U.; Novak, E.; Thompson, C.G. Effects of game-based learning on students’ mathematics achievement: A meta-analysis. J. Comput. Assist. Learn. 2019, 35, 407–420. [Google Scholar] [CrossRef]
- Anderson, J.; Barnett, M. Using Video Games to Support Pre-Service Elementary Teachers Learning of Basic Physics Principles. J. Sci. Educ. Technol. 2011, 20, 347–362. [Google Scholar] [CrossRef]
- Croxton, D.; Kortemeyer, G. Informal physics learning from video games: A case study using gameplay videos. Phys. Educ. 2017, 53, 015012. [Google Scholar] [CrossRef]
- de Aldama, C.; Pozo, J.-I. Do you want to learn Physics? Please play Angry Birds (but with epistemic goals). J. Educ. Comput. Res. 2020, 58, 3–28. [Google Scholar] [CrossRef]
- Pittman, C. Teaching With Portals: The Intersection of Video Games and Physics Education. Learn. Landsc. 2013, 6, 341–360. [Google Scholar] [CrossRef][Green Version]
- Ullman, T.D.; Spelke, E.; Battaglia, P.; Tenenbaum, J.B. Mind Games: Game Engines as an Architecture for Intuitive Physics. Trends Cogn. Sci. 2017, 21, 649–665. [Google Scholar] [CrossRef]
- Ministerio de Educación y Ciencia. Orden ECI/3960/2007, de 19 de Diciembre, por la que se Establece el Currículo y se Regula la Ordenación de la Educación Infantil. Boletín Oficial del Estado. 2008. Available online: https://www.boe.es/eli/es/o/2007/12/19/eci3960 (accessed on 13 December 2021).
- Ministerio de Educación, Cultura y Deporte. Real Decreto 126/2014, de 28 de Febrero, por el que se Establece el Currículo Básico de la Educación Primaria. Boletín Oficial del Estado 2014. Available online: https://www.boe.es/eli/es/rd/2014/02/28/126 (accessed on 13 December 2021).
- Polya, G.; Zugazagoitia, J. Cómo Plantear y Resolver Problemas, 15th ed.; Mexico, D.F., Ed.; Trillas: Mexico City, Mexico, 1989; ISBN 9682400643. [Google Scholar]
- Mason, J.; Burton, L.; Stacey, K. Pensar Matemáticamente, 2nd ed.; Labor: Barcelona, Spain, 1992; ISBN 8433551396. [Google Scholar]
- Quintanilla Batallanos, V.A.; Gallardo Romero, J. Identificar experiencias emocionales para mejorar la comprensión en matemáticas. Uno Rev. De Didáctica De Las Mat. 2020, 88, 24–33. [Google Scholar]
- Di Leo, I.; Muis, K.R.; Singh, C.A.; Psaradellis, C. Curiosity… Confusion? Frustration! The role and sequencing of emotions during mathematics problem solving. Contemp. Educ. Psychol. 2019, 58, 121–137. [Google Scholar] [CrossRef]
- Caballero, A.; Blanco, L.J.; Guerrero, E. Problem-solving and emotional education in Initial Primary Teacher Education. EURASIA J. Math. Sci. Technol. Educ. 2011, 7, 281–292. [Google Scholar] [CrossRef]
- Hanin, V.; Van Nieuwenhoven, C. Developing an expert and reflexive approach to problem-solving: The place of emotional knowledge and skills. Psychology 2018, 9, 280–309. [Google Scholar] [CrossRef]
- Trezise, K.; Reeve, R.A. Cognition-emotion interactions: Patterns of change and implications for math problem solving. Front. Psychol. 2014, 5, 840. [Google Scholar] [CrossRef]
- Hernández-Sabaté, A.; Albarracín, L.; Calvo, D.; Gorgorió, N. EyeMath: Identifying Mathematics problem solving processes in a RTS video game. In Proceedings of the Games and Learning Alliance: 5th International Conference, GALA 2016, Utrecht, The Netherlands, 5–7 December 2016; Springer: Cham, Switzerland, 2016; pp. 50–59. [Google Scholar]
- Bavelier, D.; Green, C.S.; Pouget, A.; Schrater, P. Brain plasticity through the life span: Learning to learn and action video games. Annu. Rev. Neurosci. 2012, 35, 391–416. [Google Scholar] [CrossRef] [PubMed]
- Blumberg, F.C.; Rosenthal, S.F.; Randall, J.D. Impasse-driven learning in the context of video games. Comput. Hum. Behav. 2008, 24, 1530–1541. [Google Scholar] [CrossRef]
- de Aguilera, M.; Mendiz, A. Video games and education. Comput. Entertain. 2003, 1, 1–10. [Google Scholar] [CrossRef]
- Shute, V.J.; Ventura, M.; Ke, F. The Power of Play: The effects of Portal 2 and Lumosity on Cognitive and Noncognitive Skills. Comput. Educ. 2015, 80, 58–67. [Google Scholar] [CrossRef]
- Shute, V.; Wang, L. Measuring Problem Solving Skills in Portal 2. In E-Learning Systems, Environments and Approaches; Isaías, P., Spector, J., Ifenthaler, D., Sampson, D., Eds.; Springer: Cham, Switzerland, 2015; pp. 11–24. [Google Scholar] [CrossRef]
- Avry, S.; Chanel, G.; Bétrancourt, M.; Molinari, G. Achievement appraisals, emotions and socio-cognitive processes: How they interplay in collaborative problem-solving? Comput. Hum. Behav. 2020, 107, 106267. [Google Scholar] [CrossRef]
- Chorianopoulos, K.; Giannakos, M. Design principles for serious video games in Mathematics Education: From theory to practice. Int. J. Serious Games 2014, 1, 51–59. [Google Scholar] [CrossRef]
- Creswell, J.W. Research Design: Qualitative, Quantitative, and Mixed Methods Approaches, 3rd ed.; SAGE Publications: Newbury Park, CA, USA, 2009. [Google Scholar]
- Novak, E.; Tassell, J. Using video game play to improve education-majors’ mathematical performance: An experimental study. Comput. Hum. Behav. 2015, 53, 124–130. [Google Scholar] [CrossRef]
- Gómez-Chacón, I.M. Affective influences in the knowledge of Mathematics. Educ. Stud. Math. 2000, 43, 149–168. [Google Scholar] [CrossRef]
- Vahlo, J.; Karhulahti, V.M. Challenge Types in Gaming Validation of Videogame Challenge Inventory (CHA). Int. J. Hum. Comput. Stud. 2020, 143, 102473. [Google Scholar] [CrossRef]
- Qaffas, A.A. An Operational Study of Video Games’ Genres. Int. J. Interact. Mob. Technol. 2020, 14, 175–194. [Google Scholar] [CrossRef]
- Quwaider, M.; Alabed, A.; Duwairi, R. The Impact of Video Games on the Players Behaviors: A Survey. Procedia Comput. Sci. 2019, 151, 575–582. [Google Scholar] [CrossRef]
- Tan, D.Y.; Cheah, C.W. Developing a gamified AI-enabled online learning application to improve students’ perception of university physics. Comput. Educ. Artif. Intell. 2021, 2, 100032. [Google Scholar] [CrossRef]
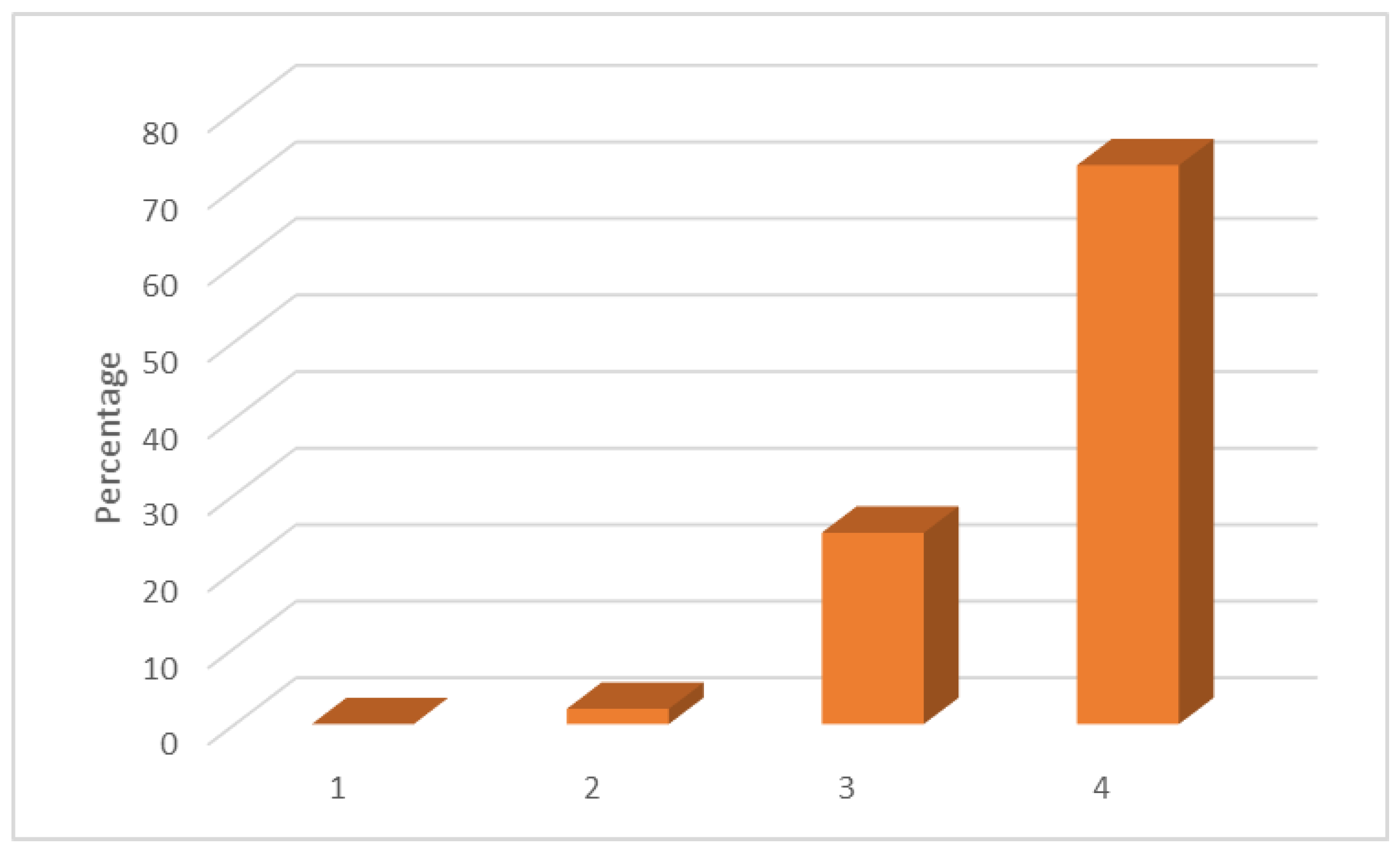
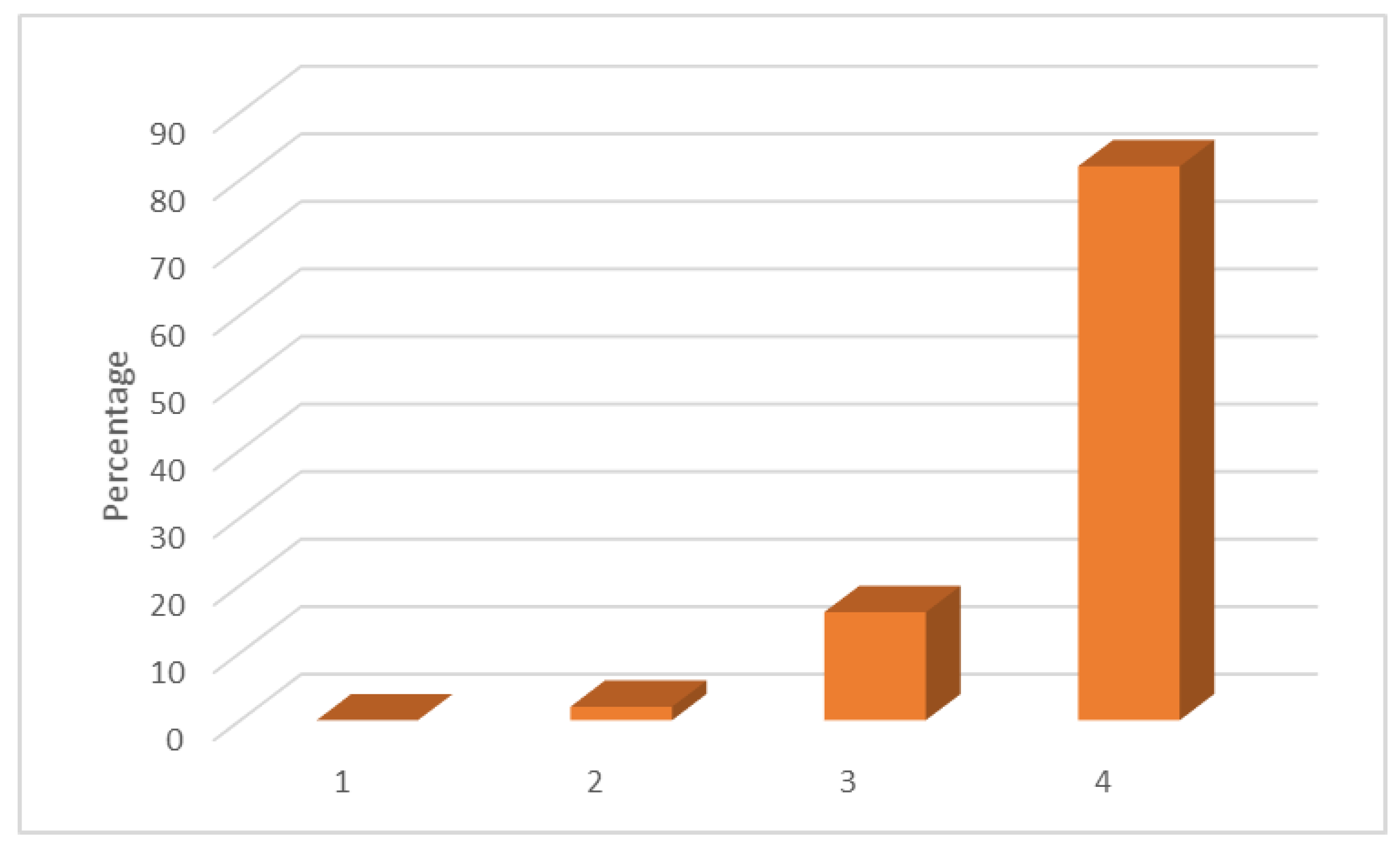

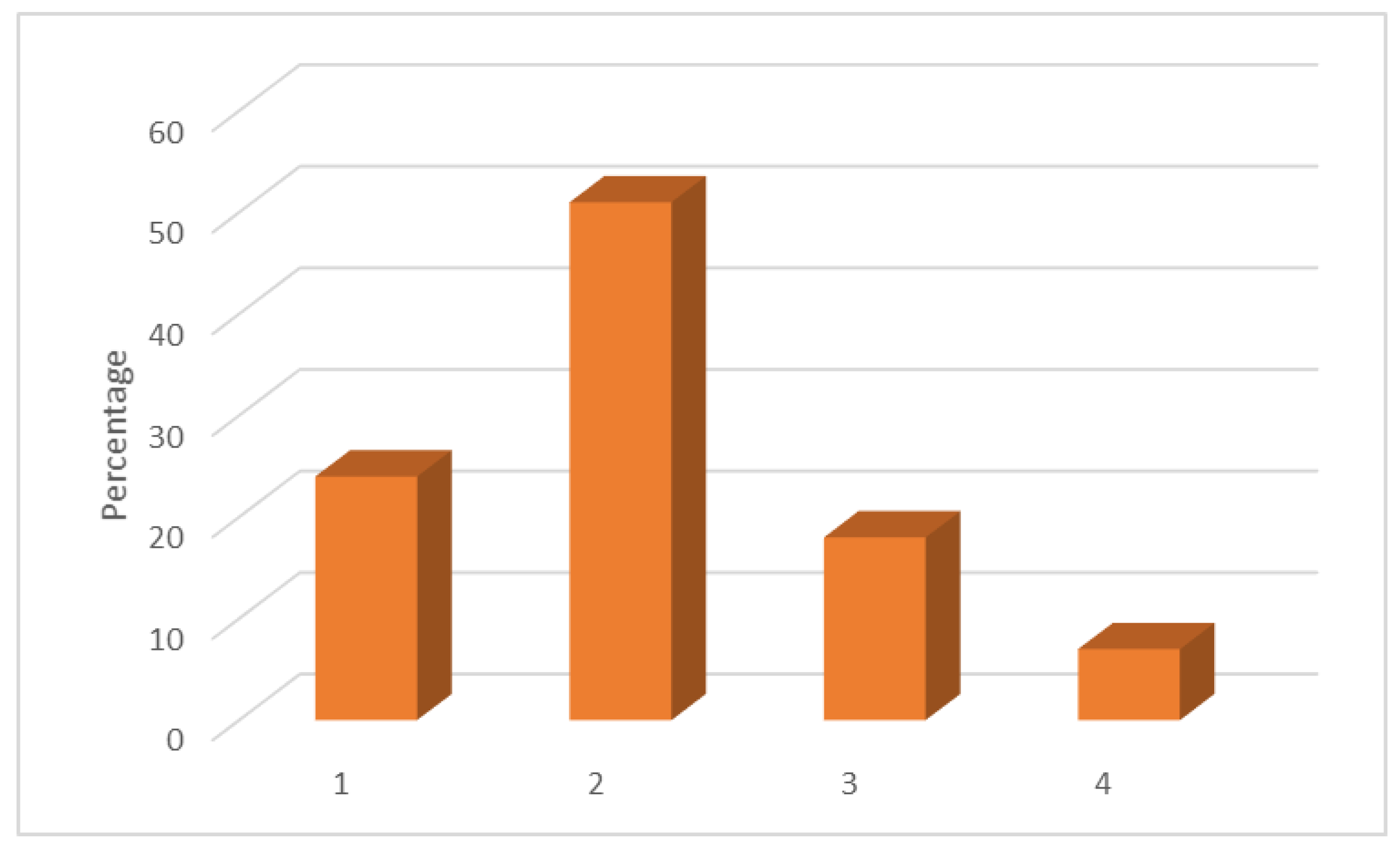
| Phases | Questions |
|---|---|
| Understanding the problem | What is the unknown? What data do I have? What is the condition? Is it enough to find the unknown? Is it redundant, contradictory, or insufficient? |
| Devising a plan | Have I seen this problem before? Do I know of any similar problems? |
| Carrying out the plan | Am I sure that each step is correct? Can I prove that the step is correct? |
| Looking back | Can I check the result and the reasoning? Can I derive the solution differently? |
| Phases | Processes | Issues or Propositions | States |
|---|---|---|---|
| Entry | Specialising | What do I KNOW? What do I WANT? What can I INTRODUCE? | STUCK! |
| Attack | CONJECTURE | ||
| Generalising | Try (Attempt) Check and distrust (Maybe) But why? | AHA! | |
| Review | CHECK the resolution REFLECT on the key ideas and key moments GENERALISE to a wider context |
| Principles | Video Game | Problem-Solving |
|---|---|---|
| 1st. Hero or heroine. Their story | The video game’s main character is trapped in a futuristic laboratory, controlled by an artificial intelligence called GLaDOS, from which she must escape to save her life. | Statement. Understand the problem, the objectives, and the challenges posed. |
| 2nd. Use of known techniques in the video game | The main character must identify the elements that appear on the screen that can help her pass the level. In order to do so, she can use a portal gun to move objects and open portals in search of items that will allow her to accomplish the mission. | Find known mathematical procedures from the data provided by the statement. |
| 3rd. Involve people in the trial-and-error method. | The completion of different tests forces the main character to open portals in different walls that make up the room to find the evidence. | Find the most appropriate solution to the problem, facilitating its resolution. |
| 4th. Collaborative learning | The video game provides a multiplayer option, with which collaborative learning is developed to pass the different logic games posed. | Analysis and critical-reflective debate that lead to the peers solving the problem amongst themselves. |
| Session | Activity | Duration (Minutes) |
|---|---|---|
| Session 0 | 1. Presentation of the activity | 15 |
| 2. Video game installation | 20 | |
| 3. Video game configuration | 5 | |
| 4. Free play | 30 | |
| 5. Sharing of views | 20 | |
| Session 1 | 1. Introduction to the session | 5 |
| 2. Free play | 25 | |
| 3. Discussion and analysis of the video game | 25 | |
| 4. Blocks I and II of the questionnaire | 25 | |
| Session 2 | 1. Introduction to the session | 5 |
| 2. Presentation of the two problem-solving models | 15 | |
| 3. Discussion and analysis of the answers given in Block II of Session 1 in terms of the two models | 30 | |
| 4. Block III of the questionnaire | 25 | |
| 5. Finishing the activity | 5 |
| Frequency | Percentage (%) | |
|---|---|---|
| Female | 161 | 95 |
| Male | 9 | 5 |
| Total | 170 | 100 |
| Female | Male | |||
|---|---|---|---|---|
| Frequency | Percentage (%) | Frequency | Percentage (%) | |
| Yes | 41 | 26 | 5 | 56 |
| No | 114 | 71 | 4 | 44 |
| DK/NR | 6 | 3 | 0 | 0 |
| Total | 161 | 100 | 9 | 100 |
| Phase | Explanation |
|---|---|
| Understanding the problem | “I must leave this level. The objective is to open the exit door. I have to look for the clues on the screen and match them. The clues can be in this room or in the rooms next door.” |
| Devising a plan | “The clues tell me that I must first perform an action to get to the push button to open the door. I will follow the clues to see what I have to do.” |
| Carrying out a plan | “I will open the necessary portals to follow the clues. If some portals do not work for me, I can always go back. I have to be careful, as some portals can confuse me when I see the main character moving. In addition, I will move objects that may be in the way or that need to be moved to open the level’s exit door.” |
| Looking back | “I have managed to open this level’s exit door. I can pass it, but I have opened more portals than necessary. My peers have passed before me with fewer moves. I have learned techniques to move around the level.” |
| Phase | Explanation |
|---|---|
| Entry | “I know I have to exit the level through the door that appears and is locked. In order to do this, I have to look at the clues on the walls and objects on the screen. To do this, I can use the portal gun to search for clues or objects that are in other rooms of the level.” |
| Attack | “When I see the clues, I have to relate them to the actions I have to perform. I will open the necessary portals and move objects to block push buttons. If my decisions are right, I will get close to the exit door, and I will be able to open it. I must check the portals, so I do not get lost in the game.” |
| Review | “I have passed the level. I was able to match the clues that appeared in the level. I have seen actions that will help me for the following levels.” |
| Phase | Explanation |
|---|---|
| Understanding the problem | “I have to open the door that appears on the screen to pass to the next level. There are enough clues in the level to pass. I must follow them.” |
| Devising a plan | “I must follow the clues and match them. I have to go through the necessary walls or move objects with the portal gun in order to solve the puzzles.” |
| Carrying out a plan | “I recognised the clues and tried to follow them. I opened portals, but I got lost in them and did not know how to get out. I saw a character running and tried to follow her, thinking it was a clue. I ended up getting disoriented. I had to stop and look at the clues again and realised that the character I was chasing was myself.” |
| Looking back | “I know I need to find the best place to open the portals so that they do not become more of a problem in the end. I need to look carefully at the clues and think them through before opening a portal or moving an object”. |
| Phase | Explanation |
|---|---|
| Entry | “The objective is to open the exit door to pass the level. I have to look at the clues that appear and match them. The portals will help me find objects and new clues.” |
| Attack | “I had to follow clues and open portals. In some cases, the portals led me to new clues and, in other cases, to twists and turns. I got disoriented. I had to stop playing for a while because I did not understand anything. In some cases, I had to restart the level.” |
| Review | “I have to check the clues and not open portals for the sake of opening them, as I will eventually lose perspective of the game and not know where I am or what I am doing.” |
| Phase | Explanation |
|---|---|
| Understanding the problem | “I have to open the exit door that will allow me to pass the level. To do this, I have to follow some clues, looking for them on the walls, objects, and in other rooms that make up the level.” |
| Devising a plan | “I have to follow the clues and open the necessary portals to get to the exit door and open it.” |
| Carrying out a plan | “After opening portals for a while, I do not quite know where I am anymore. I am disoriented and I do not know what to do anymore because I do not even know where the clues are.” |
| Looking back | (Students do nothing) |
| Phase | Explanation |
|---|---|
| Entry | “I must reach the exit door and open it to pass the level. I have to follow the clues that appear in the level.” |
| Attack | “I opened portals so I could search for clues in the other rooms of the level. At the end, I had many portals opened and I saw someone moving, so to follow her I opened more portals and I did not know how to return. It made me disoriented, I got lost and did not know what to do.” |
| Review | (Students don’t write anything) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Antequera-Barroso, J.A.; Revuelta-Domínguez, F.-I.; Guerra Antequera, J. Similarities in Procedures Used to Solve Mathematical Problems and Video Games. Educ. Sci. 2022, 12, 172. https://doi.org/10.3390/educsci12030172
Antequera-Barroso JA, Revuelta-Domínguez F-I, Guerra Antequera J. Similarities in Procedures Used to Solve Mathematical Problems and Video Games. Education Sciences. 2022; 12(3):172. https://doi.org/10.3390/educsci12030172
Chicago/Turabian StyleAntequera-Barroso, Juan Antonio, Francisco-Ignacio Revuelta-Domínguez, and Jorge Guerra Antequera. 2022. "Similarities in Procedures Used to Solve Mathematical Problems and Video Games" Education Sciences 12, no. 3: 172. https://doi.org/10.3390/educsci12030172
APA StyleAntequera-Barroso, J. A., Revuelta-Domínguez, F.-I., & Guerra Antequera, J. (2022). Similarities in Procedures Used to Solve Mathematical Problems and Video Games. Education Sciences, 12(3), 172. https://doi.org/10.3390/educsci12030172







