GESUS, an Interactive Computer Application for Teaching and Learning the Space Groups of Symmetry
Abstract
:1. Introduction
2. A Crystallographic Overview and Its Implications for GESUS
3. Objective, Motivation, and Significance
- (a)
- Teaching one to recognize the operations carried out by the symmetry operators and their combinations with the lattice translations.
- (b)
- Recognizing and using symbols to represent symmetry operators, according to their arrangement in space, in representations projected on the “a-b” plane.
- (c)
- Identification of the crystal system, crystal class (point group), and space group (Hermann–Mauguin international notation) from the operators that have been graphically drawn.
- (d)
- Solving problems related to conventions that are usually used by agreement (e.g., the imposition of an origin, different settings in the monoclinic system, etc.).
4. Target Users
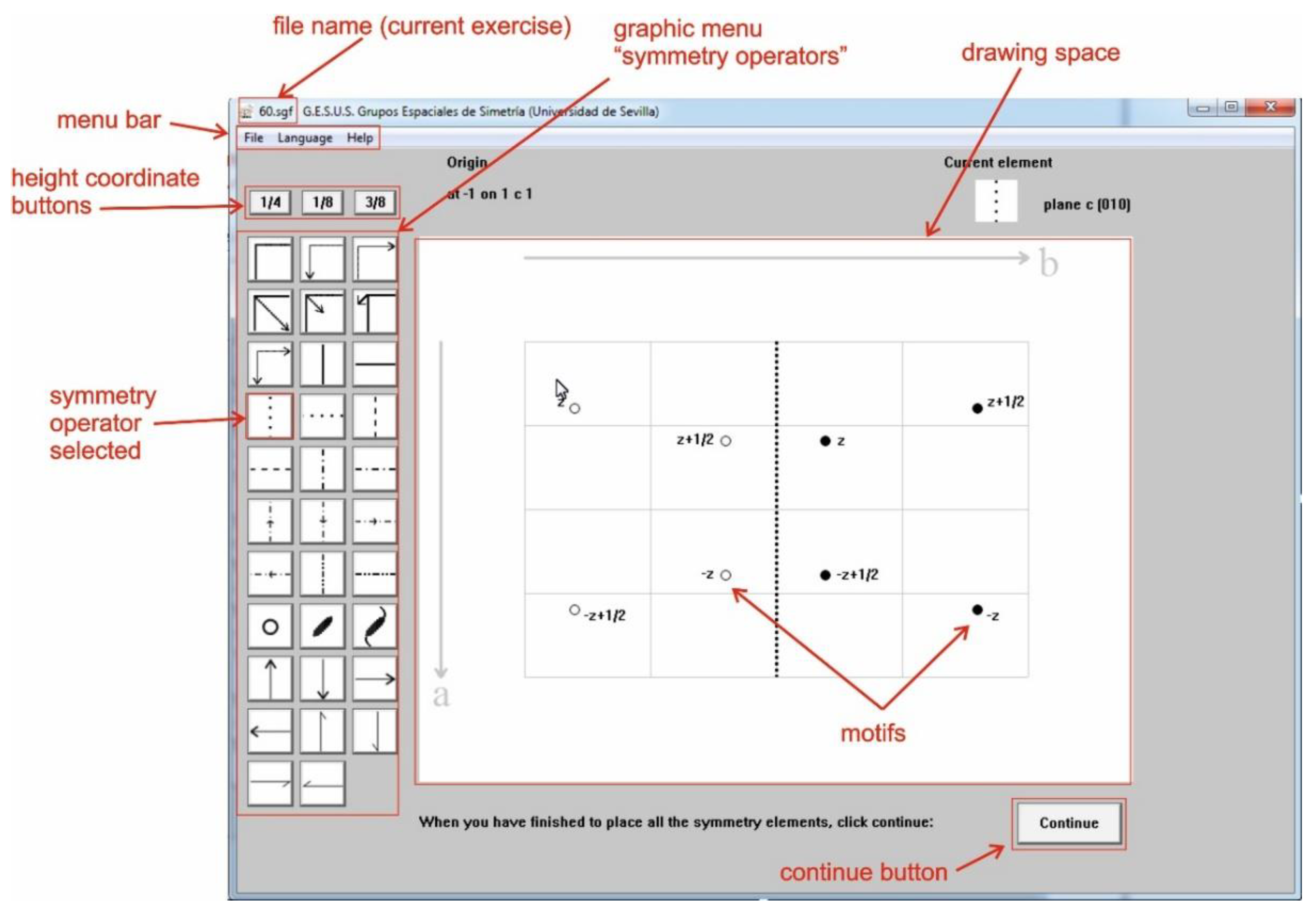
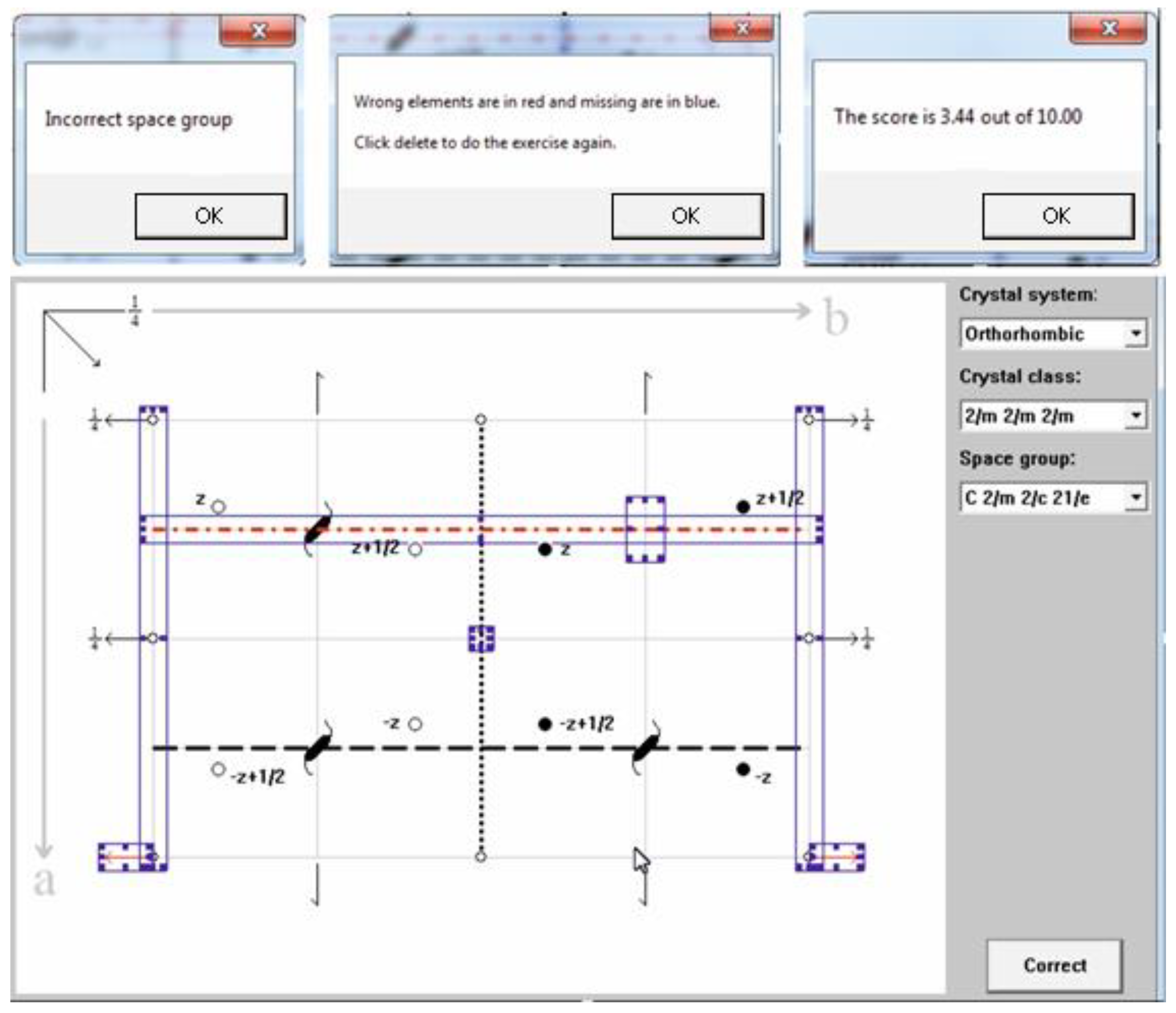
5. Software Design and Functionalities
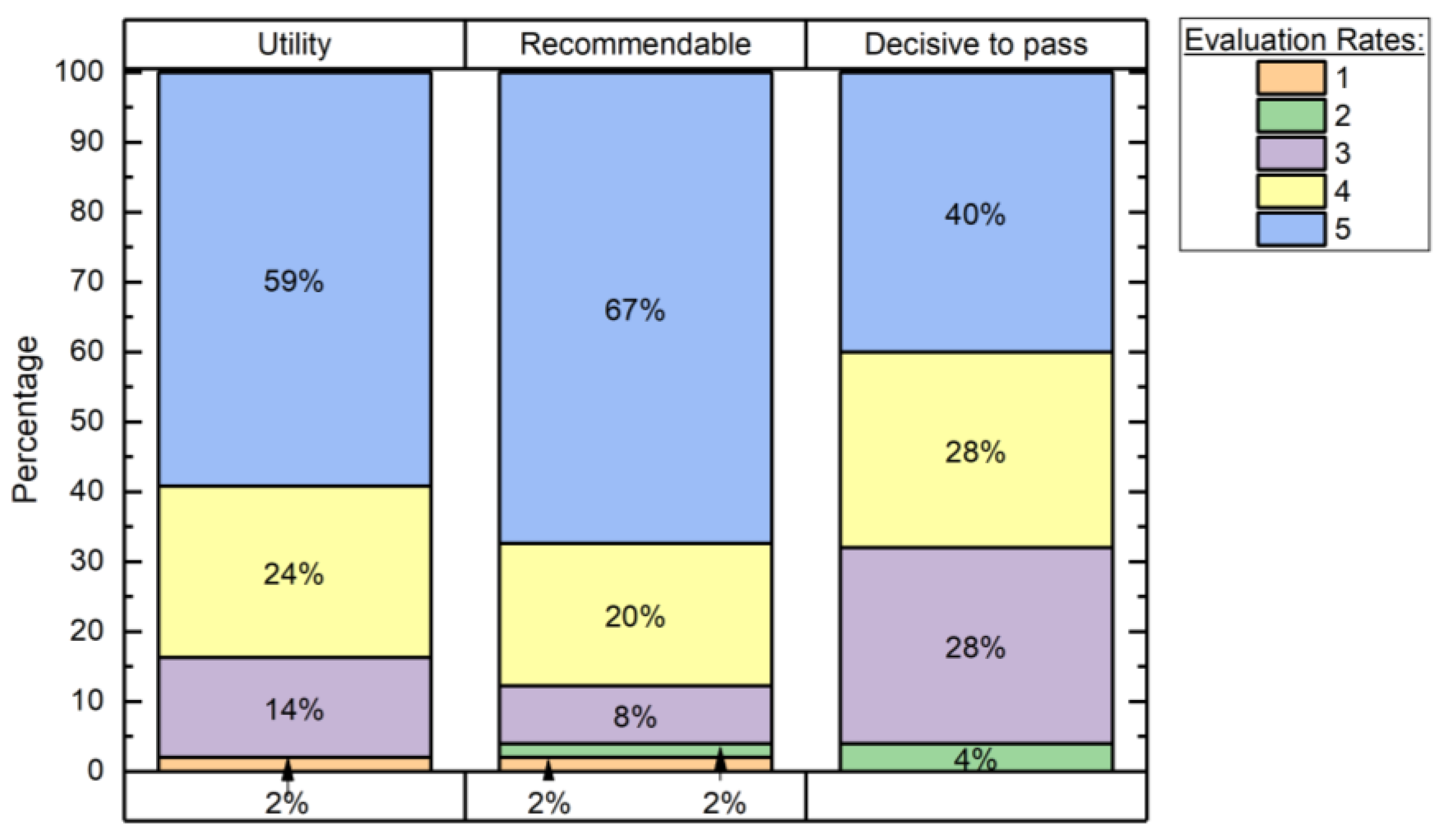
6. Impact and Student Impression
7. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Filippini, G.; Gavezzotti, A. A quantitative analysis of the relative importance of symmetry operators in organic molecular crystals. Acta Crystallogr. Sect. B Struct. Sci. 1992, 48, 230–234. [Google Scholar] [CrossRef] [Green Version]
- Malgrange, C.; Ricolleau, C.; Schlenker, M. Symmetry and Physical Properties of Crystals; Springer: New York, NY, USA, 2014; ISBN 9401789932. [Google Scholar]
- Powell, R.C. Symmetry, Group Theory, and the Physical Properties of Crystals; Springer: New York, NY, USA, 2010; Volume 824, ISBN 1441975977. [Google Scholar]
- Neumann, F.E. Vorlesungen über Die Theorie der Elastizität der Festen Körper und des Lichtäthers; Druck und Verlag Von B.G. Teubner: Leipzig, Germany, 1885. [Google Scholar]
- Chapuis, G. Initiatives in crystallographic education. Crystallogr. Rev. 2011, 17, 187–204. [Google Scholar] [CrossRef]
- Schoeni, N.; Hardaker, W.; Chapuis, G. Escher Web Sketch; The Swiss Federal Institute of Technology: Zurich, Switzerland, 1996. [Google Scholar]
- Cockcroft, J. A Hypertext Book of Crystallographic Space Group Diagrams and Tables; Birkbeck College, University of London: London, UK, 1999; Available online: http//img.chem.ucl.ac.uk/sgp/mainmenu.htm (accessed on 3 March 2020).
- Perwass, C.; Hitzer, E. Space Group Visualizer. In Proceedings of the International Symposium on Advanced Mechanical Engineering 2006, Shanghai, China, 26–29 October 2006; pp. 172–181. [Google Scholar]
- Jasinski, J.P.; Foxman, B.M. Symmetry and Space Group Tutorial; Brandeis University: Waltham, MA, USA, 2007. [Google Scholar]
- Rakovan, J. Computer Programs for Drawing Crystal Shapes and Atomic Structures. Rocks Miner. 2018, 93, 60–64. [Google Scholar] [CrossRef]
- Hoffmann, F.; Sartor, M.; Fröba, M. The Fascination of Crystal and Symmetry. Massive Open Online Course (Universität Hamburg). Available online: https://iversity.org/en/courses/the-fascination-of-crystals-and-symmetry (accessed on 3 March 2020).
- Hoffmann, F. Introduction to Crystallography; Springer Nature: New York, NY, USA, 2020; ISBN 3030351106. [Google Scholar]
- Meyer, D.E.; Sargent, A.L. An interactive computer program to help students learn molecular symmetry elements and operations. J. Chem. Educ. 2007, 84, 1551–1552. [Google Scholar] [CrossRef]
- Charistos, N.D.; Tsipis, C.A.; Sigalas, M.P. 3D Molecular Symmetry Shockwave: A Web Application for Interactive Visualization and Three-Dimensional Perception of Molecular Symmetry. J. Chem. Educ. 2005, 82, 1741. [Google Scholar] [CrossRef]
- Casas, L.; Estop, E. Virtual and Printed 3D Models for Teaching Crystal Symmetry and Point Groups. J. Chem. Educ. 2015, 92, 1338–1343. [Google Scholar] [CrossRef]
- Ruiz, G.N.; Johnstone, T.C. Computer-Aided Identification of Symmetry Relating Groups of Molecules. J. Chem. Educ. 2020, 97, 1604–1612. [Google Scholar] [CrossRef]
- Hitzer, E.; Perwass, C. Interactive 3D space group visualization with CLUCalc and the Clifford Geometric Algebra description of space groups. Adv. Appl. Clifford Algebr. 2010, 20, 631–658. [Google Scholar] [CrossRef] [Green Version]
- Aroyo, M.I. International Tables for Crystallography, 6th ed.; John Wiley & Sons Ltd.: Hoboken, NJ, USA, 2016; ISBN 0470974214. [Google Scholar]
- De Wolff, P.M.; Billiet, Y.; Donnay, J.D.H.; Fischer, W.; Galiulin, R.B.; Glazer, A.M.; Hahn, T.; Senechal, M.; Shoemaker, D.P.; Wondratschek, H. Symbols for symmetry elements and symmetry operations. Final report of the IUCr Ad-Hoc Committee on the Nomenclature of Symmetry. Acta Crystallogr. Sect. A Found. Crystallogr. 1992, 48, 727–732. [Google Scholar] [CrossRef] [Green Version]
- Zander, S.; Wetzel, S.; Bertel, S. Rotate it!—Effects of touch-based gestures on elementary school students’ solving of mental rotation tasks. Comput. Educ. 2016, 103, 158–169. [Google Scholar] [CrossRef]
- Gražulis, S.; Sarjeant, A.A.; Moeck, P.; Stone-Sundberg, J.; Snyder, T.J.; Kaminsky, W.; Oliver, A.G.; Stern, C.L.; Dawe, L.N.; Rychkov, D.A. Crystallographic education in the 21st century. J. Appl. Crystallogr. 2015, 48, 1964–1975. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pett, V.B. Teaching crystallography to undergraduate physical chemistry students. J. Appl. Crystallogr. 2010, 43, 1139–1143. [Google Scholar] [CrossRef] [Green Version]
- Rossi, M.; Berman, H.M. Symposium on teaching Crystallography-Introduction. J Chem. Educ. 1988, 65, 472–473. [Google Scholar] [CrossRef]


| Symmetry Element | Geometry | Operation |
|---|---|---|
| Mirror plane “m” | planes | reflection through plane |
| Glide plane “a, b, c, n, d, e” | planes | glide reflection through plane and a lattice-translation vector |
| Rotation axis “n” | line | rotation around line, angle 2p/n, n = 2, 3, 4, or 6 |
| Screw axis “nj” | line | Screw rotation around line, angle 2p/n, j/n time shortest lattice translation along line, right-hand screw, n = 2, 3, 4 or 6, j = 1,…(n − 1) |
| Rotoinversion axis | line and point on line | rotation around the line, angle 2p/n, followed by inversion through the point, n = 3, 4, 6 |
| Centre | point | inversion through point |
| Printed Symbol | Symmetry Axis | Graphic Symbol | Nature of the Screw Translation 1 |
|---|---|---|---|
| 1 | Identity | none | none |
| −1 | Inversion | o | none |
| 2 | Rotation diad or twofold rotation axis |  | none |
| 2 1 | Screw diad of twofold screw axis |  | c/2 a/2 or b/2 |
| Printed Symbol | Symmetry Plane | Graphic Symbol | Nature of Glide Translation 1 | |
|---|---|---|---|---|
| Normal to Plane of Projection | Parallel to the Plane of Projection | |||
| m | Reflection plane (mirror) |  | 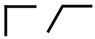 | None |
| a, b | Axial glide plane |  | 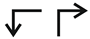 | a/2 or b/2 |
| c |  | none | c/2 | |
| n | Diagonal glide plane (net) |  |  | (a + b)/2 or (b + c)/2 or (a + c)/2 |
| d | “Diamond” glide plane | 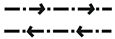 |  | (a ± b)/4 or (b ± c)/4 or (a ± c)/4 |
| e | “Double” glide plane |  | 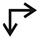 | (a/2 + c/2) or (b/2 + c/2) or (a/2 + b/2) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Miras, A.; Cota, A.; Martín, D. GESUS, an Interactive Computer Application for Teaching and Learning the Space Groups of Symmetry. Educ. Sci. 2022, 12, 85. https://doi.org/10.3390/educsci12020085
Miras A, Cota A, Martín D. GESUS, an Interactive Computer Application for Teaching and Learning the Space Groups of Symmetry. Education Sciences. 2022; 12(2):85. https://doi.org/10.3390/educsci12020085
Chicago/Turabian StyleMiras, Adolfo, Agustín Cota, and Domingo Martín. 2022. "GESUS, an Interactive Computer Application for Teaching and Learning the Space Groups of Symmetry" Education Sciences 12, no. 2: 85. https://doi.org/10.3390/educsci12020085
APA StyleMiras, A., Cota, A., & Martín, D. (2022). GESUS, an Interactive Computer Application for Teaching and Learning the Space Groups of Symmetry. Education Sciences, 12(2), 85. https://doi.org/10.3390/educsci12020085







