Abstract
After experiencing years of procedural teaching in K-12 mathematics classrooms, many students arrive at college with ideas about, and approaches towards, mathematics that are not helpful to their learning. Students’ prior experiences and misconceptions can then negatively impact their experiences in university STEM courses. This paper describes a short course in the “big ideas” of calculus, that offered students an approach of problem-based learning, combined with mindset messages, otherwise known as a “mathematical mindset approach”. The mixed-method study considered how a ‘mathematical mindset’ teaching intervention impacted the learning, achievement, and beliefs of incoming college students, finding that the intervention significantly changed students’ ideas about mathematics, their own potential, and the value of collaboration. At the end of the course students also significantly improved their achievement on assessments of problem solving and collaboration. Importantly the course allowed students to believe in their own potential and to approach mathematics with a growth mindset, suggesting a role for such courses in students’ mathematics pathways.
1. Introduction
In response to the global challenge of inspiring and recruiting more students into STEM pathways, two ideas have been well researched, although typically, they are implemented and studied separately. One of the ideas is to use a problem-based or project-based teaching approach in science and mathematics, in which students are engaged actively using rich tasks with multiple solution paths. Many research studies have shown that project-based and problem-based approaches increase student achievement and interest significantly [1,2,3,4,5,6,7,8,9,10,11,12]. A second idea is to develop students’ growth mindsets so they know they have the potential to achieve [13,14], and they have ideas that can challenge stereotyped messages they may encounter [15,16]. This seems particularly important in STEM environments, which have been found to be particularly “chilly” for women and students of color [17]. This paper shares the results of a teaching intervention that combined the two approaches, infusing mindset ideas into a calculus summer course taught to 99 incoming students at a US university in 2019 with the research question: How does a mathematical mindset teaching intervention impact the learning and beliefs of incoming college students?
1.1. Problem-Based Approaches in Mathematics
Project-based learning and problem-based instruction are flagship pedagogical approaches that position students actively as they explore the content they are learning [12,18]. Both approaches to instruction are found in all areas of education, including mathematics [6,12,18] and science [19], as well as other fields such as engineering, medical, and professional education [20,21,22]. Research on these approaches has shown that they improve students’ self-efficacy in mathematics [23], understanding [6] and, with proper support, help them transfer mathematics skills to contexts such as astronomy [1]. Problem and project-based learning approaches also enhance valuable practices such as teamwork, problem solving and communication [24]; though effective collaboration practices and intrinsic motivation remain understudied aspects of these approaches [21].
Project and problem-based approaches vary in their design and implementation, and the ways they are assessed, but they usually include the provision of more open tasks that engage students in problem solving and reasoning [25]. Open and rich tasks, which are at the center of problem-based approaches, offer students opportunities not only to collaborate, but to engage in deeper learning and to shift their beliefs about mathematics and about themselves. Traditional mathematics questions that require the application of a predetermined procedure leading to one correct answer communicate a narrow vision of mathematics where mathematical knowledge and practice consist of a series of facts and steps to memorize. Narrow mathematics is typically only accessible to a narrow group of students [26]. This type of work is in stark contrast to rich mathematics tasks, in which students are required to “connect different aspects of mathematics together, to devise solution strategies for themselves and to explore more than one pathway to solutions” [25] (p. 129). Open and rich tasks broaden the opportunities for student learning to move beyond the memorization of procedures and rules to the exploring and connecting of ideas across subject areas [27], thus providing a wider range of learning opportunities compared to traditional mathematics problems [28]. Problem-based learning with open tasks allows students to engage in the type of thinking and practice that more closely aligns with what Stein and colleagues call “doing mathematics”, that is: “framing and solving problems, looking for patterns, making conjectures, examining constraints, making inferences from data, abstracting, inventing, explaining, justifying, challenging, and so on” [29] (p. 456).
1.2. Infusing Mindset and Shifting Students’ Beliefs
Research on the effectiveness of mindset—instilling in students the idea that their intelligence is malleable, and that struggle is an important part of learning—has been conducted with students of different ages, in different subjects, showing the critical importance of such messages [13,14,30]. However, some of the research has been based on mindset interventions that deliver these messages but do not change the teaching that surrounds them, with students often receiving counter messages through educational practices [31]. When students are told they can learn anything, but are then presented with closed questions, requiring one method and one answer, the positive messages regarding mindset often fall flat [32]. This has led to criticism of the idea of mindset [33] and to research studies that show no impact [34]. In contrast, studies that consider the impact of delivering mindset ideas and infusing them through teaching practices show significant impact [10,35,36,37]. When questions are open-ended and engage students in meaningful contexts [28,38], students can see that they can learn and grow, and mindset ideas can more readily take root.
A critical feature of an approach to teaching that infuses mindset ideas is one that encourages and values student struggle, a key condition for brain growth and development [39]. This happens when teachers provide complex tasks and communicate to students that struggle is expected and valued. Teachers may offer messages such as “we are giving you this complex task so that you can struggle, which is really good for your brain and learning.” This practice and communication require a relocation of value and attention from mathematics answers to mathematical thought and reasoning. In a study of Harvard students learning calculus-based physics, which compared a lecture-based approach with a problem-based approach that centered struggle, referred to as ‘active learning,’ students believed that they learned more from lectures when they actually learned more in the active learning condition, as shown by tests of achievement [40]. The authors of the study concluded that the students felt less comfortable when engaged in active learning as they were not used to struggling and the additional cognitive effort that was required when engaged in rich and open tasks. Nor had the students ever learned that struggle was especially good for their learning and understanding.
This infusion of mindset ideas into the teaching of mathematics is important, as research shows that students tend to hold beliefs about mathematics and the nature of mathematical knowledge that serve as hindrances to their own mathematical learning. Muis conducted a meta-analysis of 33 studies on student beliefs about mathematics which included studies from early childhood through adulthood [41]. The analysis found that regardless of age, mathematics students tend to hold various “nonavailing” beliefs about mathematics, that is, they hold beliefs about mathematics that either have a negative impact on their learning of mathematics or are highly correlated with low mathematics achievement. According to the meta-analysis, in general, students believe that mathematical knowledge is unchanging, and passively received from some mathematical authority (i.e., the teacher or the textbook). Problem-based approaches that combine open tasks and mindset messages can help to shift students toward availing beliefs about mathematics that support their learning [41,42].
1.3. Collaboration
Studies of collaboration, sometimes referred to as cooperative learning [43], have shown that when students work together, their solutions tend to be more sophisticated and they learn more [11,44,45,46]. Mathematical communication and collaboration can simultaneously raise student achievement and work against inequities [11,47,48]. Capar and Tarim conducted a meta-analysis of research on cooperative mathematics learning including studies across pre-kindergarten and through the university level [49]. They found that the mean effect size of a cooperative teaching method on student grades was 0.59, indicating that this teaching method is more influential in terms of student achievement in comparison to traditional methods.
Although learning collaboratively is beneficial for students, instructors are sometimes faced with resistance when implementing a learning environment that centers collaboration [50,51]. Undergraduate students may be resistant toward collaboration for several reasons: they are resentful of the added responsibility for their own learning [52], they feel the instructor is not holding up their end of the education agreement of telling them the information directly [53], they do not see peers as resources of information [54], and/or they resent peers who may move at a slower pace [55]. To ameliorate these barriers, a key component of building successful collaborative learning environments is that students are given agency within the classroom to use their own ideas and resources to solve problems [56]. One way to do this is through “Complex Instruction” (CI), a pedagogical approach to group work that counters status differences between students and highlights positive ways to work in groups, and that was drawn on in the teaching intervention in this study [57]. Studies of CI in high school math classrooms have shown increases in effective collaborative work [58], in students’ appreciation for one another’s mathematical ideas [59], and in students’ achievement [11]. CI aligns well with problem-based learning, as it requires departing from traditional lecture-style pedagogies and narrow content and, instead, supporting students to collaborate on open tasks.
1.4. A Mathematical Mindset Approach to Problem-Based Learning
Problem-based learning approaches and the ideas of mindset naturally combine. Open and rich tasks offer opportunities for students to struggle, for teachers to share positive messages about the value of struggle, and for students to embrace mindset ideas and shift their beliefs. Yet studies that consider the integration of mindset messages into STEM content have rarely been conducted. When mindset messages are infused through problem-based mathematics content, we define the approach as a ‘mathematical mindset’ approach.
This approach has been found to be effective in shifting students’ learning and beliefs across K-12 settings. In one professional development study, teachers learned about the mathematical mindset approach and infused it into their classroom teaching, which resulted in significant positive improvements in student beliefs and achievement [35]. In a research program studying the impact of problem-based mathematics summer camps on middle school students’ achievement and mathematical beliefs, three iterations of the camp—all of which taught concepts through problems that were visual and encouraged multiple approaches—resulted in students significantly increasing their achievement on a standardized test of conceptual mathematics and reasoning. The first iteration of the camp program, which took place without the infusion of mindset ideas, significantly increased students’ achievement and changed their mathematics beliefs, as students worked through rich, problem-based tasks [60]. When the approach was repeated with the infusion of mindset ideas, including brain growth and the importance of struggle, the impact on achievement, on a standardized test of algebraic content, was twice as large [10]. Students in this camp were shown the evidence that brains are consistently changing and growing, that struggle is helpful for our brains, and that there is no such thing as a “math brain”. They were also reminded of the value of struggling when they worked on difficult content. This effect held when the camp curriculum, with accompanying mindset messages, was scaled beyond the initial researcher teachers and taught by teachers in 10 different school districts [37].
This paper extends this line of inquiry to the university context, asking the following research question: How does a mathematical mindset teaching intervention impact the learning and beliefs of incoming college students? We report on the study of a short teaching intervention with a ‘mathematical mindset’ approach taught through a calculus course. The course was taught in a program offered to students the summer before their first year in a four-year US college. The majority of students who attended the program were students of color, approximately 50% of the students were female identifying, and all were previously high achieving—although not necessarily in mathematics. Importantly, they believed, like most students, in a range of harmful myths about mathematics that could have impeded their mathematics progress that the short course was designed to change [41]. To examine the impact of the course on students’ learning and beliefs, this case study combined mixed methods, including student surveys, analysis of student reflections, and a pre- and post-assessment of problem solving and collaboration.
Calculus was chosen as the content to teach, as students’ experiences with calculus are often pivotal in their college careers [61,62,63]. Given that the majority of the students in the program had taken calculus to high levels, they had experienced what many describe as the “race to calculus” [64,65]. Most high schools in the US offer calculus as the highest-level class and require four classes to be taken in preparation. As high school is a four-year program, this means students need to be “advanced” in middle school to get there—missing or compressing middle school content, and taking high school algebra in middle school. Research has shown the ineffectiveness of this system. Bressoud studied 800,000 US students who took calculus in high school and found that the majority of them went on to repeat calculus or take a lower-level course in college [66]. Strogatz describes the teaching of calculus in many US high schools as an “avalanche of methods” that few students have opportunities to understand [67].
The mathematical mindset approach to calculus, that is the subject of this paper, strove to offer something different to students, by bringing together two ideas: problem-based learning and mindset. This is among the first studies of the impact of a college course combining these dimensions of learning and could offer scholars and teachers ideas for the teaching of calculus and other topics.
1.5. Course Design
A mathematical mindset approach was taught in a three-and-a-half-week summer course to 99 students in the summer before the students’ first year at the University. Of the 99 students enrolled in the course, 70 students came from a program for students interested in engineering who were from backgrounds underrepresented in engineering, which will be referred to as the Engineering Program (EP), and 29 students came from a program for first-generation (first in their family to attend college) and low-income students which will be referred to as the Leadership Program (LP). In both cases, students were invited to campus before the start of their first year to receive support. The course met for two hours per day, for 3.5 weeks, and both groups of students were taught together by one professor and four graduate students – including the paper authors. Of the 99 students in the class, 96 agreed to participate in the research study. Fortunately, given such a large class size, the classes took place in a large and modern classroom with multiple screens and tables that could support groupwork.
The short course in the “big ideas” [68,69] of calculus was designed to share with students a mindset approach to calculus - this involved a set of tasks that were open and inquiry-based, and that encouraged students to engage in and appreciate struggle and to see calculus as a multidimensional subject that could be approached in different ways. The students entered the course with varied prior achievement in calculus, as shown in their applications to EP and LP. Most had taken a calculus course of some kind in school, although a small subgroup had not; some students shared that they had understood calculus in school, while others noted that they had taken the course, but had little understanding. For these, and other reasons, the content of the course was oriented around the “big ideas” of calculus—core, overarching concepts rather than a narrow set of skills [68]—as set out in Strogatz’s Infinite Powers [67]. The teaching goal was that students with previous procedural understanding would receive access to a conceptual framing, into which they could place methods they had learned, and that students who had never taken calculus would see the subject through an initial lens of interest and wonder.
During the course, the students were introduced to a number of present-day mathematicians and engineers—through video conferences, in-person meetings, and consideration of their work. To tackle stereotyped assumptions about STEM, and to reflect the students in the course, the instructors invited as speakers, or introduced students to the work of, mathematicians and engineers who were mainly women and people of color. The group included: Allison Okamura, Yahya Tabesh, Keith Devlin, Steve Strogatz, Tai-Denae Bradley, and Maryam Mirzakhani. The pedagogy of the course centered on collaborative work, so that students could appreciate the different ideas and perspectives different people bring to calculus problem solving. Inspired by decades of studies that have shown that mathematical communication and collaboration can simultaneously work against inequities and raise student achievement [11,47,48], the course carefully encouraged and supported students to collaborate on calculus and other mathematical tasks in small groups, drawing from the principles and practices of Complex Instruction [57]. The tasks in the course all had the feature of being “low floor and high ceiling”—they were accessible to all students (low floor) but led to high levels of mathematical thinking (high ceiling)—and engaged students in visual and, at times, creative thinking [10,70]. See Appendix A for the task schedule.
2. Materials and Methods
2.1. Data Sources
The mixed methods case study of the course combined qualitative and quantitative data [71]. A number of data sources were collected during the course including surveys, mathematics assessments, reflections, and interviews. Prior to the start of the course, students wrote a ‘math history’ describing their experiences with mathematics before entering college and took a pre-course survey that included questions about identity and belonging [72]. On the first and last day of class, students completed a mathematics assessment, taken in pairs. Throughout the course, the students were asked to complete short reflections ranging in topics from the course readings to the tasks. Upon the completion of the course, students submitted final reflection essays and responded to the post-course survey with the same questions as the pre-survey.
2.2. Data Analysis
2.2.1. Student Written Reflections
All written work collected from participants underwent a rigorous coding process. For each of the written data sources (mathematics history essays, short reflections, and final reflection essays), a separate codebook was developed through a multiple round process that included open coding from which bottom-up codes emerged [73], followed by discussion and adjudication to collaboratively develop an initial codebook [74].
Each codebook was validated through an iterative process of coding a subset of essays to confirm applicability and assess whether any additional codes were needed. The finalized codebook was then uploaded into Dedoose qualitative coding software so the remainder of the data could be coded. After coding was complete, thematic analysis was conducted for relevant codes to synthesize results.
An additional layer of analysis was applied to the final reflection essays. A categorization of extremely positive, positive, neutral, or negative was developed to capture the students’ overall impressions of the course. The rubric for these ratings is presented below in Table 1.

Table 1.
Final Reflection Rating Rubric.
2.2.2. Pre and Post Mathematical Problem-Solving Assessment
The students came to the class with very different experiences with calculus, some having learned it for two years and some not at all, so a pre- and post-assessment was chosen that did not assess calculus. Instead, a mathematics investigative problem was chosen that could be given in parallel forms (pre and post) that assessed content that was learned by all students prior to the course—combinatorics and probabilistic reasoning (see Appendix B). The course did not include grades or timed tests of narrow questions because such methods are inconsistent with the mindset messages of growth and problem-based mathematics that were central to the course. The instructors of this course had the freedom to make this choice as the placement of the course in a summer program did not necessitate specific grading of students or structural constraints such as a common final exam.
Two low-floor high-ceiling problems were given as a pre- and post-assessments to pairs of students. The assessments allowed for the researchers to measure students’ development during the course. The students were required to work in pairs, to preserve another message of the course—that mathematical collaboration is valuable—and to diminish any anxiety students would have from being given an individual assessment, especially on the first day. The tasks had a mathematically equivalent structure (see Table 2) and the integrity of student pairs was maintained for the pre- and post-assessment in order to measure any changes in the students’ collaboration as they worked. The two students in the pair used different color pens so the contributions each student made could be easily distinguished.

Table 2.
Prompts for Pre- and Post-tasks.
The pre- and post-assessments were analyzed in two different ways: through a rubric assessing mathematical problem solving and through a measure of collaboration. The tasks were rated by pairs of coders to measure changes in mathematical thinking and in collaboration. In the first round of analysis, all pre-tests were coded and in the cases where the two pairs of coders disagreed on the rating, a discussion took place and a consensus rating was recorded.
To evaluate their mathematical thinking, the student work was assessed using a rubric of mathematical reasoning, developed for the two equivalent tasks. The rubric gave positive points for appropriate strategies such as: creating a visual, a table, a tree diagram, or finding a smaller case, and for giving mathematical justification. Additional points were given for a correct method, a correct answer, for solving creatively or in two different ways. Negative points were given for the use of inappropriate algebra, mathematically unreasonable answers (such as 100 million), or for low-quality work.
Collaboration was measured by first looking for the integration of both pen colors together across the ideas written on the paper and the connectivity between ideas written by each person in the pair. The second round of analysis determined whether collaboration from the pre- to the post-assessments improved, stayed the same, or declined. A pair was rated as having “improved” their collaboration if their ideas, written in different colors, were more physically integrated on the page, as well as more conceptually connected. A pair was rated as having “declined” in their collaboration, if both their physical and conceptual integration had decreased.
2.2.3. Survey Analysis
The survey included twelve statements with a Likert scale from strongly disagree to strongly agree. The survey was taken by 97 of the 99 students as part of surveys given by the two programs. The pre- and post-survey were statistically analyzed using a principal components analysis, with associated alpha and omegas and t-tests for significance of changes from pre to post [75].
3. Results
3.1. A Shift in Students’ Mindset and Beliefs about Mathematics
Students came to the course with a history of school success, and many of the students displayed strong confidence in their mathematics histories, but the success was accompanied by widespread beliefs that mathematics success involves memorization and speedy thinking. In the pre-course survey, nearly half of the students agreed with the statement: “People who really understand math will get an answer quickly” and over half agreed with the statement: “Math involves mostly facts and procedures that need to be memorized.” Students also gave insights into the ‘performance culture’ [76] they had experienced and frequently rated themselves, referring to tests, grades, and their performance in comparison to other people. Of the 58 students who rated themselves as good at math coming into the course, 88% referred to mathematics as a subject of competitions, speed, perfectionism, grades, test scores, correct answers, and rewards. Many of these beliefs about mathematics overlap with what Muis terms “nonavailing beliefs” that can have a negative impact on students’ learning [41].
Thematic analysis of the math histories revealed that many students believed that struggle with mathematical ideas was a sign of weakness. Fifty-five percent of students referenced struggle in their histories, with the majority of students describing struggle negatively, as something to be avoided. In the pre-survey, 65% of students agreed with the statement, “When I make a mistake in math, I feel bad.” The evidence showing students’ negative associations with struggle seemed important, as struggle is a process in which all learners need to engage and has been shown to increase brain activity and growth [39]. The course was specifically designed to change students’ ideas about struggle and to help them value the times when they needed to work through difficulties.
Multiple forms of evidence showed that students’ beliefs about mathematics and their own potential, as well as their ability to engage in problem solving (see Section 2), improved. Seventy-eight percent of students’ final reflections showed a change in perspective, indicating changes to students’ beliefs about the nature of mathematics, as illustrated by Claude’s reflection: “This class opened my eyes and helped me realize that math is more than just memorizing, but instead, a way of thinking.” Many of the students shared that the course had helped them erase a single incorrect idea that had caused them to doubt themselves: the idea that only fast thinkers can be good at mathematics. Eliza described this in the following way: “Before this class, I knew I liked maths but I didn’t feel confident in my maths skills...I wanted to major in it, but of course I never would have because I [thought] I was far too slow.” A further 57% of final course reflections described changed ideas about the value of collaboration in mathematics (see Section 2).
The third important change the students described was a change in their beliefs about their own potential. Most of the students arrived in the course with fixed ideas about their and others’ potential. They believed that people were born with a “math brain” or they were not. By sharing the neuroscience of brain growth and the importance of struggle to the development of brain connections [42], the students changed their ideas about their own potential in mathematics. Some students even described the ways that mindset messages had changed their approach to their lives:
Upon coming to this class, I began to see math differently, as something creative, something without a right or wrong answer, but rather a means of positive struggle, where I embraced all my missteps as part of a growing experience. I took the growth mindset to heart--not only did I apply it academically, I began going to the gym regularly, taking on a vegan diet, and doing even the little things that used to scare me, such as karaoke night (which, might I add, was extremely fun.) (Michelle, Final reflection)
Importantly, the change in the students’ ideas about themselves came from a different approach to mathematics, rather than disconnected mindset messages. Evidence of this connection was provided by the 40% of code co-occurrence between growth mindset and changed relationship with mathematics in students’ final reflections. Ricardo’s reflection on his changed ideas about his future in STEM highlight the importance of connecting mindset messages to a changed approach to mathematics:
My relationship with math going in was awful, trash, garbage. I hated it and, to be frank, it didn’t make much sense. The way it had been taught to me hadn’t clicked and it didn’t look like it was going to click anytime soon. I was scared for math in college, and honestly considering going from Chemistry to Linguistics to avoid having to take calculus and physics. I am no longer considering switching. (Ricardo, Final Reflection)
Evidence for the students’ changed ideas and beliefs also came from changes between the pre- and post-survey. A principal component analysis of the surveys produced four different components, two components: “nature of math” and “mindset” were statistically significant, triangulating the changes students described in their reflections. Table 3 shows the principal components and individual survey questions.

Table 3.
Survey Analysis.
The students’ final reflections were also coded to assess their reaction to the course, which showed that 6% of students were negative, 13% neutral, 47% of students were positive, and a further 34% experienced the course as “extremely positive.”
3.2. A Shift in Students’ Problem Solving and Collaborative Skills
The students’ changed beliefs about and approach towards mathematics were supported by improvements in their learning of both mathematical problem solving and collaborative skills. Analysis of students’ maths histories revealed that, prior to the course, 87% of students had experienced highly individualized classroom environments in which they engaged with mathematics independently, rather than in collaboration with peers. Of the 13% of students who did mention collaboration in their maths histories, these experiences were discussed as a social endeavor, a way to obtain help from peers when struggling, or as a competition, rather than genuine collaborative problem solving. These findings were corroborated by a collaborative problem-solving pre-assessment given on the first day, in which 53% of students completed the task individually, despite being asked to work in pairs.
In this same pre-assessment, the students also showed limited ability to engage in problem solving, with only 6% of the students solving the problem. Problematically, 35% of the students tried to convert the problem into a linear equation (which was inappropriate) or another mathematical formula, and 52% of students gave a mathematically unreasonable answer (such as 100 million). Very few of the students made use of problem-solving strategies such as using a smaller case to find a pattern (2%) or making visuals (11%) or tables (7%) to gain insight into the problem.
Analyses of the post-intervention outcomes showed that students’ collaboration and problem-solving skills improved and were associated with each other. In the pre-assessment, only 19 of the 43 pairs of students demonstrated collaborative work, while the other 24 pairs did not collaborate (i.e., only one person wrote, as indicated by the different color pens, or both people wrote, but their ideas were neither physically nor conceptually integrated). On the post assessment, however, the majority of pairs demonstrated collaborative work. In particular, 35% of pairs (n = 15) improved their collaboration and 37% of pairs (n = 16) demonstrated the same level of collaboration on both pre- and post-assessment (see Figure 1). Importantly, out of the 24 pairs that did not demonstrate collaboration on the pre-assessment, 63% of these pairs (n = 15) demonstrated collaboration on the post-assessment. This represents a significant shift for students who entered the course with a disposition to work independently (see Appendix B for an example). Importantly, the level of collaboration among students was positively and significantly associated with their total score on the mathematics assessment (n = 81, p < 0.05), with solving the problem in more than one way (n = 81, p < 0.001), and with justifying with words (n = 81, p < 0.05).
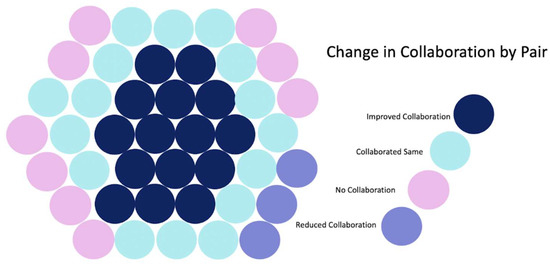
Figure 1.
Each circle represents the same pair of students that completed both pre- and posts-assessments at the beginning and end of the course.
In the final course reflection, some of the students reflected on their changed approach to problem solving between the pre-assessment on the first day and the post-assessment at the conclusion of the short course:
I was made sure of this today when we approached a problem nearly identical to the one we attempted to solve on the first day. Instead of jumping straight into the concepts we learned in statistics and calculus, my partner and I made visual representations of our thoughts and identified the patterns within the problem. Even as we were doing it, my partner and I realized the differences in our thought processes and how that led to us finding an equation that could represent what we were trying to solve. (Kim, Final Reflection)
In addition to this shift in collaborative practices, thematic analysis of final reflections revealed that students’ perceptions of collaboration significantly changed throughout the course. The majority of students (57%) stated in their final reflections that they had learned how to collaborate, gained communication skills, and changed the way they viewed collaboration. As Tasha wrote:
This class taught me how to think. It taught me how to make connections within the realm of calculus and with the people around me. Because of this class, I am looking forward to working collaboratively on work, especially math, because I have found that some of the best learning comes from learning with others. (Tasha, Final Reflections)
The students not only expressed general appreciation for collaboration, but also articulated appreciation for the specific benefits of collaboration. The students indicated that engaging with varying perspectives, making their mathematical arguments clear to others, and participating in collaborative divergent thinking and problem-solving helped them build a deeper conceptual understanding of calculus concepts. In recognizing their peers as contributing to their learning, the students began to view themselves and their group members as co-constructors of mathematical knowledge, rather than passive recipients.
3.3. Centering Mindset through Mathematics Problems: An Example
Problem-based learning encompasses many effective teaching practices, such as the use of authentic and open tasks, learning through problem-solving, and valuing multiple perspectives for the same problem. Research has shown that problem-based mathematics combined with mindset messages, or mathematical mindset teaching, enhances student learning [10,37]. As discussed earlier, the analysis of student final reflections on the short course produced a 40% code co-occurrence between growth mindset and changed relationship with mathematics, with comments such as Chantelle’s:
When we began to engage in more of the hands-on activities, I started to shift my mindset and continue to try things out. The moment that I believe changed me the most was the cube task. In that task, we worked so well together, and the work was distributed pretty evenly. I felt accomplished, as well as did my group surrounding me. (Chantelle, Final Reflection)
Chantelle’s reflection that her mindset changed through engagement in open tasks that were collaborative illustrates the importance of infusing mindset through the mathematics students learned. This supports previous research that has shown the importance of mindset messages being integrated into the teaching approaches, rather than delivered outside of content [31,35].
The interconnectivity of mathematics tasks and mindset is further illustrated by a description of student engagement with a task given in the course to find the volume of a geometric solid. The day before the lesson, the students read the first chapter of Infinite Powers [67], the course reader. The chapter tells the story of the origins of calculus, including the contributions of lively characters such as Archimedes and Newton, the “allure” of infinity, and the importance of limits to the solving of problems in the historical and modern world. The class of 99 students sat in small groups, each of which was given a lemon and asked to find its volume. They were also provided access to a resource table that included knives, cutting boards, play-doh, vases, bowls, pipe cleaners, string, painter’s tape, sticky notes, a funnel, meter sticks, rulers, and digital calipers (Figure 2). The students were told that they could use any two resources at one time.

Figure 2.
Resources Table for Lemon Task.
Students were advised not to cut their lemon until their group had come to consensus on the approach they would use. From there, students were given 40 minutes to explore together, with the reminder that they respect each other’s thinking and work to include all group members (Figure 3). They were also told to make a poster sharing their ideas, which they would present to the class at the conclusion of the exploration.

Figure 3.
Two student groups working on the Lemon Task.
During the time spent exploring the task, students proposed different approaches to the problem, a sample of which is shown in Table 4.

Table 4.
Sampling of Student Strategies for the Lemon Task.
A detailed lesson plan and films showing student group work and presentations is available at: https://www.youcubed.org/exploring-calculus (accessed on 7 June 2022).
An important aspect of supporting a growth mindset is opening problems so that students can see different possible pathways. The Lemon task provided the reason for students to appreciate the multiplicity of ways people can contribute to mathematics, and from there the potential they had to learn any mathematics, as Esther noted:
The first problem that really helped open my eyes was the lemon problem. My group thought really creatively about the three methods that we tried, and actually physically manipulating the lemon helped me see why the different methods worked well. But it was at the end of it, when we discussed the problem as a class, that I saw all of my groups’ solutions were basically just different ways to perform summation/integration. It was the first time that I saw the integration formula/graph, and it actually made sense to me. Since that problem I have been riding a kind of high in the class. I now feel like if I try hard enough, and if I think creatively enough, then I can genuinely figure anything out. (Esther, Final Reflection)
Esther’s reflection, similarly to Chantelle’s, illustrates the interrelated role played by the tasks students were given, the opportunities to collaborate, and the change in student mindset. Analysis of student reflections indicated that the experience of working on tasks in an environment that valued different perspectives on the problems, changed students’ perspective on mathematics going forward.
3.4. Students Who Resisted the Messages of the Course
At the beginning of the course, many students were uncomfortable with the need to engage with problems that were not well-defined with specific methods to apply. Students reflected on this challenge in their final reflections, with some sharing that the need to think and problem solve exposed a weakness in their understanding of mathematics, which made them uncomfortable, as Marina expressed:
Being forced to learn math at a fundamental level was very frustrating at first because beneath the memorization of formulas and functions, it made me feel like I didn’t actually understand it at all. (Marina, Final Reflection)
While the majority of students in the course overcame this initial discomfort, a small group of students noted in their final reflections that they did not overcome their discomfort, sharing statements such as Adriana’s: “I tried to be as engaged as I could be, but I often felt lost.” Analyses of student mathematics histories revealed that these students were slightly more likely to have been coded as experiencing ‘mathematics anxiety’ coming into the course [77]. Classroom observations showed that some of these students engaged less with the tasks and appeared hesitant to participate in group discussions.
The finding that students’ inability to embrace the messages of the course may be in part driven by mathematics anxiety and a discomfort in being challenged with more conceptual work seems important for our field. Despite the challenges faced by the students whose final reflections were coded “negative”, the final problem-solving assessment results showed that the improvement of this group of students was greater than for those with “extremely positive” or “positive” reflections, suggesting that their discomfort in the course was not matched by their learning of mathematics. The students who expressed negative sentiments in their final course reflection were the lowest scoring group on the problem-solving assessment coming into the course (Kruskal–Wallis test, H = 5.77, p = 0.025) and the significantly highest scoring group on the post-test (Kruskal–Wallis test, H = 4.51, p = 0.025).
The mismatch between the students’ comfort with the course and their relative achievement echoes the finding of Deslauriers and colleagues, who found that students who felt they learned more from, and preferred lectures, actually learned more through an active approach in which they were encouraged to problem solve and struggle [40]. Student discomfort with active learning, in which they are required to increase their cognitive effort, is important, as it can create negative teaching conditions and limit the effectiveness of the approach. Such discomfort for students also highlights the importance of interventions such as this one, that work to change students’ beliefs and comfort with active engagement and with collaboration, especially as most students will be required to engage actively in university courses in their future, as well as any work in the STEM industry. Deslauriers and colleagues increased students’ willingness to engage actively, in a follow-up course, by sharing the evidence of negative correlations between learning and perceptions of effectiveness [40]. At the end of their course, 65% of students reported that their feelings about active learning had significantly improved [40]. The current study adds to the findings of Deslauriers and colleagues that negative student perceptions and discomfort with active learning do not necessarily match their learning—these students improved their achievement during the course, even more so than the students who expressed comfort with and enjoyment in the course [40].
4. Discussion and Conclusions
The main goals of the course were to improve students’ relationships with mathematics and support students to develop a growth mindset through a conceptual, problem-based approach to calculus, giving meaning to procedures that many students had learned in traditional mathematics courses. Students often cite their experiences in calculus as the reason for leaving STEM [62,63] and this short course was designed to change students’ ideas and mathematical approaches to help avert such departures. Mathematics, and the topic of calculus, can be experienced in completely different ways. In one version, experienced by the majority of people, students learn to memorize methods, to follow rules, and to “perform” through frequent testing and grading. However, there is another version of the subject, described by mathematician Francis Su as a mathematics of “human flourishing”, that was the goal of the 3.5-week course offered to students [78]. This is a mathematics approach that is not based around grades or narrow tests, and that centralizes human contributions to the development of concepts. The students in the course learned to value each other’s ideas and it was important that mindset messages—centralizing struggle and the potential of all students—were woven throughout the course. It was ultimately the combination of mindset and open, collaborative mathematics that supported the majority of students to shift their “nonavailing” beliefs [41] and engage differently with mathematics. Positive collaboration, in particular, was highly meaningful for the students, in contrast with the individualized version of mathematics most of the students had experienced in school.
Some people might argue that students who had been achieving highly in mathematics in school do not need such an intervention; however, students’ reflections and initial work on a mathematics pre-assessment suggested otherwise, as described by Briaunna:
Taking this class has been my best decision at college so far. I feel like I will go into my first-year maths courses knowing a secret that no one else knows: Maths does not have to be intimidating. It is not maths’ fault that it has been portrayed to be an evil subject only conquered by "geniuses" and/or white males. With a little love and understanding, maths can be kind, compassionate, and even fun to be around. (Briaunna, Final Reflection)
Briaunna’s assertion that this is “a secret that no one else knows” speaks to the widespread nature of the “nonavailing” beliefs held by students about mathematics [41]. Many teachers, at the high school and college levels, would argue that a course focused on mindset and open, collaborative mathematics is not possible, as there are so many methods and concepts to teach, that there is no time for exploration and collaboration. This is why the provision of such a course as a short experience that could prelude other content-focused courses seems important. Our students shared that they had never experienced “mathematical freedom” before, where they were able to separate mathematical thinking from the pressures of performance, nor had they ever seen the “human” side of mathematics.
To change ideas about something as deeply historical as mathematics and calculus is not easy, and the course was not successful in changing the perceptions of all the students. The inverse association between the students’ acceptance of the approach and the learning they experienced is an important addition to previous research highlighting this curious relationship [40]. The field would benefit from further research in this area.
One study of more than 600 K-12 teachers found that 98% of teachers believed that mindset teaching had the potential to positively impact students and their achievement, but only 20% reported confidence in their own ability to foster a growth mindset in students [79]. This mismatch in teachers’ beliefs in the importance of mindset and their ideas about ways to encourage growth mindsets may be understood more readily when considering the findings of this study, which highlight the importance of collaboration and of seeing many different approaches to mathematics problems, in developing growth mindsets. Many people believe that students’ mindsets can be changed with shared messages about potential, but this study suggests that teaching needs to be completely reconceived in order for mindset ideas to take root. It may be that widespread student mindset change will only come about when repetition of procedures is replaced by exploration of ideas.
Mathematical mindset teaching, a combination of problem-based instruction and mindset messages, allows for a robust exploration of mathematical ideas while tending to student perceptions of themselves as doers of mathematics. A shift from traditional mathematics instruction to problem-based learning is a big ask of teachers, particularly when they are striving to achieve goals of content coverage and narrow test improvement. Teachers of middle and high school, as well as college, often have extensive amounts of content to teach, causing teachers to believe they do not have time to engage students in deeper activities that value students’ multiple ideas and thoughts. The results of this study highlight the need to change this situation, and to shift secondary and college policies to make room for a “mathematical mindset” approach.
This study had limitations—the research was conducted around a short intervention, and with a particular group of students—high-achieving university students. Yet the results may still be important, not only for teachers of STEM subjects, but for all teachers whose students do not believe in their own potential, and believe incorrect ideas about learning. As stated in the introduction, other work [10,37,60] has shown the effectiveness of this approach with middle school students of varying achievement levels. These studies, combined with the results of the intervention shared in this paper, suggest that such an approach has broad implications for improving interest and achievement.
An important area for future investigation will be implementing this approach in more diverse contexts with a wide range of students. We hope this article lays out some important ideas for consideration in course design and thinking for people who might implement courses like this in the future. We also hope it adds evidence for the efficacy of centering student thinking and active learning in STEM classrooms [80]. The results show the potential of short interventions that precede students’ attendance in regular mathematics programs, in high school or in college. If universities chose to illuminate the true and humanizing nature of mathematics through short programs such as this one, we may halt the widespread exit of students from STEM, particularly for women and underrepresented students of color, and change the inequitable patterns of participation that have dominated higher levels of mathematics for centuries. Problem-based learning has a long and important history of success with students; this study has shared the additional impact that may be achieved when mindset ideas are not only shared, but infused throughout the content.
Author Contributions
Conceptualization, J.B., K.B., T.L., M.L. and M.S.-A.; methodology, J.B., K.B., T.L., M.L. and M.S.-A.; formal analysis, J.B., K.B., T.L., M.L. and M.S.-A.; investigation, J.B., K.B., T.L., M.L. and M.S.-A.; data curation, M.L. and M.S.-A.; writing—original draft preparation, J.B., K.B., T.L., M.L. and M.S.-A.; writing—review and editing, J.B., K.B., T.L., M.L. and M.S.-A.; visualization, K.B. and T.L.; supervision, J.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
The study was conducted in accordance with the Declaration of Helsinki, and approved by the Human Subjects Institutional Review Board of Stanford University (protocol code #51389 and date of approval: 8 July 2019).
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
The data for this study are not publicly available to protect participant privacy. Materials used in the course described along with videos of some activities can be found at: https://www.youcubed.org/exploring-calculus.
Acknowledgments
The authors would like to thank Montse Cordero for their contributions to the design, teaching, and analysis of the course, Cathy Williams for her thought partnership and feedback throughout the process and Graciela Pérez-Núñez for her work running various statistical analyses. We would also like to thank Jack Dieckmann for his support with study design, and Kristina Dance, Estelle Woodbury, Maximiño Manzanares, Katherine Radziwonski, and Jessica Method for their support with the course.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Table A1.
A Table of the tasks covered each day in the class.
Table A1.
A Table of the tasks covered each day in the class.
| Mathematics | Calculus | |
|---|---|---|
| Day 1 | Maths Pre-Task Opening Algebra | |
| Day 2 | Rod Trains | |
| Day 3 | Negative Space | |
| Days 4 & 5 | Lemon Task Volume of a round object and integrals as Riemann sums | |
| Day 6 | Koch Snowflake Task Geometric Series | |
| Day 7 | Bicycle Path Task Derivatives as tangent lines | |
| Days 8 & 9 | Galileo’s Investigation Derivatives as movement | |
| Day 10 | Collatz Conjecture/Four 4’s | |
| Day 11 | Walking the graph Derivatives as velocity and acceleration | |
| Day 12 | Donut to Coffee Mug Topology | |
| Day 13 | Curved Shapes Task Integrals as Riemann Sums | |
| Day 14 | Maths Post-Task |
Appendix B

Table A2.
One pair of students’ pre- and post-assessments, coded non-collaborative at pre, and collaborative at post.
Table A2.
One pair of students’ pre- and post-assessments, coded non-collaborative at pre, and collaborative at post.
| Non-Collaborative Pre-Assessment | Collaborative Post-Assessment |
|---|---|
 |  |
References
- Wilhelm, J.; Sherrod, S.; Walters, K. Project.-based learning environments: Challenging preservice teachers to act in the moment. J. Educ. Res. 2008, 101, 220–233. [Google Scholar] [CrossRef]
- Merritt, J.; Lee, M.Y.; Rillero, P.; Kinach, B.M. Problem-based learning in K–8 mathematics and science education: A literature review. Interdiscip. J. Probl.-Based Learn. 2017, 11. [Google Scholar] [CrossRef]
- LaForce, M.; Noble, E.; Blackwell, C. Problem-Based Learning (PBL) and Student Interest in STEM Careers: The Roles of Motivation and Ability Beliefs. Educ. Sci. 2017, 7, 92. [Google Scholar] [CrossRef]
- Ellis, B.; Larsen, S.; Voigt, M.; Vroom, K. Where Calculus and Engineering Converge: An Analysis of Curricular Change in Calculus for Engineers. Int. J. Res. Undergrad. Math. Educ. 2021, 7, 379–399. [Google Scholar] [CrossRef]
- Laursen, S.; Rasmussen, C. I on the prize: Inquiry approaches in undergraduate mathematics. Int. J. Res. Undergrad. Math. Educ. 2019, 5, 129–146. [Google Scholar] [CrossRef]
- Boaler, J. Experiencing School Mathematics: Traditional and Reform Approaches to Teaching and Their Impact on Student Learning; Revised and Expanded Edition; Lawrence Erlbaum Associates Inc: Mahwah, NJ, USA, 2002. [Google Scholar]
- Boaler, J. What’s Math Got to Do with it?: How Parents and Teachers Can Help Children Learn to Love Their Least Favorite Subject; Penguin Books: New York, NY, USA, 2009. [Google Scholar]
- Wilhelm, J.; Wilhelm, R.; Cole, M. Creating Project-Based STEM Environments: The REAL Way; Springer Nature: Cham, Switzerland, 2019. [Google Scholar]
- Boaler, J. Open and closed mathematics: Student experiences and understandings. J. Res. Math. Educ. 1998, 29, 41–62. [Google Scholar] [CrossRef]
- Boaler, J. Prove It to Me! Math. Teach. Middle Sch. 2019, 24, 422–428. [Google Scholar] [CrossRef]
- Boaler, J.; Staples, M. Creating Mathematical Futures through an Equitable Teaching Approach: The Case of Railside School. Teach. Coll. Rec. 2008, 110, 608–645. [Google Scholar] [CrossRef]
- Schoenfeld, A.H. Mathematical Problem Solving; Elsevier: Amsterdam, The Netherlands, 2014. [Google Scholar]
- Blackwell, L.; Trzesniewski, K.; Dweck, C. Implicit theories of intelligence predict achievement across an adolescent transition: A longitudinal study and an intervention. Child Dev. 2007, 78, 246–263. [Google Scholar] [CrossRef]
- Dweck, C.S. Mindset: The New Psychology of Success; Ballantine Books trade pbk., ed.; Ballantine Books: New York, NY, USA, 2008. [Google Scholar]
- Good, C.; Rattan, A.; Dweck, C. Why Do Women Opt Out? Sense of Belonging and Women’s Representation in Mathematics. J. Personal. Soc. Psychol. 2012, 102, 700–717. [Google Scholar] [CrossRef] [PubMed]
- Steele, C. Stereotype threat and African-American student achievement. In Social Stratification; Routledge: London, UK, 2018; pp. 752–756. [Google Scholar]
- Herzig, A. Becoming mathematicians: Women and students of color choosing and leaving doctoral mathematics. Rev. Educ. Res. 2004, 74, 171–214. [Google Scholar] [CrossRef]
- Polya, G. How to Solve It: A New Aspect of Mathematical Method; Princeton University Press: Princeton, NJ, USA, 2014. [Google Scholar]
- Gallagher, S.A.; Sher, B.T.; Stepien, W.J.; Workman, D. Implementing Problem-Based Learning in Science Classrooms. Sch. Sci. Math. 1995, 95, 136–146. [Google Scholar] [CrossRef]
- Barrows, H.S.; Tamblyn, R.M. Problem-Based Learning: An Approach to Medical Education; Springer Pub. Co.: New York, NY, USA, 1980. [Google Scholar]
- Hmelo-Silver, C. Problem-based learning: What and how do students learn? Educ. Psychol. Rev. 2004, 16, 235–266. [Google Scholar] [CrossRef]
- Davidson, N.; Major, C.H. Boundary crossings: Cooperative learning, collaborative learning, and problem-based learning. J. Excell. Coll. Teach. 2014, 25, 7–55. [Google Scholar]
- Masitoh, L.F.; Fitriyani, H. Improving students’ mathematics self-efficacy through problem based learning. Malikussaleh J. Math. Learn. 2018, 1, 26–30. [Google Scholar] [CrossRef]
- Abdullah, N.; Tarmizi, R.; Abu, R.; Ayub, A. The Effects of Problem Based Learning on Mathematics Performance and Affective Attributes in Learning Statistics at Form Four Secondary Level. Procedia-Soc. Behav. Sci. 2010, 8, 370–376. [Google Scholar] [CrossRef]
- Sullivan, P.; Askew, M.; Cheeseman, J.; Clarke, D.; Mornane, A.; Roche, A.; Walker, N. Supporting teachers in structuring mathematics lessons involving challenging tasks. J. Math. Teach. Educ. 2015, 18, 123–140. [Google Scholar] [CrossRef]
- Louie, N. The Culture of Exclusion in Mathematics Education and Its Persistence in Equity-Oriented Teaching. J. Res. Math. Educ. 2017, 48, 488–519. [Google Scholar] [CrossRef]
- Sullivan, P.; Clarke, D.; Clarke, B. Teaching with Tasks for Effective Mathematics Learning; Springer: New York, NY, USA, 2013. [Google Scholar]
- Schoenfeld, A.H. Learning to Think Mathematically: Problem Solving, Metacognition, and Sense Making in Mathematics (Reprint)-Alan H. Schoenfeld, 2016. J. Educ. 2016, 196, 1–38. [Google Scholar] [CrossRef]
- Stein, M.; Grover, B.; Henningsen, M. Building student capacity for mathematical thinking and reasoning: An analysis of mathematical tasks used in reform classrooms. Am. Educ. Res. J. 1996, 33, 455–488. [Google Scholar] [CrossRef]
- Cutts, Q.; Cutts, E.; Draper, S.; O’Donnell, P.; Saffrey, P. Manipulating Mindset to Positively Influence Introductory Programming Performance. In Proceedings of the 41st ACM technical symposium on Computer science education, Milwaukee, WI, USA, 10–13 March 2010; pp. 431–435. [Google Scholar]
- De Kraker-Pauw, E.; Van Wesel, F.; Krabbendam, L.; Van Atteveldt, N. Teacher Mindsets Concerning the Malleability of Intelligence and the Appraisal of Achievement in the Context of Feedback. Front. Psychol. 2017, 8, 1594. [Google Scholar] [CrossRef] [PubMed]
- LaMar, T.; Leshin, M.; Boaler, J. The derailing impact of content standards–an equity focused district held back by narrow mathematics. Int. J. Educ. Res. Open 2020, 1, 100015. [Google Scholar] [CrossRef]
- Kohn, A. The “Mindset” Mindset: What We Miss by Focusing on Kids’ Attitudes. 2015. Available online: https://www.washingtonpost.com/news/answer-sheet/wp/2015/08/24/the-mindset-mindset-what-we-miss-by-focusing-on-kids-attitudes/ (accessed on 7 June 2022).
- Li, Y.B.; Bates, T.C. You can’t change your basic ability, but you work at things, and that’s how we get hard things done: Testing the role of growth mindset on response to setbacks, educational attainment, and cognitive ability. J. Exp. Psychol. Gen. 2019, 148, 1640–1655. [Google Scholar] [CrossRef] [PubMed]
- Anderson, R.; Boaler, J.; Dieckmann, J. Achieving Elusive Teacher Change through Challenging Myths about Learning: A Blended Approach. Educ. Sci. 2018, 8, 98. [Google Scholar] [CrossRef]
- Lee, H.; Jamieson, J.; Miu, A.; Josephs, R.; Yeager, D. An Entity Theory of Intelligence Predicts Higher Cortisol Levels When High School Grades Are Declining. Child Dev. 2019, 90, E849–E867. [Google Scholar] [CrossRef]
- Boaler, J.; Dieckmann, J.; LaMar, T.; Leshin, M.; Selbach-Allen, M.; Perez-Nunez, G. The Transformative Impact of a Mathematical Mindset Experience Taught at Scale. Front. Educ. 2021, 6. [Google Scholar] [CrossRef]
- Henningsen, M.; Stein, M. Mathematical tasks and student cognition: Classroom-based factors that support and inhibit high-level mathematical thinking and reasoning. J. Res. Math. Educ. 1997, 28, 524–549. [Google Scholar] [CrossRef]
- Moser, J.S.S.; Heeter, C.H.S.; Moran, T.P.; Lee, Y.H. Mind your errors: Evidence for a neural mechanism linking growth mind-set to adaptive post error adjustments. Psychol. Sci. 2011, 22, 1484–1489. [Google Scholar] [CrossRef]
- Deslauriers, L.; McCarty, L.; Miller, K.; Callaghan, K.; Kestin, G. Measuring actual learning versus feeling of learning in response to being actively engaged in the classroom. Proc. Natl. Acad. Sci. USA 2019, 116, 19251–19257. [Google Scholar] [CrossRef]
- Muis, K. Personal epistemology and mathematics: A critical review and synthesis of research. Rev. Educ. Res. 2004, 74, 317–377. [Google Scholar] [CrossRef]
- Boaler, J. Limitless Mind: Learn, Lead, and Live without Barriers, 1st ed.; HarperOne, an Imprint of HarperCollinsPublishers: New York, NY, USA, 2019; p. 248. [Google Scholar]
- Faust, J.L.; Paulson, D.R. Active learning in the college classroom. J. Excell. Coll. Teach. 1998, 9, 3–24. [Google Scholar]
- Barron, B. Achieving coordination in collaborative problem-solving groups. J. Learn. Sci. 2000, 9, 403–436. [Google Scholar] [CrossRef]
- Deslauriers, L.; Schelew, E.; Wieman, C. Improved Learning in a Large-Enrollment Physics Class. Science 2011, 332, 862–864. [Google Scholar] [CrossRef] [PubMed]
- Diez-Palomar, J.; Chan, M.; Clarke, D.; Padros, M. How does dialogical talk promote student learning during small group work? An exploratory study. Learn. Cult. Soc. Interact. 2021, 30, 100540. [Google Scholar] [CrossRef]
- Fullilove, R.; Treisman, P. Mathematics achievement among African American undergraduates at the University of California, Berkeley: An evaluation of the mathematics workshop program. J. Negro Educ. 1990, 59, 463–478. [Google Scholar] [CrossRef]
- Organisation for Economic Co-operation and Development. PISA 2015 Results (Volume V): Collaborative Problem Solving; OCED: Paris, France, 2017. [Google Scholar]
- Capar, G.; Tarim, K. Efficacy of the Cooperative Learning Method on Mathematics Achievement and Attitude: A Meta-Analysis Research. Educ. Sci. Theory Pract. 2015, 15, 553–559. [Google Scholar]
- Stover, S.; Holland, C. Student Resistance to Collaborative Learning. Int. J. Scholarsh. Teach. Learn. 2018, 12. [Google Scholar] [CrossRef]
- Tharayil, S.; Borrego, M.; Prince, M.; Nguyen, K.; Shekhar, P.; Finelli, C.; Waters, C. Strategies to mitigate student resistance to active learning. Int. J. Stem Educ. 2018, 5, 7. [Google Scholar] [CrossRef]
- Felder, R.M. Random thoughts: Sermons for grumpy campers. Chem. Eng. Educ. 2007, 41, 183–184. [Google Scholar]
- Howard, J.R. Discussion in the College Classroom: Getting Your Students Engaged and Participating in Person and Online; Jossey-Bass: San Francisco, CA, USA, 2015. [Google Scholar]
- Taylor, A. Top 10 reasons students dislike working in small groups... and why i do it anyway. Biochem. Mol. Biol. Educ. 2011, 39, 219–220. [Google Scholar] [CrossRef]
- Felder, R.M.; Brent, R. Navigating the Bumpy Road to Student-Centered Instruction. Coll. Teach. 1996, 44, 43–47. [Google Scholar] [CrossRef]
- Engle, R.; Conant, F. Guiding principles for fostering productive disciplinary engagement: Explaining an emergent argument in a community of learners classroom. Cogn. Instr. 2002, 20, 399–483. [Google Scholar] [CrossRef]
- Cohen, E.G.; Lotan, R.A. Designing Groupwork: Strategies for the Heterogeneous Classroom, 3rd ed.; Teachers College Press: New York, NY, USA, 2014. [Google Scholar]
- Staples, M.E. Promoting student collaboration in a detracked, heterogeneous secondary mathematics classroom. J. Math. Teach. Educ. 2008, 11, 349–371. [Google Scholar] [CrossRef]
- Boaler, J. Promoting ‘relational equity’ and high mathematics achievement through an innovative mixed-ability approach. Br. Educ. Res. J. 2008, 34, 167–194. [Google Scholar] [CrossRef]
- Boaler, J.; Sengupta-Irving, T. The many colors of algebra: The impact of equity focused teaching upon student learning and engagement. J. Math. Behav. 2016, 41, 179–190. [Google Scholar] [CrossRef]
- Nortvedt, G.; Siqveland, A. Are beginning calculus and engineering students adequately prepared for higher education? An assessment of students’ basic mathematical knowledge. Int. J. Math. Educ. Sci. Technol. 2019, 50, 325–343. [Google Scholar] [CrossRef]
- Seymour, E.; Hewitt, N.M. Talking about Leaving : Why Undergraduates Leave the Sciences; Westview Press: Boulder, CO, USA, 1997. [Google Scholar]
- Rasmussen, C.; Ellis, J. Students Who Switch out of Calculus and the Reasons They Leave. In Proceedings of the 35th Annual Meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education, Chicago, IL, USA, 14–17 November 2013; pp. 73–80. [Google Scholar]
- Burdman, P. Why Calculus? Why Indeed? 2019. Available online: https://pamela-80683.medium.com/why-calculus-why-indeed-be4809f5637c (accessed on 4 June 2022).
- Rockmore, D. Is It Time to Kill Calculus? 2020. Available online: https://www.salon.com/2020/09/26/teaching-data-science-instead-of-calculus-high-schools-math-debate (accessed on 4 June 2022).
- Bressoud, D. The Role of Calculus in the Transition from High School to College Mathematics; Mathematical Association of America: Washington, DC, USA, 2017; Available online: https://www.maa.org/sites/default/files/RoleOfCalc_rev.pdf (accessed on 4 June 2022).
- Strogatz, S.H. Infinite Powers: How Calculus Reveals the Secrets of the Universe; Mariner Books: Boston, MA, USA, 2019. [Google Scholar]
- Nasir, N.i.S.; Cabana, C.; Shreve, B.; Woodbury, E.; Louie, N. (Eds.) Mathematics for Equity: A Framework for Successful Practice; Teachers College Press: New York, NY, USA, 2014; p. 273. [Google Scholar]
- Bransford, J.D.; Brown, A.L.; Cocking, R.R.; Donovan, S.M.; Pellegino, J.W. (Eds.) How People Learn: Brain, Mind, Experience, and School: Expanded Edition; National Academies Press: Washington, DC, USA, 2000; p. 386. [Google Scholar]
- Boaler, J. Mathematical Mindsets: Unleashing Students’ Potential through Creative Math, Inspiring Messages, and Innovative Teaching; Jossey-Bass: San Francisco, CA, USA, 2016. [Google Scholar]
- Creswell, J.W.; Plano Clark, V.L. Designing and Conducting Mixed Methods Research; SAGE Publications: Thousand Oaks, CA, USA, 2017. [Google Scholar]
- Gopalan, M.; Brady, S. College Students’ Sense of Belonging: A National Perspective. Educ. Res. 2020, 49, 134–137. [Google Scholar] [CrossRef]
- Emerson, R.M.; Fretz, R.I.; Shaw, L.L. Writing Ethnographic Fieldnotes, 2nd ed.; The University of Chicago Press: Chicago, IL, USA, 2011. [Google Scholar]
- Saldaña, J. The Coding Manual for Qualitative Researchers, 4th ed.; SAGE Publications: Thousand Oaks, CA, USA, 2021. [Google Scholar]
- McDonald, R.P. Test Theory: A Unified Treatment, 1st ed.; Psychology Press: New York, NY, USA, 1999. [Google Scholar]
- Jansen, A. Rough-draft thinking and revising in mathematics. Math. Teach. Learn. Teach. PK-12 2020, 113, e107–e110. [Google Scholar] [CrossRef]
- Ashcraft, M.; Kirk, E. The relationships among working memory, math anxiety, and performance. J. Exp. Psychol.-Gen. 2001, 130, 224–237. [Google Scholar] [CrossRef]
- Su, F.E.; Jackson, C. Mathematics for Human Flourishing; Yale University Press: New Haven, CT, USA, 2020. [Google Scholar]
- Yettick, H.; Lloyd, S.; Harwin, A.; Riemer, A.; Swanson, C.h.B. Mindset in the Classroom: A National Study of K-12 Teachers. Editorial Projects in Education Inc.: Bethesda, MD, USA. 2016. Available online: https://www.edweek.org/research-center/research-center-reports/mindset-in-the-classroom-a-national-study-of-k-12-teachers (accessed on 4 June 2022).
- Freeman, S.; Eddy, S.; McDonough, M.; Smith, M.; Okoroafor, N.; Jordt, H.; Wenderoth, M. Active learning increases student performance in science, engineering, and mathematics. Proc. Natl. Acad. Sci. USA 2014, 111, 8410–8415. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).