Abstract
A concern in Mathematics Education is the professional development of the teacher and to promote effective training programs. The literature provides principles guiding the design of such programs, which were considered for an instruction intended to strengthen the teacher’s practice in relation to the development of mathematical skills. The objective of this work was to study if the designed program was effective, in relation to the impact on the teacher’s teaching. A case study on a group of in-service teachers focused on the ability of mathematical modeling (MM) and their perspectives of this skill was carried out. This was divided into three moments: before, during, and after the program. The findings show that, before the program, teachers conceived modeling from epistemological, pragmatic and conceptual perspectives; during the program, they focused on the pragmatic and educational perspectives; and at the end of the program, the group was stripped of the pragmatic, epistemological and conceptual perspectives to move towards the educational and socio-critical. They were also able to justify the choice or disassociation of one or more of them. The study advances towards the concretion of more specific and robust professional development programs for mathematics teachers.
1. Introduction
Teacher professional development (TPD) involves a process of continuous and personal learning and growth, in which teachers participate voluntarily. This development process gradually provides confidence and autonomy and contributes to deepen their knowledge and skills to improve their practice so that they are able to address the learning challenges of their students [1,2,3]. The training programs in which teachers participate play an important role in identifying how they evolve in their TPD [4]. Unfortunately, for three decades, in-service teacher training has yielded disappointing results (qualitatively and quantitatively) with respect to effective training proposals in terms of helping teachers to improve their practices and even more disappointing in relation to the impact on student learning [5,6,7,8].
This calls for effective TPD programs, defined according to the improvement of the participating teachers’ practice and their students’ learning [5,8] as key elements of a TPD.
There is a vast body of research that focuses on identifying principles for effective TPD programs [9,10,11]. Ref. [12] proposes principles of effective programs exclusive to the field of mathematics education. The purpose of this paper is to advance in this line, presenting evidence of how these principles are operationalized in a specific context, designing a TPD program based on them and analyzing the impact on the participating teachers.
Specifically, in 2020, under the perspective of the principles for effective mathematics TPD programs [12], a specific instruction was designed with the purpose of strengthening the teacher’s practice in relation to the development of the four mathematical skills promoted by the Chilean Ministry of Education: representing, problem solving, modeling, and communicating and arguing [13]. When implementing this TPD program in a remote-working modality, the question arose whether the program was effective or not; that is, did it have an impact on the teaching of the participating teachers? This led to studying if the designed program impacted the teaching of its participating teachers, analyzing its repercussion in one of the groups of teachers, particularly, the one that addressed the ability of modeling. Given the complexity of teaching, investigating it implies observing a wide range of aspects, such as their knowledge, their way of interacting with students, or their reflection on their practice. For this work, we analyze the teacher’s teaching based on how the group positions itself in relation to the perspectives of MM in three key moments: before, during, and after the program.
In relation to modeling skills, authors such as [14,15] point out that, although modeling skills have existed for some time, efforts focused on teachers through TPD programs have only been made in recent years. Ref. [16] notes that, compared to pre-service teachers, research has paid more attention to in-service teachers’ TPD programs, as they are often linked to funded projects that include a research and evaluation study. In the field of teacher education, the literature has been concerned with the design of teaching materials to encourage modeling, the positioning of teachers with regard to modeling, and the relevance of providing teachers with modeling situations to serve as examples of teaching practices [17,18]. Along the same lines, Ref. [19] states the importance that pre- and in-service teachers face modeling tasks to promote reflection based on their own experience.
Ref. [20] reports that teachers face two main challenges when promoting the use of MM practices and activities in the classroom. Firstly, there seems to be misconceptions or confusion among teachers about what MM and its practices are [21,22]. Modeling is often misperceived or misinterpreted as drawing a model or step-by-step representation of solving a mathematical problem [14,23]. Secondly, difficulties are associated with the constraints of assessment systems, leading to limitations in time management and learning from MM activities in the classroom [23].
These challenges motivated us to study the impact that a specific professional development program had on a group of teachers focused on the ability of modeling, observing how they evolve in relation to the perspectives on MM. The perspectives, discussed in the literature, will be detailed in the following section.
2. Perspectives of Mathematical Modeling
The theoretical underpinning that supports this study is based on the notion of MM and its perspectives. The teaching of this skill constitutes a topic of specific interest in mathematics education [24] that can be addressed from different perspectives [25]. These different theoretical approaches have an impact on disparate issues, which, when observed as a whole, allow us to form a global idea of how MM is understood in the educational field.
Several authors [26,27,28,29] consider two ways of treating MM in the classroom: as a means and as an end. In the first one, modeling is an instrument that allows the learning of mathematical content, which gives rise to the conceptual perspective [26] or educational perspective (learning mathematics) [30]. In the second, the class is planned thinking about developing the competence of MM in students, highlighting the educational perspective (learning modeling) [28,30]. Under this premise, Ref. [31] defined the ability of modeling as a component of mathematical competence to be developed at the school stage. Developing such modeling competence involves different stages. Ref. [32] proposed a cyclical scheme where MM is explained from the different stages of the process. Similarly, Ref. [33] proposed a diagram-based description of the temporal sequence of activities performed by students when solving Fermi problems. Discussions on the process-based approach and other examples of MM cycles can be found in [34] or [35].
From another current, Ref. [36] adopts a socio-critical perspective of mathematics education in relation to MM. This author highlights the critical appreciation that can be given to the process of construction and use of mathematical models. This view considers MM as a means to achieve citizens who are critical of society. Ref. [37] carried out a documentary analysis of what some authors understand by MM from a contextualized perspective, considering critical mathematics education, the realist approach, the socio-epistemological and anthropological theory of didactics. The authors indicate that, in this process of transferring the real world to mathematics, the teacher plays an important role, since he or she must contextualize the situation to be worked with students, allowing them to work with contexts of everyday life or with phenomena where they can relate their mathematical knowledge to the situation to be modeled.
When mathematics is seen in a utilitarian way, that is, as a means to solve practical problems of everyday life, we are faced with the pragmatic, realistic, or applied perspective [28]. In this perspective, MM is seen as a means to model real-life situations, where students understand and solve real-world situations. In it, in order to understand and handle real-world situations, models must be dealt with explicitly. Modeling arises from a question about a certain system [38], so it is associated with problem-solving. In this regard, Ref. [39] identified MM and problem-solving, while other researchers pointed out that the purpose of MM should be the production of knowledge about the system under study, not just answering a specific question [40].
When the main interest is to reconstruct mathematics through MM, we are in the presence of the epistemological or theoretical perspective [30]. The justification for this perspective lies in considering relations with the extra-mathematical world as indispensable for an adequate image of mathematics as a science [21]. MM is subordinated to the development of more general theories for the teaching and learning of mathematics, where the goal is oriented to theory and to the promotion of theory development [28], that is, the situation posed is focused on understanding the theoretical aspects that underlie it; the models are constructed starting from a situation that then leads to the development of a mathematical theory. In this perspective, students are shown authentic examples of how strongly mathematics shapes the world or epistemological examples that provide some insight on mathematics as a science (including ethnomathematical examples). In both cases, the role of mathematics and its relations to the real world should be made more conscious [21]. In addition, both mathematical and extra-mathematical topics can be addressed, where the former are described as “intra-mathematical modeling”, and where relations to the extra-mathematical world are indispensable for an adequate picture of mathematics as a science in a broad sense. Every mathematical activity is identified as modeling where MM is not limited to the mathematization of non-mathematical questions. Modeling involves working with a mathematical model, or end product of MM [41], which involves a language shift between the real world and mathematics [42], or also between different mathematical descriptions [27].
When MM is used in the sense of wanting to increase students’ interest in mathematics, motivating—through real world examples—their understanding and retention, then we are in the presence of the psychological or pedagogical perspective [43].
These perspectives and others are collected by [21], who complements them with the ideas of [44] in order to distinguish six MM perspectives, considering the notion of “perspective”, even more formally, by means of pairing “objective/suitable examples” as follows: applied perspective (pragmatic/authentic), educational perspective (formative/cognitively rich), socio-critical perspective (cultural with an emancipatory/authentic intention), epistemological perspective (cultural in relation to mathematics/epistemologically rich), pedagogical perspective (psychological with marketing/motivational intention), and conceptual perspective (psychological/mathematically rich).
These perspectives make it possible for the student to make sense of the activity of modeling, understanding by the “sense” of an activity the subjective meaning that you can give to this activity by which you can understand its purpose. Each of these perspectives offers learners a specific aspect of meaning:
- “applied”: understanding and mastery of real-world situations;
- “educational”: the realization of the growth of one’s own competence;
- “socio-critical”: understanding the role of mathematics in society;
- “epistemological”: understanding of mathematics as a science;
- “pedagogical”: the enjoyment of doing mathematics;
- “conceptual”: the understanding of mathematical concepts.
Ref. [44] emphasizes that one of the points to address was the need to separate didactic approaches from research perspectives because the lack of this distinction causes difficulties for researchers and practitioners as they often work with several perspectives.
This paper adheres to the ideas of [21,45] in relation to the different perspectives that can be adopted from the MM, according to the scenario and context where you want to use it. For this study, we have focused on observing which perspective(s) is (are) present in the discourse of the teachers studied, inquiring into the robustness of their arguments and the degree of depth in the skill itself.
In this sense, Ref. [46] indicates that the main emphasis in these perspectives is on the aspects that are put into play, and that the direct or indirect implications that they have in the classroom should be considered. The author foresees two trends, one referring to the role of the student and the other to that of the teacher. In the latter, reference is made to the fact that the teacher chooses contexts or phenomena depending on his/her knowledge, thematic contents, and institutional reality. The author points out some MM situations that have been carried out in other studies and that can be seen from different perspectives, inviting them to be reproduced. He also emphasizes that MM should offer freedom to students and teachers to recognize the different socio-cultural contexts, situations where mathematical knowledge can be the engine to “read the world”, which requires from teachers the ability to emancipate themselves from routines that seem to be justified in traditional educational contexts.
3. Materials and Methods
A qualitative case study was conducted, analyzing the perspectives of MM of a group of teachers attending an instruction when designing, implementing, and evaluating a class focused on this skill.
3.1. Context and Teacher Training Program
The study was framed within a specific program called “Professional Development from the Lesson Study with a focus on mathematical skills” conducted at a university in Chile. Lesson Study is a methodology for promoting TPD, of Japanese origin, that enables teachers to improve and reflect on their practices. It involves a cycle of three key stages: design, implementation, and evaluation of a lesson, which is conducted in a collaborative environment [47].
This program was designed considering the principles of effective programs for mathematics teachers [12] (Table 1).

Table 1.
Principles for effective professional development programs for mathematics teachers [12].
The training program had two stages. In the first stage, called the “Examining and design stage” (which lasted one week), the teachers began the process by designing, in groups, a class around one of the mathematical skills, to socialize with peers and trainers. Afterwards, the trainers further examined the skills so that the teachers could acquire theoretical and didactic support for their implementation in the classroom. As a result, the groups reformulated the lesson plans. The improvement continued by asking each group to carry out the Didactic Analysis related to the designed class, which was shared with their peers and trainers, leading to a new reformulation of the lesson plan, based on the feedback provided. The Didactic Analysis is a methodological tool that is used in teacher training to examine a learning unit. It contains five sub-analyses: conceptual, content, cognitive, instructional, and evaluation [48].
At the end of this week, the groups presented a report with the didactic analysis carried out and the reformulated lesson plan, which they implemented in the following stage, where they carried out cycles of Lesson Study around what they designed in this stage.
The second stage of the training program, called the “Lesson Study stage”, was based on the Lesson Study methodology, in which each group, starting from the class designed in the intensive week, carried out cycles of this methodology, where the implementations were recorded to be analyzed as a group. Once a month, the teachers and trainers met to analyze and reflect on the implemented classes, observing the elements that needed to be reformulated. This process lasted 6 months, culminating in the delivery of a final report where each group presented the Lesson Study cycles, the reformulations of the classes, the analysis of their implementations, and their reflections on the process carried out. The stages of the program are illustrated in Figure 1.
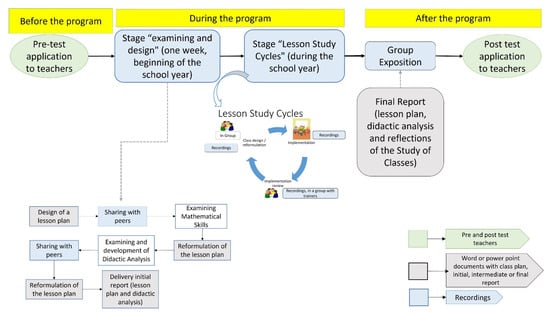
Figure 1.
Stages of the program, data collection instruments, typology, and temporality.
These two stages that structure the program allow the presence of principle 3 (inquiry and reflection), especially through the Lesson Study methodology, which also favors the presence of principle 6 (communities of practice), where the exchange of opinions and collaborative work was encouraged. In addition, the program considered sufficient time for the appropriation of the topics to be addressed, both disciplinary and didactic. This causes principle 5 (time) to be present in the design of the TPD.
Given that the purpose of the program was to strengthen the practice and specialized knowledge of the teacher in relation to the development of mathematical skills, it considered in its design principle 1 (focus on teaching) and principle 2 (focus on knowledge).
As mentioned above, the program revolves around the four mathematical skills promoted by the national curriculum. This emphasis on one element of the curriculum is present in the design of the training program in principle 4 (external links), providing balance and coherence between mathematics and the curriculum.
Furthermore, in stage 2 of the program, the importance of collecting data from the classroom can be seen, present in principle 7, which accounts for the instance of collecting data from the classroom.
Finally, in its design, principle 8 was considered: expert facilitation, i.e., it was taken into account that the program should be directed by experts in mathematics didactics and mathematical skills. It was initially taught by three trainers specialized in the didactics of mathematics, one of them specialized in the ability of argumentation, another in the ability of problem solving and modeling, and the third in the ability of representation. Subsequently, two specialists in the same area were incorporated, one of them a specialist in the ability of modeling and the other in the ability of problem solving.
3.2. Study Subjects
Twenty-two primary and secondary school teachers participated. These teachers enrolled on the training program of their own free will. Of these 22 teachers, this study paid attention to the only 1 group of 4 teachers that voluntarily chose to address the skill of modeling. The teachers in the group range in age from 38 to 43 years and have between 11 and 15 years of teaching experience. Two of them work in vulnerable schools (those whose students are of high social risk and low socio-economic level), and these same teachers have taken the Teacher Evaluation (placing them in the “outstanding” category) and the Disciplinary and Pedagogical Knowledge Test (with a performance level above B). In Chile, teachers must take the Teacher Evaluation every few years, which gives levels of performance: outstanding, competent, basic, unsatisfactory. They must also take the Disciplinary and Pedagogical Knowledge Test, which assigns the teacher to a specific bracket: A, B, C, and D, where A is the bracket with the best performance and D the lowest performance.
Three of the four teachers (Teacher 1, Teacher 2, and Teacher 3) have as initial training the title of secondary mathematics teacher and have completed a postgraduate degree in some specialty related to the didactics of mathematics. The implementation of the designed class was carried out by Teacher 1 and Teacher 2, with the support of Teacher 3, with secondary school students aged 12 and 13 and in virtual mode. The first class was implemented in a group of 30 students and the second in a class of 9 students. Both classes had no experience with modeling activities.
Based on the above, the research design of this study follows a “case study”, in which the aim is to investigate and analyze in depth a single case [49,50] of a group of four teachers during a specific time, participating in a didactic-mathematical specialty training course. This group was chosen because it was the only one that voluntarily focused on modeling skills. The group of teachers stated that they had chosen this skill because they considered it to be the most complex of the four promoted by the Ministry of Education.
We have focused on studying the impact of the program on this group of teachers, prioritizing, in the first instance, the enquiry into how this improvement directly affected the teachers. It should be noted that we are aware of the need to address the impact of the program not only on teachers but also on their students and consider that this aspect is on the horizon of the present work. However, given the magnitude of this teacher-centered study, the impact on students will be the subject of a subsequent paper.
3.3. Data Collection
For the data collection, we used various sources: recordings of different moments of the program and of the classes implemented, Word or PowerPoint documents with the lesson plan designed and reformulated, Word documents with the initial and final reports, and the pre- and post-tests applied to teachers. Figure 1 illustrates the different data collection instruments according to the moment when they were applied (before, during, or after the program).
The objective of the pre- and post-test was to gather information about the initial (before the program) and final (at the end of the program) conceptions about MM. The pre-test contained two items and was designed considering a validation by experts in didactics of mathematics, especially in MM. The items considered in the pretest were as follows:
- In mathematics education, what do you understand by the ability of modeling?
- Give an example of an activity or task you would do for your students to develop this skill.
In order to maintain the degree of difficulty, the post-test included the same items as the pre-test, but a third item was added to lead the teachers to a global reflection of the process carried out in the program. The third item of the post-test was:
- 3.
- Provide a brief reflection on the main learning you have achieved in the program. Also comment on the positive and negative aspects of the program, the methodology used, the focus (skills), among others.
3.4. Data Analysis
For the data analysis, the content analysis method was adopted, considering as units the paragraphs or set of paragraphs with a common idea, both in the writings and in the recordings. Each unit of analysis was codified by Teacher 1, Teacher 2, Teacher 3, etc., when the interventions were of teachers participating in the program and by Trainer 1, Trainer 2, Trainer 3, etc., when they were the trainers. The categories of analysis, linked to the perspectives of the MM, are detailed in Table 2.

Table 2.
Categories of analysis used in the study.
4. Results
The results are presented according to the MM perspectives presented by the teachers before, during, and after the program.
4.1. Before the Program
At this stage, there are two instruments for data collection, the pre-test and the initial lesson plan.
4.1.1. Results of the Application of the Pre-Test
Before starting the training process, a pre-test was applied to the teachers. Their answers show that three of the four teachers in the group proposed a conception of MM centered on the pragmatic perspective. An example of this is shown below, where Teacher 2 proposed MM as a means to model real-life situations, in which students understand and solve real-world situations:
- In mathematics education, what do you understand by the ability of modeling?That the student can use mathematical tools to codify or symbolize an everyday situation and, if possible, give a solution to it thanks to these utilities of mathematics.
- 2.
- Give an example of an activity or task you would do for your students to develop this skill.They are presented with an everyday problem situation involving money, and they must use algebraic language as a means to translate and model this situation and provide a solution.
It should be noted that the fourth member of the group (Teacher 4) evidenced an epistemological perspective of MM, since he considered it as a process that involves determining the algebraic representation associated with a mathematical situation, emphasizing the importance of studying the behavior of the numerical sequence, as illustrated in the following text:
Modeling consists of expressing a situation or problem using algebraic language in such a way that the generalization of the problem can be sought. Example: Add the first “n” consecutive natural numbers.
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 +…+ n = [n (n + 1)]/2
To achieve the skill, you must first study the behavior, this could be made at first by adding the first 10 numbers.
4.1.2. Initial Lesson Plan Results
At the beginning of the training program, and before intervening with the teachers, the group was urged to design a lesson plan whose purpose was to develop modeling skills in their students. Although this instance took place at the beginning of the program, it is considered, for the purposes of the study, as “before the program”, since no didactic intervention had yet been carried out on the teachers by the trainers. The group discussed what elements such a lesson should contain, giving rise to the dialogue shown in Table 3.

Table 3.
Group discussion on what is MM.
In the group discussion, what was observed in the pre-test is confirmed regarding a conception of the ability of modeling centered on the process of constructing the mathematical model. This model is viewed as an algebraic representation associated with a mathematical situation, where the teacher emphasizes the importance of studying the behavior of the numerical sequence. This, therefore, suggests the epistemological perspective. It can be seen that they did not contemplate a problem of everyday life (intra-mathematical approach), nor did they consider the stages of solving and validating as part of the MM, confusing it with the ability of representation and conceiving it as the process that leads to the generalization of numerical expressions. In other words, it seems that the group conceived MM as a mathematical practice that allows generalizing mathematical expressions, trying to look for epistemologically rich examples that shed some light on mathematics as a science, which is close to the epistemological perspective. When they shared with the rest of their peers and trainers, they were asked about the type of context that involves MM, and they affirmed that it could be real or mathematical.
On the other hand, when analyzing the lesson plan (that teachers structured in three main moments: beginning, development, and closing), the focus was centered primarily on content over skill. The main goal of the lesson was to arrive to the algebraic expression involved in the problem (Figure 2), which makes the conceptual perspective of the MM emerge.

Figure 2.
Slides designed by the teachers for the beginning and closing of their class in its initial version.
4.2. During the Program
The results are shown in the two stages of the program: the stage of examining and design at the beginning and at the stage of Lesson Study, where there was a monthly meeting with teachers.
4.2.1. Examining and Design Stage
After the teachers present their lesson plans, the trainers delved further into each mathematical skill. In the case of the group of teachers working with the MM skill, it was observed that these clarifications provoked in them strong changes to their conceptions. Examples in relation to the role of the context (of real life), data collection and the importance of solving the problem are illustrated in the dialogue shown in Table 4. This provides evidence that the teachers discarded the epistemological perspective from their conceptions and focused more attention on the pragmatic or educational perspective, which became clearer as they advanced in the training process.

Table 4.
Group discussion on what modeling is after examining.
Subsequently, teachers were encouraged to develop the didactic analysis associated with the learning unit, which involved identifying the errors, difficulties, and returns of the class, the possible responses of students, among other aspects. This process led them to reformulate their lesson plan on several occasions. Finally, at the end of the examining and design stage, teachers submitted a report that included the lesson plan and the didactic analysis associated.
All this allowed us to observe changes in the group in relation to their initial positions on MM. When observing the lesson plan that teachers carried out (which, in its first version, evidenced the epistemological and conceptual perspectives), a greater relevance to the ability over the mathematical content was observed, giving presence to the educational and pragmatic perspectives:
- The beginning of the lesson focused on a video (https://www.youtube.com/watch?v=szmxbpJM24M, accessed date: 15 December 2021) that was intended to bring the students into a specific context (contagion by a disease such as COVID-19);
- Development aimed to solve a problem related to the contagion of a disease, where, under certain conditions, they must find the number of infected for a certain time;
- The closing (Figure 3) dealt with the definition of MM from an educational perspective, by trying to emphasize its phases, and from a pragmatic perspective, by highlighting the relevance of solving a problem of everyday life.

 Figure 3. Slides presented by the teachers for the closing of the lesson (images adapted from https://theconversation.com/covid-19-pandemia-de-modelos-matematicos-136212, accessed date: 18 December 2021; https://minciencia.gob.cl/comunidad-covid19/, accessed date: 18 December 2021).
Figure 3. Slides presented by the teachers for the closing of the lesson (images adapted from https://theconversation.com/covid-19-pandemia-de-modelos-matematicos-136212, accessed date: 18 December 2021; https://minciencia.gob.cl/comunidad-covid19/, accessed date: 18 December 2021).
4.2.2. Lesson Study Stage
As the academic year progressed, the group carried out two cycles of Lesson Study (design, implementation, and evaluation of the class). In the first implementation, it was observed that the implementing teacher (Teacher 1) focused her attention on getting her students to solve a contextualized problem, introducing the pragmatic perspective. However, in the closing, the educational perspective emerged, since the teacher explained that “the process you did mainly addresses a very important skill that has to do with modeling”. After that, the teacher presented its definition as illustrated in Figure 3, where the emphasis was also on the phases of the MM. After the first implementation, in the program sessions, together with peers and trainers, the most relevant moments of the class were shared. On that occasion, the group mentioned that “we were able to address the objective of the class, which was to be able to implement this problematic situation, so that the children, through their modeling, could reach the result”, which gives a glimpse of the pragmatic perspective.
There was a discussion about what happened in the class, where trainers and peers raised several questions to the group, among which we highlight: (a) how to favor in the class that the students manage to move from one stage to another? For this, it was suggested to add initial indications, for example: “explain to your partner what you understand about the problem”, in order to help to go through the stage of understanding the problem in the MM; (b) how to start the class in a way that is coherent with the skill to be developed, suggesting incorporating questions such as “what steps would you do if you had to conduct an investigation?”, which will provoke a brainstorming session that can be taken up again at the end, formalizing the MM; (c) how to take advantage of the solutions found by the students in relation to the MM?—suggested to promote instances of validation of results (contrasting with the context), the last phase of the MM; and (d) do you want the students to develop the whole process of MM or some of its phases? (to position oneself as to what the emphasis will be).
In this regard, teachers reformulated the lesson plan and implemented it again. The methodology implied that the class was implemented by the different members of the group, after the reflections and reformulations were made. On this occasion, the teacher who implemented (Teacher 2) again focused her attention on getting her students to solve the contextualized problem, as happened in the first implementation, giving the impression of maintaining the pragmatic perspective. However, it should be noted that the teacher did not take the time to reach the correct answer and immediately moved on to the closing of the class, where the educational perspective emerges, as she presented the definition of MM and the cyclical model illustrated in the center of Figure 3.
After the implementation, in the monthly meeting, a reflection of the class was carried out, where the trainers raised certain questions such as “why at the beginning of the class is it not proposed to introduce the stages of the MM?”, to which the group argued that their intention was that the children carried out the process with the tools they handle, and at the end of this work, it was explained to them that they carried out the modeling process. This can show us that the group manifested an educational perspective, where they highlighted the importance of carrying out the MM process (with or without the teacher’s help).
Another query that arose from the trainers was in relation to the phase of understanding the problem, where they were shown the need to return to this stage when necessary, for example, when it was observed in the following phase that the students did not arrive at a correct model. In this regard, the group stated that when they saw that their students did not find the model, it was difficult to move forward and that they were now aware that it is possible to go back to the phase of understanding the problem.
They were also questioned about how to take advantage of the wrong models, where they were led to consider the validation phase, where the important thing is not to evaluate the skill but to carry it out. This became relevant in the group when they stated that they thought that the important thing was to get to the right model (pragmatic perspective). Throughout this process, it can be observed that the discussion continued to revolve around the educational perspective and with some glimpses of the pragmatic perspective.
Finally, the importance of leading the students to reflect on the usefulness of MM was emphasized. Teachers highlighted that this type of problem situation can be found on other occasions, they are tools for everyday life, and that this is why this skill is worked on at school, trying to include the socio-critical perspective. In this respect, the group did not express an opinion, but it seems that they reflected on it, as is evidenced in the following stage.
4.3. After the Program
At the end of the program, the groups submitted a final report, presenting the main ideas of the process carried out and answering the post-test. The results of these three activities are detailed below.
4.3.1. Final Report
In relation to the final report, the group studied showed evidence of stripping itself of the pragmatic perspective, which is evident in the final joint reflection of the report, an excerpt of which is presented below:
At the beginning we were all very focused on the students getting to the solution of the problem, rather than on the process of developing the skill. This was changing in the course of the application of the lesson study system that involves the three stages of preparation, realization and evaluation. By receiving the comments and reviews of the experts and making the necessary adjustments, we managed to focus on the students working on the skill rather than on obtaining a correct result of the problem.
There is also an intention to detach from the conceptual perspective and move towards the educational perspective, for example, when they indicated, “I have tried to put aside the conceptual to focus on the skill and its phases. In this way, I realized the richness that is achieved in the students.”. In addition, they also highlighted the importance of promoting the stages of MM:
As for the ability of mathematical modeling, as a tool to solve real-life problem situations, it was possible to work during the development of the classes, specifically the second class of 90 min, by virtual platform, emphasizing the understanding of the problem, promoting the stages of mathematical modeling together with the students, allowing them to be the main actors of their own learning.
4.3.2. Final Exhibition
After the delivery of the report, a last meeting of the program was held, where each group presented its reflections on the process carried out. On this occasion, one of the trainers presented them with three statements (linked to some perspectives of the MM) and asked them which of them they felt most identified with, which provoked the dialogue illustrated in Table 5.

Table 5.
Dialogue between the trainer and the teachers on the prospects of MM.
Moreover, one of the trainers asked them about the learning achieved in the program, giving rise to the dialogue shown in Table 6.

Table 6.
Dialogue between the trainer and the teachers about the learning achieved in the program.
Several aspects can be observed from this dialogue. In the first place, it seems that the teachers recognized that initially they conceived MM from an epistemological perspective, with a strictly mathematical approach (in relation to the initial lesson plan that they propose). Subsequently, they stated that, for them, in the process of MM, it is not relevant to reach the solution, but to carry out the MM cycle, especially to find models that must be validated, which gives evidence that they moved from the pragmatic perspective to the educational one. Finally, the group manifested the importance of achieving critical and reflective citizens, as part of the process involved in MM, which shows that they were becoming aware of the socio-critical perspective of this skill.
4.3.3. Post Test Results
At the end of the process, the teachers take the post-test. In it, it can be seen that the four teachers in the group maintained the educational perspective, as evidenced in one of the answers of Teacher 3:
In mathematics education, what do you understand by the ability of modeling?
The ability of modeling corresponds to being able to go through a circuit that involves a problematic situation in real life, going through the understanding and analysis of the situation, creating a model that allows to give a solution to this situation, such as pictorial representations, numerical or algebraic expressions, solving this model to be able to later re-analyze the situation and see if this model responds or gives a solution to the problem posed.
Furthermore, from the reflection question added to this test it can be seen that Teacher 3 again shifted to the pragmatic perspective, as illustrated below:
Having been able to participate in the two class implementations has allowed me to experience firsthand how students work, in this case, the skill of modeling, where we, as teachers, are often concerned that they reach a solution and not that they work on the skill.
To summarize the results, a synthesis of how they evolve in the perspectives of the MM is illustrated in Figure 4, where the dotted lines in red indicate a shedding of the indicated perspective.
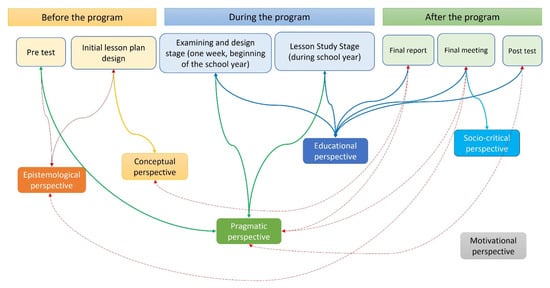
Figure 4.
Summary of the perspectives presented before, during, and after the program.
Figure 4 shows that teachers started the process from a conception of MM based on epistemological, conceptual, and pragmatic perspectives. During the program, they oriented their views towards the pragmatic and educational perspective. At the end of the program, they had a clearer posture, where they stated that they moved away from the epistemological, pragmatic, and conceptual posture to concentrate on the educational perspective. In addition, it is interesting to note that in this final stage the socio-critical perspective emerged and that at no time during the program did the motivational perspective emerge. In summary, although throughout the process they modified their positions on the perspectives of MM, at the end of the program, the teachers were able to justify their choice or disassociation from one or several of them.
5. Discussion
We have set out to study whether the professional development program designed has an impact on the improvement of the teacher’s teaching. To this end, we have focused our attention on the different perspectives on MM expressed by teachers at three key moments: before, during, and after the program.
Before the program, teachers conceived MM focused on epistemological and conceptual perspectives, as is reflected in the pre-test and in the initial lesson plan. Likewise, they recognized difficulties in distinguishing MM from problem solving, a fact that was also identified by [20] when developing a TPD program focused on modeling and 3D printers. Indeed, authors such as [51,52] acknowledge that there is no simple blueprint for describing and defining universal problem-solving method or modeling processes.
Furthermore, the bewilderment shown by teachers in confusing the ability of modeling with the ability of representation may be rooted in what [22] explains about modeling mathematics and mathematical modeling. While the former refers to using representations to communicate mathematical concepts or ideas, the essence of the latter lies in dealing with a variety of real-world problems where the main task is to translate a problem into mathematical form. From the teachers’ comments in the pre-test, it appears that they were thinking about modeling mathematics. This confusion also seems to be reflected in the lack of real contexts in the initial tasks they proposed, since, by placing themselves in the conception of modeling mathematics, the process begins in the mathematical world rather than in the real world, as occurs in mathematical modeling.
The difficulty of teachers to pose situations in real context found among the participants of this study has also been highlighted by [19], who state the importance that pre-service teachers as well and in-service teachers face this type of situations based on MM so that, through what they can experience, they reflect on the characteristics and difficulties that can be observed in order to seek strategies. In the same way, Ref. [53] states that teachers’ professional development courses should be improved, offering occasions to face modeling activities based on rich and realistic contexts, as well as developing prototypes of practices and textbooks based on realistic problematic contexts available for all school levels.
During the program, in the examining and design stage, teachers gradually discarded the epistemological perspective from their conceptions, focusing more attention on the pragmatic and educational perspectives. When they focused on the educational perspective, they became aware of the importance of the validation stage, which went largely unnoticed by students, an aspect that was also identified by [32,54]. In stage two of the program (during the school year), a tendency for the educational perspective was manifested.
Finally, after the program, the group of teachers manifested the intention of stripping themselves of the pragmatic and conceptual perspectives in order to move towards the educational perspective. It can be seen how in the last stages of the process, the socio-critical perspective emerged. The fact of becoming aware of this perspective brings teachers closer to international positions that have pointed out the educational value of involving students in the modeling activity [55], especially if mathematics education is understood as a means to promote responsible citizenship [25].
In summary, although throughout the process they modified their positions on the perspectives of MM, in the final stage they were able to justify the choice or disengagement of one or more of them with arguments that go beyond the anecdotal. They approached what [56] notes as a reflective view of MM itself, causing teachers and students to engage with these issues.
This global view of the program allows us to visualize that it enabled teachers to face a skill that was initially complex and confusing for them. This process highlights that the program has forced teachers to emancipate themselves from routines that seemed legitimate to them, such as the fact of stripping themselves of certain perspectives to focus on others. This enabled them to look at the classroom from a more refined position in relation to this skill, ratifying the ideas of [46], who indicates that the direct or indirect implications that the perspectives of MM have in the classroom should be considered. In this sense, we agree with [21,57], who state that TPD can improve teachers’ knowledge of mathematical modeling.
Moreover, taking into account the complexity of teaching, we have considered studying the teacher’s teaching from the perspectives of the MM. This may be a limitation for the study, since the teacher’s teaching, given its complex nature, involves many other aspects, such as personal knowledge, reflection, and way of interacting in the classroom, among others. However, at the same time, we consider that this study is a contribution to the scientific community given that we have materialized the perspectives of MM in a specific TPD program for mathematics teachers, a complex issue to deal with as stated by [44], owing to the need to separate didactic approaches from research perspectives.
Another limitation of the study has to do with the context where the TPD program is located, since, due to the pandemic conditions, it was not possible to carry out the training in person but by remote means, which hindered communication and the impact on teachers. This context also had to consider the work overload that the participating teachers had. Given the change of focus that they had to make in their classes (from face-to-face to remote or hybrid), even teachers who were already using online environments in their practices had to adapt suddenly to the new teaching context with the advent of emergency remote education due to COVID-19 [58]. Even so, we also consider that this study is a contribution to the scientific community, as it was possible to demonstrate that, despite the pandemic and working remotely, it was possible to advance in the training of mathematics teachers and achieve satisfactory results from them.
This study has focused on observing whether the program studied was effective or not, through its impact on the teaching of its participating teachers. Considering that effectiveness involves observing both the teaching of the teacher and the learning of their students [8], we projected this study by analyzing its impact on the learning of the students of these teachers. To do so, we have proposed to follow up with these teachers and their students in order to see their impact in the longer term.
Other lines of research can be directed towards observing how each of the principles of effective programs influence the teaching of the teacher or the learning of their students. This would allow for increasingly specific and robust TPD programs for mathematics teachers that will ultimately have an impact on the education of future generations.
Author Contributions
Conceptualization, E.R.-R., E.F.-A. and A.M.-S.; methodology, E.R.-R., E.F.-A. and A.M.-S.; formal analysis, E.R.-R.; investigation, E.R.-R., E.F.-A. and A.M.-S.; resources, E.R.-R.; writing—original draft preparation, E.R.-R., E.F.-A. and A.M.-S.; writing—review and editing, E.F.-A.; funding acquisition, E.R.-R. All authors have read and agreed to the published version of the manuscript.
Funding
This research and the APC were funded by the National Research and Development Agency (ANID) of the Government of Chile, through FONDECYT project 11190553, and by the Department for Research and Advanced Studies of the Pontifical Catholic University of Valparaiso, project 039.396/2019.
Institutional Review Board Statement
The study was conducted in accordance with the guidelines of the 2005 UNESCO Declaration on Bioethics and Human Rights and was approved by the Ethics Committee of the Pontifical Catholic University of Valparaiso (BIOEPUCV-H 313-2029, 14 October 2019).
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Acknowledgments
The authors thank the teachers participating in the postgraduate course for their valuable contributions and continuous reflection on their practice. Special thanks go to the group of teachers who addressed the skill of mathematical modelling.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Avalos, B. Teacher professional development in Teaching and Teacher Education over ten years. Teach. Teach. Educ. 2011, 27, 10–20. [Google Scholar] [CrossRef]
- Bautista, A.; Oretga-Ruiz, R. Teacher professional development: International perspectives and approaches. Psychol. Soc. Educ. 2017, 7, 240–251. [Google Scholar] [CrossRef] [Green Version]
- Mizell, H. Why Professional Development Matters; Learning Forward: Oxford, OH, USA, 2010; ISBN 978-0-9800393-9-9. [Google Scholar]
- Ramos-Rodríguez, E. Reflexión Docente Sobre la Enseñanza del Álgebra en un Curso de Formación Continua; Universidad de Granada: Granada, Spain, 2014. [Google Scholar]
- Montecinos, C. Desarrollo profesional docente y aprendizaje colectivo. Psicoperspectivas. Individuo Soc. 2003, 2, 105–128. [Google Scholar]
- Vaillant, D. El desarrollo profesional y su incidencia en la tarea del maestro. Rev. Int. Magisterio. Educ. Pedagog. 2016, 1–7. [Google Scholar]
- Darling-hammond, L.; Hyler, M.E.; Gardner, M. Effective Teacher Professional Development; Learning Policy Institute: Palo Alto, CA, USA, 2017. [Google Scholar]
- Desimone, L.M.; Pak, K. Instructional Coaching as High-Quality Professional Development. Theory Pract. 2017, 56, 3–12. [Google Scholar] [CrossRef]
- Loucks-Horsley, S.; Stiles, K.; Hewson, P. Principles of effective professional development for mathematics and science education: A synthesis of standards. NISE Br. 1996, 1, 3–8. [Google Scholar]
- Reitzug, U.C. Professional development. In School reform proposals: The research evidence; Molnar, A., Ed.; EPSL. Education Policy Research Unit: Gainesville, FL, USA, 2002; pp. 289–316. [Google Scholar]
- Korthagen, F.; Loughran, J.; Russell, T. Developing fundamental principles for teacher education programs and practices. Teach. Teach. Educ. 2006, 22, 1020–1041. [Google Scholar] [CrossRef]
- Ramos Rodriguez, E.; Bustos, B.; Morales, A. Identification of the Principles of Effective Professional Development Programs and Their Impact: An Investigation of the Guidelines of a Mathematics Didactic Graduate Program and a Case Study Focused on Teacher Training. Int. J. Sci. Math. Technol. Learn. 2021, 29, 1–16. [Google Scholar] [CrossRef]
- Bases Curriculares Primero a Sexto Básico; Ministerio de Educación: Santiago, Chile, 2018.
- Chan, C.M.E. Initial perspectives of teacher professional development on mathematical modelling in Singapore: Conceptions of mathematical modelling. In Teaching Mathematical Modelling: Connecting to Research and Practice. International Perspectives on the Teaching and Learning of Mathematical Modelling; Stillman, G., Kaiser, G., Blum, W., Brown, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 405–413. [Google Scholar]
- Borromeo Ferri, R. Learning How to Teach Mathematical Modeling in School and Teacher Education; Springer International Publishing: Cham, Switzerland, 2018; ISBN 978-3-319-68071-2. [Google Scholar]
- Cai, J.; Cirillo, M.; Pelesko, J.A.; Ferri, R.B.; Borba, M.; Geiger, V.; Stillman, G.; English, L.D.; Wake, G.; Kaiser, G.; et al. Mathematical Modeling in School Education: Mathematical, Cognitive, Curricular. In Proceedings of the Proceedings of the Joint Meeting of PME 38 and PME-NA 36, PME-NA, Vol.1; Liljedahl, P., Nicol, C., Oesterle, S., Allan, D., Eds.; PME: Vancouver, BC, Canada, 2014; pp. 145–172. [Google Scholar]
- Guerrero-Ortiz, C.; Mena-Lorca, J.; Soto, A.M. Fostering Transit between Real World and Mathematical World: Some Phases on the Modelling Cycle. Int. J. Sci. Math. Educ. 2018, 16, 1605–1628. [Google Scholar] [CrossRef]
- Huincahue, J.; Borromeo-Ferri, R.; Mena-Lorca, J. Math modeling knowledge from reflection in math teachers initial training. Enseñanza Ciencias 2018, 36, 99–115. [Google Scholar] [CrossRef]
- Zaldívar Rojas, J.D.; Quiroz Rivera, S.A.; Medina Ramírez, G. La modelación matemática en los procesos de formación inicial y continua de docentes. Rev. Investig. Educ. Rediech 2017, 8, 87–110. [Google Scholar] [CrossRef]
- Asempapa, R.S.; Love, T.S. Teaching math modeling through 3D-printing: Examining the influence of an integrative professional development. Sch. Sci. Math. 2021, 121, 85–95. [Google Scholar] [CrossRef]
- Blum, W. Quality Teaching of Mathematical Modelling: What Do We Know, What Can We Do? In The Proceedings of the 12th International Congress on Mathematical Education; Cho, S.J., Ed.; Springer International Publishing: Cham, Switzerland, 2015; pp. 73–96. ISBN 9783319126883. [Google Scholar]
- Cirillo, M.; Pelesko, J.A.; Felton-Koestler, M.D.; Rubel, L. Perspectives on modeling in school mathematics. In Annual perspectives in Mathematics Education 2016: Mathematical Modeling and Modeling Mathematics; Hirsch, C.R., McDuffie, A.R., Eds.; National Council of Teachers of Mathematics: Reston, VA, USA, 2016; pp. 3–16. ISBN 978-0-87353-974-6. [Google Scholar]
- Lehrer, R.; Schauble, L. Origins and evaluation of model-based reasoning in mathematics and science. In Beyond Constructivism: Models and Modeling Perspectives on Mathematics Problem Solving, Learning, and Teaching; Lesh, R., Doerr, H.M., Eds.; Lawrence Erlbaum: Mahwah, NJ, USA, 2003; pp. 59–70. [Google Scholar]
- Blum, W.; Galbraith, P.; Henn, H.W.; Niss, M. Modelling and Applications in Mathematics Education: The 14th ICMI Study; Springer: New York, NY, USA, 2007. [Google Scholar]
- Kaiser, G. The teaching and learning of mathematical modelling. In Compendium for Research in Mathematics Education; J. Cai, Ed.; National Council of Teachers of Mathematics: Reston, VA, USA, 2017; pp. 267–291. [Google Scholar]
- Julie, C. Making Relevance Relevant in Mathematics Teacher Education. In Proceedings of the Proceedings of the 2nd International Conference on the Teaching of Mathematics; Vakalis, I., Hallett, D.H., Quinney, D., Kourouniotis, C., Eds.; Wiley: New York, NY, USA, 2002. [Google Scholar]
- Bosch, M.; García, F.; Gascón, J.; Ruíz-Higueras, L. La modelización matemática y el problema de la articulación de la matemática escolar. Una propuesta desde la teoría de antropológica de lo didáctco. Educ. Matemática 2006, 18, 37–74. [Google Scholar]
- Kaiser, G.; Sriraman, B. A global survey of international perspectives on modelling in mathematics education. ZDM 2006, 38, 302–310. [Google Scholar] [CrossRef]
- Ikeda, T. Pedagogical reflections on the role of modelling in mathematics instruction. In Teaching Mathematical Modelling: Connecting to Research and Practice; Stillman, G.A., Kaiser, G., Blum, W., Brown, J.P., Eds.; Springer: London, UK, 2013; pp. 255–276. [Google Scholar]
- Blomhøj, M. Different perspectives in research on the teaching and learning mathematical modelling. In Proceedings of the Mathematical Applications and Modelling in the Teaching and Learning of Mathematics: Proceedings from Topic Study Group 21 at the 11th International Congress on Mathematical ducation in Monterrey, Monterrey, Mexico, 6–13 July 2008; Blomhøj, M., Carreira, S., Eds.; Roskilde Universitet. IMFUFA-tekst: Roskilde, Denmark, 2009. i, om og med matematik og fysik No. 461, 2. pp. 1–18. [Google Scholar]
- Niss, M.A.; Højgaard, T. Competencies and Mathematical Learning: Ideas and Inspiration for the Development of Mathematics Teaching and Learning in Denmark; Niss, M.A., Højgaard, T., Eds.; Roskilde Universitet. IMFUFA-tekst: Roskilde, Denmark, 2011; i, om og med matematik og fysik No. 485. [Google Scholar]
- Blum, W.; Leiß, D. How do Students and Teachers Deal with Modelling Problems? In Mathematical Modelling: Education, Engineering and Economics; Haines, C., Galbraith, P., Blum, W., Khan, S., Eds.; Chichester: New South Wales, Australia, 2007; pp. 222–231. [Google Scholar]
- Ärlebäck, J.B.; Albarracín, L. An extension of the MAD framework and its possible implication for research. In 11th Congress of the European Society for Research in Mathematics Education; Jankvist, U.T., van den Heuvel-Panhuizen, M., Veldhuis, M., Eds.; Freudenthal Group & Freudenthal Institute, Utrecht University, Netherlands: Utrecht, The Netherlands, 2019; pp. 1232–1239. [Google Scholar]
- Ferri, R.B. Theoretical and empirical differentiations of phases in the modelling process. ZDM 2006, 38, 86–95. [Google Scholar] [CrossRef]
- Greefrath, G.; Vorhölter, K. Teaching and Learning Mathematical Modelling: Approaches and Developments from German Speaking Countries. In Teaching and Learning Mathematical Modelling. ICME-13 Topical Surveys; Springer: Cham, Switzerland, 2016; ISBN 9783319450049. [Google Scholar]
- Barbosa, J.C. Mathematical modelling in classroom: A socio-critical and discursive perspective. ZDM 2006, 38, 293–301. [Google Scholar] [CrossRef]
- Luquez Herazo, J.; Pacheco Fernández, J.; De La Hoz Molinares, E. Modelización matemática desde la perspectiva contextualizada. Rev. Boletín REDIPE 2021, 10, 463–480. [Google Scholar] [CrossRef]
- Velten, K. Mathematical Modeling and Simulation; WILEY-Springer: Weinheim, Germany, 2009; ISBN 978-3-527-40758-8. [Google Scholar]
- Castro, E.; Castro, E. Representaciones y modelización. In La Educación Matemática en la Enseñanza Secundaria; Rico, L., Ed.; Horsori: Barcelona, Spain, 1997; pp. 95–124. [Google Scholar]
- Montoya Delgadillo, E.; Viola, F.; Vivier, L. Choosing a Mathematical Working Space in a modelling task: The influence of teaching. In Proceedings of the CERME 10; Dooley, T., Gueudet, G., Eds.; DCU Institute of Education and ERME: Dublin, Ireland, 2017; pp. 956–963. [Google Scholar]
- Sriraman, B. Conceptualizing the model-eliciting perspective of mathematical problem solving. In Proceedings of the CERME 4; Bosch, M., Ed.; FUNDEMI IQS, Universitat Ramon Llull: Sant Feliu de Guíxols, Spain, 2006; pp. 1686–1695. [Google Scholar]
- Blum, W.; Borromeo, R. Mathematical Modelling: Can It Be Taught And Learnt? J. Math. Model. Appl. 2009, 1, 45–58. [Google Scholar]
- Blum, W. Can Modelling Be Taught and Learnt? Some Answers from Empirical Research. In Trends in Teaching and Learning of Mathematical Modelling. International Perspectives on the Teaching and Learning of Mathematical Modelling; Kaiser, G., Blum, W., Borromeo Ferri, R., Stillman, G., Eds.; Springer: Dordrecht, The Netherlands, 2011; pp. 15–30. [Google Scholar]
- Kaiser, G.; Sriraman, B.; Blomhøj, M.; Garcia, F.J. Report from the working group modelling and applications—differentiating perspectives and delineating commonalities. In Proceedings of the Fifth Congress of the European Society for Research in Mathematics Education; Pitta-Pantazi, D., Philippou, G., Eds.; University of Cyprus: Nicosia, Republic of Cyprus, 2007; pp. 2035–2041. [Google Scholar]
- Kaiser, G. Mathematical Modelling and Applications in Education. In Encyclopedia of Mathematics Education; Lerman, S., Ed.; Springer Netherlands: Dordrecht, The Netherlands, 2014; pp. 396–404. ISBN 978-94-007-4978-8. [Google Scholar]
- Villa-Ochoa, J.A. Miradas y actuaciones sobre la modelación matemática en el aula de clase. In Proceedings of the VIII Conferência Nacional sobre Modelagem Matemática na Educação Matemática; Centro Universitário Franciscano: Santa María-Rio Grande do Sul, Brazil, 2013; pp. 1–8. [Google Scholar]
- Isoda, A.; Arcavi, A.; Mena, A. El estudio de Clases Japonés en Matemáticas: Su Importancia Para el Mejoramiento de los Aprendizajes en el Escenario Global; Ediciones Universitarias de Valparaiso: Valparaiso, Chile, 2012. [Google Scholar]
- Rico Romero, L. El método del Análisis Didáctico. Unión. Rev. Iberoam. Educ. Matemática 2013, 33, 11–27. [Google Scholar]
- Stake, R. Investigación con Estudio de Casos, 4th ed.; Morata: Madrid, Spain, 2007. [Google Scholar]
- Yin, R.K. Case Study Research and Applications: Design and Methods; SAGE Publications: Thousand Oaks, CA, USA, 2018. [Google Scholar]
- Niss, M.; Blum, W.; Galbraith, P.L. Introduction. In Modelling and Applications in Mathematics Education. The 14th ICMI Study; Blum, W., Galbraith, P.L., Henn, H.-W., Mogens, N., Eds.; Springer: New York, NY, USA, 2007; pp. 3–32. [Google Scholar]
- Powell, S.G.; Baker, K.R. Management Science: The Art of Modeling with Spreadsheets; Wiley: New York, NY, USA, 2013; ISBN 978-1-119-29842-7. [Google Scholar]
- Passarella, S. Mathematics teachers’ inclusion of modelling and problem posing in their mathematics lessons: An exploratory questionnaire. Eur. J. Sci. Math. Educ. 2021, 9, 43–56. [Google Scholar] [CrossRef]
- Montejo-Gámez, J.; Fernández-Ahumada, E.; Adamuz-Povedano, N. Modelización matemática en el proceso de resolución de problemas contextualizados. ¿Cómo surge un modelo? In Investigación en Educación Matemática XXII; Rodríguez-Muñiz, L.J., Muñiz-Rodríguez, L., Aguilar-González, A., Alonso, P., García García, F.J., Bruno, A., Eds.; SEIEM: Gijón, Spain, 2018; pp. 368–377. [Google Scholar]
- Shahbari, J.; Daher, W. Pre-service teachers’ mathematical models’ features. Eur. J. Sci. Math. Educ. 2016, 4, 523–533. [Google Scholar]
- Brady, C. Modelling and the representational imagination. ZDM Math. Educ. 2018, 50, 45–59. [Google Scholar] [CrossRef]
- Kertil, M.; Gurel, C. Mathematical Modeling: A Bridge to STEM Education. Int. J. Educ. Math. Sci. Technol. 2016, 4, 44–55. [Google Scholar] [CrossRef]
- Godoy, L.D.; Falcoski, R.; Incrocci, R.M.; Versuti, F.M.; Padovan-Neto, F.E. The Psychological Impact of the COVID-19 Pandemic in Remote Learning in Higher Education. Educ. Sci. 2021, 11, 473. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).