On the Potential of Augmented Reality for Mathematics Teaching with the Application cleARmaths
Abstract
:1. Introduction
1.1. Aims and Structure of the Research
1.2. Concept of Augmented Reality
2. The Potential of AR for Teaching Mathematics
2.1. Didactical Fundamentals of Augmented Reality
2.1.1. Influence of Augmented Reality on the Learning Process
2.1.2. Importance of Spatial Imagination
2.2. An Overview of Augmented Reality Applications in Teaching Mathematics
3. CleARmaths: A Simple and Robust AR Application for Teaching Vector Geometry
3.1. Concept and Functions of the Application
- Fields for displaying the object equations.
- The keyboard opens when 1 is pressed. The buttons with arrow symbols allow to activate and edit the input fields one after the other. Touching individual input fields has the same effect. An active field is highlighted in light blue.
- Selection between the object equations of plane, line and point.
- Buttons for canceling input and closing the keyboard.
- Buttons (from top to bottom) for general information, a short user manual, scaling and pausing the visualization and displaying/ hiding the intersection
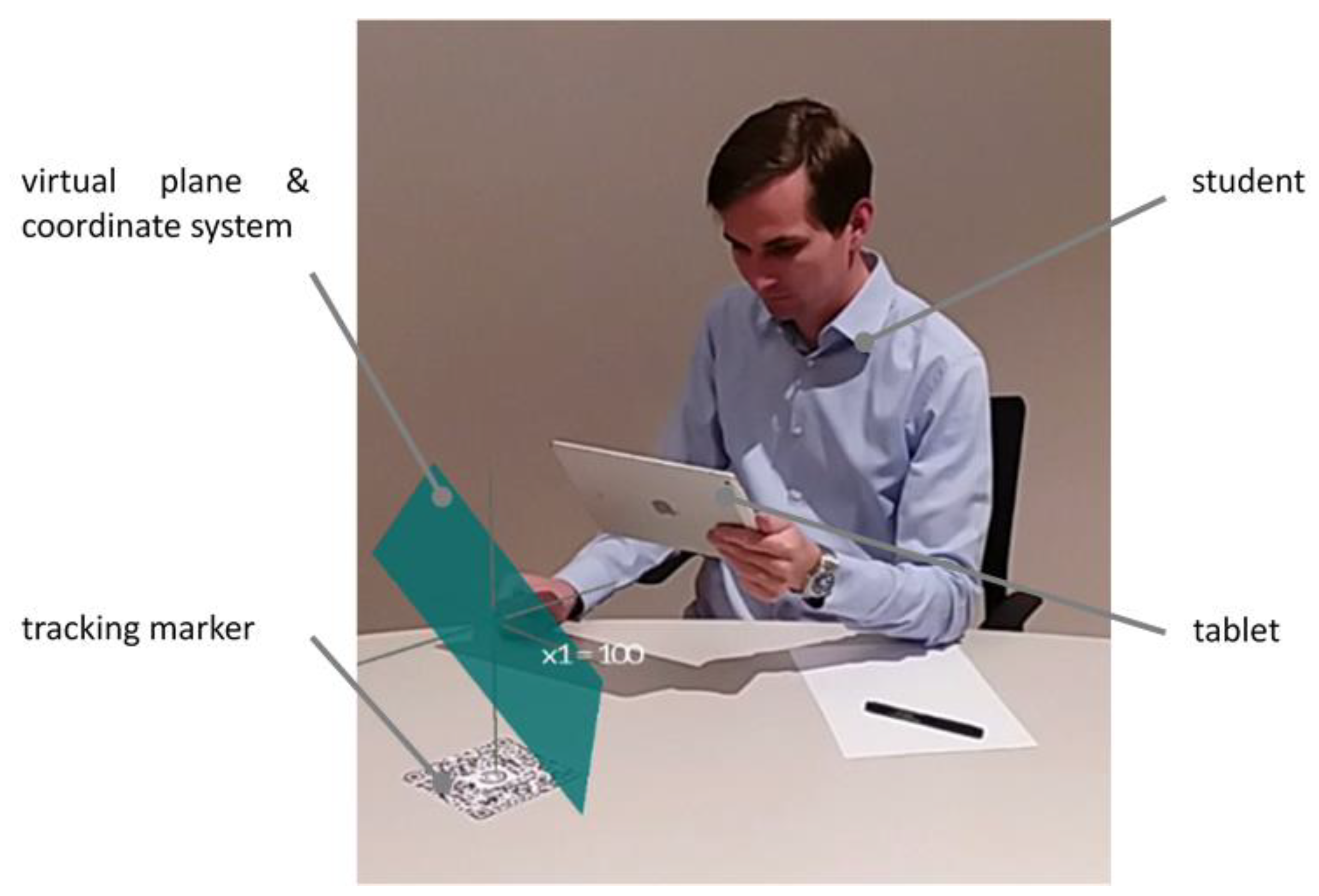
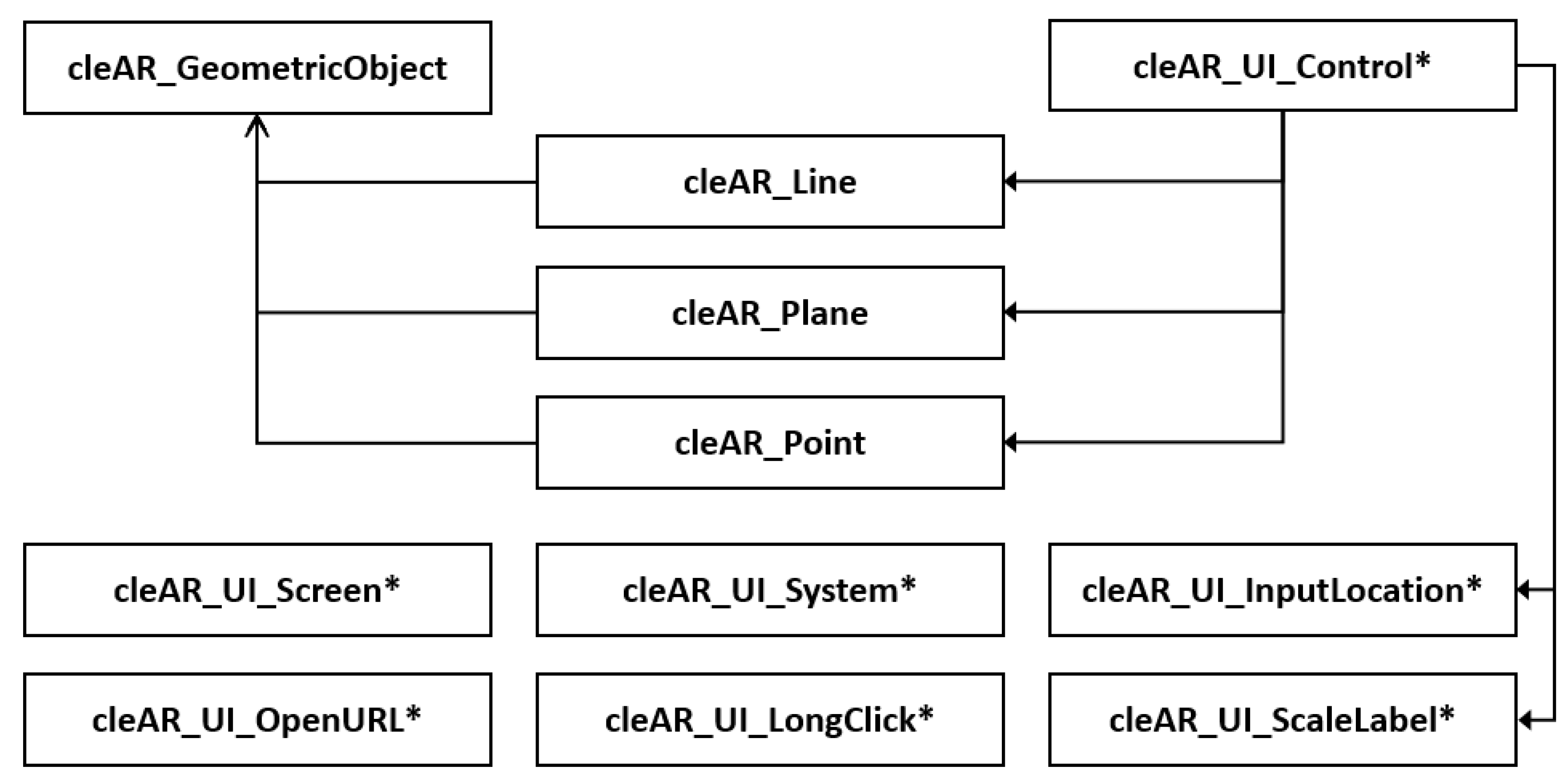
3.2. Technical Realization
3.3. Didactical Concept
4. Evaluation of the cleARmaths App in a Mathematics Class
4.1. Types of Exercises Proposed
4.2. Feedback from the Students
- Usefulness;
- Ease of use;
- Relevance of the tasks performed; and
- Need for optimization.
4.3. Feedback from the Teacher and Conclusion of the Study
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
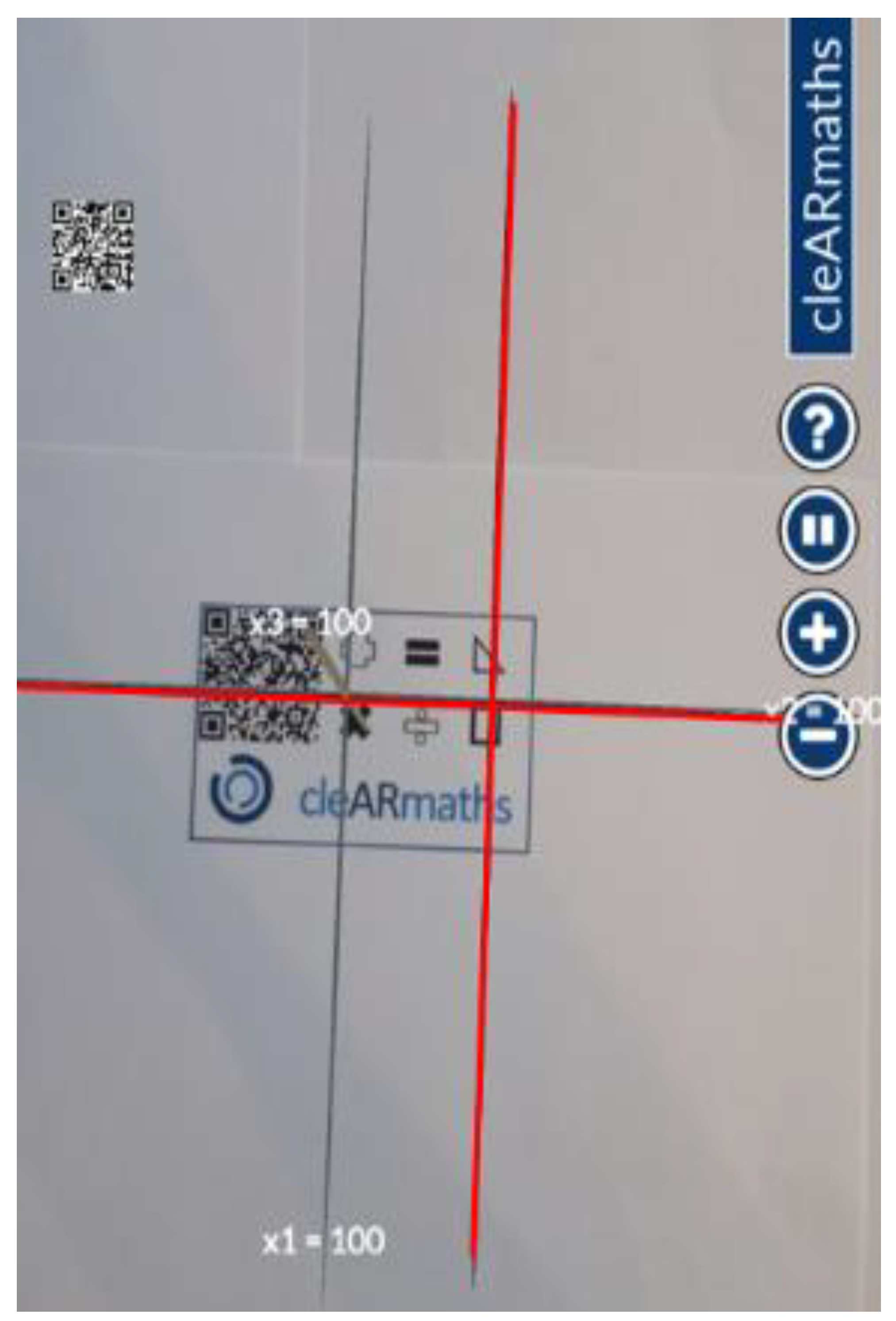
Appendix A. Designing a Teaching Unit Using QR Codes
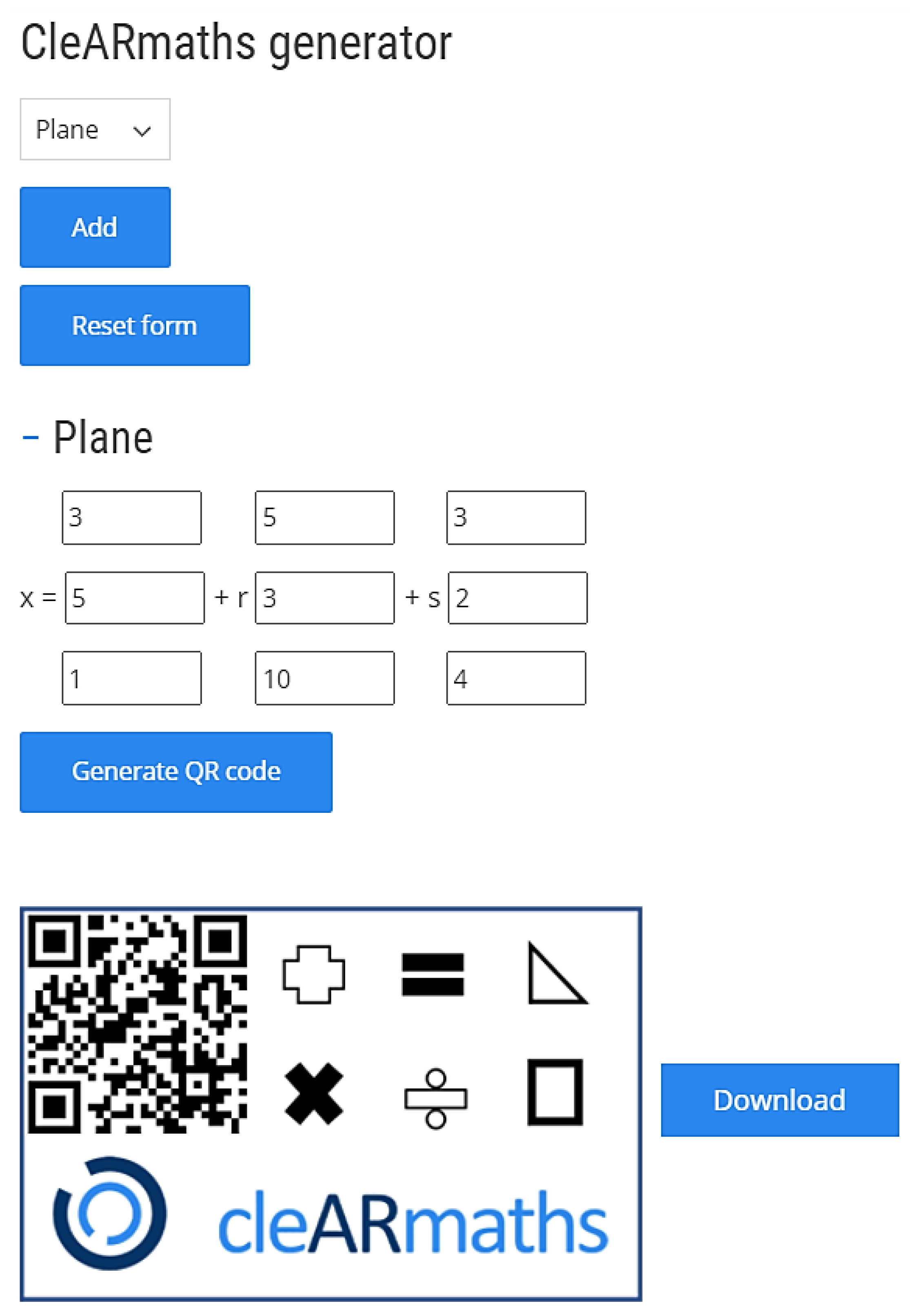

Appendix B. Exemplary Design of a Teaching Unit with Manual Input
References
- Ashcraft, M.H.; Moore, A.M. Mathematics Anxiety and the Affective Drop in Performance. J. Psychoeduc. Assess. 2009, 27, 197–205. [Google Scholar] [CrossRef] [Green Version]
- Chang, H.; Beilock, S. The math anxiety-math performance link and its relation to individual and environmental factors: A review of current behavioral and psychophysiological research. Current Opinion in Behavioral Sciences. Neurosci. Educ. 2016, 10, 33–38. [Google Scholar]
- Dowker, A.; Sarkar, A.; Looi, C.Y. Mathematics Anxiety: What Have We Learned in 60 Years? Front. Psychol. 2016, 7, 508. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ellis, J.; Fosdick, B.K.; Rasmussen, C. Women 1.5 Times More Likely to Leave STEM Pipeline after Calculus Compared to Men: Lack of Mathematical Confidence a Potential Culprit. PLoS ONE 2016, 11, 7. [Google Scholar] [CrossRef] [PubMed]
- Khan, M.; Trujano, F.; Maes, P. Mathland: Constructionist Mathematical Learning in the Real World Using Immersive Mixed Reality. In Immersive Learning Research Network. Communications in Computer and Information Science; Springer: Berlin/Heidelberg, Germany, 2018; pp. 133–147. [Google Scholar]
- Feenan, K. Social Resiliency in Digital Games. In Proceedings of the Immersive Learning Research Network 4th International Conference, iLRN 2018, Missoula, MT, USA, 24–29 June 2018; Springer: Chan, Switzerland, 2018; pp. 189–197. [Google Scholar]
- Prensky, M. Digital Natives, Digital Immigrants. On Horiz. 2001, 9, 1–6. [Google Scholar]
- Feierabend, S.; Plankenhorn, T.; Rathgeb, T. JIM-Studie 2016. Jugend, Information, (Multi-) Media; Medienpädagogischer Forschungsverbund Südwest: Stuttgart, Germany, 2016. [Google Scholar]
- Azuma, R.T. A survey of augmented reality. Presence Teleoper. Virtual Environ. 1997, 6, 355–385. [Google Scholar] [CrossRef]
- Dörner, R.; Jung, B.; Grimm, P.; Broll, W.; Göbel, M. Introduction. In Virtual und Augmented Reality (VR/AR); Springer: Berlin/Heidelberg, Germany, 2013; pp. 1–31. [Google Scholar]
- Grimm, P.; Herold, R.; Hummel, J.; Broll, W. VR-Eingabegeräte. In Virtual und Augmented Reality (VR/AR); Springer: Berlin/Heidelberg, Germany, 2013; pp. 97–125. [Google Scholar]
- Broll, W. Augmentierte Realität. In Virtual und Augmented Reality (VR/AR); Springer: Berlin/Heidelberg, Germany, 2013; pp. 241–294. [Google Scholar]
- Martin-Gutierrez, J.; Mora, C.; Añorbe, B.; González-Marrero, A. Virtual Technologies Trends in Education. Eurasia J. Math. Sci. Technol. Educ. 2017, 13, 469–486. [Google Scholar]
- Wittmann, E. Christian Grundfragen des Mathematikunterrichts, 6th ed.; Vieweg + Teubner Verlag: Wiesbaden, Germany, 1981. [Google Scholar]
- Radu, I. Augmented reality in education: A meta-review and cross-media analysis. Pers. Ubiquitous Comput. 2014, 18, 1533–1543. [Google Scholar] [CrossRef]
- Morrison, A.; Oulasvirta, A.; Peltonen, P.; Lemmela, S.; Jacucci, G.; Reitmayr, G.; Näsänen, J.; Juustila, A. Like bees around the hive: A comparative study of a mobile augmented reality map. In Proceedings of the SIGCHI Conference on Human Factors in Computing Systems, Boston, MA, USA, 4–9 April 2009; pp. 1889–1898. [Google Scholar]
- Kaufmann, H.; Dünser, A. Summary of Usability Evaluations of an Educational Augmented Reality Application. In Virtual Reality; Springer: Berlin/Heidelberg, Germany, 2007; pp. 660–669. [Google Scholar]
- Freitas, R.; Campos, P. SMART: A System of Augmented Reality for Teaching 2nd Grade Students. In Proceedings of the 22nd British HCI Group Annual Conference on People and Computers: Culture, Creativity, Interaction, Liverpool, UK; 2008; Volume 2, pp. 27–30. [Google Scholar]
- Chen, Y. A study of comparing the use of augmented reality and physical models in chemistry education. In Proceedings of the ACM International Conference on Virtual Reality Continuum and Its Applications, Hong Kong, China; 2006; pp. 369–372. [Google Scholar]
- Baumgartner, P.; Herber, E. Höhere Lernqualität durch interaktive Medien?—Eine kritische Reflexion. In Erziehung & Unterricht; Österreichischer Bundesverlag Schulbuch GmbH & Co. KG: Wien, Österreich, 2013. [Google Scholar]
- Fowler, C. Virtual reality and learning: Where is the pedagogy? Br. J. Educ. Technol. 2015, 46, 412–422. [Google Scholar] [CrossRef]
- Mikropoulos, T.A.; Natsis, A. Educational virtual environments: A ten-year review of empirical research (1999–2009). Comput. Educ. 2011, 56, 769–780. [Google Scholar] [CrossRef]
- Mohler, J.L. Using interactive multimedia technologies to improve student understanding of spatially-dependent engineering concepts. In Proceedings of the GraphiCon, Nizhny, Novgorod, 10–15 September 2001. [Google Scholar]
- Thurstone, L.L. Primary Mental Abilities; University of Chicago Press: Chicago, IL, USA, 1938. [Google Scholar]
- Dornheim, D. Prädiktion von Rechenleistung und Rechenschwäche: Der Beitrag von Zahlen-Vorwissen und Allgemein-Kognitiven Fähigkeiten; Logos Verlag Berlin GmbH: Berlin, Germany, 2008. [Google Scholar]
- Weigand, H.; Filler, A.; Hölzl, R.; Kuntze, S.; Ludwig, M.; Roth, J.; Schmidt-Thieme, B.; Wittmann, G. Didaktik der Geometrie für die Sekundarstufe I; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Henn, H.-W.; Filler, A. Analytische Geometrie. In Didaktik der Analytischen Geometrie und Linearen Algebra; Springer: Berlin/Heidelberg, Germany, 2015; pp. 149–238. [Google Scholar]
- Kaufmann, H.; Schmalstieg, D.; Wagner, M. Construct3D: A Virtual Reality Application for Mathematics and Geometry Education. Educ. Inf. Technol. 2000, 5, 263–276. [Google Scholar] [CrossRef]
- Schnabel, M.A.; Kvan, T. Spatial Understanding in Immersive Virtual Environments. Int. J. Archit. Comput. 2003, 1, 435–448. [Google Scholar] [CrossRef]
- Mantovani, F. VR Learning: Potential and Challenges for the Use of 3D Environments in Education and Training; Galimberti, C., Riva, G., Eds.; IOS Press: Amsterdam, The Netherlands, 2001; pp. 207–225. [Google Scholar]
- Shin, D.H.; Dunston, P.S.; Wang, X. View changes in augmented reality computer-aided-drawing. ACM Trans. Appl. Percept. TAP 2005, 2, 1–14. [Google Scholar] [CrossRef]
- Math-VR App. Available online: https://www.ace-learning.com/app/math-vr (accessed on 11 June 2021).
- Augmented Maths. Available online: http://www.et.iitb.ac.in/labs/am/index.html (accessed on 11 June 2021).
- Rebollo, C.; Remolar, I.; Rossano, V.; Lanzilotti, R. Multimedia augmented reality game for learning math. Multimed. Tools Appl. 2021, 1–18. [Google Scholar] [CrossRef]
- Radu, I.; McCarthy, B.; Kao, Y. Discovering educational augmented reality math applications by prototyping with elementary-school teachers. In Proceedings of the 2016 IEEE Virtual Reality (VR), Greenville, SC, USA, 19–23 March 2016; pp. 271–272. [Google Scholar]
- Auliya, R.N.; Munasiah, M. Mathematics learning instrument using augmented reality for learning 3D geometry. J. Phys. Conf. Ser. 2019, 1318, 12069. [Google Scholar] [CrossRef]
- Cai, S.; Liu, E.; Yang, Y.; Liang, J.C. Tablet-based AR technology: Impacts on students’ conceptions and approaches to learning mathematics according to their self-efficacy. Br. J. Educ. Technol. 2019, 50, 248–263. [Google Scholar] [CrossRef]
- Geogebra Augmented Reality. Available online: https://www.geogebra.org/m/agpb7bq7 (accessed on 11 June 2021).
- CleARmaths Website. Available online: https://www.clearmaths.org/en (accessed on 10 May 2021).
- Zxing. Github. Available online: https://github.com/zxing/zxing (accessed on 10 May 2021).
- Qrcode.js. Available online: https://davidshimjs.github.io/qrcodejs/ (accessed on 10 May 2021).
- WordPress. Available online: https://wordpress.org (accessed on 10 May 2021).
- Bujak, K.R.; Radu, I.; Catrambone, R.; Macintyre, B.; Zheng, R.; Golubski, G. A psychological perspective on augmented reality in the mathematics classroom. Comput. Educ. 2013, 68, 536–544. [Google Scholar] [CrossRef]



| [32] | [33] | [34] | [35] | [36] | [37] | |
|---|---|---|---|---|---|---|
| Year | X 1 | 2019 | 2021 | 2016 | 2019 | 2019 |
| Country | Singapore | India | Spain/Italy | USA | Indonesia | China |
| Cost | 20$/6 months | Free | X | X | X | X |
| Availability | Apple store | Website (apk) | Not public | Not public | Not public | Not public |
| Platform | iOS | Android | Android | X | X | X |
| Subject | 3D solids, graphs, trigonometry | 3D geometric objects | Multiplication tables | Operations, numbers, measures | 3D geometric objects | Statistics & probability |
| Age group | X | 14 years old | 8–9 years old | 6–7 years old | 14–15 years old | 13–15 years old |
| Type of AR marker | 2D image | 2D image/textbook page | Ground plane | 2D image | 2D image | 2D image |
| Development soft-ware | Unity/ARKit | Unity/Vuforia | Unity/Vuforia | X | Augment | X |
| Interaction level | Limited (view only) | Good (exercises) | Good (mini-games) | Good (exercises) | Moderate | Good |
| Feedback from study | X | X | Good enjoyment/easy to use/no stress | Teachers were enthusiastic/reveals potential and need for AR for math classes | Easy to under-stand/fun/interactive | Results dependent on student self-efficacy. Overall good results |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schutera, S.; Schnierle, M.; Wu, M.; Pertzel, T.; Seybold, J.; Bauer, P.; Teutscher, D.; Raedle, M.; Heß-Mohr, N.; Röck, S.; et al. On the Potential of Augmented Reality for Mathematics Teaching with the Application cleARmaths. Educ. Sci. 2021, 11, 368. https://doi.org/10.3390/educsci11080368
Schutera S, Schnierle M, Wu M, Pertzel T, Seybold J, Bauer P, Teutscher D, Raedle M, Heß-Mohr N, Röck S, et al. On the Potential of Augmented Reality for Mathematics Teaching with the Application cleARmaths. Education Sciences. 2021; 11(8):368. https://doi.org/10.3390/educsci11080368
Chicago/Turabian StyleSchutera, Stefanie, Marc Schnierle, Mathilde Wu, Tim Pertzel, Jonathan Seybold, Patricia Bauer, Dennis Teutscher, Matthias Raedle, Natascha Heß-Mohr, Sascha Röck, and et al. 2021. "On the Potential of Augmented Reality for Mathematics Teaching with the Application cleARmaths" Education Sciences 11, no. 8: 368. https://doi.org/10.3390/educsci11080368
APA StyleSchutera, S., Schnierle, M., Wu, M., Pertzel, T., Seybold, J., Bauer, P., Teutscher, D., Raedle, M., Heß-Mohr, N., Röck, S., & Krause, M. J. (2021). On the Potential of Augmented Reality for Mathematics Teaching with the Application cleARmaths. Education Sciences, 11(8), 368. https://doi.org/10.3390/educsci11080368







