Inferential Statistical Reasoning of Math Teachers: Experiences in Virtual Contexts Generated by the COVID-19 Pandemic

Abstract

The COVID-19 pandemic generated a new scenario in education, where technological resources mediate teaching and learning processes. This paper presents the development of a virtual teacher training experience aimed at promoting inferential reasoning in practicing and prospective mathematics teachers using inference problems on the Chi-square statistic. The objective of this article is to assess the implemented or intended institutional meanings and the degree of availability and adequacy of the material and temporal resources necessary for the development of the training experience. For this purpose, we use theoretical and methodological notions introduced by the Ontosemiotic Approach to Mathematical Knowledge and Instruction (OSA), among which are the notions of practice and suitability criteria. The participants of this experience were divided into three groups; one of them was comprised of practicing teachers and the other two of prospective teachers. The intervention used different virtual modalities that enabled the development of the participants’ inferential reasoning in a similar way.

1. Introduction

In the past few decades, we have observed a growing interest in the training of citizens in the ability to interpret and critically evaluate the results of statistical studies. Thus, statistics are incorporated into school curricula since primary education. It is also worth noting that several countries have incorporated statistical inference topics into their secondary education curricula [1,2]. However, the notions involved in statistical inference are often complex for students and teachers to understand. Several studies have identified errors and difficulties presented by both when making inferences, for example, on the understanding of the significance level, type I and type II error, the logic of hypothesis testing, the formulation of statistical hypotheses and sampling distributions, and the relationship between the statistic and the parameter [3,4,5,6]. In this sense, the incorporation of statistical inference in years before university education presents a challenge for secondary school teachers, who must now face the challenge of teaching topics such as hypothesis testing or confidence intervals. For this reason, teachers seek to take continuing education courses or workshops on statistics and statistical inference.

In response to these challenges, research has been conducted, on the one hand, on how to approach inference from an informal perspective, called informal inferential reasoning (IIR) [7,8,9,10] and, on the other hand, on the need to introduce stepwise inference; in other words, how to promote formal inferential reasoning progressively (FIR) on the basis of IIR [9,10,11,12,13,14].

In addition to this, the COVID-19 pandemic opened new scenarios where teachers and teacher educators must face one more challenge: we must teach online. According to UNESCO, as a result of the global pandemic, 82.8% of the total number of students enrolled worldwide, approximately 1.5 billion, and their teachers had to leave traditional classrooms. In order to face this challenge and continue learning during confinement, educational institutions have sought alternatives by undertaking programs such as “I learn at home”, “I learn online”, or “digital learning.” These programs have used physical booklets, television classes, and synchronous virtual classes through platforms such as Zoom, Google Meet, and Microsoft Teams and asynchronous virtual classes through platforms such as Moodle. Thus, to teach in this scenario, teachers need to have adequate digital literacy [15,16,17].

According to the National Council of Teachers of Mathematics (NCTM), technology is a primary tool for mathematical learning in the 21st century [18]. Therefore, teachers should take advantage of the potential of technology (e.g., software and applets) to stimulate students’ interest and enhance their understanding of mathematics topics. In this sense, in the current context, we must take advantage of all the technological resources available to us to generate spaces for learning and interaction.

The present study focuses on the development of a training experience aimed at promoting the inferential reasoning of practicing and prospective teachers by using problems with the Chi-square statistic. Hypothesis testing with this statistic makes an essential contribution in medicine, psychology, genetics, agronomy, aquaculture, biology, financial analysis, econometrics, industry, and marketing research. In order to make inferences based on these tests, it is necessary that students and teachers have a deep understanding of the Chi-square statistic and can connect with the notions related to this statistic. When students present difficulties in connecting statistical notions, they may focus on algorithms or procedures. This could imply that they cannot identify the type of data or choose the statistic, the distribution, or test needed to solve a real problem [19].

In this sense, this article aims to assess the extent to which the institutional meanings implemented or intended represent the reference meaning and the degree of availability and adequacy of the material and temporal resources necessary for the development of the teacher training experience aimed at promoting inferential reasoning in practicing and prospective mathematics teachers, using inference problems with the Chi-square statistic.

2. Theoretical Framework

For the development of this research, we used some theoretical-methodological notions of the Ontosemiotic Approach (OSA) to Mathematical Knowledge and Mathematical Instruction [20,21]. The OSA is an inclusive theoretical system that tries to articulate various approaches and theoretical models used in research in mathematics education [22]. OSA recognizes the dual nature of mathematics as a system of objects and practices. The notion of practice plays a fundamental role. It is understood as “any performance or manifestation (verbal, graphic, etc.) carried out by someone to solve mathematical problems, to communicate the solution obtained to others, to validate it or generalize it to other contexts and problems” [23] (p. 334).

This approach adopts a global perspective that considers various facets (epistemic, cognitive, affective, interactional, mediational, and ecological) and their relationships. Thus, it recognizes the complexity of the processes of teaching and learning mathematics. The OSA proposes five levels of didactical analysis for the facets mentioned above: practices, configurations, standards, and suitability. These levels of analysis refer, respectively, to the practices or actions of the agents involved in the teaching and learning processes, the ‘networks’ of objects and processes involved in the practices, the norms that condition and support the implementation of the practices, and the assessment of the suitability of the educational process as a whole [24].

The notion of didactical suitability and its breakdown into criteria, components, and indicators is included in the OSA as a systemic criterion for optimizing a mathematical instruction process. Godino, Batanero, and Font [25] define it as the degree to which the instructional process (or part of it) meets certain characteristics allowing it to be classified as adequate to achieve the adaptation between the students’ personal meanings (learning) and the intended or implemented institutional meanings (teaching), taking into account the circumstances and resources available (environment). Figure 1 shows the six components into which the suitability criteria are broken down (this figure is presented just for illustration).

In this study, we will focus on epistemic and mediational suitability. On the one hand, it is understood that a mathematical study process (e.g., this training experience) has greater epistemic suitability to the extent that the implemented or intended institutional meanings represent the reference meaning. This reference meaning must be relative to the educational level at which the training experience is to be implemented [26]. The components and indicators of epistemic suitability are presented in

Table 1. Components and indicators of epistemic suitability (retrieved from [26]).

Components	Indicators
Situations/Problems	A representative and articulated sample of situations is presented, including contextualization, exercising, and application situations. Problem-generating situations (problematization) are proposed.
Languages	Using different modes of mathematical expression (verbal, graphic, symbolic …) and translations and conversions between them. Use of appropriate language for the students. Situations of mathematical expression and interpretation are proposed.
Rules (Definitions, propositions, procedures)	Definitions and procedures are clear and accurate and are adapted to the educational level. Statements and fundamental procedures of the topic for the educational level given are presented. Situations where students have to generate or negotiate definitions, propositions, or procedures are proposed.
Arguments	Explanations, verifications, and demonstrations are appropriate to the educational level treated. Situations where students have to argue are promoted.
Relations	Mathematical objects (problems, definitions, propositions, etc.) are related and connected between them. The different meanings of the objects involved in the practices are identified and articulated.

.

On the other hand, mediational suitability allows us to assess the degree of availability and adequacy of the material and time resources necessary to develop the teaching and learning processes.

Table 2. Components and indicators of mediational suitability (retrieved from [26]).

Components	Indicators
Material resources (manipulatives, calculators, computers)	The use of manipulatives and technology, which give way to favorable conditions, language, procedures, and arguments, adapted to the intended content. Definitions and properties are contextualized and motivated using concrete situations, models, and visualizations.
Number of students, scheduling, and classroom conditions	The number and distribution of students enable the desired teaching to take place. The timetable of the course is appropriate (e.g., not all the classes are held late). The classroom and the distribution of the students are appropriate for the development of the intended instructional method.
Time (for group teaching/tutorials; for learning)	The intended content is accommodated to the available time (contact or non-contact hours). The devotion of time to the most important contents of the topic is appropriate. The devotion of time to topic areas that present more difficulty is appropriate.

presents the components and indicators of mediational suitability.

According to the NCTM principles, technology is essential in teaching and learning mathematics; it influences the mathematics that are taught, and enhances students’ learning [18]. This principle on technology is related to mediational suitability, especially with the first component, material resources, which is where technological resources are incorporated.

3. Methodology

This study is framed within the qualitative paradigm [27]. It seeks to analyze a teacher training experience aimed at promoting inferential reasoning in prospective and practicing mathematics teachers through inference problems with the Chi-square statistic. This analysis is performed using the OSA epistemic and mediational suitability tool described in the previous section.

Three different groups participated in this training experience. One of the groups was comprised of practicing teachers and the other two of prospective teachers. We worked with them using different virtual modalities.

Table 3. Characteristics of the participating groups.

	Group 1	Group 2	Group 3
Participating teachers	28 prospective teachers	41 high school practicing teachers	22 prospective teachers
Probability and statistics courses taken so far	First university course on the subject	Completed all the university courses on the subject. In addition, they teach at the high school level.	Completed all the university courses on the subject
Country	Mexico	Latin America (Argentina, Chile, Colombia, Guatemala, Mexico, and Peru)	Costa Rica

shows a brief summary of the characteristics of each group.

The first group was comprised of 28 prospective teachers from a Mexican university who were taking their first course in probability and statistics. Nevertheless, they have not yet taken courses on inferencing. As part of the course, these prospective teachers took a two-week workshop on statistical reasoning, which, due to the pandemic, was conducted virtually and synchronously through the Zoom platform, which acted as the primary resource for interaction. During the workshop, the prospective teachers worked in teams on activities on the Chi-square statistic. The aim of this was to prompt the discussion of their solution strategies and carry them out. After that, they shared their solutions with their peers and the trainer in charge of the workshop (the first author of this article). It is important to note that the composition of the teams was random.

The second group was made up of 41 high school teachers from different nationalities in Latin America, specifically Argentina, Chile, Colombia, Guatemala, Mexico, and Peru. These practicing teachers enrolled in a workshop on statistical reasoning organized by a Chilean university for secondary school mathematics teachers. This activity lasted one week and was conducted virtually synchronously and asynchronously because of the pandemic. During the workshop week, the teachers were encouraged to solve activities on the Chi-square statistic and discuss their solutions with their peers and the trainers who moderated the workshop (both authors of this article). The proposed activities were solved in teams, which were randomly formed. The synchronous sessions were carried out through Zoom, while the asynchronous ones were through a Moodle-type platform. Furthermore, the teachers sent written documents with the development of the activities and interacted with their peers and workshop trainers through forums.

The third group was made up of 22 prospective teachers from various universities in Costa Rica. They enrolled in a one-week virtual and asynchronous workshop on statistical reasoning, which two universities in the country organized. In this workshop, participants solved activities on the Chi-square statistic individually, due to the workshop modality, and had the opportunity to interact with their peers and the trainer (the first author of this article) through a forum and videos, using a Moodle-type platform.

For the design of the activities (problem-situations) with the Chi-square statistic, we considered the following criteria: (1) that they admit different mathematical practices to solve the activity (intuitive, pre-formal, or formal elements) as suggested by research that has focused on introducing stepwise inference and informal inferential reasoning [7,8,12,14]; (2) representativeness of the meanings of the Chi-square statistic, for which activities were designed to attend to each meaning of this statistic (goodness-of-fit, independence, and homogeneity); and (3)more general aspects were considered such as the use of accessible and interesting contexts and use of diverse representations (natural language, tables, figures).

Concerning the validation of the activities design, we resorted to validation by content. This type of validation determines whether the activities fairly and completely cover the domain or elements they are intended to cover [27].

4. Development of the Teacher Training Experience

Next, we describe the training experience aimed at promoting inferential reasoning on three groups of teachers through the use of inference problems with the Chi-square statistic. Furthermore, we analyze the resources used in the development of this training experience. It is worth noting that three problems were at the center of the training experience and that they were presented to the three groups of teachers. For reasons of space, we analyzed one problem for each group; however, we can anticipate that the practices developed by the teachers around such activities were consistent in the three groups. We resorted to the didactical suitability criteria to perform this analysis, specifically to the mediational and epistemic suitability described in the theoretical framework section.

4.1. Group 1 of Prospective Teachers

At the beginning, the trainer introduced the workshop by initiating a dialogue with the prospective teachers about their conceptions of statistics and its usefulness and presence in their work and daily life. Subsequently, in the same instance, the trainer asked them about the notions they consider essential in probability and statistics. The prospective teachers mentioned that they considered important the sample, population, sampling, distributions, statistics such as mean and standard deviation, and parameters. Then, the trainer introduced Heitele’s fundamental ideas [28] and discussed the relationship between a sample and a population and the role of statistical inference in this relationship. In addition, he introduced the definitions of statistical inference of Moore [29] and Rossman [30].

According to Moore [29], statistical inference moves beyond the data in hand and draws conclusions about some wider universe, taking into account that variation is pervasive and the conclusions are uncertain. For Roosman [30], inferences are more than a conclusion—they must also include the evidence and reasoning on which they are made.

Based on the above definitions, a dialogue was opened on what statistical reasoning is. Once the participants had given their points of view and consensus was gathered, the trainer referred to Ben-Zvi and Garfield’s definition [31] and emphasized the importance of reasoning in making inferences.

In a second stage of the workshop, the trainer commented that teams would be formed randomly and that these would solve some activities. Each of the six teams (four five-member teams and two four-member teams) would have a virtual room (via Zoom’s small group tool) and would have 15 min to complete the activity. Once they were in their rooms, they were asked to discuss the strategies by which they could solve the problem. They could use paper and pencil, calculator, software, or whatever means they felt more comfortable with to solve the problem. Once they solved the activity, they would return to the general room to share with the group their solutions and the strategies they followed.

Then, they were presented with activity 1 (Figure 2). They all read it together, and when the trainer asked if there were any doubts, the questions asked by the prospective teachers were focused on what to use to solve it, if they had to use the mean, make graphs, or use probability. It was mentioned to them that there was no single way to solve the activity, that they could use whatever they considered appropriate, and that this was precisely what they had to discuss with their team.

Once the teams finished the activity, they returned to the general Zoom room, presented their practices, and commented on why they had decided to solve the activity following this strategy. To summarize, the six teams used technological tools to solve the activity: five teams used Microsoft Excel and one team used Minitab statistical software. Their mathematical practices were quite similar. They created line graphs, bar graphs, and dot plots. The prospective teachers commented that they used graphs because they helped them better visualize the frequency distributions’ shape. In addition, they noted that the observed frequencies appeared to have greater dispersion than the expected frequencies. In Figure 3, we present the solution strategy of team 1.

To finish with activity 1, the trainer and prospective teachers established a new solution strategy for activity 1, which involved graphs as developed by the various teams and statistical measures such as quartiles. This is because an intuitive meaning of the Chi-square statistic was taken into account; we refer to Galton’s graphical method [32].

For activities 2 and 3, which were carried out in the third and fourth stages of the workshop, respectively, the same dynamics were followed as for activity 1. The dynamics consist of (1) presenting the activity to the general group and clarifying doubts and (2) the teams going to the small rooms’ section of Zoom, and (3) once everyone returns to the general room, they present the practices they developed to solve the activity, explain their reasoning, and answer questions from the trainer and their peers; then, (4) the prospective teachers and the trainer generate an alternative solution to the activity, to show new solution strategies that involve the use of key notions of inferential reasoning.

As could be observed, activity 1 is in the context of arrow shooting in an amateur archery tournament and corresponds to the meaning of goodness-of-fit [32]. The activity uses a language appropriate for the educational level of the participants. On the one hand, natural language and tabular and iconic representations are used to present the activity and the data. On the other hand, in their mathematical practice, the prospective teachers in Group 1 used graphic representations and natural and symbolic languages. To support their conclusions, conjured in the context of the problem, the teachers resorted mainly to the “bell-like” shape of the graphs and the apparent greater dispersion of the observed data. In the mathematical practices developed on this activity, it was observed that mathematical objects are related to each other, for example, definitions such as observed and expected frequency, frequency distribution, dispersion, and the normal distribution proposition.

During the workshop, it was observed that the prospective teachers had some difficulties when solving the activities. For example, they had complications when calculating statistical measures (e.g., mean and standard deviation) because they confused the variable’s possible values with the sample size. These difficulties were addressed in two moments. The first moment was when interacting with the prospective teachers as they presented their solutions. The second moment was when the trainer and the participating teachers generated an alternative solution to the activity.

The material resource we used to interact with the prospective teachers and introduce this training activity was the Zoom platform. From this, we can highlight the “general” room where the initial dialogue, the reading of the activities, and the prospective teachers’ presentations on the mathematical practices that they developed to solve such activities took place. In such presentations, prospective teachers had the opportunity to interact with the members of their groups, the trainer, and their peers. In this same platform, we also emphasize the use of small groups. This option allowed us to have an adequate number of participating teachers per team to solve the activities. On the other hand, the resources used by the prospective teachers and the trainer to solve and present the activities were Excel, Word, and Minitab. These resources helped them to generate calculations of statistical measures, different representations such as bar and line graphs; from the visualization, mainly, the prospective teachers were able to establish conjectures or conclude in the context of the activities.

As mentioned in the methodology section, this group consisted of 28 prospective teachers, which was a manageable number of participants for most stages of the workshop. However, it was necessary to work with teams of 5 and 4 members when discussing solution strategies and to solve the activity. The workshop was held at the last period of the prospective teachers’ class schedule, at 8:00 p.m., and each session lasted one hour.

4.2. Group 2 of Practicing Teachers

The modality of the statistical reasoning workshop for practicing teachers was both synchronous and asynchronous. Before the first session, a video was uploaded to the Moodle platform where the workshop trainers introduced themselves and briefly introduced the workshop. In the video, they assigned the first activity, which consisted of commenting on the forum (activated on the same platform) about how statistical reasoning can be promoted in the classroom, based on their teaching experience. Through this forum, teachers interacted with their peers and the workshop trainers.

In the first session of the workshop (synchronous), as with the prospective teachers in Group 1, we initiated a dialogue with the practicing teachers on the importance of statistics in everyday life, the notions they consider important in probability and statistics, and in general on the fundamental ideas of Heitele [28]. In addition, we asked the teachers what statistical inference is and what are the notions they identify in inference. Their answers highlighted notions such as sampling, sample and population, hypotheses, and confidence intervals. We also discussed the applications of statistical inference and at what educational level notions of inference are declared in the curriculum, highlighting that in several countries, as is the case of Chile, inference topics are found in the 11th and 12th years of school [33]. In addition, teachers were encouraged to take up some comments on how to promote statistical reasoning in the forum.

Subsequently, the activities were presented, including activity two, which can be seen in Figure 4.

The procedure was very similar to that of the previous group. First, the general indications were given, and the activity was presented in the general room. Then, teams were randomly formed (four of eight members and one of nine members). Activity 2 was presented, and the teams were asked if they had any doubts. This activity was also on the Moodle platform so that the teams could access it in the group rooms. The teachers had 15 min to solve the activity, after which time they returned to the general Zoom room to present and explain their solutions. During the presentations, their peers and the trainers interacted with the participants.

The practicing teachers created pie charts and tree diagrams and used conditional probability, with the help of Microsoft Excel, to answer the activity question. In Figure 5, we present the mathematical practice developed by the practicing teachers of team 5.

To finish with activity 2, the practicing teachers and trainers developed a new solution strategy for the activity. That strategy revolved around the association coefficient Q developed by Yule [34] because an intuitive meaning of the Chi-squared statistic was considered when used for a test of independence [32]. In addition, teachers were asked to continue the discussion of their solution strategies in the activity forum.

At the end of the three activities, we proceeded to present and comment on mathematical practices developed to solve these activities with different formality levels and identify among all the features of inferential reasoning observed in their practices and in the practices presented by the trainers (Figure 6). Based on the features identified, we proposed to “construct”, in a consensual manner, levels of inferential reasoning with different levels of formality. Figure 6 shows this construction of levels and its guidelines.

For the construction of such levels, teachers were asked which traits could be placed on the first, second, third, and fourth level. Then, the teachers used the chat and raised their hands to indicate these traits. Below is an excerpt of the teachers’ participation during the construction of the levels:

Teacher 1:

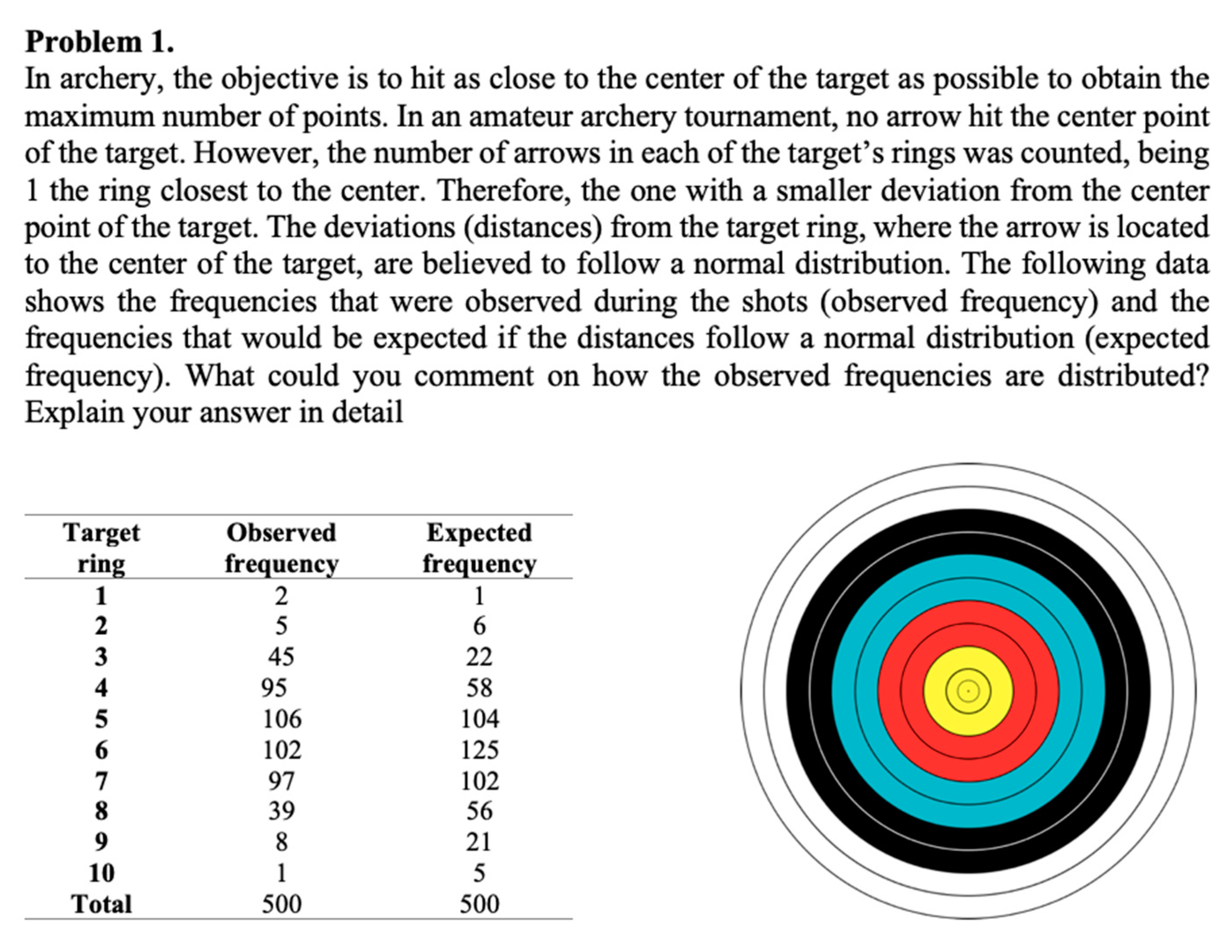
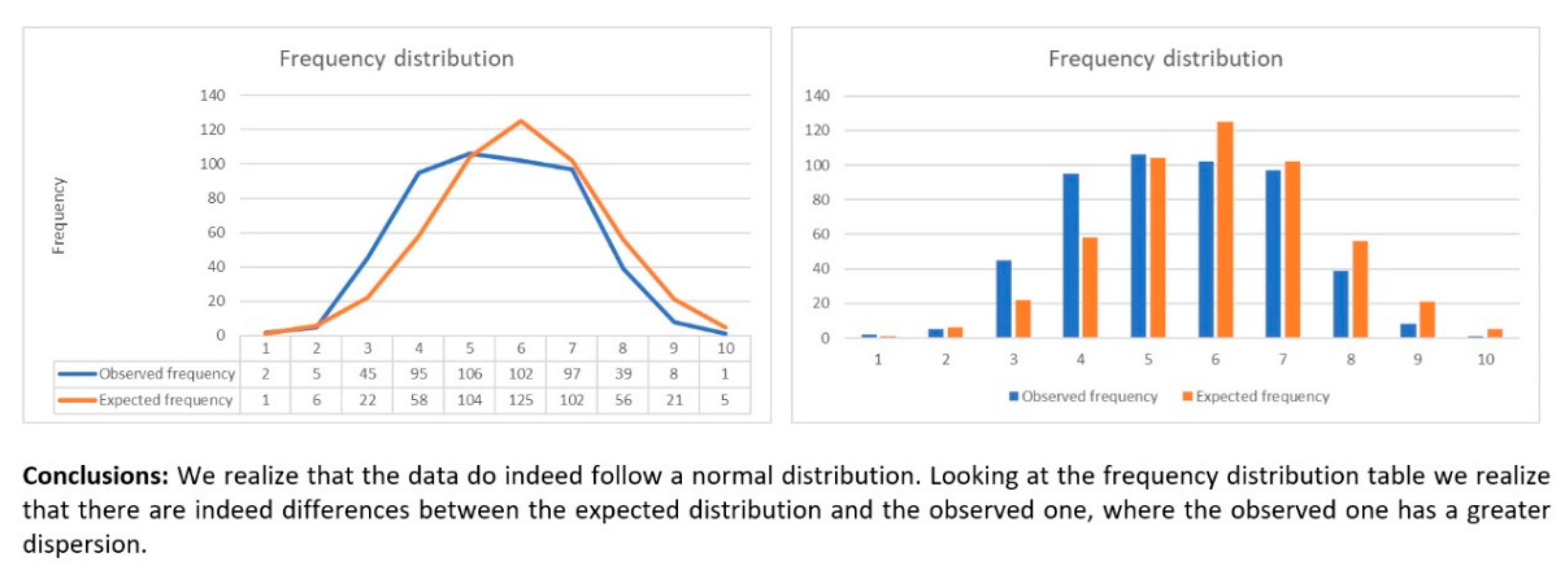
In our team, we used the graphs, their shape, and how the data looked like to answer the problem.

Teacher educator 1:

So, you used visualization to make your conjectures, and this can be done only with graphs? What did the other teams do?

Teacher 2:

We first analyzed the composition of the data in the table and then resorted to making graphs.

Teacher educator 1:

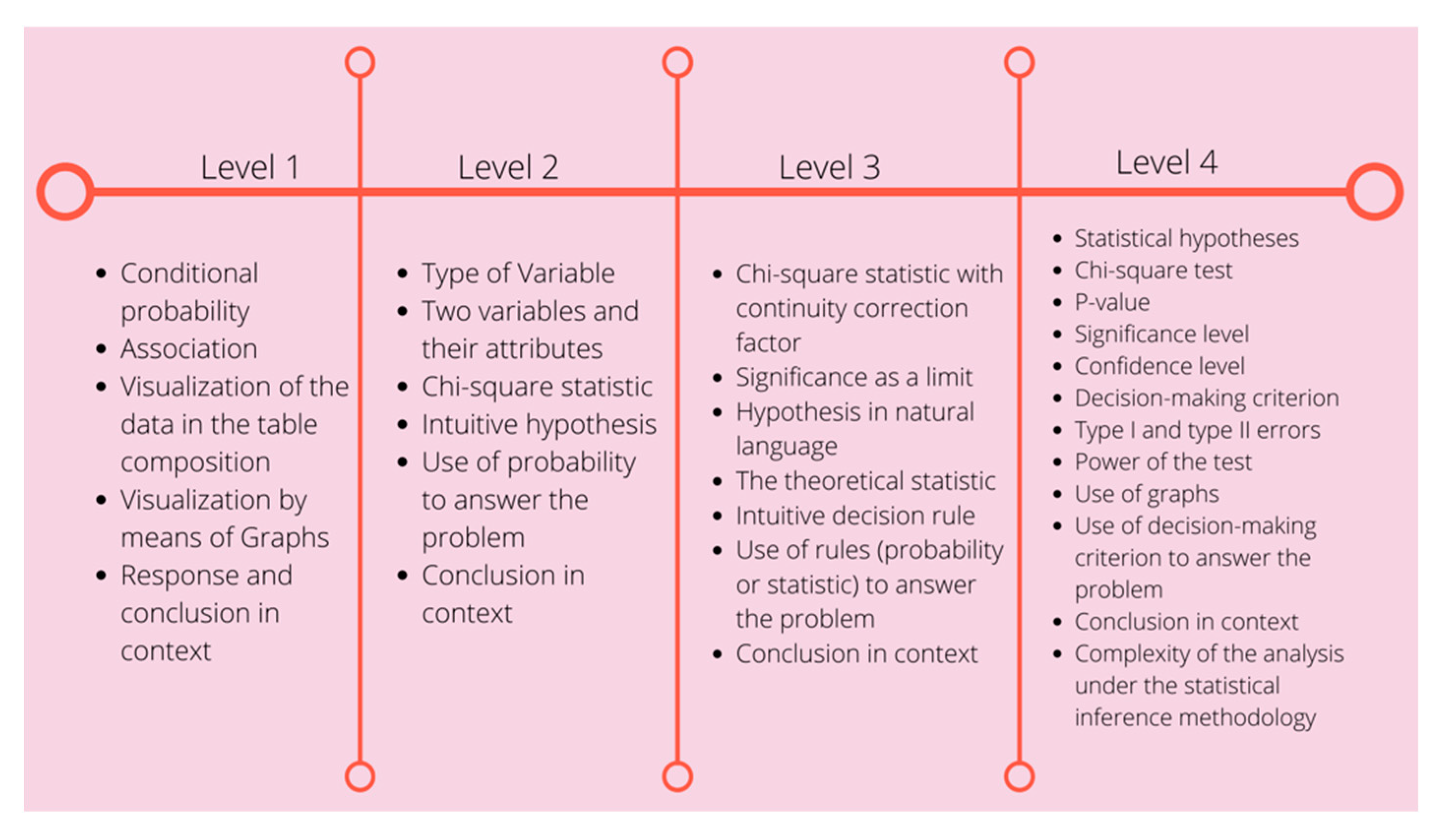
We could say that an important part of the conclusions or conjectures made by the different teams is the visualization, so let’s include the visualization of the data in the composition of the table and the visualization through the graphs.

Teacher educator 2:

What other aspect could we include at this level?

Teacher 3:

For the problem number two, we used conditional probability.

Teacher educator 1:

Should we include it in Level 1 too or in Level 2?

Teacher 5:

I think in Level 1, too.

Teacher 6:

Me too.

Teacher educator 1:

Okay [includes conditional probability in Level 1].

Teacher educator 2:

In the chat, teacher 4 says that it is important that the answer is given in terms of the problem.

Teacher educator 2:

Teacher 7, in the chat, tells us that answering in terms of the problem should be included in all levels, which is a central aspect for statistical reasoning.

Teacher educator 1:

Okay, we include the conclusions in the context of the problem.

Teacher 8:

In our team, we looked at the data, which is already at level one, we identified the type of variable and we also needed to define zero, what does zero mean for this variable.

Teacher educator 1:

Another important feature of the reasoning, then, is the identification of the type of variable. What about significance? I think team two mentioned it when presenting their strategies.

Teacher 9:

We used significance but in the sense of being far from the mean.

Teacher 10:

We also used it in the same sense.

Teacher educator 1:

Ok, we could include significance as a limit in Level 3, because of the complexity that this notion implies.

Teacher 11:

I think all the teams mentioned what we wanted to test, such as the non-increase in sleeping hours, now that we have seen other practices maybe this would be a kind of hypothesis.

Teacher educator 1:

We could include it as an intuitive hypothesis in Level 2, and in some solutions that we presented we saw the null and alternative hypothesis in natural language, that we could include it in Level 3.

Teacher 8:

In Level 4, we could include both hypotheses posed with statistical terms.

Teacher educator 2:

That’s right, so…

Figure 6 shows the elements that make up the teachers’ types of practices, which the teachers and trainer presented to solve the activity. The practices associated with Level 1 are characterized by the use of graphical representations (e.g., double bars, lines, and pie), some statistical measures (e.g., quartiles, mean and standard deviation), and the use of conditional probability; teachers based their conjectures on the visualization of graphical features and statistical measures, thus showing informal inferential reasoning. This way of conjecturing and arguing whether the data in a sample follow a normal distribution through the elements present in the graphs is similar to how the first part of task 1 is approached to promote the IIR of Zieffler et al. [7], where students are asked to speculate about the graphical characteristics of the unknown population based solely on the graph of a sample.

On the other hand, the guidelines for Level 2 report on practices that emphasized the use of the Chi-square statistic, the formulation of an intuitive hypothesis, and the recognition of the variable(s). The formulation of an intuitive hypothesis can be considered as a first approximation to statistical hypotheses. In this sense, the statistical enquiry cycle PPDAC has as its first component the generation of a research question, which must be given in a particular context that is to be investigated. Some investigations [35,36,37] have taken up this first component, recognizing that most of these questions have the form of conjecture or hypothesis.

In the Level 3 guidelines, we highlight natural language hypotheses, significance as a limit, and the use of an intuitive decision rule. Significance as a significant limit can be seen as an intuitive version of the significance level. It is also important to highlight that significance is a key concept in statistical inference, and in the mathematical practices that gave rise to this guideline, it is used only as a limit [38] that enables it to have a critical point for decision-making.

In the guidelines for Levels 2 and 3, we can find the three key principles (generalization, use of data as evidence, and the use of probabilistic language) that Makar and Rubin [8] indicate as essential for informal statistical inference.

Regarding Level 4 guidelines, we find the hypothesis statement, the Chi-square statistic and distribution, the critical value rule for decision-making, and the significance level. These indicators correspond to formal inferential reasoning and are essential for the student to make decisions based on the statistical techniques of the hypothesis testing methodology. However, at this point, we want to focus on the validity of the procedures and the inferences made (e.g., power of the test and type I and type II errors). In this regard, some investigations have raised the importance of a deep understanding of probability in hypothesis testing, especially emphasizing that students do not confuse conditional probabilities involved in type I and type II errors, p-value, and significance level, with single event probabilities [3,39,40]. In addition, Hoekstra [41] and Riemer and Seebach [42] motivate students to go beyond inference through hypothesis testing by performing validation of their inferences.

A constant in the guidelines of the four levels was the conclusion in the context of the activity. In this sense, we recognize that the interpretation, together with the arguments, evidence the understanding and connections that the students make of statistical notions [43,44]. In addition, we highlight that various studies have indicated the importance of working with problem situations in contexts that are close or accessible to students [43,45,46,47,48,49].

It is important to clarify that the activity that led to the construction of levels and their guidelines for developing inferential reasoning was carried out with the three groups of teachers. However, we exemplified it with Group 2 because the guidelines provided by this group included the guidelines provided by the other two groups.

To close the workshop, the trainers offered a final reflection where they emphasized the importance of promoting inferential reasoning in students and that the development of this type of reasoning can be initiated in primary education, under the perspective of informal inferential reasoning, and progressively continue to promote it until formal inferential reasoning is developed.

Activity 2 is in the context of a smallpox epidemic and corresponds to the meaning of independence [32] since it is of interest to establish whether there is any relationship between the presence of vaccine scarring and smallpox recoveries. The activity is presented to the teachers with natural language and tabular representation, while in the mathematical practices developed by the teachers, we observed the use of natural language to conclude in the context of the problem, graphical representations, and symbolic language (e.g., percentages and probability); natural language was also used to communicate their practices. The teachers supported their conclusions by making use of conditional probability, percentages, and visualization of graphs. In addition, in the mathematical practices, we observed that they related mathematical objects such as definitions, sample, association, variable, conditional probability, and conditional distribution.

The practicing teachers presented difficulties in posing the hypotheses (null and alternative). Hypotheses are fundamental in hypothesis testing and have been reported as one of the main difficulties presented by students and teachers in statistical inference [3,19,50,51].

The material resources used for the development of this workshop were the Zoom platform for synchronous interaction and a Moodle-type platform for asynchronous interaction. As previously mentioned, for asynchronous interaction, we resorted to videos and forums. The first forum was used for statistical reasoning, while the second to discuss the different solution strategies followed by the teachers when solving the activities. Spaces were also provided for the teams to upload to the platform the mathematical practices they developed to solve the activities. Regarding the resources used by the teachers to solve the activities, the use of Microsoft Excel and Word stood out. These resources helped the teachers create graphs, diagrams, probability calculations, and presentations. The teams that opted for charting based their guesses on the visualization and percentages of patients who died and had the scar and those who survived and did not have the scar. On the other hand, those who chose to calculate probabilities using tree diagrams or directly under the expression of Bayes’ theorem formula used these probabilities to support their conclusion in the context of the activity.

We mentioned earlier that we had to form teams to carry out the activities. However, these teams are larger than the ones created in Group 1 of teachers. This was because Group 2 was larger, and we had less time for synchronous interaction than with Group 1. The timetable for synchronous interactions was from 16:30 to 18:00 h, while asynchronous work was free.

We consider that using synchronous and asynchronous modalities for the workshop allowed us to dedicate sufficient time to promote inferential statistical reasoning in the teachers, remarkably close to what was achieved with the teachers in Group 1.

4.3. Group 3 of Prospective Teachers

With the prospective teachers in Group 3, the workshop modality was totally asynchronous. In this workshop, the trainer produced several videos and uploaded them to the Moodle platform provided by the event organizers. In the first video, the trainer dealt with topics such as the current importance of statistics in work and daily life, the incorporation of probability and statistics in the curricula of primary, secondary, and university education, and the fundamental notions of Heitele [28]—some answers had been obtained in other workshops on what statistics is—and then provided the definitions of Cabria [52] and Moore [29] in which the importance of statistical reasoning was emphasized. Additionally, the trainer commented that according to Bakker and Derry [45], one of the main challenges facing the teaching of statistics is that notions are treated in isolation. In other words, they are taught detached from each other as from the context from which the data arises. Moreover, in this regard, Makar and Ben-Zvi [47] indicated that this type of teaching contrasts with the holistic approach required to learn to reason statistically. The trainer also showed what some research on statistical reasoning indicates [31]; from this, participating teachers were asked to address the forum and comment their thoughts on how they felt statistical reasoning could be promoted in the classroom. As a result, teachers pointed out that statistical reasoning could be promoted by using problems in contexts close to the students and favoring the use of software or applets that provide dynamic representations of the notions involved (e.g., distributions).

Once the prospective teachers participated in the forum and interacted with each other and the trainer, they accessed the second video. The second video began with an introduction to statistical inference and some key aspects, such as sample-population and statistic-parameter relationships, sampling, and hypotheses. Moore’s [29] and Rossman’s [30] definitions of statistical inference were also introduced, emphasizing the importance of reasoning in inferences. Finally, three activities were presented, and the teachers were asked to solve them individually. Figure 7 shows activity 3 as an example.

Once the prospective teachers submitted their resolutions, either through the platform or via e-mail, they entered the activities forum, where they commented on their strategies for solving the activities. This space allowed the participating teachers to interact with the trainer and their peers since, in addition to presenting their strategies, they raised the doubts and difficulties they had had in solving the activities. Figure 8 shows a type of practice characteristic of this activity among prospective teachers in Group 3.

In Figure 8, we can see that the prospective teacher performed a homogeneity test with the Chi-square statistic, and to support his conclusion, he based his decision on the criterion of the critical value, as the critical value is less than the value of the calculated statistic, then the null hypothesis is not rejected.

In general, the prospective teachers developed double bar and double line graphs, obtained percentages and the conditional distribution by rows, and used the homogeneity test with the Chi-square statistic to infer whether homogeneity exists between groups. Some difficulties identified were misunderstanding the p-value decision criterion because when they compare the significance level with the p-value, they decide to reject the null hypothesis when the criterion indicates that if the p-value is greater than the significance level, the null hypothesis is not rejected. However, the calculation and interpretation of the p-value are major difficulties in inferencing that have been reported in several investigations [51,53,54].

In addition, some prospective teachers identified that the activity could be solved by means of a test with the Chi-square statistic, obtained the expected frequencies, and calculated the statistic; however, they were unable to continue with the test because they indicated that they did not know what else to do, so they resorted to the differences between the observed and expected frequencies, and to making graphs to visualize whether there could be homogeneity between the groups. Additionally, we highlight that the prospective teachers did not use the Chi-square statistic with continuity correction as suggested when having small expected frequencies. We have observed this difficulty in research proposing activities to work Chi-square tests with students [55,56,57]. It is very common not to use the continuity correction factor when working with software because some of them (e.g., Minitab) do not have the option to use this factor. Therefore, teachers must understand when and why this factor is used and what is behind the processes or procedures performed by some software in data analysis.

The trainer showed and explained various solution strategies for the activities in a third video, with varying degrees of formality. These solution strategies were useful to identify inferential reasoning features and build inferential reasoning levels with different levels of formality (Figure 6). Based on the guidelines for developing inferential reasoning from this construct, the workshop trainer conducted a reflection on the importance of progressively promoting inferential reasoning, linking to research in statistics education [11,12,14].

Activity 3 is in the context of lung cancer disease and corresponds to the meaning of homogeneity [32] because we are interested in knowing whether there is homogeneity between two groups (men and women) who have lung cancer with respect to race. The activity uses a language appropriate for the educational level of the participants; on the one hand, natural language and tabular representation are used to present the activity and the data; furthermore, in their mathematical practice, the prospective teachers of this group used graphic representations and natural and symbolic languages. To support their conclusions, the teachers relied mainly on the differences in percentages (probability) between the groups by race category, the differences they observed in both the graphs and the conditional probabilities, and the critical value criterion for decision-making. In the mathematical practices developed on this activity, we also observed that mathematical objects are related to each other, for example, the definitions sample, variables, categories, observed frequencies, expected frequencies and hypotheses, and the propositions conditional probability and the Chi-square statistic.

As a first resource to carry out the workshop asynchronously, we had to use a Moodle-type platform and create videos and forums to teach the workshop and interact with the participants. To solve the activities and present their mathematical practices, the teachers used material resources such as calculators, the freely available statistical software R, online probability calculators, Chi-square probability distribution tables, drawing tablets, Microsoft Excel, Word, and documents in PDF format. In this group, the presentation of the practices was only in written form, which was more restrictive than in the two previous groups. Teacher groups 1 and 2 had the opportunity to show the development of their practice with visual support and explain orally, referring to each part of the practice. This last aspect was not possible with the resources used by the participants of Group 3 (e.g., Word and PDF) since they usually chose to explain the practice in a single moment.

When the trainer presented several practices to solve the activities, he used technological resources such as Microsoft Excel and the statistical software Minitab and G*Power. These resources supported the calculation of the Chi-square statistic, the critical value, and the p-value. The trainer also used graphs to visualize the probability of committing the type I and type II errors, the probability associated with the test statistic, and the critical value.

With a small number of participants, it was possible to meet the needs of interaction through forums and e-mail, which was indispensable for conducting a workshop asynchronously. Overall, through the responses to the activities and the interactions that were had with the participating teachers in Group 3, we felt that the time devoted to this workshop was adequate. Nevertheless, some participants expressed the need for more time to carry out the activities requested during the workshop.

5. Final Reflections

In this study, we set out to assess whether the institutional meanings, implemented or intended, represent the meaning of reference, the degree of availability, and adequacy of the material and time resources necessary for the development of the training experience to promote inferential reasoning in practicing and prospective mathematics teachers, by means of inference problems using the Chi-square statistic.

Regarding the meanings implemented with activities 1, 2, and 3, the goodness of fit, independence, and homogeneity, we could say that they correspond to the three main reference meanings of the Chi-squared statistic [32]. The activities of the training experience are in contexts close to the prospective teachers and practicing teachers. In addition, we observed that the teachers participating in this study use different languages (e.g., natural language, symbolic, graphical, and tabular representations). They also use in their practices definitions, propositions, and procedures in different degrees of formality, such as the definitions sample, observed frequency, expected frequency, frequency distribution, dispersion, association, variable(s), categories, and hypothesis; and the propositions’ normal distribution, conditional probability, conditional distribution, and the Chi-square statistic.

However, we also identified some errors and difficulties presented by the prospective and practicing teachers, such as with the calculation of statistical measures (e.g., mean and standard deviation), mainly in activity 1. In particular, the prospective teachers in Group 1 confused the possible values taken by the variable with the sample size; the practicing teachers in Group 2 presented difficulties formulating the hypotheses (null and alternative); furthermore, prospective teachers in Group 3 presented complications in understanding the decision criterion of the p-value. We also observed that in the practices developed by the teachers of the three groups, the Chi-square statistic with continuity correction factor was not used when appropriate. This difficulty can be frequently generated when using technological resources since some software tools do not have the option of using this factor. In this sense, teachers or teacher educators should pay particular attention and encourage students to understand when and why the Chi-square statistic with correction factor is used, especially in virtual contexts where this type of resource is frequently used.

The workshop activities included constructing levels with guidelines for developing inferential reasoning with the three groups of teachers (see Figure 6). This construction, which underlies the practices developed by the teachers and the trainer, is not developed in-depth. However, Pfannkuch, Arnold, and Wild [12] propose stages to promote formal inferential reasoning from informal reasoning. They indicate some fundamental concepts for informal inference (e.g., “making a call”, sample-population ideas, sampling variability) and formal inference (e.g., resampling method and randomization method), which can be worked on at various times in the school curriculum. This construction of levels with guidelines for developing inferential reasoning can constitute a starting point for further exploration and systematic research on guidelines for progressively promoting formal inferential reasoning. For future research on the construction of progressive levels of inferential reasoning, we consider important the epistemological nature of the mathematical objects (e.g., the Chi-square statistic) and the contributions of the scientific literature on informal and formal inferential reasoning and on the progression from IIR to FIR [58]. Furthermore, considering that the focus of this study was to analyze epistemic and mediational suitability, future research could analyze interactional, affective, cognitive, and ecological suitability. Likewise, we think it is important to carry out workshops that include activities with other statistics, and analyze the meanings promoted with certain activities/problems.

Regarding the media resources, we used the Zoom platform for connection and interaction with prospective teachers from Group 1, whose workshop was carried out in a synchronous modality. Regarding practicing teachers from Group 2, we used the Zoom platform for the synchronous modality and a Moodle-type platform for the asynchronous modality. Concerning prospective teachers from Group 3, we used a Moodle-type platform for their workshop which was developed in a synchronous modality. Furthermore, the three groups used different learning resources to solve the activities or to communicate their solutions. For example, in Group 1, they used Excel, Word, and Minitab as technological resources. They also formed smaller teams to solve the activities. Group 2, on the other hand, used resources such as videos, Excel, Word, Minitab, and G*Power. This group was also divided into teams to solve the activities. Group 3 of prospective teachers solved the activities individually. They used videos, calculators, statistical software R, Minitab, G*Power, online probability calculators, Chi-square probability distribution tables, drawing tablets, Microsoft Word, Excel, and PDF format.

As a result, it was possible to identify that, in the background, when developing experiences such as those we present in virtual mode, two types of resources and media must be adequately regulated: in the first type are those that allow establishing the connection and virtual interaction with teachers (e.g., Zoom, Google Meet, Microsoft Teams, Moodle, etc.); and in the second type are those that allow promoting learning (e.g., Minitab, R, Microsoft Excel, G*Power, etc.). The above is in accordance with the classification made by Peña, Pino-Fan, and Assis [59] on mediational norms when teaching and learning processes are developed in virtual environments. In this sense, in virtual contexts such as those promoted by COVID-19, the resources and means of an instructional process can be classified into primary and secondary, and the latter are conditioned by the resources and means for virtual connection and interaction. In other words, the resources and means for learning (secondary or second type) must be compatible with those for virtual connection and interaction (first or primary type) in order to be functional.

In general, we can say that the three groups had similar opportunities to explore solutions to the proposed activities, reflect on the practices developed to solve the activities, support their solutions, clarify doubts with the trainer and, in short, develop key elements of their inferential reasoning. As we mentioned, the modality used in each group responded to the resources that the participants had at their disposal; this gives us evidence that in the confining times we are living in, it is essential for teachers and teacher educators to be flexible with the type of resources used for teaching and to understand the changing nature of teaching and learning in a virtual education environment, but we must also consider the inherent restrictions of the resources used and understand the meaning behind the processes of each command and the results that, for example, a certain software gives us.