MAD+. Introducing Misconceptions in the Temporal Analysis of the Mathematical Modelling Process of a Fermi Problem
Abstract
:1. Introduction and Theoretical Framework
1.1. Estimation, Mathematical Modelling and Fermi Problems
1.2. Difficulties, Mistakes and Obstacles When Solving a Modelling Task
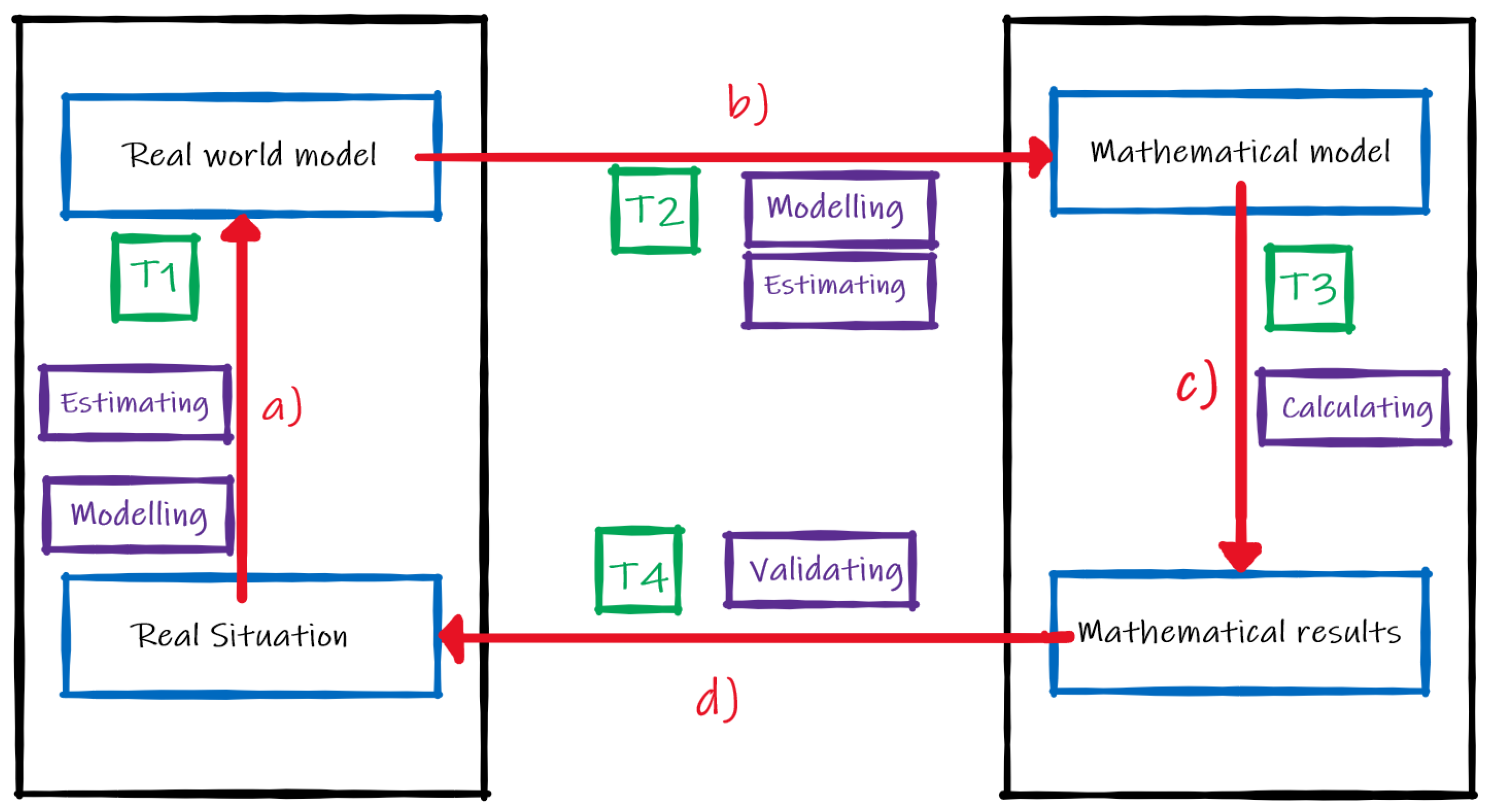
1.3. Temporal Analysis of the Resolution Process
- -
- Can the classification made by Moreno, Marín and Ramírez-Uclés [39] be adapted to the problem proposed in our research? Additionally, if this is the case, can this classification be used as the basis to detect students’ mistakes?
- -
- Does the MAD+ diagrams allow us to see which phases are the most conflicting? What interpretation can we give to the presence of mistakes of a category in the different phases of the process described in the MAD+?
2. Materials and Methods
2.1. Sample
2.2. The Fermi Problem
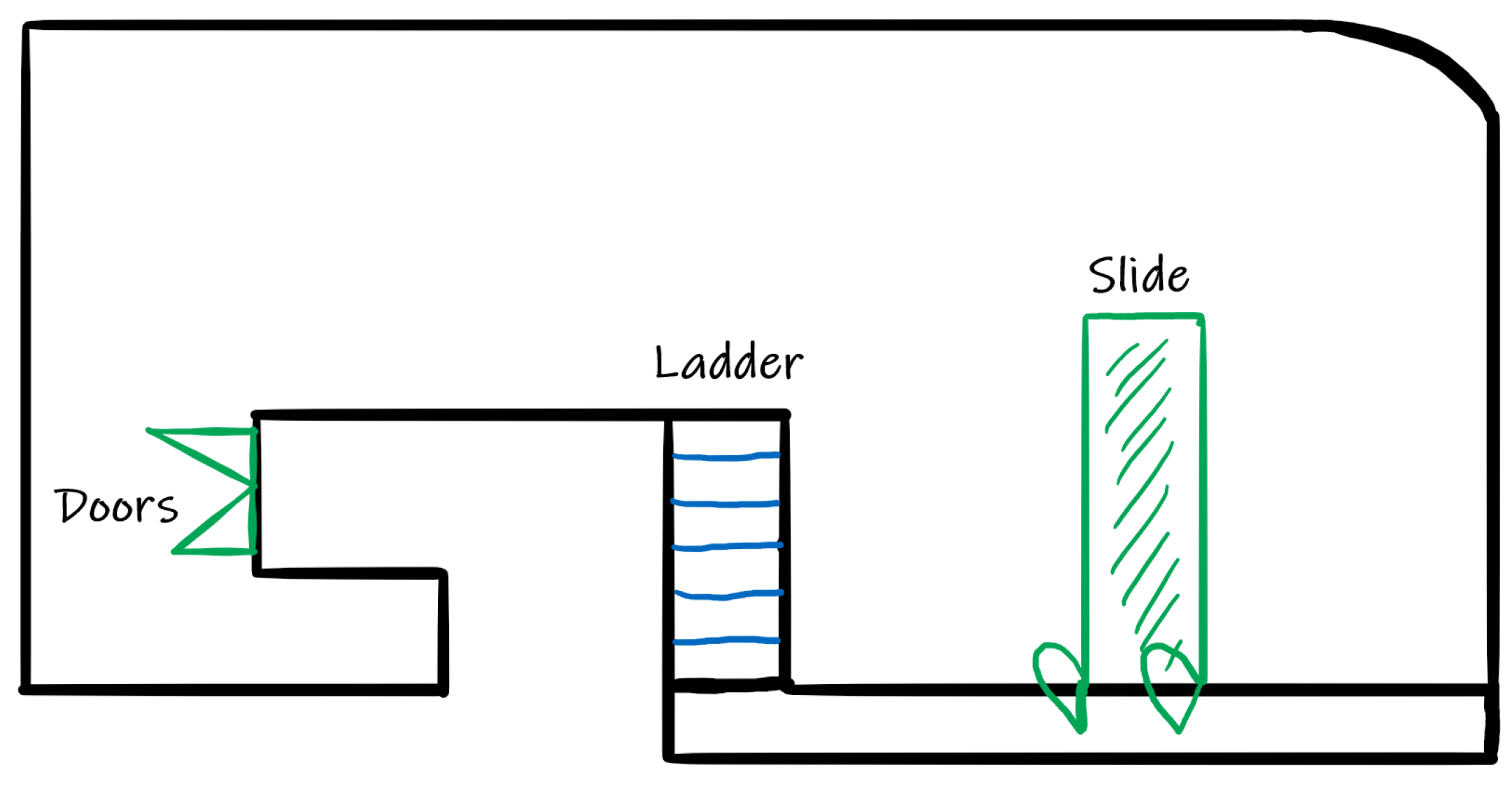
Vincent takes his little brother to a ball pit to celebrate his ninth birthday. When they enter, they realise that the pool has been filled with new balls. Vicent’s brother thinks that they’ve bought a lot of balls, probably more than 1000! Do you think Vicent’s brother has exaggerated the number? Calculate approximately how many balls fit in the pool if you have the diagram shown in Figure 2.
2.3. Methodology
3. Results and Discussion
3.1. Mistakes and Misconceptions Detection Using the Transcriptions
00:07:46 GBS2 No, because it says: how many balls did they have to buy? I’m sure it’s more than 1000. It’s like they’ve added more balls.00:07:50 GBS1 Yeah, yeah.00:07:54 GBS3 So maybe there’s a catch there.00:07:57 GBS2 Of course that’s what it is. It’s not that there’s 1000, it’s that there’s 1000 more than there were before.
00:02:45 GBS1 And we could do it scaled because you have a drawing. I mean, from the drawing you can measure, and you do it scaled but I don’t know if that would be okay.00:03:05 GBS1 Because what scale do you use? I don’t know, I don’t remember how that worked.00:03:31 GBS1 We’ve said that you must calculate the volume by taking out the slide, the staircase, and doors, right?00:04:24 GBS3 Maybe it’s crazy to take a ruler and then scale it.00:04:46 GBS1 Of course, I think the right thing to do is to do the scale, but I don’t know, is there a fixed scale for the drawing or something?00:04:57 GBS2 No. You can do whatever scale you want. I don’t think you don’t gain anything by doing the scale because the scale is whatever you want.
00:19:35 GCS2 What I would say is that the total number of balls that we’ve got is 7458, but as the balls are not going to take up all the available space, we could subtract 2000 of those balls, at a guess…00:19:47 GCS3 Yeah…2000 will certainly be left out.00:19:51 GCS2 Because, anyway, we don’t know how many balls fit in 1 square metre, we’d have to assume that…Well, yeah, we could figure it out, you know, by having the diameter of the sphere…00:20:08 GCS3 Yeah, but you can’t work out how much the little gaps take up either…00:20:13 GCS2 No, no, no…The volume that it takes up in those holes, we can’t calculate that.00:20:24 GCS3 Subtract about…2000…00:20:27 GCS2 Yeah, it’s by estimation…as these are modelling problems…00:20:44 GCS1 …minus 2000, so 5458 balls. So…, so we could say that there’s room for more than 1000 balls.
00:48:03 GAS3 37 million 44,00000:48:11 GAS1 Shall we convert it to metres?00:48:14 GAS2 Are you doing it in centimetres?00:48:29 GAS3 Okay, now better 37,044 meters.00:48:36 GAS1 cubic meters.
00:35:14 GBS1 Okay, it is 13 point 5, the whole area [of the pool picture]00:35:20 GBS2 Thirteen point 5 square meters. Ok.
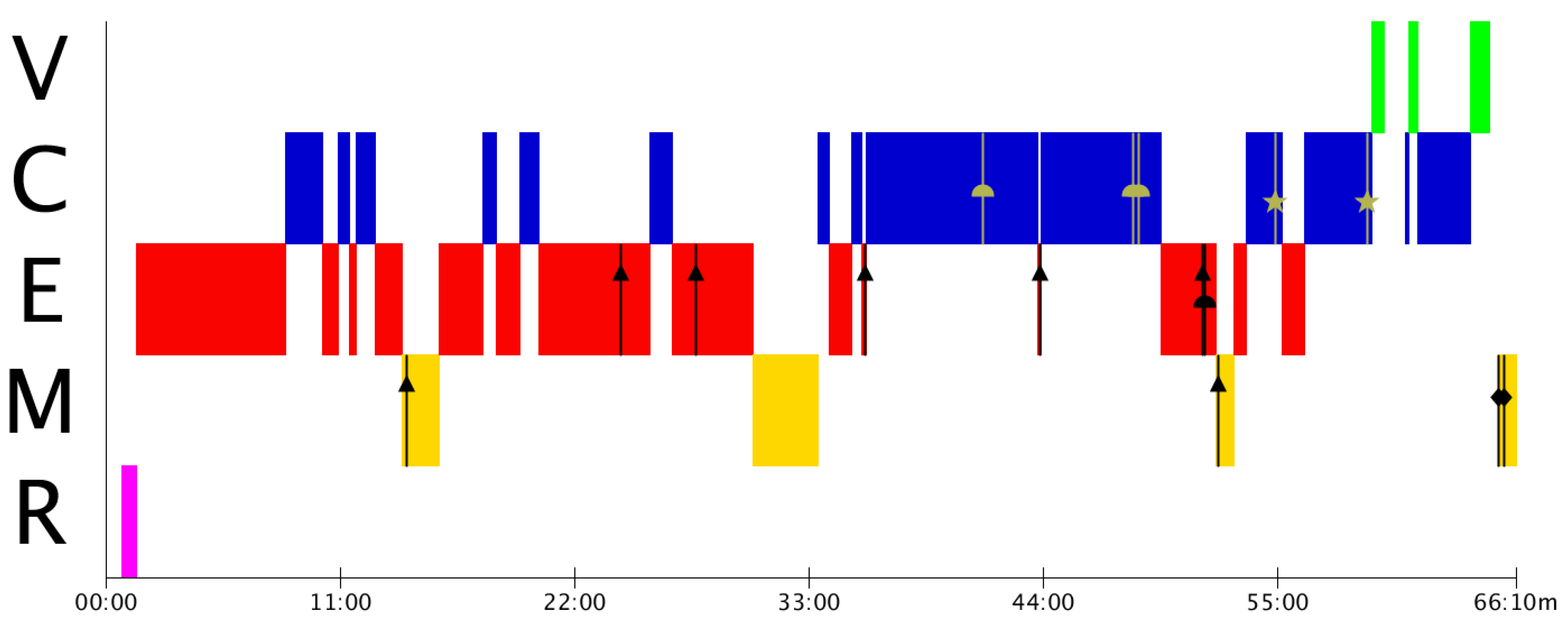
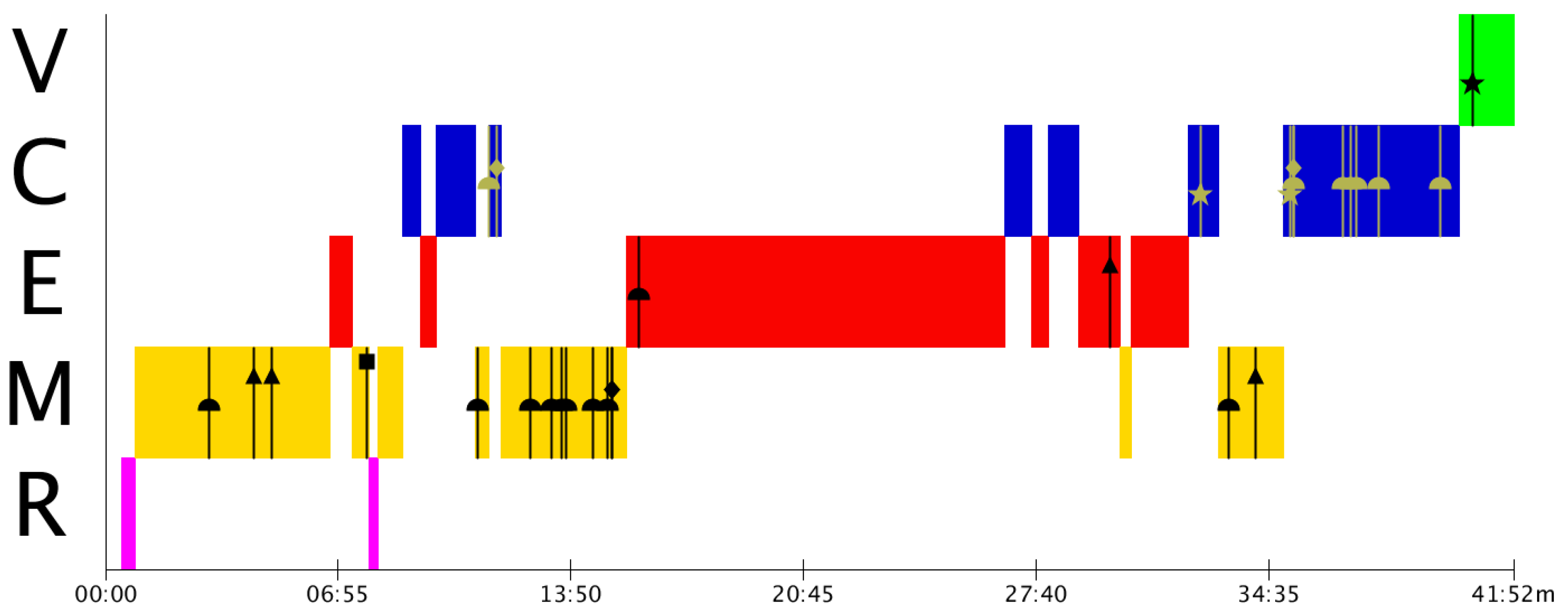
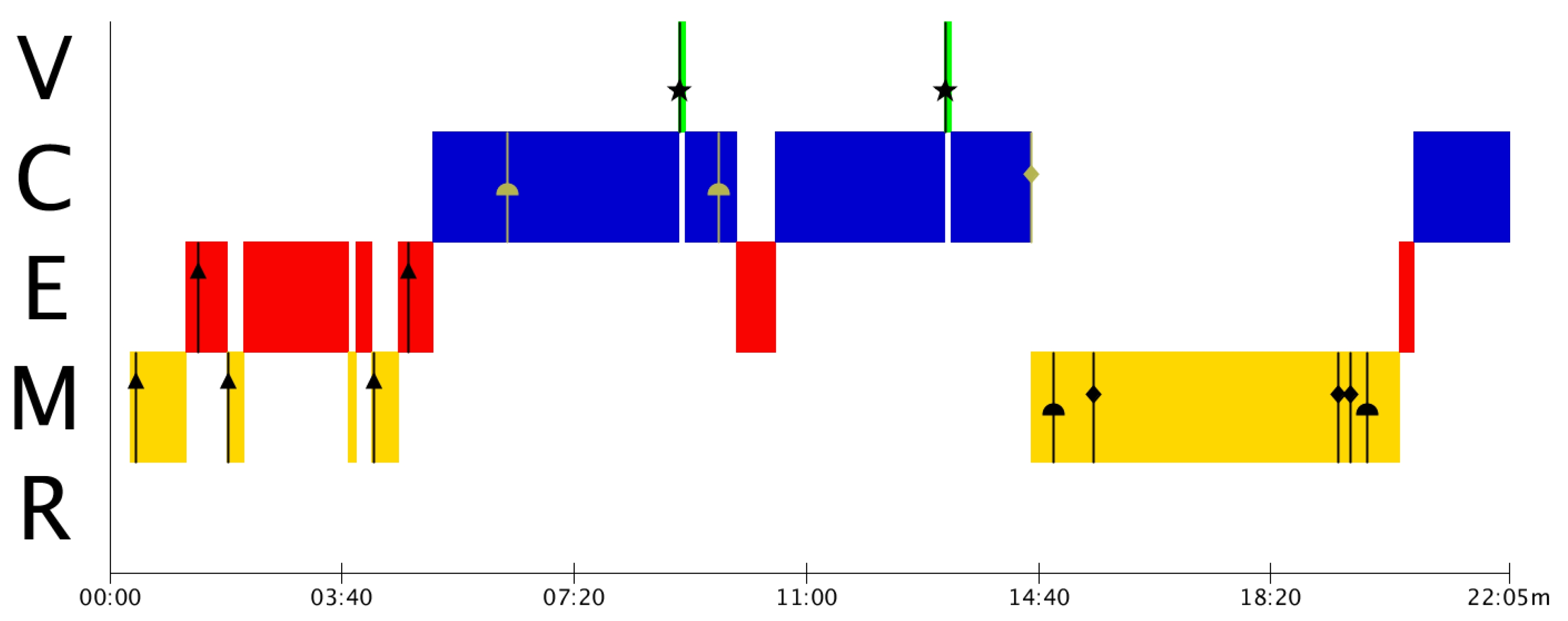
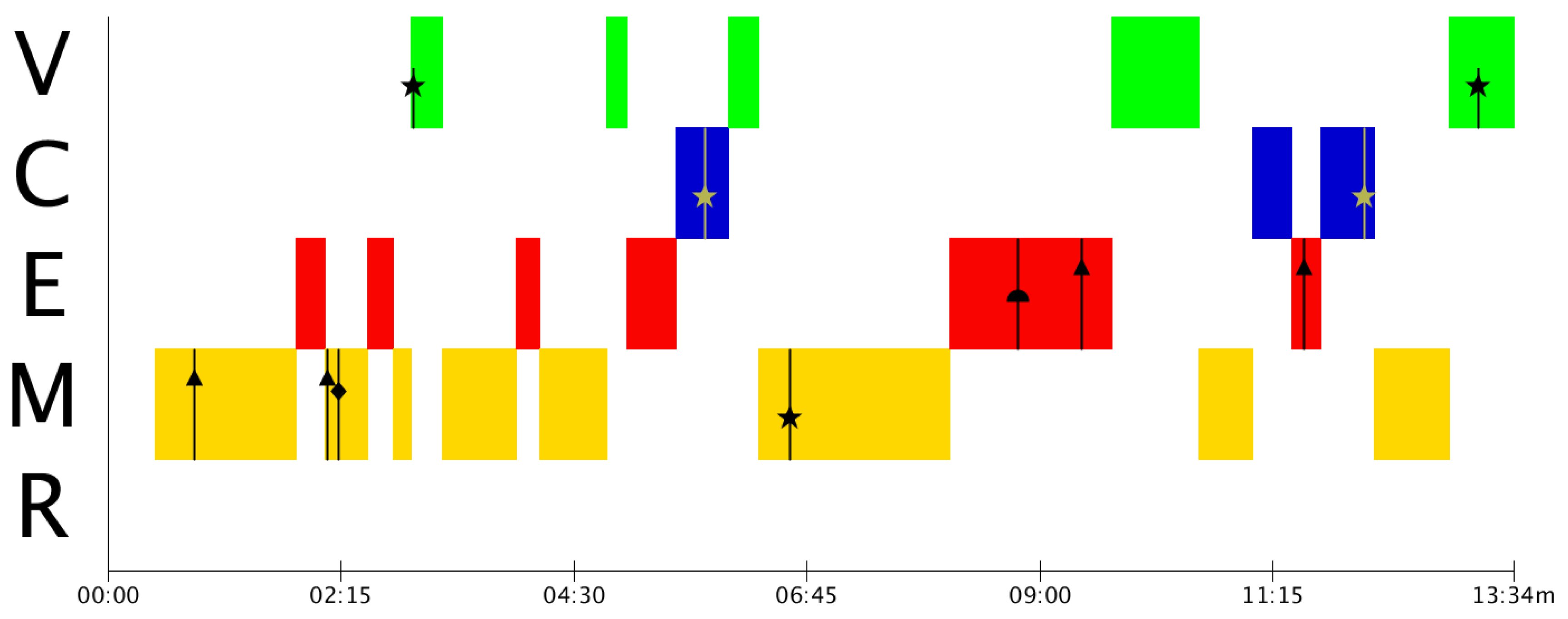
3.2. Analysis of the Mistakes’ Timeline. Construction of the MAD+ Diagrams
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| MAD | Modelling Activity Diagram |
| MAD+ | Enhanced Modelling Activity Diagram |
| TTT | Task Time Tracker |
Appendix A. Spanish Transcriptions of the Dialogues
00:07:46 GBS2 No, porque dice ¿cuántas bolas han tenido que comprar? Seguro que más de 1000. Es como que han añadido más bolas.00:07:50 GBS1 Sí, sí.00:07:54 GBS3 Entonces es que igual está la trampa ahí.00:07:57 GBS2 Claro es que es eso. Es que no es que hayan 1000, es que hay 1000 más las que ya más la que ya hubiera antes. Supuestamente
00:02:45 GBS1 Y lo podríamos hacer a escala porque tú tienes un dibujo. O sea a partir del dibujo puedes medir y lo haces a escala pero no sé si eso estaría bien.00:03:05 GBS1 Porque ¿qué escala utilizas? No sé, eso no me acuerdo cómo funcionaba00:03:31 GBS1 Hemos dicho que hay que calcular el volumen quitando tobogán, la escalera y puertas ¿no?00:04:24 GBS3 Igual es una locura pero coger una regla y luego pasarlo a escala.00:04:46 GBS1 Claro yo creo que lo más correcto es que vas a hacer la escala pero claro yo tampoco sé. ¿Hay una escala fija para los dibujos o algo?00:04:57 GBS2 No. Tú puedes poner la escala que tú quieras. Es que yo creo que haciendo la escala tampoco ganas nada porque la escala es la que tú quieras.
00:19:35 GCS2 Yo lo que pondría es que el total de bolas que hemos obtenido son 7458, pero como las bolas no van a ocupar todo el espacio disponible, podríamos restar 2000 de esas bolas, a ojo…00:19:47 GCS3 Sí…2000 seguro que se quedan fuera.00:19:51 GCS2 Porque, de todas formas, no sabemos cuántas bolas caben en 1 metro cuadrado, eso tendríamos que suponerlo…Bueno, sí, lo podríamos calcular, vaya, teniendo el diámetro de la esfera…00:20:08 GCS3 Sí, pero tampoco lo puedes calcular lo que ocupan los huequecillos esos…00:20:13 GCS2 No, no…El volumen que ocupa en esos huecos, no lo podemos calcular.00:20:24 GCS3 Réstales unas…2000…00:20:27 GCS2 Sí, es a ojo…como son problemas de modelización…00:20:44 GCS1 …menos 2000, o sea, 5458 bolas. Entonces…, por tanto podríamos decir que sí que caben más de 1000 bolas
00:48:03 GAS3 37 millones 44,00000:48:11 GAS1 lo pasamos a metros?00:48:14 GAS2 ¿Lo estáis haciendo en centímetros?00:48:29 GAS3 Vale, ahora mejor 37,044 metros.00:48:36 GAS1 metros cúbicos
00:35:14 GBS1 Vale, me da 13 con 5, toda el área [del dibujo de la piscina]00:35:20 GBS2 Trece con 5 metros cuadrados. Vale.
References
- Vorhölter, K.; Kaiser, G.; Borromeo Ferri, R. Modelling in mathematics classroom instruction: An innovative approach for transforming mathematics education. In Transforming Mathematics Instruction; Springer: Cham, Switzerland, 2014; pp. 21–36. [Google Scholar]
- Vos, P. “How Real People Really Need Mathematics in the Real World”—Authenticity in Mathematics Education. Educ. Sci. 2018, 8, 195. [Google Scholar] [CrossRef] [Green Version]
- Kaiser, G.; Sriraman, B. A global survey of international perspectives on modelling in mathematics education. ZDM 2006, 38, 302–310. [Google Scholar] [CrossRef]
- Blum, W.; Leiß, D. Investigating quality mathematics teaching–the DISUM Project. Dev. Res. Qual. Math. Teach. Learn. Proc. MADIF 2007, 5, 3–16. [Google Scholar]
- Maaß, K.; Gurlitt, J. LEMA–Professional development of teachers in relation to mathematical modelling. In Trends in Teaching and Learning of Mathematical Modelling; Springer: Dordrecht, The Netherlands, 2011; pp. 629–639. [Google Scholar]
- Erbas, A.K.; Kertil, M.; Çetinkaya, B.; Çakiroglu, E.; Alacaci, C.; Bas, S. Mathematical Modeling in Mathematics Education: Basic Concepts and Approaches. Educ. Sci. Theory Pract. 2014, 14, 1621–1627. [Google Scholar] [CrossRef]
- Bilek, M.; Machkova, V.; Musilek, M.; Simonova, I.; Manenova, M. Mascil project, or how to improve the interest in engineering studies and professions of primary and secondary school learners. In Proceedings of the 2015 International Conference on Interactive Collaborative Learning (ICL), Firenze, Italy, 20–24 September 2015; pp. 827–831. [Google Scholar]
- Kaiser, G. Mathematical modelling and applications in education. In Encyclopedia of Mathematics Education; Springer: Cham, Switzerland, 2020; pp. 553–561. [Google Scholar]
- Borromeo Ferri, R. Learning How to Teach Mathematical Modeling in School and Teacher Education; Springer: Cham, Switzerland, 2017. [Google Scholar]
- Czocher, J.A. Introducing modeling transition diagrams as a tool to connect mathematical modeling to mathematical thinking. Math. Think. Learn. 2016, 18, 77–106. [Google Scholar] [CrossRef]
- Albarracin, L.; Ärlebäck, J.; Civil, E.; Gorgorio, N. Extending Modelling Activity Diagrams as a tool to characterise mathematical modelling processes. Math. Enthus. 2019, 16, 211–230. [Google Scholar]
- Alsina, Á.; Toalongo-Guamba, X.; Trelles-Zambrano, C.; Salgado, M. Desarrollando habilidades de modelización matemática temprana en Educación Infantil: Un análisis comparativo en 3 y 5 años. Quadrante 2021, 30, 74–93. [Google Scholar]
- Ärlebäck, J.B. On the use of realistic Fermi problems for introducing mathematical modelling in school. Math. Enthus. 2009, 6, 331–364. [Google Scholar]
- Czocher, J.A. Mathematical modeling cycles as a task design heuristic. Math. Enthus. 2017, 14, 129–140. [Google Scholar]
- Maaß, J.; O’Meara, N.; Johnson, P.; O’Donoghue, J. Mathematical Modelling for Teachers: A Practical Guide to Applicable Mathematics Education; Springer: Cham, Switzerland, 2018. [Google Scholar]
- Hogan, T.P.; Brezinski, K.L. Quantitative Estimation: One, Two, or Three Abilities? Math. Think. Learn. 2003, 5, 259–280. [Google Scholar] [CrossRef]
- Albarracín, L.; Gorgorió, N. Devising a plan to solve Fermi problems involving large numbers. Educ. Stud. Math. 2014, 86, 79–96. [Google Scholar] [CrossRef]
- Kaiser, G.; Brand, S. Modelling competencies: Past development and further perspectives. In Mathematical Modelling in Education Research and Practice; Springer: Cham, Switzerland, 2015; pp. 129–149. [Google Scholar]
- Cevikbas, M.; Kaiser, G.; Schukajlow, S. A systematic literature review of the current discussion on mathematical modelling competencies: State-of-the-art developments in conceptualizing, measuring, and fostering. Educ. Stud. Math. 2021, 2021, 1–32. [Google Scholar] [CrossRef]
- Kaiser, G.; Schwarz, B. Mathematical modelling as bridge between school and university. ZDM 2006, 38, 196–208. [Google Scholar] [CrossRef]
- Borromeo Ferri, R. Theoretical and empirical differentiations of phases in the modelling process. ZDM 2006, 38, 86–95. [Google Scholar] [CrossRef]
- Borromeo Ferri, R. Personal experiences and extra-mathematical knowledge as an influence factor on modelling routes of pupils. In Proceedings of the CERME-5, WG 13 Modelling and Applications, Larnaca, Cyprus, 22–26 February 2007; pp. 2080–2089. [Google Scholar]
- Sol, M.; Giménez, J.; Rosich, N. Project modelling routes in 12–16-year-old pupils. In Trends in Teaching and Learning of Mathematical Modelling; Springer: Dordrecht, The Netherlands, 2011; pp. 231–240. [Google Scholar]
- Doerr, H.M.; Ärlebäck, J.B.; Misfeldt, M. Representations of modelling in mathematics education. In Mathematical Modelling and Applications; Springer: Cham, Switzerland, 2017; pp. 71–81. [Google Scholar]
- Ferrando, I.; Albarracín, L. Students from grade 2 to grade 10 solving a Fermi problem: Analysis of emerging models. Math. Educ. Res. J. 2021, 33, 61–78. [Google Scholar] [CrossRef]
- Ferrando, I.; Segura, C.; Pla-Castells, M. Analysis of the relationship between context and solution plan in modelling tasks involving estimations. In Mathematical Modelling Education in East and West; Springer: Cham, Switzerland, 2021; pp. 119–128. [Google Scholar]
- Julie, C.; Mudaly, V. Mathematical modelling of social issues in school mathematics in South Africa. In Modelling and Applications in Mathematics Education; Springer: Boston, MA, USA, 2007; pp. 503–510. [Google Scholar]
- Kaiser, G.; Schwarz, B.; Tiedemann, S. Future teachers’ professional knowledge on modeling. In Modeling Students’ Mathematical Modeling Competencies; Springer: Boston, MA, USA, 2010; pp. 433–444. [Google Scholar]
- Biembengut, M.S.; Faria, T.M.B. Mathematical modelling in a distance course for teachers. In Trends in Teaching and Learning of Mathematical Modelling; Springer: Dordrecht, The Netherlands, 2011; pp. 269–278. [Google Scholar]
- Socas, M.M.; Ruano, R.M.; Domínguez, J.H. Análisis Didáctico del proceso matemático de Modelización en alumnos de Secundaria. Av. Investig. Educ. Matemática 2016, 9, 21–41. [Google Scholar] [CrossRef] [Green Version]
- Şen Zeytun, A.; Çetinkaya, B.; Erbaş, A.K. Understanding prospective teachers’ mathematical modeling processes in the context of a mathematical modeling course. EURASIA J. Math. Sci. Technol. Educ. 2017, 13, 691–722. [Google Scholar] [CrossRef]
- Stillman, G.; Brown, J.; Galbraith, P. Identifying challenges within transition phases of mathematical modeling activities at year 9. In Modeling Students’ Mathematical Modeling Competencies; Springer: Boston, MA, USA, 2013; pp. 385–398. [Google Scholar]
- Galbraith, P.; Stillman, G. A framework for identifying student blockages during transitions in the modelling process. ZDM 2006, 38, 143–162. [Google Scholar] [CrossRef]
- Galbraith, P.; Stillman, G.; Brown, J.; Edwards, I. Facilitating middle secondary modelling competencies. In Mathematical Modelling: Education, Engineering and Economics-ICTMA 12; Horwood Publishing: Chichester, UK, 2007; pp. 130–140. [Google Scholar]
- Crouch, R.; Haines, C. Exemplar models: Expert-novice student behaviours. In Mathematical Modelling: Education, Engineering and Economics-ICTMA 12; Horwood Publishing: Chichester, UK, 2007; pp. 90–100. [Google Scholar]
- Große, C.S. Learning to solve story problems—Supporting transitions between reality and mathematics. Eur. J. Psychol. Educ. 2014, 29, 619–634. [Google Scholar] [CrossRef]
- Klock, H.; Siller, H.S. A Time-Based Measurement of the Intensity of Difficulties in the Modelling Process. In Mathematical Modelling Education and Sense-Making; Springer: Cham, Switzerland, 2020; p. 163. [Google Scholar]
- Maaß, K. Mathematisches modellieren im unterricht—Ergebnisse einer empirischen studie. J.-Math.-Didakt. 2004, 25, 175–176. [Google Scholar] [CrossRef]
- Moreno Verdejo, A.; Martín Arenas, M.; Ramírez Uclés, R. Errores de profesores de Matemáticas en formación inicial al resolver una tarea de modelización. PNA Rev. Investig. Didáctica Matemática 2021, 15, 109–136. [Google Scholar]
- Segura, C.; Ferrando, I. Classification and Analysis of Pre-Service Teachers’ Errors in Solving Fermi Problems. Educ. Sci. 2021, 11, 451. [Google Scholar] [CrossRef]
- Pla-Castells, M.; García-Fernández, I. TaskTimeTracker: A tool for temporal analysis of the problem solving process. Investig. Entornos TecnolÓGicos Educ. MatemÁTica 2020, 1, 9–14. [Google Scholar]
- Schoenfeld, A.H. Mathematical Problem Solving; Academic Press: Orlando, FL, USA, 1985. [Google Scholar]
- Schoenfeld, A.H. On paradigms and methods: What do you do when the ones you know don’t do what you want them to? Issues in the analysis of data in the form of videotapes. J. Learn. Sci. 1992, 2, 179–214. [Google Scholar] [CrossRef]
- Goos, M.; Galbraith, P. Do it this way! Metacognitive strategies in collaborative mathematical problem solving. Educ. Stud. Math. 1996, 30, 229–260. [Google Scholar] [CrossRef]
- Scott, N.; Stacey, K. Orientation to Deep Structure When Trying Examples: A Key to Successful Problem Solving; Hergué: La Palma Del Condado, Spain, 2000. [Google Scholar]
- Brown, J.P. An Insight into Student Understanding of Functions in a Graphing Calculator Environment. Master’s Thesis, Department of Education, The University of Melbourne, Melbourne, Australia, 2003. [Google Scholar]
- Cai, J.; Cirillo, M.; Pelesko, J.; Bommero Ferri, R.; Borba, M.; Geiger, V.; Stillman, G.; English, L.; Wake, G.; Kaiser, G. Mathematical modeling in school education: Mathematical, cognitive, curricular, instructional and teacher educational perspectives. In Proceedings of the 38th Conference of the International Group for the Psychology of Mathematics Education and the 36th Conference of the North American Chapter of the Psychology of Mathematics Education, Vancouver, BC, Canada, 15–20 July 2014; pp. 145–172. [Google Scholar]
- Blum, W. Anwendungsbezüge im Mathematikunterricht–Trends und perspektiven. Schriftenreihe Didakt. Math. 1996, 23, 15–38. [Google Scholar]
- Kaiser, G. Realitätsbezüge im Mathematikunterricht: Ein Überblick Über Die Aktuelle und Historische Diskussion; Springer: Cham, Switzerland, 1995. [Google Scholar]
- Vygotsky, L.S. Mind in Society: The Development of Higher Psychological Processes; Harvard University Press: Boston, MA, USA, 1980. [Google Scholar]
- Gillies, R.M. Structuring cooperative group work in classrooms. Int. J. Educ. Res. 2003, 39, 35–49. [Google Scholar] [CrossRef]
- Berry, J.; Sahlberg, P. Accountability affects the use of small group learning in school mathematics. Nord. Stud. Math. Educ. 2006, 11, 5–31. [Google Scholar]
- Clement, J.; Lochhead, J.; Monk, G.S. Translation difficulties in learning mathematics. Am. Math. Mon. 1981, 88, 286–290. [Google Scholar] [CrossRef]
- Crouch, R.; Haines, C. Do You Know Which Students Are Good Mathematical Modellers? Some Research Developments; Technical Report; Department of Physics, Astronomy and Mathematics, University of Hertfordshire: Hetfield, UK, 2003. [Google Scholar]
- Crouch, R.; Haines, C. Mathematical modelling: Transitions between the real world and the mathematical model. Int. J. Math. Educ. Sci. Technol. 2004, 35, 197–206. [Google Scholar] [CrossRef]
- Forrester, M.A.; Latham, J.; Shire, B. Exploring estimation in young primary school children. Educ. Psychol. 1990, 10, 283–300. [Google Scholar] [CrossRef]
- Pizarro, N.; Gorgorió, N.; Albarracín, L. La definición del concepto estimación de medida de los maestros de primaria. Acta Latinoam. Matemática Educ. 2015, 28, 1202–1209. [Google Scholar]
- Castillo-Mateo, J.; Segovia, I.; Molina, M. Estudio comparativo de la estimación de cantidades continuas que hacen los estudiantes de secundaria y futuros maestros. PNA Rev. Investig. Didáctica Matemática 2017, 12, 43–59. [Google Scholar]
| Mistake Description | Students’ Considerations | |
|---|---|---|
| T1. Simplification | 1.1. Incomplete real model associated with the lack of consideration of elements of reality | Any of the following elements are not considered:
|
| 1.2. Incomplete real model due to inconsistencies in the relationships between the elements of reality considered |
| |
| 1.3. Does not develop an objective function for the real model that can then be expressed in mathematical terms. |
| |
| 1.4. Does not build a real model. |
| |
| T2. Mathem. | 2.1. Mathem. model inconsistent with reality |
|
| 2.2 Incomplete mathematical model |
| |
| 2.3. Does not build any mathematical models |
| |
| T3. Solve | 3.1. Conceptual mistakes: failure in relation to the associated mathematical object |
|
| 3.2. Procedural mistakes in calculations |
| |
| 3.3. Incomplete resolution of the proposed mathematical model. |
| |
| T4. Interpret. | 4.1 The results obtained are not interpreted on the basis of the proposed model |
|
| 4.2. The limitations of the mathematical model in the original situation are not recognised. |
|
| T0 | T1 | T2 | T3 | T4 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Reading | Simplification | Mathematisation | Solve | Validate | |||||||||
| 0 | 1.1 | 1.2 | 1.3 | 1.4 | 2.1 | 2.2 | 2.3 | 3.1 | 3.2 | 3.3 | 4.1 | 4.2 | |
| Group A | x | x | x | x | x | x | |||||||
| Group B | x | x | x | x | x | x | x | x | |||||
| Group C | x | x | x | x | x | ||||||||
| Group D | x | x | x | x | x | x | |||||||
| MAD Categories | Description of Modelling Activities of Students from the Problem in Context |
|---|---|
| Reading | Understanding the task: The students must understand the context of the problem and to focus on the main question of the task. How many balls can fit into the pool of the ball pit? Is this number lower or greater than 1000? |
| Modelling | Transitioning from a real-world context to a mathematical interpretation of the task: Students find out how to calculate the number of balls fitting in the pool, asking themselves how to obtain the result. They have to think if any of the unit iteration, density or grid models can lead to a solution, even if they are not explicitly aware of that decision. They list the quantitative variables to be estimated. |
| Estimating | Making sense of the quantitative estimates in the problem in context: Students estimate the quantities involved in the model. |
| Calculating | Using simple mathematical concepts to calculate the missing information on the sketched diagrams or figures: Students calculate the volume of the pool and the volume of the ball, convert cm into m (or vice versa), use the proportion to calculate the scaled measures, etc. |
| Validating | Interpreting, verifying and validating the mathematical calculations: Students make sense of the mathematical results, including calculations, within the problem in context. They compare their calculation with the number given in the task formulation. |
| Type of Mistake | Code |
|---|---|
| 0. Reading | Square (∎) |
| 1. Simplification | Triangle (▲) |
| 2. Mathematisation | Diamond (♦) |
| 3. Solve | Cap (⯊) |
| 4. Validate | Star (★) |
| T0 | T1 | T2 | T3 | T4 | |
|---|---|---|---|---|---|
| V | o | ||||
| C | x | o | x | ||
| E | o | x | |||
| M | x | x | o | x | x |
| R |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pla-Castells, M.; Melchor, C.; Chaparro, G. MAD+. Introducing Misconceptions in the Temporal Analysis of the Mathematical Modelling Process of a Fermi Problem. Educ. Sci. 2021, 11, 747. https://doi.org/10.3390/educsci11110747
Pla-Castells M, Melchor C, Chaparro G. MAD+. Introducing Misconceptions in the Temporal Analysis of the Mathematical Modelling Process of a Fermi Problem. Education Sciences. 2021; 11(11):747. https://doi.org/10.3390/educsci11110747
Chicago/Turabian StylePla-Castells, Marta, Carmen Melchor, and Gisela Chaparro. 2021. "MAD+. Introducing Misconceptions in the Temporal Analysis of the Mathematical Modelling Process of a Fermi Problem" Education Sciences 11, no. 11: 747. https://doi.org/10.3390/educsci11110747
APA StylePla-Castells, M., Melchor, C., & Chaparro, G. (2021). MAD+. Introducing Misconceptions in the Temporal Analysis of the Mathematical Modelling Process of a Fermi Problem. Education Sciences, 11(11), 747. https://doi.org/10.3390/educsci11110747






