Validation of Rubric Evaluation for Programming Education
Abstract
:1. Introduction
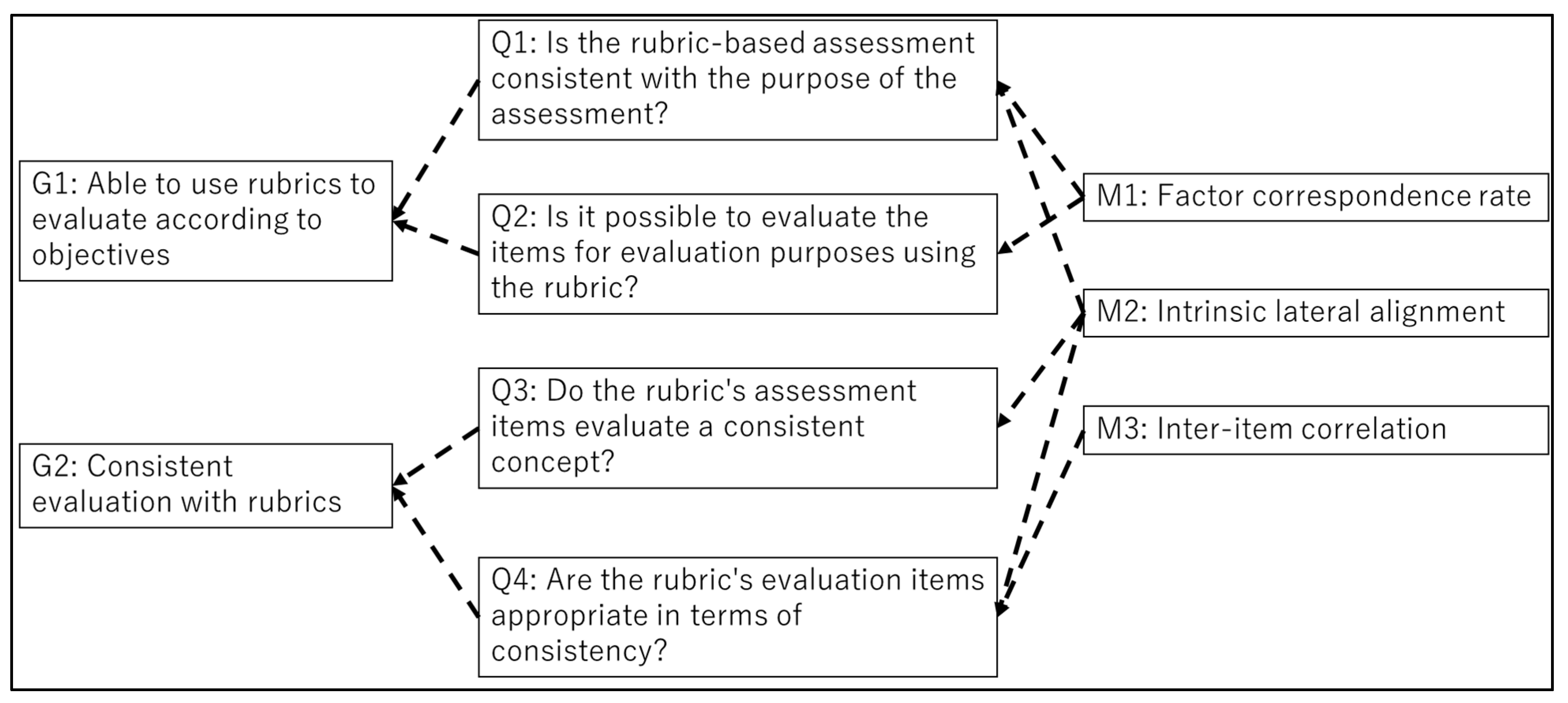
- RQ1: How do we identify statistical methods to assess the properties of rubrics?
- RQ2: How can rubrics be evaluated and analyzed to identify improvements?
- RQ3: By evaluating and analyzing the rubrics, can we confirm the generality of the evaluation?
2. Backgrounds
2.1. Definition and Required Properties of Rubrics
2.2. Evaluating the Reliability of Rubrics
2.3. About the Rubric to Be Evaluated
3. Characteristic Evaluation Framework for Rubrics
3.1. Rubric Characterization Methods
3.2. Factor Response Rate
3.3. Integration Within
3.4. Inter-Item Correlation
4. Experiment and Evaluation
4.1. Rubrics and Data to Be Covered
4.2. Class Details
4.3. Application Results of Evaluation Framework
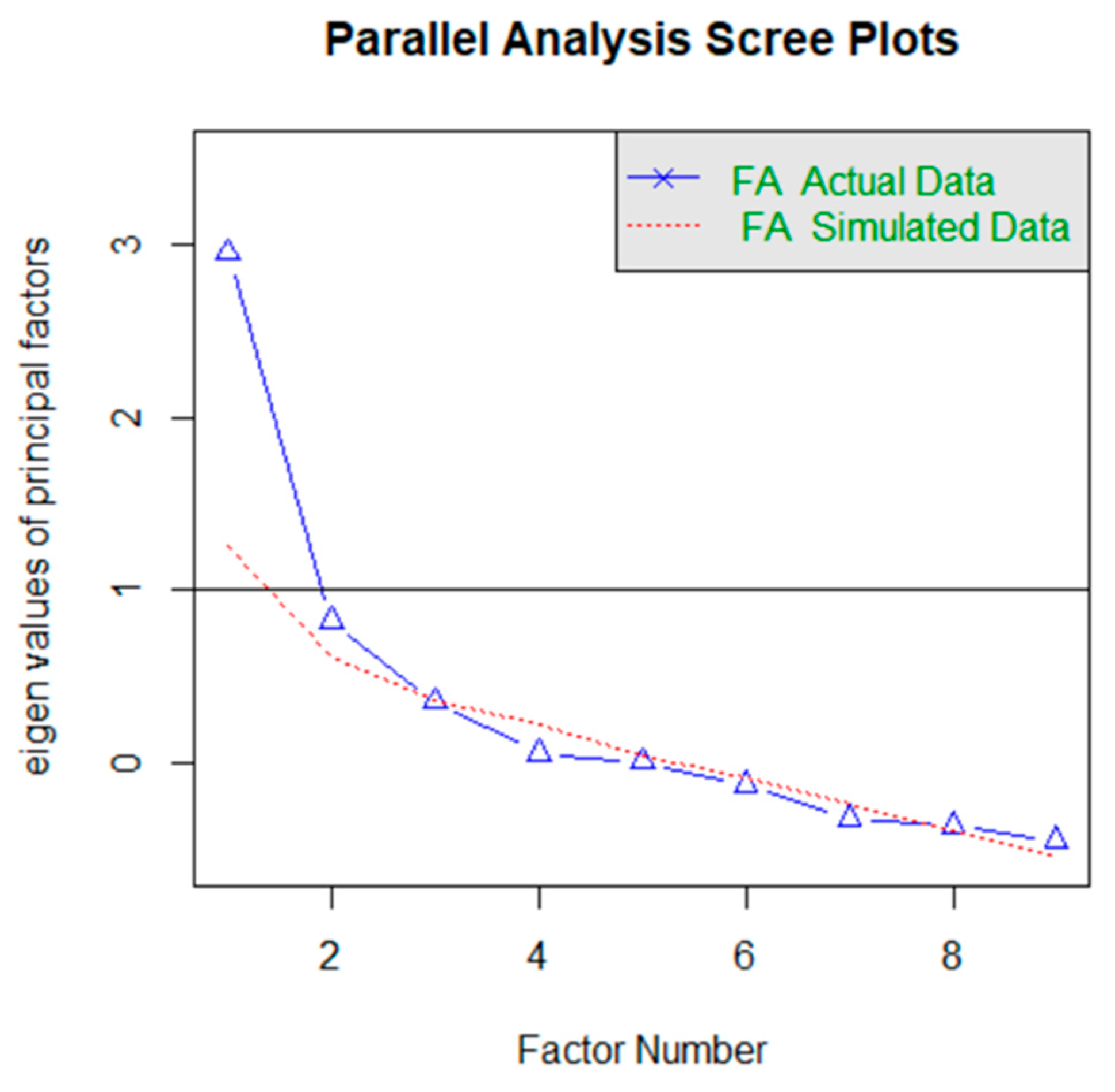
4.3.1. Factor Loadings in Evaluation Results
4.3.2. Internal Consistency in Each Evaluation Result
5. Discussion
5.1. Answers to RQs
5.1.1. RQ1: How Do We Identify Statistical Methods to Evaluate Rubric Properties?
5.1.2. RQ2: How Can Rubrics Be Evaluated and Analyzed to Identify Improvements?
5.1.3. RQ3: Can We Confirm the Generality of Evaluation by Evaluating and Analyzing Rubrics?
5.2. General Comments on the Application of the Evaluation Framework
5.3. Threats of Validity
6. Related Works
7. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Category | Item | Stage 5 | Stage 4 | Stage 3 | Stage 2 | Stage 1 |
|---|---|---|---|---|---|---|
| Understanding of the algorithm (the concept of the algorithm) | Sequence | It can be tied to understand the sequence of ideas with other ideas | Multiple things the in’s order, can be considered in conjunction | It can be multiple things the have’s order, respectively | It is possible that it is the order for one thing | Do not understand the concept of sequence |
| Branch | Able to connect the idea of branching to other ideas. | Consider the plurality of conditions for a matter can be branched in combination | It can be branched in a plurality of conditions for a matter | It can be branched at one condition for a certain matter | Do not understand the concept of branch | |
| Repetition | The concept of repetition can be combined with other ideas. | It can be used to combine multiple iterations (double loop) | You can notice from one procedure to the plurality of iterations | You can notice a certain procedure or one iteration | Do not understand the concept of repetition | |
| Variable | It is possible to link the concept of variables and other ideas | It is possible to make multiple variables associated with a certain matter | It is possible to create multiple variables for a certain matter | It is possible to make one of the variables for a certain matter | Do not understand the concept of variable | |
| Array | It is possible to link the idea of the sequence with other ideas | It can be in unity associated with some of the elements as | Can some elements into a plurality of separate unity | It can be some of the elements in one of unity | Do not understand the concept of array | |
| Function | It is possible to link the concept of a function and other ideas | Summarized the several steps in the form associated with each of the plurality of elements | It is summarized a few steps into a plurality of elements | It is summarized a few steps to one of the elements | Do not understand the concept of function | |
| Recursion | It is possible to link the concept of recursion to the other way of thinking | Notice cannot be a comeback can function, use recursion for recursion can function | For some functions, it can be issued to call the function itself in the function | For some functions, Kizukeru call the function itself in the function | Do not understand the concept of recursion | |
| Sort | It is possible to link the idea of the sort to other ideas | It can be sorted in an optimal way associated with some of the elements to the element | It is possible to sort each with some of the elements of a plurality of different ways | It can be sorted in one way some elements | Do not understand the concept of sorting |
Appendix B
| Category | Item | Stage 5 | Stage 4 | Stage 3 | Stage 2 | Stage 1 |
|---|---|---|---|---|---|---|
| Thinking in the design and creation of the program | Subdivision of the problem | Can subdivide the problem, it is possible to make the solutions and other things subdivided problem | It can be divided into several smaller problems associated with major problems | It can be separated from a big problem into smaller problems | It is possible to find one small problem from a big problem | Cannot subdivide the problem |
| Analysis of events | It is the analysis of the events, the results of the analysis can be used in problem-solving and other things | It can be found several factors (causes) related to an event | You can find multiple factors (causes) for a certain event | You can find one factor (Cause) about a certain event | Cannot analyze events | |
| Extraction operation | Operation can be extracted, the extracted operation can be utilized to solve problems and other things | It can be withdrawn a plurality of operations associated with existing matter | It is possible to extract a plurality of operations from the existing things | It is possible to extract one of the operations from the existing things | Cannot extract operation | |
| Construction of the operation | Following the purpose to build an operation, it can be used in problem-solving and other things | You can build more of the operations related to suit your purpose | You can build a plurality of operations following the purpose | You can build one operation by the purpose | Cannot build operation | |
| functionalization | Big thing can function reduction, can be utilized for their problem-solving and other things that | Can be summarized into several smaller steps associated with large things that | For large things that can be summarized into several smaller steps | Can be summarized for the big things that, one in small steps | Cannot function of | |
| Generalization | Be generalized to various things, it can be used for problem-solving and other things | It is possible to combine the common parts of the various things in the big concept | It can represent multiple things to a large concept | It can express one thing as a great concept | Cannot be generalized |
Appendix C
| Category | Item | Stage 5 | Stage 4 | Stage 3 | Stage 2 | Stage 1 |
|---|---|---|---|---|---|---|
| Thinking in the design and creation of the program | Abstraction | Big thing can abstract for, can be used for their problem-solving and other things that | Be focused on a plurality of elements associated with large things that | For large things that can focus on several important factors | For large things that can focus on one important element | Cannot be abstracted |
| inference | Hypothesized cause to the problem, it can be utilized to resolve methods (deduction and induction) were derived problem-solving and other things on the basis thereof | Hypothesized cause to the problem, derivable how to solve based thereon (deductive, inductive) | You can both the following (independent form) 1. is a hypothesis of the cause for the problem. 2. derivable how to solve the problem | You are either the following 1. is a hypothesis of the cause for the problem. 2. derivable how to solve the problem | Cannot be inferred | |
| Logical algebra | It can be used in conjunction with logical algebra and other ideas | It can be used in combination logical sum, logical product, a logical negation | Logical sum, logical product, and understand more about the logical negation | Is the logical sum, logical product, one of the logical NOT understand | Do not understand the logic of algebra | |
| operator | It is possible to use the operator in conjunction with other ideas | Can be used in conjunction to understand several types of operators | We are familiar with several types of operators | We are familiar with one type of operator (assignment operators, arithmetic operators, comparison operators, Boolean operators, bitwise) | Do not understand the operator | |
| Understanding of the program (reading, editing, and evaluation) | Understanding of the program | Comprehension of procedures and operations, evaluation, to understand the editing, can be utilized in problem-solving and other things | Comprehension of procedures and operations, evaluation, can be associated with the editing | Possible reading of procedures and operations, evaluation, editing each | It is possible to read the procedures and operations | Do not understand the program |
References
- Stegeman, M.; Barendsen, E.; Smetsers, S. Designing a rubric for feedback on code quality in programming courses. In Proceedings of the Koli Calling 2016: 16th Koli Calling International Conference on Computing Education Research, Koli, Finland, 24–27 November 2016; pp. 160–164. [Google Scholar]
- Alves, N.D.C.; von Wangenheim, C.G.; Hauck, J.C.R.; Borgatto, A.F. A large-scale evaluation of a rubric for the automatic assessment of algorithms and programming concepts. In Proceedings of the SIGCSE ‘20: The 51st ACM Technical Symposium on Computer Science Education, Portland, OR, USA, 12–14 March 2020; pp. 556–562. [Google Scholar]
- Chen, B.; Azad, S.; Haldar, R.; West, M.; Zilles, C. A validated scoring rubric for explain-in-plain-english questions. In Proceedings of the 51st ACM Technical Symposium on Computer Science Education, Portland, OR, USA, 12–14 March 2020; pp. 563–569. [Google Scholar]
- Saito, D.; Kaieda, S.; Washizaki, H.; Fukazawa, Y. Rubric for Measuring and Visualizing the Effects of Learning Computer Programming for Elementary School Students. J. Inf. Technol. Educ. Innov. Pract. 2020, 19, 203–227. [Google Scholar] [CrossRef]
- Sadhu, S.; Laksono, E.W. Development and validation of an integrated assessment for measuring critical thinking and chemical literacy in chemical equilibrium. Int. J. Instr. 2018, 11, 557–572. [Google Scholar] [CrossRef]
- Demir, K.; Akpinar, E. The effect of mobile learning applications on students’ academic achievement and attitudes toward mobile learning. Malays. Online J. Educ. Technol. 2018, 6, 48–59. [Google Scholar] [CrossRef]
- Christmann, A.; Van Aelst, S. robust estimation of Cronbach’s Alpha. J. Multivar. Anal. 2006, 97, 1660–1674. [Google Scholar] [CrossRef] [Green Version]
- Angell, K. The application of reliability and validity measures to assess the effectiveness of an undergraduate citation rubric. Behav. Soc. Sci. Libr. 2015, 34, 2–15. [Google Scholar] [CrossRef]
- Reising, D.L.; Carr, D.E.; Tieman, S.; Feather, R.; Ozdogan, Z. Psychometric testing of a simulation rubric for measuring interprofessional communication. Nurs. Educ. Perspect. 2015, 36, 311–316. [Google Scholar] [CrossRef] [PubMed]
- ISTE. Standards for Students. Available online: https://www.iste.org/standards/for-students (accessed on 25 January 2021).
- CSTA K-12. Computer Science Standards. 2017. Available online: https://www.doe.k12.de.us/cms/lib/DE01922744/Centricity/Domain/176/CSTA%20Computer%20Science%20Standards%20Revised%202017.pdf (accessed on 25 January 2021).
- Van Solingen, R.; Basili, V.; Caldiera, G.; Rombach, H.D. Goal question metric (GQM) approach. In Encyclopedia of Software Engineering; John Wiley & Sons: Hoboken, NJ, USA, 2002. [Google Scholar]
- Tsuda, N.; Washizaki, H.; Honda, K.; Nakai, H.; Fukazawa, Y.; Azuma, M.; Komiyama, T.; Nakano, T.; Suzuki, T.; Morita, S.; et al. Wsqf: Comprehensive software quality evaluation framework and benchmark based on square. In Proceedings of the 2019 IEEE/ACM 41st International Conference on Software Engineering: Software Engineering in Practice (ICSE-SEIP), Montreal, QC, Canada, 25–31 May 2019. [Google Scholar]
- Brown, T.A. Confirmatory Factor Analysis for Applied Research; The Guilford Press: New York, NY, USA, 2006. [Google Scholar]
- DeVellis, R.F. Scale Development: Theory and Applications; SAGE Publications: Thousand Oaks, CA, USA, 2003. [Google Scholar]
- Jackson, J.E. Oblimin rotation. In Wiley StatsRef: Statistics Reference Online; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- Arcuria, P.; Morgan, W.; Fikes, T.G. Validating the use of LMS-derived rubric structural features to facilitate automated measurement of rubric quality. In Proceedings of the 9th International Learning Analytics & Knowledge Conference, Tempe, AR, USA, 4–8 March 2019; pp. 270–274. [Google Scholar]
- Catete, V.; Lytle, N.; Barnes, T. Creation and validation of low-stakes rubrics for k-12 computer science. In Proceedings of the 23rd Annual ACM Conference on Innovation and Technology in Computer Science Education, Larnaca, Cyprus, 29 June–3 July 2018; pp. 63–68. [Google Scholar]
- Mustapha, A.; Samsudin, N.A.; Arbaiy, N.; Mohammed, R.; Hamid, I.R. generic assessment rubrics for computer programming courses. Turk. Online J. Educ. Technol. 2016, 15, 53–68. [Google Scholar]
- Allen, S.; Knight, J. A method for collaboratively developing and validating a rubric. Int. J. Scholarsh. Teach. Learn. 2009, 3, 10. [Google Scholar] [CrossRef] [Green Version]




| Learning Perspective | Learning Goals | |||||
|---|---|---|---|---|---|---|
| Category | Item | Stage 5 | Stage 4 | Stage 3 | Stage 2 | Stage 1 |
| Thinking in the design and creation of the program | Subdivision of the problem | Can subdivide the problem, it is possible to make the solution and other things a subdivided problem | It can be divided into several smaller problems associated with major problems | It can be reduced from a big problem into smaller problems | It is possible to find one small problem from a big problem | Cannot subdivide the problem |
| Analysis of events | It is the analysis of the events, the results of the analysis can be used in problem-solving and other things | Several factors (causes) related to an event can be found | You can find multiple factors (causes) for a certain event | You can find one factor (cause) about a certain event | Cannot analyze events | |
| Name | Definition | Details |
|---|---|---|
| Factor correspondence rate | X = A/B | A: Number of factors in the rubric that matches the evaluation objective B: Number of concepts in the evaluation objective |
| Intrinsic Consistency | X = A/(A − 1) + (1 − B/C) | A: Number of items B: Total variance of each item C: Variance of the total score |
| Item Correlation | Xn = A − Bn | A: Overall alpha coefficient Bn: Alpha coefficient when the nth item is deleted |
| Label | Subject | Number of Students | Number of Quizzes |
|---|---|---|---|
| A | Arithmetic | 47 | 13 |
| B | Science | 36 | 9 |
| C | Information | 18 | 10 |
| Q1 | Q2-1 | Q2-2 | Q2-3 | Q3-1 | Q3-2 | Q3-3 | Q3-4 | Q4-1 | Q4-2 | Q5 | Q6-1 | Q6-2 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sequence | 2 | 2 | |||||||||||
| Branch | 3 | ||||||||||||
| Repetition | 2 | 2 | |||||||||||
| Subdivision of the problem | 4 | 4 | 4 | 2 | 2 | 2 | 2 | 2 | |||||
| Analysis of events | 2 | 2 | 2 | 2 | |||||||||
| Extraction operation | 3 | 3 | |||||||||||
| Construction of the operation | 3 | 3 | |||||||||||
| functionalization | 2 | 2 | 2 | ||||||||||
| Generalization | 4 | 4 | 4 | ||||||||||
| Abstraction | 3 | 3 | 3 | ||||||||||
| Inference | 2 | 2 | 2 | ||||||||||
| Operator | 2 | 2 |
| Q1 | Q2-1 | Q2-2 | Q2-3 | Q3-1 | Q3-2 | Q4 | Q5 | Q6-1 | Q6-2 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Sequence | 2 | 2 | ||||||||
| Branch | 2 | 3 | ||||||||
| Repetition | 2 | 2 | ||||||||
| Subdivision of the problem | 2 | 2 | ||||||||
| Extraction operation | 3 | 3 | ||||||||
| Construction of the operation | 3 | 3 | ||||||||
| Operator | 2 | 2 |
| Q1 | Q2 | Q3 | Q4 | Q5 | Q6 | Q7 | Q8 | Q9 | Q10 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Sequence | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 |
| Branch | 3 | 3 | 3 | 3 | 3 | 3 | ||||
| Repetition | 3 | 3 | 3 | 3 | 3 | 3 | ||||
| Variable | 3 | 3 | 3 | 3 | 3 | 3 | ||||
| Array | 3 | |||||||||
| Function | 2 | |||||||||
| Analysis of events | 2 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 |
| Construction of the operation | 2 | |||||||||
| Functionalization | 2 | |||||||||
| Understanding of the program | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 |
| A | B | C | |
|---|---|---|---|
| KMO value | 0.519 | 0.709 | 0.541 |
| Q | Factor1 | Factor2 | Factor3 |
|---|---|---|---|
| Q1 | 0.403 | 0.099 | −0.153 |
| Q2-1 | −0.047 | 0.050 | 0.658 |
| Q2-2 | 0.163 | −0.015 | 0.700 |
| Q2-3 | 0.025 | 0.499 | 0.446 |
| Q3-1 | 0.971 | −0.087 | 0.024 |
| Q3-2 | 0.971 | −0.087 | 0.024 |
| Q3-3 | 0.928 | 0.091 | 0.008 |
| Q3-4 | 0.928 | 0.091 | 0.008 |
| Q4-1 | −0.126 | 0.869 | −0.001 |
| Q4-2 | 0.095 | 0.840 | −0.052 |
| Q5 | 0.134 | 0.263 | −0.006 |
| Q6-1 | −0.010 | −0.126 | 0.684 |
| Q6-2 | 0.352 | 0.485 | −0.076 |
| Q | Factor1 | Factor2 |
|---|---|---|
| Q1-1 | 0.18 | 0.30 |
| Q1-2 | −0.10 | 0.30 |
| Q2 | −0.11 | 0.58 |
| Q3-1 | 0.94 | −0.01 |
| Q3-2 | 0.99 | −0.01 |
| Q4 | 0.43 | 0.07 |
| Q5 | 0.03 | 0.55 |
| Q6-1 | −0.01 | 0.88 |
| Q6-2 | 0.40 | 0.46 |
| Q | Factor1 | Factor2 |
|---|---|---|
| Q1 | 0.10 | 0.68 |
| Q2 | 0.48 | 0.11 |
| Q3 | 0.10 | 0.84 |
| Q4 | 0.37 | 0.28 |
| Q5 | 0.80 | 0.03 |
| Q6 | 0.62 | −0.42 |
| Q7 | 0.48 | −0.44 |
| Q8 | 0.81 | 0.14 |
| Q9 | 0.30 | 0.28 |
| Q10 | 0.72 | 0.12 |
| A | B | C | |||
|---|---|---|---|---|---|
| Q | α | Q | α | Q | α |
| Overall | 0.841 | Overall | 0.767 | Overall | 0.778 |
| Q1 | 0.84 | Q1-1 | 0.723 | Q1 | 0.778 |
| Q2-1 | 0.841 | Q1-2 | 0.759 | Q2 | 0.756 |
| Q2-2 | 0.832 | Q2 | 0.728 | Q3 | 0.779 |
| Q2-3 | 0.831 | Q3-1 | 0.685 | Q4 | 0.760 |
| Q3-1 | 0.809 | Q3-2 | 0.677 | Q5 | 0.723 |
| Q3-2 | 0.809 | Q4 | 0.721 | Q6 | 0.769 |
| Q3-3 | 0.803 | Q5 | 0.717 | Q7 | 0.788 |
| Q3-4 | 0.803 | Q6-1 | 0.696 | Q8 | 0.714 |
| Q4-1 | 0.847 | Q6-2 | 0.685 | Q9 | 0.776 |
| Q4-2 | 0.835 | Q10 | 0.733 | ||
| Q5 | 0.847 | ||||
| Q6-1 | 0.842 | ||||
| Q6-2 | 0.831 | ||||
| Statistical Methods | A | B | C |
|---|---|---|---|
| Factor correspondence ratio | 1 | 0.86 | 0.89 |
| Internal consistency | 0.841 | 0.767 | 0.778 |
| Inter-item correlation | Q4-1/Q5/Q6-1 | N/A | Q7 |
| Question | A | B | C |
|---|---|---|---|
| Q1: Is the rubric-based assessment consistent with the purpose of the assessment? | Consistency. | Generally consistent | Generally consistent |
| Q2: Is it possible to evaluate the items for evaluation purposes using the rubric? | Evaluated | Generally evaluated | Generally evaluated |
| Q3: Do the rubric’s assessment items evaluate a consistent concept? | Evaluated | Generally evaluated | Generally evaluated |
| Q4: Are the rubric’s evaluation items appropriate in terms of consistency? | Generally appropriate | Reasonable | Generally appropriate |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saito, D.; Yajima, R.; Washizaki, H.; Fukazawa, Y. Validation of Rubric Evaluation for Programming Education. Educ. Sci. 2021, 11, 656. https://doi.org/10.3390/educsci11100656
Saito D, Yajima R, Washizaki H, Fukazawa Y. Validation of Rubric Evaluation for Programming Education. Education Sciences. 2021; 11(10):656. https://doi.org/10.3390/educsci11100656
Chicago/Turabian StyleSaito, Daisuke, Risei Yajima, Hironori Washizaki, and Yoshiaki Fukazawa. 2021. "Validation of Rubric Evaluation for Programming Education" Education Sciences 11, no. 10: 656. https://doi.org/10.3390/educsci11100656
APA StyleSaito, D., Yajima, R., Washizaki, H., & Fukazawa, Y. (2021). Validation of Rubric Evaluation for Programming Education. Education Sciences, 11(10), 656. https://doi.org/10.3390/educsci11100656







