Implementation of a Playful Microproject Based on Traditional Games for Working on Mathematical and Scientific Content
Abstract
:1. Introduction
1.1. Background
1.2. Game-Based Learning and STEAM Education
1.3. Learning Based on Traditional Games as an Intercultural Education Channel
1.4. Objectives
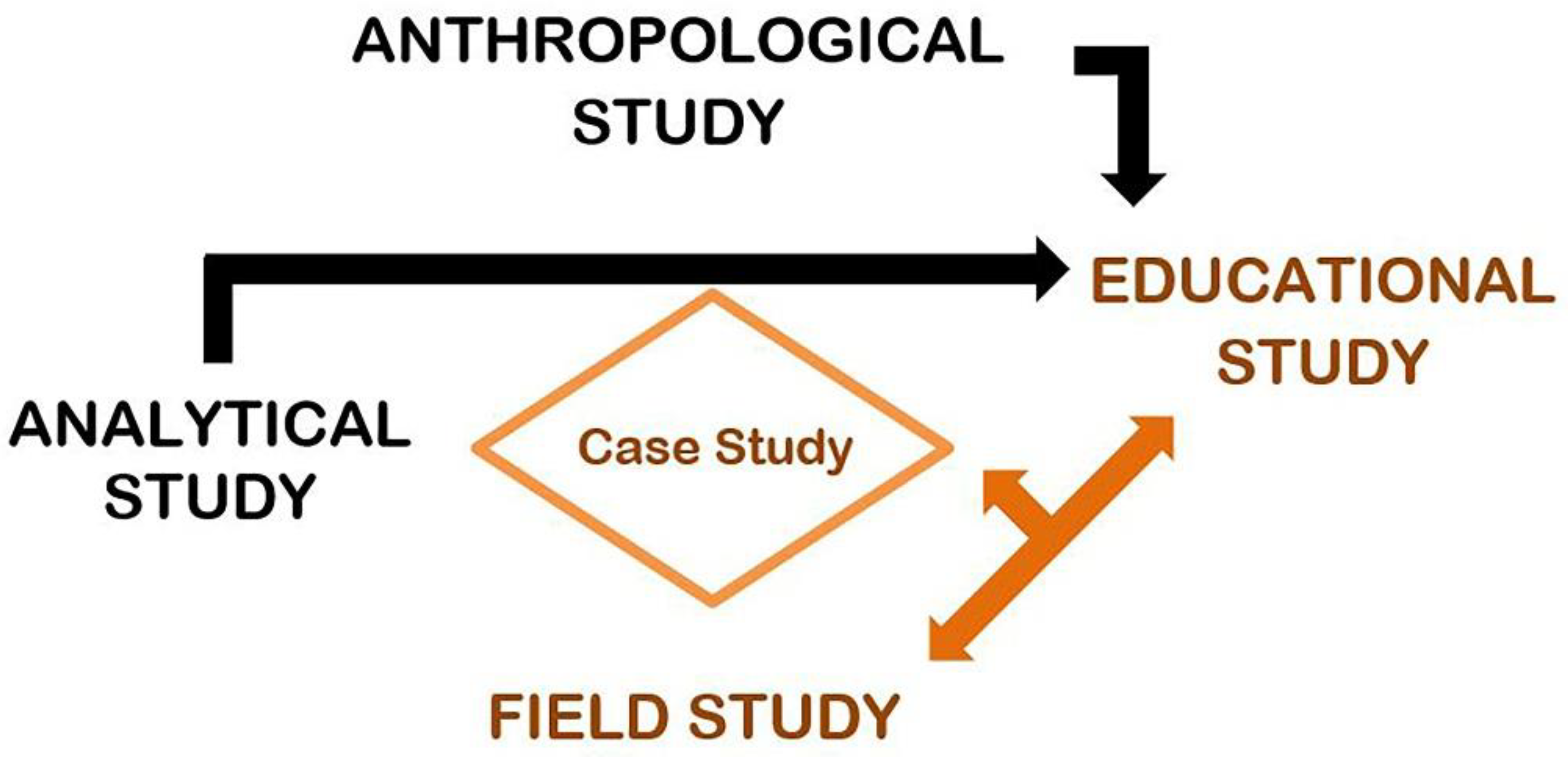
2. Materials and Methods
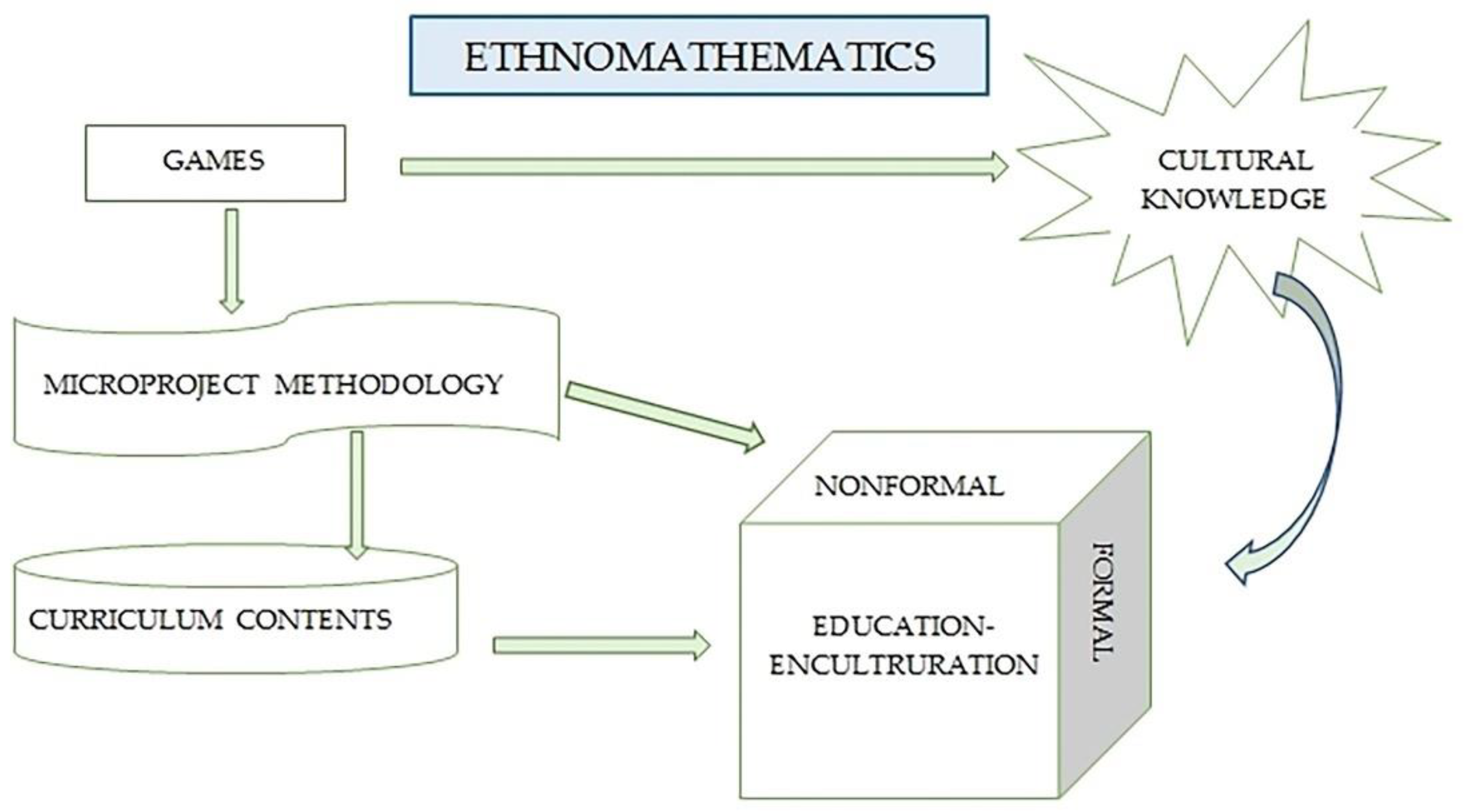
2.1. Educational Methodology. Playful Microproject
2.2. Research Methodology: Case Study
3. Results
3.1. Results of the Educational Study. Implementation of the Microproject
3.2. Research Results. Evidence of Activation of Mathematical and Scientific Content
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Player Code (N°, Boy: O/Girl: A, Years. Example: 1A9 = 1°, Girl, 9 Year Old) | Evidence Captured with Recorded Video. Quote Player Phrases or Gestures (Sessions 1–3) | Evidence Gathered by Direct Observation and Written in the Field Notebook (Sessions 1–3) | Situation: Playing (put X if applicable) | Situation: Making the Board and the Pieces (put X if applicable) |
| Category (from 1 to 21) |
| Game Pairs | Player Code | Gaming Place | Game Played |
|---|---|---|---|
| Pair 1 | 1-A-9 | ALFA play centre | The dog and the goats |
| 2-A-8 | ALFA play centre | ||
| Pair 2 | 3-O-9 | ALFA play centre | |
| 4-O-12 | ALFA play centre | ||
| Pair 3 | 5-O-7 | Neighbourhood community room | |
| 6-O-8 | Neighbourhood community room | ||
| Pair 4 | 7-A-7 | Neighbourhood community room | |
| 8-A-8 | Neighbourhood community room | ||
| Pair 5 | 9-A-8 | Maracena play centre | |
| 10-A-8 | Maracena play centre | ||
| Pair 6 | 11-A-8 | Maracena play centre | |
| 12-O-7 | Maracena play centre | ||
| Pair 7 | 13-A-7 | ALFA play centre | Torres de la Alhambra |
| 14-O-8 | ALFA play centre | ||
| Pair 8 | 15-O-8 | ALFA play centre | |
| 16-O-9 | ALFA play centre | ||
| Pair 9 | 17-A-10 | ALFA play centre | |
| 18-A-11 | ALFA play centre | ||
| Pair 10 | 19-O-11 | ALFA play centre | |
| 20-O-12 | ALFA play centre | ||
| Pair 11 | 21-O-9 | Maracena play centre | |
| 22-O-9 | Maracena play centre | ||
| Pair 12 | 23-A-10 | Maracena play centre | |
| 24-A-9 | Maracena play centre | ||
| Pair 13 | 25-A-11 | ALFA play centre | Mijnlieff |
| 26-A-11 | ALFA play centre | ||
| Pair 14 | 27-O-11 | ALFA play centre | |
| 28-O-12 | ALFA play centre | ||
| Pair 15 | 29-O-9 | Maracena play centre | |
| 30-O-9 | Maracena play centre | ||
| Pair 16 | 31-A-10 | Maracena play centre | |
| 32-A-9 | Maracena play centre |
References
- Huizinga, J. Homo Ludens, Ils 86, 1st ed.; Routledge: London, UK, 2013. [Google Scholar] [CrossRef]
- Huizinga, J. De lo lúdico y lo serio. In Acerca de los Límites Entre lo Lúdico y lo Serio en la Cultura; Aullón de Haro, P., Huizinga, J., Eds.; Casimiro Libros: Madrid, Spain, 2014; pp. 19–60. [Google Scholar]
- Benalcázar, M.M.B.; Guamán, J.L.U.; Torres-Toukoumidis, A. Análisis descriptivo del juego como herramienta para aprender sobre el patrimonio cultural: Estudio de caso. Estud. Pedagógicos 2020, 3, 33–44. [Google Scholar] [CrossRef]
- Cornellà, P.; Estebanell, M.; Brusi, D. Gamificación y aprendizaje basado en juegos. Enseñanza Cienc. Tierra 2020, 28, 5–19. [Google Scholar]
- Latorre, A.J. Juego y Educación: Aplicación de la Construcción y Uso de Juegos Educativos a los Procesos de Enseñanza y Aprendizaje; Dirección General de Promoción Educativa: Madrid, Spain, 2003. [Google Scholar]
- Glenberg, A.M.; Robertson, D.A. Indexical understanding of instructions. Discourse Process. 1999, 1, 1–26. [Google Scholar] [CrossRef]
- Garaigordobil, M. Juego Cooperativo y Socialización en el Aula, 1st ed.; Seco-Olea: Madrid, Spain, 1992. [Google Scholar]
- Piaget, J. La Formación del Símbolo en el Niño: Imitación, Juego y Sueño. Imagen y Representación; Fondo de Cultura Económica: Madrid, Spain, 2019. [Google Scholar]
- Vigotsky, L. Interacción entre enseñanza y desarrollo. Sel. Lect. Psicol. Edades 1988, 3, 37–45. [Google Scholar]
- Morris, B.; Croker, S.; Zimmerman, C.; Gill, D.; Romig, C. Gaming science: The “Gamification” of scientific thinking. Front. Psychol. 2013, 4, 607. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bergen, D. Play as the Learning Medium for Future Scientists, Mathematicians, and Engineers. Am. J. Play 2009, 4, 413–428. [Google Scholar]
- Espigares-Gámez, M.J.; Fernández-Oliveras, A.; Oliveras, M.L. Compilation of traditional games played in Jamaica: An ethnomathematical study for steam education. In Proceedings of the ICERI 2019 Conference, Sevilla, España, 11–13 November 2019; pp. 9643–9649. [Google Scholar]
- Espigares-Gámez, M.J.; Fernández-Oliveras, A.; Oliveras M., L. Games as STEAM learning enhancers. Application of traditional Jamaican games in Early Childhood and Primary Intercultural Education. Acta Sci. 2020, 4, 28–50. [Google Scholar] [CrossRef]
- Espigares-Gámez, M.J.; Fernández-Oliveras, A.; Oliveras, M.L. Instrumento para evaluar competencias matemáticas y científicas del alumnado que inicia Educación Primaria, mediante juegos. Rev. Paradig. 2020, 41, 326–359. [Google Scholar] [CrossRef]
- Bishop, A. El papel de los juegos en la educación matemática. UNO Rev. Didact. Mat. 1998, 8, 9–19. [Google Scholar]
- Espigares-Gámez, M.J.; Fernández-Oliveras, A.; Oliveras, M.L. Anthropological and analytical studies for the design of a playful microproject devoted to mathematics and science education. In Proceedings of the INTED2021 Proceedings, Online, 8–9 March 2021; pp. 1876–1881. [Google Scholar]
- Oliveras, M.L. El pensamiento creativo, la crítica y la comunicación en ICEm5. Rev. Latinoam. de Etnomatemática Perspect. Sociocult. de la Educ. Matemática 2015, 2, 4–10. [Google Scholar]
- D’Ambrosio, U.; Rosa, M. Um diálogo com Ubiratan D’Ambrosio: Uma conversa brasileira sobre etnomatemática. Rev. Latinoam. de Etnomatemática Perspect. Sociocult. de la Educ. Matemática 2008, 2, 88–110. [Google Scholar]
- D’Ambrosio, U. The program Ethnomathematics: Cognitive, anthropological, historic and socio-cultural bases. PNA 2018, 12, 229–247. [Google Scholar]
- Oliveras, M.L. Matemáticas en la Sociedad; Fuentes, J., Oliveras, M.L., Eds.; Repro Digital: Granada, Spain, 2000; ISBN 84-6070657-5. [Google Scholar]
- Oliveras, M.L. Etnomathematics and Etnodidactics. In Proceedings of the First International Conference on Ethnomathematics (ICEM 1), Granada, Spain, 2–5 September 1998; Fuentes, J., Ed.; University of Granada: Granada, Spain, 1998; pp. 91–106. [Google Scholar]
- D’Ambrosio, U. Ethnomathematics and its place in the history and pedagogy of mathematics. Learn. Math. 1985, 5, 44–48. [Google Scholar]
- Bishop, A. Mathematical Enculturation. A Cultural Perspective on Mathematics Education; Springer Science & Business Media: Berlin/Alemania, Germany, 1991. [Google Scholar]
- Gerdes, P. Ethnomathematics and Mathematics Education. In International Handbook of Mathematics Education; Bishop, A.E., Clements, K., Keitel, C., Kilpatrick, J., Laborde, C., Eds.; Kluwer Academic Publishers: Dordrecht, Germany, 1996; pp. 909–943. [Google Scholar]
- D’Ambrosio, U. Literacy, Matheracy, and Technoracy: A Trivium for Today. Math. Think. Learn. 1999, 1, 131–153. [Google Scholar] [CrossRef]
- Zaslavsky, C. Africa Counts: Number and Pattern in African Cultures; Lawrence Hill Books: Chicago, IL, USA, 1999. [Google Scholar]
- Ascher, M. Ethnomathematics. A Multicultural view of Mathematical Ideas; Brooks/Cole Co.: Pacific Grove, CA, USA, 1991. [Google Scholar]
- Powell, A.B.; Frankenstein, M. (Eds.) Ethnomathematics: Challenging Eurocentrism in Mathematics Education; State University of New York Press: Albany, NY, USA, 1997; p. 7. [Google Scholar]
- Knijnik, G.; Wanderer, F.; Giongo, I.; Duarte, C. Etnomatemática em Movi-Mento; Autentica: Belo Horizonte, Brazil, 2012. [Google Scholar]
- Barton, B. Mathematics, Education, and Culture: A Contemporary Moral Imperative. In Proceedings of the 13th International Congress on Mathematical Education, Hamburg, Germany, 24–31 July 2016; Springer: Berlin/Heidelberg, Germany, 2017; pp. 35–43. [Google Scholar] [CrossRef] [Green Version]
- Blanco-Álvarez, H.; Higuita, C.; Oliveras, M.L. Una mirada a la Etnomatemática y la Educación Matemática en Colombia: Caminos recorridos. Rev. Latinoam. de Etnomatemática Perspect. Sociocult. de la Educ. Matemática 2014, 7, 245–269. [Google Scholar]
- Fuentes Leal, C. Algunos enfoques de investigación en Etnomatemática. Rev. Latinoam. de Etnomatemática Perspect. Sociocult. de la Educ. Matemática 2014, 7, 155–170. [Google Scholar]
- D’Ambrosio, U. Etnomatemática. Entre las Tradiciones y la Modernidad; Limusa: México City, México, 2008. [Google Scholar]
- Rosa, M.; Orey, D. Etnomatemáticas: Los aspectos culturales de las matemáticas. Rev. Latinoam. de Etnomatemática Perspect. Sociocult. de la Educ. Matemática Perspect. Sociocult. Educ. Mat. 2011, 4, 32–54. [Google Scholar]
- Alsina i Pastells, À.; Planas Raig, N. Matemática Inclusiva: Propuestas Para una Educación Matemática Accesible; M Narcea: Madrid, Spain, 2008. [Google Scholar]
- De Guzmán, M. Enseñanza de las ciencias y la matemática. Rev. Iberoam. Educ. 2007, 43, 19–58. [Google Scholar]
- Espigares-Gámez, M.-J.; Fernández-Oliveras, A.; Oliveras, M.-L. Análisis de juegos. Catálogo de juegos tradicionales para trabajar áreas científicas y matemáticas. In Innovación Educativa en la Sociedad Digital; Sola, T., García, M., Fuentes, A., Rodríguez-García, A.M., López, J., Eds.; Dykinson: Madrid, España, 2019; pp. 2186–2200. [Google Scholar]
- Fernández-Oliveras, A.; Espigares-Gámez, M.J.; Oliveras, M.L. Teorizaciones para la tipificación de juegos con potencial educativo STEAM. In Innovación Educativa en la Sociedad Digital; Sola, T., García, M., Fuentes, A., Rodríguez-García, A.M., López, J., Eds.; Dykinson: Madrid, España, 2019; pp. 1645–1658. [Google Scholar]
- Chawla, L. Benefits of Nature Contact for Children. J. Plan. Lit. 2015, 4, 433–452. [Google Scholar] [CrossRef]
- Yakman, G.; Lee, H. Exploring the exemplary STEAM education in the US as a practical educational framework for Korea. J. Korean Assoc. Sci. Educ. 2012, 32, 1072–1086. [Google Scholar] [CrossRef] [Green Version]
- Cilleruelo, L.; Zubiaga, A. Una aproximación a la Educación STEAM. Prácticas educativas en la encrucijada arte, ciencia y tecnología. Actas Jorn. Psicodidáctica 2014, 4, 1–18. [Google Scholar]
- Sullivan, A.; Strawhacker, A.; Umaschi Bers, M. Dancing, Drawing, and Dramatic Robots: Integrating Robotics and the Arts to Teach Foundational STEAM Concepts to Young Children. In Robotics in STEM Education: Redesigning the Learning Experience; Khine: London, UK, 2017; pp. 231–260. [Google Scholar] [CrossRef]
- Oliveras, M.L. Etnomatemáticas Formación de Profesores e Innovación Curricular; Comares: Granada, Spain, 1996. [Google Scholar]
- Fernández-Oliveras, A.; Oliveras, M.L. Formación de maestros y Microproyectos curriculares. Rev. Latinoam. de Etnomatemática Perspect. Sociocult. de la Educ. Matemática 2015, 2, 472–495. [Google Scholar]
- Park, N.; Ko, Y. Computer education’s teaching learning methods using educational programming language based on STEAM education. In Proceedings of the 9th International Conference on Network and Parallel Computing (NPC), Gwangju, Korea, 6–8 September 2012; Park, J.J., Zomaya, A.A., Yeo, S.-S., Sahni, S.S., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 320–327. [Google Scholar]
- Oliveras, M.L. Etnomatemáticas. De la multiculturalidad al mestizaje. In Matemáticas e Interculturalidad, 2nd ed.; Goñi, J., Ed.; Graó: Barcelona, Spain, 2006; pp. 117–149. [Google Scholar]
- Craft, A. Creativity in the School; Beyond Current Horizons Project: London: UK, 2008. [Google Scholar]
- Ananiadou, K.; Claro, M. 21st Century Skills and Competences for New Millennium Learners in OECD Countries; OECD Publishing: Paris, France, 2009. [Google Scholar]
- Rotherham, A.J.; Willingham, D.T. 21st century skills, not new, but worthy challenge. Am. Educ. 2010, 1, 17–20. [Google Scholar]
- National Advisory Committee on Creative, Cultural Education. All our Futures: Creativity, Culture & Education; Department for Education and Employment: London, UK, 1999; Available online: http://sirkenrobinson.com/pdf/allourfutures.pdf (accessed on 11 July 2021).
- Pombo, L.; Marques, M.M. The potential educational value of mobile augmented reality games: The case of EduPARK app. Educ. Sci. 2020, 10, 287. [Google Scholar] [CrossRef]
- Yuste, F.C.; Piquet, J.D. Juegos manipulativos en la enseñanza de las matemáticas. UNO Rev. Didáctica Mat. 1996, 7, 71–80. [Google Scholar]
- Deulofeu, J. Una Recreación Matemática: Historias, en el Alumnado de Secundaria; Planeta: Barcelona, Spain, 2001. [Google Scholar]
- Zhao, Z.; Linaza, J.L. La importancia de los videojuegos en el aprendizaje y el desarrollo de niños de temprana edad. Electron. J. Res. Educ. Psychol. 2015, 2, 301–318. [Google Scholar] [CrossRef]
- Evans, M.A. Mobility, Games and Education. In Handbook of Research on Effective Electronic Gaming in Education; Hershley: New York, NY, USA, 2009; pp. 96–110. [Google Scholar]
- Tokac, U.; Novak, E.; Thompson, C. Effects of Game-Based Learning on Students’ Mathematics. Achievement: A Meta-Analysis. Representing Florida State University 2015. In Proceedings of the Statewide Graduate Student Research Symposium, Orlando, FL, USA, 24 April 2015. [Google Scholar]
- National Mathematics Advisory Panel. Foundations for Success: The Final Report of the National Mathematics Advisory Panel; U.S. Department of Education: Washington, DC, USA, 2008. [Google Scholar]
- Wilcox, S. Praxis Games. A Design Philosophy for Mobilizing Knowledge through Play. Am. J. Play 2019, 11, 156–182. [Google Scholar]
- González González, C.S. Estrategias para trabajar la creatividad en la Educación Superior: Pensamiento de diseño, aprendizaje basado en juegos y en proyectos. Rev. Educ. Distancia 2015, 1, 40. [Google Scholar]
- Méndez-Giménez, A.; Fernández-Río, J. Efectos del uso de materiales autoconstruidos sobre la satisfacción, el aprendizaje, las actitudes y las expectativas del alumnado de magisterio de la asignatura Juegos Tradicionales. In Proceedings of the International Congress AIESEP, A Coruña, Spain, 26–29 October 2010; pp. 26–36. [Google Scholar]
- LLeixà, T. Educación física y competencias básicas. Contribución del área a la adquisición de las competencias básicas del currículo. Tándem Didact. Educ. Física 2007, 23, 31–37. [Google Scholar]
- Perrotta, C.; Featherstone, G.; Aston, H.; Houghton, E. Game-Based Learning: Latest Evidence and Future Directions; National Foundation for Educational Research: London, UK, 2013. [Google Scholar]
- Kenny, R.; McDaniel, R. The role teachers’ expectations and value assessments of video games play in their adopting and integrating them into their classrooms. Br. J. Educ. Technol. 2011, 2, 197–213. [Google Scholar] [CrossRef]
- Kirriemuir, J.; McFarlane, A. Literature Review in Games and Learning; University of Bristol: Bristol, UK, 2004; Available online: http://www.futurelab.org.uk/download/pdfs/research/lit_reviews/Games_Review1 (accessed on 11 July 2021).
- Mitchell, A.; Savill-Smith, C. The Use of Computer and Video Games for Learning. A Review of the Literature; Learning and Skills Development Agency: London, UK, 2004; Available online: http://www.lsda.org.uk/files/PDF/1529.pdf (accessed on 11 July 2021).
- Higgins, E.; Grant, H.; Shah, J. Self-Regulation and quality of life: Emotional and nonemotional life experiences. In Well-Being: The Foundations of Hedonic Psychology; Kahneman, D., Diener, E., Schwarz, N., Eds.; Russell Sage Fundation: New York, NY, USA, 1999; pp. 244–266. [Google Scholar]
- Bonk, C.J.; Dennen, V.P. Massive Multiplayer Online Gaming: A Research Framework for Military Training and Education; University at Bloomington: Bloomington, IN, USA, 2005. [Google Scholar]
- López-Fernández, L. Aprendizaje Basado en Metodologías que Apoyan la Lúdica y el Juego. Master’s Thesis, Universidad de Almería, Almería, Spain, 2013. [Google Scholar]
- Paredes, J. Juego, Luego Soy. Teoría de la Actividad Lúdica; Wanceulen: Sevilla, Spain, 2003. [Google Scholar]
- Aroca, A. Universidad del Atlántico. Producciones Audiovisuales Etnomatematica (4 de Junio de 2021). Matemáticas Detrás de mi Casa. Serie Matemáticas en Juegos de Niñas y/o Niños. Vídeo 12. [Archivo de Vídeo]. Available online: https://www.youtube.com/watch?v=205hahmB38s (accessed on 11 July 2021).
- Aroca, A. Universidad del Atlántico. Producciones Audiovisuales Etnomatemática (19 de Junio de 2021). Matemáticas en la Gallina Pijabá. Serie Matemáticas en Juegos de Niñas y/o Niños. Vídeo 13. [Archivo de Vídeo]. Available online: https://www.youtube.com/watch?v=HTMkDKphWRU (accessed on 11 July 2021).
- Ferreira, D.; Palhares, P.; Silva, J.N. A perspective on games and patterns. In New Pedagogical Approaches in Game Enhanced Learning: Curriculum Integration; IGI Global: Hershey, PA, USA, 2013; pp. 60–80. [Google Scholar]
- Ferreira, D.; Palhares, P.; Silva, J.N. Mathematical games played by elementary school students. GRIM Quad. Ric. Didatt. Math. 2012, 22, 95–98. [Google Scholar]
- Ferreira, D.; Palhares, P.; Silva, J.N. Padrões e jogos matemáticos. Rev. Eletron. Educ. Mat. 2008, 3, 30–40. [Google Scholar]
- Palhares, P. O Jogo e o Ensino/Aprendizagem da Matemática; Instituto Politécnico de Viana do Castelo, Escola Superior de Educação: Viana do Castelo, Portugal, 2004. [Google Scholar]
- Yagüe, V. Juegos de Ayer y de Siempre; Madrid SL: Madrid, Spain, 2002. [Google Scholar]
- Trigueros, C. Nuevos Significados del Juego Tradicional en el Desarrollo Curricular de la Educación Física en Centros de Educación Primaria de Granada. Ph.D. Thesis, Universidad de Granada, Granada, Spain, 12 January 2020. [Google Scholar]
- Estrada, J.A.C.; González-Mesa, C.G.; Méndez-Giménez, A.; Fernández-Río, J. Achievement goals, social goals, and motivational regulations in physical education settings. Psicothema 2011, 1, 51–57. [Google Scholar]
- Gros, B. La dimensión socioeducativa de los videojuegos. Edutec Rev. Electron. Tecnol. Educ. 2000, 23, 1–11. Available online: http://edutec.rediris.es/Revelec2/Revelec12/gros.pdf (accessed on 11 July 2021).
- Oliveras, M.L. Microproyectos Para La Educación Intercultural En Europa. UNO Rev. Didact. Mat. 2005, 38, 70–81. [Google Scholar]
- Baute, J. Juego de la dama. Rev. Bien Me Sabe 2008, 892, 4–8. Available online: https://www.bienmesabe.org/noticia/buscar?q=833 (accessed on 11 July 2021).
- Molina, J. Conocimientos Científicos y Técnicos de los Guanches; InfoNorte Digital: Galdar, Spain, 2003. [Google Scholar]
- Bien Me Sabe. Available online: https://www.bienmesabe.org/noticia/2008/Octubre/juego-de-la-dama (accessed on 11 July 2021).
- Asociación Cultural Jugamos Todos. Las Torres de la Alhambra. Available online: https://www.jugamostodos.org/index.php/noticias-en-espana/en-produccion/3196-las-torres-de-la-ahambra (accessed on 11 July 2021).
- Gutiérrez Perera, C.S. Programación Didáctica de la Asignatura de 4° de ESO Trabajo Monográfico de Investigación: “Juegos de Mesa del Mundo y Etnomatemáticas”; University of Valencia: Valencia, Spain, 2014. [Google Scholar]
- Hoopwood Games. Available online: https://www.hopwoodgames.com/shop-1/mijnlieff (accessed on 11 July 2021).
- Attia, P. La Muy, Muy Larga Pero Imprescindible Historia de los Juegos de Mesa; Magnet: Madrid, Spain, 2016; Available online: https://magnet.xataka.com/en-diez-minutos/la-larga-historia-de-los-juegos-de-mesa (accessed on 11 July 2021).
- Cohat, I. Los Vikingos, Reyes de los Mares; Aguilar: Madrid, Spain, 1989. [Google Scholar]
- Velasco, M. Breve Historia de los Vikingos.; Nowtilus: Madrid, Spain, 2009. [Google Scholar]
- Boardspace. Available online: https://www.boardspace.net/english/about_mijnlieff.html (accessed on 11 July 2021).
- Uplayit. Available online: https://www.uplay.it/gioco-da-tavolo-Mijnlieff.html (accessed on 11 July 2021).
- The Abstract Rat. Available online: http://www.theabstractrat.com/reviews/mijnlieff (accessed on 11 July 2021).
- El Rayón Artesanías. Available online: https://elrayon.es/oraculos/24-runas-vikingas-futhark.html (accessed on 11 July 2021).
- Berelson, B. Content Analysis in Communication Researches. Foundations of Communications Research; Glencoe: New York, NY, USA, 1952. [Google Scholar]
- Bardin, L. El Análisis de Contenido; Akal: Madrid, Spain, 1986. [Google Scholar]
- D’Ambrosio, U. La integración de la matemática con las ciencias. Mat. Rev. Digit. Divulg. Mat. Real Soc. Mat. Esp. 2005, 1. Available online: http://www.matematicalia.net/index.php?option=com_content&task=view&id=27&Itemid=27 (accessed on 11 July 2021).
- Huxley, J.S. Guest editorial: Evolution cultural and biological. In Yearbook of Anthropology; The University of Chicago Press: Chicago, IL, USA, 1955; pp. 2–25. [Google Scholar]
- White, R.T. Learning Science; Basil Blackwell: Oxford, UK, 1988. [Google Scholar]
- Cano, E. The rubrics as an assessment tool of competency in higher education: Use or abuse? Profesorado 2015, 19, 265–280. Available online: https://recyt.fecyt.es/index.php/profesorado/article/view/41533 (accessed on 11 July 2021).




| Area | Type | Category | Meaning Contextualized in the Microproject Activities |
|---|---|---|---|
| Mathematics | Artefacts: Game materials | 1 Identifying flat shapes and three-dimensional bodies | Distinguishing regular polygons and polyhedrons and assigning them their name |
| 2 Situating oneself on plane and space | Distinguishing different positions with regards to some references (sides of the playing board and the outside) | ||
| Mentifacts: Game objectives and challenges | 3 Making relationships of order | Sequencing elements spatially or temporally and/or numbering them with ordinals | |
| 4 Making classifications | Grouping objects that share one or more properties, separating them from those that lack them, forming subgroups or classes | ||
| 5 Making counts | Considering the discreet quantitative aspect of a group, assigning it a natural number (can be game pieces or phases) | ||
| 6 Recognizing regularities | Appreciating that patterns are repeated | ||
| Sociofacts: Game rules | 7 Giving exact and approximate measurements | Making measurements of magnitude with units already established or conceived by the players | |
| 8 Posing numerical questions | Quantifying aspects that require communication, with the aid of numbers for explaining them | ||
| 9 Ascertaining geometric aspects | Posing questions on spatial situations and shapes | ||
| Sciences | Artefacts: Game materials | 10 Recognising length | Understanding the linear distance between two points (a dimension of the board) |
| 11 Recognizing the surface area and volume of a body | Differentiating between two and three dimensions (flat board and pieces, respectively) | ||
| 12 Identifying properties of materials | Intuitively understanding approximate values of physical properties of materials (handled for making game board and pieces) | ||
| Mentifacts: Game objectives and challenges | 13 Exercising observation | Paying attention (visually and though hearing, without speaking simultaneously) | |
| 14 Proposing hypotheses | Thinking about something that could be done and stating it | ||
| 15 Recognizing alternatives | Realizing that you can do something different to that already thought about or done | ||
| 16 Demonstrating logical reasoning | Ordering ideas with a cause-effect criterion (coming to relate moves made in the game) | ||
| 17 Designing strategies | Thinking about and expressing ways of acting (to win the game) | ||
| Sociofacts: Game rules | 18 Experimenting | Making tests before acting or doing various things to see their effects | |
| 19 Evaluating results | Observing something that happened and making an assessment of it | ||
| 20 Drawing conclusions | Making inferences or other logical reasoning with a view to guidelines for the future | ||
| 21 Predicting | Anticipating something (that could occur in the game) |
| Category | Player Code/Evidence Situation | Example |
|---|---|---|
| 1. Identifying flat shapes and three-dimensional bodies | All players show evidence of this category. Making the game board and pieces | It is observed that they all recognise square and rectangle shapes when making the board. |
| 3. Making relationships of order | Players showing evidence of this category: 1A9, 3A9, 4O12, 8A8, 9A9, 10A8, 11A9, 12O12. Making the game board and pieces and Playing | Establish a numerical order when placing the tiles while playing (1,2,3…). A player states the number of steps followed for making the board (12O12) |
| 4. Making classifications | All players show evidence of this category. Making the game board and pieces | When looking for objects to make the pieces, they classify them by colour, creating the white and the black types. A player sort the chips by shape, quantity and colour (1A9) |
| 5. Making counts | Players showing evidence of this category: 1A9, 2A8, 3A9, 4O12, 5O7, 7A7, 8A8, 9A9, 10A8, 11A9, 12O12. Making the game board and pieces | They count the white pieces |
| 6. Recognizing regularities | Players showing evidence of this category: 2A8, 3A9, 4O12, 5O7, 8A8, 9A9, 10A8, 11A9, 12O12. Making the game board and pieces and playing | “I’ve taken 2 pieces in a row, then one and now another 2” Decorate the box, in which to keep the game, drawing a red flower, followed by a rose, repeating this pattern regularly (4O12). |
| 7. Giving exact and approximate measurements | Players showing evidence of this category: 1A9, 2A8, 3A9, 4O12, 5O7, 6O8, 8A8, 9A9, 10A8, 11A9, 12O12. Making the board. | A player realises that the width of the board corresponds to a succession of various pieces in a row (12O12) |
| 8. Posing numerical questions | Players showing evidence of this category: 1A9, 2A8, 3A9, 4O12, 5O7, 7A7, 8A8, 9A9, 10A8, 11A9, 12O12. Playing | “I’ve lost 5 pieces, only 3 of the ones I’ve got left can’t be taken by the dog” “You’d take more pieces if you moved 2 rows forward” |
| 10. Recognizing length | All players show evidence of this category Playing | They estimate distances between points during their turns playing |
| 11. Recognizing the surface area and volume of a body | All players show evidence of this category Making the game board and pieces | When constructing the game materials, they distinguish flat figures (board) from three-dimensional bodies (pieces) |
| 12. Identifying properties of materials | Players showing evidence of this category: 2A8, 3A9, 4O12, 9A9, 12O12. Making the game board and pieces | They identify hardness when selecting materials to make the board and pieces |
| 13. Exercising observation | All players except one (4O12) show evidence of this category. Playing | They watch the game closely in order to know what to do while play |
| 14. Proposing hypotheses | Players showing evidence of this category: 1A9, 2A8, 3A9, 10A8, 11A9, 12O12. Playing | “I don’t think I’ll win because wherever I move he can take me” |
| 15. Recognizing alternatives | Players showing evidence of this category: 1A9, 12O12. Playing | “It’s better to keep this piece for the end of the game” |
| 16. Demonstrating logical reasoning | Players showing evidence of this category: 1A9, 2A8, 3A9, 4O12, Playing | “If I move them all together I’ll trap it” |
| 17. Designing strategies | Players showing evidence of this category: 9A9, 11A9, 12O12 Playing | “When there are fewer goats left, I’ll move the ones in the corners” |
| 18. Experimenting | Players showing evidence of this category: 1A9, 12O12. Playing | Only moves 2 pieces in order to avoid the rest being taken |
| 19. Evaluating results | Players showing evidence of this category: 1A9, 9A9, 11A9, 12O12. Playing | “I played terribly” |
| 20. Drawing conclusions | Players showing evidence of this category: 1A9, 3A9, 9A9, 11A9, 12O12. Playing | “I should have moved another piece that wasn’t so close to the dog” |
| Category | Player Code/Evidence Situation | Example |
|---|---|---|
| 1. Identifying flat shapes and three-dimensional bodies | All players show evidence of this category. Making the game board and pieces | They find the irregular shape of the board strange: “It looks like a rectangle with a square inside” (25O9). |
| 2. Situating oneself on plane and space | Players showing evidence of this category: 13A7, 14O8, 21O9, 23A10. Playing | They begin on the initial starting squares and must move to adjacent squares, not diagonally and they do it correctly |
| 3. Making relationships of order | All players show evidence of this category. Making the game board and pieces and Playing | They order temporally: they indicate that, firstly, you have to make the board and pieces and then, play |
| 4. Making classifications | All players show evidence of this category. Making the game board and pieces and Playing | They classify the pieces by their colour or design |
| 5. Making counts | All players show evidence of this category. Making the game board and pieces | They count how many pieces there are per player and in total. A player counts the tower battlements and how many towers have windows (23A10) |
| 6. Recognizing regularities | All players show evidence of this category. Making the game board and pieces | They establish a pattern of various colours when decorating the board simulating marquetry. When cutting out the battlements, a player indicates that “you have to cut one then not cut the other” (18A11), along with colouring the board with two colours. |
| 7. Giving exact and approximate measurements | A player show evidence of this category: 20O12. Making the game board and pieces | They measure with a ruler. A player calculates the measurements of the board counting the squares (20O12). |
| 8. Posing numerical questions | Players showing evidence of this category: 15O8, 16O9, 17A10, 18A11, 19O11, 20O12, 23A10, 24A9. Playing | “If I move 2 pieces I can block you”. “You’re on square 4, you can’t jump over me on 7” |
| 9. Ascertaining geometric aspects | Players showing evidence of this category: 13A7, 15O8, 16O9, 17A10, 18A11, 19O11, 20O12, 23A10, 24A9. Playing | “If I squash the tower flat, it will look like another square”. “I’m moving along the corners of the board, let’s see what happens”. |
| 10. Recognizing length | All players show evidence of this category. Playing | They estimate distances between points during their turns playing |
| 11. Recognizing the surface area and volume of a body | All players show evidence of this category. Making the game board and pieces | They differentiate flat shapes on a surface of three-dimensional bodies, as the pieces are parallelepiped towers. When they make them they ask questions and speak about it |
| 12. Identifying properties of materials | Players showing evidence of this category: 13A7, 15O8, 16O9, 17A10, 18A11, 19O11, 20O12, 22O9, 23A10, 24A9. Making the game board and pieces | They identify hardness in the board material (box lid) and flexibility in the cartons they cut out to make the pieces |
| 13. Exercising observation | All players show evidence of this category. Playing | They watch the games carefully |
| 14. Proposing hypotheses | Players showing evidence of this category: 14O8, 15O8, 16O9, 17A10, 18A11, 19O11,20O12, 21O9, 22O9, 23A10, 24A9. Playing | “If you pass the middle of the board you’ve won, because it’s easier to move forward”. “If I move this piece, you can’t move yours and I win on the next move”. |
| 15. Recognizing alternatives | Players showing evidence of this category: 18A11, 19O11, 20O12, 21O9 Playing | A player moves the piece he or she has moved incorrectly back, before ending the move (18A11). |
| 16. Demonstrating logical reasoning | Players showing evidence of this category:15O8, 16O9, 17A10, 18A11, 19O11, 20O12, 21O9, 22O9, 23A10, 24A9. Playing | “If I jump over 3, I win”. “If I go far enough past you, I win, because you’re not going to get me moving one by one”. “I move my towers together to make a barrier”. “You can’t draw” |
| 17. Designing strategies | Players showing evidence of this category: 16O9, 17A10, 18A11, 19O11, 20O12, 21O9, 22O9, 23A10, 24A9. Playing | A player tries to leave a space to take two at a time. Another only moves the forward pieces. Another doesn’t start from the initial squares, saying it’s to prevent the opponent from getting there. Another player moves the pieces together. |
| 19. Evaluating results | Players showing evidence of this category:7A10, 18A11, 19O11, 20O12, 21O9, 23A10. Playing | “I’m not going to do that anymore”. “I’m not going to start anymore”. “I should’ve moved another one”. “I don’t start first, that’s why you always get there before”. |
| 20. Drawing conclusions | Players showing evidence of this category: 18A11, 19O11, 20O12, 21O9. Playing | “I’m going to think more in the next one”. “I’ll move them all together in the next one”. “I’m not going to do that anymore”. “I’m not going to start anymore”. |
| Category | Player Code/Situations | Example |
|---|---|---|
| 1. Identifying flat shapes and three-dimensional bodies | All players show evidence of this category. Making the game board and pieces and playing. | They recognise circle, rectangle and square in the pieces and board |
| 2. Situating oneself on plane and space | All players show evidence of this category. Playing. | When playing, they understand spatial situations represented by the symbols of the pieces |
| 4. Making classifications | All players show evidence of this category. Making the game board and pieces and playing | They classify the pieces by the different symbols and colours while they make them. |
| 5. Making counts | All players show evidence of this category. Making the game board and pieces | They count the total pieces in the game and the number of different symbols |
| 6. Recognizing regularities | Players showing evidence of this category: 27O11, 28O12, 31A10, 32A9 Making the game board and pieces | They recognise the repetition of patterns in the designs of the pieces and different figures when drawing on the box (one player draws a mandala: 27O11) |
| 7. Giving exact and approximate measurements | All players show evidence of this category. Making the game board and pieces | They measure well with the ruler. Only one player tries another measuring system, placing the pieces in a row to measure the width of the box (28O12) |
| 8. Posing numerical questions | Players showing evidence of this category: 25A11, 26A11, 27O11, 28O12, 30O9, 31A10, 32-A-9. Playing. | One player establishes a number for each piece. Another calculates how many pieces the opponent has left after each move. Another player mentally divides the pieces when distributing them Another adds up the empty spaces to know how many moves he has left and to calculate whether he has enough pieces to win |
| 9. Ascertaining geometric aspects | Players showing evidence of this category: 25A11, 27O11, 28O12, 31A10, 32A9. Playing. | A player creates a mandala combining shapes (27O11). Another uses the pieces as a means for calculating the sizes of the squares that make up the board. Another player relates the shape of the pieces to the squares. |
| 10. Recognizing length | All players show evidence of this category. Making the game board and pieces | They take the measurements of the length of the board and the pieces, comparing them |
| 11. Recognizing the surface area and volume of a body | Players showing evidence of this category: 25A11, 26A11, 27O11, 28O12, 30O9, 31A10, 32-A-9. Making the game board and pieces | They differentiate flat figures (pieces and board) and three-dimensional bodies, with volume (the box) |
| 13. Exercising observation | All students show evidence of this category. Creating the board and pieces and playing | They closely observe the preparation of the materials by the other pairs and then their way of playing. |
| 14. Proposing hypotheses | Player showing evidence of this category: 30O9 Playing. | “I’m going to play this piece, because with this other one X can’t move to this square anymore and so I can move there afterwards” “If I place this piece first it’s better, because it makes it difficult for X to be able to play hers” |
| 16. Demonstrating logical reasoning | Players showing evidence of this category: 25A11, 26A11, 27O11, 28O12, Playing | “If you put the first piece in the centre it’s more difficult for you to win because the other player has more space to put his pieces”, “I’m not moving this piece because X only has one left and if I do he beats me”, “If I play this piece, X wins because then I’m not going to be able to play the one I have left” |
| 17. Designing strategies | Players showing evidence of this category: 25A11, 26A11, 27O11, 28O12, 30O9, 31A10. Playing | “I’ve done a good move because X hasn’t been able block me”, “If I move this piece, it’s not good for my opponent”. “I’m going to play this piece, because with this other one X can’t move to this square anymore and so I can move there afterwards” |
| 18. Experimenting | All students show evidence of this category. Making the board and pieces | They try out materials and designs on the construction of the pieces and the board. |
| 19. Evaluating results | All students show evidence of this category. Making the board and pieces and Playing | “This game really helps you to concentrate”, “This game is more complicated than Three in a Row because it has symbols” “At the beginning I found it hard to understand it because I got confused with the symbols, but then it was easy because the picture looked like what you had to do”. |
| 20. Drawing conclusions | All students show evidence of this category. Creating the board and pieces and Playing | “I shouldn’t have put that piece there”, “I have to practice more”, “I have good strategies which is why I always win” |
| 21. Predicting | Player showing evidence of this category: 28O12. Playing | “The next game, I’ll keep this piece for the end” |
| Category | Relative Frequency (%) | |||
|---|---|---|---|---|
| The Dog and the Goats (N = 12) | The Towers of the Alhambra (N = 12) | Mijnlieff (N = 8) | Playful Microproject (N = 32) | |
| 1 | 100 | 100 | 100 | 100 |
| 2 | 0 | 33 | 100 | 37 |
| 3 | 67 | 100 | 0 | 63 |
| 4 | 100 | 100 | 100 | 100 |
| 5 | 88 | 100 | 100 | 96 |
| 6 | 75 | 100 | 50 | 89 |
| 7 | 92 | 8 | 100 | 63 |
| 8 | 50 | 66 | 88 | 88 |
| 9 | 0 | 74 | 63 | 43 |
| 10 | 100 | 0 | 100 | 63 |
| 11 | 100 | 100 | 88 | 97 |
| 12 | 38 | 84 | 0 | 49 |
| 13 | 92 | 100 | 100 | 97 |
| 14 | 50 | 92 | 13 | 56 |
| 15 | 16 | 33 | 0 | 19 |
| 16 | 33 | 83 | 50 | 56 |
| 17 | 25 | 75 | 75 | 56 |
| 18 | 16 | 0 | 95 | 30 |
| 19 | 33 | 50 | 100 | 56 |
| 20 | 42 | 33 | 100 | 53 |
| 21 | 0 | 0 | 13 | 3 |
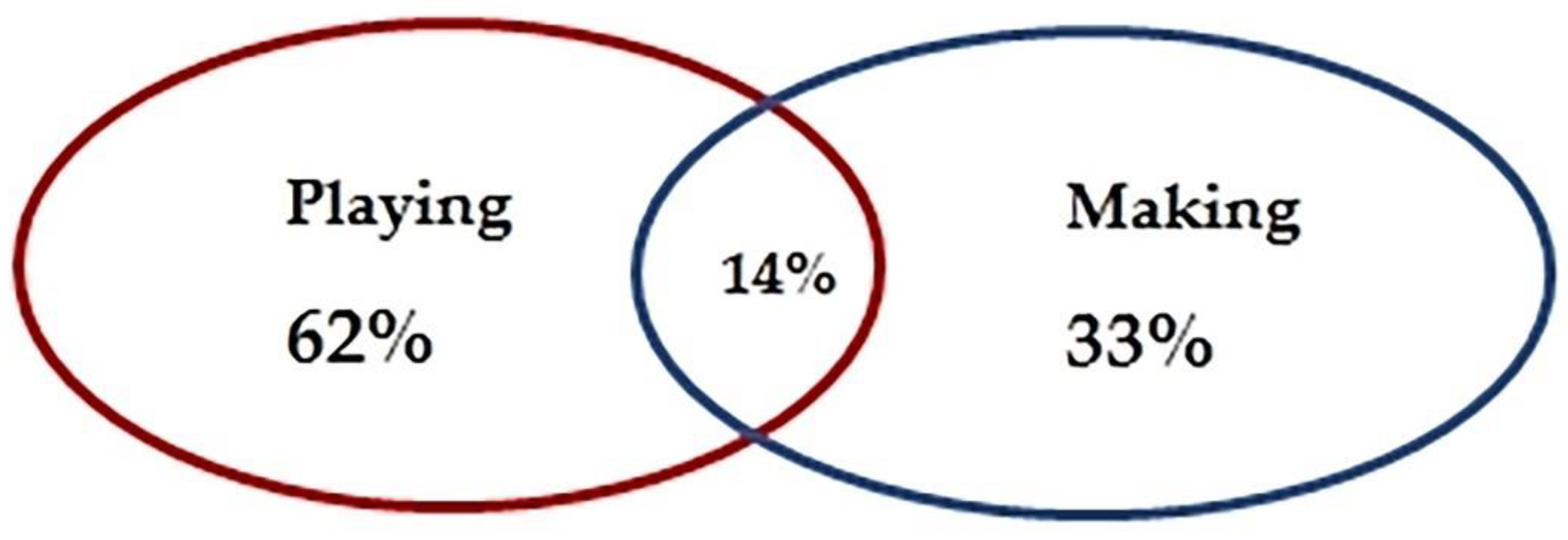
| Situations | Playing | Making the Board and Pieces | ||||||
|---|---|---|---|---|---|---|---|---|
| Total Evidence/Category | Total Evidence/Category | |||||||
| Games | The Dog and the Goats | The Towers of the Alhambra | Mijnlieff | The Dog and the Goats | The Towers of the Alhambra | Mijnlieff | ||
| Category | ||||||||
| 1. Identifying flat shapes and three- dimensional bodies | X | X | 2 | X | X | X | 3 | |
| 2. Situating oneself on plane and space | X | X | 2 | 0 | ||||
| 3. Making relationships of order | X | X | 2 | X | X | 2 | ||
| 4. Making classifications | X | 1 | X | 1 | ||||
| 5. Making counts | X | X | 2 | X | X | X | 3 | |
| 6. Recognizing regularities | 0 | X | X | X | 3 | |||
| 7. Giving exact and approximate measurements | X | 1 | X | X | X | 3 | ||
| 8. Posing numerical questions | 0 | X | X | X | 3 | |||
| 9. Ascertaining geometric aspects | X | X | X | 3 | 0 | |||
| 10. Recognizing length | X | X | 2 | 0 | ||||
| 11. Recognizing the surface area and volume of a body | X | X | X | 3 | X | 1 | ||
| 12. Identifying properties of materials | 0 | X | X | 2 | ||||
| 13. Exercising observation | 0 | X | X | X | 3 | |||
| 14. Proposing hypotheses | 0 | X | X | 2 | ||||
| 15. Recognizing alternatives | X | X | 2 | 0 | ||||
| 16. Demonstrating logical reasoning | X | X | X | 3 | X | 1 | ||
| 17. Designing strategies | X | X | X | 3 | 0 | |||
| 18. Experimen-ting | X | X | 2 | 0 | ||||
| 19. Evaluating results | X | X | 2 | 0 | ||||
| 20. Drawing conclusions | X | X | X | 3 | 0 | |||
| 21. Predicting | X | 1 | X | 1 | ||||
| Total game/evidences | 15 | 13 | 12 | 8 | 9 | 10 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fernández-Oliveras, A.; Espigares-Gámez, M.J.; Oliveras, M.L. Implementation of a Playful Microproject Based on Traditional Games for Working on Mathematical and Scientific Content. Educ. Sci. 2021, 11, 624. https://doi.org/10.3390/educsci11100624
Fernández-Oliveras A, Espigares-Gámez MJ, Oliveras ML. Implementation of a Playful Microproject Based on Traditional Games for Working on Mathematical and Scientific Content. Education Sciences. 2021; 11(10):624. https://doi.org/10.3390/educsci11100624
Chicago/Turabian StyleFernández-Oliveras, Alicia, María José Espigares-Gámez, and María Luisa Oliveras. 2021. "Implementation of a Playful Microproject Based on Traditional Games for Working on Mathematical and Scientific Content" Education Sciences 11, no. 10: 624. https://doi.org/10.3390/educsci11100624
APA StyleFernández-Oliveras, A., Espigares-Gámez, M. J., & Oliveras, M. L. (2021). Implementation of a Playful Microproject Based on Traditional Games for Working on Mathematical and Scientific Content. Education Sciences, 11(10), 624. https://doi.org/10.3390/educsci11100624






