Using Cases as a Means to Discuss Errors in Mathematics Teacher Education

Abstract

Errors are a major component of the pedagogical content knowledge (PCK) needed for teaching mathematics. In this study, 25 prospective teachers (PTs) in high schools were invited to solve a trigonometric task that had been assigned to high-school students and, subsequently, to relate to an authentic solution containing mathematical errors, which was presented in a dialogue by a pair of students. While all PTs reached the final, correct solution, eight provided only one of the two results in one step of the solution. Almost all (23) PTs identified at least one of the students’ errors. The case raised issues regarding the steps that should be written in a solution and the role of drawings in mathematical problems. This article suggests that exposing PTs to authentic teaching cases provides opportunities to discuss subtle issues related to their own mathematical knowledge and to obstacles that their future students might encounter when solving such tasks.

1. Introduction

An important trend in mathematics education has been the study of students’ ways of thinking about mathematical concepts and processes. This body of knowledge includes numerous documented instances of errors that are frequently made by students during the learning process [1,2,3]. A complementary body of knowledge (e.g., [4,5,6]) describes teachers’ knowledge and their attitudes towards students’ mathematical errors, and provides evidence that mathematics teachers’ content knowledge and their beliefs about errors that might occur during the learning process have considerable impact on their error-handling practices and on their teaching. Accordingly, there are consistent calls to raise the issue of addressing students’ errors in the education of mathematics teachers.

One way of educating mathematics teachers on how to address errors is through presenting and discussing cases of students’ mistakes [7,8,9]. This article describes a case that was presented to prospective secondary mathematics teachers during their studies towards a certificate for mathematics teaching in secondary schools. The case relates to a trigonometric task that was assigned to students in grade 11, focusing on a dialogue containing mathematical errors between two students who were solving the task. The prospective teachers (PTs) were asked to solve the task and to evaluate the incidences in the students’ dialogue.

The article centers on two essential steps that a teacher should take before determining how to handle an error. The first is to correctly solve the related task, and the second is identify the error (or the errors) that the students made when solving the task. Accordingly, this article describes the prospective teachers’ solutions to the trigonometric task and their reactions to the dialogue. This article focuses on two specific questions: a) In what ways (correct and incorrect) did the PTs solve the task? b) What errors did the PT’s identify in the students’ dialogue and how did they explain why they were errors?

2. Theoretical Background

Diverse views of errors, their role in the learning process, and approaches to student errors that occur during the teaching process are described in the mathematics education literature. Some articles and books describe attempts to create sequences of error-free instruction (e.g., [10]), while others suggest ways of using the information that errors provide for diagnosing students’ difficulties and consequently implementing remediation [1,11]. A different approach calls for using errors as a productive platform for stimulating student thinking about mathematical concepts and procedures (see, for instance, [12,13,14,15]). Regardless of the specific view of errors and their role in the learning and teaching process, teachers should be able to provide a correct solution to a given task and differentiate between correct and incorrect solutions that are given by their students to this task. In addition, teachers should be able to identify students’ misconceptions and the possible reasons for those misconceptions.

The views that errors are a natural, unavoidable part of the learning process, that they are part of the students’ ways of thinking, and that they occur during the learning process are regarded as some of the major components of the PCK needed for teaching in general [16] and for teaching mathematics in particular [17]. The realization of the important role that PCK plays in instruction has led to various suggestions of ways to address students’ ways of thinking in mathematics teacher education, in teacher education, and in the professional development of mathematics teachers [18,19]. One way that has been suggested is to describe cases showcasing students’ ways of thinking, and to analyze these cases. This paper focuses on such a case.

Case use in teacher education began intensively in 1986, when Lee Shulman proposed ”case knowledge” as a component of teacher knowledge. In his seminal work entitled ”Those who understand: Knowledge growth in teaching”, Shulman asserts that case knowledge is an essential form of knowledge needed for instruction. He noted that a case should be ”a case of something… or an instance of a larger case” [16] (p. 11). This paper focuses on one instance of a larger case; namely, a case of using errors to enhance prospective mathematics teachers’ mathematical knowledge and PCK.

Common types of cases that are employed in mathematics teacher education include exemplars [20], narratives [21,22], video cases [23], and problem situations [24,25]. The case presented in this paper could be categorized as a specific type of problem situation case. Problem situation cases are classroom situations involving mathematics, in which a problem, dilemma, debate, or some form of tension is involved [26]. They may be real events that took place in the classroom, or hypothetical situations based on students’ ways of thinking and conceptions as identified by researchers and, through teachers’ personal experience. Problem situations are relatively short; some focus on fostering mathematical content knowledge, which might be challenging for the learners. Others focus on didactical issues, aiming to enhance the learners’ PCK by addressing issues, such as what the students understands and what they do not understand.

Problem situations often introduce an erroneous solution proposed by students. The case presented in the current study is such a case. The PTs were invited to provide their own solutions to the task and to detect the errors in the solutions provided by the students. The aim of presenting this problem situation to the PTs was twofold: to enhance the PTs’ own mathematical content knowledge, and to increase their sensitivity towards possible factors that may constitute hurdles for their future students.

This paper focuses on PTs’ own solutions (correct and incorrect) to a given task and on their evaluation of the correctness of a solution that was provided by a pair of students to this task.

3. Method

Twenty-five prospective teachers (labelled PT1–PT25) participated in a workshop as part of their studies towards a teaching certificate for high-school mathematics at a large, urban university. During the workshop, among other activities, they were asked to address mathematical, pedagogical, and didactical aspects of cases. The cases that were presented to them were collected from authentic classroom observations in high-school mathematics classes (10th–12th graders) over several years. The observations were audiotaped, and data written on the whiteboard were photographed. The information gathered was transcribed, discussed by faculty members, and divided into 15 segments to present instances that were identified as worthwhile cases.

The PTs’ reactions were to a case that introduced an erroneous solution provided during a dialogue between two 11th-grade students while solving a trigonometric task. This case was chosen for three main reasons: firstly, it exhibits a typical error made when solving trigonometric equations, namely, finding only one possible solution and not the entire solution system, and then disqualifying some of the solutions, if necessary; secondly, the typical error in this case led to the correct solution to the task; finally, this case raises doubts about the role of drawings in solving geometric and trigonometric tasks.

The PTs were invited to provide their own solutions to the trigonometric task and to detect the errors in the students’ solutions. The trigonometric task and the dialogue between the two 11th-grade students are presented below.

The Trigonometric Task (Figure 1):

Given

O is the center of a circle with radius R

AB the diameter

String CD intersects AB at point E (see drawing)

$<\mathrm{BAC}=<\mathrm{BOD}=\mathsf{\alpha }$.

(i) Express the area of triangle BCD by means of R and α

(ii) Find R, if $\mathrm{CB}=\sqrt{3}\mathrm{R}$.

and the area of BCD is $8\sqrt{3}$.

The Sue and Ron Case:

The case as presented in the workshop, i.e., the dialogue between two 11th graders, Sue and Ron, while solving item b of the task:

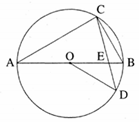
• Sue: “We already found in the previous item that $\mathrm{CB}=2\mathrm{Rsin}\mathsf{\alpha }$.”
• Ron: “Right. Now if $\mathrm{CB}=\sqrt{3}\mathrm{R}$ it means that $2\mathrm{Rsin}\mathsf{\alpha }=\sqrt{3}\mathrm{R}$=”
• Both write in their notebooks: $2\sin \mathsf{\alpha }=\sqrt{3}$
• $\sin \mathsf{\alpha }=\frac{\sqrt{3}}{2}$
• $\mathsf{\alpha }=60°$
• Sue (Hesitantly): Ehh. Ohm. Ah. It seems to me that something is wrong…In the given (pause) about CB. $\mathsf{\alpha }=60°$ is impossible.”
• Ron: “Why?”
• Sue: “If $\mathsf{\alpha }=60°$ then:
  $<\mathrm{CBD}=180°-\frac{3}{2}\mathsf{\alpha }=180°-\frac{3}{2}·60°-180°-90°=90°$180
  and CBD is an inscribed angle, and a right angle.”
• Ron: “Ah. Right. An inscribed angle, that is a right angle, is on the diameter. So... CD is also a diameter in this circle. Can’t be. Can’t be that the circle has two centers.”
• (Ron and Sue go over their solution)
• Ron (Enthusiastically): “Ah. Found it… we forgot the possibility of $\mathsf{\alpha }=120°$”
• Sue: “Great! Now, let’s continue. We’ll use the area of the triangle to find the radius.”

In the workshop, the PTs submitted, individually, their written answers to the trigonometric task. Then, they were presented with the “Sue and Ron case” and asked to answer the following questions: Are there are any errors in the Sue and Ron case? If there are, identify and relate to each error (on which line is the error? What kind of error is it? Why is it an error?). The PTs submitted their written responses to these questions.

The PTs’ own solutions to the trigonometric task and their responses to the questions about the “Sue and Ron case” comprised the body of data for this study. I first examined the different ways in which the PTs solved the task and the correctness of the final answer that they provided to the task. Then, I carefully studied each of the steps towards the solutions given by each PT, marking incorrect instances in each step.

Regarding the PTs’ evaluation of the dialogue between Sue and Ron, one researcher categorized the responses of the PTs according to the types of errors identified in the dialogue, the errors that the PTs mentioned, and their explanations to the question: why is it an error? Another researcher verified the categorization and coded the data according to these categories. Full agreement was attained.

4. Findings

As mentioned above, the workshop session included two parts: I. Solve—the PTs’ solutions to the trigonometric task; and II. Evaluate—the PTs’ evaluations of the errors in the case.

In the sections below, I follow the stages of the study according to these two parts.

4.1. Solve—Prospective Teachers’ Solutions

The trigonometric task posed two questions, (i) and (ii). The first question was correctly solved by Sue and Ron and by all the PTs. The solution was ${\mathrm{S}}_{\mathrm{BCD}}=2{\mathrm{R}}^2\cdot \sin \mathsf{\alpha }\cdot \sin \frac{\mathsf{\alpha }}{2}\cdot \sin \frac{3}{2}\mathsf{\alpha }$.

In response to question (ii), all PTs reached the correct solution, which was $\mathrm{R} =4$.

Almost all PTs (24 of the 25) provided a trigonometric solution. One PT (PT11) provided a geometric solution.

Two main processes of solving the tasks were identified among the 24 PTs who provided a trigonometric solution. Sixteen PTs correctly examined two options for $\sin \mathsf{\alpha }=\frac{\sqrt{3}}{2}$ (${\mathsf{\alpha }}_1=60°$; ${\mathsf{\alpha }}_2=180°-{\mathsf{\alpha }}_1=120°$), and correctly dismissed the option of 120°; but eight PTs only addressed the option of ${\mathsf{\alpha }}_1=60°$.

The solution that was provided by the 15 of the 16 PTs who correctly examined the two options for $\mathsf{\alpha }$(line (f) of solution 1) was:

Solution 1: A trigonometric solution

(a)

$\mathrm{CB}=2\mathrm{Rsin}\mathsf{\alpha }$/from part a

(b)

$\mathrm{CB}=\sqrt{3}\mathrm{R}$/given

(c)

$2\mathrm{Rsin}\mathsf{\alpha }=\sqrt{3}\mathrm{R}$/from lines 1 and 2

(d)

$2\sin \mathsf{\alpha }=\sqrt{3}$

(e)

$\sin \mathsf{\alpha }=\frac{\sqrt{3}}{2}$

(f)

${\mathsf{\alpha }}_1=60°$ or ${\mathsf{\alpha }}_2=180°-{\mathsf{\alpha }}_1=120°$

(g)

But: $<\mathrm{BAC}=\mathsf{\alpha }$ is in a right-angle triangle, so ${\mathsf{\alpha }}_2=120°$

(h)

$\mathsf{\alpha }=60°$

(i)

${\mathrm{S}}_{\mathrm{BCD}}=2{\mathrm{R}}^2·\sin \mathsf{\alpha }·\sin \frac{\mathsf{\alpha }}{2}·\sin \frac{3}{2}\mathsf{\alpha }$/solution part a

(j)

${\mathrm{S}}_{\mathrm{BCD}}=8\sqrt{3}$/given

(k)

$2{\mathrm{R}}^2·\sin 60°·\sin 30°·\sin 90°=8\sqrt{3}$/from lines (i) and (g)

(l)

$2{\mathrm{R}}^2\cdot \frac{\sqrt{3}}{2}\cdot \frac{1}{2}\cdot 1=8\sqrt{3}$

(m)

$2{\mathrm{R}}^2=16$

(n)

$\mathrm{R}=\mp 4$

(o)

$\mathrm{R}=4$/radius

One of the 16 PTs (PT3) who wrote in step (f) both ${\mathsf{\alpha }}_1=60°$ and ${\mathsf{\alpha }}_2=120°$, excluded the 120° by substituting ${\mathsf{\alpha }}_2=120°$ in the expression of the area. PT3 wrote:

“${\mathrm{S}}_{\mathrm{BCD}}=2{\mathrm{R}}^2\cdot \sin \mathsf{\alpha }\cdot \sin \frac{\mathsf{\alpha }}{2}\cdot \sin \frac{3}{2}\mathsf{\alpha }$

$2{\mathrm{R}}^2\cdot \sin 120\cdot \sin 60\cdot \sin 180=0$

This is a contradiction.”

The eight PTs who mentioned only ${\mathsf{\alpha }}_1=60°$ skipped steps (f) and (g) in solution 1.

The solution of the PT (PT11) who provided a geometrical solution was correct.

PT11 wrote:

Solution 2: A geometrical solution

Δ CBA a right-angle triangle

$\mathrm{AB}=2\mathrm{R}$/given

$\mathrm{CB}=\sqrt{3}\mathrm{R}$/given

${\mathrm{AC}}^2+{\mathrm{CB}}^2={\mathrm{AB}}^2$/Pythagorean theorem

${\mathrm{AC}}^2+3{\mathrm{R}}^2=4{\mathrm{R}}^2$

$\mathrm{AC}=\mathrm{R}$

Δ ACO is an equilateral triangle

$\mathsf{\alpha }=60°$

4.2. Evaluate—Prospective Teachers’ Evaluations of Correctness in the Case

As mentioned above, the PTs were asked whether any errors existed in the Sue and Ron case, and, if so, they were requested to specify in what lines each error occurred, identify what the error is, and explain why it is an error.

One prospective teacher (PT13) did not answer the questions, and another (PT2) provided a detailed, yet ambiguous response to which I will refer at the end of this section. The other 23 PTs wrote that the case contained mathematical errors, and they pointed to one or more of the following:

Ignoring the case of sin (180°– 60°): Eight prospective teachers wrote that this error appears in lines 4 and 5, where Sue and Ron solved $\mathsf{\alpha }=60°$ instead of ${\mathsf{\alpha }}_1=60°$, ${\mathsf{\alpha }}_2=120°$. The PTs explained that although 120° turns out to be impossible, at this stage it should have been presented, and only afterwards should the reason for rejecting ${\mathsf{\alpha }}_2=120°$ be given.

They wrote, for instance:

“There is another possibility on top of $\mathsf{\alpha }$ here, that of ($180-\mathsf{\alpha }$).

It is necessary to check all the possibilities and rule out one of them.” (PT3)

“It is impossible to deduce that ${\mathsf{\alpha }}_1=60°$. One needs to examine the option of ${\mathsf{\alpha }}_2=120°$, and then reject it.” (PT6)

It should be noted that five of these eight PTs referred in their own solutions (in the first “Solve” stage) to both ${\mathsf{\alpha }}_1=60°$ and ${\mathsf{\alpha }}_2=120°$, and three reached only $\mathsf{\alpha }=60°$.

Rejecting the case of ${\mathsf{\alpha }}_1=60°$: Eighteen PTs pointed to lines 6–10 (or part of these lines), where Sue and Ron decided that for geometrical reasons, ${\mathsf{\alpha }}_1=60°$ cannot be a solution. The PTs wrote, for instance:

“They (Sue and Ron) grasped that CBD is a right angle, and therefore CD is a diameter in this circle. They claimed that this is impossible, because a circle cannot have two different centers. But, in the case of this problem, nothing contradicts the possibility of points O and E merging, and all the other angles are fine when this happens.” (PT1)

“The idea that a circle cannot have two centers is correct. The error is that E and O are not necessarily different points. They can merge.” (PT9)

Seven of the 18 PTs made some reference to the misleading role that the drawing played in Sue and Ron’s decisions:

“The error is the students’ claim that “$\mathsf{\alpha }=60°$ is impossible”. This error evolves from their understanding of the drawing that accompanies the problem. In the drawing, points E and O are two separate points. This is definitely fine for question (i). However, the two points can join together to make a single point (and actually, according to the information given in (ii), they do merge). The contradictory mismatch between the drawing and the given information is what caused Sue’s hesitation, and this was followed by her taking the wrong decision and relying on the misleading drawing. Both were influenced by the visual information, rather than by mathematical considerations. The figure that they were given imposed itself on their [logical] reasoning… Visual, figural-intuitive information forcefully and fiercely overpowered the formal knowledge.” (PT5)

“The students made an assumption, without checking, that CD cannot be a diameter. It might be that they were confused by the drawing.” (PT21)

“Sue finds the solution for the angle that they reached to be problematic, as she explains in line 6, and from the contradiction [that she arrives at], she concludes that, consequently, CB, as it is [probably presented in the drawing] is impossible. Her error is probably rooted in the drawing, from which she concluded that E and O are different points.” (PT22)

Two of these PTs went on to add a comment criticizing the phrasing of the problem and the presentation of the drawing:

“There is no doubt that the drawing in this problem is confusing, and has led to the erroneous conclusions.” (PT17)

“The error is quite understandable, and makes sense, because of the phrasing of the problem that clearly refers to the intersection of CD at point E, and which also states “see drawing”.” (PT22)

Tending to view ${\mathsf{\alpha }}_2=120°$ as the solution: Fifteen PTs wrote that the error is in lines 11 and 12, where Sue and Ron suddenly recollected that they had neglected the option of ${\mathsf{\alpha }}_2=120°$ as a solution in line 4, treating the ${\mathsf{\alpha }}_2=120°$ solution as a rescue from the dead end that they had reached by the erroneous decision that ${\mathsf{\alpha }}_1=60°$ was impossible. They wrote:

“In line 12, the students forget a “marginal and insignificant” detail, that the angle by the hypotenuse in a right-angle triangle in necessarily less than 90°.” (PT5)

“Line 11 is problematic. The students say that ${\mathsf{\alpha }}_2=120°$, however the angle belongs to a right-angle triangle, and therefore it can’t be bigger than 90°.” (PT8)

“On line 11, the student said that α is 120°, and this is wrong, because then we would have a triangle with three angles that sum up to more than 180°.” (PT11)

As mentioned above, one prospective teacher (PT2), who originally solved the problem with no mention of ${\mathsf{\alpha }}_2=120°$ $\mathsf{\alpha }=10°$, wrote that in line 5 the students should have also considered the case of ${\mathsf{\alpha }}_2=120°$ $\mathsf{\alpha }=12°$. He further implied in a vague manner that α = 120° is the solution:

“In line 5 they wrote that $\mathsf{\alpha }=60°$, and this indicates that they believed that the equation in line 4 has a unique solution. However, the equation in line 4 has an infinite number of solutions, and therefore there are two solutions between 0° and 360°. Only in lines 11 and 12 did they (the students) realize that the solution is indeed ${\mathsf{\alpha }}_2=120°$. Had they noticed it beforehand, the confusion about CD being the diameter would have been avoided.”

Three PTs were impressed by the students’ careful, yet in this case detrimental, checking of their solution. Although they were not asked to address this issue, these PTs volunteered comments, such as:

“It should be said, in their favor, that it is nice that they were not satisfied with their solution and did not settle for merely blindly substituting the values for the variables, but adopted a critical attitude and examined whether their solution makes sense. Unfortunately, this is precisely what made them fail.” (PT1)

“The students activated a process of control, checking whether their solution makes sense. This is nice! It’s really nice that they initiated a self-check of their solution. This doesn’t happen often. My dilemma is how to react. What should I say to them?” (PT12)

5. Summary and Discussion

In this paper, I posed two questions: In what ways (correct and incorrect) did the prospective teachers (PTs) solve the task? What errors did PT’s identify in the students’ dialogue and how did they explain why they are errors? In this section, I summarize the findings with reference to these questions, and present how the data give rise to several broader pedagogical issues.

In their own solutions to the task, all the PTs reached R = 4, which is the correct solution. Seventeen of the 25 PTs correctly wrote a full sequence of steps. Sixteen of these 17 used a trigonometric approach and correctly examined two options (${\mathsf{\alpha }}_1=60°$ and ${\mathsf{\alpha }}_2=180°-{\mathsf{\alpha }}_1-120°$) for the equation $\sin \mathsf{\alpha }=\frac{\sqrt{3}}{2}$. Subsequently, they justified the rejection of ${\mathsf{\alpha }}_2=120°$. One of these 17 PTs provided an adequate geometrical solution that led only to $\mathsf{\alpha }=60°$. Still, the other eight prospective teachers, who also presented a trigonometric solution, provided only the option of $\mathsf{\alpha }=60°$ as a result of the equation $\sin \mathsf{\alpha }=\frac{\sqrt{3}}{2}$. This raises some doubts regarding their solution and some concerns regarding their trigonometric knowledge. One option is that their reference only to ${\mathsf{\alpha }}_1=60°$ is an outcome of a thoughtful, knowledgeable action in which they examined ${\mathsf{\alpha }}_2=120°$ and rightly ruled it out. Another option is that they erroneously omitted the option of $180°-{\mathsf{\alpha }}_1$ as a solution to $\sin \mathsf{\alpha }=\frac{\sqrt{3}}{2}$ and considered only one of the two possible solutions, namely ${\mathsf{\alpha }}_1=60°$. However, since the ($180°-\mathsf{\alpha }$) option is rejected at a later stage of the task-solving process, and the final solution is based only on ${\mathsf{\alpha }}_1=60°$, the data do not allow an examination of each of these two possible options. Even the information that three of these eight PTs did write, in response to the case, that examining the option of $180-\mathsf{\alpha }$, and justifying its rejection, is absolutely necessary (i.e., that it is an essential part of the solution), does not provide sufficient ground to choose between the two options.

One possible way to examine this aspect is to ask the PTs, immediately after solving the trigonometric task and before exposing them to the Sue and Ron case, to solve a trigonometric equation, similar to ${\mathsf{\alpha }}_1=60°$. This diagnostic task could provide the information needed to determine whether the omission is a result of a careful consideration or of erroneously neglecting one of the possible solutions of the equation. Such a refinement enhances the opportunities to openly discuss the PTs’ own solutions, their uncertainties regarding their own knowledge, the ways of constructing diagnostic tasks, and the ways of diagnosing learners’ knowledge. Discussing these aspects could contribute to additional aspects of PCK such as knowledge about diagnosing and assessing learners’ ways of thinking [27,28].

In their responses to the case, almost all (23) PTs identified at least one of the errors. They pointed out that Sue and Ron erroneously overlooked the solution of $180-\mathsf{\alpha }$ (eight PTs), that they erroneously rejected the solution of ${\mathsf{\alpha }}_1=60°$ (18 PTs), and that they tended to accept the incorrect option of ${\mathsf{\alpha }}_2=120°$ (15 PTs). One prospective teacher did not submit this task, and another wrote an answer which implies that for them, much like for Ron and Sue, ${\mathsf{\alpha }}_2=120°$ is the correct solution.

Notably, the prospective teachers’ reactions to this case highlight mathematical properties that need to be addressed in their future classes, two of which are the solutions to trigonometric equations, and the steps that should be written in the stages of a solution. Moreover, the case brought up a specific dilemma pertaining to the role of drawings in the presentation of a mathematical problem. The drawing that accompanied the task describes a general situation, but this general situation implies that E and O are two distinct points, while the solution requires that E and O be the same point. Fischbein [29], who proposed the theory of figural concepts, describes the tension between the general nature of the geometrical drawing and the nature of the specific drawing in the following way:

“When you draw a certain ABC triangle on a sheet of paper in order to check some of its properties (for instance, the property of its heights to be concurrent) you do not refer to the respective particular drawing but to a certain shape which may be the shape of an infinite class of objects. Even the particular shape drawn by you with its given sides and angles may be the shape of an infinity of objects. As a matter of fact, we deal with a hierarchy of shapes, from an apparently particular one—but in fact corresponding to an infinity of possible objects—to the universal category of triangles” (p. 141).

In the trigonometric problem that serves as the basis for the case presented in this paper, the general drawing was a major cause of the difficulty experienced by the students while solving the trigonometric task. The questions that naturally emerge are: Is it good practice to present such a drawing? Is it good practice mathematically? Is it good practice pedagogically? Is it good practice emotionally? These issues should be further studied by mathematics educators and discussed with prospective teachers, teachers, and their students.

Finally, in this study, high-school PTs were invited to solve a task that was assigned to high-school students and to relate to an authentic solution given by a pair of students to this task. Confronting high-school students with such tasks provides opportunities to discuss, during teacher education, subtle issues related to both their own mathematical knowledge and understanding, and possible obstacles that their future students might encounter when solving these tasks. It could also lead to a discussion regarding the types of trigonometric and geometric tasks that are assigned to high-school students and to the kind of drawings accompanying these tasks. Enhancing these dimensions of teacher knowledge is advocated in contemporary theories of proficiency in teaching mathematics [15,17,30]. Hence, presenting PTs with rich, authentic cases is definitely one way of occasioning these essential dimensions of mathematics knowledge for teaching. More generally, analyzing cases of students’ errors and discussing them can raise teachers’ awareness of students’ ways of thinking. Such a process is evidently an important source of learning for teachers.