Next Article in Journal
Experiences of Preservice and In-Service Teachers in a Comprehensive School Physical Activity Infusion Curriculum
Previous Article in Journal
Literacy Teacher Educators Creating Space for Children’s Literature
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Education Sciences
Volume 10
Issue 10
10.3390/educsci10100289
education-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Kinds of Mathematical Reasoning Addressed in Empirical Research in Mathematics Education: A Systematic Review

by
Alexandra Hjelte
1,*,
Maike Schindler
2 and
Per Nilsson
1
1
School of Science and Technology, Örebro University, SE-701 82 Örebro, Sweden
2
Department of Special Education and Rehabilitation, Faculty of Human Sciences, University of Cologne, DE-50931 Cologne, Germany
*
Author to whom correspondence should be addressed.
Educ. Sci. 2020, 10(10), 289; https://doi.org/10.3390/educsci10100289
Submission received: 23 September 2020 / Revised: 13 October 2020 / Accepted: 14 October 2020 / Published: 17 October 2020
Browse Figures
Versions Notes

Abstract

:
Mathematical reasoning is gaining increasing significance in mathematics education. It has become part of school curricula and the numbers of empirical studies are growing. Researchers investigate mathematical reasoning, yet, what is being under investigation is diverse—which goes along with a diversity of understandings of the term reasoning. The aim of this article is to provide an overview on kinds of mathematical reasoning that are addressed in mathematics education research. We conducted a systematic review focusing on the question: What kinds of reasoning are addressed in empirical research in mathematics education? We pursued this question by searching for articles in the database Web of Science with the term reason* in the title. Based on this search, we used a systematic approach to inductively find kinds of reasoning addressed in empirical research in mathematics education. We found three domain-general kinds of reasoning (e.g., creative reasoning) as well as six domain-specific kinds of reasoning (e.g., algebraic reasoning). The article gives an overview on these different kinds of reasoning both in a domain-general and domain-specific perspective, which may be of value for both research and practice (e.g., school teaching).

1. Introduction

Mathematical reasoning is an important topic in mathematics education—both in research and in practice (e.g., at school). According to the Cambridge English Dictionary, reasoning is “the process of thinking about something in order to make a decision” [1]. Mathematical reasoning has often been connected to mathematical proving and the logical process that comes with it [2]. However, other scholars take the concept of reasoning in a broader sense, in which reasoning is not restricted to a logical way of thinking but can be based on what makes sense to the person giving the reasons—logical or not [3]. Researchers point out that—on a methodological level—investigating students’ mathematical reasoning helps both teachers and researchers to understand students’ understanding and learning of mathematics. On the other hand, reasoning is seen as the process of learning itself, where the learner builds on knowledge through reasoning [2].
In recent years, mathematical reasoning has become an integral part of mathematical curricula in many countries—not least since PISA has highlighted mathematical process competencies in mathematics teaching and learning, such as modelling, problem-solving, and reasoning. The increased interest in mathematical processes [4] such as problem solving, reasoning and proof, and communication [5] is evident in curricula documents all over the world [6]. In the Nordic countries, the so-called KOM-framework (Competencies and the Learning of Mathematics) spells out eight distinct competencies that describe “someone’s insightful readiness to act appropriately in response to a specific sort of mathematical challenge in given situations” [7] (p. 14), whereof one is mathematical reasoning, which means “to analyse or produce arguments (i.e., chains of statements linked by inferences) put forward in oral or written form to justify mathematical claims” [7] (p. 16). Likewise, in Sweden, for instance, teachers are supposed to foster students’ mathematical reasoning abilities [8].
Given the increasing significance of mathematical reasoning, it has become crucially important for practitioners (e.g., schoolteachers) and researchers to be aware of what reasoning is—in particular, of the different conceptualizations of reasoning. Researchers and practitioners need to know what it is that is supposed to be fostered—and they need to know about the different kinds of mathematical reasoning that can be addressed. Furthermore, for researchers it is important to monitor what is understood by mathematical reasoning: For research to systematically build on and connect to previous works, it is necessary to monitor in what ways mathematical reasoning is conceptualized and what different kinds of mathematical reasoning are addressed.
In existing works, we find that mathematical reasoning is a term that is used in different ways and often in a broad sense. In simplified terms, reasoning can almost be everything or nothing. Likewise, Lithner and Palm state that “the term ‘reasoning’ is mostly used among mathematics educators without defining it, under the implicit assumption that there is a universal agreement on its meaning” [3] (p. 285). Yet, such agreement does not exist—there are several ways in which mathematical reasoning is used and conceptualized [2]. For instance, mathematical reasoning is sometimes conceptualized as a general ability, sometimes as a means to solve problems, or as a topic-related ability to draw conclusions within a certain mathematical domain. Because of these different uses of the term (mathematical) reasoning, it is difficult for practitioners to know what and how to support students adequately; and for research, the fuzziness of the use of the term mathematical reasoning hinders a systematic development of the scientific knowledge about mathematical reasoning.
One recent effort to circumvent the fuzziness of the use of the term mathematical reasoning was made by Jeannotte and Kieran, who conducted a literature review. They aimed to clarify and conceptualize mathematical reasoning. The outcome of their research is a model of mathematical reasoning, structured according to a structural aspect and a process aspect. The structural aspect refers to the form of mathematical reasoning, to the way an ordered system describes both the elements of the system and their relation. Deduction, induction, and abduction are three general reasoning structures. The process aspect refers to the temporality and axiological nature of mathematical reasoning. Jeannotte and Kieran’s approach—examining a given body of studies, searching for commonalties and ways to summarize them accurately and succinctly—is an important purpose of a systematic literature review [6]. However, another purpose of a literature review can be to fan out the diversity of conceptualizations of a phenomenon among studies that share a common focus (see, e.g., [9]). For mathematical reasoning, we feel that there is a research desideratum unfolding the different kinds of mathematical reasoning that are addressed in current mathematics education research. (In this article, we use the term “kind” to refer to phenomena or things sharing common characteristics.)
The aim of this article is, thus, to provide an overview on kinds of mathematical reasoning addressed in mathematics education research. We ask the research question, What kinds of reasoning are addressed in empirical research in mathematics education? We intend to investigate the kinds of reasoning that are addressed in empirical studies with school students, since these kinds of reasoning will have most practical relevance for mathematics teaching at school, so that the results of our review—an overview on kinds of mathematical reasoning—can be useful both to researchers and practitioners (e.g., school teachers) (see Section 4).

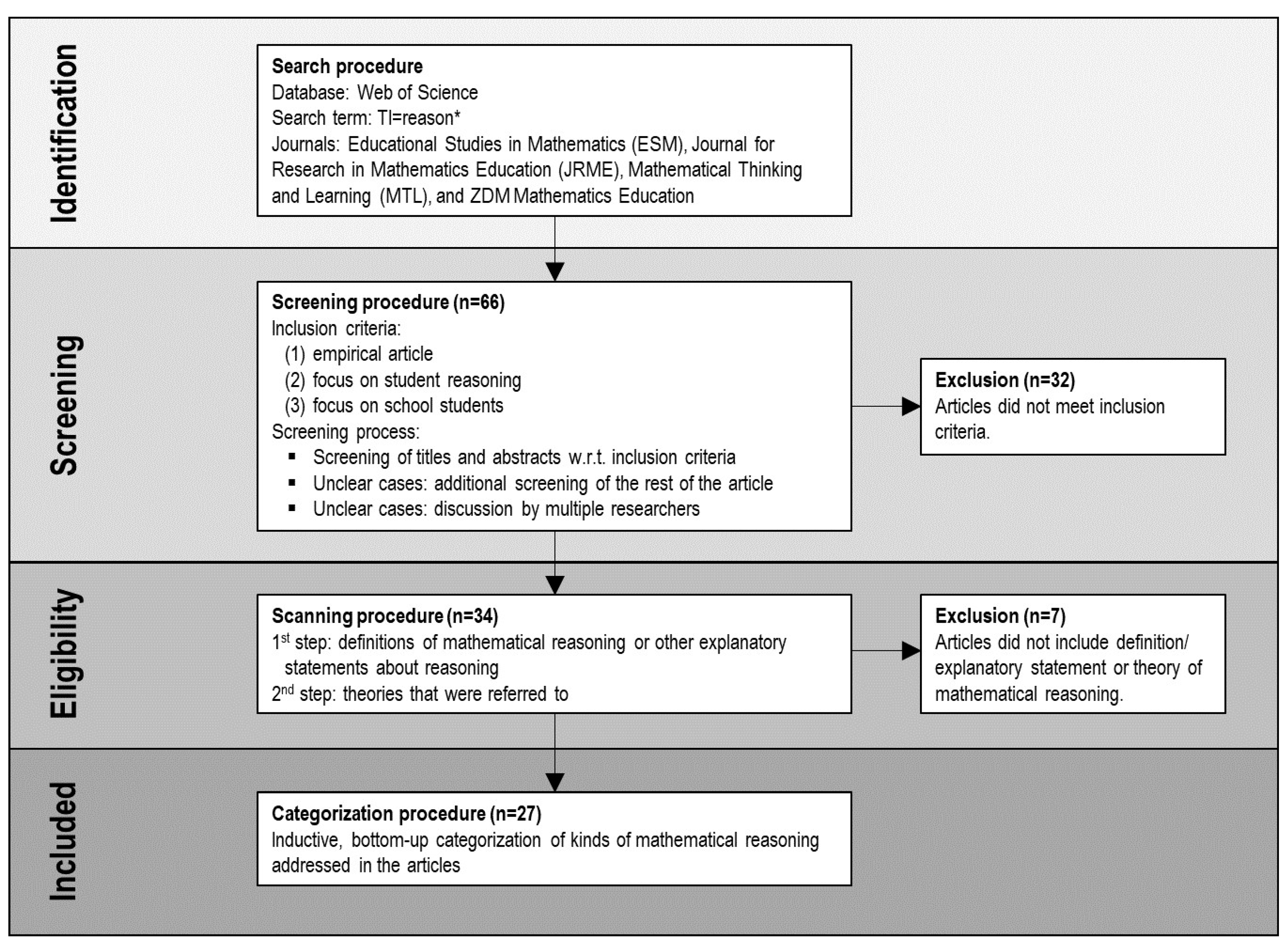
2. Methods

The research question of this article is pursued by means of a systematic literature review. We conducted this review through systematically searching and screening for relevant research articles through a database search and analyzing them with the purpose of answering our scientific enquiry [10]. With regard to PRISMA (Preferred Reporting Items for Systematic Reviews and Meta-Analyses), we implemented four steps (as described in the following subsections in more detail). In the initial identification step, we conducted a search procedure that consisted of a database search; for screening, we defined and used inclusion criteria (similar to [11]); for eligibility, we further scanned for definitions/statements/theories and reasoning; and in the inclusion step, we finally categorized kinds of reasoning inductively, bottom up, as shown in Figure 1.

2.1. Identification: Search Procedure

In order to find articles that addressed reasoning in mathematics education, the term reason* was used in a title search in Web of Science, using the format [TI = reason*]. We used the Web of Science database since we wanted to include high level journals. We limited our search to journals with a focus of mathematics education research, since our intention was to focus on mathematical reasoning in mathematics education. The following journals were included: Educational Studies in Mathematics (ESM), Journal for Research in Mathematics Education (JRME), Mathematical Thinking and Learning (MTL), and ZDM Mathematics Education. To get an overview of recent research, the time for article publications was set to 2008 until 2017. Further, we limited the search to articles that were published in English. Our search resulted in a hit of 66 articles from the database.

2.2. Screening Basis: Criteria for Inclusion of Articles

From the list of 66 articles with reason* in the title, we manually singled out articles that addressed students’ reasoning in mathematics. We used the following inclusion criteria:
  • The article was an empirical article. We included empirical articles, in which students’ reasoning was investigated, since we wanted to investigate the kinds of reasoning addressed in empirical research (see research question). With this focus, we wanted to account for the kinds of mathematical reasoning addressed in empirical studies in mathematics education.
  • The article addressed students’ reasoning. Articles that focused on, for example, teachers’ reasoning [12] or reasoning within different task formulations [13], were excluded.
  • The article focused on school students. Articles with a focus on reasoning at university level [14] were excluded. Our main reason for narrowing our focus to primary and secondary school years was to get a manageable selection of articles to be included in the review. Besides, since the topic of reasoning is mostly related to the curriculum in primary and secondary school years, the restriction to these school years appeared appropriate. This restriction also was in line with our intention to draw conclusions for school practice (see Section 4).

2.3. Screening Process: Focus on Titles and Abstracts

The titles and abstracts of the 66 articles were read by one researcher to determine if the articles met the inclusion criteria. In some cases, the information given in title and abstract was not sufficient to decide if the article should be included. In those cases, parts of the articles were read; the research questions, the method of the study, and sometimes the results and conclusions. After this process, when there still remained uncertainties if the article should be included or not, the article was read and discussed by multiple researchers. This process resulted in 34 articles that were included after the manual inclusion process.

2.4. Eligibility and Inclusion: Scanning and Categorization

To find the kinds of reasoning in mathematics educational research, the introduction and theoretical background of the articles were read. If the articles were structured in a way where these parts were not included, the articles were read until the methodology was presented. The data analysis followed an inductive approach as detailed below.
First step: To investigate what kinds of reasoning were addressed in the respective articles, we first looked at definitions of mathematical reasoning or other explanatory statements about reasoning in the articles. For instance, Mata-Pereira and da Ponte are explicit about the kind of mathematical reasoning they address, pointing out that they take mathematical reasoning as making justified inferences and using deductive, inductive, and abductive processes [15] (and refer to [16,17,18]). We also checked if the definitions or explanatory statements about mathematical reasoning involved a reference—like in the given example by Mata-Pereira and da Ponte. We did so since we wanted to see whether they were anchored in prior works. We scanned all articles looking for definitions or explanatory statements for mathematical reasoning.
Second step: In the next step of the analysis, we looked for if and what theories were referred to, to describe the kind of mathematical reasoning. To count as a case of a reference to a theory, the respective theories needed to be explicitly stated and backed up with a reference. For instance, Hackenberg and Lee [19] stated explicitly that they used Thompson’s theory of quantitative reasoning [20,21]. We did not include statements about theories without a reference; likewise, we did not include something as theory, where only a reference was given without a statement. In the latter case, we wanted to prevent something to be counted as a theory use, which did not have direct significance for the respective paper and the kind of reasoning addressed.
Through these two steps (looking for definitions/statements and for theories), we found that seven out of 34 articles, did not include a definition or explanatory statement for mathematical reasoning with a reference, nor did they refer to theories on mathematical reasoning. These articles were—in line with the above criteria—not integrated in the further categorization.
Finally, the 27 resulting articles were then categorized inductively, bottom-up. The articles were grouped together based on similarities and distinguished based on differences regarding the kinds of reasoning that were addressed.

3. Results

In the following, we present our findings with respect to the kinds of reasoning, including the scholars’ definitions or explanatory statements about reasoning and the theories on reasoning that were referred to. We present these findings together: We give an overview on the kinds of reasoning addressed, elaborating on what definitions are given and what theories are referred to.
In our analyses, two main categories emerged. We found that some articles regard reasoning as domain-general and others as domain-specific (connected to a specific mathematical topic). Through categorizing the articles further, we were able to find different kinds of reasoning addressed. Accordingly, we present the domain-general kinds of reasoning (Section 3.1) and the domain-specific kinds of reasoning (Section 3.2).

3.1. Mathematical Reasoning in a Domain-General View

In nine articles, the term mathematical reasoning is used in a domain-general way, without a restriction to certain mathematical sub-domains. For instance, Barmby, Harries, Higgins, and Suggate take reasoning as the process of drawing conclusions [22], and Meletiou-Mavrotheris and Paparistodemou use hierarchic interactionism to look at internal and external factors in mathematical reasoning and learning [23].
In this category, the focus is on how the students give reasons for a specific standpoint, solution, or conclusion. The mathematics is necessary for the reasoning to take place, but the understanding of how the reasoning is taking form is not tied to a specific mathematical content. Table 1 gives an overview on what domain-general kinds of reasoning are addressed in the articles in our review. Each of the kinds of reasoning addressed in this table will be elaborated on in the following.

3.1.1. Definitions and Explanatory Statements

Four of the nine articles [15,22,24,25] present a definition or explanatory statement for reasoning along with a reference. In that regard, they all give the reader an understanding for how they view mathematical reasoning. These articles connect reasoning to activities such as making inferences, drawing conclusions, justifying, and problem solving.
Barmby et al. connect reasoning to understanding and state that they have a broad notion of reasoning with an emphasis on drawing conclusions and making inferences. In particular, they “choose to consider reasoning (…) ‘as the process of drawing conclusions’ (Leighton 2004) [26]” [22] (p. 220). They also refer to Christou and Papageorgiou who emphasize that reasoning involves drawing inferences from principles and from evidence to new conclusions [27]. Mata-Pereira and da Ponte also relate mathematical reasoning to making inferences. They point out that they “consider mathematical reasoning as making justified inferences (Brousseau & Gibel, 2005; Pólya, 1954; Rivera & Becker, 2009) [16,17,18] using deductive, inductive, and abductive processes” [15] (p. 170).
Bjuland et al. refer to reasoning strategies, whom they connect to problem solving, referring to Pólya [28,29]. In particular, they state that “[r]easoning strategies are defined as a branch of strategies well-known in problem-solving research, which are cognitive operations that are typically helpful in solving mathematical problems (Pólya, 1957) [29]” [24] (p. 272). They further refer to mathematical reasoning as semiotic activity [30].
Hohensee relates reasoning to backward transfer and states that the construction and generalization of (new) knowledge has influences “on one’s ways of reasoning about related mathematical concepts that one has encountered previously” [25] (p. 136). In this vein, Hohensee uses the term ways of reasoning “in a similar way to how Gravemeijer (2004) [31], and McClain, Cobb, and Gravemeijer (2000) [32], use this phrase to represent the mathematical activities that students engage in while solving, explaining, justifying, identifying, and so on” [25] (p. 136).

3.1.2. Creative and Imitative Reasoning

One framework used within mathematics education research about reasoning is the framework of imitative and creative reasoning. Three articles in our review use this framework to conceptualize students’ reasoning [33,34,35]. Reasoning is regarded as a line of thought that results in assertions and conclusions [33]. Within this framework, there are different kinds of reasoning presented—the two main categories are creative and imitative reasoning. Whereas in both kinds of reasoning, students use previously learned facts, algorithms, or mathematical procedures to solve a task or a problem, it is only in creative reasoning that they use reasoning that is new to them. This new way of reasoning however still needs to be anchored in mathematics, that is it needs to follow the mathematical rules connected to the reasoning [34].
The theory of creative and imitative reasoning [4] is one of the predominant theories used in the empirical articles investigated in our review. It is presented as a conceptual framework with the aim of increasing both the understanding of mathematical reasoning and developing the teaching. It gives the perspective of viewing reasoning as the product of the process that the student goes through while solving an assignment. The product takes “the form of a sequence of reasoning that starts in a task and ends in an answer” [4] (p. 257).

3.1.3. The Structure of the Learned Outcomes (SOLO) Taxonomy

One of the articles in our review [36] uses the theory of Structure of the Learned Outcomes (SOLO) (developed by Biggs and Collis [37]) as a framework for mathematical reasoning. The theory takes students’ reasoning as a complex, emerging, and developing system. The development of the reasoning follows a hierarchical system of levels, which follows the stages of Piaget’s cognitive development. Within each stage, the student advances through the levels of the SOLO taxonomy; prestructural, unistructural, multistructural, relational, and extended abstract [37]. The SOLO taxonomy can be used to describe the development of students’ reasoning in different subjects and in varying age groups [36]. It is used by Jurdak and Mouhayar to understand different kinds of student reasoning and generalizations and to look at how students’ reasoning can develop and become more advanced through the use of different kinds of tasks [36].

3.1.4. Hierarchic Interactionism

One of the articles in our review [23] uses the theory of hierarchic interactionism [38] as a framework for mathematical reasoning. In hierarchic interactionism, it is important to take into account both internal and external factors to understand mathematical reasoning and learning. Meletiou-Mavrotheris and Paparistodemou use this theory to investigate how students use their prior knowledge and their informal language to understand and make sense of new mathematical concepts and data [23].

3.2. Mathematical Reasoning in Domain-Specific Views

We found that in 18 articles, mathematical reasoning is connected to a specific mathematical topic or content. In these cases, reasoning is often presented as being different ways of solving mathematical tasks in a specific mathematical domain. Using different tools or concepts that are connected to a specific mathematical area, the students’ different ways of solving a task are viewed as different kinds of reasoning. These are often being rated from a lower kind of reasoning to a more advanced (and mathematically correct) kind of reasoning. Table 2 gives an overview on the domain-specific views and the respective articles that refer to them. In the following, we elaborate on these domain-specific kinds of reasoning and point out what theories were used, respectively.

3.2.1. Spatial Reasoning

Spatial, or geometrical, reasoning is explained as understanding and explaining what happens when working with geometrical tasks, using different subject-related entities such as geometrical objects, diagrams, measuring tools, or even gestures [39]. By using these entities, the students can, among other things, discuss the relation between different geometrical objects, relations between length, area, and volume. Four articles in our review focus on students’ spatial or geometrical reasoning.
Hallowell, Okamoto, Romo, and La Joy investigate students’ reasoning about plane and geometric shapes presented in 2D diagrams. With reasoning, they address students’ spatial skills to transform a 2D description of an object into a 3D understanding. They look at students’ geometrical reasoning to understand how the students make sense of 2D representations of 3D objects [40]. They use Herbst’s [41] description on how to make “reasoned conjectures” [40] (p. 134) and how that builds geometrical knowledge [40].
Chen and Herbst also use Herbst’s description [41] in their study on geometrical reasoning. They emphasize the need for the students to have diagrams, possibilities to create representations of geometrical objects, and the opportunity to anticipate different relationships within and between these objects. When students make these “reasoned conjectures” [42] (p. 134), they construct mathematical knowledge. Chen and Herbst also emphasize the social aspects of geometrical reasoning, in which the students discuss, make claims, and give arguments for these claims [42].
Gómez-Chacón, Romero Albaladejo, and del Mar García López [43] draw on Lakatos [44] to describe reasoning not as a linear process but as a course that goes zig-zag. In this process, it is assumed that students use different aspects, both physical and mental, in their reasoning process. These aspects can be artifacts or references like a geometrical object, as well as visualizations and proofs [44].
Spatial reasoning is also taken as seeing the surrounding world and objects with regard to, for instance, symmetry, balance, location, orientation, navigation, scales, transformations, and visualization. Spatial reasoning is therefore understood both as actions and cognition—as the sensation of the surroundings, the perception of the surroundings, as well as the physical bodies in the surroundings, and cognition and actions made in this context [39].

3.2.2. Informal Inferential Reasoning

Informal Inferential Reasoning (IIR) deals with how students use and reason about information drawn from data [45]. It is about how the students understand data in an informal way and how they draw conclusions about a larger group than the dataset at hand [46]. Four articles in our review use IIR as a theoretical framework for explaining how students reason in statistics [45,46,47,48]. IIR is therefore one of theoretical frameworks in this review that is referred to most often.
IIR focuses on how students interpret data that they produce or receive. This process of interpretation contains many different aspects and sources. The process is about finding meaning in a dataset by identifying statistical patterns, deviations in the dataset, and then about deciding if a claim can be made from the data, deciding if that data can justify certain conclusions, and so on [46]. IIR is therefore understood as a cognitive process in which a person draws conclusions about a wider universe based on a smaller sample, while at the same time also taking into consideration the limitations of that sample [45].
The theory that is referred to most often as the foundation for reasoning in IIR is the framework for Informal Statistical Inference (ISI) by Makar and Rubin. It is a domain-specific theory on how informal inferences in statistics are made [49]. It includes the reasoning process that occurs when making generalizations from data. This theory is about how students use statistics to make conclusions beyond the dataset that they have [47].

3.2.3. Additive, Multiplicative, and Distributive Reasoning

These kinds of reasoning describe how students handle and understand numerical operations and actions. Due to this common denominator they are presented together. They describe how different understandings for numbers can lead to different kinds of reasoning.
The concept of additive reasoning is described as the students’ ability to understand the logic of part–whole relationships [50]. It is described as the students’ ability to understand the inverse relationship between addition and subtraction. The idea is to grasp how the students use this relationship when they calculate different types of addition and subtraction tasks. It focuses on the kinds of inferences the students make, and the ability to make inferences based on the part–whole relationship within and between numbers [50].
Multiplicative reasoning addresses students’ understanding of numbers in a one-to-many relationship. This means that the students need to understand the ratio between quantities and how to find the product between quantities. Sometimes the students may be told the quantities and be asked to find the ratio. Sometimes it may be the other way around. Multiplicative reasoning addresses how students deal with these types of problems and what understanding they have [50].
Finally, distributive reasoning is associated with students’ work with fractions. Here, they need to understand how a quantity or multiple quantities can be divided equally. When the students have this understanding and can show it by using it in multiple situations, this is understood as the students showing distributive reasoning skills [19].

3.2.4. Algebraic Reasoning

Algebraic reasoning regards reasoning as the students’ ability to make abstractions and generalizations from arithmetic [19]. Using the theory of Kaput [51], algebraic reasoning is presented by Bishop, Lamb, Philipp, Whitacre, and Schappelle as the process in which students work with numbers and develop new understandings for numbers [52]. This is, for example, the case when students investigate relations between numbers and develop an understanding for the operation 2 − (−2) = 4 through investigating 2 − 1 = 1, 2 − 0 = 2, 2 − (−1) = 3, and so on. An approach like this is presented as a formal way to approach numbers. However, algebraic reasoning goes beyond the arithmetic understanding. It is when the students use letters as unknown entities, without understanding them as a temporary placeholder for numbers, that the students are engaged in algebraic reasoning [19].

3.2.5. Proportional and Covariational Reasoning

Proportional and covariational reasoning both address the understanding for variations and the relation between and within varying entities. Because they both address students’ understanding of variation they are presented together.
Proportional reasoning focuses on the understanding of rates, and the understanding of what happens when rates change; for example, continuous variation in rates [53]. Within proportional reasoning, there are multiple levels of reasoning skills. The more mathematically advanced and sophisticated the students’ reasoning becomes, the higher their reasoning level is perceived [53]. Proportional reasoning also involves co-variation in a sense that the students have to be able to make comparisons between different entities. The students need to acquire multiple skills, including relational thinking, to be able to reason proportionally [54].
Covariational reasoning is explained as reasoning in which the students work with two different quantities, focusing on how these two quantities change in relation to each other [55]. Reasoning in this way is central to developing an understanding for ratio and rate. Johnson describes five levels of reasoning, where the reasoning becomes more and more sophisticated [55]. One way to understand the change between and within these two different quantities it described as chunky resp. smooth understanding. The smooth way of seeing variation entails understanding the variation as a continuous variation, in which the quantities are changeable and where individual quantities can be put together to a new quantity. This understanding is viewed as more sophisticated than the chunky understanding, where students view different quantities as separated and different from each other [56].

3.2.6. Quantitative Reasoning

The articles that hold the perspective of quantitative reasoning mostly use Thompson’s theory of quantitative reasoning [20,57]. Five of the articles [19,50,53,56,58] in our review use this theory, where the students’ quantitative operations are enacted both through thought and action. It builds on Piaget’s notion of internalization, interiorization, mental operation, and scheme—and quantities are understood as conceptual entities. One part of quantitative reasoning is the process of quantification, which involves understanding that some attributes can be measured, finding an appropriate unit of measure, and understanding the relationship of the attributes and the unit [56]. Quantitative reasoning is explained as the way the students analyze a situation and incorporate it into a quantitative structure. The structure is set up by a network of quantities and relationships between these quantities. It is these relationships between quantities that is the most important content in quantitative reasoning [58]. Quantitative reasoning is therefore a foundation for the students to be able to develop other kinds of reasoning, such as algebraic reasoning [19].
There is also one article referring to quantitative reasoning that does not draw on Thompson’s theory. This article also use the concepts of chunky and smooth, however they use them to describe the students’ development of understanding quantities, focusing on how students’ reasoning can be developed from discrete to continued as the students’ understanding of quantities develops from chunky to smooth [59].

3.2.7. Transformational Reasoning

Transformational reasoning [60] is not connected to a specific mathematical topic but is used by two of the articles in combination with a domain-specific view on reasoning. Reasoning is here described as to include not only an ability for a specific mental activity, but also the understanding for how a certain activity fits into a specific mathematical situation [55]. The role of reasoning is to create a change in students’ understanding for particular mathematical relationships, their ability to think about these relationships, and how they perceive them. The process of change is supported by letting students work together with the same mathematical task. Through collaborative work with the task, and through reasoning and giving account for their understanding on how to solve the task, the students develop their understanding [53].

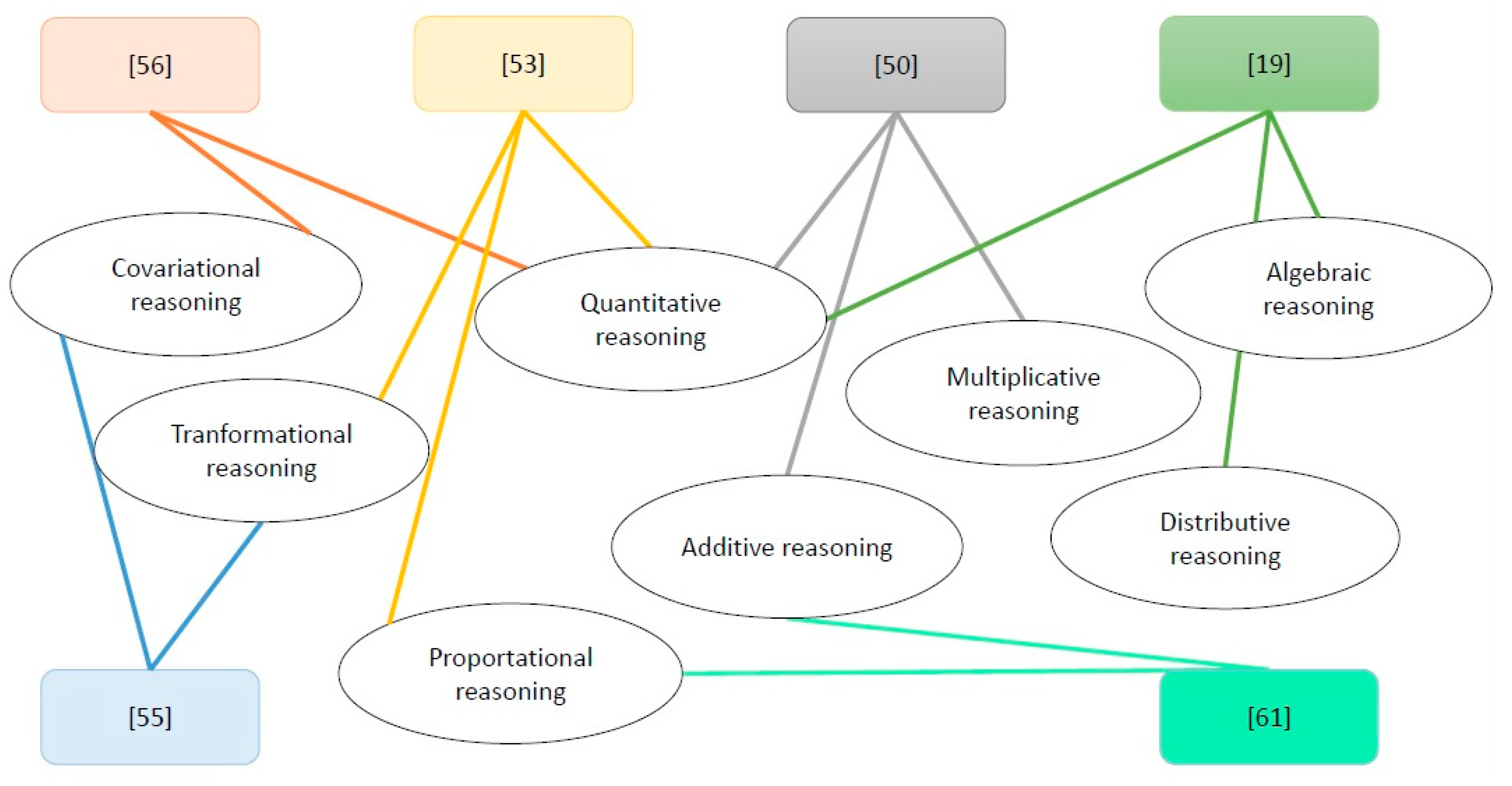
3.2.8. Combinations of Kinds of Reasoning

In six articles [19,50,53,55,56,61], the scholars combine different kinds of mathematical reasoning, as shown in Figure 2. The different kinds of reasoning are used in different ways, for instance, to exemplify how the researchers understand reasoning [53], or to explain relationships between different kinds of topics related to reasoning [56]. One example of this is Hackenberg and Lee, who describe how quantitative and algebraic reasoning are connected to each other and build on one another [19].

4. Discussion

The aim of this article was to provide an overview on kinds of mathematical reasoning addressed in mathematics education research. In particular, we reviewed existing empirical studies on mathematical reasoning. Of course, our study has the limitation that with N = 27 articles incorporated, it cannot claim to be generalizable. More importantly, we incorporated only articles from high-level journals, and most certainly the results would have been different if other journals or conference proceedings had been considered. This said, the following results should be regarded against the backdrop that they may be biased through our choices. Yet, we think that future research can overcome the limitations of our review through integrating a broader database (e.g., articles from more different journals) and could accordingly come to deeper scientific conclusions with respect to the concept of mathematical reasoning.

4.1. Discussion of the Results

In our review, we found that almost one in five articles were not explicit about the kind of mathematical reasoning addressed. This confirms the impression that many scholars have—that reasoning is a term that is often used in an intuitive way, without explicit definitions or theory use [2].
We found that scholars either had a domain-general or domain-specific view on mathematical reasoning. In the domain-general view, reasoning is not bound to a specific mathematical topic but can be applied in any mathematical task or subject. In this category, the focus is on how the students give reasons for a specific standpoint, solution, or conclusion. One of the theories most often used was Lithner’s theory on creative and imitative reasoning [4]. This theory describes reasoning as “the line of thought” [4] (p. 257)—as a process when solving mathematical tasks, from starting with a question or the task that needs to be solved, to a conclusion, when the solution of that task is reached. Within this theory, reasoning is not related to proof or correctness, but only has to be reasonable to the person. Lithner presents two main categories of reasoning: imitative and creative reasoning. This theory is domain-general in that it focuses on the domain of mathematical reasoning, however not with restriction to a specific mathematical content or topic. It is therefore possible to use this theory within different areas of mathematics [4].
In the domain-specific view, we found the following kinds of reasoning (in alphabetical order): additive reasoning, algebraic reasoning, covariational reasoning, distributive reasoning, informal inferential reasoning, multiplicative reasoning, proportional reasoning, quantitative reasoning, and transformational reasoning. Within these kinds of reasoning, quantitative reasoning was addressed often—together with Thompson’s theory of quantitative reasoning [20,57]. This theory was used to conceptualize reasoning as a process that includes understanding, quantification, and relationships between quantities. Furthermore, Informal Inferential Reasoning (IIR) [47] was among those kinds of reasoning addressed often. IIR provides specific tools for understanding and investigating reasoning related to statistics. IIR builds on the theory of Informal Statistical Inference (ISI) by Makar and Rubin [49]. In this theory, the reasoning is described as a process in which students use a dataset to draw conclusions about the world, while also understanding the limitations for the conclusions that accompany the specific data set [45]. On the other hand, multiplicative reasoning and distributive reasoning are examples of kinds of reasoning that were only used in single cases of articles.
Further, it is noteworthy that approximately a fourth of the studies in our review combined different domain-specific kinds of reasoning, indicating the interplay of different mathematical domains in students’ mathematical reasoning.

4.2. Implications for School Practice

What do the insights from our review imply for school practice? We found that the kinds of reasoning addressed in the empirical studies with school students can be broadly divided into domain-general and domain-specific.
One domain-general kind of reasoning that can be useful for mathematics teachers to know about is Lithner’s idea of creative and imitative reasoning. It is not restricted to a specific content but puts emphasis on how students reason—with already known facts, or in a way that is creative, and new to them. We think that for teachers, creative and imitative reasoning can be useful didactical categories. They can help teachers to be aware of what mathematical reasoning can be and what to support, for instance, in whole-class discussions, in group work, or individual work [4]. The framework offered by Lithner can not only help teachers to understand students’ mathematical reasoning, but also to develop the teaching—in a way that it focuses less on rote-learning but more on creative reasoning and on trying new things, which connects to the aim to prepare students for their present and future lives in increasingly automated and interconnected societies and economies, where creative solutions are required [62].
Further, we think that it is important for teachers to be aware that there are different domain-specific kinds of reasoning, with different obstacles and affordances. Spatial, geometrical reasoning is, for example, different from Informal Inferential Reasoning (IIR). Whereas in spatial reasoning, the focus is on relations between geometrical entities and the changes and consequences happening when working with these entities, in IRR the focus is on making conclusions from data that go beyond the data at hand. Reasoning in different sub-domains has different focuses, different difficulties, and different characteristics. It would be valuable for teachers to know that reasoning in different mathematical domains comes with different characteristics and that students who are excelling in reasoning in one domain, may have difficulties in another. Being able to reason creatively in domain A does not guarantee for doing likewise in domain B.
Further, we think it is important for practitioners to be aware of the interplay that the domain-specific kinds of reasoning often are in. We found that, for instance, additive and multiplicative reasoning are partially studied together and that some ways of reasoning are basic to other ones. For instance, quantitative reasoning is a foundation for the students to be able to engage in algebraic reasoning [19]. These connections are important to know for teachers to support students in their learning adequately. Especially when students encounter difficulties in mathematical reasoning, it is valuable to know what the “predecessors” are, etc.

5. Conclusions

Through our review, we were able to provide an overview on different kinds of reasoning addressed in empirical mathematics education research both in a domain-general and domain-specific perspective. We think that our work may be of interest both for researchers and practitioners (e.g., teachers), who want to study or support mathematical reasoning and who need to navigate through the diversity of notions of mathematical reasoning, and the diverse landscape on research about it. We think that we may have indicated that reasoning is not almost everything or nothing—like stated in the introduction—but that it can be regarded in certain ways; either domain-general or -specific, with different theoretical anchors, etc. Finally, we hope that our work may be a springboard for further research on mathematical reasoning and that it can fuel the discussion on this important mathematical activity.

Author Contributions

Conceptualization, A.H., M.S., and P.N.; methodology, A.H.; analysis, A.H.; investigation, A.H., M.S. and P.N.; writing, A.H., M.S., and P.N.; visualization, A.H. and M.S.; supervision, M.S. and P.N. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Conflicts of Interest

The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.

References

  1. Cambridge University Press. Reasoning: Cambridge English Dictionary. Available online: https://dictionary.cambridge.org/dictionary/english/reasoning (accessed on 7 November 2018).
  2. Yackel, E.; Hanna, G. Reasoning and proof. In A Research Companion to Principles and Standards for School Mathematics; Kilpatrick, J., Martin, W.G., Schifter, D., Eds.; National Council of Teachers of Mathematics: Reston, VA, USA, 2003; pp. 227–236. ISBN 0873535375/9780873535373. [Google Scholar]
  3. Lithner, J.; Palm, T. Learning Difficulties and Mathematical Reasoning. In The First Sourcebook on Nordic Research in Mathematics Education: Norway, Sweden, Iceland, Denmark, and Contributions from Finland; Sriraman, B., Bergsten, C., Goodchild, S., Pálsdóttir, G., Dahl, B., Haapasalo, L., Eds.; Information Age Pub: Charlotte, NC, USA, 2010; pp. 283–298. ISBN 1617351008/9781617351006. [Google Scholar]
  4. Lithner, J. A research framework for creative and imitative reasoning. Educ. Stud. Math. 2008, 67, 255–276. [Google Scholar] [CrossRef]
  5. National Council of Teachers of Mathematics. Principles and Standards for School Mathematics; The Council: Reston, VA, USA, 2000. [Google Scholar]
  6. Jeannotte, D.; Kieran, C. A conceptual model of mathematical reasoning for school mathematics. Educ. Stud. Math. 2017, 96, 1–16. [Google Scholar] [CrossRef] [Green Version]
  7. Niss, M.; Højgaard, T. Mathematical competencies revisited. Educ. Stud. Math. 2019, 102, 9–28. [Google Scholar] [CrossRef]
  8. Skolverket. Läroplan för Grundskolan, Förskoleklassen och Fritidshemme; Lgr 11 (Rev. ed.); Skolverket: Stockholm, Sweden, 2019. [Google Scholar]
  9. Baker, S.; Gersten, R.; Lee, D.S. A synthesis of empirical research on teaching mathematics to low-achieving students. Elem. Sch. J. 2002, 103, 51–73. [Google Scholar] [CrossRef]
  10. Eriksson, K.B.; Forsberg, C.; Wengström, Y. Systematiska Litteraturstudier i Utbildningsvetenskap: Vägledning vid Examensarbeten och Vetenskapliga Artiklar; Natur & Kultur: Stockholm, Sweden, 2013; ISBN 9789127134119. [Google Scholar]
  11. Nilsson, P.; Schindler, M.; Bakker, A. The nature and use of theories in statistics education. In International Handbook of Research in Statistics Education; Ben-Zvi, D., Makar, K., Garfield, J., Eds.; Springer: Cham, Switzerland, 2018; pp. 359–386. ISBN 9783319661933. [Google Scholar]
  12. Dyer, E.B.; Sherin, M.G. Instructional reasoning about interpretations of student thinking that supports responsive teaching in secondary mathematics. ZDM 2016, 48, 69–82. [Google Scholar] [CrossRef]
  13. Otten, S.; Gilbertson, N.J.; Males, L.M.; Clark, D.L. The mathematical nature of reasoning-and-proving opportunities in geometry textbooks. Math. Think. Learn. 2014, 16, 51–79. [Google Scholar] [CrossRef] [Green Version]
  14. Dawkins, P.C.; Cook, J.P. Guiding reinvention of conventional tools of mathematical logic: Students’ reasoning about mathematical disjunctions. Educ. Stud. Math. 2017, 94, 241–256. [Google Scholar] [CrossRef]
  15. Mata-Pereira, J.; da Ponte, J.-P. Enhancing students’ mathematical reasoning in the classroom: Teacher actions facilitating generalization and justification. Educ. Stud. Math. 2017, 96, 169–186. [Google Scholar] [CrossRef]
  16. Brousseau, G.; Gibel, P. Didactical handling of students’ reasoning processes in problem solving situations. Educ. Stud. Math. 2005, 59, 13–58. [Google Scholar] [CrossRef]
  17. Pólya, G. Mathematics and Plausible Reasoning: Induction and Analogy in Mathematics; University Press: Princeton, NJ, USA, 1954; Volume 1, ISBN 4871878333/978-4871878333. [Google Scholar]
  18. Rivera, F.; Becker, J. Algebraic reasoning through patterns. Math. Teach. Middle Sch. 2009, 15, 213–221. [Google Scholar] [CrossRef]
  19. Hackenberg, A.J.; Lee, M.Y. Students’ distributive reasoning with fractions and unknowns. Educ. Stud. Math. 2016, 93, 245–263. [Google Scholar] [CrossRef]
  20. Thompson, P.W. Quantitative reasoning, complexity, and additive structures. Educ. Stud. Math. 1993, 25, 165–208. [Google Scholar] [CrossRef]
  21. Thompson, P.W. Quantitative reasoning and mathematical modeling. In New Perspectives and Directions for Collaborative Research in Mathematics Education; Chamberlin, S., Hatfield, L.L., Eds.; University of Wyoming: Laramie, WY, USA, 2010; pp. 33–57. [Google Scholar]
  22. Barmby, P.; Harries, T.; Higgins, S.; Suggate, J. The array representation and primary children’s understanding and reasoning in multiplication. Educ. Stud. Math. 2009, 70, 217–241. [Google Scholar] [CrossRef] [Green Version]
  23. Meletiou-Mavrotheris, M.; Paparistodemou, E. Developing students’ reasoning about samples and sampling in the context of informal inferences. Educ. Stud. Math. 2015, 88, 385–404. [Google Scholar] [CrossRef]
  24. Bjuland, R.; Luiza Cestari, M.; Borgersen, H.E. The interplay between gesture and discourse as mediating devices in collaborative mathematical reasoning: A multimodal approach. Math. Think. Learn. 2008, 10, 271–292. [Google Scholar] [CrossRef]
  25. Hohensee, C. Backward transfer: An investigation of the influence of quadratic functions instruction on students’ prior ways of reasoning about linear functions. Math. Think. Learn. 2014, 16, 135–174. [Google Scholar] [CrossRef]
  26. Leighton, J.P. Defining and describing reason. In The Nature of Reasoning; Leighton, J.P., Sternberg, R.J., Eds.; Cambridge University Press: Cambridge, UK, 2004; pp. 3–11. ISBN 0521009286/978-0521009287. [Google Scholar]
  27. Christou, C.; Papageorgiou, E. A framework of mathematics inductive reasoning. Learn. Instr. 2007, 17, 55–66. [Google Scholar] [CrossRef]
  28. Pólya, G. How to Solve it; University Press: Princeton, NJ, USA, 1945. [Google Scholar]
  29. Polya, G. How to Solve it; University Press: Princeton, NJ, USA, 1957; Original work published 1945. [Google Scholar]
  30. Presmeg, N. Semiotics and the “connections” standard: Significance of semiotics for teachers of mathematics. Educ. Stud. Math. 2006, 61, 163–182. [Google Scholar] [CrossRef]
  31. Gravemeijer, K. Local instruction theories as means of support for teachers in reform mathematics education. Math. Think. Learn. 2004, 6, 105–128. [Google Scholar] [CrossRef]
  32. McClain, K.; Cobb, P.; Gravemeijer, K. Supporting students’ ways of reasoning about data. In Learning Mathematics for a New Century, 2000 Yearbook; Burke, M.J., Curcio, R.F., Eds.; National Council of Teachers of Mathematics: Reston, VA, USA, 2000; pp. 174–187. ISBN 978-0873534796/0873534794. [Google Scholar]
  33. Boesen, J.; Lithner, J.; Palm, T. The relation between types of assessment tasks and the mathematical reasoning students use. Educ. Stud. Math. 2010, 75, 89–105. [Google Scholar] [CrossRef]
  34. Hershkowitz, R.; Tabach, M.; Dreyfus, T. Creative reasoning and shifts of knowledge in the mathematics classroom. ZDM 2017, 49, 25–36. [Google Scholar] [CrossRef]
  35. Lithner, J. Principles for designing mathematical tasks that enhance imitative and creative reasoning. ZDM 2017, 49, 937–949. [Google Scholar] [CrossRef] [Green Version]
  36. Jurdak, M.; El Mouhayar, R. Trends in the development of student level of reasoning in pattern generalization tasks across grade level. Educ. Stud. Math. 2014, 85, 75–92. [Google Scholar] [CrossRef]
  37. Biggs, J.B.; Collis, K.F. Evaluating the Quality of Learning: The Solo Taxonomy; Academic Press: New York, NY, USA, 1982; ISBN 0120975505. [Google Scholar]
  38. Clements, D.; Sarama, J. Learning and Teaching Early Math: The Learning Trajectories Approach; Routledge: New York, NY, USA, 2009; ISBN 978-0-415-82850-5. [Google Scholar]
  39. Khan, S.; Francis, K.; Davis, B. Accumulation of experience in a vast number of cases: Enactivism as a fit framework for the study of spatial reasoning in mathematics education. ZDM 2015, 47, 269–279. [Google Scholar] [CrossRef]
  40. Hallowell, D.A.; Okamoto, Y.; Romo, L.F.; La Joy, J.R. First-graders’ spatial-mathematical reasoning about plane and solid shapes and their representations. ZDM 2015, 47, 363–375. [Google Scholar] [CrossRef]
  41. Herbst, P. Interaction with diagrams and the making of reasoned conjectures in geometry. Zent. Didakt. Math. 2004, 36, 129–139. [Google Scholar] [CrossRef] [Green Version]
  42. Chen, C.-L.; Herbst, P. The interplay among gestures, discourse, and diagrams in students’ geometrical reasoning. Educ. Stud. Math. 2013, 83, 285–307. [Google Scholar] [CrossRef] [Green Version]
  43. Gómez-Chacón, I.M.; Romero Albaladejo, I.M.; del Mar García López, M. Zig-zagging in geometrical reasoning in technological collaborative environments: A Mathematical working space-framed study concerning cognition and affect. ZDM 2016, 48, 909–924. [Google Scholar] [CrossRef]
  44. Lakatos, I. Proofs and Refutations: The Logic of Mathematical Discovery; Cambridge University Press: New York, NY, USA, 1979; ISBN 0521290384/9780521290388. [Google Scholar]
  45. Gil, E.; Ben-Zvi, D. Explanations and context in the emergence of students’ informal inferential reasoning. Math. Think. Learn. 2011, 13, 87–108. [Google Scholar] [CrossRef]
  46. Pfannkuch, M. The role of context in developing informal statistical inferential reasoning: A classroom study. Math. Think. Learn. 2011, 13, 27–46. [Google Scholar] [CrossRef] [Green Version]
  47. Makar, K. Young children’s explorations of average through informal inferential reasoning. Educ. Stud. Math. 2014, 86, 61–78. [Google Scholar] [CrossRef] [Green Version]
  48. Pfannkuch, M.; Arnold, P.; Wild, C. What I see is not quite the way it really is: Students’ emergent reasoning about sampling variability. Educ. Stud. Math. 2015, 88, 343–360. [Google Scholar] [CrossRef]
  49. Makar, K.; Rubin, A. A framework for thinking about informal statistical inference. Stat. Educ. Res. J. 2009, 8, 82–105. [Google Scholar]
  50. Nunes, T.; Bryant, P.; Evans, D.; Barros, R. Assessing quantitative reasoning in young children. Math. Think. Learn. 2015, 17, 178–196. [Google Scholar] [CrossRef]
  51. Kaput, J.J. Transforming algebra from an engine of inequity to an engine of mathematical power by “algebrafying” the K–12 curriculum. In the Nature and Role of Algebra in the K–14 Curriculum, Proceedings of a National Symposium Washington, DC, USA, 27–28 May 1997; National Council of Teachers of Mathematics & Mathematical Sciences Education Board, Ed.; National Academies Press: Washington, DC, USA, 1998. [Google Scholar] [CrossRef]
  52. Bishop, J.P.; Lamb, L.L.; Philipp, R.A.; Withacre, I.; Schappelle, B.P.; Lewis, M.L. Obstacles and affordances for integer reasoning: An analysis of children’s thinking and the history of mathematics. J. Res. Math. Educ. 2014, 45, 19–61. [Google Scholar] [CrossRef]
  53. Lobato, J.; Hohensee, C.; Rhodehamel, B.; Diamond, J. Using student reasoning to inform the development of conceptual learning goals: The case of quadratic functions. Math. Think. Learn. 2012, 14, 85–119. [Google Scholar] [CrossRef]
  54. Hilton, A.; Hilton, G.; Dole, S.; Goos, M. Promoting middle school students’ proportional reasoning skills through an ongoing professional development programme for teachers. Educ. Stud. Math. 2016, 92, 193–219. [Google Scholar] [CrossRef]
  55. Johnson, H.L. Secondary students’ quantification of ratio and rate: A framework for reasoning about change in covarying quantities. Math. Think. Learn. 2015, 17, 64–90. [Google Scholar] [CrossRef]
  56. Johnson, H.L.; McClintock, E.; Hornbein, P. Ferris wheels and filling bottles: A case of a student’s transfer of covariational reasoning across tasks with different backgrounds and features. ZDM 2017, 49, 851–864. [Google Scholar] [CrossRef]
  57. Thompson, P.W. The development of the concept of speed and its relationship to concepts of rate. In The Development of Multiplicative Reasoning in the Learning of Mathematics; Harel, G., Confrey, J., Eds.; State University of New York Press: Albany, NY, USA, 1994; pp. 181–234. ISBN 978-0791417645/0791417646. [Google Scholar]
  58. Nunes, T.; Bryant, P.; Evans, D.; Bell, D.; Barros, R. Teaching children how to include the inversion principle in their reasoning about quantitative relations. Educ. Stud. Math. 2012, 79, 371–388. [Google Scholar] [CrossRef]
  59. de Beer, H.; Gravemeijer, K.; van Eijck, M. Discrete and continuous reasoning about change in primary school classrooms. ZDM 2015, 47, 981–996. [Google Scholar] [CrossRef] [Green Version]
  60. Simon, M.A. Beyond inductive and deductive reasoning: The search for a sense of knowing. Educ. Stud. Math. 1996, 30, 197–209. [Google Scholar] [CrossRef]
  61. Noll, J.; Shaughnessy, J.M. Aspects of students’ reasoning about variation in empirical sampling distributions. J. Res. Math. Educ. 2012, 43, 509–556. [Google Scholar] [CrossRef]
  62. OECD. Pisa 2012 Results: Creative Problem Solving: Students’ Skills in Tackling Real-Life Problems. In PISA 2012 results: Organisation for Economic Co-operation and Development, Programme for International Student Assessment; OECD Publishing: Paris, France, 2014; Volume 5, Available online: http://www.oecd.org/pisa/keyfindings/PISA-2012-results-volume-V.pdf (accessed on 15 October 2020).
Education 10 00289 g001 550
Figure 1. PRISMA Flow Diagram.
Figure 1. PRISMA Flow Diagram.
Education 10 00289 g001
Education 10 00289 g002 550
Figure 2. Different Domain-Specific Kinds of Reasoning Used Together.
Figure 2. Different Domain-Specific Kinds of Reasoning Used Together.
Education 10 00289 g002
Table
Table 1. Domain-general kinds of reasoning addressed by the studies included in the review.
Table 1. Domain-general kinds of reasoning addressed by the studies included in the review.
Kind of ReasoningArticles
(Reference No.)		Numbers of Articles per Kind of Reasoning
Definitions and explanatory statements15, 22, 24, 25 4
Creative and imitative reasoning33, 34, 353
SOLO-taxonomy361
Hierarchic interactionism231
Table
Table 2. Domain-Specific Kinds of Reasoning Addressed by the Studies Included in the Review.
Table 2. Domain-Specific Kinds of Reasoning Addressed by the Studies Included in the Review.
Kind of ReasoningArticles
(Reference No.)		Numbers of Articles per Kind of Reasoning
Spatial reasoning39, 40, 42, 434
Informal Inferential Reasoning (IIR)45, 46, 47, 484
Additive, multiplicative and distributive reasoning19, 50, 613
Algebraic reasoning19, 52 2
Proportional and covariational reasoning53, 54, 55, 56, 615
Quantitative reasoning19, 50, 53, 56, 58, 59 6
Transformational reasoning53, 552
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Hjelte, A.; Schindler, M.; Nilsson, P. Kinds of Mathematical Reasoning Addressed in Empirical Research in Mathematics Education: A Systematic Review. Educ. Sci. 2020, 10, 289. https://doi.org/10.3390/educsci10100289

AMA Style

Hjelte A, Schindler M, Nilsson P. Kinds of Mathematical Reasoning Addressed in Empirical Research in Mathematics Education: A Systematic Review. Education Sciences. 2020; 10(10):289. https://doi.org/10.3390/educsci10100289

Chicago/Turabian Style

Hjelte, Alexandra, Maike Schindler, and Per Nilsson. 2020. "Kinds of Mathematical Reasoning Addressed in Empirical Research in Mathematics Education: A Systematic Review" Education Sciences 10, no. 10: 289. https://doi.org/10.3390/educsci10100289

APA Style

Hjelte, A., Schindler, M., & Nilsson, P. (2020). Kinds of Mathematical Reasoning Addressed in Empirical Research in Mathematics Education: A Systematic Review. Education Sciences, 10(10), 289. https://doi.org/10.3390/educsci10100289

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop