The Response of Housing Construction to a Copper Price Shock in Chile (2009–2020)

Abstract

The copper price is a leading indicator of real estate activity. Price increases are statistically related to increasing numbers of applications for residential building permits. However, this reciprocity is not instantaneous as permit numbers lag price rises by 9 to 10 months. This dynamic is implicit in various transmission channels: from the first effects on investment plans and demand for durable goods due to better expectations from investors and consumers to the real impact of higher copper revenues on the economy’s aggregate production and demand (multiplier or second-round effect). In this paper, we proposed the impulse-response functions of a vector autoregressive model to capture the dynamic between the copper price and house building permits. Therefore, it would be expected that the recent copper price increase will boost construction and real estate activity. The effects could materialize this year and extend into early 2022.

1. Introduction

The international copper price has tended to rise sharply since the end of 2020, consistent with improved global economic prospects. Better performance of China’s industrial production and improved prospects for investors due to 2021 global economic growth have contributed to the most recent copper price recovery (International Monetary Fund 2021). In particular, the inoculation process to prevent COVID-19, already initiated in various regions of the world, is contributing to rising expectations regarding the performance of financial markets. The copper price rose 54% during December 2020 compared to its lowest level registered in April that year (USD 2.29/pound) (Banco Central de Chile 2021).

Chile considerably benefits from this high-price scenario as it is a key copper producer (Astudillo et al. 2020; Carrasco et al. 2020). The country has the largest copper reserves in the world, estimated at 210 million metric tons in 2015 (Comisión Chilena del Cobre 2021). For every 10% increase in the copper price, Chile’s GDP could grow between 0.05% and 0.7% annually, depending on whether the government follows a structural surplus rule (Medina and Soto 2007). Furthermore, the world’s main copper deposits are in north Chile, specifically, in the Antofagasta Region (see Figure 1), so increased mining activity could be reflected in potentially higher demand for real estate—similar to what was observed during the 2011 mining boom, when the copper price averaged USD 4/pound (Cámara Chilena de la Construcción 2011). During 2011 it was observed that the increase in new hires in the mining sector and higher household income closely tracked with mining activity, resulting in higher housing demand, mainly in that part of the country. This development could be partially explained by workers’ preference to live near the workplace.

Figure 1. Study area restricted to Chile’s northern regions.

Given the current context, it is relevant to analyze the potential of a quantitative impact of the copper price on real estate activity and how far in advance the higher copper price stimulates the development of residential building works (Contreras-Reyes and Idrovo-Aguirre 2020; Idrovo-Aguirre and Contreras-Reyes 2019, 2021). From a real estate market perspective, residential building permits—requested by construction companies from the municipality where the project will be carried out—“naturally” precede effective real estate investment. Idrovo and Lozano (2018) showed statistically that the average period from granting a housing construction permit to the start of works (real or effective investment), is around 12 months for Chile’s northern regions. Therefore, building permits can be considered a leading investment indicator for the real estate sector.

The objective of this study is to answer the questions initially posed through a model that captures the dynamic relationship between the copper price and house building permits approved in the north of Chile, using the impulse-response functions of a vector autoregressive (VAR) model (Ozcelebi 2021). This way, our VAR model’s impulse response functions aim to collect the short-term transmission mechanism of the international copper price in real estate investments reflected in new housing permits. In this regard, it is crucial to consider that the real estate sector’s infrastructure segment is labor intensive, with 70% of workers engaged in residential building construction. In addition, real estate investments account for a third of construction investments and represent 22% of the national total. Therefore, this analysis could provide an early activity warning indicator for decision makers to adjust economic policy. This link between the copper price and the real estate market also figures in the results of studies on the Chinese case (Chen and Tongurai 2021).

This paper therefore proceeds as follows: After this introduction, data and variables used in this studies are widely described. Section 3 explains the methodology of cointegration analysis, VAR model and impulse response function. The main results of the selected VAR model are shown in Section 4. Conclusions are then addressed in Section 5.

2. Data Description

The database (available at https://dx.doi.org/10.13140/RG.2.2.23553.79200 (accessed on 28 February 2021)) contains the historical copper price series (in USD/pound) and the variables of approved permits for housing construction in the north of Chile. Figure 2 shows each variable’s evolution (original and with logarithmic transformation), and Table 1 describes each variable to be used in the VAR model. Permits are measured both in quantity (number of permits granted) and in the authorized area (m²). Building permits are disaggregated into a north zone and a north-central zone, as established by the CORFO (Corporación de Fomento de la Producción 2021) and the Odeplan (Oficina de Planificación Nacional 2021). The approach should capture possible heterogeneities in the impact of the copper price in the real estate market in the northern zone; above all because the Antofagasta Region, which concentrates most mining activity in Chile, is in the north. The analysis period runs monthly from January 2009 to December 2012 (144 observations). Therefore, the period or cycle covering the boom would be 2011. Copper price evolution and building the permit series are based on the data source from the Banco Central de Chile (2021) and the Instituto Nacional de Estadísticas (2021), respectively.

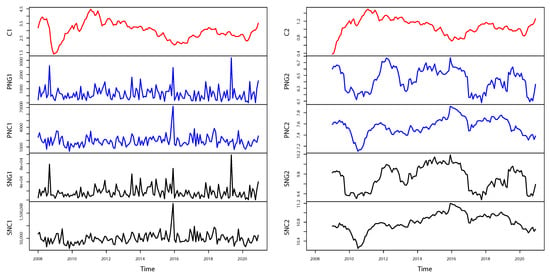
Figure 2. Copper price evolution (C1: original, C2: transformed), permits (PNG1: original north, PNG2: transformed north, PNC1: original north-central, PNC2: transformed north-central), and surface (SNG1: original north, SNG2: transformed north, SNC1: original north-central, SNC2: transformed north-central) of residential construction (January 2009–December 2020). The transformation of the original series (left column) corresponds to the logarithm of the 12-month moving average (right column).

Table 1. Definition of variables of the VAR Model. BCCh: Banco Central de Chile; INE: Instituto Nacional de Estadísticas de Chile.

Variables (VAR Model)	Abbreviation	Short Description	Resource
C2: Logarithm of the copper price.	$y_{1t}$	The copper price is measured in USD per pound, and its value as listed on the London Metal Exchange.	BCCh
PNG2: Logarithm of the 12-month moving average of the number of housing permits approved in the northern zone.	$y_{2t}$	Number of permits approved by municipalities for residential construction (northern zone).	INE
SNG2: Logarithm of the 12-month moving average of the area (m2) authorized for housing construction in the northern zone.	$y_{3t}$	Area approved by municipalities for housing construction (northern zone).	INE
PNC2: Logarithm of the 12-month moving average of the number of approved housing permits in the north-central zone.	$y_{4t}$	Number of permits approved by municipalities for housing construction (north-central zone).	INE
SNC2: Logarithm of the 12-month moving average of the area (m2) authorized for housing construction in the north-central zone.	$y_{5t}$	Area approved by municipalities for housing construction (north-central zone).	INE

The database considered is relevant for the following reasons:

• House building permit data are useful because permits precede real or effective real estate investment. Idrovo and Lozano (2018) showed statistically that the average time from permit granting until construction start (real or effective investment) is around 12 months for the regions that concentrate mining activity in Chile. For its part, the copper price is among the primary transmission channels of external shocks in the Chilean economy. Therefore, it functions as an early economic warning indicator.
• All public and private institutions involved in real estate activity in Chile can benefit from this database. In particular, the VAR model used here enables systematic measurement of how the copper price impacts housing construction progress in north Chile, which hosts the world’s main copper deposits. Therefore, higher mining activity could be related to potentially higher demand for real estate, resembling the scenario of the 2011 mining boom.
• An additional value of the data is that they are of high frequency, easily accessible, and provided by official sources. They are published monthly by local and international organizations of high technical prestige. This allows the impulse-response functions of the VAR model, estimated here, to be a source of additional information for policymakers who make decisions on housing.

3. Methods

The permit series (quantity and area) are transformed as the logarithm of the 12-month moving average. In particular, this technique of smoothing housing permits provides a reasonable approximation of the dynamics of effective monthly real estate investment (Idrovo and Lozano 2018).

3.1. The VAR Model

The VAR model is specified as a dynamic system of simultaneous equations between the copper price logarithm and the building permit series logarithm—previously transformed into 12-month moving averages (proxy variable of the effective real estate investment) (Ozcelebi 2021). Formally, we have:

$${\mathbf{y}}_t=\mathbf{c}+\sum _{j=1}^p{\mathsf{\Phi }}_j{\mathbf{y}}_{t-j}+{\mathbf{\epsilon }}_t,$$

with

$${\mathbf{\epsilon }}_t{\sim }^{\mathrm{i}.\mathrm{i}.\mathrm{d}.}N(\mathbf{0},\mathsf{\Omega }),$$

where ${\mathbf{y}}_t$ is a vector ($n\times 1$), n is the number of variables that are part of the equations system, and $\mathsf{\Omega }$ is the matrix ($n\times n$) of variances-covariances of the innovations $\left\{{\mathbf{\epsilon }}_t\right\}$ (Contreras-Reyes 2021). The model assumes that ${\mathbf{y}}_t$ is governed by a Gaussian autoregressive process of order p (Maleki et al. 2020). On the other hand, $\mathbf{c}$ and ${\left\{{\mathsf{\Phi }}_j\right\}}_{j=1}^p$ are parameter matrices that describe the degree of autocorrelation of the model variables (Contreras-Reyes and Hernández-Santoro 2020). The VAR model is assumed to be stationary, that is, the roots of the characteristic polynomial would lie within the unit circle (Contreras-Reyes and Palma 2013; Hamilton 1994).

3.2. Impulse-Response Function

The estimate of the impulse-response functions of an unrestricted VAR model is proposed to measure the response of housing construction activity to copper price variations. The impulse-response functions (Chung 2001) are obtained from the representation of the VAR model as an MA(∞) process:

$${\mathbf{y}}_t=\mathbf{\mu }+\sum _{s=1}^{\infty }{\mathsf{\Psi }}_s{\mathbf{\epsilon }}_{t-s}+{\mathbf{\epsilon }}_t,$$

where $\mathbf{\mu }$ is a non-stochastic drift vector parameter and

$${\mathsf{\Psi }}_s=\frac{\partial {\mathbf{y}}_{t+s}}{\partial {\mathbf{\epsilon }}_t}$$

corresponds to the impulse-response matrix. In particular, the element of row i, column j, of matrix ${\mathsf{\Psi }}_s$ measures the response of the ith variable at time $t+s$ ($y_{i,t+s}$) to an innovation (or shock) of the jth variable of the system (${\epsilon }_{jt}$). Finally, the maximum likelihood method is used for the estimation strategy of the VAR(p) model parameters (Contreras-Reyes 2021; Contreras-Reyes and Hernández-Santoro 2020).

4. Results

Regarding the historical evolution of the data, Table 2 shows the traditional Dickey–Fuller (Dickey and Fuller 1979) and Phillips–Perron (Phillips and Perron 1988) unit root statistical tests. The Zivot–Andrews (ZA) (Zivot and Andrews 1992) left-tailed test is also shown and contrasts the unit root hypothesis with the presence of endogenous structural breaks at the level and/or trend of the time series. Using statistical DFA and PP tests, it appears that all series are non-stationary or I(1) at 1% significance. This result was corroborated by the statistical ZA left-tailed test, whose calculated values were located in the region of non-rejection of the unit root null hypothesis. However, if we consider a significance level of 5% in the DFA and PP tests of block (a), the copper price is weakly stationary. Likewise, under this criterion, the statistical values calculated for the variable “number of homes approved for construction in the northern zone” are close to their critical values, giving rise to imprecise conclusions about unit root presence. Thus, it cannot be ruled out that the VAR system of the variables expressed in levels is globally stationary.

Table 2. Unit root statistic tests. (a) Equation includes only constant; (b) equation includes constant and trend. DFA: augmented Dickey–Fuller test. PP: Phillips–Perron test. ZA: Zivot–Andrews sequential test of structural breaks. The variables are described in Table 1.

	Levels (a)			Levels (b)			Difference (a)
Indicators	DFA	PP	ZA	DFA	PP	ZA	DFA	PP
$y_{1t}$	−2.91	−3.38	−4.96	−3.48	−3.93	−4.91	−7.09	−8.17
$y_{2t}$	−2.88	−2.88	−4.68	−2.86	−2.89	−4.63	−4.84	−12.02
$y_{3t}$	−2.26	−2.29	−3.77	−2.26	−2.28	−3.71	−4.67	−11.96
$y_{4t}$	−2.07	−1.90	−3.23	−2.11	−1.87	−3.41	−7.70	−9.84
$y_{5t}$	−1.64	−1.53	−2.92	−1.50	−1.35	−3.51	−7.61	−9.83
Critical Value
1%	−3.50	−3.50	−5.34	−4.03	−4.03	−5.57	−3.50	−3.50
5%	−2.89	−2.89	−4.80	−3.45	−3.44	−5.08	−2.89	−2.89

Once the theoretical framework has been defined, we proceed to estimate the impact of the higher copper price on housing construction permits, disaggregated by the north zone and north-central zone according to the division by the CORFO (Corporación de Fomento de la Producción 2021) and the Odeplan (Oficina de Planificación Nacional 2021). This facilitates the evaluation of possible heterogeneities in the impact of the copper price on the real estate market in the northern zone; above all, because the Antofagasta Region, which concentrates most mining activity in Chile, is in the north (Figure 1).

Table 3 shows the values of information criteria for the selection of the order of lags p of the VAR model that will be estimated later. Therefore, the VAR model with $p=4$ lags was selected as the best fit because it has the lowest final prediction error (FPE) and the Akaike Information Criterion (AIC) (Akaike 1974) values. The parameters estimated by the maximum likelihood of the VAR(4) model are shown in Supplementary Material (GAUSS software output), due to the extensiveness of the results. In addition, Table 4 summarizes several general results of the VAR model estimation, where the high correlation coefficients ($R^2>0.85$) were a result of the good fit of each variable and the large number of observations (140). Figure 3 shows that the estimated VAR model is statistically stable (or weakly stationary), since all the characteristic roots lie within the unit circle (Contreras-Reyes and Palma 2013).

Table 3. Selection criteria for the order of lags (p) of the VAR model. * Determines the optimal order of lags p. LL: log-likelihood; LR: likelihood ratio; FPE: final prediction error; AIC: Akaike information criterion; BIC: Bayesian information criterion.

Lag (p)	LL	LR	FPE	AIC	BIC
0	603.475	-	1.3 × 10−10	−8.61116	−8.5056
1	1384.07	1561.2	2.4 × 10−15	−19.4831	−18.8497 *
2	1410.6	53.059	2.3 × 10−15	−19.5051	−18.344
3	1440.3	59.395	2.2 × 10−15	−19.5727	−17.8838
4	1468.86	57.126	2.1 × 10−15 *	−19.6239 *	−17.4072
5	1491.97	46.213 *	2.2 × 10−15	−19.5967	−16.8522

Table 4. Summary of the estimation of the VAR(4) model. $y_{1t}$: logarithm of the copper price; $y_{2t}$: logarithm of the 12-month moving average of the number of housing permits approved in the northern zone; $y_{3t}$: logarithm of the 12-month moving average of the area (m²) authorized for housing construction in the northern zone; $y_{4t}$: logarithm of the 12-month moving average of the number of approved housing permits in the north-central zone; $y_{5t}$: logarithm of the 12-month moving average of the area (m²) authorized for housing construction in the north-central zone.

Sample: May 2009–December 2020				No. of Observations = 140
Log-likelihood = 1475.396				AIC = −19.57708
FPE = 2.19 × 10−15				BIC = −17.37085
$|{\mathbf{\Omega }}_{\mathit{ML}}|$ = 4.83 × 10−16
Variable	No. Parameters	RMSE	R2	χ2	$\mathbb{P}>{\mathbf{\chi }}^{\mathbf{2}}$
$y_{1t}$	21	0.040717	0.9569	3109.384	0.0000
$y_{2t}$	21	0.074309	0.8555	829.0199	0.0000
$y_{3t}$	21	0.083274	0.9011	1275.525	0.0000
$y_{4t}$	21	0.043851	0.9346	2000.234	0.0000
$y_{5t}$	21	0.040084	0.9612	3471.823	0.0000

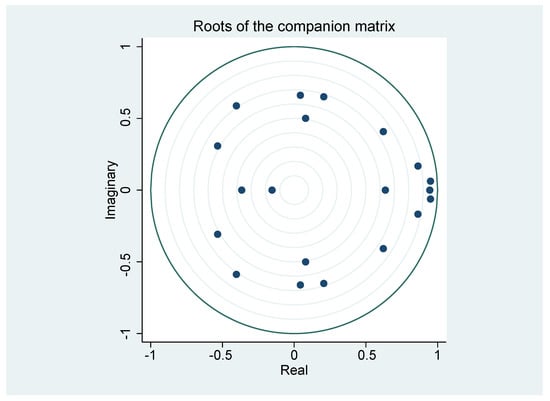
Figure 3. Characteristic roots of estimated parameters of the VAR(4) model.

Figure 4 shows the impulse-response functions, from which several results emerge. Faced with an average 4% monthly copper price rise, the 12-month moving average of housing construction permits in the northern zone responded significantly to this increase or price shock. In particular, the most significant and positive effects on housing permits are observed from the ninth month after the shock. This dynamic is common both for permits measured in a number of dwellings and in the authorized area, with increases that could exceed 2% per month (27% annualized), respectively.

Figure 4. Analysis of a shock to the copper price and the response of housing construction permits (January 2009–December 2020). (a) Copper price shock at $t_0$, equivalent to a rise of one standard deviation of its historical monthly growth rate. Response of the number (b) and surface (c) of authorized dwellings to the copper price shock in the north (monthly growth rate). Response of the number (d) and surface (e) of authorized dwellings to the copper price shock in the north-central area (monthly growth rate).

Therefore, if the 12-month moving average of building permits constitutes a reasonable approximation of northern housing investments (Idrovo and Lozano 2018), impulse-response functions (b) and (c) indicate that, on average, the innovations (or increases) in the copper price can anticipate the largest real estate investment by 9 to 10 months. Intuitively, this period would not only capture the initial effect of construction investors’ improved expectations for new opportunities but also the real impact of higher copper revenues on the aggregate demand of the economy (second-round effect of higher copper prices on consumer decisions for durable goods).

However, the higher copper price did not significantly influence housing permits corresponding to the north-central zone. This could be due to reasons that may not be mutually exclusive. One is that it is effectively an initiation of the heterogeneity of the copper price impact in areas with low concentrations of copper projects compared to zones with many projects, such as the northern area. However, it cannot be ruled out that the low impact of the copper price on building projects in the north-central zone is related to the limitations inherent to the reduced form that specify the VAR models. Therefore, it is not possible to identify or discriminate first and second-round effects of the higher copper price in real estate activity in areas with less mining activity.

Some stylized facts that support our findings are key. From 2011 to 2013, the copper supercycle peaked in Chile around a decade after it started. In this period, the northern zone-led by mining production in the Antofagasta Region stood out for the significant cross-sectional improvement in economic activity indicators compared to the country’s other regions (Centro de Sistemas Públicos 2019). In particular, the area approved for housing construction grew 18% per year on average during the peak of the mining boom from 2011 to 2013, thrice the average growth rate seven years before. In the short term, the largest applications for building permits approved in this mining area constitute initiatives to increase investment in the real estate market. In part, this situation reflects higher expectations of companies regarding housing demand. For example, in 2011, the monthly construction business confidence index recorded a historical maximum on the expectations of labor hiring, with 68 percentage points versus the neutral value of 50 percentage points. In this context, the impulse response functions of our VAR model attempt to capture this short-term transmission mechanism of the copper price in real estate investment initiatives-reflected in the number of new housing permits. This link between copper price and the real estate market also figures in the results of studies on the case of China (Chen and Tongurai 2021).

During the maturation of this macroeconomic scenario of higher income from copper and general mining investment, the northern Antofagasta Region reached the highest level of real family income among the country’s regions (Centro de Sistemas Públicos 2019). This coincides with the impact higher spending had on the increase of real wages, employment and hours worked (Kirchner et al. 2016). The dynamism was also reflected in the composition of capital goods imports for the mining and construction sectors (Banco Central de Chile 2018). These events materialized in an environment of increasingly favorable financial conditions with easy access to real estate credit for companies and individuals, according to a Central Bank survey on bank loans.

5. Conclusions

The impulse-response functions of the estimated VAR(4) model show that in the face of an average 4% monthly copper price rise, the 12-month moving average of residential building permits in the northern zone responds significantly to this increase, or shock, in the price of the mineral. In particular, the greatest significant and positive effects on housing permits are observed as of the ninth month after the shock occurred. This dynamic is common both for permits measured in the number of dwellings and in the authorized area, with increases that could exceed 2% per month (27% annualized), respectively.

In this way, it is statistically proven that copper price cycles are an anticipator of housing construction cycles—since the 12-month moving average of permits constitutes a reasonable approximation of the dynamics of real estate investment in Chile. In addition, it would be expected that the current copper price rise will boost construction and real estate activity, with effects that could be seen from this year and extend into 2022. In summary, investigating the short-term relationship between the international copper price and the sentiment of the real estate market—reflected in building permit dynamics—is essential to anticipate boom periods in this market. Crucially, the real estate sector’s infrastructure segment is labor intensive. Approximately 70% of construction workers are engaged in residential building construction (Cámara Chilena de la Construcción 2019). Furthermore, real estate investments account for a third of construction investments and represent 22% of the national total (Cámara Chilena de la Construcción 2021). Therefore, this analysis could provide an early activity warning indicator for decision makers to adjust economic policy.

Further study could be the analysis of the influence of other external factors in copper prices and for Chile’s northern regions, e.g., using additional variables like gross domestic product (GDP) of the economy, construction GDP, investment in the economy and sectoral investment (Idrovo-Aguirre and Contreras-Reyes 2019), or home loans (Devlin 2002).