Corruption and Tax Burden: What Is the Joint Effect on Total Factor Productivity?
Abstract
1. Introduction
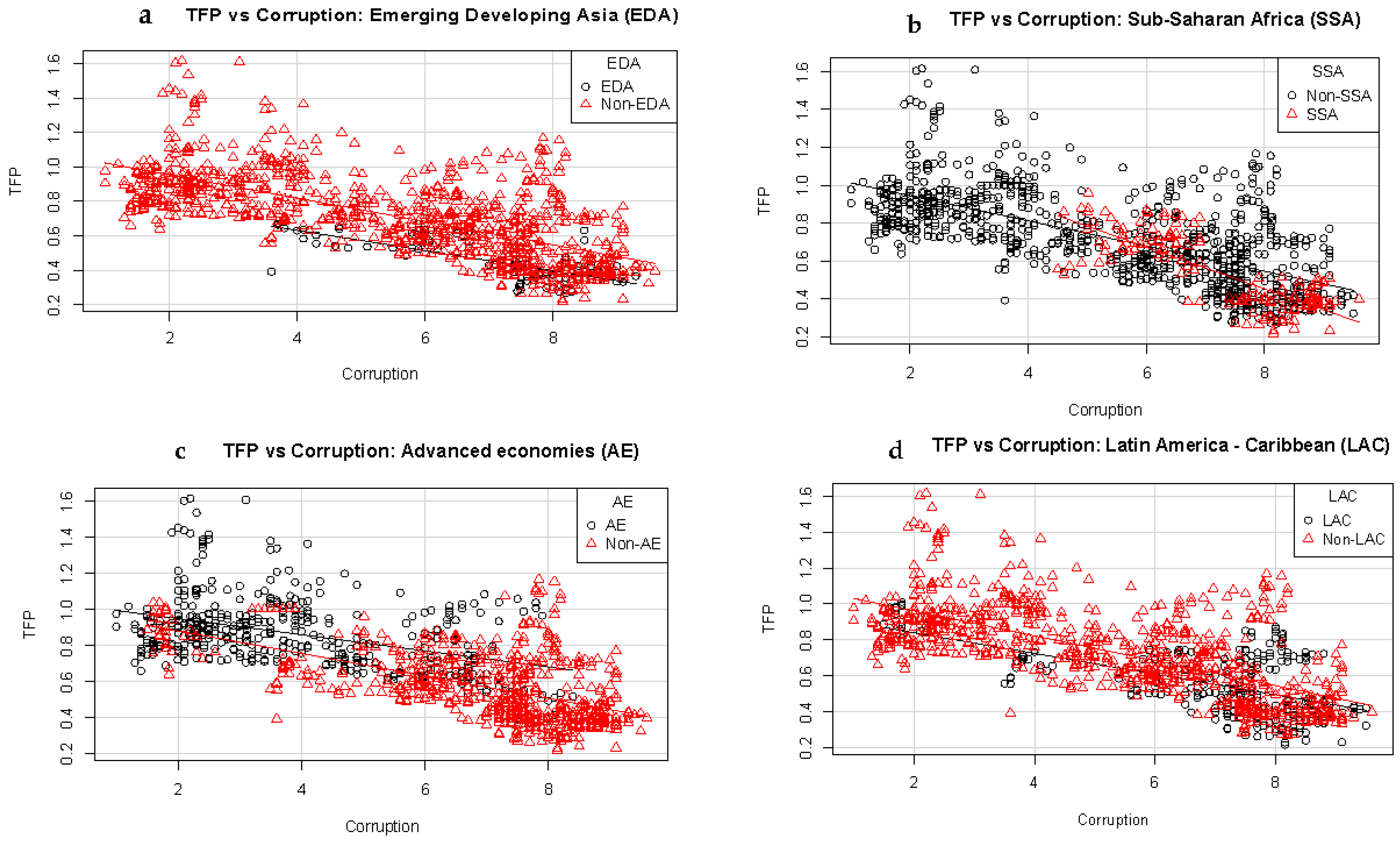
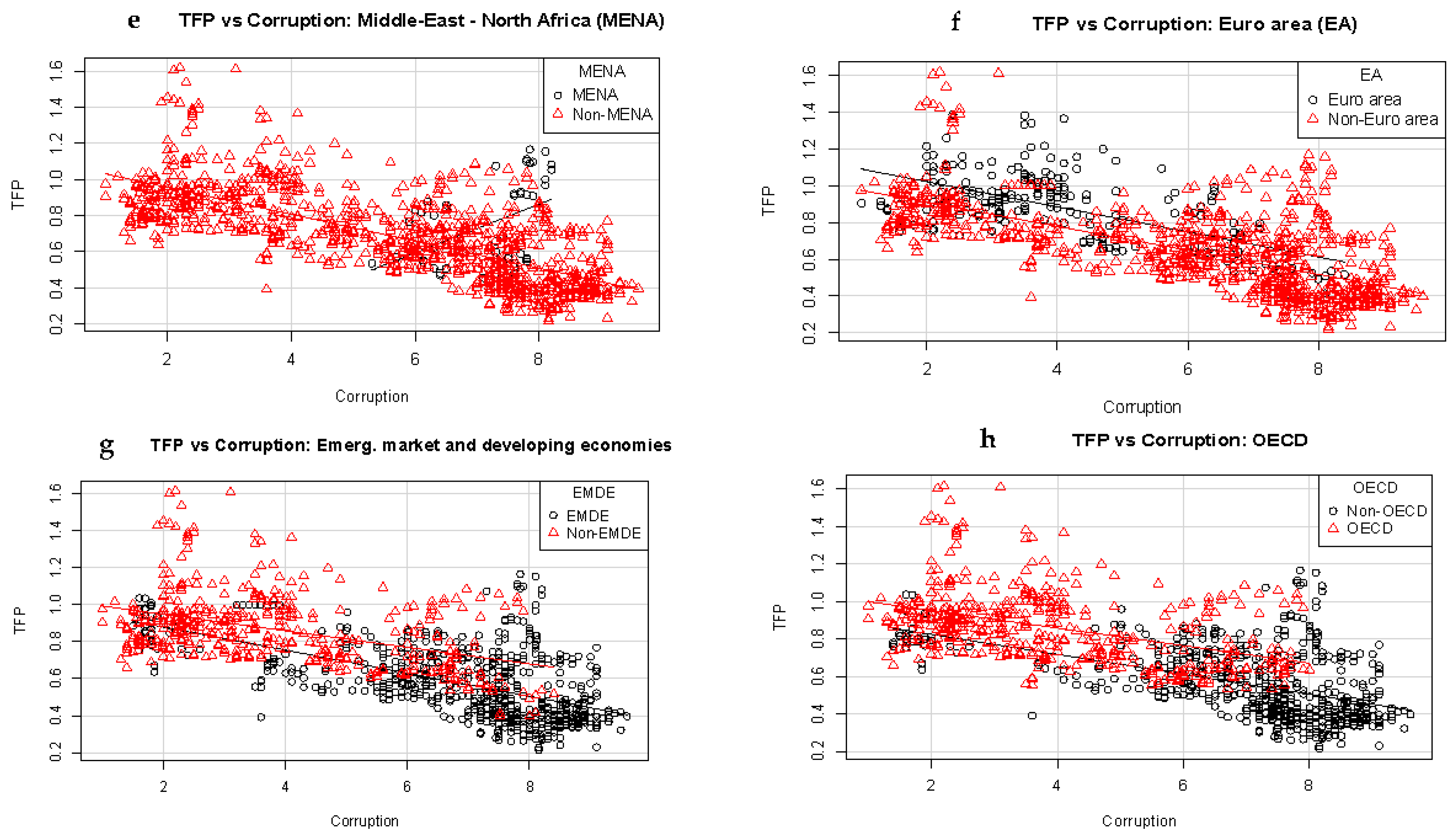
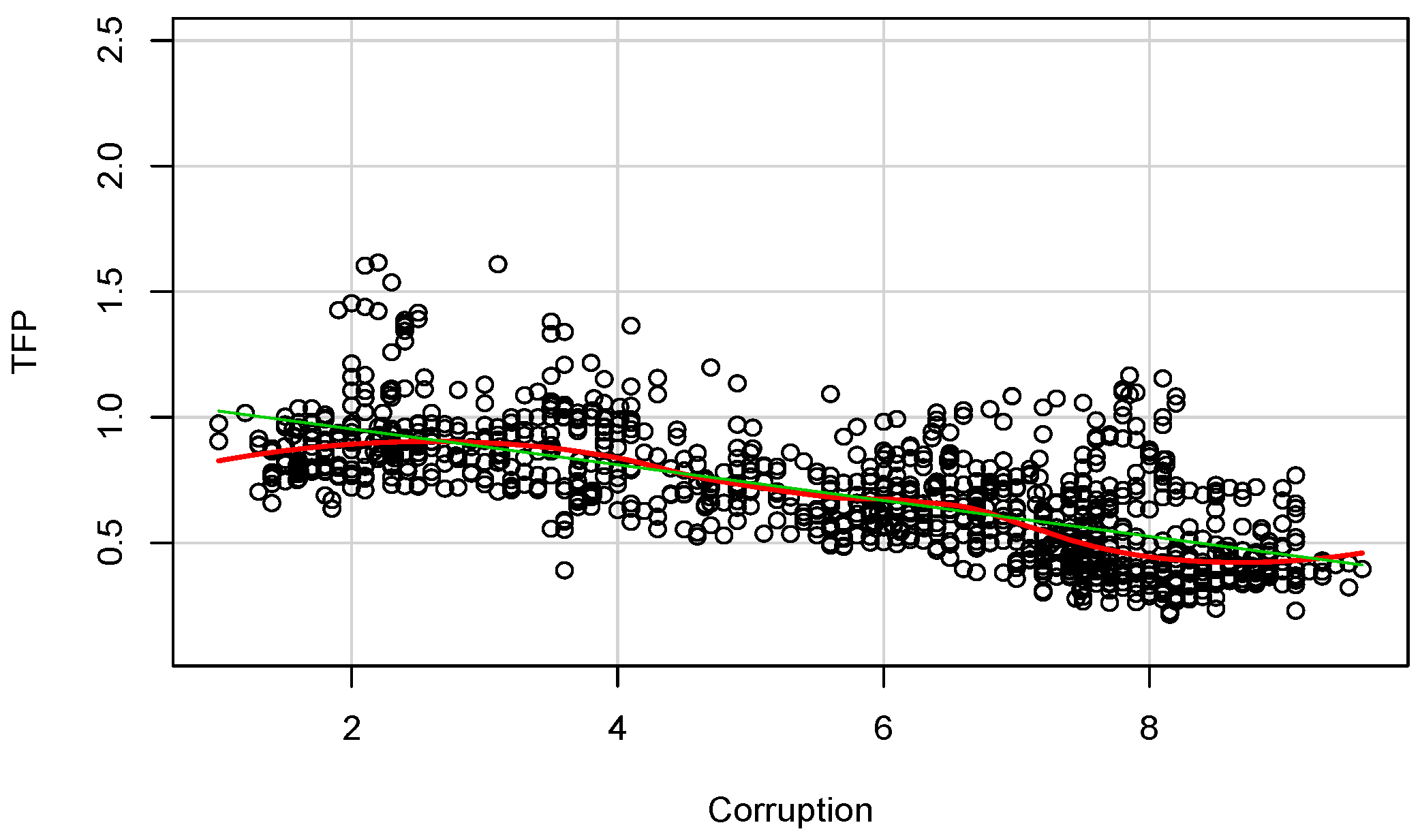
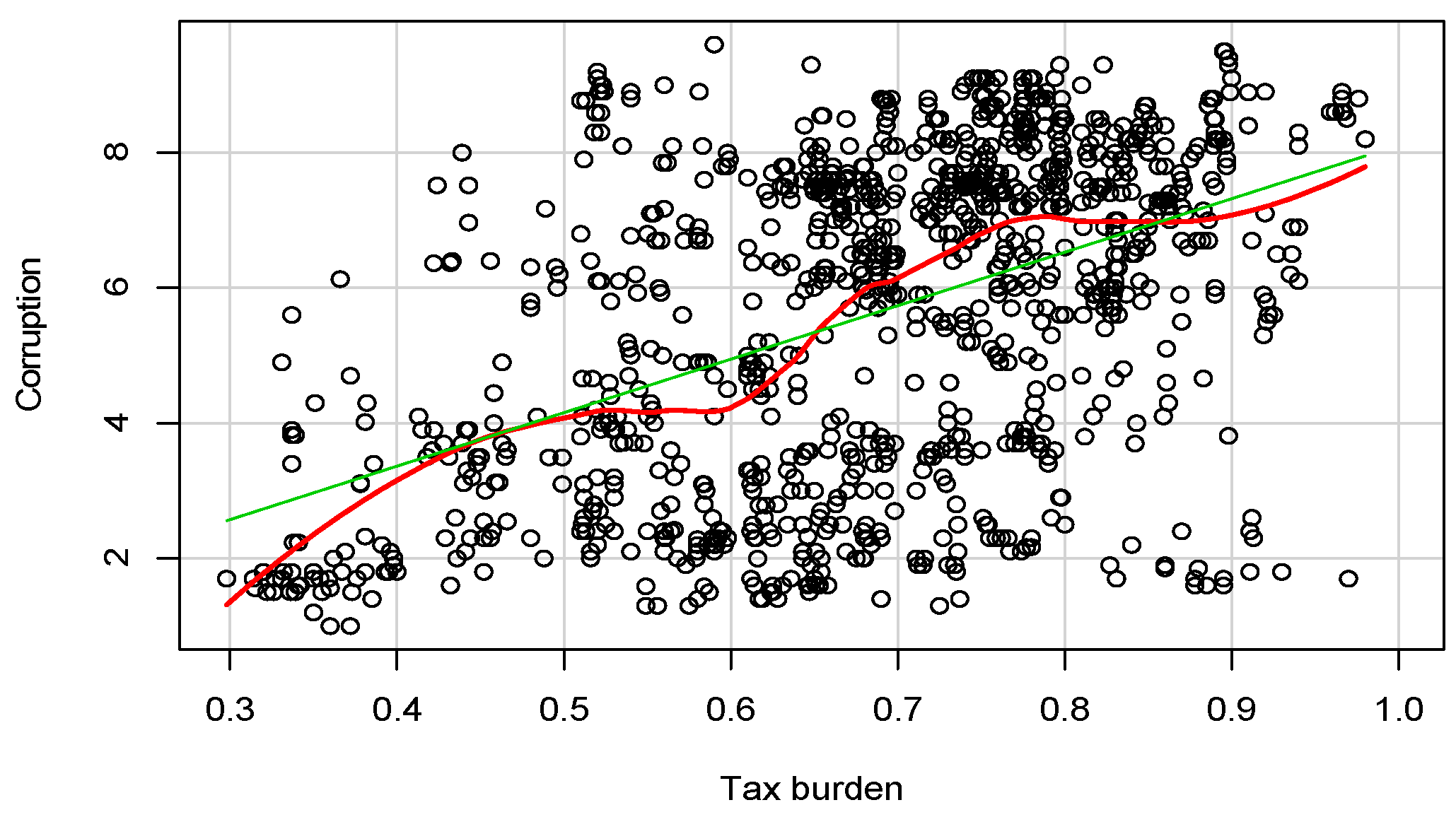
2. Data, Modeling, and Methods
3. Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Argentina, Australia, Austria, Bahrain, Barbados, Belgium, Benin, Bolivia, Botswana, Brazil, Bulgaria, Burundi, Cameroon, Canada, Central African Republic, Chile, China, Colombia, Costa Rica, Cote d’Ivoire, Cyprus, Denmark, Dominican Republic, Egypt, Finland, France, Gabon, Germany, Greece, Guatemala, Honduras, Hungary, Iceland, India, Indonesia, Iran, Ireland, Israel, Italy, Jamaica, Japan, Jordan, Kenya, Kuwait, Laos, Lesotho, Luxembourg, Malaysia, Malta, Mauritania, Mauritius, Mexico, Mongolia, Morocco, Mozambique, Namibia, Netherlands, New Zealand, Niger, Norway, Panama, Paraguay, Peru, Philippines, Poland, Portugal, Qatar, Republic of Korea, Romania, Rwanda, Saudi Arabia, Senegal, Sierra Leone, Singapore, South Africa, Spain, Sri Lanka, Swaziland, Sweden, Switzerland, Tanzania, Thailand, Togo, Trinidad and Tobago, Tunisia, Turkey, United Kingdom, United States, Uruguay, Venezuela. |
| Variable | Augmented Dickey−Fuller | Phillips−Perron | ||
|---|---|---|---|---|
| DF Statistics | p-Value | DF Statistics | p-Value | |
| TFP | −9.846 | <0.01 | −31.332 | 0.01 |
| Corruption | −10.778 | <0.01 | −32.583 | 0.01 |
| Openness | −10.035 | <0.01 | −31.959 | 0.01 |
| Property rights | −9.953 | <0.01 | −31.645 | 0.01 |
| Inflation | −10.821 | <0.01 | −31.664 | 0.01 |
| Tax burden | −10.104 | <0.01 | −30.934 | 0.01 |
| Government spending | −9.720 | <0.01 | −29.000 | 0.01 |
| Health expenditure | −10.977 | <0.01 | −32.182 | 0.01 |
| Improved sanitation | −10.886 | <0.01 | −31.853 | 0.01 |
| Electricity | −9.306 | <0.01 | −30.809 | 0.01 |
| Transport service | −10.045 | <0.01 | −32.198 | 0.01 |
| Energy use | −9.249 | <0.01 | −30.904 | 0.01 |
| OLS 1 | OLS 2 | OLS 3 | OLS 4 | Fixed Effects 1 | Fixed Effects 2 | |
|---|---|---|---|---|---|---|
| Constant | 3.054 *** (0.047) | 4.162 *** (0.021) | 2.742 *** (0.053) | 2.732 *** (0.014) | ||
| Corruption1996 | −0.141 *** (0.036) | −0.049 *** (0.028) | ||||
| Government spendingt | 0.218 *** (0.091) | 0.205 *** (0.133) | 0.073 *** (0.025) | 0.061 *** (0.032) | ||
| Military expenditure | 0.002 *** (0.073) | 0.001 ** (0.033) | 0.003 ** (0.042) | 0.001 ** (0.040) | ||
| Corruptiont−1 | 0.012 ** (0.037) | 0.0014 ** (0.021) | ||||
| Corruptiont−2 | −0.004 * (0.001) | −0.0034 * (0.001) | ||||
| Inflationt | 0.013 *** (0.035) | |||||
| Property rightt | 0.044 ** (0.018) | |||||
| Health expenditure | 0.014 * (0.364) | |||||
| Improved sanitationt | −0.053 (0.016) | |||||
| Adjusted-R2 | 0.0381 | 0.1271 | 0.023 | 0.1506 | 0.1073 | 0.2454 |
| Number of obs. | 1088 | 1088 | 1088 | 1088 | 1088 | 1088 |
| Fisher test (p-value) | 8.44 × 10−8 *** | <2.2 × 10−16 *** | <2.2 × 10−16 *** | <2.2 × 10−16 *** |
| OLS 5 | OLS 6 | OLS 7 | OLS 8 | Fixed Effects 3 | |
|---|---|---|---|---|---|
| Constant | 2.547 *** (0.028) | 2.830 *** (0.037) | 3.135 *** (0.015) | 2.652 *** (0.027) | |
| Corruption | −0.392 *** (0.026) | −0.149 *** (0.046) | −0.272 *** (0.183) | −0.248 *** (0.082) | −0.149 *** (0.053) |
| Tax Burden | −0.164 *** (0.015) | −0.103 *** (0.014) | −0.117 *** (0.011) | −0.209 *** (0.013) | −0.018 *** (0.035) |
| Residual (OLS 1) | 0.043 *** (0.061) | ||||
| Residual (OLS 2) | 0.162 *** (0.038) | ||||
| Residual (OLS 3) | 0.217 *** (0.051) | ||||
| Residual (OLS 4) | 0.251 *** (0.028) | ||||
| Residual (Fixed effects 1) | 0.169 ** (0.009) | ||||
| Adjusted−R2 | 0.3312 | 0.4607 | 0.5028 | 0.6376 | 0.3401 |
| Number of obs. | 1088 | 1088 | 1088 | 1088 | 1088 |
| Wu−Hausman (p-value) | 2.16 × 10−16 *** | 2.0 × 10−12 | <2.2 × 10−16 *** | <2.2 × 10−16 *** | <2.2 × 10−16 *** |
| Conclusion | IV | IV | IV | IV | IV |
References
- Abramovitz, Moses. 1956. Resource and output trends in the United States since 1870. American Economic Review, Papers and Proceedings 46: 5–23. [Google Scholar]
- Abramovitz, Moses, and Paul A. David. 2000. American macroeconomic growth in the era of knowledge-based progress: The long-run perspective. In The Cambridge economic history of the United States, Volume II, The Twentieth Century. Edited by Stanley L. Engerman and Robert E. Gallman. Cambridge: Cambridge University Press, pp. 1–92. [Google Scholar]
- Ades, Alberto, and Rafael Di Tella. 1999. Rents, competition, and corruption. American Economic Review 89: 982–93. [Google Scholar] [CrossRef]
- Aidt, Toke S. 2016. Rent seeking and the economics of corruption. Constitutional Political Economy 27: 142–57. [Google Scholar] [CrossRef]
- Aidt, Toke, Jayasri Dutta, and Vania Sena. 2008. Governance regimes, corruption and growth: Theory and evidence. Journal of Comparative Economics 36: 195–220. [Google Scholar] [CrossRef]
- Alm, James, Jorge Martinez-Vazquez, and Chandler McClellan. 2016. Corruption and firm tax evasion. Journal of Economic Behavior & Organization 124: 146–63. [Google Scholar]
- Al-Marhubi, Fahim A. 2000. Corruption and inflation. Economics Letters 66: 199–202. [Google Scholar] [CrossRef]
- Aschauer, David Alan. 1989. Is public expenditure productive? Journal of Monetary Economics 23: 177–200. [Google Scholar] [CrossRef]
- Auzina-Emsina, Astra. 2014. Labour productivity, economic growth and global competitiveness in post-crisis period. Procedia Social and Behavioral Sciences 156: 317–21. [Google Scholar] [CrossRef]
- Baier, Scott L., Gerald P. Dwyer, Jr., and Robert Tamura. 2006. How important are capital and total factor productivity for economic growth. Economic Inquiry 44: 23–49. [Google Scholar] [CrossRef]
- Baltagi, Badi Hani. 1995. Econometric Analysis of Panel Data. New York: Wiley. [Google Scholar]
- Bardhan, Pranab. 1997. Corruption and development: A review of the issues. Journal of Economic Literature 35: 1320–46. [Google Scholar]
- Blundell, Richard, and Stephen Bond. 1998. Initial conditions and moment restrictions in dynamic panel data models. Journal of Econometrics 87: 115–43. [Google Scholar] [CrossRef]
- Bryant, Charles E., and Rajshekhar G. Javalgi. 2016. Global economic integration in developing countries: The role of corruption and human capital investment. Journal of Business Ethics 136: 437–50. [Google Scholar] [CrossRef]
- Cieślik, Andrzej, and Łukasz Goczek. 2018. Control of Corruption, International Investment, and Economic Growth—Evidence from panel data. World Development 103: 323–35. [Google Scholar] [CrossRef]
- Cole, Matthew A., and Eric Neumayer. 2006. The impact of poor health on factor productivity. Journal of Development Studies 42: 918–38. [Google Scholar] [CrossRef]
- Davoodi, Hamid Reza, and Vito Tanzi. 1997. Corruption, public investment, and growth. In IMF Working Paper. WP/97/139. Washington: International Monetary Fund. [Google Scholar]
- Del Mar Salinas-Jiménez, Ma, and Javier Salinas-Jiménez. 2011. Corruption and total factor productivity: Level or growth effects. Portuguese Economic Journal 10: 109–28. [Google Scholar] [CrossRef]
- Delavallade, Clara. 2006. Corruption and distribution of public spending in developing countries. Journal of Economics and Finance 30: 222–39. [Google Scholar] [CrossRef]
- Dridi, Mohamed. 2014. Corruption and education: Empirical evidence. International Journal of Economics and Financial Issues 4: 476–93. [Google Scholar]
- Dzhumashev, Ratbek. 2014. The two-way relationship between government spending and corruption and its effects on economic growth. Contemporary Economic Policy 32: 403–19. [Google Scholar] [CrossRef]
- Feenstra, Robert C., Robert Inklaar, and Marcel P. Timmer. 2015. The next generation of the Penn World Table. American Economic Review 105: 3150–82. [Google Scholar] [CrossRef]
- Fisman, Raymond, and Miriam A. Golden. 2017. Corruption: What Everyone Needs to Know. New York: Oxford University Press. [Google Scholar]
- Fisman, Raymond, and Jakob Svensson. 2007. Are corruption and taxation really harmful to growth? Firm level evidence. Journal of Development Economics 83: 63–75. [Google Scholar] [CrossRef]
- Frankel, Jeffrey A., and David H. Romer. 1999. Does trade cause growth. American Economic Review 89: 379–99. [Google Scholar] [CrossRef]
- Gillanders, Robert. 2013. Corruption and infrastructure at the country and regional level. The Journal of Development Studies 50: 803–19. [Google Scholar] [CrossRef]
- Goerke, Laszlo. 2008. Bureaucratic corruption and profit tax evasion. Economics of Governance 9: 177–96. [Google Scholar] [CrossRef]
- Gründler, Klaus, and Niklas Potrafke. 2019. Corruption and Economic Growth: New empirical evidence. European Journal of Political Economy 60: 101810. [Google Scholar] [CrossRef]
- Hall, Robert E., and Charles I. Jones. 1999. Why do some countries produce so much more output per worker than others? ” The Quarterly Journal of Economics 114: 83–116. [Google Scholar] [CrossRef]
- Huntington, Samuel. 1968. Political Order in Changing Societies. New Haven: Yale University Press. [Google Scholar]
- Isaksson, Anders. 2007. Determinants of total factor productivity: A literature review. In Staff Working Paper 02. Vienna: United Nations Industrial Development Organization. [Google Scholar]
- Jorgenson, Dale, Frank M. Gollop, and Barbara Fraumeni. 1987. Productivity and U.S. economic growth. In Harvard Economic Studies. Cambridge: Harvard University Press, p. 159. [Google Scholar]
- Kendrick, John. 1961. Productivity trends in the United States. In Princeton University Press for the National Bureau of Economic Research. New York: Princeton University Press. [Google Scholar]
- Knack, Stephen, and Philip Keefer. 1995. Institutions and economics performance: Cross−country tests using alternative institutional measures. Economics and Politics VII: 207–27. [Google Scholar] [CrossRef]
- Lachler, Ulrich, and David Alan Aschauer. 1998. Public investment and economic growth in Mexico. In Policy Research Working Paper N° 1964. Washington: The World Bank. [Google Scholar]
- Lambsdorff, J. Graf. 1999. The Impact of Corruption of Capital Productivity. Göttingen: Göttingen University, Unpublished manuscript. [Google Scholar]
- Lane, Philip R. 1997. Inflation in open economies. Journal of International Economies 42: 327–47. [Google Scholar] [CrossRef]
- Leff, Nathaniel H. 1964. Economic development through bureaucratic corruption. American Behavioral Scientist 8: 8–14. [Google Scholar] [CrossRef]
- Leys, Colin. 1965. What is the problem about corruption? Journal of Modern African Studies 3: 215–30. [Google Scholar] [CrossRef]
- Maddison, Angus. 1997. Causal influences on productivity performance 1820–992: A global perspective. Journal of Productivity Analysis 8: 325–60. [Google Scholar] [CrossRef]
- Maddison, Angus. 1999. Perspective on global economic progress and human development—Economic progress: The last half century in historical perspective. In Annual Symposium 1999. Canberra: Academy of the Social Sciences. [Google Scholar]
- Mauro, Paolo. 1995. Corruption and growth. The Quarterly Journal of Economics 110: 681–712. [Google Scholar] [CrossRef]
- Mauro, Paolo. 1998. Corruption and the composition of government expenditure. Journal of Public Economics 69: 263–79. [Google Scholar] [CrossRef]
- McBride, William. 2012. What Is the Evidence on Taxes and Growth? Tax Foundation, December 18, Special Report no. 207. [Google Scholar]
- Méndez, Fabio, and Facundo Sepúlveda. 2006. Corruption, growth and political regimes: Cross-country evidence. European Journal of Political Economy 22: 82–98. [Google Scholar] [CrossRef]
- Méon, Pierre-Guillaume, and Khalid Sekkat. 2005. Does corruption grease or sand the wheels of corruption? Public Choice 122: 69–97. [Google Scholar] [CrossRef]
- Méon, Pierre-Guillaume, and Laurent Weill. 2010. Is Corruption an Efficient Grease? World Development 38: 244–59. [Google Scholar] [CrossRef]
- Mo, Pak Hung. 2001. Corruption and growth. Journal of Comparative Economics 29: 66–79. [Google Scholar] [CrossRef]
- Nordhaus, William D. 2002. Productivity growth and the new economy. In Brookings Paper on Economic Activity, Economic Studies Program. Washington: The Brookings Institution, pp. 211–65. [Google Scholar]
- Olson, Mancur, Naveen Sarna, and Anand V. Swamy. 2000. Governance and growth: A simple hypothesis explaining cross-country differences in productivity growth. Public Choice 102: 341–64. [Google Scholar] [CrossRef]
- Paldam, Martin. 1999. The Big Pattern of Corruption. Economics, Culture, and the Seesaw Dynamics. Aarhus: Aarhus University, Unpublished manuscript. [Google Scholar]
- Pellegrini, Lorenzo, and Reyer Gerlagh. 2004. Corruption’s effect on growth and its transmission channels. Kyklos 57: 429–56. [Google Scholar] [CrossRef]
- Przeworski, Adam, and Fernando Limongi. 1993. Political regimes and economic growth. Journal of Economic Perspectives 7: 51–69. [Google Scholar] [CrossRef]
- Reinikka, Ritva, and Jakob Svensson. 2005. Fighting corruption to improve schooling: Evidence from a newspaper campaign in Uganda. Journal of the European Economic Association 3: 259–67. [Google Scholar] [CrossRef]
- Romer, David. 1993. Openness and inflation. The Quarterly Journal of Economics 108: 869–903. [Google Scholar] [CrossRef]
- Sanyal, Amal, Ira N. Gang, and Omkar Goswami. 2000. Corruption, tax evasion, and the Laffer curve. Public Choice 105: 61–78. [Google Scholar] [CrossRef]
- Seka, Pierre Roche. 2013. Corruption, growth and human capital: What relationship? Africa Development 38: 133–50. [Google Scholar]
- Shleifer, Andrei, and Robert W. Vishny. 1993. Corruption. Quarterly Journal of Economics 108: 599–617. [Google Scholar] [CrossRef]
- Solow, Robert M. 1956. A Contribution to the theory of economic growth. Quarterly Journal of Economics 70: 65–94. [Google Scholar] [CrossRef]
- Solow, Robert M. 1957. Technical change and the aggregate production function. Review of Economics and Statistics 39: 312–20. [Google Scholar] [CrossRef]
- Swan, Trevor W. 1956. Economic growth and capital accumulation. Economic Record 32: 334–61. [Google Scholar] [CrossRef]
- Treismann, Daniel. 2000. The causes of corruption: A cross-national study. Journal of Public Economics 76: 399–457. [Google Scholar] [CrossRef]
- Ulubasoglu, Mehmet A., and Chris Doucouliagos. 2004. Institutions and economic growth: A systems approach. In Mimeo. Melbourne: School of Accounting, Economics and Finance, Deakin University. [Google Scholar]
- Wei, Shang-Jin. 2000. How taxing is corruption on international investors? Review of Economics and Statistics 82: 1–11. [Google Scholar] [CrossRef]
- Wu, Dong Frank, and Friedrich Schneider. 2019. Nonlinearity between the Shadow Economy and Level of Development. In IZA Institute of Labor Economics, Discussion Papers. Bonn: IZA Institute of Labor Economics. [Google Scholar]

| Variables | Mean | Standard Deviation | Minimum | Maximum | Sources |
|---|---|---|---|---|---|
| TFP (level at current PPPs, in million 2011 US dollars) | 0.680 | 0.324 | 0.105 | 2.492 | Feenstra et al. (2015), Penn World Table 9.0 |
| Inflation (price level of household consumption, US GDP in 2011 = 1) | 0.615 | 0.311 | 0.143 | 1.713 | Feenstra et al. (2015), Penn World Table 9.0 |
| Openness (sum of shares of merchandise exports and imports in GDP, at current) | −0.042 | 0.162 | −0.846 | 0.588 | Feenstra et al. (2015), Penn World Table 9.0 |
| Corruption (Corruption Perception Index) | 5.633 | 2.373 | 1.000 | 9.600 | Transparency International |
| Property rights/100 (overall quality of legal framework) | 0.561 | 0.242 | 0.100 | 0.950 | The Heritage Foundation |
| Tax burden/100 (% of tax revenue to GDP) | 0.703 | 0.145 | 0.298 | 0.999 | The Heritage Foundation |
| Government spending (government consumption and all transfer)/100 | 0.663 | 0.219 | 0.100 | 0.993 | The Heritage Foundation |
| Improved sanitation/100, rural (facilities, % of rural population with access) | 0.683 | 0.339 | 0.021 | 1.000 | World Development Indicators, World Bank |
| Energy use/10,000 (kg of oil equivalent per capita) | 0.297 | 0.338 | 0.0009 | 2.276 | World Development Indicators, World Bank |
| Transport service (% of commercial services exports/100) | 0.236 | 0.149 | 0.0007 | 0.880 | World Development Indicators, World Bank |
| Electricity (Electric power consumption (in kWh per capita)/10,000) | 1.030 | 3.786 | 1.030 | 55.578 | World Development Indicators, World Bank |
| Military expenditure (% GDP) | 2.612 | 3.943 | 0.000 | 63.100 | World Development Indicators, World Bank |
| Dependent Variable: Total Factor Productivity (TFP) | ||||||||
|---|---|---|---|---|---|---|---|---|
| Fixed Effects | IV-2SLS | System GMM | ||||||
| 1 | 2 | 3 | 4 | 5 | 6 | |||
| Corruption | −0.024 *** (0.005) | −0.264 *** (0.063) | −0.041 *** (0.024) | −0.319 *** (0.073) | −0.463 *** (0.091) | −0.383 *** (0.073) | ||
| TFPt−1 | 1.094 *** (0.027) | 1.305 *** (0.092) | 1.760 *** (0.104) | 1.514 *** (0.261) | ||||
| Openness | 0.174 ** (0.184) | 0.106 ** (0.317) | 0.384 ** (0.258) | |||||
| Property rights | −0.273 *** (0.056) | −0.153 ** (0.042) | −0.559 ** (0.069) | |||||
| Improved sanitation | 0.092 ** (0.195) | 0.219 ** (0.395) | 0.407 ** (0.201) | |||||
| Energy use | −0.031 * (0.039) | |||||||
| Electricity | 0.025 (0.107) | |||||||
| Transport service | 0.001 (0.038) | |||||||
| Intercept | 2.434 *** (0.069) | |||||||
| R−Squared | 0.018 | 0.031 | ||||||
| Sargan test (p-value) | 0.268 | 0.325 | 0.195 | 0.271 | ||||
| AR (1) (p-value) | 0.0048 | 0.001 | 0.000 | 0.003 | ||||
| AR (2) (p-value) | 0.170 | 0.371 | 0.309 | 0.103 | ||||
| Wald test, coefficients (p-value) | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | |||
| Wald test, dummies (p-value) | 0.000 | 0.000 | 0.000 | 0.000 | ||||
| Number of observations | 1088 | 1088 | 1984 | 1877 | 1606 | 1828 | ||
| Dependent Variable: Total Factor Productivity (TFP) | ||||||||
|---|---|---|---|---|---|---|---|---|
| System GMM | ||||||||
| 7 | 8 | 9 | 10 | 11 | 12 | |||
| Corruption | −0.043 *** (0.012) | −0.074 *** (0.024) | −0.067 *** (0.021) | −0.068 *** (0.034) | −0.084 *** (0.017) | −0.055 *** (0.022) | ||
| TFPt−1 | 0.946 *** (0.032) | 0.984 *** (0.020) | 0.961 *** (0.034) | 0.904 *** (0.031) | 0.917 *** (0.024) | 0.984 *** (0.038) | ||
| Openness | 0.071 *** (0.031) | 0.077 *** (0.035) | 0.068 *** (0.027) | 0.069 *** (0.031) | 0.072 ** (0.030) | 0.081 ** (0.032) | ||
| Property rights | −0.061 *** (0.023) | −0.057 ** (0.024) | −0.071 ** (0.038) | −0.038 ** (0.044) | −0.064 *** (0.028) | −0.051 ** (0.032) | ||
| Improved sanitation | 0.071 ** (0.047) | 0.073 ** (0.041) | 0.061 *** (0.034) | 0.063** (0.051) | 0.071 *** (0.063) | 0.083 *** (0.074) | ||
| Energy use | 0.017 (0.005) | 0.008 * (0.005) | ||||||
| Government spending | −0.012 * (0.025) | −0.043 * (0.031) | −0.014 * (0.045) | |||||
| Inflation | −0.016 ** (0.036) | −0.027 *** (0.024) | −0.034 *** (0.031) | −0.039 *** (0.042) | −0.041 *** (0.031) | −0.051 *** (0.042) | ||
| Electricity | 0.015 (0.027) | 0.027 (0.061) | ||||||
| Transport service | 0.053 ** (0.041) | 0.049 * (0.038) | ||||||
| Sargan test (p−value) | 0.732 | 0.537 | 0.342 | 0.479 | 0.529 | 0.268 | ||
| AR (1) (p−value) | 0.003 | 0.001 | 0.028 | 0.019 | 0.010 | 0.008 | ||
| AR (2) (p−value) | 0.695 | 0.720 | 0.648 | 0.746 | 0.681 | 0.539 | ||
| Wald test, coeffic. (p−value) | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | ||
| Wald test, dumm. (p−value) | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | ||
| Number of observations | 1877 | 1846 | 1606 | 1586 | 1828 | 1803 | ||
| Dependent Variable: Total Factor Productivity (TFP) | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| System GMM | |||||||||
| 13 | 14 | 15 | 16 | 17 | 18 | 19 | |||
| Corruption | −0.023 *** (0.004) | −0.011 *** (0.002) | −0.015 *** (0.002) | −0.022 *** (0.007) | −0.021 *** (0.006) | −0.017 *** (0.002) | −0.023 *** (0.006) | ||
| TFPt−1 | 0.945 *** (0.012) | 0.956 *** (0.013) | 0.964 *** (0.014) | 0.971 *** (0.011) | 0.977 *** (0.013) | 0.963 *** (0.016) | 0.960 *** (0.014) | ||
| Openness | 0.063 *** (0.019) | 0.050 *** (0.017) | 0.089 *** (0.024) | 0.081 *** (0.025) | 0.062 ** (0.025) | 0.071 ** (0.021) | |||
| Property rights | −0.081 *** (0.015) | −0.094 ** (0.018) | −0.068 ** (0.017) | −0.047 ** (0.020) | −0.084 *** (0.019) | −0.082 ** (0.017) | |||
| Improved sanitation | 0.052 ** (0.014) | 0.041 ** (0.016) | 0.037 * (0.018) | 0.038 ** (0.016) | 0.039 ** (0.016) | 0.040 ** (0.017) | |||
| Energy use | 0.011 * (0.012) | 0.012 (0.013) | |||||||
| Inflation | −0.061 *** (0.033) | −0.042 *** (0.032) | −0.051 ** (0.031) | −0.063 *** (0.043) | −0.075 ** (0.057) | −0.082 ** (0.061) | |||
| Tax burden | −0.033 *** (0.063) | −0.031 *** (0.06) | −0.018 *** (0.066) | −0.024 *** (0.072) | −0.023 *** (0.081) | −0.037 *** (0.059) | −0.022 *** (0.061) | ||
| Corruption × Tax burden | 0.042 *** (0.017) | 0.023 *** (0.006) | 0.028 *** (0.007) | 0.025 *** (0.006) | 0.027 ** (0.007) | ||||
| Corruption × Inflation | 0.006 ** (0.005) | 0.006 ** (0.004) | |||||||
| Electricity | 0.007 (0.006) | 0.006 * (0.003) | |||||||
| Transport service | 0.047 * (0.019) | 0.033 ** (0.020) | |||||||
| Sargan test (p-value) | 0.250 | 0.536 | 0.438 | 0.594 | 0.749 | 0.631 | 0.537 | ||
| AR (1) (p-value) | 0.002 | 0.005 | 0.005 | 0.018 | 0.019 | 0.010 | 0.001 | ||
| AR (2) (p-value) | 0.427 | 0.841 | 0.980 | 0.958 | 0.974 | 0.850 | 0.964 | ||
| Wald test, coeffic. (p-value) | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | ||
| Wald test, dumm. (p-value) | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | ||
| Number of observations | 1980 | 1877 | 1873 | 1602 | 1602 | 1828 | 1824 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kéïta, K.; Laurila, H. Corruption and Tax Burden: What Is the Joint Effect on Total Factor Productivity? Economies 2021, 9, 26. https://doi.org/10.3390/economies9010026
Kéïta K, Laurila H. Corruption and Tax Burden: What Is the Joint Effect on Total Factor Productivity? Economies. 2021; 9(1):26. https://doi.org/10.3390/economies9010026
Chicago/Turabian StyleKéïta, Kouramoudou, and Hannu Laurila. 2021. "Corruption and Tax Burden: What Is the Joint Effect on Total Factor Productivity?" Economies 9, no. 1: 26. https://doi.org/10.3390/economies9010026
APA StyleKéïta, K., & Laurila, H. (2021). Corruption and Tax Burden: What Is the Joint Effect on Total Factor Productivity? Economies, 9(1), 26. https://doi.org/10.3390/economies9010026






