Japan’s Productivity and GDP Growth: The Role of Private, Public and Foreign R&D 1967–2017
Abstract
1. Introduction
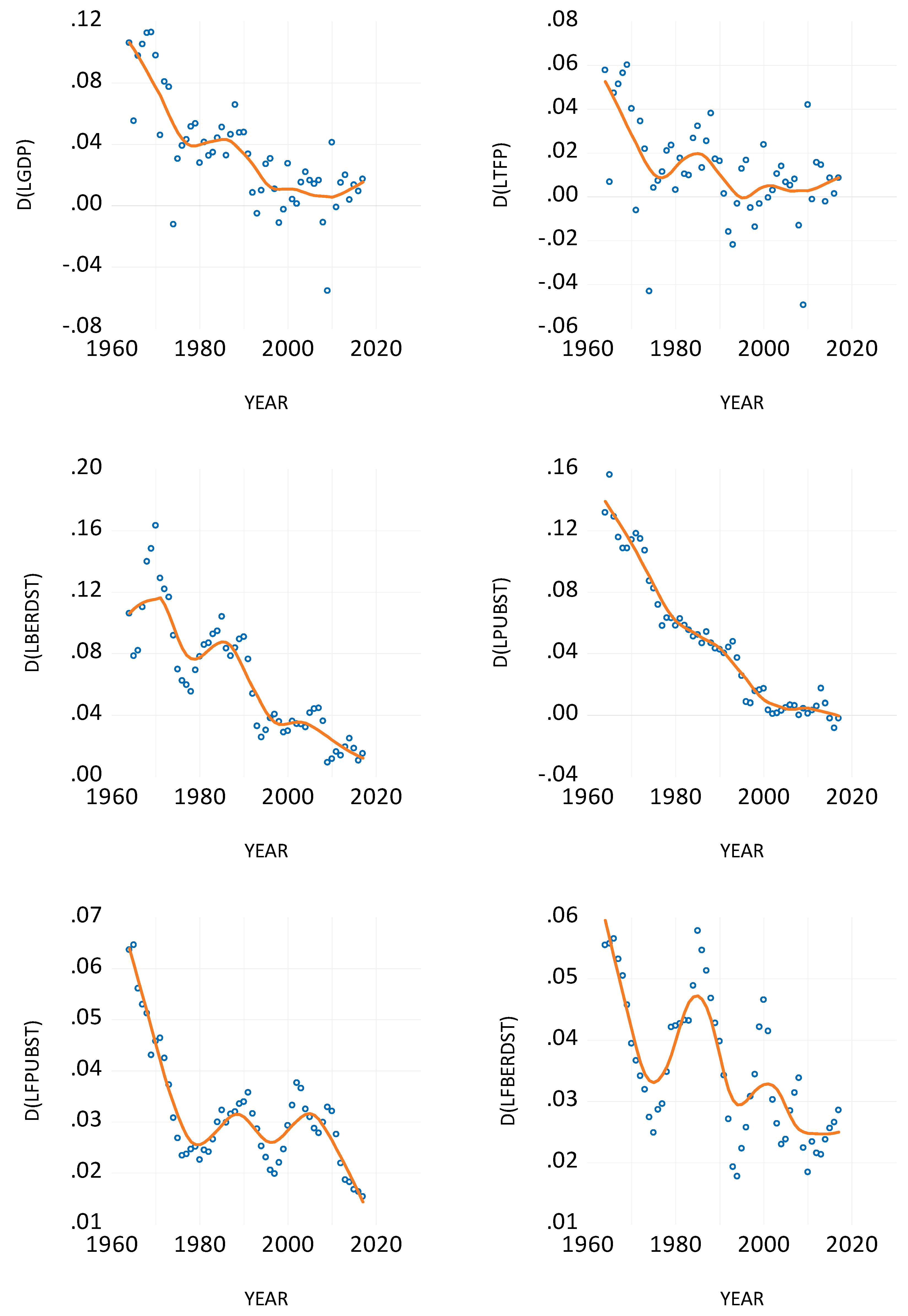
2. Data
3. Methodology
3.1. The Cointegrated VAR Approach
3.2. Net Gains and Internal Rates of Return
4. Estimation Results
4.1. Unit Root and Cointegration Tests
4.2. The Model with Five Cointegrating Equations
[−23.44] [3.2]
[−32.16] [−5.98]
[16.75] [−9.2]
[16.22] [−9.71]
[28.2] [−7.42]
[2.89] [−2.92] [4.79] [−4.75] [5.63]
[1.77] [−1.4] [3.34] [−3.2] [2.24]
[−2.53] [NA] [−3.04] [2.86] [−0.97]
[NA] [NA] [−1.274] [NA] [2.14]
[4.5] [NA] [5.66] [−5.72] [5.9]
[2.42] [3.02] [3.88] [−4.05] [−2.33]
4.3. Relations with the Literature on Japan’s Growth
- (i)
- Branstetter and Nakamura (2003) defend stagnant human capital supply as a cause of stagnant R&D employment for PhD-level engineers, and Arora et al. (2013) for IT software and Kim (2016) for durable manufactured goods. Arora et al. (2013) argue that Japanese immigration practices are restrictive, offshoring is not used much, and domestic graduates are scarce. Goto (2000) mentions the low number of PhD grants in Japan. Consequently, Japanese firms do software skill-intensive research in the USA and patent there. Overall, stagnant R&D employment caused by a limit in human capital supply is an interesting explanation; R&D expenditures then only drive up human capital prices.
- (ii)
- (iii)
- The number of researchers as a share of the population may be too high in Japan (see Goto 2000, Table 1), leaving too few high skilled workers for production. If many are doing research, there may be an insufficient number of scientists and engineers to cooperate in development and production; a given accounting number at the macro level may go together with an imbalance between the number of researchers and applying engineers (see Grossman 1989 for the theoretical underpinning). The Japanese tax system may support such an imbalance because it allows deducting changes rather than levels in R&D expenditure from the sum of taxes paid (Goto 2000). The incentive then is to go beyond optimum R&D expenditures. This may be a reason why Japanese firms have possibly strengthened research at the cost of productivity in production. The literature studied so far for this paper shows that R&D in Japan is strong in every type of input, but it does not look at engineers in production. Moreover, if all researchers are fully employed, additional R&D expenditure may increase wages more than hiring, which increases GDP but makes TFP-enhancing projects less profitable.
- (iv)
- Shifts of sector shares to low productivity sectors may be an important element. Interpreting macro TFP as a weighted sum of sectoral TFPs, sectors with below average productivity possibly gain in shares of GDP in the period with negative growth rates when old industries are defended against the market trends and exiting firms are more productive than staying firms (Fukao and Kwon 2004). An example is government subsidies for specific technologies such as a smelting process (see Peck et al. 1987), which goes beyond technological neutrality. The negative national spillovers found by Bernstein and Yan (1996) and the decreasing spillovers from large to smaller firms found by Fukao (2013) may be part of this. In recent years, the fall of Japanese sectors behind their US competitors (Branstetter and Nakamura 2003) may have continued this effect. Fukao and Kwon (2004) state that “while TFP growth decelerated in many manufacturing industries, it picked up in non-manufacturing industries”13; the strongest counterpart in the rise of services as a share of GDP is the fall of non-manufacturing industries, implying that sectors with stronger TFP growth are shrinking relatively more.
- (v)
- Falling capacity utilization and exit of efficient firms may have contributed to this (Jones and Yokoyama 2006).
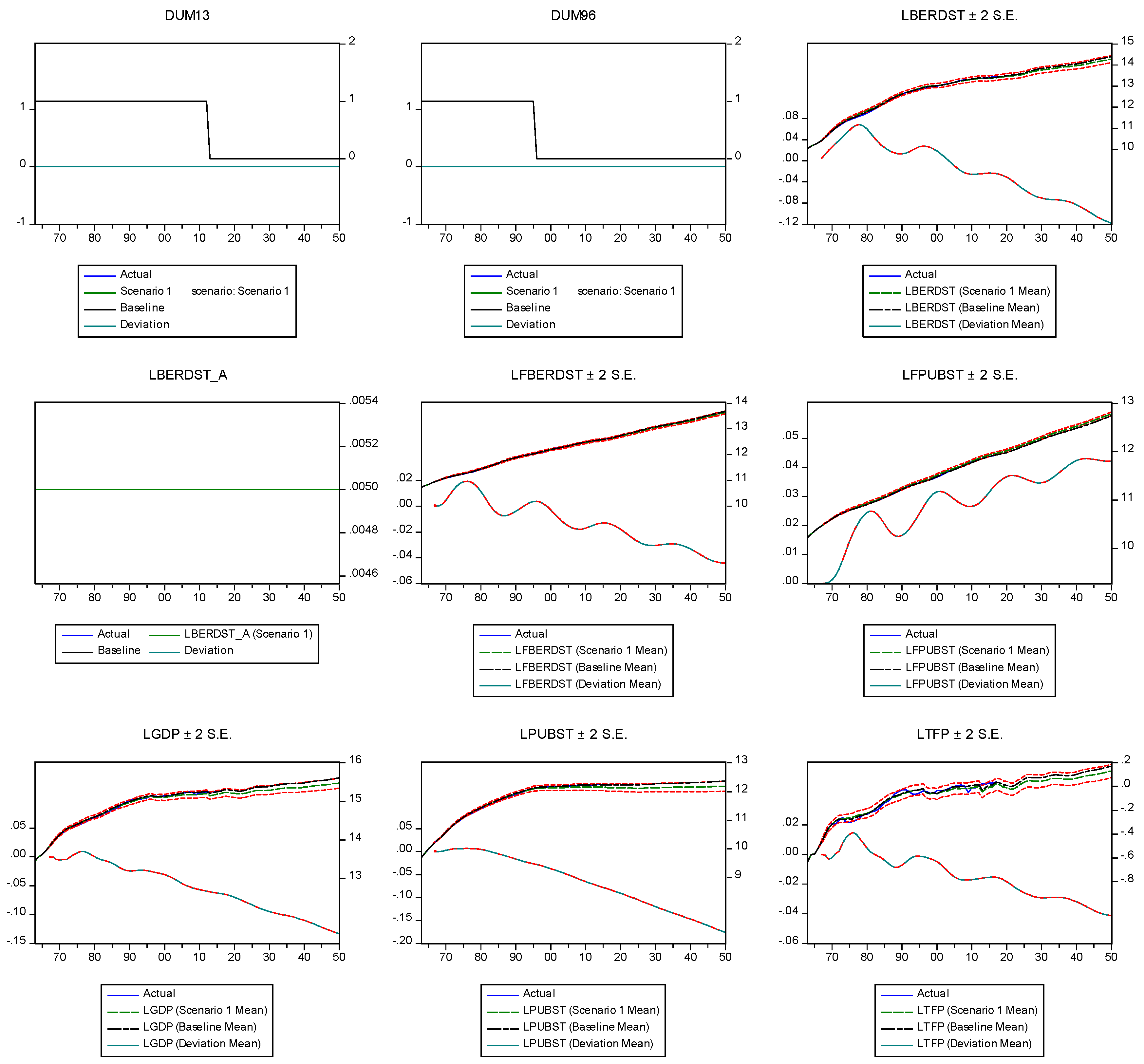
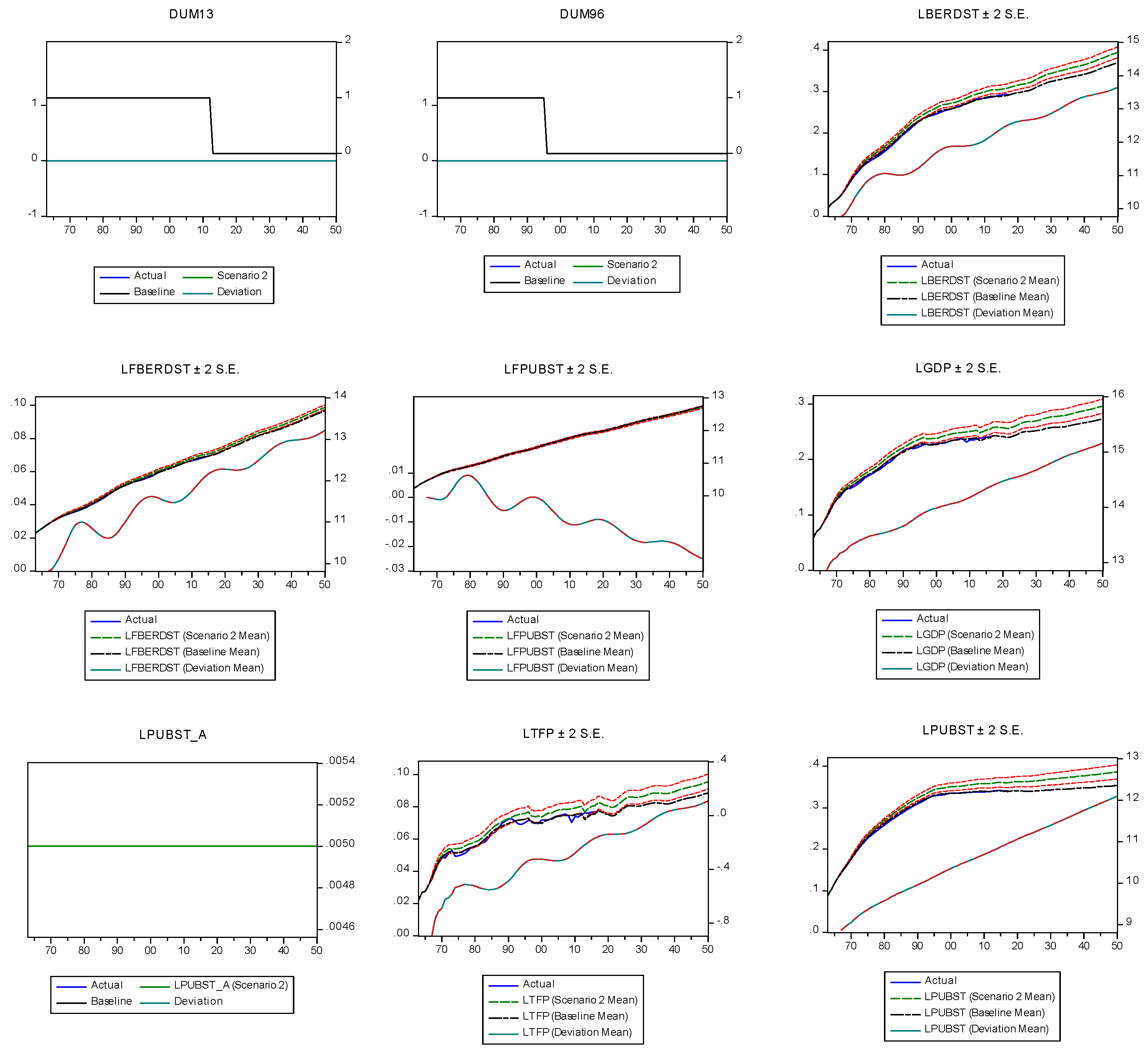
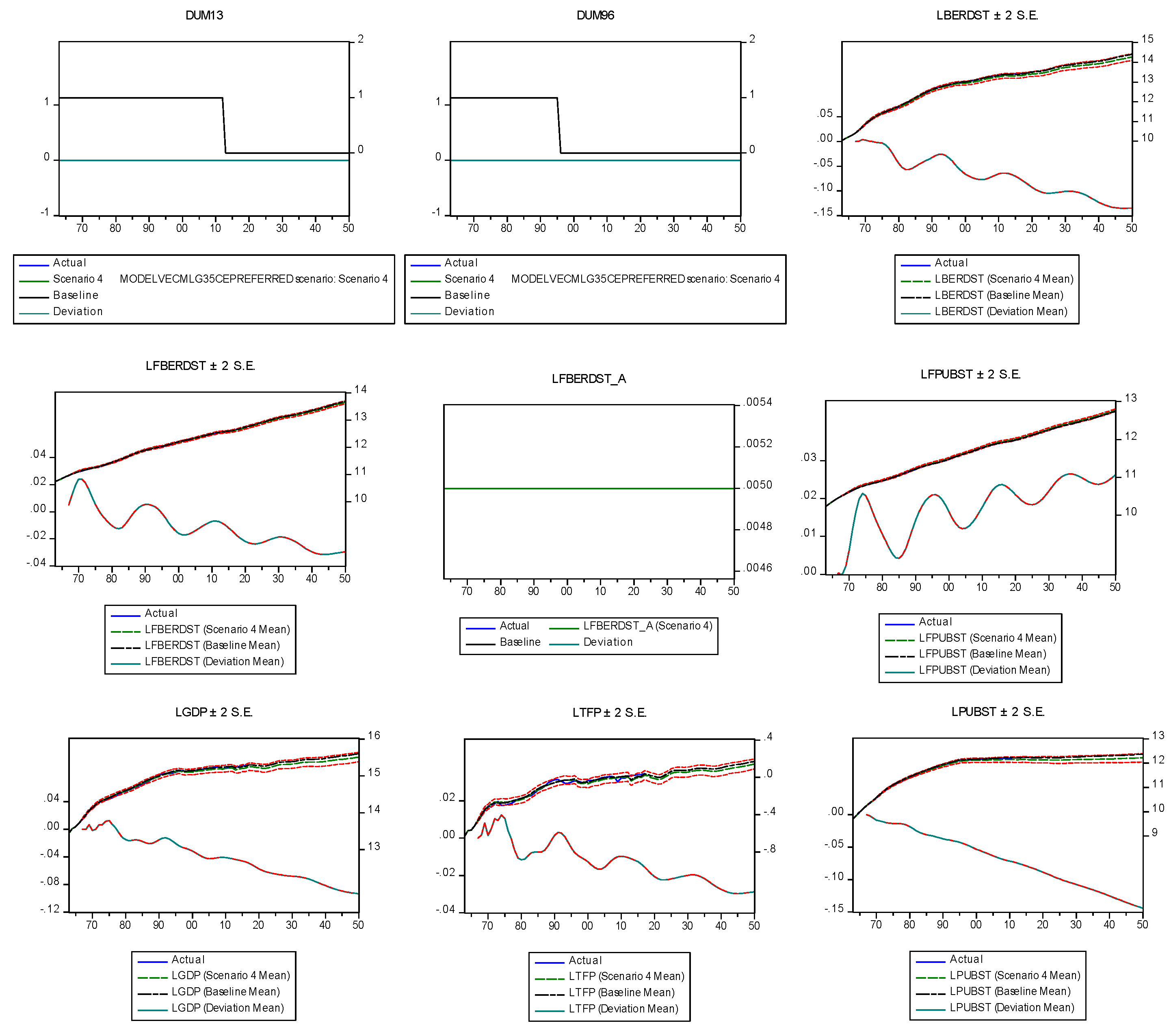
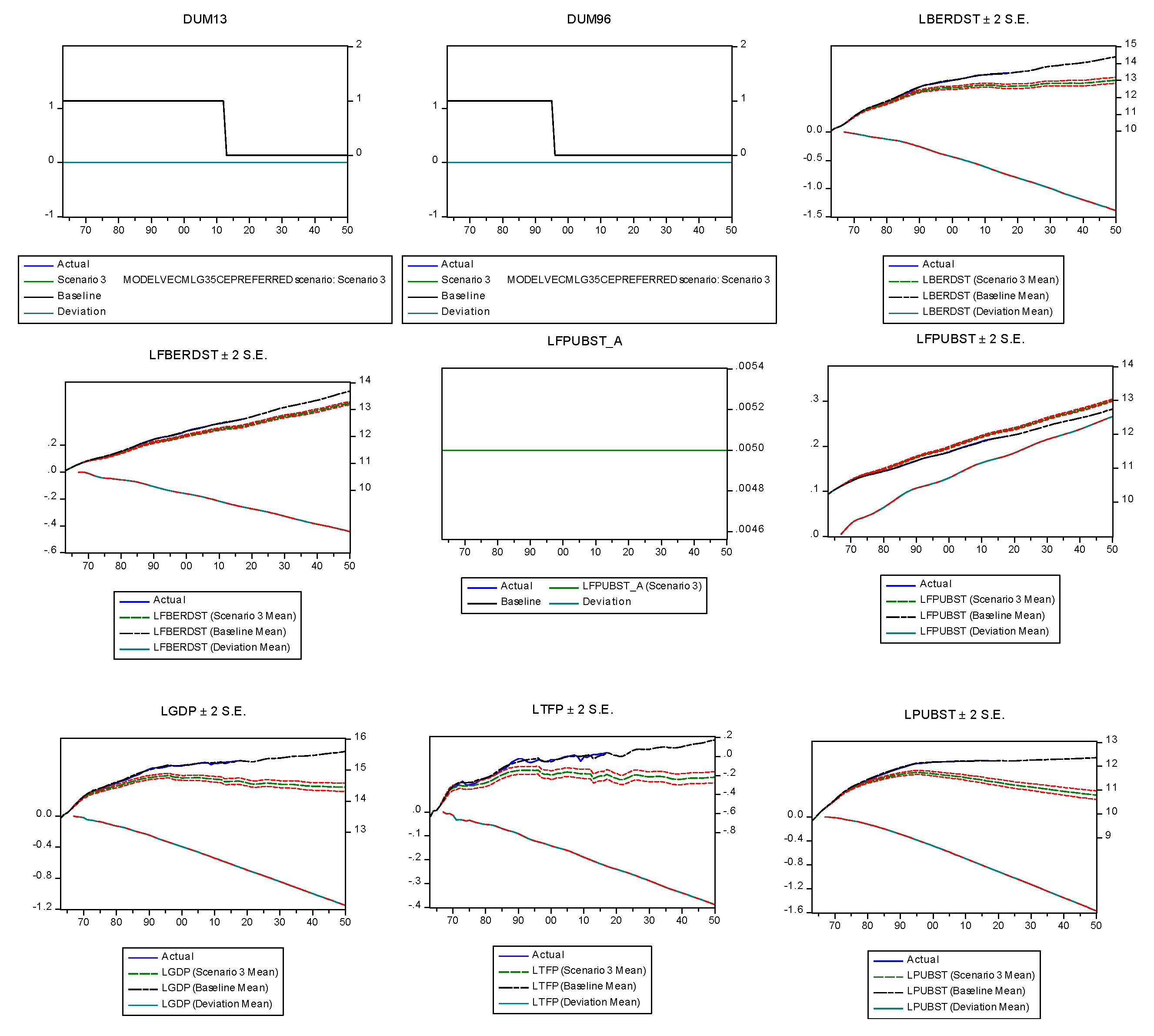
5. Simulation Results
5.1. Results for Permanent Private and Public R&D Policy Changes
5.2. Results for Changes of Foreign Private and Public R&D
5.3. Checking Cyclically of Public R&D: The Effects of a Temporary GDP Change
5.4. VES Parameters from VECM Estimates
6. Summary and Conclusions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Unit Roots
| Variable | LGDP | LTFP | LBERDST | LPUBST | LFBERDST | LFPUBST |
|---|---|---|---|---|---|---|
| Dickey–Fuller GLS without breakpoints. Dependent Variable: D(GLSRESIDUAL); coefficient of lagged residual. | ||||||
| Coefficient | 0.019 | −0.035 | −0.008 | −0.0056 | −0.0099 | −0.0068 |
| t-value (p-value) | −1.246 (0.219) | −1.011 (0.3167) | −1.36 (0.1796) | −1.61 (0.113) | −1.001 (0.32) | −0.875 (0.3857) |
| Zivot–Andrews unit-root test with breakpoint determination for intercept and trend. | ||||||
| t-value (c) unit root | −3.454 yes | −3.4478 yes | −4.393 yes | −2.45 yes | −4.2876 yes | −3.3235 yes |
| Break year | 1988 | 1987 | 1988 | 1987 | 1984 | 2008 |
| ADF unit-root test with break | ||||||
| Coeff. (b) | 0.85 0.81 | 0.51 0.75 | 0.88 0.92 | 0.952 0.93 | 0.72 0.91 | 0.90 0.965 |
| p-value (c) | 0.75 0.19 | 0.0155 0.47 | 0.0194 0.2 | 0.45 0.21 | 0.21 0.70 | 0.30 0.99 |
| Break date (d) | 1992 1986 | 1992 1992 | 1997 1997 | 1994 1988 | 2000 1987 | 1974 1971 |
Appendix B. Cointegration Details
| Hypothesis Test | No Cointeg. Equations | At Most 1 | At Most 2 | At Most 3 | At Most 4 | At Most 5 |
|---|---|---|---|---|---|---|
| Trace | 0 | 0 | 0 | 0.0373 | 0.2122 | 0.4051 |
| Max eigenv. | 0 | 0 | 0 | 0.0882 | 0.266 | 0.4051 |
| Eigenvalue | 0.85 | 0.76 | 0.624 | 0.37 | 0.237 | 0.119 |
Appendix C. First-Difference Terms as Equilibrium Version of the Estimated VECM Model
| D(LTFP(−1)) | −1.473017 | −0.750921 | 0.813472 | 0.006889 | −1.942158 | −0.015236 |
| (0.79493) | (0.49591) | (0.31552) | (0.15381) | (0.90171) | (0.19044) | |
| [−1.85302] | [−1.51423] | [2.57822] | [0.04479] | [−2.15387] | [−0.08000] | |
| D(LTFP(−2)) | −1.378858 | −1.466363 | 0.334274 | −0.080010 | −1.773803 | −0.439539 |
| (0.79501) | (0.49596) | (0.31555) | (0.15383) | (0.90181) | (0.19046) | |
| [−1.73438] | [−2.95659] | [1.05933] | [−0.52012] | [−1.96694] | [−2.30774] | |
| D(LTFP(−3)) | 0.162058 | 0.021131 | 0.276971 | 0.081857 | 0.217982 | 0.045294 |
| (0.69671) | (0.43464) | (0.27653) | (0.13481) | (0.79030) | (0.16691) | |
| [0.23261] | [0.04862] | [1.00158] | [0.60721] | [0.27582] | [0.27137] | |
| D(LBERDST(−1)) | 0.440968 | 0.757832 | −0.083943 | 0.027450 | 0.588813 | 0.012469 |
| (0.40664) | (0.25368) | (0.16140) | (0.07868) | (0.46126) | (0.09742) | |
| [1.08443] | [2.98739] | [−0.52009] | [0.34887] | [1.27653] | [0.12799] | |
| D(LBERDST(−2)) | −0.061206 | 0.170539 | 0.052219 | 0.010755 | −0.236406 | 0.126510 |
| (0.43974) | (0.27433) | (0.17454) | (0.08509) | (0.49880) | (0.10535) | |
| [−0.13919] | [0.62167] | [0.29918] | [0.12640] | [−0.47395] | [1.20088] | |
| D(LBERDST(−3)) | 0.350605 | −0.046460 | 0.092931 | 0.023594 | 0.387288 | −0.104288 |
| (0.36545) | (0.22798) | (0.14505) | (0.07071) | (0.41454) | (0.08755) | |
| [0.95938] | [−0.20379] | [0.64068] | [0.33367] | [0.93426] | [−1.19117] | |
| D(LPUBST(−1)) | 0.735582 | 0.443396 | 0.642661 | −0.046334 | 0.843053 | 0.127155 |
| (0.42287) | (0.26381) | (0.16784) | (0.08182) | (0.47968) | (0.10131) | |
| [1.73948] | [1.68076] | [3.82892] | [−0.56627] | [1.75754] | [1.25513] | |
| D(LPUBST(−2)) | −1.176531 | −0.406026 | −0.226454 | 0.054214 | −1.482269 | −0.135491 |
| (0.42863) | (0.26740) | (0.17013) | (0.08294) | (0.48621) | (0.10269) | |
| [−2.74485] | [−1.51843] | [−1.33107] | [0.65368] | [−3.04862] | [−1.31945] | |
| D(LPUBST(−3)) | 0.262465 | −0.096724 | 0.036400 | −0.099835 | 0.230811 | −0.101310 |
| (0.31682) | (0.19764) | (0.12575) | (0.06130) | (0.35937) | (0.07590) | |
| [0.82844] | [−0.48939] | [0.28946] | [−1.62859] | [0.64226] | [−1.33477] | |
| D(LFPUBST(−1)) | −1.465028 | −1.255798 | −0.350081 | 0.621725 | −1.549172 | 0.427905 |
| (1.26280) | (0.78779) | (0.50122) | (0.24434) | (1.43243) | (0.30253) | |
| [−1.16014] | [−1.59408] | [−0.69846] | [2.54449] | [−1.08150] | [1.41442] | |
| D(LFPUBST(−2)) | 2.053474 | 1.031291 | 0.472678 | −0.348314 | 2.576915 | −0.466600 |
| (1.40493) | (0.87645) | (0.55763) | (0.27184) | (1.59365) | (0.33658) | |
| [1.46162] | [1.17666] | [0.84765] | [−1.28131] | [1.61699] | [−1.38630] | |
| D(LFPUBST(−3)) | −3.229958 | −0.456770 | −0.268731 | −0.017361 | −3.900740 | 0.354862 |
| (1.12791) | (0.70364) | (0.44768) | (0.21824) | (1.27942) | (0.27021) | |
| [−2.86367] | [−0.64916] | [−0.60027] | [−0.07955] | [−3.04884] | [1.31326] | |
| D(LGDP(−1)) | 1.551809 | 1.034306 | −0.600743 | 0.019399 | 1.837188 | 0.057341 |
| (0.79890) | (0.49839) | (0.31709) | (0.15458) | (0.90622) | (0.19139) | |
| [1.94243] | [2.07530] | [−1.89452] | [0.12550] | [2.02731] | [0.29960] | |
| D(LGDP(−2)) | 1.307990 | 1.294019 | −0.083448 | 0.062646 | 1.495243 | 0.317541 |
| (0.75231) | (0.46932) | (0.29860) | (0.14557) | (0.85336) | (0.18023) | |
| [1.73864] | [2.75722] | [−0.27946] | [0.43036] | [1.75218] | [1.76186] | |
| D(LGDP(−3)) | 0.058895 | −0.029050 | −0.133908 | −0.096507 | −0.016041 | −0.071775 |
| (0.70918) | (0.44242) | (0.28148) | (0.13722) | (0.80444) | (0.16990) | |
| [0.08305] | [−0.06566] | [−0.47573] | [−0.70330] | [−0.01994] | [−0.42245] | |
| D(LFBERDST(−1)) | −1.288669 | −0.421379 | −0.277412 | −0.094861 | −1.939679 | 0.673374 |
| (0.85077) | (0.53075) | (0.33768) | (0.16462) | (0.96506) | (0.20382) | |
| [−1.51470] | [−0.79393] | [−0.82152] | [−0.57625] | [−2.00991] | [ 3.30376] | |
| D(LFBERDST(−2)) | −0.038445 | 0.476176 | 0.022386 | 0.246485 | 0.347866 | −0.054771 |
| (1.04397) | (0.65127) | (0.41437) | (0.20200) | (1.18420) | (0.25011) | |
| [−0.03683] | [0.73115] | [0.05402] | [1.22022] | [0.29375] | [−0.21899] | |
| D(LFBERDST(−3)) | −2.490940 | −0.623034 | 0.172032 | −0.069436 | −3.499444 | −0.218439 |
| (0.89454) | (0.55805) | (0.35505) | (0.17309) | (1.01470) | (0.21431) | |
| [−2.78461] | [−1.11645] | [0.48453] | [−0.40116] | [−3.44875] | [−1.01929] | |
| C | 0.093034 | −0.014553 | 0.032592 | 0.019087 | 0.160230 | 0.003539 |
| (0.05274) | (0.03290) | (0.02093) | (0.01020) | (0.05982) | (0.01263) | |
| [1.76406] | [−0.44234] | [1.55699] | [1.87041] | [2.67839] | [0.28008] | |
| DUM96 | −0.006613 | −0.016577 | 0.017396 | −0.001350 | −0.002797 | −0.004137 |
| (0.01271) | (0.00793) | (0.00505) | (0.00246) | (0.01442) | (0.00305) | |
| [−0.52015] | [−2.09003] | [ 3.44726] | [−0.54869] | [−0.19396] | [−1.35816] | |
| DUM13 | 0.044408 | 0.027929 | −0.008401 | 0.002148 | 0.056505 | 0.009046 |
| (0.01306) | (0.00814) | (0.00518) | (0.00253) | (0.01481) | (0.00313) | |
| [3.40150] | [ 3.42921] | [−1.62131] | [0.85037] | [3.81558] | [2.89217] | |
| R-squared | 0.859830 | 0.984454 | 0.993251 | 0.967802 | 0.926455 | 0.967858 |
| Adj. R-squared | 0.719659 | 0.968908 | 0.986502 | 0.935605 | 0.852911 | 0.935716 |
| Sum sq. resids | 0.003124 | 0.001216 | 0.000492 | 0.000117 | 0.004019 | 0.000179 |
| S.E. equation | 0.011178 | 0.006973 | 0.004437 | 0.002163 | 0.012679 | 0.002678 |
| F-statistic | 6.134176 | 63.32537 | 147.1688 | 30.05810 | 12.59717 | 30.11201 |
| Log likelihood | 174.9996 | 199.0643 | 222.1255 | 258.7680 | 168.5715 | 247.8737 |
| Akaike AIC | −5.843120 | −6.786835 | −7.691196 | −9.128158 | −5.591038 | −8.700928 |
| Schwarz SC | −4.858268 | −5.801983 | −6.706344 | −8.143305 | −4.606186 | −7.716076 |
| Mean dependent | 0.010904 | 0.061460 | 0.041079 | 0.029655 | 0.030934 | 0.034193 |
| S.D. dependent | 0.021111 | 0.039546 | 0.038187 | 0.008523 | 0.033060 | 0.010562 |
| Determinant resid covariance(dof adj.) | 2.67E−30 | |||||
| Determinant resid covariance | 3.71E−32 | |||||
| Log likelihood | 1410.897 | |||||
| Akaike information criterion | −47.83911 | |||||
| Schwarz criterion | −40.60423 | |||||
| Number of coefficients | 191 | |||||
Appendix C.1. Appendix Alternative Models
Appendix C.2. The Model with Four Cointegrating Equations
[−3.5] [−8.53] [−1.72]
[−27.6] [−4.65] [2.12]
[−6.53] [−40.3] [ 8.54]
[−1.54] [−24.0] [−5.44]
Appendix C.3. The Model with Three Cointegrating Equations
LFPUBST(−1) + 0.89LPUBST(−1) − 0.56LBERDST(−1) − 0.435LGDP(−1) − 0.009t – 8.07
[33.5] [−23.8] [−10.4] [−6.49]
LBERDST(−1) −1.366LPUBST(−1) − 2.169LFPUBST(−1) + 1.15LTFP(−1) + 0.0276t + 27.3
[−31.98] [−45.7] [11.44] [10.96]
LFBERDST(−1) − 0.945LFPUBST(−1) −0.72LPUBST(−1) − 0.42LBERDST(−1) −0.0149t + 2.4
[−17.05] [−18.37] [13.27] [−6.67]
Appendix C.4. Comparing the Models
| No. of Cointegrat. Eqs. | Three | Four | Five |
|---|---|---|---|
| Normal distr. (a) | 0.0423 | 0.2321 | 0.0592 |
| Serial correl. (b) | Lag 1 | Lags 1, 2, 3, 4 | Lags 1, 2 |
| Heteroscedast. (c) | 0.2556 | 0.2613 | 0.3003 |
| Adj. R-sq. (d) | 0.837, 0.67, 0.91, 0.96, 0.985, 0.94 | 0.85, 0.725, 0.94, 0.966, 0.986, 0.94 | 0.85, 0.72, 0.936, 0.97, 0.986, 0.936 |
| Log likelihood | 1392.489 | 1403.463 | 1410.897 |
| AIC | −48.137 | −48.057 | −47.839 |
| SIC | −41.89 | −41.315 | −40.604 |
| Unstable models: end year, start year | None, 1969 | 2014, 1969, 1970 | 2014, 1969, 1970 |
| No. of different signs in long-term relations (e) | 2016: 1 of 15; 2015: 1; 2014: 8; 1968: 6;1969: 6; 1970: 10; Sum:32 | 2016: 2; 2015: 3; 2014: 4; 1968: 0; 1969:1; 1970:2. Sum: 12. | 2016:3; 2015: 0; 2014: 0; 1968:0; 1969:0; 1970:0. Sum: 3. |
| No. of different sign in adjustment coefficients (e) | 2016: 0 of 17; 2015: 1; 2014: 5; 1968:11; 1969: 11; 1970: 10. Sum: 38 | 2016: 0 of 20; 2015: 3; 2014: 4; 1968: 0; 1969: 1; 1970: 2. Sum: 10. | 2016: 8; 2015: 0; 2014: 0; 1968: 0; 1969:1; 1970: 1. Sum: 10. |
| Cointegration test per set of variables in a cointegrating equation (f) | Each quadruple of any ce has more than one ce. | Each triple of any ce has more than one ce | Five pairs of cointegrating equations |
References
- Archibugi, Daniele, and Andrea Filippetti. 2018. The retreat of public research and its adverse consequences on innovation. Technological Forecasting and Social Change 127: 97–111. [Google Scholar] [CrossRef]
- Arora, Ashish, Lee G. Branstetter, and Matej Drev. 2013. Going soft: How the rise of software-based innovation led to the decline of Japan’s IT industry and the resurgence of Silicon Valley. The Review of Economics and Statistics 95: 757–75. [Google Scholar] [CrossRef]
- Bernstein, Jeffrey I., and Pierre Mohnen. 1998. International R&D spillovers between U.S. and Japanese R&D intensive sectors. Journal of International Economics 44: 315–38. [Google Scholar]
- Bernstein, Jeffrey I., and Xiaoyi Yan. 1996. Canadian–Japanese R&D spillovers and productivity growth. Applied Economics Letters 3: 763–67. [Google Scholar]
- Bottazzi, Laura, and Giovanni Peri. 2007. The international dynamics of R&D and innovation in the long run and in the short run. The Economic Journal 117: 486–511. [Google Scholar]
- Branstetter, Lee, and Yoshiaki Nakamura. 2003. Structural Impediments to Growth in JAPAN. NBER Conference Report series; Chicago and London: University of Chicago Press, pp. 191–223. [Google Scholar]
- Coe, David T., and Elhanan Helpman. 1995. International R&D spillovers. European Economic Review 39: 859–87. [Google Scholar]
- Davidson, R., and J.G. MacKinnon. 2004. Econometric Theory and Methods. New York: Oxford University Press. [Google Scholar]
- De Loo, Ivo, and T. Ziesemer. 2000. Sectoral Average Wage and Employment Growth Rates in a Specific Factors Model with International Capital Movements. In The Unemployment Debate: Current Issues. Edited by Peter. de Gijsel, Ralph Olthoff and Thomas Zwick. Marburg: Metropolis, pp. 227–41. [Google Scholar]
- Eaton, Jonathan, and Samuel Kortum. 1997. Engines of growth: Domestic and foreign sources of innovation. Japan and the World Economy 9: 235–59. [Google Scholar] [CrossRef]
- Enders, Walter. 2015. Applied Econometric Time Series, 4th ed. Hoboken: Wiley. [Google Scholar]
- Feenstra, Robert C., Robert Inklaar, and Marcel P. Timmer. 2015. The Next Generation of the Penn World Table. American Economic Review 105: 3150–82. [Google Scholar] [CrossRef]
- Fisher, Lance A., Hyeon-Seung Huh, and Adrian R. Pagan. 2016. Econometric Methods for Modelling Systems with a Mixture of I(1) And I(0) Variables. Journal of Applied Econometrics 31: 892–911. [Google Scholar] [CrossRef]
- Fukao, Kyoji, and Hyeog Ug Kwon. 2004. Japan’s Productivity and Economic Growth: An Empirical Analysis Based on Industry-Level and Firm-Level Data. (In Japanese). Available online: https://ideas.repec.org/p/hst/hstdps/d04-33.html (accessed on 31 August 2020).
- Fukao, Kyoji, and Hyeog Ug Kwon. 2006. Why Did Japan’s TFP Growth Slow Down in The Lost Decade? An Empirical Analysis Based On Firm-Level Data of Manufacturing Firms. The Japanese Economic Review 57: 195–228. [Google Scholar] [CrossRef]
- Fukao, Kyoji. 2013. Explaining Japan’s Unproductive Two Decades. Asian Economic Policy Review 8: 193–213. [Google Scholar] [CrossRef]
- Fukao, Kyoji, Tatsuji Makino, and Tokihiko Settsu. 2019. Structural Change, Capital Deepening, and TFP Growth in Japan: 1885–1970. Discussion Paper Series a No. 693; Tokyo: Hitotsubashi University Repository. [Google Scholar]
- Gospodinov, Nikolay, Ana María Herrera, and Elena Pesavento. 2013. Unit roots, cointegration and pretesting in VAR models. Advances in Econometrics 31: 81–115. [Google Scholar]
- Goto, Akira. 2000. Japan’s national innovation system: Current status and problems. Oxford Review of Economic Policy 16: 103–13. [Google Scholar] [CrossRef]
- Grossman, Gene M. 1989. Explaining Japan’s innovation and Trade: A Model of quality competition and Dynamic Comparative Advantage. New York: NBER. [Google Scholar]
- Hall, Brownwyn, Jacques Mairesse, and Pierre Mohnen. 2010. Measuring the Returns to R&D. In Handbook of the Economics of Innovation. Edited by Bronwyn H. Hall and Nathan Rosenberg. Amsterdam: NorthHolland, vol. 2, pp. 1033–82. [Google Scholar]
- Hayashi, Fumio, and Edward C. Prescott. 2002. The 1990s in Japan: A Lost Decade. Review of Economic Dynamics 5: 206–35. [Google Scholar] [CrossRef]
- Herzer, Dierk. 2020. An Empirical Note on the Long-Run Effects of Public and Private RD on TFP, MPRA Paper No. 10075729, May. Available online: https://mpra.ub.uni-muenchen.de/100757/ (accessed on 31 July 2020).
- Hjalmarsson, Erik, and Pär Österholm. 2010. Testing for cointegration using the Johansen methodology when variables are near-integrated: Size distortions and partial remedies. Empirical Economics 39: 51–76. [Google Scholar] [CrossRef]
- Johansen, Søren, Rocco Mosconi, and Bent Nielsen. 2000. Cointegration analysis in the presence of structural breaks in the deterministic trend. Econometrics Journal 3: 216–49. [Google Scholar] [CrossRef]
- Johansen, Søren. 1996. Likelihood-based inference in Cointegrated Vector Autoregressive Models, 2nd ed. Oxford: Oxford University Press. [Google Scholar]
- Jones, R., and T. Yokoyama. 2006. Upgrading Japan’s Innovation System to Sustain Economic Growth. In OECD Economics Department Working Papers. Paris: OECD Publishing. [Google Scholar] [CrossRef]
- Jusélius, Katarina. 2006. The Cointegrated VAR Model: Methodology and Application. Oxford: Oxford University Press. [Google Scholar]
- Kaihatsu, Sohei, and Takushi Kurozumi. 2014. What caused Japan’s Great Stagnation in the 1990s? Evidence from an estimated DSGE model. Journal of the Japanese Int. Economies 34: 217–35. [Google Scholar] [CrossRef]
- Kilian, L., and H. Lütkepohl. 2017. Structural Vector Autoregressive Analysis. New York and Cambridge: Cambridge University Press. [Google Scholar]
- Kim, Sangho. 2016. Factor Determinants of Total Factor Productivity Growth for the Japanese Manufacturing Industry. Contemporary Economic Policy 34: 572–86. [Google Scholar] [CrossRef]
- Kurita, Takamitsu. 2020. Normalising cointegrating relationships subject to long-run exclusion. Economics Letters 192: 1–4. [Google Scholar] [CrossRef]
- Lau, Sau-Him Paul. 1997. Using stochastic growth models unit roots and breaking. Journal of Economic Dynamics and Control 21: 1645–67. [Google Scholar] [CrossRef]
- Lau, Sau-Him Paul. 2008. Using an error-correction model to test whether endogenous long-run growth exists. Journal of Economic Dynamics & Control 32: 648–76. [Google Scholar]
- Luintel, Kul B., and Mosahid Khan. 2004. Are International R&D Spillovers Costly for the United States? The Review of Economics and Statistics 86: 896–910. [Google Scholar]
- Luintel, Kul B., Mosahid Khan, and Konstantinos Theodoridis. 2014. On the robustness of R&D. Journal of Productivity Analysis 42: 137–155. [Google Scholar]
- Lütkepohl, H. 2005. New Introduction to Multiple Time Series Analysis. Heidelberg and New York: Springer. [Google Scholar]
- MacKinnon, James G., Alfred A. Haug, and Leo Michelis. 1999. Numerical Distribution Functions of Likelihood Ratio Tests for Cointegration. Journal of Applied Econometrics 14: 563–77. [Google Scholar] [CrossRef]
- Maddala, G. S., and I.-M. Kim. 1998. Unit Roots, Cointegration and Structural Change. Cambridge: Cambridge University Press. [Google Scholar]
- Mazzucato, Mariana. 2018. Mission-Oriented Innovation Policy: Challenges and Opportunities. In European Commission. Science, Research and Innovation Performance of the EU 2018. Brussels: Strengthening the Foundations for Europe’s Future, pp. 396–427. Available online: https://ec.europa.eu/info/sites/info/files/rec-17-015-srip-report2018_mep-web-20180228.pdf (accessed on 24 September 2020).
- Miyagawa, Tsutomu, and Takayuki Ishikawa. 2019. On the Decline of R&D Efficiency. RIETI Discussion Paper Series 19-E-052; Tokyo: RIETI. [Google Scholar]
- Mukerji, V. 1963. A Generalized S.M.A.C. Function with Constant Ratios of Elasticity of Substitution. The Review of Economic Studies 30: 233–36. [Google Scholar] [CrossRef]
- Patterson, K. 2000. An Introduction to Applied Econometrics: A Time-Series Approach. Houndmills and New York: Palgrave Macmillan. [Google Scholar]
- Peck, Merton J., Richard C. Levin, and Akira Goto. 1987. Picking Losers: Public Policy toward Declining Industries in Japan. The Journal of Japanese Studies 13: 79–123. [Google Scholar] [CrossRef]
- Pellen, Maikel, Bettina Peters, Christian Rammer, and Georg Licht. 2017. Public Investment in R&D in Reaction to Economic Crises-A Longitudinal Study for OECD Countries. ZEW WP 2017-1113. Mannheim: ZEW, November. [Google Scholar]
- Pesaran, M. Hashem. 2015. Time Series and Panel Data Econometrics. Oxford: Oxford University Press. [Google Scholar]
- Revankar, Nagesh S. 1971. A class of variable elasticity of substitution production functions. Econometrica 39: 61–71. [Google Scholar] [CrossRef]
- Soete, Luc, Bart Verspagen, and Thomas Ziesemer. 2020a. The productivity effect of public R&D in the Netherlands. Economics of Innovation and New Technology 29: 31–47. [Google Scholar]
- Soete, Luc, Bart Verspagen, and Thomas Ziesemer. 2020b. The Economic Impact of Public R&D: An International Perspective. UNU-MERIT Working Paper 2020-014. Maastricht: UNU-MERIT. [Google Scholar]
- Sussex, Jon, Yan Feng, Jorge Mestre-Ferrandiz, Michele Pistollato, Marco Hafner, Peter Burridge, and Jonathan Grant. 2016. Quantifying the economic impact of government and charity funding of medical research on private research and development funding in the United Kingdom. BMC Med. 14: 32. [Google Scholar] [CrossRef]
- Thach, Ngoc N. 2020. Macroeconomic Growth in Vietnam Transitioned to Market: An Unrestricted VES Framework. Economies 8: 58. [Google Scholar] [CrossRef]
- Van Elk, Roel, Bas ter Weel, Karen van der Wiel, and Bram Wouterse. 2019. Estimating the Returns to Public R&D Investments: Evidence from Production Function Models. De Economist 167: 45–87. [Google Scholar]
- Wooldridge, Jeffrey M. 2013. Introductory Econometrics: A Modern Approach, 5th ed. Mason: South-Western. [Google Scholar]
- Ziesemer, Thomas. 2019. Japan’s productivity and GDP growth: The role of GBAORD, public and foreign R&D. UNU-MERIT Working Papers 2019-029. Maastricht: UNU-MERIT. [Google Scholar]
- Ziesemer, Thomas. 2020. Semi-endogenous growth models with domestic and foreign private and public R&D linked to VECMs. Economics of Innovation and New Technology. [Google Scholar] [CrossRef]
| 1 | For earlier periods, see Fukao et al. (2019). |
| 2 | Public R&D stocks are obtained from accumulation of GERD-BERD (gross expenditure on R&D minus business expenditure on R&D) as explained below. |
| 3 | Special thanks go to Bart Verspagen for providing these data from the UNU-MERIT database. |
| 4 | In contrast, OECD measures of TFP do include human capital as only labour and capital are subtracted from GDP. As R&D also includes human capital, a regression of both including a third human capital variable as found in some articles is likely to be strong because of the common human capital data included and may lead to collinearity. |
| 5 | Nearest neighbor or loess fit uses 30% of the data for a weighted least squares regression and attributes the slope to the middle observation, and then shifts one observation further to repeat the procedure, resulting in a non-linear line. |
| 6 | Unlike other areas, we do not assume that there is another model with contemporaneous regressors behind it. |
| 7 | Other definitions of exogeneity deal with having also no impact on a variable y from other variables in the differenced part because of zero elements in B of Equation (2) (Patterson 2000). Then we will have an additional exogenous variable x with coefficient matrix F extended and the number of endogenous variables is reduced by one. The differenced equation then does not depend on any other variable and is a purely autoregressive process of a variable in differenced form if it has a unit root. |
| 8 | This method using the exact time resolution from a VECM for the rate of return calculation was first developed and used in the related R&D literature by Soete et al. (2020a). Sussex et al. (2016) also estimated a VECM for medical research, but they did not carry out dynamic simulations of the model with all feedback to get an internal rate of return. |
| 9 | The numbers give only a rough first indication. We also found a variable with p > 0.05 for a unit root when the coefficient was only 0.3 rather than unity in related work. See the example of Enders (2015, p. 236). We do not use a fractionally cointegrated VAR because “easy interpretation is lost for fractionally differenced variables... reliable estimation of fractionally integrated processes requires larger samples than typically available in macroeconomics”; “how well this approach works in small samples is not known”. (Kilian and Lütkepohl (2017, pp. 23 and 99). |
| 10 | We do not use a theoretical model here, but (3) and (4) can be related to the marginal products of TFP with respect to BERDST and PUBST for a generalization of the CES function for TFP generation. See Section 5.4. |
| 11 | See Appendix C for other statistics. |
| 12 | Miyagawa and Ishikawa (2019) disaggregate the macro variables according to sectors and find decreasing R&D efficiency in some sectors. |
| 13 | Most studies discussed in Fukao and Kwon (2006) seem to show the opposite result, however. |
| 14 | |
| 15 | We often use the word “shock” for intercept changes rather than for residuals as the SVAR (structural vector-autoregression) literature is doing (Kilian and Lütkepohl 2017). |
| 16 | Under the opposite assumption of equal marginal products of private and public R&D in TFP production, it is possible to obtain the parameters of a VES production function from the VECM estimates (see Section 5.4 “VES parameters from VECM estimates”). |
| 17 | An asymmetric VAR with up to four lags (not shown) shows slightly lower effects than our preferred model, but the trace test would require accepting a p-value of 40 percent for the hypothesis of “at most five cointegrating equations” (Table A2). |
| 18 | A companion paper includes GBA(O)RD, government appropriations for mission-oriented social objectives implying availability of data for fewer periods. |

| Test (a) | Trace Test | Trace Test | Max-Eigenvalue | Max-Eigenvalue |
|---|---|---|---|---|
| Hypothesis | No coint. equation | At most 1 | No coint. equation | At most 1 |
| TFP, BERDST | 0.0017 | 0.1803 | 0.0028 | 0.1803 |
| BERDST, PUBST | 0.0001 | 0.2415 | 0.0001 | 0.2415 |
| PUBST, FPUBST (b) | 0.0013 | 0.2459 | 0.0014 | 0.2459 |
| FPUBST, GDP | 0.0074 | 0.1770 | 0.0140 | 0.1770 |
| GDP, FBERDST | 0.0022 | 0.1686 | 0.0040 | 0.1686 |
| Effects → (a) from Policy ↓ | Domestic Private R&D | Domestic Public R&D | Foreign Public R&D | Foreign Private R&D | TFP | GDP |
|---|---|---|---|---|---|---|
| Private R&D (VECM) | −0.019 | −0.067 | 0.028 | −0.0133 | −0.0146 | −0.054 |
| public R&D (VECM) | 0.18 | 0.18 | −0.008 | 0.049 | 0.052 | 0.129 |
| Effects → of Permanent Policy Change on ↓ | Years of Gains; Average Gain/GDP (a) | Sum DPV (4%) in Bill. $ | Internal Rate of Return (Payback Period) (b) | Remarks |
|---|---|---|---|---|
| private R&D (VECM) | 1972–1982; 0.004 | 95.445 | 43.66% (16) | (c) |
| public R&D (VECM) | 1968–2050; 0.044 | 2483 | 425.5% (4) | (d) |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ziesemer, T. Japan’s Productivity and GDP Growth: The Role of Private, Public and Foreign R&D 1967–2017. Economies 2020, 8, 77. https://doi.org/10.3390/economies8040077
Ziesemer T. Japan’s Productivity and GDP Growth: The Role of Private, Public and Foreign R&D 1967–2017. Economies. 2020; 8(4):77. https://doi.org/10.3390/economies8040077
Chicago/Turabian StyleZiesemer, THW. 2020. "Japan’s Productivity and GDP Growth: The Role of Private, Public and Foreign R&D 1967–2017" Economies 8, no. 4: 77. https://doi.org/10.3390/economies8040077
APA StyleZiesemer, T. (2020). Japan’s Productivity and GDP Growth: The Role of Private, Public and Foreign R&D 1967–2017. Economies, 8(4), 77. https://doi.org/10.3390/economies8040077





