Do DJIA Firms Reflect Stationary Debt Ratios?
Abstract
1. Introduction
2. Data and Empirical Model
2.1. Data
2.2. Empirical Model
H0: δi < 0, regarding certain i, (nonlinear stationarity).
- (1)
- The flexibility and power to detect mean reversion trend for the series;
- (2)
- Classification of the whole panel into two group series, i.e., stationary and nonstationary, respectively;
- (3)
- Clear identification of how many and which series in the panel are stationary processes;
- (4)
- Use of stationarity tests based on a nonlinear framework for the nonlinear adjustment of economic variables because of the cycle and government policy implementation.
- (1)
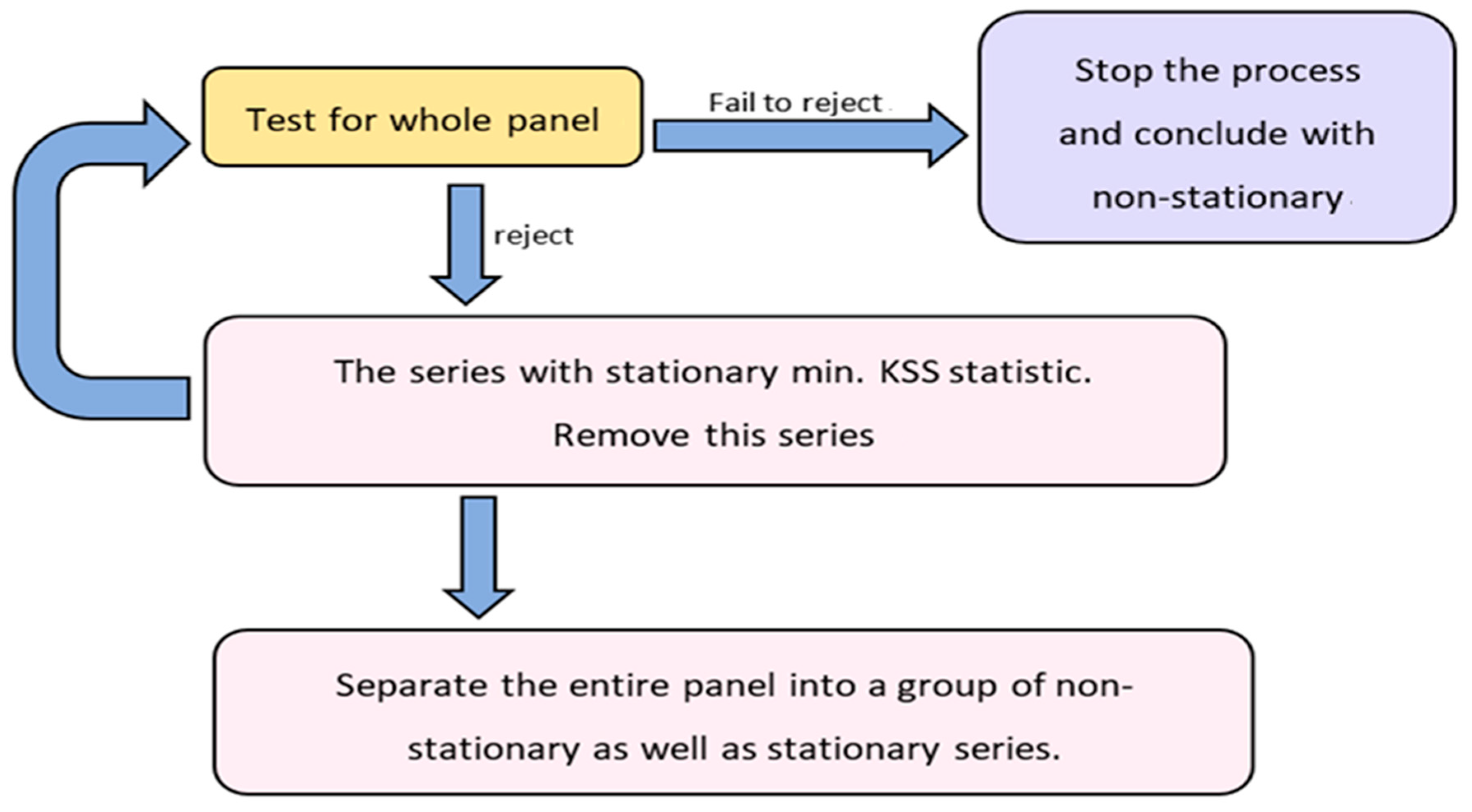
- KSS PURTs with a Fourier function are associated with the whole panel debt ratio. The process discontinues and whole panel series are not stationary, therefore, the null assumption is not refused. Step 2 is initiated if the null is refused;
- (2)
- The series is removed via the minimum KSS statistic due to its classified stationarity;
- (3)
- The first step is returned to in case of the rest of the series, otherwise, the process is stopped with the whole panel-disconnected series.
3. Empirical Results
3.1. Results
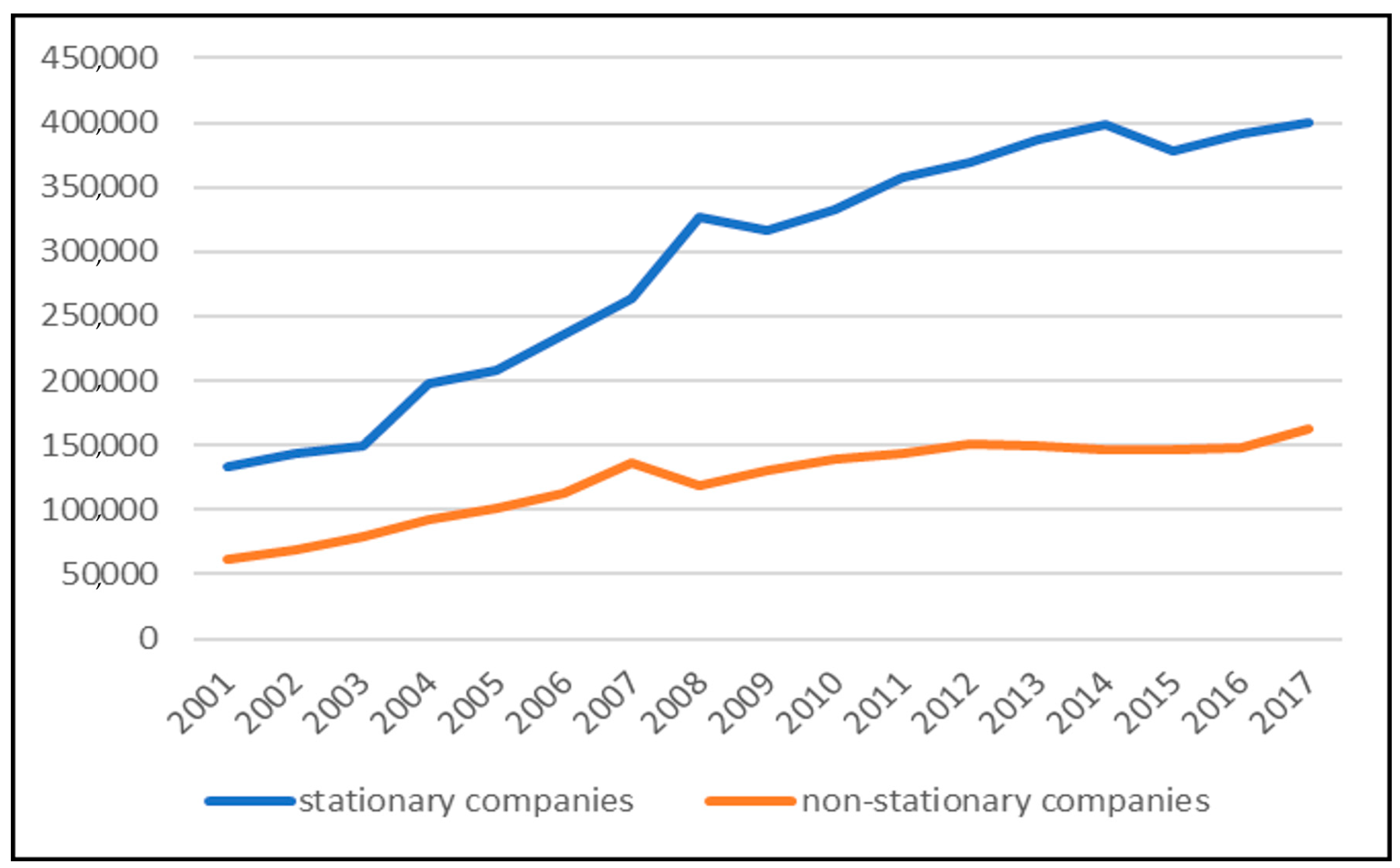
3.2. Discussion of the Results
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Abor, Joshua. 2005. The effect of capital structure on profitability: An empirical analysis of listed firms in Ghana. Journal of Risk Finance 6: 438–45. [Google Scholar] [CrossRef]
- Ahmad, Rubi, and Oyebola Fatima Etudaiye-Muhtar. 2017. Dynamic model of optimal capital structure: Evidence from Nigerian listed firms. Global Business Review 18: 590–604. [Google Scholar] [CrossRef]
- Ahsan, Tanveer, Man Wang, and Muhammad Azeem Qureshi. 2016. Mean reverting financial leverage: Theory and evidence from Pakistan. Applied Economics 48: 379–88. [Google Scholar] [CrossRef]
- Bai, Jushan, and Serena Ng. 2004. A Panic Attack on Unit Roots and Cointegration. Econometrica 72: 1127–77. [Google Scholar] [CrossRef]
- Banerjee, Saugata, Almas Heshmati, and Clas Wihlborg. 2004. The dynamics of capital structure. Research in Banking and Finance 4: 275–97. [Google Scholar]
- Becker, Ralf, Walter Enders, and Stan Hurn. 2004. A general test for time dependence in parameters. Journal of Applied Econometrics 19: 899–906. [Google Scholar] [CrossRef]
- Botta, Marco. 2019. Financing Decisions and Performance of Italian SMEs in the Hotel Industry. Cornell Hospitality Quarterly 60: 335–54. [Google Scholar] [CrossRef]
- Brealey, Richard A., and Stewart Myers. 2003. Principles of Corporate Finance, 7th ed. Pennsylvania: McGraw Hill Irwin. [Google Scholar]
- Chadha, Saurabh, and Anil K. Sharma. 2015. Determinants of capital structure: An empirical evaluation from India. Journal of Advances in Management Research 12: 3–14. [Google Scholar] [CrossRef]
- Chang, Chun, and Xiaoyun Yu. 2010. Informational efficiency and liquidity premium as the determinants of capital structure. Journal of Financial and Quantitative Analysis 45: 401–40. [Google Scholar] [CrossRef]
- Chang, Chingfu, Alice C. Lee, and Cheng F. Lee. 2009. Determinants of capital structure choice: A structural equation modeling approach. The Quarterly Review of Economics and Finance 49: 97–213. [Google Scholar] [CrossRef]
- Chen, Zhiyao, Jarrad Harford, and Avraham Kamara. 2019. Operating leverage, profitability, and capital Structure. Journal of Financial and Quantitative Analysis 54: 369–92. [Google Scholar] [CrossRef]
- Choi, In. 2001. Unit root tests for panel data. Journal of International Money and Finance 20: 249–272. [Google Scholar] [CrossRef]
- Choi, In. 2002. Combination unit root tests for cross-sctionally correlated panels. In The Econometric Theory and Practice: Frontiers of Analysis and Applied Research. Edited by Peter Charles Bonest Phillips, Dean Corbae, Steven N. Durlauf and Bruce E. Hansen. Cambridge: Cambridge University Press, pp. 311–33. [Google Scholar] [CrossRef]
- Chortareas, Georgios, and George Kapetanios. 2009. Getting PPP right: Identifying mean-reverting real exchange rates in panels. Journal of Banking and Finance 33: 390–404. [Google Scholar] [CrossRef]
- Christopher, Green, and Guanqun Tong. 2005. Pecking order or trade-off hypothesis? Evidence on the capital structure of Chinese companies. Applied Economics 37: 2179–89. [Google Scholar] [CrossRef]
- Črnigoj, Matjaž, and Dušan Mramor. 2009. Determinants of capital structure in emerging European economies: Evidence from Slovenian firms. Emerging Markets Finance & Trade 45: 72–89. [Google Scholar] [CrossRef]
- Daskalakis, Nikolaos, and Maria Psillaki. 2008. Do country or firm factors explain capital structure? Evidence from SMEs in France and Greece. Applied Financial Economics 18: 87–97. [Google Scholar] [CrossRef]
- DeAngelo, Harry, and Richard Roll. 2015. How stable are corporate capital structures? The Journal of Finance 70: 373–418. [Google Scholar] [CrossRef]
- Dierker, Martin, Inmoo Lee, and Sung Won Seo. 2019. Risk changes and external financing activities: Tests of the dynamic trade-off theory of capital structure. Journal of Empirical Finance 52: 178–200. [Google Scholar] [CrossRef]
- Elsas, Ralf, and David Florysiak. 2011. Heterogeneity in the speed of adjustment toward target leverage. International Review of Finance 11: 181–211. [Google Scholar] [CrossRef]
- Enders, Walter, and Junsoo Lee. 2009. The Flexible Fourier Form and Testing for Unit Roots: An Example of the Term Structure of Interest Rates. Working Paper. Tuscaloosa: Department of Economics, Finance & Legal Studies, University of Alabama. Available online: http://cba.ua.edu/~wenders2/wp-content/uploads/2009/11/enders_lee_april_29_20091.pdf (accessed on 22 August 2020).
- Enders, Walter, and Junsoo Lee. 2012. A unit roots test using a Fourier series to approximate smooth Breaks. Oxford Bulletin of Economics and Statistics 74: 574–99. [Google Scholar] [CrossRef]
- Fama, Eugene F., and Kenneth R. French. 2002. Testing trade-off and pecking order predictions about dividends and debt. Review of Financial Studies 15: 1–3. [Google Scholar] [CrossRef]
- Flannery, Mark, and Kasturi P. Rangan. 2006. Partial adjustment toward target capital structures. Journal of Financial Economics 79: 469–506. [Google Scholar] [CrossRef]
- Frank, Murray Z., and Vidhan K. Goyal. 2009. Capital structure decisions: Which factors are reliably important? Financial Management 38: 1–37. [Google Scholar] [CrossRef]
- Gallant, Ronald. 1981. On the basis in flexible functional form and an essentially unbiased form: The flexible Fourier form. Journal of Econometrics 15: 211–353. [Google Scholar] [CrossRef]
- Hackbarth, Dirk, Christopher Hennessy, and Hayne Leland. 2007. Can the tradeoff theory explain debt structure? Review of Financial Studies 20: 1389–428. [Google Scholar] [CrossRef]
- Hovakimian, Armen, Tim Opler, and Sheridan Titman. 2001. The debt-equity choice. Journal of Financial and Quantitative Analysis 36: 1–24. [Google Scholar] [CrossRef]
- Im, Kyung So, M. Hashem Pesaran, and Yongcheol Shin. 2003. Testing for unit roots in heterogeneous panels. Journal of Econometrics 115: 53–74. [Google Scholar] [CrossRef]
- Jarallah, Shaif, Ali. Salman Saleh, and Ruhul Salim. 2019. Examining pecking order versus trade-off theories of capital structure: New evidence from Japanese firms. International Journal of Finance & Economics 24: 204–11. [Google Scholar] [CrossRef]
- Ju, Nengjiu, Robert Parrino, Allen M. Poteshman, and Michael S. Weisbach. 2005. Horses and rabbits? Trade-Off Theory and Optimal Capital Structure. The Journal of Financial and Quantitative Analysis 40: 259–81. [Google Scholar] [CrossRef]
- Kapetanios, George, Andy Snell, and Yongcheol Shin. 2003. Testing for unit root in the nonlinear STAR framework. Journal of Econometrics 112: 359–79. [Google Scholar] [CrossRef]
- Kwiatkowski, Denis, Peter C. B. Phillips, Peter Schmidt, and Yongcheol Shin. 1992. Testing the null hypothesis of stationarity against the alternative of a unit root. Journal of Econometrics 54: 159–78. [Google Scholar] [CrossRef]
- Leary, Mark T., and Michael Roberts. 2005. Do firms rebalance their capital structures? Journal of Finance 60: 2575–619. [Google Scholar] [CrossRef]
- Leland, Hayne E. 1994. Corporate debt value, bond covenants, and optimal capital structure. Journal of Finance 49: 1213–52. [Google Scholar] [CrossRef]
- Levin, Andrew, Chien-Fu Lin, and Chia-Shang Chu. 2002. Unit root in panel data: Asymptotic and finite-sample properties. Journal of Econometrics 108: 1–24. [Google Scholar] [CrossRef]
- Lin, Woon Leong, Nick Yip, Murali Sambasivan, and Jo Ann Ho. 2018. Corporate debt policy of Malaysian SMEs: Empirical evidence from firm dynamic panel data. Int. Journal of Economics and Management 12: 491–508. [Google Scholar]
- Maddala, Gangadharrao S., and Shaowen Wu. 1999. A comparative study of unit root tests with panel data and a new simple test. Oxford Bulletin of Economics and Statistics 61: 631–52. [Google Scholar] [CrossRef]
- Miller, Merton H. 1977. Debt and taxes. The Journal of Finance 32: 261–75. [Google Scholar] [CrossRef]
- Modigliani, Franco, and Merton H. Miller. 1958. The cost of capital, corporation finance, and the theory of investment. American Economic Review 48: 261–97. [Google Scholar]
- Moon, Hyungsik Roger, and Benoit Perron. 2004. Testing for a unit root in panels with dynamic factors. Journal of Econometrics 122: 81–126. [Google Scholar] [CrossRef]
- Myers, Stewart C. 1984. The capital structure puzzle. Journal of Finance 39: 574–92. [Google Scholar] [CrossRef]
- Myers, Stewart C., and Nicholas S. Majluf. 1984. Corporate financing and investment decisions when firms have information that investors do not have. Journal of Financial Economics 13: 187–221. [Google Scholar] [CrossRef]
- Nehrebecka, Natalia, and Aneta Dzik-Walczak. 2018. The dynamic model of partial adjustment of the capital structure: Meta-analysis and a case of Polish enterprises. Zbornik radova Ekonomskog fakulteta u Rijeci/Proceedings of Rijeka Faculty of Economics 36: 55–81. [Google Scholar] [CrossRef]
- Newey, Whitney K., and Kenneth D. West. 1994. Automatic lag selection in covariance matrix estimation. Review of Economic Studies 61: 631–653. [Google Scholar] [CrossRef]
- Ozkan, Aydin. 2001. Determinants of capital structure and adjustment to long run target: Evidence from UK company panel data. Journal of Business Finance & Accounting 28: 175–98. [Google Scholar] [CrossRef]
- Paul, Kosakowski. 2019. Why the Dow Matters. Investopedia. November 14. Available online: https://www.investopedia.com/articles/stocks/08/dow-history.asp (accessed on 23 August 2020).
- Perron, Pierre. 1989. The great crash, the oil price shock and the unit root hypothesis. Econometrica 57: 1361–401. [Google Scholar] [CrossRef]
- Pesaran, M. Hashem. 2007. A Simple Panel Unit Root Test in the Presence of Cross Section Dependence. Journal of Applied Econometrics 22: 265–312. Available online: https://www.jstor.org/stable/25146517 (accessed on 22 August 2020).
- Phillips, Peter C. B., and Pierre Perron. 1988. Testing for a unit root in time series regression. Biometrica 75: 335–46. [Google Scholar] [CrossRef]
- Rajan, Raghran. G., and Luigi Zingales. 1995. What do we know about capital structure? Some evidence from international data. The Journal of Finance 50: 1421–60. [Google Scholar] [CrossRef]
- Sani, Abdullahi, and Mohd Norfian Alifiah. 2020. Determinants of the capital structure of Nigerian listed firms: A dynamic panel model. International Journal of Psychosocial Rehabilitation 24: 991–99. [Google Scholar] [CrossRef]
- Shyam-Sunder, Lakshmi, and Stewart C. Myers. 1999. Testing static tradeoff against pecking order models of capital structure. Journal of Financial Economics 51: 219–44. [Google Scholar] [CrossRef]
- Sogorb Mira, Francisco, and José López-Gracia. 2003. Pecking Order versus Trade-Off: An Empirical Approach to the Small and Medium Enterprise Capital Structure. Working Paper. Valencia: Instituto Valenciano de Investigationes Económicas, S.A. [Google Scholar] [CrossRef]
- Solomon, Ezra. 1963. Theory of Financial Management. New York: Columbia University Press. [Google Scholar] [CrossRef]
- Ucar, Nuri, and Tolga Omay. 2009. Testing for unit root in nonlinear heterogeneous panels. Economics Letters 104: 5–8. [Google Scholar] [CrossRef]
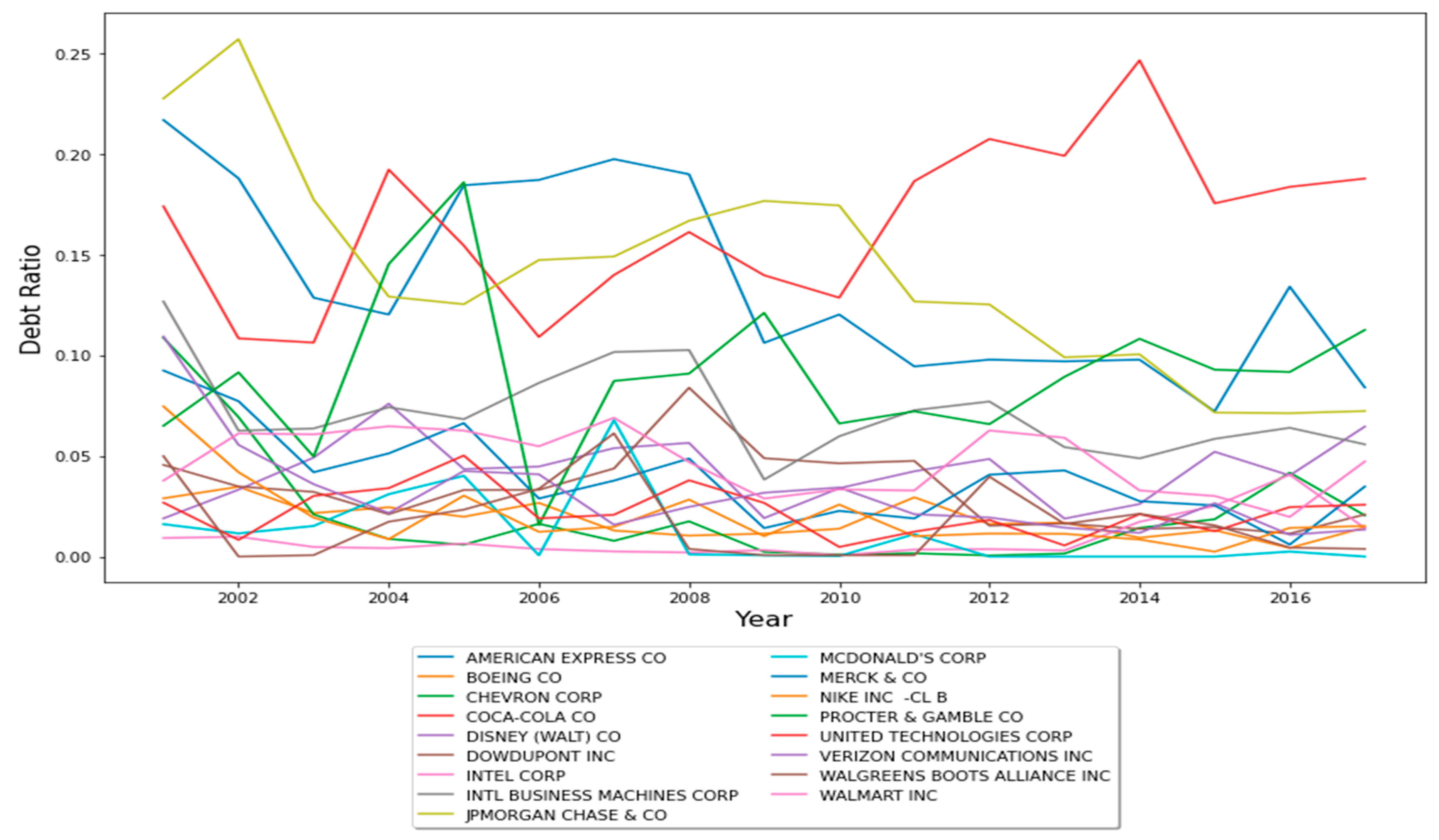
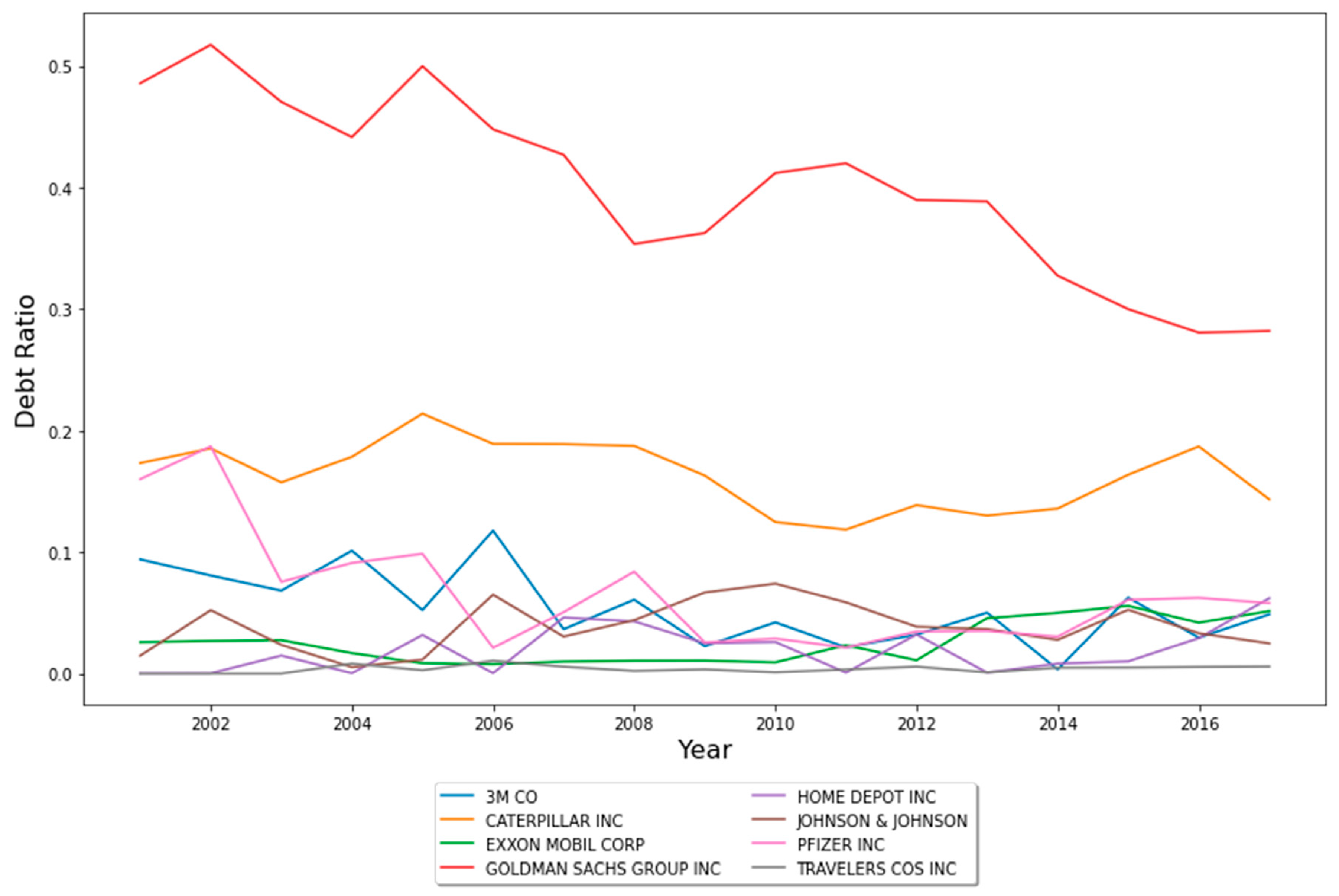
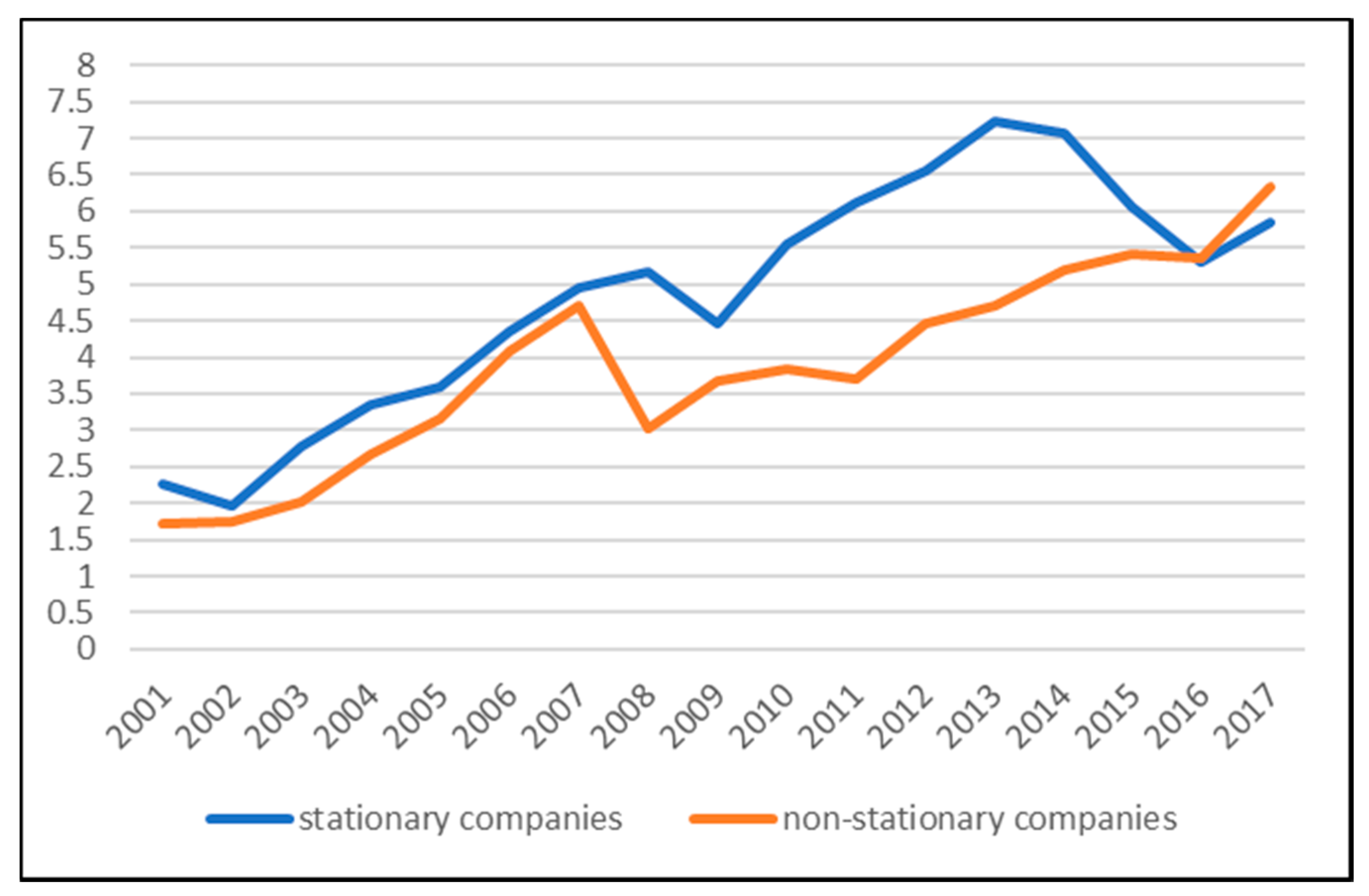
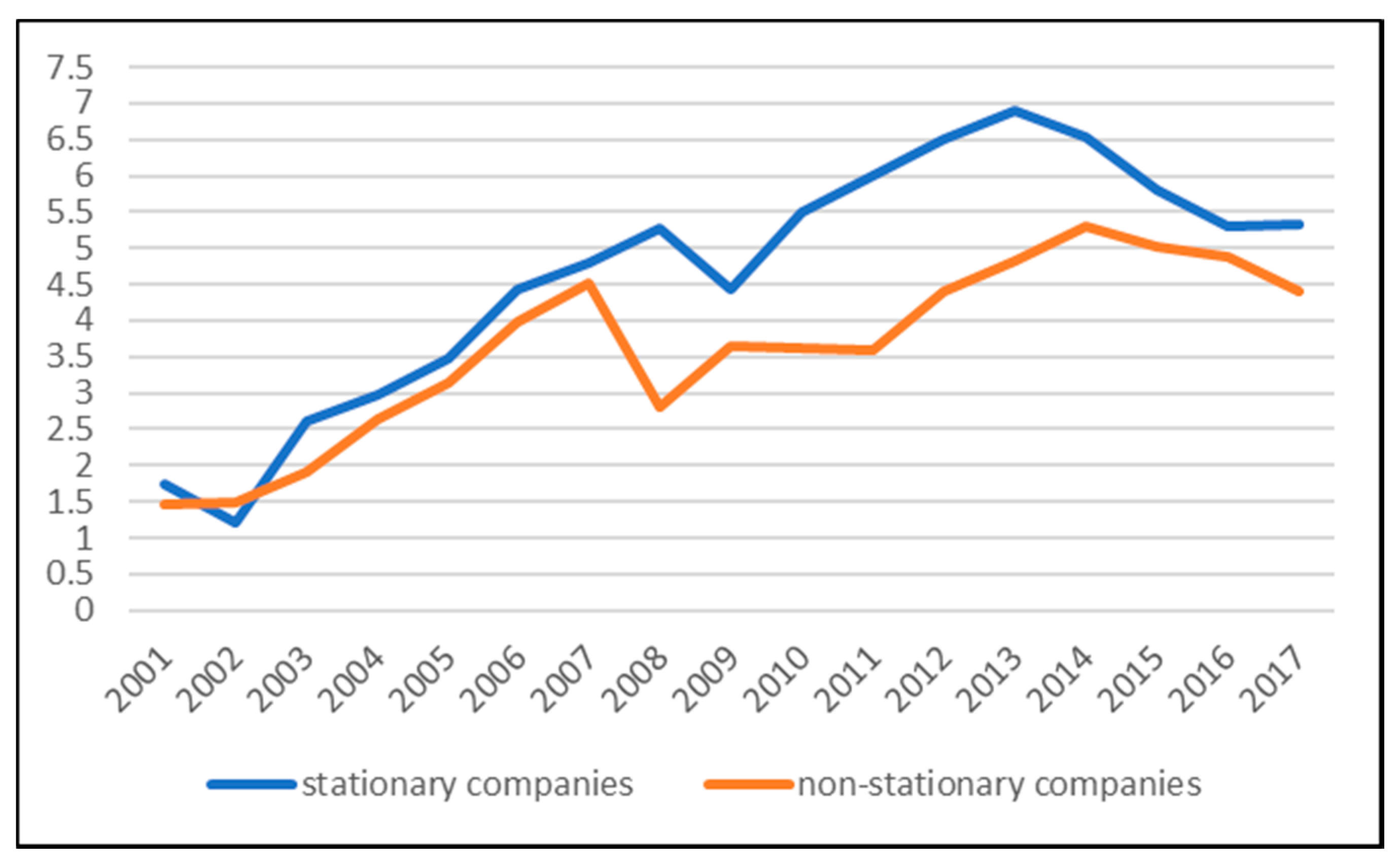

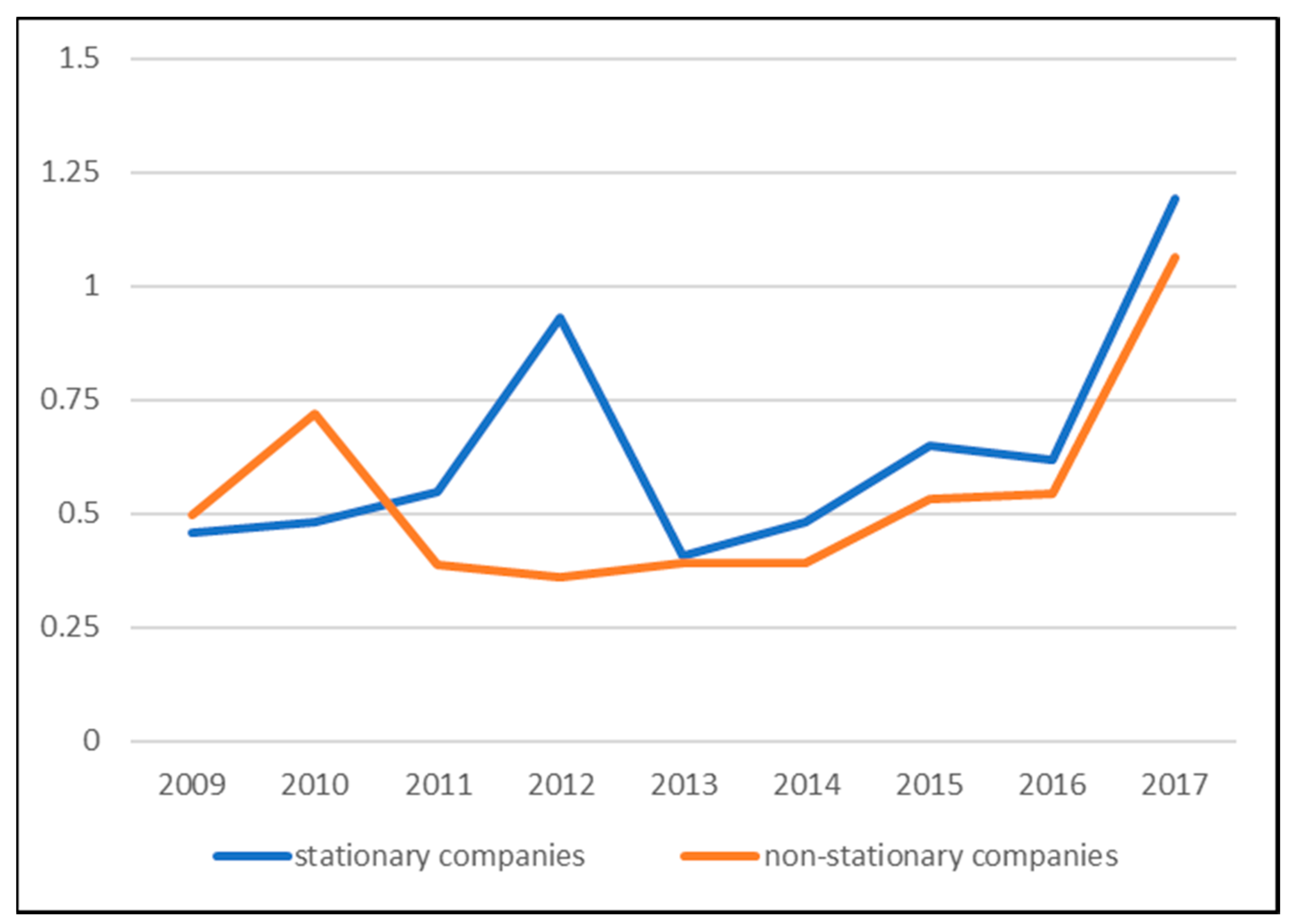
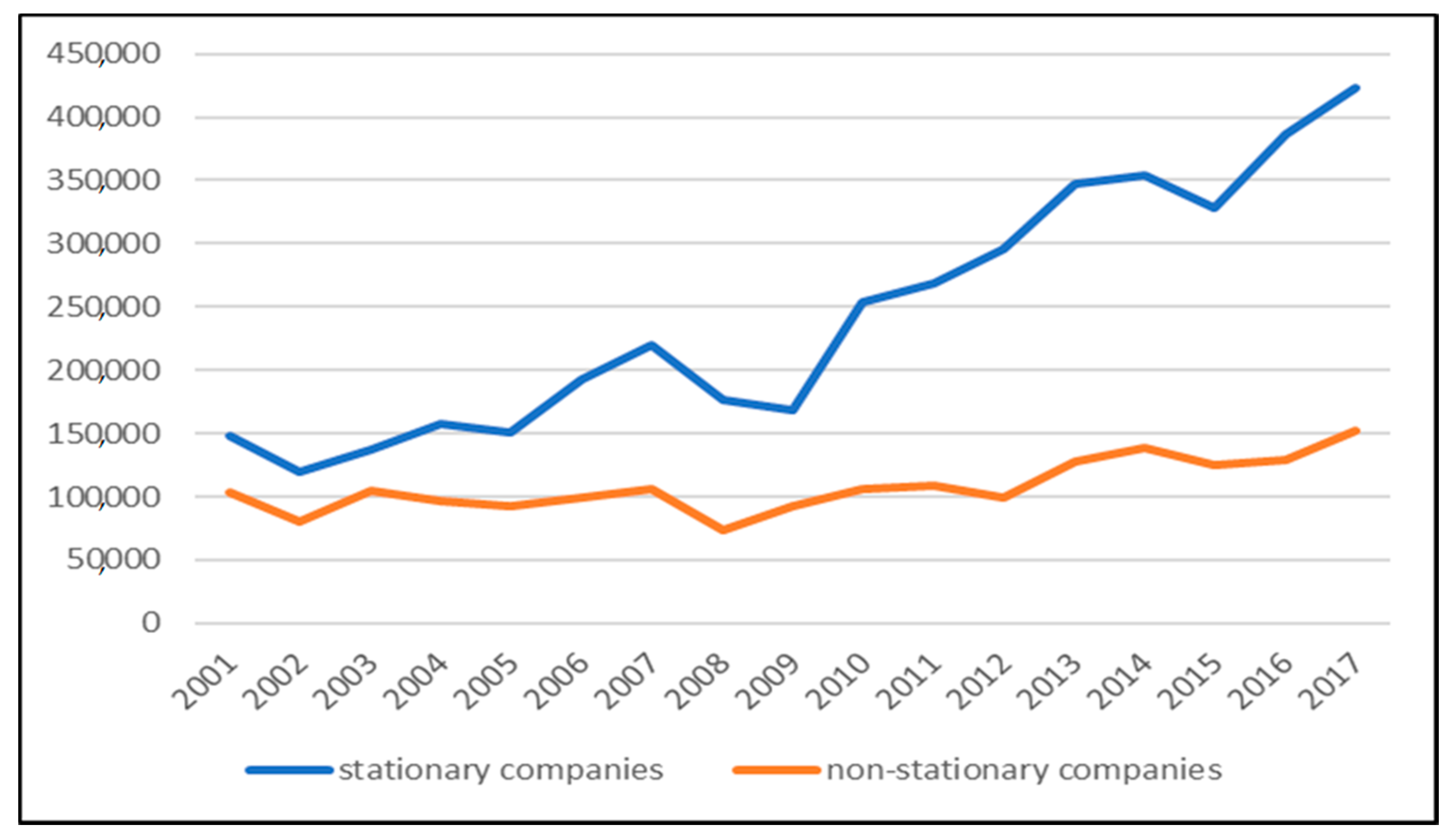
| Companies | Mean | Max. | Min. | Std.Dev. | Skew. | Kurt. | J-B |
|---|---|---|---|---|---|---|---|
| 3M CO. | 0.217 | 0.369 | 0.119 | 0.073 | 0.994 | 2.922 | 2.807 |
| AMERICAN EXPRESS CO. | 0.375 | 0.548 | 0.227 | 0.094 | −0.074 | 2.066 | 0.633 |
| BOEING CO. | 0.172 | 0.275 | 0.091 | 0.061 | 0.508 | 1.979 | 1.468 |
| CATERPILLAR INC. | 0.498 | 0.547 | 0.425 | 0.043 | −0.306 | 1.517 | 1.823 |
| CHEVRON CORP. | 0.110 | 0.225 | 0.048 | 0.058 | 0.620 | 2.145 | 1.605 |
| COCA-COLA CO. | 0.317 | 0.543 | 0.153 | 0.128 | 0.519 | 1.822 | 1.748 |
| DISNEY (WALT) CO. | 0.225 | 0.289 | 0.179 | 0.034 | 0.225 | 1.910 | 0.984 |
| DOWDUPONT INC. | 0.274 | 0.342 | 0.177 | 0.049 | −0.429 | 2.234 | 0.937 |
| EXXON MOBIL CORP. | 0.064 | 0.129 | 0.035 | 0.031 | 1.044 | 2.737 | 3.140 |
| GOLDMAN SACHS GROUP INC. | 0.584 | 0.641 | 0.510 | 0.041 | −0.510 | 2.056 | 1.368 |
| HOME DEPOT INC. | 0.267 | 0.607 | 0.040 | 0.180 | 0.348 | 2.165 | 0.836 |
| INTEL CORP. | 0.092 | 0.223 | 0.019 | 0.076 | 0.712 | 1.886 | 2.316 |
| INTL BUSINESS MACHINES CORP. | 0.285 | 0.374 | 0.210 | 0.054 | 0.176 | 1.794 | 1.117 |
| JOHNSON & JOHNSON | 0.128 | 0.220 | 0.046 | 0.048 | −0.032 | 2.356 | 0.296 |
| JPMORGAN CHASE & CO. | 0.250 | 0.317 | 0.195 | 0.039 | 0.265 | 1.769 | 1.273 |
| MCDONALD’S CORP. | 0.440 | 0.874 | 0.291 | 0.173 | 1.759 | 4.647 | 10.684 *** |
| MERCK & CO. | 0.190 | 0.278 | 0.119 | 0.046 | 0.507 | 2.260 | 1.115 |
| NIKE INC-CLUB | 0.087 | 0.172 | 0.025 | 0.046 | 0.724 | 2.371 | 1.764 |
| PFIZER INC. | 0.192 | 0.255 | 0.069 | 0.054 | −0.800 | 2.556 | 1.955 |
| PROCTER & GAMBLE CO. | 0.280 | 0.395 | 0.225 | 0.056 | 0.886 | 2.314 | 2.556 |
| TRAVELERS COS INC. | 0.058 | 0.064 | 0.041 | 0.006 | −1.048 | 3.542 | 3.322 |
| UNITED TECHNOLOGIES CORP. | 0.198 | 0.284 | 0.140 | 0.042 | 0.698 | 2.304 | 1.722 |
| VERIZON COMMUNICATIONS INC. | 0.307 | 0.487 | 0.167 | 0.101 | 0.543 | 1.940 | 1.632 |
| WALGREENS BOOTS ALLIANCE INC. | 0.098 | 0.262 | 0.001 | 0.077 | 0.590 | 2.355 | 1.280 |
| WALMART INC. | 0.259 | 0.281 | 0.227 | 0.016 | −0.556 | 2.393 | 1.137 |
| Level | 1st Difference | |||||
|---|---|---|---|---|---|---|
| ADF | PP | KPSS | ADF | PP | KPSS | |
| 3M CO. | −2.732(2) | −1.265(0) | 0.114[2] | −3.096(0) | −3.129(1) | 0.062(1) |
| AMERICAN EXPRESS CO. | −5.745(3) ** | −1.097(1) | 0.157[2] ** | −4.002(0) ** | −4.024(1) ** | 0.076(0) |
| BOEING CO. | −3.613(3) * | −2.028(2) | 0.124[0] * | −3.581(0) * | −4.739(6) *** | 0.231(5) *** |
| CATERPILLAR INC. | −2.726(3) | −2.028(2) | 0.107[1] | −3.389(1) | −3.278(11) | 0.261[8] *** |
| CHEVRON CORP. | −1.286(2) | −1.555(5) | 0.177[2] ** | −2.178(1) | −1.876(4) | 0.185[5] ** |
| COCA-COLA CO. | −5.75(3) *** | −3.541(15) * | 0.166[2] ** | −3.874(0) ** | −3.939(6) ** | 0.500[15] *** |
| DISNEY (WALT) CO. | −1.215(0) | −1.587(1) | 0.142[1] * | −4.663(0) *** | −4.877(3) *** | 0.147[1] ** |
| DOWDUPONT INC. | −2.681(2) | −1.550(1) | 0.085[2] | −2.693(2) | −2.502(1) | 0.103[1] |
| EXXON MOBIL CORP. | −1.403(0) | −1.381(2) | 0.169[2] ** | −3.202(0) | −2.842(4) | 0.161[4] ** |
| GOLDMAN SACHS GROUP INC. | −2.834(0) | −2.821(3) | 0.144[1] ** | −3.801(0) ** | −4.621(5) *** | 0.296[10] *** |
| HOME DEPOT INC. | −2.677(1) | −1.734(1) | 0.087[2] | −2.400(0) | −2.396(2) | 0.094[0] |
| INTEL CORP. | −1.993(0) | −1.996(12) | 0.163[2] ** | −4.730(1) *** | −5.001(13) *** | 0.394[12] *** |
| INTL BUSINESS MACHINES CORP. | −3.398(1) * | −4.006(7) ** | 0.137[1] * | −3.503(1) * | −4.186(14) ** | 0.216[5] ** |
| JOHNSON & JOHNSON | −3.164(1) | −1.686(0) | 0.067[1] | −2.903(0) | −2.903(0) | 0.073[1] |
| JPMORGAN CHASE & CO. | −2.347(2) | −1.832(1) | 0.100[2] | −3.270(0) * | −3.333(1) * | 0.082[0] |
| MCDONALD’S CORP. | 0.376(2) | 0.616(4) | 0.163[2] ** | −3.652(1) * | −3.081(7) | 0.115[3] |
| MERCK & CO. | −1.770(0) | −1.741(6) | 0.176[2] ** | −4.616(0) *** | −8.472(14) *** | 0.500[15] *** |
| NIKE INC-CLUB | 0.019(3) | −0.987(15) | 0.183[2] | −6.111(2) *** | −8.907(8) *** | 0.302[8] *** |
| PFIZER INC. | −3.679(3) * | −2.387(3) | 0.123[1] * | −4.660(0) *** | −4.602(1) *** | 0.187[6] ** |
| PROCTER & GAMBLE CO. | −2.083(0) | −2.022(2) | 0.149[1] | −3.998(1) ** | −8.487(13) *** | 0.469[14] *** |
| TRAVELERS COS INC. | −4.999(0) *** | −4.999(0) *** | 0.099[3] | −7.270(0) *** | −16.669(14) *** | 0.500[15] *** |
| UNITED TECHNOLOGIES CORP. | −3.394(0) * | −3.535(8) * | 0.155[2] ** | −4.809(2) *** | −12.878(11) *** | 0.500[15] *** |
| VERIZON COMMUNICATIONS INC. | −2.134(0) | −2.570(8) | 0.163[2] ** | −3.524(1) * | −3.506(12) * | 0.228{8} *** |
| WALGREENS BOOTS ALLIANCE INC. | −2.904(2) | −8.148(13) *** | 0.153[3] ** | −7.117(1) *** | −4.954(7) *** | 0.235[9] *** |
| WALMART INC. | −2.521(0) | −2.521(0) | 0.141[1] ** | −5.883(0) *** | −7.958(5) *** | 0.500[15] *** |
| Levin et al. (2002) | |||||
| 10.059 (1.000) | −0.333 *** (0.001) | 10.965 (1.000) | 16.755 (1.000) | ||
| Im et al. (2003) | |||||
| −2.042 | 0.591 (0.723) | −2.748 *** (0.003) | −2.048 | −2.778 *** (0.003) | |
| Maddala and Wu (1999) | |||||
| 46.049 (0.633) | −0.395 (0.654) |
| Bai and Ng (2004) | |||||
| 4.0 | 0.482 (0.315) | 54.824 (0.297) | 3 | 4 | |
| Moon and Perron (2004) | |||||
| −10.29 *** (0.000) | −5.964 *** (0.000) | 0.777 | −9.487 *** (0.000) | −5.824 *** (0.000) | |
| Choi (2002) | |||||
| −0.077 (0.531) | 0.349 (0.637) | 0.571 (0.716) | |||
| Pesaran (2007) | |||||
| 2 | −1.747 (0.460) | −1.747 (0.460) |
| Sequence | OU Statistic | Min. KSS Statistic | Series |
|---|---|---|---|
| 1 | −2.1923 (0.0000) | −3.8103 | VERIZON COMMUNICATIONS INC |
| 2 | −2.1249 (0.0000) | −3.7087 | TRAVELERS COS INC. |
| 3 | −2.0560 (0.0000) | −3.6905 | JPMORGAN CHASE & CO. |
| 4 | −1.9817 (0.0000) | −3.5692 | PROCTER & GAMBLE CO. |
| 5 | −1.9061 (0.0004) | −3.4705 | JOHNSON & JOHNSON |
| 6 | −1.8279 (0.0002) | −3.4109 | WALGREENS BOOTS ALLIANCE INC |
| 7 | −1.7446 (0.0002) | −2.9576 | CHEVRON CORP. |
| 8 | −1.6772 (0.0008) | −2.7664 | INTL BUSINESS MACHINES CORP |
| 9 | −1.6131 (0.0004) | −2.6667 | EXXON MOBIL CORP. |
| 10 | −1.5473 (0.0020) | −2.4373 | MCDONALD’S CORP. |
| 11 | −1.4879 (0.0094) | −2.1723 | GOLDMAN SACHS GROUP INC. |
| 12 | −1.4390 (0.0022) | −2.1411 | UNITED TECHNOLOGIES CORP. |
| 13 | −1.3850 (0.0114) | −2.1392 | INTEL CORP. |
| 14 | −1.3222 (0.0336) | −2.1057 | COCA-COLA CO. |
| 15 | −1.2510 (0.1056) | −1.828 | PFIZER INC. |
| 16 | −1.1933 (0.1580) | −1.8243 | MERCK & CO. |
| 17 | −1.1231 (0.3002) | −1.7788 | NIKE INC-CLUB |
| 18 | −1.0412 (0.4726) | −1.7505 | AMERICAN EXPRESS CO. |
| 19 | −0.9399 (0.4806) | −1.6941 | WALMART INC. |
| 20 | −0.8141(0.6098) | −1.3689 | CATERPILLAR INC. |
| 21 | −0.7032 (0.5528) | −1.1822 | DOWDUPONT INC. |
| 22 | −0.5835 (0.5634) | −1.1095 | 3M CO. |
| 23 | −0.4081 (0.7492) | −0.5161 | BOEING CO. |
| 24 | −0.3541 (0.4586) | −0.3554 | HOME DEPOT INC. |
| 25 | −0.3529 (0.4456) | −0.3529 | DISNEY (WALT) CO. |
| Sequence | OU Statistic | Min. KSS | Series | |
|---|---|---|---|---|
| 1 | −3.0469 (0.0000) | −3.8103 | 2 | VERIZON COMMUNICATIONS INC. |
| 2 | −2.9080 (0.0002) | −3.7087 | 2 | TRAVELERS COS INC. |
| 3 | −2.5176 (0.0018) | −3.5692 | 2 | PROCTER & GAMBLE CO. |
| 4 | −2.4212 (0.0026) | −3.4705 | 2 | JOHNSON & JOHNSON |
| 5 | −2.4163 (0.0038) | −3.4109 | 2 | WALGREENS BOOTS ALLIANCE INC. |
| 6 | −2.3273 (0.0064) | −2.9576 | 2 | CHEVRON CORP |
| 7 | −2.2102 (0.0092) | −2.9001 | 2 | JPMORGAN CHASE & CO. |
| 8 | −2.1989 (0.0098) | −2.7664 | 2 | INTL BUSINESS MACHINES CORP. |
| 9 | −2.2092 (0.0102) | −2.755 | 2 | EXXON MOBIL CORP. |
| 10 | −2.0459 (0.0266) | −2.4373 | 2 | MCDONALD’S CORP. |
| 11 | −1.8590 (0.1128) | −2.1723 | 2 | GOLDMAN SACHS GROUP INC. |
| 12 | −1.8014 (0.1190) | −2.1411 | 2 | UNITED TECHNOLOGIES CORP. |
| 13 | −1.7682 (0.1110) | −2.1392 | 2 | INTEL CORP. |
| 14 | −1.7444 (0.1260) | −2.1057 | 2 | COCA-COLA CO. |
| 15 | −1.6280 (0.2860) | −1.828 | 2 | PFIZER INC. |
| 16 | −1.7476 (0.1892) | −1.8243 | 2 | MERCK & CO. |
| 17 | −1.7021 (0.3084) | −1.7788 | 2 | NIKE INC-CLUB |
| 18 | −1.4255 (0.5604) | −1.7505 | 2 | AMERICAN EXPRESS CO. |
| 19 | −1.0974 (0.7500) | −1.7238 | 2 | 3M CO. |
| 20 | −1.0386 (0.8828) | −1.6941 | 2 | WALMART INC. |
| 21 | −0.7026 (0.9342) | −1.3689 | 2 | CATERPILLAR INC |
| 22 | −0.3800 (0.9428) | −1.1822 | 2 | DOWDUPONT INC |
| 23 | 0.1372 (0.9512) | −0.5161 | 2 | BOEING CO. |
| 24 | 0.2777 (0.8470) | −0.3554 | 2 | HOME DEPOT INC. |
| 25 | −1.0739 (0.4550) | −0.3529 | 2 | DISNEY (WALT) CO. |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, F.-L. Do DJIA Firms Reflect Stationary Debt Ratios? Economies 2020, 8, 76. https://doi.org/10.3390/economies8040076
Lin F-L. Do DJIA Firms Reflect Stationary Debt Ratios? Economies. 2020; 8(4):76. https://doi.org/10.3390/economies8040076
Chicago/Turabian StyleLin, Feng-Li. 2020. "Do DJIA Firms Reflect Stationary Debt Ratios?" Economies 8, no. 4: 76. https://doi.org/10.3390/economies8040076
APA StyleLin, F.-L. (2020). Do DJIA Firms Reflect Stationary Debt Ratios? Economies, 8(4), 76. https://doi.org/10.3390/economies8040076





