The Impact of International Sanctions on Russian Financial Markets
Abstract
1. Introduction
2. Literature Review
3. Data and Methodology
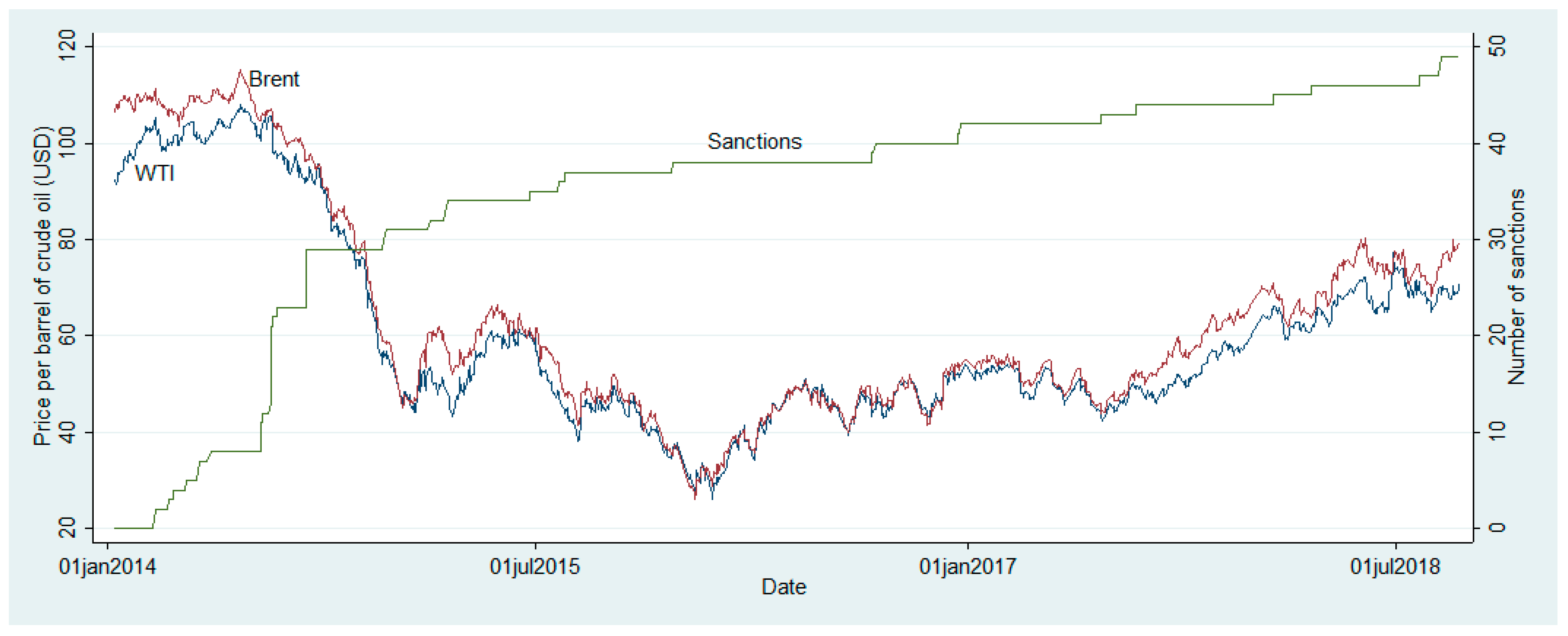
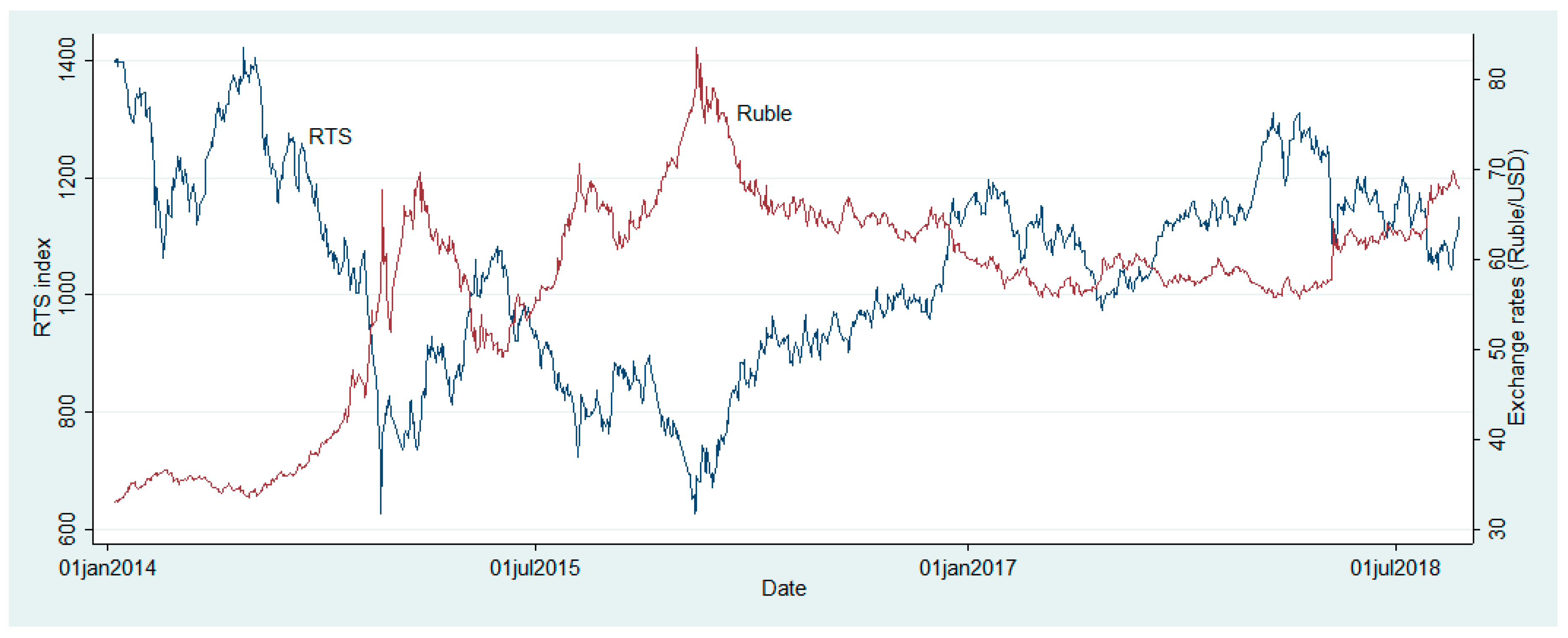
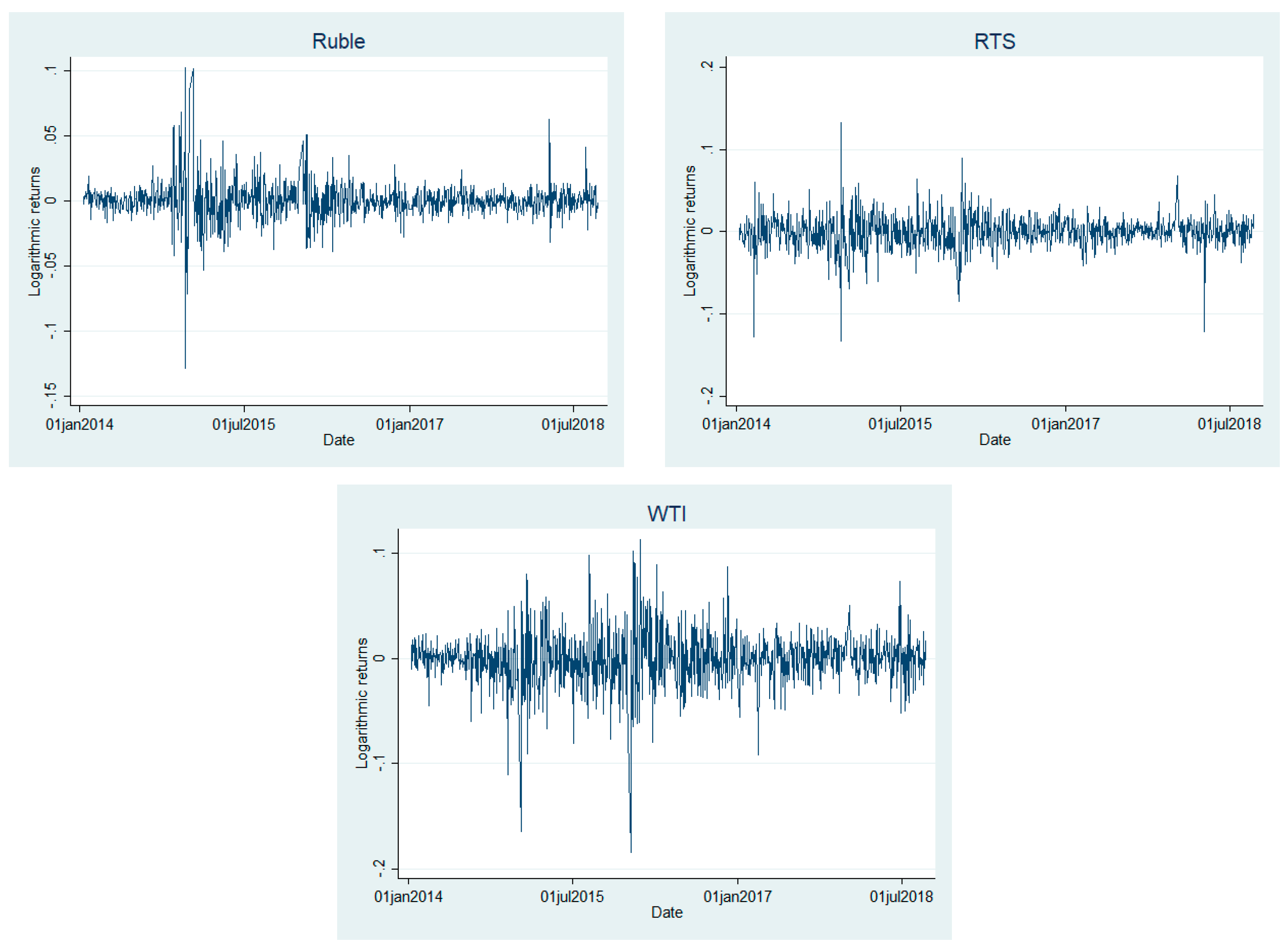
3.1. Data Description
3.2. Methodology
4. Empirical Findings
4.1. Short-Term Impact of Sanctions
4.2. Long-Term Impact of Sanctions
5. Concluding Remarks
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Exchange Rate Logarithmic Returns (Ruble) | Stock Price Index Logarithmic Returns (RTS) | |||
|---|---|---|---|---|
| Model 1 | Model 2 | Model 1 | Model 2 | |
| Mean equation | ||||
| 0.0314 (0.0308) | 0.0291 (0.0307) | 0.0077 (0.0339) | 0.0067 (0.0342) | |
| −0.0071 (0.0305) | −0.0080 (0.0299) | |||
| −0.0664 ** (0.0310) | −0.0682 ** (0.0309) | |||
| −0.0420 *** (0.0134) | −0.0409 *** (0.0131) | 0.0757 *** (0.0247) | 0.0766 *** (0.0247) | |
| Sanction dummy | ||||
| All | 0.0003 * (0.0001) | −0.0003 (0.0004) | ||
| Economic | 0.0012 (0.0011) | 0.0008 (0.0024) | ||
| Financial | 0.0005 (0.0011) | −0.0014 (0.0020) | ||
| Corporate | −0.0010 ** (0.0005) | −0.0003 (0.0011) | ||
| 0.0001 (0.0003) | 0.0003 (0.0003) | 0.0003 (0.0005) | 0.0002 (0.0005) | |
| Variance equation | ||||
| 0.2418 *** (0.0771) | 0.2490 *** (0.0796) | 0.0448 *** (0.0156) | 0.0443 *** (0.0153) | |
| −0.1586 * (0.0829) | −0.1584 ** (0.0800) | |||
| 0.9002 *** (0.0436) | 0.8893 *** (0.0340) | 0.9419 *** (0.0180) | 0.9427 *** (0.0174) | |
| 34.6010 ** (17.6391) | 35.0140 ** (13.9890) | −29.8911 *** (4.0547) | −32.4463 *** (9.3880) | |
| Sanction dummy | ||||
| All | −0.0041 (0.1558) | 0.0578 (0.2011) | ||
| Economic | −4.1096 ** (1.9771) | −0.3556 (1.2357) | ||
| Financial | 2.2812 *** (0.6123) | 0.6020(1.3912) | ||
| Corporate | 0.1225 (0.4235) | −0.3278 (1.2867) | ||
| −13.2686 *** (0.6430) | −13.1121 *** (0.5508) | −12.7489 *** (0.6241) | −12.7487 *** (0.6228) | |
| Portmanteau (Q) statistic, lags (5) | ||||
| Standardized residuals | 5.2971 (0.3807) | 5.0564 (0.4090) | 2.3588 (0.7976) | 2.4653 (0.7817) |
| Standardized residuals (squared) | 1.0890 (0.9551) | 0.8887 (0.9710) | 1.1713 (0.9476) | 1.1225 (0.9521) |
| Exchange Rate Logarithmic Returns (Ruble) | Stock Price Index Logarithmic Returns (RTS) | |||
|---|---|---|---|---|
| Model 1 | Model 2 | Model 1 | Model 2 | |
| Mean equation | ||||
| 0.0319 (0.0309) | 0.0304 (0.0312) | 0.0083 (0.0337) | 0.0082 (0.0339) | |
| −0.0043 (0.0303) | −0.0136 (0.0304) | |||
| −0.0648 ** (0.0308) | −0.0718 ** (0.0311) | |||
| −0.0423 *** (0.0132) | −0.0386 *** (0.0136) | 0.0761 *** (0.0246) | 0.0738 *** (0.0249) | |
| Sanction dummy | ||||
| All | −2.6 × 10−5 (−1.7 × 10−5) | −4.6 × 10−5 (−3.7 × 10−5) | ||
| Economic | −0.0010 ** (0.0004) | 0.0014 * (0.0008) | ||
| Financial | 0.0011 ** (0.0005) | −0.0016 * (0.0009) | ||
| Corporate | −1.5 × 10−5 (0.0001) | −4.7 × 10−5 (0.0002) | ||
| 0.0012 * (0.0007) | 0.0007 (0.0008) | −0.0016 (0.0015) | −0.0009 (0.0017) | |
| Variance equation | ||||
| 0.2538 *** (0.0803) | 0.2239 *** (0.0769) | 0.0435 *** (0.0147) | 0.0361 *** (0.0127) | |
| −0.1679 ** (0.0855) | −0.1323 (0.0818) | |||
| 0.8974 *** (0.0443) | 0.8729 *** (0.0572) | 0.9364 *** (0.0186) | 0.9379 *** (0.0200) | |
| Sanction dummy | 36.2570 ** (14.9062) | 33.7129 *** (9.8200) | −29.9437 *** (3.1247) | −26.3059 *** (4.3985) |
| All | ||||
| Economic | −0.0042 (0.0096) | −0.0238 ** (0.0108) | ||
| Financial | −0.1272 (0.2216) | −0.1769 (0.2116) | ||
| Corporate | 0.3305 (0.2357) | 0.3398 (0.2412) | ||
| −0.0934 (0.0583) | −0.0978 (0.0644) | |||
| Portmanteau (Q) statistic, lags (5) | ||||
| Standardized residuals | 5.4528 (0.3632) | 3.7706 (0.5829) | 2.7245 (0.7424) | 2.3909 (0.7928) |
| Standardized residuals (squared) | 0.8988 (0.9703) | 0.6960 (0.9832) | 1.1098 (0.9532) | 0.6692 (0.9846) |
References
- Bollerslev, Tim. 1986. Generalised autoregressive conditional hetroscedasticity. Journal of Econometrics 31: 307–27. [Google Scholar] [CrossRef]
- Bollerslev, Tim, Ray Chou, and Kenneth Kroner. 1992. ARCH modeling in finance: A review of the theory and empirical evidence. Journal of Econometrics 52: 5–59. [Google Scholar] [CrossRef]
- Box, George, and David Pierce. 1970. Distribution of residual autocorrelations in autoregressive-integrated moving average time series models. Journal of the American Statistical Association 65: 1509–26. [Google Scholar] [CrossRef]
- Central Bank of Russia. 2020. Dynamics of the Official Exchange Rates. Moscow, Russia. Available online: https://www.cbr.ru/eng/currency_base/dynamics/ (accessed on 10 May 2020).
- Council of the European Union. 2014. Council Regulation (EU) No 833/2014 of 31 July 2014 Concerning Restrictive Measures in View of Russia’s Actions Destabilising the Situation in Ukraine, Official Journal, L 229/1. pp. 1–11. Available online: http://data.europa.eu/eli/reg/2014/833/oj (accessed on 31 July 2014).
- Dickey, Alan, and Arthur Wayne Fuller. 1979. Distribution of the estimators for autoregressive time series with a unit root. Journal of the American Statistical Association 74: 427–31. [Google Scholar]
- Dickey, Alan, and Arthur Wayne Fuller. 1981. Likelihood ration statistics for autoregressive time series with a unit root. Econometrica 49: 1057–72. [Google Scholar] [CrossRef]
- Doxey, Margaret. 1987. International Sanctions in Contemporary Perspective. London: Palgrave Macmillan. [Google Scholar]
- Dreger, Christian, Jarko Fidrmuc, Konstantin Kholodilin, and Dirk Ulbricht. 2015. The Ruble between the Hammer and the Anvil: Oil Prices and Economic Sanctions. Discussion Papers 1488. Berlin: DIW Berlin, German Institute for Economic Research. [Google Scholar]
- Engle, Robert. 1982. Autoregressive conditional heteroscedasticity with estimates of the variance of United Kingdom inflation. Econometrica 50: 987–1007. [Google Scholar] [CrossRef]
- Galtung, Johan. 1967. On the effects of international economic sanctions, with examples from the case of Rhodesia. World Politics 19: 378–416. [Google Scholar] [CrossRef]
- Glosten, Lawrence, Ravi Jagannathan, and David Runkle. 1993. On the relation between the expected value and the volatility of the nominal excess return on stocks. Journal of Finance 48: 1779–801. [Google Scholar] [CrossRef]
- Hufbauer, Gary, Jeffrey Schott, and Kimberly Elliott. 1990. Economic Sanctions Reconsidered: History and Current Policy, 2nd ed. Washington: Institute for International Economics. [Google Scholar]
- Jing, Chao, William Kaempfer, and Anton Lowenberg. 2003. Instrument choice and the effectiveness of international sanctions: A simultaneous equations approach. Journal of Peace Research 40: 519–35. [Google Scholar] [CrossRef]
- Kholodilin, Konstantin, and Aleksei Netšunajev. 2019. Crimea and punishment: the impact of sanctions on Russian economy and economies of the euro area. Baltic Journal of Economics 19: 39–51. [Google Scholar] [CrossRef]
- Korhonen, Iikka, Heli Simola, and Laura Solanko. 2018. Sanctions, Countersanctions, and Russia—Effects on Economy, Trade, and Finance. BOFIT Policy Brief 4/2018. Helsinki: Institute for Economies in Transition, Bank of Finland. [Google Scholar]
- Lindsay, James. 1986. Trade sanctions as policy instruments: A re-examination. International Studies Quarterly 30: 153–73. [Google Scholar] [CrossRef]
- Ljung, Greta, and George Box. 1978. On a measure of lack of fit in time series models. Biometrika 65: 297–303. [Google Scholar] [CrossRef]
- Nelson, Daniel. 1991. Conditional heteroskedasticity in asset returns: A new approach. Econometrica 59: 347–70. [Google Scholar] [CrossRef]
- Nureev, Rustem. 2017. Reasons and content of economic sanctions. In Economic Sanctions against Russia: Expectations and Reality. Edited by R. Nureev. Moscow: Knorus, pp. 8–21. [Google Scholar]
- Primakov, Yevgeniy. 2015. Russia: Hope and Anxiety. Moscow: CJSC Tsentrpoligraph. [Google Scholar]
- Radio Free Europe/Radio Liberty. 2018. A Timeline of all Russia-related sanctions: A detailed look at all the sanctions levied against Russia, and its countersanctions, since 2014. Paper presented at Ivan Gutterman, Wojtek Grojec, and RFE/RL’s Current Time, Prague, Czechia, September 19. [Google Scholar]
- Schmıdbauer, Harald, Angi Rösch, Erhan Ulucevız, and Narod Erkol. 2016. The Russian Stock Market during the Ukrainian Crisis: A Network Perspective. Journal of Economics and Finance 66: 478–509. [Google Scholar]
- Schwert, William. 1989. Why does stock market volatility change over time? Journal of Finance 44: 1115–53. [Google Scholar] [CrossRef]
- Smeets, Maarten. 2018. Can Economic Sanctions be Effective? Staff Working Paper ERSD-2018-03, Economic Research and Statistics Division. Geneva: World Trade Organization. [Google Scholar]
- Stone, Mark. 2017. The Response of Russian Security Prices to Economic Sanctions: Policy Effectiveness and Transmission; Working Paper February 2017; Washington: Office of the Chief Economist, U.S. Department of State.
- Taylor, Stephen. 1986. Modelling Financial Time Series. Chichester/York: Wiley. [Google Scholar]
- Tyll, Ladislav, Karel Pernica, and Markéta Arltová. 2018. The impact of economic sanctions on Russian economy and the RUB/USD exchange rate. Journal of International Studies 11: 21–33. [Google Scholar] [CrossRef] [PubMed]
- United States Congress. 2014. Support for the sovereignty, integrity, democracy, and economic stability of Ukraine act of 2014, H.R. 4152. Paper presented at 113th Congress, WA, USA, March 4. [Google Scholar]
- Weber, Patrick, and Gerald Schneider. 2020. Post-Cold War Sanctioning by the EU, the UN, and the US: Introducing the EUSANCT Dataset. Conflict Management and Peace Science. Available online: https://journals.sagepub.com/doi/full/10.1177/0738894220948729 (accessed on 27 August 2020).
- World Bank. 2015. Russia Economic Report: The Dawn of a New Economic Era? Moscow: The World Bank. [Google Scholar]
- World Bank. 2020a. Fuel Exports (% of Merchandise Exports). World Development Indicators. Washington, USA. Available online: https://data.worldbank.org/indicator/TX.VAL.FUEL.ZS.UN (accessed on 15 May 2020).
- World Bank. 2020b. Exports of Goods and Services (BoP, current US$). World Development Indicators. Washington, USA. Available online: https://data.worldbank.org/indicator/BX.GSR.GNFS.CD (accessed on 15 May 2020).
- World Bank. 2020c. Imports of Goods and Services (BoP, current US$). World Development Indicators. Washington, USA. Available online: https://data.worldbank.org/indicator/BM.GSR.GNFS.CD (accessed on 15 May 2020).
| Sanctions | 2014 | 2015 | 2016 | 2017 | 2018 |
|---|---|---|---|---|---|
| Economic | US 8 | US 2 | US 0 | US 0 | US 1 |
| EU 4 | EU 0 | EU 0 | EU 0 | EU 0 | |
| Financial | US 5 | US 1 | US 0 | US 0 | US 1 |
| EU 5 | EU 0 | EU 0 | EU 0 | EU 0 | |
| Corporate | US 5 | US 3 | US 4 | US 1 | US 2 |
| EU 4 | EU 1 | EU 0 | EU 1 | EU 1 |
| Variables | Mean | SD | Skewness | Kurtosis | ARCH LM | ADF |
|---|---|---|---|---|---|---|
| Ruble | 0.00062 | 0.01421 | 0.41435 | 17.5496 | 224.263 *** | −4.49400 *** |
| RTS | −0.00015 | 0.01979 | −0.49856 | 10.8321 | 148.697 *** | −6.64800 *** |
| WTI | −0.00029 | 0.02489 | −0.49078 | 9.24029 | 11.0290 *** | −6.34300 *** |
| Brent | −0.00030 | 0.02306 | −0.93690 | 15.6977 | 2.07200 | −6.44800 *** |
| Exchange Rate Logarithmic Returns (Ruble) | Stock Price Index Logarithmic Returns (RTS) | |||||
|---|---|---|---|---|---|---|
| Model 0 | Model 1 | Model 2 | Model 0 | Model 1 | Model 2 | |
| Mean equation | ||||||
| 0.0306 *** (0.0110) | 0.0177 (0.0316) | 0.0222 (0.0452) | 0.0472 (0.0302) | 0.0054 (0.0319) | 0.0069 (0.0343) | |
| −0.0388 *** (0.0139) | −0.0386 *** (0.0148) | 0.0827 *** (0.0236) | 0.0829 *** (0.0250) | |||
| Sanction dummy | ||||||
| All | 0.0003 *** (3.06 × 10−5) | −0.0004 (0.0004) | ||||
| Economic | 0.0017 (0.0033) | 0.0010 (0.0022) | ||||
| Financial | −0.0001 (0.0032) | −0.0014 (0.0019) | ||||
| Corporate | −0.0009 (0.0011) | −0.0006 (0.0012) | ||||
| 0.0003 ** (0.0001) | 0.0001 (0.0002) | 0.0002 (0.0004) | −2.15×10−5 (0.0004) | 0.0001 (0.0005) | 0.0001 (0.0005) | |
| Variance equation | ||||||
| 0.0887 *** (0.0231) | 0.0913 *** (0.0305) | 0.0950 *** (0.0309) | −0.0697 *** (0.0171) | −0.0640 *** (0.0203) | −0.0666 *** (0.0212) | |
| 0.2167 *** (0.0602) | 0.2113 *** (0.0684) | 0.1980 ** (0.0836) | 0.1036 *** (0.0210) | 0.0954 *** (0.0213) | 0.0977 *** (0.0217) | |
| 0.9758 *** (0.0122) | 0.9750 *** (0.0148) | 0.9810 *** (0.0158) | 0.9870 *** (0.0050) | 0.9875 *** (0.0047) | 0.9879 *** (0.0049) | |
| 0.1284 (1.6477) | −0.1593 (1.7934) | −0.8046 (0.9038) | −0.7817 (0.9732) | |||
| Sanction dummy | ||||||
| All | −0.0031 (0.0066) | −0.0014 (0.0033) | ||||
| Economic | −0.0432 (0.0541) | −0.0104 (0.0221) | ||||
| Financial | 0.0170 (0.0503) | −0.0016 (0.0207) | ||||
| Corporate | 0.0209 (0.0313) | 0.0082 (0.0147) | ||||
| −0.2133 * (0.1092) | −0.2193 * (0.1312) | −0.1677 (0.1397) | −0.1038 *** (0.0398) | −0.1005 *** (0.0375) | −0.0974 ** (0.0393) | |
| Portmanteau (Q) statistic, lags (5) | ||||||
| Standardized residuals | 8.6763 (0.1227) | 8.4741 (0.1320) | 9.4724 (0.0916) | 2.7498 (0.7385) | 3.1364 (0.6790) | 3.0381 (0.6941) |
| Standardized residuals (squared) | 1.5730 (0.9045) | 2.0981 (0.8354) | 2.2723 (0.8103) | 0.6548 (0.9854) | 0.6738 (0.9844) | 0.7043 (0.9827) |
| Exchange Rate Logarithmic Returns (Ruble) | Stock Price Index Logarithmic Returns (RTS) | |||
|---|---|---|---|---|
| Model 3 | Model 4 | Model 3 | Model 4 | |
| Mean equation | ||||
| 0.0190 (0.0392) | 0.0196 (0.0179) | 0.0087 (0.0337) | 0.0074 (0.0349) | |
| −0.0398 *** (0.0145) | −0.0360 *** (0.0084) | 0.0822 *** (0.0250) | 0.0795 *** (0.0254) | |
| Sanction dummy | ||||
| All | −2.02 × 10−5 (2.99 × 10−5) | 3.30 × 10−5 (4.15 × 10−5) | ||
| Economic | −0.0012 *** (8.10 × 10−6) | 0.0013 *** (7.61 × 10−6) | ||
| Financial | 0.0014 *** (1.16 × 10−5) | −0.0016 *** (7.58 × 10−6) | ||
| Corporate | 2.89 × 10−5 ** (1.18 × 10−5) | −1.28 × 10−5 (9.72 × 10−6) | ||
| 0.0010 (0.0011) | 0.0005 * (0.0003) | −0.0013 (0.0016) | −0.0004 *** (0.0001) | |
| Variance equation | ||||
| 0.0917 *** (0.0323) | 0.1111 *** (0.0399) | −0.0625 *** (0.0205) | −0.0771 *** (0.0228) | |
| 0.2195 *** (0.0723) | 0.2313 *** (0.0756) | 0.0962 *** (0.0219) | 0.0911 *** (0.0207) | |
| 0.9748 *** (0.0152) | 0.9464 *** (0.0322) | 0.9865 *** (0.0054) | 0.9782 *** (0.0078) | |
| 0.2684 (1.6964) | 1.5265 (2.0971) | −0.7297 (0.9304) | −0.1153 (1.0102) | |
| Sanction dummy | ||||
| All | 5.72 × 10−5 (5.15 × 10−4) | −0.0002 (0.0003) | ||
| Economic | −0.0215 * (0.0129) | −0.0042 (0.0046) | ||
| Financial | 0.0411 ** (0.0200) | 0.0091 * (0.0053) | ||
| Corporate | −0.0060 (0.0061) | −0.0028 (0.0017) | ||
| −0.2250 (0.1385) | −0.5476 * (0.3267) | −0.1006 ** (0.0405) | −0.1789 *** (0.0629) | |
| Portmanteau (Q) statistic, lags (5) | ||||
| Standardized residuals | 8.6127 (0.1255) | 6.9248 (0.2263) | 3.1183 (0.6818) | 2.7005 (0.7460) |
| Standardized residuals (squared) | 2.3667 (0.7964) | 1.3744 (0.9271) | 0.6078 (0.9876) | 0.5419 (0.9905) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sultonov, M. The Impact of International Sanctions on Russian Financial Markets. Economies 2020, 8, 107. https://doi.org/10.3390/economies8040107
Sultonov M. The Impact of International Sanctions on Russian Financial Markets. Economies. 2020; 8(4):107. https://doi.org/10.3390/economies8040107
Chicago/Turabian StyleSultonov, Mirzosaid. 2020. "The Impact of International Sanctions on Russian Financial Markets" Economies 8, no. 4: 107. https://doi.org/10.3390/economies8040107
APA StyleSultonov, M. (2020). The Impact of International Sanctions on Russian Financial Markets. Economies, 8(4), 107. https://doi.org/10.3390/economies8040107





