Model Selection Procedures in Bounds Test of Cointegration: Theoretical Comparison and Empirical Evidence

Abstract

Only unstructured single-path model selection techniques, i.e., Information Criteria, are used by Bounds test of cointegration for model selection. The aim of this paper was twofold; one was to evaluate the performance of these five routinely used information criteria {Akaike Information Criterion (AIC), Akaike Information Criterion Corrected (AICC), Schwarz/Bayesian Information Criterion (SIC/BIC), Schwarz/Bayesian Information Criterion Corrected (SICC/BICC), and Hannan and Quinn Information Criterion (HQC)} and three structured approaches (Forward Selection, Backward Elimination, and Stepwise) by assessing their size and power properties at different sample sizes based on Monte Carlo simulations, and second was the assessment of the same based on real economic data. The second aim was achieved by the evaluation of the long-run relationship between three pairs of macroeconomic variables, i.e., Energy Consumption and GDP, Oil Price and GDP, and Broad Money and GDP for BRICS (Brazil, Russia, India, China and South Africa) countries using Bounds cointegration test. It was found that information criteria and structured procedures have the same powers for a sample size of 50 or greater. However, BICC and Stepwise are better at small sample sizes. In the light of simulation and real data results, a modified Bounds test with Stepwise model selection procedure may be used as it is strongly theoretically supported and avoids noise in the model selection process.

1. Introduction

The concept of avoiding the spurious regression in case the time series under consideration are I(1) was firstly explored by (Engle and Granger 1987) in their seminal paper. They argued that spurious cointegration could be avoided if the I(1) time series are cointegrated, i.e., having a long-run relationship. Following their paper, numerous tests were developed, and empirical studies were carried out to find the long-run relationship between time series. Since the development of the first cointegration test, various cointegration tests have been developed, and one of them is the Bounds cointegration test developed by (Pesaran et al. 2001). Since the development of the Bounds test of cointegration by (Pesaran et al. 2001), it has been widely and frequently used by researchers to examine the level relationship between different macroeconomic and financial variables (Adeleye et al. 2018; Tsoulfidis and Tsaliki 2014; Tang 2014).

The information criteria/unstructured model selection procedures are used by the Bounds test of cointegration for plausible model selection. The five unstructured procedures, commonly known as information criteria, are Akaike Information Criterion (AIC) developed by (Akaike 1973b), Akaike Information Criterion Corrected (AICC) formulated by (Hurvich and Tsai 1989), Bayesian or Schwarz Information Criterion (BIC or SIC) developed by (Schwarz 1978), Bayesian or Schwarz Information Criterion Corrected (BICC or SICC) developed by (McQuarrie and Tsai 1998) and an information criterion proposed by (Hannan and Quinn 1979) generally abbreviated as HQC. These criteria were developed for the lag selection in different testing approaches. In addition to these information criteria, there are other model selection procedures such as Forward Selection (FS), Backward Elimination (BW) and Stepwise (SW) Regression, which can be used for plausible model selection. These three model selection procedures are known as single-path structured procedures which were developed by (Efroymson 1960) and are routinely used in SPSS and STATA for plausible model selection.

Bounds cointegration test has some additional features as compared to its single-equation rivals as it is based on an Error Correction form of the equation, and it does not require pretesting for unit root. Furthermore, if cointegration is found, then the same error correction form serves as the famous error correction model, and if it is not found, then it is a simple autoregressive model in difference of the variables. Therefore, for the Bounds cointegration test, it is not a simple problem of lag selection, it is a very vital and crucial problem of model selection as the same model will be used for policy implications.

The performance of these model selection techniques has been assessed in numerous studies; however, one should note that the performance of these model selection techniques has yet not been evaluated for Bounds test. Moreover, single-path procedures’ performance has also not been assessed for the Bounds test so far. However, scholars have frequently and widely applied the Bounds test to explore the level relationship between several financial and macroeconomic series.

Therefore, it is worth exploring the efficiency and assessing the performance of the different techniques and procedures which can be used by Bounds test for selecting a plausible model. This paper, therefore, fills the existing vacuum in the literature by finding an appropriate model selection technique from these eight model selection procedures by investigating their size and power properties on the basis of Monte Carlo simulations. Furthermore, this study also assesses the behavior of these model selection procedures by evaluating the existence of cointegration between different macroeconomic variables for BRICS (Brazil, Russia, India, China, and South Africa) member countries. Moreover, as the Bounds test has not been used for cross-country comparison of level relationship in the literature for BRICS, a cross-country comparison was also carried out, based on the existence of long-run relationships between different macroeconomic variables for BRICS economies.

These cross-country or cross-regions comparisons have been carried out in literature in several studies like (Sari 2015; Mayor and Patuelli 2015; Delbecq et al. 2013) and many more. We consider three different pairs of variables, i.e., Energy Consumption (EC) and Gross Domestic Product (GDP), Oil Price (OP) and GDP, and Broad Money (BM) and GDP, to ensure the robustness of our findings.

The rest of the paper is structured as follows. The next section presents the literature review, tracked by methodology; Section 4 presents the empirical results, and Section 5 concludes the article.

2. Literature Review

Some of the studies assessing the long-run relationship between time series after the development of cointegration include the following: long-run performance of Slovenia apple markets illustrates an almost perfect price transmission along the marketing chain with an elasticity close to unity. Economic theory generally explains this as an indicator of market productivity (Hassouneh et al. 2015). The price-level variations mainly favor retailers by increasing their marketing margins. Increases in international wheat stocks reduce producer prices, while higher interest rates boost their instability (Hassouneh et al. 2017).

A spatial price transmission is analyzed from several perspectives, using a variety of econometric techniques to shed light upon the degree of integration, adjustment asymmetries, and the role of market share upon price transmission. A linear and nonlinear Vector Error Correction (VEC) model were found to be capable of adequately depicting the long-run wheat producer price relationship between Hungary and Slovenia (Bakucs et al. 2015). The cointegration relation implies a common stochastic trend of variables, which are modelled in the empirical analysis. Inflation rate and hospitality industry prices are found to be integrated of order one with a nonzero mean, suggesting that the present level of costs can be composed as a sum of all the previous shocks to inflation and hospitality industry prices. The general price level influences hospitality industry prices in the short run, but less in the long-term equilibrium price relation in the dynamic specifications (Gričar and Bojnec 2013).

The eight model selection approaches along with other approaches were compared using Monte Carlo simulations and real data in numerous studies such as (Hoover and Perez 1999; Hendry and Krolzig 1999; Kudo and Sklansky 2000; Castle et al. 2011) and many more having mixed conclusions. For a detailed survey of the comparison of model selection techniques, please read (Rashid 2014). (Rashid 2014) concluded that stepwise regression performs better than the rest of the single-path and unstructured model selection techniques. Moreover, (Rashid 2014) also showed that for small sample sizes, AIC is the second better performer, and BIC is the second better performer at large sample sizes.

The existence of a long-run relationship between EC and GDP has been explored in numerous studies like (Shahbaz et al. 2018; Belke et al. 2011; Mehrara 2007) and many more. Similarly, the relationship between OP and GDP has been explored in a number of studies like (Foudeh 2017; Ghalayini 2011; Du et al. 2010) and many more. A lot of studies have explored the dynamics between BM and GDP, such as (Denbel et al. 2016; Ogunmuyiwa and Ekone 2010; Liu and Jin 2005), but they are not restricted to these. The panel cointegration analysis and cointegration regression used Fully Modified Ordinary Least Squares (FMOLS) and Dynamic Ordinary Least Squares (DOLS) for 31 OECD (Organization for Economic Co-operation and Development) countries covering the time span 1990–2016. It shows that there is strong bidirectional causality between variables. The energy consumption elasticities of high-technology exports are comparatively high compared to medium- and low-tech exports (Şanlı 2019).

The causality tests disclosed the following: (1) unidirectional causality running from energy consumption to real GDP in Egypt, Iran, Lebanon, and Tunisia; (2) unidirectional causality running from real GDP to energy consumption in Algeria, Morocco, and Saudi Arabia; (3) bidirectional causality in Oman and the United Arab Emirates; and (4) no causality between energy consumption and real GDP in Bahrain and Malta. These conclusions suggest that energy conservation policies can be implemented in Algeria, Bahrain, Malta, Morocco, and Saudi Arabia (Ozturk 2017). The magnitude of the coefficient estimates of Natural Gas Consumption (NGC) becomes substantially smaller in the long run, and the sign of short-run estimates of NGC shifts to negative after accounting for capital and labor as well. The direction of causality between growth rate (GR) and NGC using the vector error correction model Granger causality approach revealed the evidence of feedback hypothesis for Turkey (Dogan 2015).

The higher oil prices transform income from oil-importing countries to oil-exporting countries. So, increases in oil prices have a negative impact on the economy of oil importers. Moreover, it has a significant impact on economic growth. Trade openness also has a positive and significant impact on economic output. Long-run results indicate that the coefficient of government investment has a positive and significant impact on growth. Long-run and short-run dynamics between variables, respectively, used annual data from 1972 to 2011 in the context of Pakistan. Through examining the results, the long-run and dynamic relationships have detected for all the variables except industrial oil consumption, and oil price variables for the model have no short-run impact on GDP. Oil prices impact real GDP negatively in the long run but positively in the short run (Nazir and Qayyum 2014).

The oil prices have no vital impact on the most variables during the short term, with the exception that they have a positive effect on inflation and negative effect on the real effective exchange rate. The result of Variance Decomposition (VD) analysis is consistent with the Impulse Response Function (IRF) in that there is a positive impact in the long term of oil prices on the real GDP (RGDP) and inflation (INF). On the other hand, there is a negative impact on the real effective exchange rate (REER) and unemployment rate (UNE), with no effect at all on Money supply (M2) (Bouchaour and Al-Zeaud 2012).

3. Methodology

The details of the Bounds Cointegration test and model selection procedures are laid out. The data generating process (DGP) and the details of data sources with their description are also given.

3.1. Bounds Test of Cointegration

The Bounds test of cointegration uses the following form of the Error Correction Model (ECM hereafter):

$$\Delta y_t=c_0+c_{1}t+\varphi \left({\pi }_0+{\pi }_{1}t+\alpha y_{t-1}+\beta X_{t-1}\right)+{\displaystyle \sum _{i=1}^p{\gamma }_i\Delta y_{t-i}+{\displaystyle \sum _{i=0}^q{\delta }_i\Delta X_{t-i}}}+{\epsilon }_t$$

(1)

where $y_t$ is a $T\times 1$ vector of endogenous/dependent variable, $X_t$ is a $T\times k$ vector of $k$ regressors, i.e., $\left(x_{1t},x_{2t},-------x_{kt}\right)$, ${\epsilon }_t$ is a $T\times 1$ vector of random errors and $p$, and q is the maximum number of lags of Y and X, respectively. The parameters of interest are $c_0$, the unrestricted intercept, $c_1$ the unrestricted linear time trend, ${\pi }_0$ the restricted intercept, and ${\pi }_1$ the restricted linear time trend. (Pesaran et al. 2001) considered the following five different models, i.e.,

Model-1: No intercepts, No trends: In ECM (1) $c_0=c_1={\pi }_0={\pi }_1=0$ and it becomes

$$\Delta y_t=\varphi \left(\alpha y_{t-1}+\beta X_{t-1}\right)+{\displaystyle \sum _{i=1}^p{\gamma }_i\Delta y_{t-i}+{\displaystyle \sum _{i=0}^p{\delta }_i\Delta X_{t-i}}}+{\epsilon }_t$$

(2)

Model-2: Restricted intercept, No trends: In ECM (1) $c_0=c_1={\pi }_1=0$ and it becomes

$$\Delta y_t=\varphi \left({\pi }_0+\alpha y_{t-1}+\beta X_{t-1}\right)+{\displaystyle \sum _{i=1}^p{\gamma }_i\Delta y_{t-i}+{\displaystyle \sum _{i=0}^p{\delta }_i\Delta X_{t-i}}}+{\epsilon }_t$$

(3)

Model-3: Unrestricted intercept, No trends: In ECM (1) $c_1={\pi }_0={\pi }_1=0$ and it becomes

$$\Delta y_t=c_0+\varphi \left(\alpha y_{t-1}+\beta X_{t-1}\right)+{\displaystyle \sum _{i=1}^p{\gamma }_i\Delta y_{t-i}+{\displaystyle \sum _{i=0}^p{\delta }_i\Delta X_{t-i}}}+{\epsilon }_t$$

(4)

Model-4: Unrestricted intercept, Restricted trends: In ECM (1) $c_1={\pi }_0=0$ and it becomes

$$\Delta y_t=c_0+\varphi \left({\pi }_{1}t+\alpha y_{t-1}+\beta X_{t-1}\right)+{\displaystyle \sum _{i=1}^p{\gamma }_i\Delta y_{t-i}+{\displaystyle \sum _{i=0}^p{\delta }_i\Delta X_{t-i}}}+{\epsilon }_t$$

(5)

Model-5: Unrestricted intercept, Unrestricted trend: In ECM (1) ${\pi }_0={\pi }_1=0$ and it becomes

$$\Delta y_t=c_0+c_{1}t+\varphi \left(\alpha y_{t-1}+\beta X_{t-1}\right)+{\displaystyle \sum _{i=1}^p{\gamma }_i\Delta y_{t-i}+{\displaystyle \sum _{i=0}^p{\delta }_i\Delta X_{t-i}}}+{\epsilon }_t$$

(6)

For the testing of the existence of a long-run relationship, the null hypothesis of no cointegration, i.e.,

$$H_0: \phi =0 \left(No Long-run relationship\right)$$

(7)

is tested against the alternative hypothesis of cointegration, i.e.,

$$H_A: \phi \ne 0 \left(Long-run relationship exists\right)$$

(8)

(Pesaran et al. 2001) used the standard $F-test$ for linear restrictions to test $H_0$, i.e.,

$$F=\frac{\raisebox{1ex}{$\left(RSSR-RSSU\right)$}\!\left/ \!\raisebox{-1ex}{$q$}\right.}{\raisebox{1ex}{$RSSU$}\!\left/ \!\raisebox{-1ex}{$\left(T-k\right)$}\right.}$$

(9)

where $RSSR$ is the Residual Sum of Squares for Restricted Regression, $RSSU$ is the Residual Sum of Squares for Unrestricted Regression, $q$ is the number of restrictions, and $k$ is the total number of parameters estimated. Two critical values of $F-stat$ were obtained; one was named as lower bound, denoted as $F_{LB}$ and it was the $100\left(1-\alpha \right)th$ percentile of $F$ when $X_t$ are generated as $I\left(0\right)$, i.e., integrated of order zero. The other was named as upper bound denoted as $F_{UB}$ and it was the $100\left(1-\alpha \right)th$ percentile of $F$ when $X_t$ are generated as $I\left(1\right)$, i.e., integrated of order one. The $\alpha$ is the assumed significance level. The null hypothesis of no cointegration is rejected when $F\ge F_{UB}$ and it is concluded that there is a long-run relationship between $y_t$ and $X_t$. If $F\le F_{LB}$, then it is concluded that there is no long-run relationship between $y_t$ and $X_t$. However, if $F_{LB}<F<F_{UB}$, then it is concluded that the test is inconclusive.

For the selection of a plausible model, the following eight model selection procedures are used belonging to two types of structured and unstructured model selection procedures.

3.2. Structured Model Selection Procedures

These procedures and algorithms use Several Linear Regression models and their conclusions for the selection of a plausible and parsimonious model from a set of candidate variables. These algorithms were first developed by (Efroymson 1960) and are routinely used by social scientists. The details of these three algorithms are below.

3.2.1. Forward Selection (FS) Procedure

It is a unidirectional algorithm that first estimates the model with no candidate variable, and then it estimates the linear regression model for all candidate variables separately one by one. Let $Y$ be the dependent variable, $X_i for i=1, 2, 3, \dots \dots \dots \dots , k$ be $k$ independent variables,  be $k$ respective regression coefficients, and $\epsilon$ be the random error, then FS algorithm estimates $k$ linear regressions, i.e.,

$$Y=X_i{\beta }_i+\epsilon \forall k=1, 2, 3, \dots \dots \dots \dots ,k$$

(10)

The independent variable having the minimum significant p-value or maximum significant t-stat is chosen. Then this variable is maintained in the model throughout the further selection technique. In the next step, again $k-1$ linear regressions are estimated, and another most significant variable is chosen from remaining $k-1$ candidate variables. This process is continued until either there is no significant variable to be included or all variables have been included.

3.2.2. Backward Elimination (BW) Procedure

It is also a unidirectional algorithm that first estimates that the most general multiple linear regression model was having all the candidate variables. Say that $Y$ is the $\left(T\times 1\right)$ vector of the dependent variable, $X$ is $\left(T\times k\right)$ matrix of independent variables, $\beta$ is $\left(k\times 1\right)$ vector of respective regression coefficients, and $\epsilon$ is the $\left(T\times 1\right)$ vector of random errors, then BW algorithm estimates the multiple linear regression model:

$$Y=X\beta +\epsilon$$

(11)

In this estimated model, the independent variable, either having the maximum insignificant p-value or minimum insignificant t-stat, is dropped, and the model is reduced to $k-1$ regressors. Again, the same procedure is adopted for the remaining regressors, and another variable is dropped, and the model is reduced to $k-2$ regressors. This procedure continues until either there is no insignificant variable to be dropped or all of the variables have been dropped.

3.2.3. Stepwise (SW) Regression Procedure

There are two algorithms, i.e., Stepwise with Forward Selection and Stepwise with Backward Elimination, whose details are below:

Stepwise with Forward Selection

It is a bidirectional selection algorithm, which uses both forward selection and backward elimination for plausible and parsimonious model selection. Take the same model as it is in forward selection, i.e., let $Y$ be the dependent variable, $X_i for i=1, 2, 3, \dots \dots \dots \dots , k$ be $k$ independent variables, ${\beta }_i for i=1, 2, 3, \dots \dots \dots \dots , k$ be $k$ respective regression coefficients, and $\epsilon$ be the random error. Then for the first two steps, the forward selection is used to select two variables, i.e., FS algorithm estimates $k$ linear regressions separately:

$$Y=X_i{\beta }_i+\epsilon \forall k=1, 2, 3, \dots \dots \dots \dots ,k$$

(12)

The independent variable having the minimum significant p-value or maximum significant t-stat is chosen as the valid first regressor. Then, this variable is retained in the model for the second-step selection procedure. In the second step, again $k-1$ separate linear regressions are estimated, and another most significant variable is chosen from remaining $k-1$ candidate variables as the second valid regressor. Then, backward elimination is run on these two selected valid regressors by FS to drop the variable, which is insignificant in the model if there is any. In the third step again, forward selection is used to select another valid variable if it is significant, and then again, backward elimination is used to drop the insignificant regressors. This process continues until all the candidate regressors are accounted for.

Stepwise with Backward Elimination

In this algorithm for the first two steps, backward elimination is used to drop the two most insignificant variables, and then in the forward selection is used to check whether the two dropped variables may or may not be included again. In the third step again, backward elimination is used to drop another most insignificant variable (if any), and then again forward selection is used. This process continues until a parsimonious model is obtained.

3.2.4. Unstructured Model Selection Procedures

These methods are generally known as Information Criteria in Statistics and Econometrics. These are no-parametric methods, which calculate the information lost by imposing penalties. The models having the minimum value of these information criteria are selected as the most plausible and parsimonious model. The general procedure of all these methods is the same; however, they differ in penalty. The general form is as follows:

$$IC=c·ln\left({\sigma }^2\right)+Penalty$$

(13)

where $c$ is a constant, ${\sigma }^2$ is the estimated error variance, and $Penalty$ is a function which differs with type.

In order to implement the information criteria for model selection, first, all possible models are estimated, and for each model, information criteria are calculated. Then, the model having the minimum information criteria is selected as the most plausible model. If there are $k$ candidate variables, then there will be $(2^k-1)$ possible models, and all these models are to be estimated. So, if there are a large number of candidate variables, say $k=15$, then there will be $(2^{15}-1=\mathrm{32,767})$ possible models to be estimated, which is a massive task. For all information criteria, let there be $k$ candidate variables; $l$ is the value of the log-likelihood function of the estimated model, $T$ is the total number of observations, and ${\sigma }^2$ is the estimated variance of the model. The five information criteria’s performance is assessed in this paper and their details are:

3.2.5. Akaike Information Criterion (AIC)

It was developed by (Akaike 1973a), and it is a measure of goodness of fit of the model. It is given as

$$AIC=ln\left({\sigma }^2\right)+2\left(k+1\right)/T$$

(14)

Its likelihood form is

$$AIC=-2l+2k$$

(15)

3.2.6. Akaike Information Criterion Corrected (AICC)

This criterion is a modification of AIC, modified by (Hurvich and Tsai 1989). It is given as

$$AICC=ln\left({\sigma }^2\right)+\left(T+k+1\right)/\left(T-k-3\right)$$

(16)

Its likelihood form is

$$AIC=-2\left(l/T\right)+2\left(k/T\right)$$

(17)

3.2.7. Bayesian Information Criterion (BIC)

BIC was developed by (Schwarz 1978), also known as Schwarz Information Criterion (SIC) in literature. Analytically, it is given as

$$BIC=ln\left({\sigma }^2\right)+\left(k+1\right)·ln\left(T\right)/T$$

(18)

Its likelihood form is

$$BIC=-2l+k·ln\left(T\right)$$

(19)

3.2.8. Bayesian Information Criterion Corrected (BICC)

BICC is a modification of BIC and modified by (McQuarrie and Tsai 1998). BICC is also known as Schwarz Information Criterion Corrected (SICC). It is given as

$$BICC=ln\left({\sigma }^2\right)+\left(k+1\right)·ln\left(T\right)/\left(T-k-3\right)$$

(20)

Its likelihood form is

$$BIC=-2\left(l/T\right)+k·ln\left(T\right)/T$$

(21)

3.2.9. Hannan-Quinn Information Criterion (HQC)

HQC was developed by (Hannan and Quinn 1979). It is given as

$$HQC=ln\left({\sigma }^2\right)+2k·ln\left(ln\left(T\right)\right)$$

(22)

Its likelihood form is

$$HQC=-2\left(l/T\right)+2k·ln\left(ln\left(T\right)\right)/T$$

(23)

3.3. Data Generating Process (DGP)

The ECM specified in Equation (1) has been used as DGP. However, $X$ is a single regressor in our DGP and being generated as a random walk without drift and trend. The performance of model selection procedures is free of nuisance parameters (a different set of values of nuisance parameters were taken, and it was observed that they do not affect the size or power), so their values are set to 1, i.e.,

$$c_0=c_1={\pi }_0={\pi }_1=\alpha =\beta =1$$

(24)

Under the null hypothesis of no cointegration, $\phi =0$ and under the alternative hypothesis of cointegration $\phi =\left\{0.005, 0.008, 0.011\right\}$ have been considered.

3.4. Basis of Monte Carlo Comparison

Eight model selection procedures have been compared on the basis of size and power using Monte Carlo simulations. The size and power are defined as

$$\begin{gathered} Size=Probability \left(Rejection of H_0/ H_0 is True\right) \\ Power=Probability \left(Rejection of H_0/ H_0 is False\right) \end{gathered}$$

(25)

50,000 simulation has been carried out for estimation of size and power.

3.5. Data Description and Source

In our empirical analysis, we used the data for BRICS (Brazil, Russia, India, China, and South Africa) member countries. We considered these countries because BRICS is one of the essential alliances of five nations, and these are five rapidly emerging economies representing four different continents (Lissovolik and Vinokurov 2019; Huang and Osborne 2017). Three pairs of variables have been considered to assess the cointegration among them, and these are {Energy Consumption (EC hereafter) and Gross Domestic Product (GDP hereafter)}, {Oil Price (OP hereafter) and GDP} and {Broad Money (BM hereafter) and GDP}. The annual data for three considered pairs of macroeconomic variables of BRICS member countries have been taken from WDI (World Bank’s online data source). The data covers the period from 1990 to 2017. Data of “GDP per Capita in current US$” for each of the BRICS members is taken as GDP for the first two pairs, and “GDP in Current Local Currency Unit (LCU)” has been taken as GDP for the third pair as BM is also in LCU. The data of “Energy use (kg of oil equivalent per capita)” has been taken as Energy Consumption (EC), and “Cushing, OK WTI Spot Price FOB (US$ per Barrel)” are taken as Oil Prices (OP).

4. Results and Discussion

To evaluate the relative performance of all eight model selection procedures, the findings of Monte Carlo experiments are discussed first and then the findings of real data are discussed.

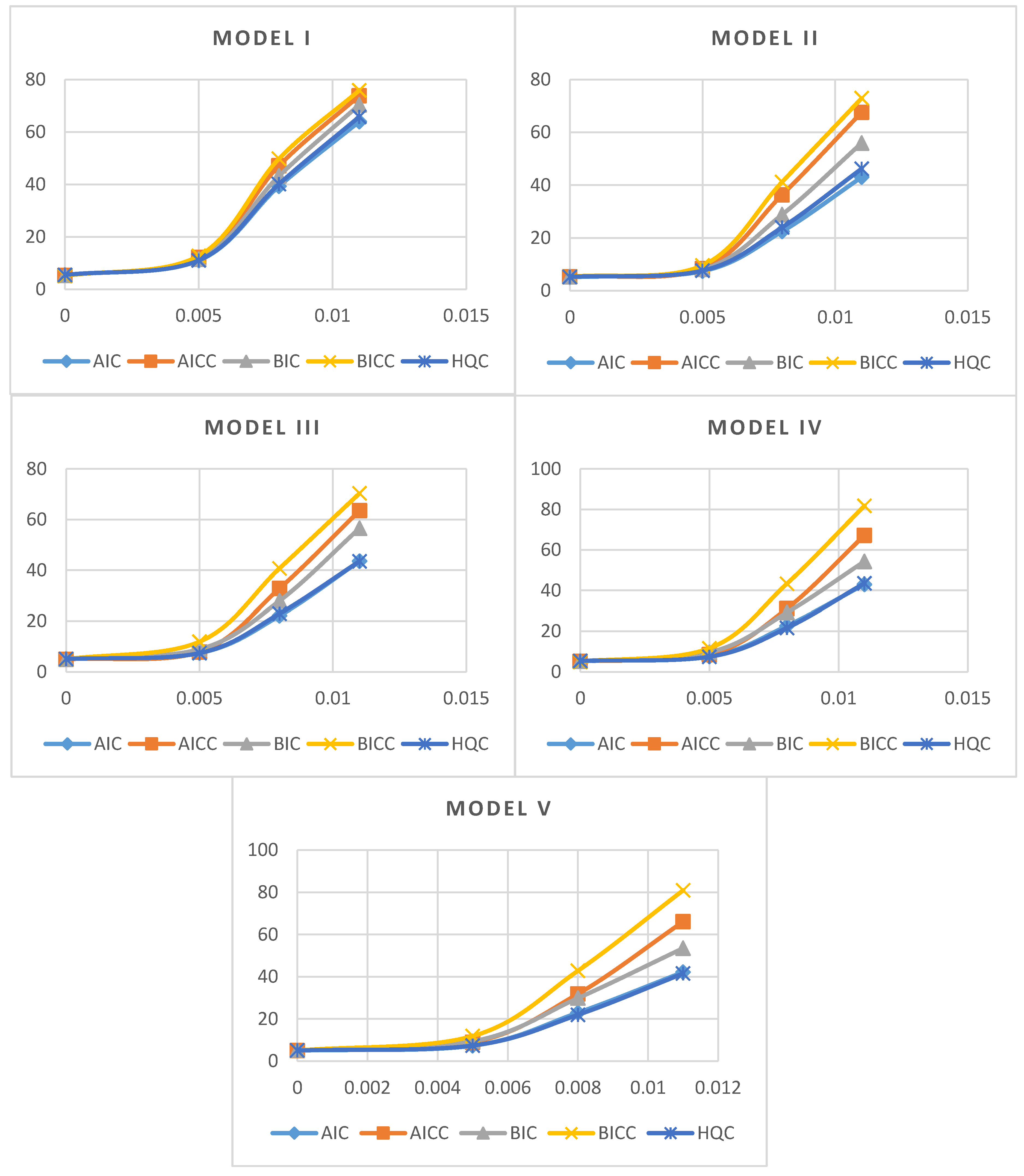
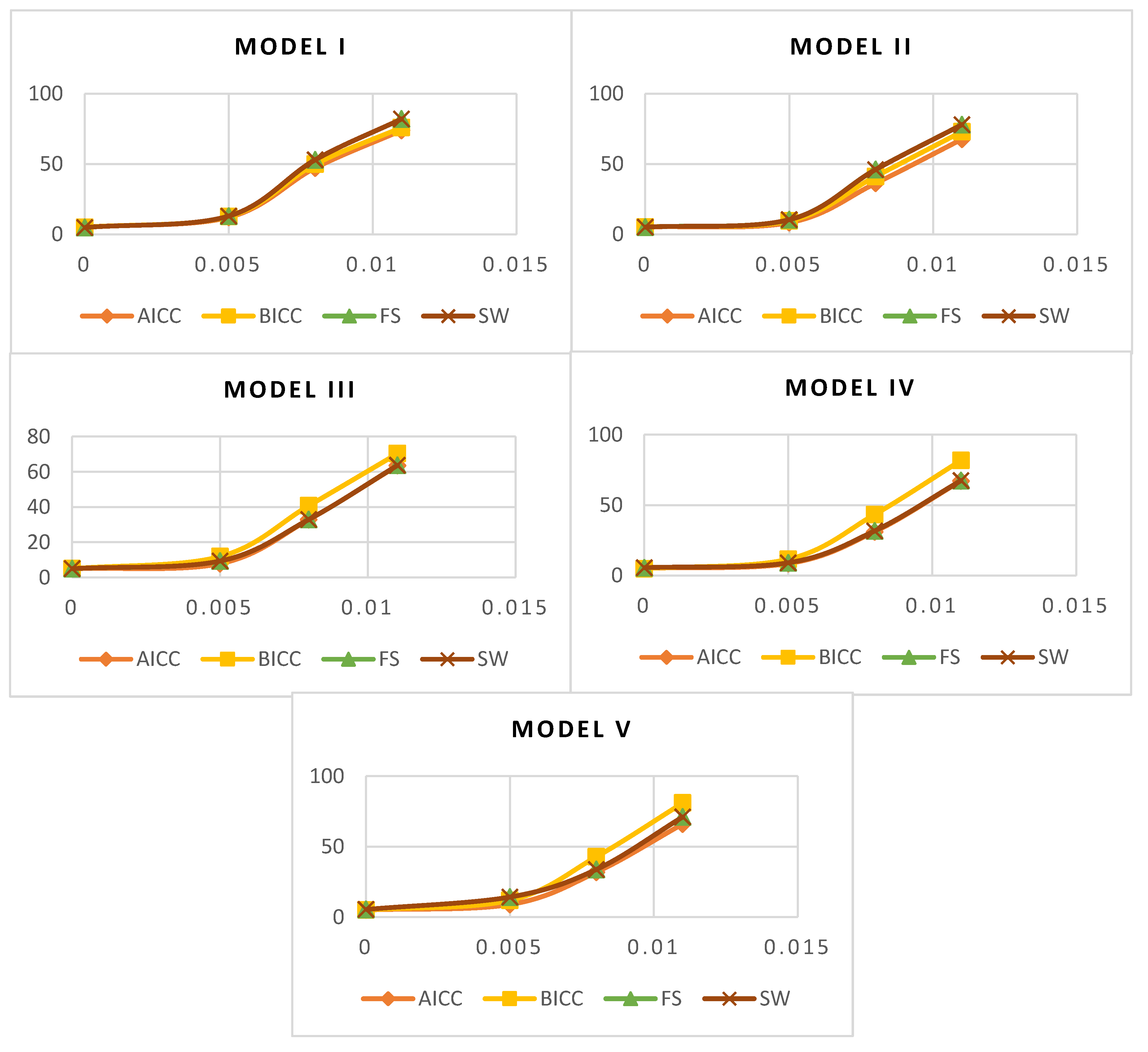
4.1. Theoretical Comparison

The size of the Auto-Regressive Distributed Lags (ARDL) Bounds test is assessed considering all five models at four different time dimensions of 25, 50, 100, and 200 using asymptotic critical values at a 5% level of significance as given in (Pesaran et al. 2001). These sizes are displayed in

Table A1. Size of Model Selection Procedures when Asymptotic Critical Values are used.

T	AIC	AICC	BIC	BICC	HQC	BW	FS	SW
Model I
25	30.25	21.29	25.92	17.2	29.43	21	13.84	13.84
50	12.76	11.71	10.39	9.81	11.62	9.85	8.96	8.96
100	8.56	8.45	7.67	7.61	8.04	6.88	6.74	6.74
200	6.41	6.33	5.93	5.91	6.14	5.86	5.85	5.85
Model II
25	47.01	30.1	41.29	24.63	46.39	34.01	19.72	19.72
50	19.4	16.66	14.42	12.68	17.05	13.84	11.65	11.65
100	10.54	10.21	8.42	8.22	9.3	8.5	8.12	8.12
200	7.67	7.57	6.55	6.51	7.01	6.47	6.4	6.4
Model III
25	39.84	25.31	35.1	20.82	39.33	29.05	16.45	16.45
50	17.27	15.21	12.97	11.52	15.45	12.29	10.42	10.43
100	10.31	9.92	8.4	8.2	9.2	8.22	7.81	7.81
200	7.42	7.29	6.6	6.59	6.85	6.14	6.12	6.12
Model IV
25	58.09	33.83	53.66	27.58	58.09	47.08	23.22	23.22
50	24.89	20.52	17.47	14.77	21.89	16.67	13.05	13.06
100	13.74	12.96	10.29	10.05	11.71	10.16	9.55	9.56
200	9.24	9.14	7.82	7.77	8.48	7.42	7.28	7.28
Model V
25	50.17	30.06	46.79	24.25	50.24	41.58	20.18	20.21
50	19.99	16.61	14.38	11.87	17.56	13.53	10.61	10.61
100	14.07	13.82	13.18	13.14	13.57	8.97	8.74	8.74
200	8.53	8.47	8.29	8.28	8.36	7.39	7.38	7.38

Note: Size is in % when the Nominal Size is 5%.

in the Appendix A. At the smallest time dimension/sample size of $T=25$, all model selection procedures have high size distortions as the empirical sizes are way higher than the assumed nominal size of 5%. However, when gradually the time dimension T is increased, the empirical size of each model selection procedure also improves, with varying convergence rates. FS, SW, BIC, and BICC have a better convergence rate than others.

To find the size-adjusted power, simulated critical values are obtained and are displayed in

Table A2. Simulated Critical Values.

T	Type of CV	AIC	AICC	BIC	BICC	HQC	BW	FS	SW
Model I
25	$\mathbf{UB}\mathbf{:}{\mathit{X}}_{\mathit{t}}\mathbf{~}\mathit{I}\mathbf{\left(}\mathbf{1}\mathbf{\right)}$	10.40	8.63	10.04	7.52	10.46	8.91	6.69	6.69
	$\mathbf{LB}\mathbf{:}{\mathit{X}}_{\mathit{t}}\mathbf{~}\mathit{I}\mathbf{\left(}\mathbf{0}\mathbf{\right)}$	8.54	7.02	8.32	6.12	8.61	7.39	5.34	5.34
50	$\mathbf{UB}\mathbf{:}{\mathit{X}}_{\mathit{t}}\mathbf{~}\mathit{I}\mathbf{\left(}\mathbf{1}\mathbf{\right)}$	5.98	5.76	5.38	5.20	5.78	5.24	4.99	4.99
	$\mathbf{LB}\mathbf{:}{\mathit{X}}_{\mathit{t}}\mathbf{~}\mathit{I}\mathbf{\left(}\mathbf{0}\mathbf{\right)}$	5.13	4.86	4.50	4.30	4.87	4.51	4.08	4.08
100	$\mathbf{UB}\mathbf{:}{\mathit{X}}_{\mathit{t}}\mathbf{~}\mathit{I}\mathbf{\left(}\mathbf{1}\mathbf{\right)}$	4.92	4.84	4.67	4.66	4.76	4.47	4.43	4.43
	$\mathbf{LB}\mathbf{:}{\mathit{X}}_{\mathit{t}}\mathbf{~}\mathit{I}\mathbf{\left(}\mathbf{0}\mathbf{\right)}$	4.29	4.21	3.80	3.78	4.01	3.94	3.72	3.72
200	$\mathbf{UB}\mathbf{:}{\mathit{X}}_{\mathit{t}}\mathbf{~}\mathit{I}\mathbf{\left(}\mathbf{1}\mathbf{\right)}$	4.41	4.41	4.30	4.29	4.32	4.29	4.28	4.28
	$\mathbf{LB}\mathbf{:}{\mathit{X}}_{\mathit{t}}\mathbf{~}\mathit{I}\mathbf{\left(}\mathbf{0}\mathbf{\right)}$	4.00	3.98	3.71	3.70	3.82	3.75	3.56	3.56
Model II
25	$\mathbf{UB}\mathbf{:}{\mathit{X}}_{\mathit{t}}\mathbf{~}\mathit{I}\mathbf{\left(}\mathbf{1}\mathbf{\right)}$	11.47	9.52	11.47	8.03	11.46	10.77	7.34	7.34
	$\mathbf{LB}\mathbf{:}{\mathit{X}}_{\mathit{t}}\mathbf{~}\mathit{I}\mathbf{\left(}\mathbf{0}\mathbf{\right)}$	9.50	7.68	9.54	6.55	9.56	8.53	6.01	6.01
50	$\mathbf{UB}\mathbf{:}{\mathit{X}}_{\mathit{t}}\mathbf{~}\mathit{I}\mathbf{\left(}\mathbf{1}\mathbf{\right)}$	6.42	6.14	5.80	5.51	6.17	5.81	5.39	5.40
	$\mathbf{LB}\mathbf{:}{\mathit{X}}_{\mathit{t}}\mathbf{~}\mathit{I}\mathbf{\left(}\mathbf{0}\mathbf{\right)}$	5.41	5.26	4.97	4.71	5.29	4.97	4.58	4.58
100	$\mathbf{UB}\mathbf{:}{\mathit{X}}_{\mathit{t}}\mathbf{~}\mathit{I}\mathbf{\left(}\mathbf{1}\mathbf{\right)}$	5.04	5.01	4.75	4.72	4.88	4.74	4.71	4.71
	$\mathbf{LB}\mathbf{:}{\mathit{X}}_{\mathit{t}}\mathbf{~}\mathit{I}\mathbf{\left(}\mathbf{0}\mathbf{\right)}$	4.61	4.55	4.24	4.22	4.44	4.21	4.05	4.05
200	$\mathbf{UB}\mathbf{:}{\mathit{X}}_{\mathit{t}}\mathbf{~}\mathit{I}\mathbf{\left(}\mathbf{1}\mathbf{\right)}$	4.63	4.61	4.46	4.45	4.51	4.42	4.40	4.40
	$\mathbf{LB}\mathbf{:}{\mathit{X}}_{\mathit{t}}\mathbf{~}\mathit{I}\mathbf{\left(}\mathbf{0}\mathbf{\right)}$	4.21	4.18	4.00	3.99	4.07	4.04	3.93	3.93
Model III
25	$\mathbf{UB}\mathbf{:}{\mathit{X}}_{\mathit{t}}\mathbf{~}\mathit{I}\mathbf{\left(}\mathbf{1}\mathbf{\right)}$	15.21	12.67	15.43	10.74	15.40	14.71	9.60	9.60
	$\mathbf{LB}\mathbf{:}{\mathit{X}}_{\mathit{t}}\mathbf{~}\mathit{I}\mathbf{\left(}\mathbf{0}\mathbf{\right)}$	12.36	9.81	12.42	8.63	12.48	11.49	7.66	7.66
50	$\mathbf{UB}\mathbf{:}{\mathit{X}}_{\mathit{t}}\mathbf{~}\mathit{I}\mathbf{\left(}\mathbf{1}\mathbf{\right)}$	8.75	8.34	7.85	7.44	8.40	7.68	7.19	7.19
	$\mathbf{LB}\mathbf{:}{\mathit{X}}_{\mathit{t}}\mathbf{~}\mathit{I}\mathbf{\left(}\mathbf{0}\mathbf{\right)}$	7.37	7.02	6.56	6.22	7.13	6.71	6.02	6.02
100	$\mathbf{UB}\mathbf{:}{\mathit{X}}_{\mathit{t}}\mathbf{~}\mathit{I}\mathbf{\left(}\mathbf{1}\mathbf{\right)}$	7.05	7.00	6.61	6.58	6.84	6.48	6.37	6.37
	$\mathbf{LB}\mathbf{:}{\mathit{X}}_{\mathit{t}}\mathbf{~}\mathit{I}\mathbf{\left(}\mathbf{0}\mathbf{\right)}$	6.21	6.17	5.80	5.77	6.01	5.77	5.48	5.48
200	$\mathbf{UB}\mathbf{:}{\mathit{X}}_{\mathit{t}}\mathbf{~}\mathit{I}\mathbf{\left(}\mathbf{1}\mathbf{\right)}$	6.40	6.39	6.19	6.18	6.27	6.12	6.12	6.12
	$\mathbf{LB}\mathbf{:}{\mathit{X}}_{\mathit{t}}\mathbf{~}\mathit{I}\mathbf{\left(}\mathbf{0}\mathbf{\right)}$	5.77	5.72	5.38	5.37	5.56	5.49	5.35	5.35
Model IV
25	$\mathbf{UB}\mathbf{:}{\mathit{X}}_{\mathit{t}}\mathbf{~}\mathit{I}\mathbf{\left(}\mathbf{1}\mathbf{\right)}$	15.13	12.38	15.64	10.35	15.32	15.07	9.56	9.56
	$\mathbf{LB}\mathbf{:}{\mathit{X}}_{\mathit{t}}\mathbf{~}\mathit{I}\mathbf{\left(}\mathbf{0}\mathbf{\right)}$	12.79	10.24	13.11	8.79	12.83	12.61	7.99	7.99
50	$\mathbf{UB}\mathbf{:}{\mathit{X}}_{\mathit{t}}\mathbf{~}\mathit{I}\mathbf{\left(}\mathbf{1}\mathbf{\right)}$	8.26	7.83	7.39	6.87	7.99	7.47	6.75	6.75
	$\mathbf{LB}\mathbf{:}{\mathit{X}}_{\mathit{t}}\mathbf{~}\mathit{I}\mathbf{\left(}\mathbf{0}\mathbf{\right)}$	6.97	6.66	6.37	5.99	6.75	6.57	5.94	5.94
100	$\mathbf{UB}\mathbf{:}{\mathit{X}}_{\mathit{t}}\mathbf{~}\mathit{I}\mathbf{\left(}\mathbf{1}\mathbf{\right)}$	6.54	6.46	6.04	5.99	6.29	6.03	5.92	5.92
	$\mathbf{LB}\mathbf{:}{\mathit{X}}_{\mathit{t}}\mathbf{~}\mathit{I}\mathbf{\left(}\mathbf{0}\mathbf{\right)}$	5.93	5.82	5.42	5.38	5.65	5.59	5.32	5.33
200	$\mathbf{UB}\mathbf{:}{\mathit{X}}_{\mathit{t}}\mathbf{~}\mathit{I}\mathbf{\left(}\mathbf{1}\mathbf{\right)}$	5.91	5.90	5.65	5.64	5.78	5.57	5.56	5.56
	$\mathbf{LB}\mathbf{:}{\mathit{X}}_{\mathit{t}}\mathbf{~}\mathit{I}\mathbf{\left(}\mathbf{0}\mathbf{\right)}$	5.45	5.44	5.20	5.18	5.33	5.21	5.09	5.09
Model V
25	$\mathbf{UB}\mathbf{:}{\mathit{X}}_{\mathit{t}}\mathbf{~}\mathit{I}\mathbf{\left(}\mathbf{1}\mathbf{\right)}$	20.41	16.87	21.13	14.02	20.65	20.64	12.85	12.86
	$\mathbf{LB}\mathbf{:}{\mathit{X}}_{\mathit{t}}\mathbf{~}\mathit{I}\mathbf{\left(}\mathbf{0}\mathbf{\right)}$	17.16	13.87	17.92	11.86	17.38	17.12	10.95	10.98
50	$\mathbf{UB}\mathbf{:}{\mathit{X}}_{\mathit{t}}\mathbf{~}\mathit{I}\mathbf{\left(}\mathbf{1}\mathbf{\right)}$	11.21	10.59	10.07	9.35	10.79	10.04	9.19	9.18
	$\mathbf{LB}\mathbf{:}{\mathit{X}}_{\mathit{t}}\mathbf{~}\mathit{I}\mathbf{\left(}\mathbf{0}\mathbf{\right)}$	9.69	9.16	8.71	8.18	9.32	8.83	7.93	7.93
100	$\mathbf{UB}\mathbf{:}{\mathit{X}}_{\mathit{t}}\mathbf{~}\mathit{I}\mathbf{\left(}\mathbf{1}\mathbf{\right)}$	7.03	6.90	6.48	6.43	6.74	6.35	6.22	6.22
	$\mathbf{LB}\mathbf{:}{\mathit{X}}_{\mathit{t}}\mathbf{~}\mathit{I}\mathbf{\left(}\mathbf{0}\mathbf{\right)}$	6.25	6.18	5.88	5.82	6.07	5.84	5.57	5.57
200	$\mathbf{UB}\mathbf{:}{\mathit{X}}_{\mathit{t}}\mathbf{~}\mathit{I}\mathbf{\left(}\mathbf{1}\mathbf{\right)}$	4.00	3.98	3.83	3.82	3.90	3.85	3.83	3.83
	$\mathbf{LB}\mathbf{:}{\mathit{X}}_{\mathit{t}}\mathbf{~}\mathit{I}\mathbf{\left(}\mathbf{0}\mathbf{\right)}$	4.34	4.31	3.88	3.87	4.01	4.02	3.77	3.77

in the Appendix A. All eight model selection procedures are evaluated based on their powers using these simulated critical values. To summarize, first, the information criteria are compared on the basis of powers, and it is found that AICC and BICC outperform the rest in a small sample size of $T=25$. However, as $T$ increases, all five information criteria tend to have the same powers. The power comparison of these five information criteria for $T=25$ are displayed in Figure A1 in Appendix A. For the rest of the time dimensions considered in this paper, i.e., $T=50, 100, \mathrm{and} 200$, all five information criteria have the same powers (see

Table A3. Powers in % of Information Criteria for T = 50, 100, and 200.

T = 50						T = 100					T = 200
Model I
Phi	AIC	AICC	BIC	BICC	HQC	AIC	AICC	BIC	BICC	HQC	AIC	AICC	BIC	BICC	HQC
0	5.55	5.43	5.44	5.35	5.35	4.63	4.82	4.45	4.46	4.61	4.63	4.82	4.45	4.46	4.61
0.005	27.14	28.01	28.83	29.35	27.92	48.83	49.4	49.99	49.98	49.8	48.83	49.4	49.99	49.98	49.8
0.008	68.77	69.93	71	71.48	69.93	84.55	84.75	84.87	84.87	84.81	84.55	84.75	84.87	84.87	84.81
0.011	89.19	89.98	90.69	91	89.99	95.34	95.38	95.55	95.54	95.44	95.34	95.38	95.55	95.54	95.44
Model II
0	5.03	4.96	4.98	5.08	5.02	5.13	4.96	4.86	4.86	4.97	5.13	4.96	4.86	4.86	4.97
0.005	20.87	22.08	22.82	23.05	22.04	43.64	43.77	44.58	44.77	44.28	43.64	43.77	44.58	44.77	44.28
0.008	62.04	63.91	65.3	66.06	63.82	81.53	81.76	82.13	82.27	82.05	81.53	81.76	82.13	82.27	82.05
0.011	85.54	87.19	87.94	88.49	87.12	94.86	94.93	95.14	95.15	95.09	94.86	94.93	95.14	95.15	95.09
Model III
0	4.89	4.71	5.03	5.09	4.79	5.15	4.99	5.05	4.95	5.01	5.15	4.99	5.05	4.95	5.01
0.005	20.25	22.17	23.14	23.98	22.19	42.56	42.89	43.42	45.39	42.48	42.56	42.89	43.42	45.39	42.48
0.008	61.26	62.08	64.13	65.03	62.16	80.14	80.32	81.07	83.14	80.72	80.14	80.32	81.07	83.14	80.72
0.011	84.57	86.61	86.93	87.43	86.56	93.92	94.03	94.62	96.59	93.13	93.92	94.03	94.62	96.59	93.13
Model IV
0	4.85	5.05	5.23	5.23	5.03	5.31	5.18	5.35	5.5	5.27	5.31	5.18	5.35	5.5	5.27
0.005	22.07	22.95	23.76	24.93	22.61	42.24	42.86	43.36	44.94	42.91	42.24	42.86	43.36	44.94	42.91
0.008	61.46	62.99	63.28	65.14	61.48	80.81	81.87	81.99	83.65	80.94	80.81	81.87	81.99	83.65	80.94
0.011	84.17	85.02	85.71	88.26	84.55	99.78	99.82	100	100	99.8	99.78	99.82	100	100	99.8
Model V
0	4.86	4.64	4.79	4.99	4.87	4.74	4.74	4.9	4.94	4.65	4.74	4.74	4.9	4.94	4.65
0.005	20.86	22.83	23.79	24.7	20.95	33.32	34.22	34.83	37.78	32.14	33.32	34.22	34.83	37.78	32.14
0.008	61.73	62.65	63.56	66.43	61.74	76.57	77.41	79.42	79.79	78.31	76.57	77.41	79.42	79.79	78.31
0.011	84.68	85.38	85.97	88.97	85.11	99.98	99.98	100	100	99.98	99.98	99.98	100	100	99.98

). Similarly, the three structured model selection procedures, i.e., BW, FS, and SW, were compared on the basis of their powers, and it was found that FS and SW are better as compared to the BW at the smallest time dimension of $T=25$. However, with the increase of $T$, the three structured procedures have the same powers. The power comparison for three structured procedures at $T=25$ are displayed in Figure A2 in the Appendix A. At other larger time dimensions, the three structured procedures have the same powers (see Appendix

Table A4. Powers in % of Structured Procedures for T = 50, 100, and 200.

T = 50				T = 100			T = 100
Model I
Phi	BW	FS	SW	BW	FS	SW	BW	FS	SW
0	4.76	4.81	4.81	4.92	5	5	4.89	4.9	4.9
0.005	29.26	29.86	29.87	51.09	51.3	51.3	72.31	72.31	72.31
0.008	72.52	73.27	73.27	85.14	85.23	85.23	93.88	93.85	93.85
0.011	90.67	91.1	91.1	95.83	95.88	95.88	98.57	98.57	98.57
Model II
0	4.75	4.75	4.75	4.95	4.9	4.9	4.55	4.66	4.66
0.005	21.77	23.14	23.12	44.8	44.77	44.77	68.14	68.26	68.26
0.008	66.76	67.79	67.79	82.75	82.74	82.74	92.63	92.67	92.67
0.011	88.9	89.47	89.47	95.04	95.05	95.05	98.43	98.43	98.43
Model III
0	5.59	5.61	5.61	5.33	5.34	5.34	4.57	4.47	4.47
0.005	22.89	23.28	23.28	43.51	43.54	43.54	65.36	65.46	65.46
0.008	65.03	66.91	66.92	81.06	81.22	81.22	81.79	81.86	81.86
0.011	85.35	87.57	87.57	94.13	94.43	94.43	96.54	96.54	96.54
Model IV
0	5.27	5.37	5.38	5.29	5.28	5.29	4.98	4.86	4.86
0.005	22.59	23.97	24	42.95	42.96	42.96	64.85	64.96	64.97
0.008	67.75	68.29	68.29	80.95	80.99	80.99	80.99	81.56	81.56
0.011	84.03	85.45	85.45	93.99	94.09	94.1	95.97	95.97	95.97
Model V
0	5.13	4.78	4.82	4.83	4.87	4.88	4.53	4.49	4.49
0.005	22.87	23.86	23.87	41.92	42.79	42.79	64.82	64.9	64.9
0.008	66.07	66.67	66.68	82.3	82.89	82.89	80.95	81.09	81.09
0.011	83.63	84.22	84.26	93.91	94.1	94.11	95.91	95.91	95.91

).

The two better-performing information criteria, i.e., AICC and BICC, are compared with two better-performing structured model selection procedures, i.e., FS and SW at T = 25, 50, 100, and 200. The comparison at T = 25 is displayed in Figure 1. However, for T >= 50, all these four procedures have approximately the same power. From Figure 1, it is clearly evident that for Models I and II, SW and FS have slightly higher powers than BICC and AICC. However, for Models III, IV, and V, BICC has higher powers than the rest of the three, and the rest of the three have the same powers. Even for these three models (III, IV, and V), the maximum gap is around 10% between the BICC’s power and the powers of the other three (AICC, SW, and FS).

4.2. Real Economic Applications

Coming to the real economic data application, we estimated the five error correction models, i.e., Model-1, Model-2, Model-3, Model-4, and Model-5, using the annual data of GDP1 and Energy Consumption (EC)2 of BRICS countries from 1990 to 2014. The eight model selection techniques have been used to select a plausible model with maximum lag length p = 2. The results are presented in

Table 1. Bounds Test Results for Energy Consumption and GDP.

Type of ECM	Model Selection Procedure
	AIC	AICC	BIC	BICC	HQC	FS	BW	SW
BRAZIL
Model-1	2.619	2.619	2.619	2.619	2.619	1.349	2.619	1.349
	(0.172)	(0.173)	(0.166)	(0.166)	(0.172)	(0.463)	(0.174)	(0.463)
Model-2	2.261	2.046	2.046	2.046	2.046	0.947	2.046	0.947
	(0.352)	(0.417)	(0.409)	(0.409)	(0.414)	(0.851)	(0.414)	(0.851)
Model-3	2.927	2.408	2.408	2.408	2.408	0.246	2.408	0.246
	(0.337)	(0.454)	(0.447)	(0.447)	(0.451)	(0.964)	(0.452)	(0.964)
Model-4	2.848	4.236	2.848	4.234	2.848	4.234	4.233	4.234
	(0.417)	(0.138)	(0.408)	(0.129)	(0.411)	(0.132)	(0.133)	(0.132)
Model-5	4.246	6.225	4.246	6.225	4.246	6.225	6.225	6.224
	(0.327)	(0.110)	(0.322)	(0.105)	(0.324)	(0.107)	(0.107)	(0.107)
RUSSIA
Model-1	1.735	1.735	1.735	0.478	1.735	0.478	0.478	0.478
	(0.351)	(0.350)	(0.346)	(0.796)	(0.345)	(0.7961)	(0.796)	(0.796)
Model-2	7.037 ***	6.116 ***	7.037 ***	6.116 ***	7.037 ***	6.1164 ***	7.037 ***	6.116 ***
	(0.002)	(0.006)	(0.001)	(0.007)	(0.002)	(0.007)	(0.002)	(0.007)
Model-3	10.546 ***	7.335 **	10.546 ***	7.335 **	10.546 ***	7.335 ***	10.546 ***	7.335 **
	(0.001)	(0.017)	(0.001)	(0.016)	(0.001)	(0.017)	(0.001)	(0.017)
Model-4	6.980 **	4.644	6.980 ***	4.644 *	6.980 ***	4.644 *	6.980 ***	4.644 *
	(0.011)	(0.102)	(0.009)	(0.096)	(0.009)	(0.099)	(0.009)	(0.099)
Model-5	10.454 ***	6.763 *	10.454 ***	6.763 *	10.454 ***	6.763 *	10.454 ***	6.763 *
	(0.010)	(0.082)	(0.007)	(0.077)	(0.008)	(0.077)	(0.01)	(0.077)
INDIA
Model-1	0.789	1.285	1.285	1.285	0.789	10.114 ***	10.114 ***	10.114 ***
	(0.668)	(0.484)	(0.477)	(0.477)	(0.664)	(0.000)	(0.000)	(0.000)
Model-2	1.182	0.817	0.817	0.817	1.182	6.51 4***	6.514 ***	6.514 ***
	(0.759)	(0.896)	(0.894)	(0.894)	(0.760)	(0.003)	(0.003)	(0.003)
Model-3	0.681	0.110	0.110	0.110	0.681	0.125	0.125	0.125
	(0.883)	(0.988)	(0.986)	(0.986)	(0.881)	(0.985)	(0.985)	(0.985)
Model-4	4.339	3.528	3.528	2.535	4.339	1.427	1.427	1.427
	(0.126)	(0.247)	(0.234)	(0.497)	(0.121)	(0.876)	(0.874)	(0.876)
Model-5	6.422	5.205	5.205	3.780	6.422 *	1.927	1.927	1.927
	(0.095)	(0.198)	(0.189)	(0.409)	(0.094)	(0.808)	(0.809)	(0.808)
CHINA
Model-1	1.236	1.372	1.236	1.372	1.236	1.372	1.372	1.372
	(0.503)	(0.461)	(0.493)	(0.451)	(0.497)	(0.457)	(0.458)	(0.457)
Model-2	6.999 ***	35.701 ***	19.89 ***	35.701 ***	8.546 ***	35.701 ***	35.678 ***	35.702 ***
	(0.002)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)
Model-3	8.726 ***	23.109 ***	18.453 ***	23.109 ***	10.97 ***	23.109 ***	17.830 ***	23.109 ***
	(0.005)	(0.000)	(0.000)	(0.000)	(0.001)	(0.000)	(0.000)	(0.000)
Model-4	19.618 ***	16.871 ***	19.618 ***	15.653 ***	19.618 ***	16.871 ***	16.871 ***	16.871 ***
	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)
Model-5	29.313 ***	25.264 ***	29.313 ***	23.099 ***	29.313 ***	25.264 ***	25.264 ***	25.264 ***
	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)
SOUTH AFRICA
Model-1	0.597	1.01	0.597	1.01	0.596	0.863	0.863	0.863
	(0.748)	(0.583)	(0.748)	(0.574)	(0.750)	(0.634)	(0.636)	(0.634)
Model-2	7.153 ***	7.153 ***	7.153 ***	7.153 ***	7.153 ***	1.415	7.153 ***	1.415
	(0.002)	(0.002)	(0.000)	(0.000)	(0.0018)	(0.662)	(0.002)	(0.662)
Model-3	9.131 ***	9.131 ***	9.131 ***	9.131 ***	9.131 ***	1.784	9.131 ***	1.784
	(0.004)	(0.004)	(0.004)	(0.004)	(0.004)	(0.601)	(0.004)	(0.601)
Model-4	3.855	5.815 **	3.855	2.012	3.855	3.215	3.855	3.215
	(0.188)	(0.032)	(0.178)	(0.686)	(0.182)	(0.301)	(0.182)	(0.301)
Model-5	5.551	7.932 **	5.551	3.017	5.551	4.734	5.551	4.734
	(0.163)	(0.043)	(0.155)	(0.575)	(0.156)	(0.247)	(0.158)	(0.247)

Note: ***, ** and * indicate the existence of cointegration at 1%, 5%, and 10% level of significance, respectively, p-values are given in parenthesis.

. It is apparent from the table that, for all five BRICS countries, if only first ECM (Model-1) is considered, then there is no significant evidence for the existence of cointegration using any of the model selection techniques except for India, where cointegration exists at the 1% level of significance only using the three single-path procedures, i.e., FS, BW, and SW. For the second ECM (Model-2), cointegration does not exist for Brazil using any of the model selection approaches. Similarly, for India, cointegration does not exist using any of the information criteria (AIC, AICC, BIC, BICC, and HQC). In the same manner, cointegration does not exist for South Africa using FS and SW. However, cointegration exists at the 1% level of significance for Russia and China using any model selection techniques. Similarly, cointegration exists at the 1% level of significance for South Africa using any of the model selection approaches except two, i.e., FS and SW. In the same manner, cointegration exists at the 1% level of significance for India, using only three structured model selection approaches, i.e., FS, BW, and SW.

For Model-3, there is no significant evidence about the existence of cointegration for Brazil and India using any of the model selection approaches. However, cointegration exists at the 1% level of significance for Russia and China using any of the model selection approaches. Similarly, for South Africa, cointegration exists at the 1% level of significance using any of the model selection techniques except two, i.e., FS and SW. When the fourth ECM (Model-4) is considered, then there is no evidence about the existence of cointegration for Brazil and India using any of the model selection procedures. Similarly, cointegration does not exist for South Africa using any of the model selection techniques except AICC. Cointegration exists for Russia and China using any of the model selection procedures. If the fifth ECM (Model-5) is assumed, then cointegration does not exist for Brazil and India using any of the model selection approaches. Similarly, cointegration does not exist for South Africa using any of the model selection procedures except AICC. However, cointegration exists for Russia and China using any of the model selection techniques. From the overall 25 cases (5 ECMs and 5 BRICS countries), cointegration is detected only 10 times when AIC is used. Similarly, cointegration is detected 11, 10, 10, 11, 10, 12, and 10 times when AICC, BIC, BICC, HQC, FS, BW, and SW are used, respectively.

As far as the cross-country comparison is concerned, for Brazil, there is no evidence of a long-run relationship between EC and GDP, irrespective of the model selection technique. However, the long-run relationship between the said macroeconomic variables exists for Russia, considering all models except Model-1. In the same manner, there is evidence of a long-run relationship between EC and GDP for India when Model-1 or Model-2 are considered, and structured model selection techniques are used. Coming to China, it is evident that there is a long-run relationship between EC and GDP for all models except Model-1. Finally, the long-run relationship between EC and GDP exists for South Africa when Model-2 and Model-3 are considered majorly.

For the detection of cointegration between Oil Prices (OP) and GDP, the five ECMs, i.e., Model 1, Model 2, Model 3, Model 4, and Model 5 have been estimated using the annual data of GDP3 and Oil Prices4 from 1990 to 2016 for all BRICS member countries by considering Oil Prices as an exogenous and GDP as an endogenous variable. The results are given in

Table 2. Bounds Test Results for Oil Prices and GDP.

Type of ECM	Model Selection Procedure
	AIC	AICC	BIC	BICC	HQC	FS	BW	SW
BRAZIL
Model-1	1.725	1.725	1.725	1.725	1.725	1.725	1.725	1.725
	(0.353)	(0.353)	(0.348)	(0.348)	(0.348)	(0.345)	(0.345)	(0.345)
Model-2	1.09	1.09	1.09	1.09	1.09	1.09	1.09	1.09
	(0.798)	(0.799)	(0.796)	(0.796)	(0.800)	(0.800)	(0.800)	(0.800)
Model-3	1.634	1.634	1.634	1.634	1.634	1.634	1.634	1.634
	(0.642)	(0.643)	(0.633)	(0.633)	(0.635)	(0.636)	(0.636)	(0.636)
Model-4	1.545	1.545	1.545	1.545	1.545	1.545	1.545	1.545
	(0.849)	(0.848)	(0.845)	(0.845)	(0.846)	(0.846)	(0.845)	(0.846)
Model-5	1.605	1.605	1.605	1.605	1.605	1.605	1.605	1.605
	(0.868)	(0.868)	(0.864)	(0.864)	(0.864)	(0.864)	(0.865)	(0.864)
RUSSIA
Model-1	1.916	0.737	0.737	0.737	1.916	0.737	0.737	0.737
	(0.309)	(0.691)	(0.688)	(0.687)	(0.310)	(0.689)	(0.691)	(0.689)
Model-2	2.028	5.840 ***	5.840 ***	5.840 ***	5.840 ***	5.840 ***	5.840 ***	5.840 ***
	(0.423)	(0.009)	(0.008)	(0.008)	(0.008)	(0.008)	(0.008)	(0.008)
Model-3	3.026	8.253 ***	8.253 ***	8.253 ***	8.253 ***	8.253 ***	8.253 ***	8.253 ***
	(0.321)	(0.008)	(0.007)	(0.007)	(0.008)	(0.007)	(0.008)	(0.007)
Model-4	2.110	5.247 *	5.247 *	5.247 *	2.110	5.247 *	5.247 *	5.247 *
	(0.661)	(0.06)	(0.052)	(0.052)	(0.652)	(0.056)	(0.056)	(0.056)
Model-5	2.209	6.754 *	6.754 *	6.754 *	2.209	6.754 *	6.754 *	6.754 *
	(0.754)	(0.083)	(0.077)	(0.077)	(0.753)	(0.078)	(0.079)	(0.078)
INDIA
Model-1	13.106 ***	13.106 ***	13.106 ***	13.106 ***	13.106 ***	16.131 ***	16.131 ***	16.131 ***
	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)
Model-2	12.867 ***	13.045 ***	13.98 ***	13.045 ***	13.98 ***	10.985 ***	10.985 ***	10.985 ***
	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)
Model-3	3.063	1.885	2.833	1.885	2.833	0.418	0.418	0.418
	(0.316)	(0.577)	(0.353)	(0.574)	(0.3537)	(0.936)	(0.937)	(0.936)
Model-4	4.553	3.302	4.469	2.327	4.552	1.190	1.190	1.190
	(0.1077)	(0.292)	(0.109)	(0.565)	(0.105)	(0.935)	(0.936)	(0.935)
Model-5	6.820 *	4.874	6.621 *	3.490	6.820 *	1.782	1.782	1.782
	(0.080)	(0.233)	(0.083)	(0.469)	(0.075)	(0.834)	(0.835)	(0.8340)
CHINA
Model-1	0.916	1.417	0.916	1.417	0.916	1.417	1.417	1.417
	(0.62)	(0.446)	(0.614)	(0.437)	(0.615)	(0.443)	(0.443)	(0.443)
Model-2	48.58 ***	48.024 ***	48.04 ***	108.765 ***	48.024 ***	48.024 ***	48.024 ***	48.024 ***
	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)
Model-3	41.635 ***	40.717 ***	40.717 ***	23.929 ***	40.717 ***	40.717 ***	40.718 ***	40.718 ***
	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)
Model-4	28.219 ***	20.553 ***	28.219 ***	16.195 ***	28.219 ***	2.189	25.504 ***	2.189
	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.626)	(0.000)	(0.626)
Model-5	41.975 ***	30.798 ***	41.975 ***	24.279 ***	41.975 ***	3.21	38.204 ***	3.21
	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.54)	(0.000)	(0.54)
SOUTH AFRICA
Model-1	0.884	1.405	0.884	0.411	0.884	0.769	1.405	0.77
	(0.632)	(0.449)	(0.625)	(0.829)	(0.629)	(0.673)	(0.447)	(0.673)
Model-2	11.656 ***	10.417 ***	11.656 ***	1.521	11.656 ***	1.521	10.909 ***	1.521
	(0.000)	(0.000)	(0.000)	(0.617)	(0.000)	(0.615)	(0.000)	(0.615)
Model-3	17.117 ***	14.937 ***	17.118 ***	1.821	17.117 ***	1.821	16.283 ***	1.821
	(0.000)	(0.000)	(0.000)	(0.589)	(0.000)	(0.590)	(0.000)	(0.590)
Model-4	10.384 ***	5.174 *	10.745 ***	1.661	10.384 ***	1.661	10.745 ***	1.661
	(0.0003)	(0.064)	(0.000)	(0.810)	(0.000)	(0.811)	(0.000)	(0.811)
Model-5	15.383 ***	7.503 *	15.301 ***	2.378	15.383 ***	2.378	15.301 ***	2.378
	(0.000)	(0.053)	(0.000)	(0.716)	(0.000)	(0.716)	(0.000)	(0.716)

Note: *** and * indicate the existence of cointegration at 1%, 5%, and 10% level of significance, respectively. p-values are given in parenthesis.

. For the first ECM (Model 1), cointegration does not exist between Oil Prices and GDP for Brazil, Russia, China, and South Africa using any of the model selection procedures. However, cointegration exists between Oil Prices and GDP for India using any of the model selection approaches. When the second ECM, i.e., Model 2, is considered, then only for Brazil cointegration does not exist using any of the model selection techniques. From the rest of the four countries, cointegration exists for India and China using any of the model selection procedures. For Russia, cointegration exists using any of the model selection approaches except AIC. Similarly, for South Africa, cointegration exists using any of the model selection approaches except BIC, FS, and SW.

If the third ECM, i.e., Model 3, is assumed, then cointegration does not exist for Brazil and India using any of the model selection techniques. However, cointegration exists for China using any of the model selection techniques. For Russia, cointegration exists using any of the model selection approaches except AIC. Similarly, for South Africa, cointegration exists using any of the model selection procedures except BICC, FS, and SW. In the same manner, when the fourth ECM, i.e., Model 4, is considered, then cointegration does not exist for Brazil and India using any of the model selection techniques. Cointegration exists at the 1% level of significance for China using any of the model selection procedures except two, i.e., FS and SW. Similarly, for Russia, cointegration is detected at the 10% level of significance using six model selection techniques (AICC, BIC, BICC, FS, BW, and SW) and using the rest of two (AIC and HQC), cointegration is not detected. Similarly, for South Africa, there is evidence about the existence of cointegration using any of the model selection techniques except three, i.e., BICC, FS, and SW.

When the fifth ECM, i.e., Model 5, is assumed, then for only Brazil, cointegration does not exist using any of the model selection procedures. Similarly, cointegration does not exist for India using five model selection techniques (AICC, BICC, FS, BW, and SW) and using the rest of three (AIC, BIC, and HQC) cointegration exists. However, cointegration between oil prices and GDP exists at the 1% level of significance for China using any of the model selection approaches except two, i.e., FS and SW. In the same manner, cointegration exists at the 10% level of significance for Russia using any of the model selection procedures except two, i.e., AIC and HQC. Similarly, cointegration between oil prices and GDP exists for South Africa using any of the model selection approaches except three, i.e., BICC, FS, and SW. From the overall 25 cases (5 ECMs and 5 BRICS countries), cointegration between oil price and GDP is detected 11 times using AIC as a model selection technique. Similarly, cointegration is detected 14, 15, 10, 13, 8, 14, and 8 times using AICC, BIC, BICC, HQC, FS, BW, and SW as the model selection techniques, respectively.

Coming to cross-country comparison, there is no evidence of the long-run relationship between OP and GDP for Brazil, positive evidence for Russia when mainly Model-2 and Model-3 are considered, positive evidence for India when majorly Model-1 and Model-2 are considered, strong evidence for China when all models are considered except Model-1 and strong evidence for South Africa considering all models except Model-1.

For the detection of cointegration between Broad Money (BM) and GDP by Bounds test for all five BRICS member countries, the five Error Correction Models (ECMs), i.e., Model 1, Model 2, Model 3, Model 4, and Model 5 have been estimated considering Broad Money as exogenous and GDP as an endogenous variable. The annual data of Broad Money5 and GDP6 from 1993 to 2015 have been used for this purpose. The results are given in

Table 3. Bounds Test Results for Broad Money and GDP.

Type of ECM	Model Selection Procedures
	AIC	AICC	BIC	BICC	HQC	FS	BW	SW
BRAZIL
Model-1	1.221 ***	104.171 ***	0.63	104.171 ***	1.221	92.133 ***	104.171 ***	92.133 ***
	(0.508)	(0.000)	(0.734)	(0.000)	(0.503)	(0.000)	(0.000)	(0.000)
Model-2	9.156 ***	20.129 ***	20.129 ***	20.129 ***	9.156 ***	20.129 ***	20.129 ***	20.129 ***
	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)
Model-3	10.117 ***	13.052 ***	13.052 ***	13.052 ***	10.117 ***	13.052 ***	13.052 ***	13.052 ***
	(0.001)	(0.000)	(0.000)	(0.000)	(0.001)	(0.000)	(0.000)	(0.000)
Model-4	5.930 **	9.151 ***	6.084 **	9.151 ***	6.084 ***	9.151	5.895 **	9.151
	(0.03)	(0.001)	(0.021)	(0.001)	(0.022)	(0.001)	(0.028)	(0.001)
Model-5	8.889 **	13.719 **	9.113 **	13.719 ***	9.113 **	13.719 ***	8.450 **	13.719 ***
	(0.023)	(0.001)	(0.018)	(0.001)	(0.019)	(0.001)	(0.028)	(0.001)
RUSSIA
Model-1	9.457 ***	9.457 ***	9.457 ***	9.457 ***	9.457 ***	1.450	9.457 ***	1.450
	(0.001)	(0.001)	(0.000)	(0.000)	(0.001)	(0.433)	(0.001)	(0.433)
Model-2	16.706 ***	22.609 ***	16.706 ***	50.177 ***	16.706 ***	50.177 ***	22.884 ***	50.177 ***
	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)
Model-3	25.06 ***	32.784 ***	25.06 ***	56.533 ***	25.06 ***	56.533 ***	32.650 ***	56.533 ***
	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)
Model-4	21.124 ***	45.165 ***	52.81 ***	47.882 ***	55.647 ***	45.165 ***	52.809 ***	45.165 ***
	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)
Model-5	7.328 *	13.834 ***	17.221 ***	14.844 ***	18.021 ***	13.834 ***	17.221 ***	13.834 ***
	(0.061)	(0.001)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.001)
INDIA
Model-1	1.457	5.965 ***	5.965 ***	5.965 ***	5.965 ***	5.965 ***	1.682	5.965 ***
	(0.434)	(0.009)	(0.007)	(0.007)	(0.008)	(0.008)	(0.364)	(0.008)
Model-2	4.619 **	3.427	5.468 **	3.427	4.619 **	3.427	3.427	3.427
	(0.032)	(0.126)	(0.014)	(0.115)	(0.033)	(0.119)	(0.12)	(0.119)
Model-3	6.907 **	3.057	7.163 **	3.057	6.907 **	3.057	3.057	3.057
	(0.020)	(0.316)	(0.017)	(0.307)	(0.02)	(0.311)	(0.313)	(0.311)
Model-4	6.316 **	1.915	6.316 **	1.915	6.316 **	1.915	5.000 *	1.915
	(0.020)	(0.733)	(0.016)	(0.728)	(0.017)	(0.732)	(0.076)	(0.732)
Model-5	8.793 **	2.872	8.793 **	2.872	8.793 **	2.872	6.412 *	2.872
	(0.025)	(0.614)	(0.022)	(0.605)	(0.023)	(0.610)	(0.097)	(0.610)
CHINA
Model-1	0.126	1.443	0.125	1.443	0.126	1.443	0.175	1.443
	(0.949)	(0.438)	(0.950)	(0.430)	(0.949)	(0.434)	(0.926)	(0.434)
Model-2	5.332 **	23.521 ***	23.521 ***	23.521 ***	23.521 ***	23.521 ***	23.521 ***	23.521 ***
	(0.015)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)
Model-3	5.629 *	32.121 ***	32.12 ***	32.121 ***	32.121 ***	32.121 ***	32.121 ***	32.121 ***
	(0.049)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)
Model-4	9.676 ***	20.572 ***	9.676 ***	20.572 ***	9.676 ***	20.572 ***	9.676 ***	20.572 ***
	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)
Model-5	14.498 ***	30.725 ***	14.498	30.725 ***	14.498 ***	30.725 ***	14.498 ***	30.725 ***
	(0.000)	(0.000)	(0.0003) ***	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)
SOUTH AFRICA
Model-1	16.257 ***	16.257 ***	16.257 ***	16.257 ***	16.257 ***	16.257 ***	16.257 ***	16.257 ***
	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)
Model-2	17.830 ***	17.651 ***	17.651 ***	17.651 ***	17.830 ***	13.836 ***	17.651 ***	13.836 ***
	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)
Model-3	11.63 ***	11.657 ***	11.657 ***	11.657 ***	11.63 ***	1.555	11.657 ***	1.555
	(0.001)	(0.001)	(0.000)	(0.000)	(0.000)	(0.658)	(0.001)	(0.658)
Model-4	7.053 **	2.284	7.222 ***	2.284	7.222 ***	2.284	7.222 ***	2.284
	(0.011)	(0.591)	(0.006)	(0.579)	(0.007)	(0.583)	(0.007)	(0.583)
Model-5	9.555 **	2.807	9.608 **	2.807	9.608 **	2.807	9.608 **	2.807
	(0.017)	(0.628)	(0.013)	(0.617)	(0.014)	(0.620)	(0.015)	(0.620)

Note: ***, ** and * indicate the existence of cointegration at 1%, 5%, and 10% level of significance, respectively. p-values are given in parenthesis.

. When the first ECM, i.e., Model 1, is assumed and estimated, then cointegration does not exist using any of the model selection procedures for China. However, cointegration is detected at the 1% level of significance using any of the model selection procedures for South Africa. Similarly, cointegration exists using any of the model selection approaches except two, i.e., FS, and SW for Russia. In the same manner, there is evidence of cointegration at the 1% level of significance for India using any of the model selection methods except two, i.e., AIC and BW. Continuingly, there is evidence about the existence of cointegration at the 1% level of significance for Brazil using only five model selection methods, and these five are AICC, BICC, FS, BW, and SW.

If the second ECM (Model 2) is considered and estimated for the detection of cointegration, then there is evidence about existence of cointegration at the 1% level of significance for Brazil, Russia, China, and South Africa using any of the model selection procedures. However, cointegration is detected at the 5% level of significance for India using only three model selection methods, and these are AIC, BIC, and HQC. When the third ECM, i.e., Model 3, is estimated for the detection of cointegration, then there is evidence about the existence of cointegration at the 1% level of significance for Brazil, Russia, and China using any of the model selection methods. However, for India, cointegration at the 5% level of significance is detected using only three model selection approaches, and these three are AIC, BIC, and HQC. Similarly, for South Africa, detection of cointegration is possible when six model selection methods are used and these six are AIC, AICC, BIC, BICC, HQC, and BW. If the fourth ECM (Model 4) is considered for the detection of cointegration between them, there is evidence about the existence of cointegration for Brazil, Russia, and China. Similarly, cointegration exists for India using only four model selection methods, and these four are AIC, BIC, HQC, and BW. In the same manner, when these same four model selection methods are used for the detection of cointegration in the case of South Africa, then there is evidence about the existence of cointegration.

If the fifth ECM (Model 5) is estimated for detection of cointegration, then cointegration exists for Brazil, Russia, and China using any of the model selection methods. Continuingly, for India only, the use of four model selection methods results in the existence of cointegration and these four are AIC, BIC, HQC, and BW. Similar is the case of South Africa, where use of the same four model selection techniques (AIC, BIC, HQC, and BW) results in the existence of cointegration. From the overall 25 (5 ECMS and 5 BRICS member countries) cases, 22 times cointegration has been detected when AIC is used as the model selection method. Similarly, cointegration has been detected 18, 23, 18, 23, 16, 21, and 16 times using AICC, BIC, BICC, HQC, FS, BW, and SW as the model selection methods, respectively.

The long-run relationship between BM and GDP has significant evidence of its existence for Brazil, Russia, and South Africa irrespective of any of the five models considered, for India when Model-1 is considered only and for China when all models are considered except Model-1.

5. Conclusions and Recommendations

This paper aimed to find a better model selection technique and to assess the performance of eight different model selection techniques for Bounds test of cointegration by comparing the performance of these eight model selection techniques. Furthermore, it is also aimed to compare the structured model selection procedures with unstructured, i.e., information criteria. Moreover, it was also investigated how these information criteria are behaving for real data, i.e., whether they behave similar to the unstructured ones or differently.

The Monte Carlo experiment suggests and concludes that, for a small sample size of 25, these are performing slightly different. However, for moderate and large sample sizes, they behave the same. These results and conclusions are partially in line with (Castle et al. 2011; Rashid 2014). The difference in the result is due to the model as, in the current study, error correction model is considered which has not been explored and considered earlier for assessing model selection procedures. From the results of real data analysis using three pairs of macroeconomic variables for BRICS member countries, the first pair is of Energy Consumption and GDP, and for this pair nearly all model selection procedures have the same behavior when they are used in the Bounds test to detect the cointegration between Energy Consumption and GDP. However, three model selection approaches, two are the information criteria, i.e., Akaike Information Criterion Corrected (AICC) and Bayesian Information Criterion (BIC) and one is the structured single-path model selection approach, i.e., Backward Elimination (BW), have the most common behavior than the rest. Similarly, for the detection of cointegration between Oil Price and GDP, three model selection procedures have the same behavior when these are used in the Bounds test for model selection. From these three similarly behaving model selection techniques, two are information criteria, i.e., Akaike Information Criterion Corrected (AICC) and Bayesian Information Criterion (BIC), and one is the structured single-path model selection approach, i.e., Backward Elimination (BW). Continuingly, for the testing of existence of cointegration between Broad Money and GDP, the behavior of three model selection information criteria, i.e., Akaike Information Criterion (AIC), Bayesian Information Criterion (BIC), and Hannan and Quinn Information Criterion (HQC), is the same. However, for the same pair, the Backward Elimination (BW) procedure of model selection also behaves similar to the three.

Carrying out the cross-country comparison, it is concluded that strong and compelling evidence of a long-run relationship between EC and GDP exists only for the two large economies from BRICS, i.e., Russia and China. For India and South Africa, there is evidence in favor of and against a long-run relationship between EC and GDP. Strong and compelling evidence is found that there is no long-run relationship between EC and GDP for Brazil. The same is the case for the pair of OP and GDP, with one exception that now strong evidence is also found for South Africa. However, for the last pair of BM and GDP, except India, all five economies of BRICS have strong evidence of level relationship.

In the light of the above conclusions, it is concluded that, in general, information criteria and structured model selection procedures have the same behavior and they select the same model for the Bounds cointegration test. However, as structured model selection procedures are strongly supported by econometric theory, so they may be preferred over the unstructured ones, i.e., information criteria. This is due to the fact that, in testing of cointegration using Bounds test, the problem is model selection, not lag selection, because the same test equation will act as an error correction model if cointegration is found and will be used for policy implications. Furthermore, the structured model selection procedures may be preferred greatly in dealing with a large number of candidate variables due to their quick and easy calculation.

The current study has certain limitations in terms of data availability as it has time series of length less than 30. Furthermore, it also does not account for model validation using residual diagnostics and stability testing, because the model selection procedures compared here in the study do not consider model validation. Therefore, it will be a worthy investigation in the future as to how the model procedures with model validation (like Autometrics) are performing and also how the performance of these procedures change when there is enough length of time series.