How Does a Policymaker Rank Regional Income Distributions across Years? A Study on the Evolution of Greek Regional per Capita Income
Abstract
1. Introduction
2. Methodology
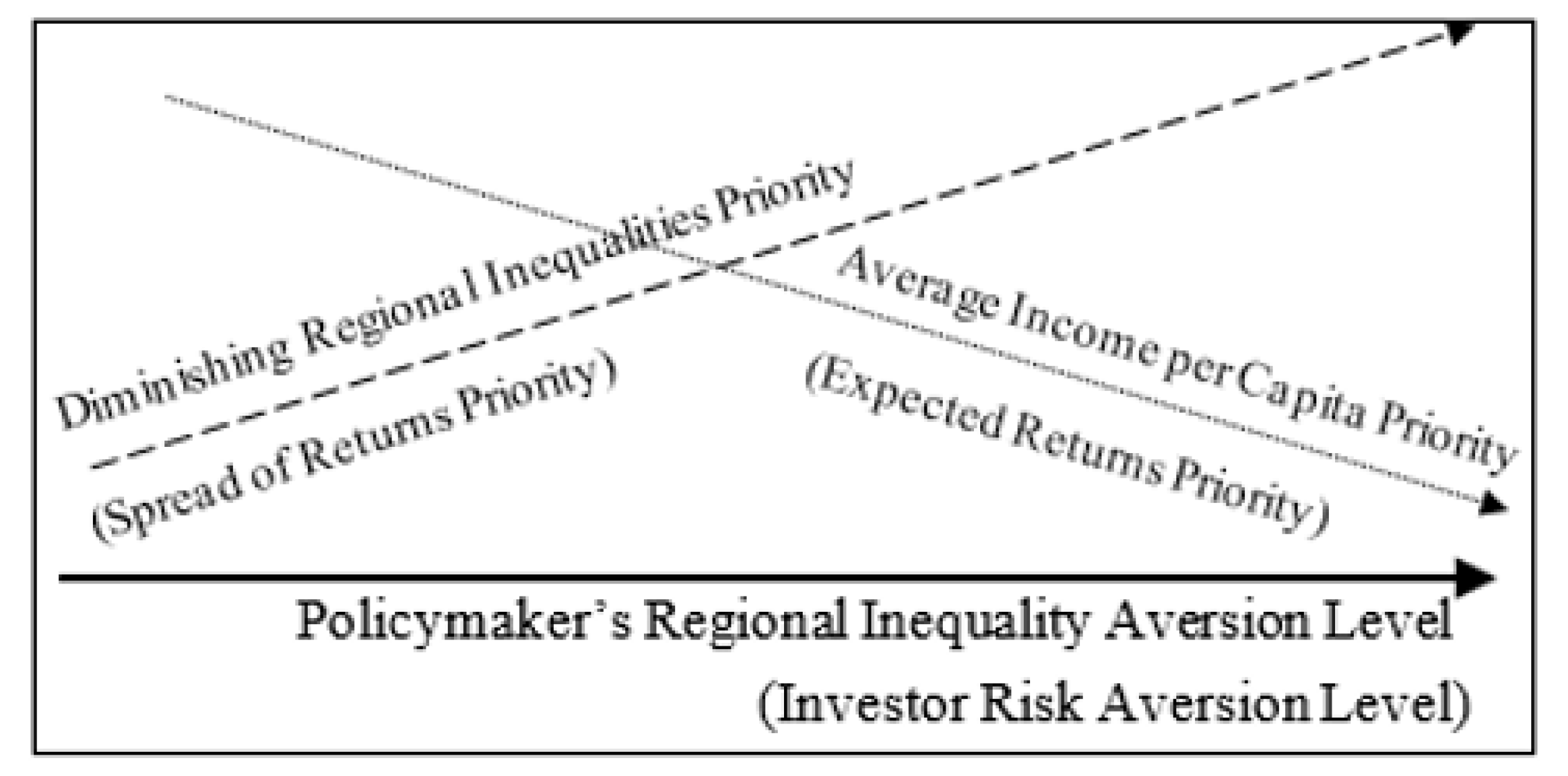
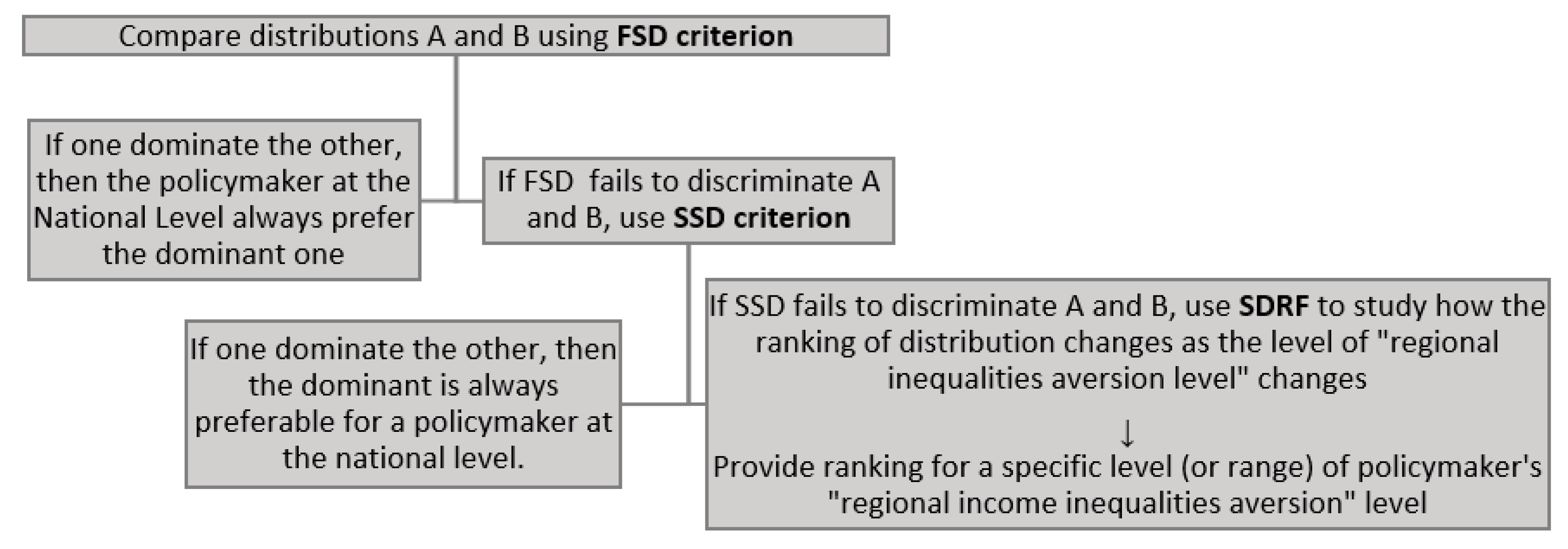
Stochastic Dominance Analysis
- High expected returns to low expected returns and;
- Low spread of returns to high spread. Analogously, a policymaker prefers:
- High average regional income per capita to low average income per capita and;
- Low level of dispersion (which coincides with diminishing regional inequalities) to a high level of dispersion (which coincides with increasing regional inequalities).
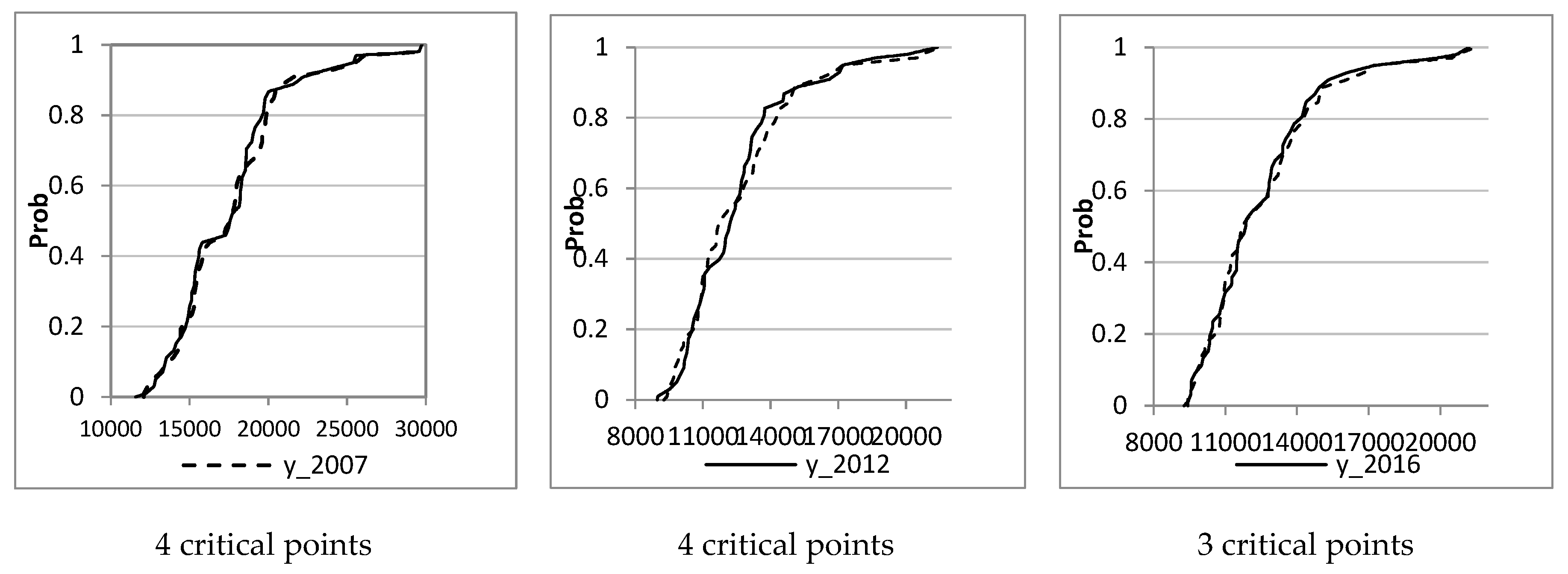
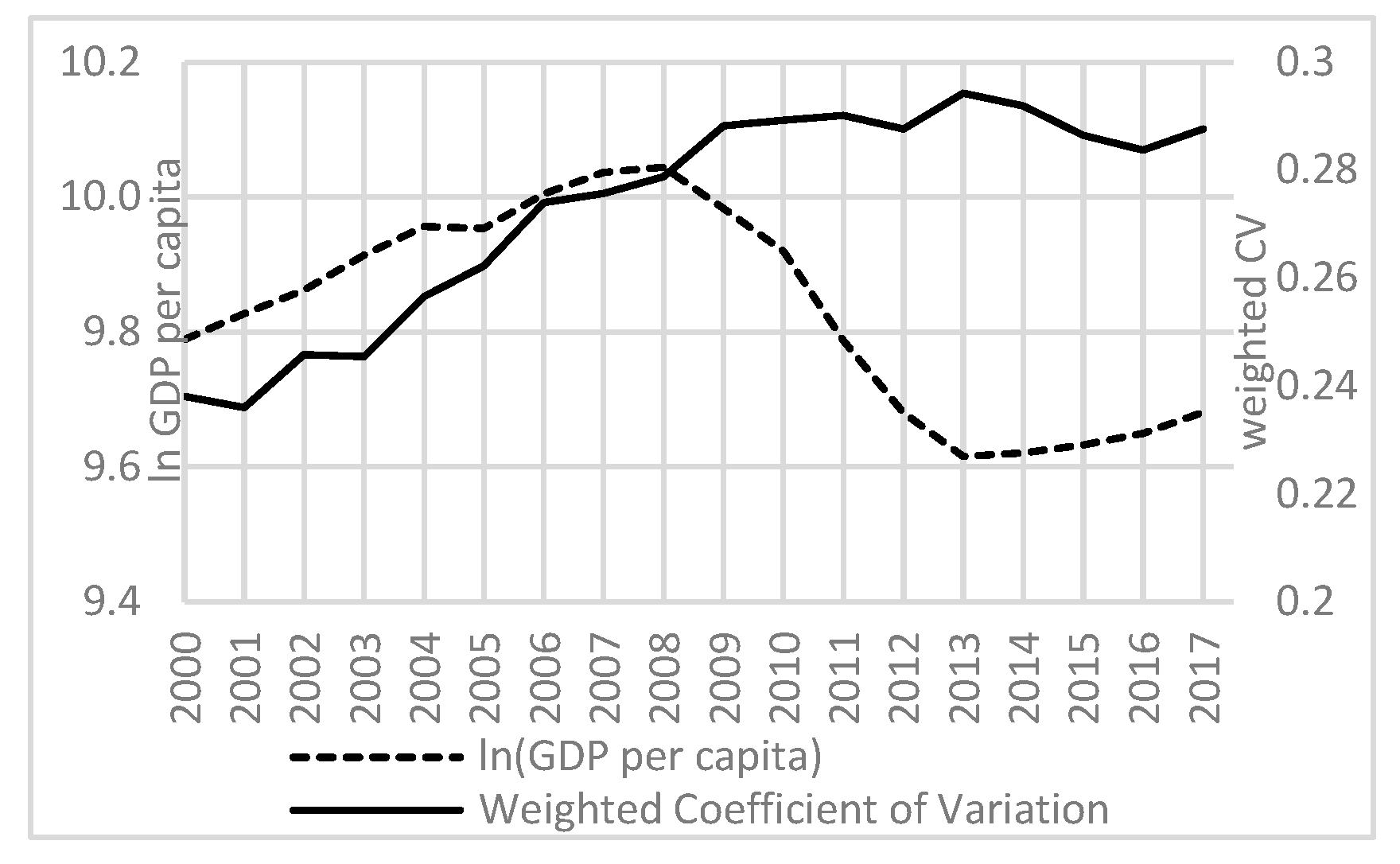
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Anderson, Gordon. 2004. Making Inferences about the Polarization, Welfare and Poverty of Nations: A Study of 101 Countries 1970–1995. Journal of Applied Econometrics 19: 537–50. [Google Scholar] [CrossRef]
- Anderson, Gordon, and Ying Ge. 2009. InterCity Income Inequality, Growth and Convergence in China. Journal of Income Distribution 18: 70–89. [Google Scholar]
- Angrist, Joshua D., and Jörn Steffen Pischke. 2008. Mostly Harmless Econometrics: An Empiricist’s Companion. In Mostly Harmless Econometrics: An Empiricist’s Companion. Princeton: Princeton University Press. [Google Scholar]
- Barro, Robert J., Xavier Sala-I-Martin, Olivier Jean Blanchard, and Robert E. Hall. 1991. Convergence Across States and Regions. Brookings Papers on Economic Activity 1991: 107–82. [Google Scholar] [CrossRef]
- Bishop, John A., John P. Formby, and Paul D. Thistle. 1991. Rank Dominance and International Comparisons of Income Distributions. European Economic Review 35: 1399–409. [Google Scholar] [CrossRef]
- Carrington, Anca. 2006. Regional Convergence in the European Union: A Stochastic Dominance Approach. International Regional Science Review 29: 64–80. [Google Scholar] [CrossRef]
- Christofakis, Manolis, Eleni Gaki, and Dimitrios Lagos. 2019. Τhe Impact of Economic Crisis on Regional Disparities and the Allocation of Economic Branches in Greek Regions. Bulletin of Geography 44: 7–21. [Google Scholar]
- Coes, Donald V. 2008. Income Distribution Trends in Brazil and China: Evaluating Absolute and Relative Economic Growth. Quarterly Review of Economics and Finance 48: 359–69. [Google Scholar] [CrossRef]
- Freund, Rudolf J. 1956. The Introduction of Risk into a Programming Model. Econometrica 24: 253–63. [Google Scholar]
- Hardaker, J. Brian, Ruud B.M. Huirne, Jock R. Anderson, and Gudbrand Lien. 2004. Coping with Risk in Agriculture. Wallingford: CABI Publishing. [Google Scholar]
- Ioannides, Yannis M., and George Petrakos. 2000. Regional Disparities in Greece: The Performance of Crete, Peloponnese and Thessaly. EIB Papers 5: 30–58. [Google Scholar]
- Islam, N. 1995. Growth Empirics: A Panel Data Approach. The Quarterly Journal of Economics 110: 1127–70. [Google Scholar] [CrossRef]
- Jmaii, Amal, and Besma Belhadj. 2017. Fuzzy Regional Inequality Measurement: A New Stochastic Dominance Approach with Application to Tunisia. International Journal of Intelligent Engineering Informatics 5: 296–307. [Google Scholar] [CrossRef]
- Karahasan, Burhan Can, and Vassilis Monastiriotis. 2017. Spatial Structure and Spatial Dynamics of Regional Incomes in Greece. In Political Economy Perspectives on the Greek Crisis: Debt, Austerity and Unemployment. Cham: Palgrave Macmillan. [Google Scholar]
- Koudoumakis, Panagiotis, George Botzoris, Angelos Protopapas, and Vassilios Profillidis. 2019. The Impact of the Economic Crisis in the Process of Convergence of the Greek Regions. Regional Science Inquiry 11: 25–32. [Google Scholar]
- Liontakis, Angelos, Christos T Papadas, and Irene Tzouramani. 2010. Regional Economic Convergence in Greece: A Stochastic Dominance Approach. Louvain-la-Neuve: European Regional Science Association (ERSA). Available online: https://www.econstor.eu/bitstream/10419/119147/1/ERSA2010_1188.pdf (accessed on 24 May 2020).
- Maasoumi, Esfandiar, Jeff Racine, and Thanasis Stengos. 2007. Growth and Convergence: A Profile of Distribution Dynamics and Mobility. Journal of Econometrics 136: 483–508. [Google Scholar] [CrossRef]
- Meyer, Jack. 1977. Second Degree Stochastic Dominance with Respect to a Function. International Economic Review 18: 477–87. [Google Scholar] [CrossRef]
- Meyer, Jack, and Michael B. Ormiston. 1985. Strong Increases in Risk and Their Comparative Statics. International Economic Review 26: 425–37. [Google Scholar] [CrossRef]
- Meyer, Jack, and Michael B. Ormiston. 1994. The Effect on Optimal Portfolios of Changing the Return to a Risky Asset: The Case of Dependent Risky Returns. International Economic Review 35: 603–12. [Google Scholar] [CrossRef]
- Monastiriotis, Vassilis. 2008. The Geography of Spatial Association across the Greek Regions: Patterns of Persistence and Heterogeneity. Reg. Anal. Policy, 17–39. [Google Scholar]
- Monastiriotis, Vassilis. 2009. Examining the Consistency of Spatial Association Patterns across Socio-Economic Indicators: An Application to the Greek Regions. Empirical Economics 37: 25–49. [Google Scholar] [CrossRef]
- Monastiriotis, Vassilis. 2014. Convergence through Crisis? The Impact of the Crisis on Wage Returns across the Greek Regions. Région et Développement 39: 35–66. [Google Scholar]
- Petrakos, George, and Yannis Psycharis. 2004. Regional Development in Greece. New York: Springer. [Google Scholar]
- Petrakos, George, and Yannis Psycharis. 2016. The Spatial Aspects of Economic Crisis in Greece. Cambridge Journal of Regions, Economy and Society 9: 137–52. [Google Scholar] [CrossRef]
- Petrakos, George, and Yiannis Saratsis. 2000. Regional Inequalities in Greece. Papers in Regional Science 79: 57–74. [Google Scholar] [CrossRef]
- Psycharis, Yannis, Dimitris Kallioras, and Panagiotis Pantazis. 2014. Economic Crisis and Regional Resilience: Detecting the ‘Geographical Footprint’ of Economic Crisis in Greece. Regional Science Policy & Practice 6: 121–41. [Google Scholar]
- Psycharis, Yannis, Antonis Rovolis, Vassilis Tselios, and Panayotis Pantazis. 2016. Economic Crisis and Regional Development in Greece. Reg. et dev. 39: 67–85. [Google Scholar]
- Rey, Sergio J., Wei Kang, and Levi John Wolf. 2019. Regional Inequality Dynamics, Stochastic Dominance, and Spatial Dependence. Papers in Regional Science 98: 861–81. [Google Scholar] [CrossRef]
- Richardson, James W., Keith D. Schumann, and Paul A. Feldman. 2008. Simetar: Simulation and Econometrics to Analyze Risk. Handbuch Zum Excel Add-In Simetar. College Station: Texas A&M University. [Google Scholar]
- Siriopoulos, Costas, and Dimitrios Asteriou. 1998. Testing for Convergence across the Greek Regions. Regional Studies 32: 537–46. [Google Scholar] [CrossRef]
- Topaloglou, Lefteris, George Petrakos, and Victor Cupcea. 2019. Deliverable 6.2 National Report-Greece (v.2). Available online: https://relocal.eu/wp-content/uploads/sites/8/2019/10/RELOCAL-National-Report_Greece_AD_Checked.pdf (accessed on 1 May 2020).
- Zarco, Ismael Ahamdanech, and Carmelo García Pérez. 2007. Welfare, Inequality and Poverty Rankings in the European Union Using an Inference-Based Stochastic Dominance Approach. Research on Economic Inequality 14: 159. [Google Scholar]
- Zarco, Ismael Ahamdanech, Carmelo García Pérez, and Mercedes Prieto Alaiz. 2010. Convergence of Spanish Regions, 1990–2003. A New Approach Using Stochastic Dominance Techniques. Journal of Income Distribution 19: 33–47. [Google Scholar]
| Year | Average | Min | Max | Range | Median | Std. Dev | Skewness | Kurtosis |
|---|---|---|---|---|---|---|---|---|
| 2000 | 14,775 | 10,217 | 27,016 | 16,799 | 13,931 | 3432 | 1.35 | 2.36 |
| 2001 | 15,305 | 10,745 | 28,240 | 17,495 | 14,607 | 3513 | 1.42 | 2.76 |
| 2002 | 15,500 | 10,570 | 26,996 | 16,426 | 14,600 | 3377 | 1.26 | 1.93 |
| 2003 | 16,422 | 11,175 | 28,219 | 17,044 | 15,510 | 3709 | 1.17 | 1.35 |
| 2004 | 16,953 | 11,705 | 27,642 | 15,937 | 16,101 | 3831 | 1.09 | 0.98 |
| 2005 | 16,781 | 11,314 | 28,219 | 16,905 | 16,446 | 3909 | 1.12 | 1.18 |
| 2006 | 17,279 | 11,268 | 28,455 | 17,187 | 16,819 | 4033 | 1.02 | 0.95 |
| 2007 | 17,816 | 12,092 | 29,711 | 17,619 | 17,666 | 4040 | 1.15 | 1.60 |
| 2008 | 17,697 | 11,559 | 29,744 | 18,185 | 17,647 | 4014 | 1.19 | 1.76 |
| 2009 | 16,939 | 11,204 | 28,992 | 17,788 | 16,678 | 3689 | 1.27 | 2.21 |
| 2010 | 15,456 | 10,593 | 26,387 | 15,794 | 15,281 | 3284 | 1.36 | 2.48 |
| 2011 | 13,715 | 9570 | 23,457 | 13,887 | 13,543 | 2913 | 1.51 | 2.90 |
| 2012 | 12,628 | 8978 | 21,425 | 12,447 | 12,244 | 2691 | 1.42 | 2.23 |
| 2013 | 12,148 | 8839 | 20,714 | 11,875 | 11,759 | 2664 | 1.60 | 2.77 |
| 2014 | 12,309 | 8802 | 20,849 | 12,047 | 11,672 | 2753 | 1.37 | 1.84 |
| 2015 | 12,531 | 9116 | 21,066 | 11,950 | 11,986 | 2815 | 1.31 | 1.65 |
| 2016 | 12,595 | 9425 | 21,217 | 11,792 | 11,866 | 2761 | 1.49 | 2.42 |
| 2017 | 12,681 | 9266 | 21,530 | 12,264 | 11,803 | 2887 | 1.42 | 2.06 |
| Year | 2000 | 2001 | 2002 | 2003 | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2000 | |||||||||||||||||
| 2001 | F2001 | ||||||||||||||||
| 2002 | F2002 | I | |||||||||||||||
| 2003 | F2003 | F2003 | F2003 | ||||||||||||||
| 2004 | F2004 | S2004 | F2004 | S2004 | |||||||||||||
| 2005 | F2005 | F2005 | F2005 | I | S2004 | ||||||||||||
| 2006 | F2006 | F2006 | F2006 | S2006 | I | I | |||||||||||
| 2007 | F2007 | F2007 | F2007 | F2007 | S2007 | F2007 | S2007 | ||||||||||
| 2008 | F2008 | F2008 | F2008 | F2008 | I | S2008 | S2008 | I | |||||||||
| 2009 | F2009 | F2009 | F2009 | S2009 | I | I | I | F2007 | F2008 | ||||||||
| 2010 | S2010 | I | I | F2003 | F2004 | F2005 | F2006 | F2007 | F2008 | F2009 | |||||||
| 2011 | F2000 | F2001 | F2002 | F2003 | F2004 | F2005 | F2006 | F2007 | F2008 | F2009 | F2010 | ||||||
| 2012 | F2000 | F2001 | F2002 | F2003 | F2004 | F2005 | F2006 | F2007 | F2008 | F2009 | F2010 | F2011 | |||||
| 2013 | F2000 | F2001 | F2002 | F2003 | F2004 | F2005 | F2006 | F2007 | F2008 | F2009 | F2010 | F2011 | S2012 | ||||
| 2014 | F2000 | F2001 | F2002 | F2003 | F2004 | F2005 | F2006 | F2007 | F2008 | F2009 | F2010 | F2011 | S2012 | I | |||
| 2015 | F2000 | F2001 | F2002 | F2003 | F2004 | F2005 | F2006 | F2007 | F2008 | F2009 | F2010 | F2011 | I | S2015 | S2015 | ||
| 2016 | F2000 | F2001 | F2002 | F2003 | F2004 | F2005 | F2006 | F2007 | F2008 | F2009 | F2010 | F2011 | I | S2016 | S2016 | S2016 | |
| 2017 | F2000 | F2001 | F2002 | F2003 | F2004 | F2005 | F2006 | F2007 | F2008 | F2009 | F2010 | F2011 | I | F2017 | S2017 | S2017 | I |
| ARIAC = 0 | ARIAC = 0.00089 | ARIAC = 0.0092 | ARIAC = +∞ | |||||
|---|---|---|---|---|---|---|---|---|
| Year | CE | Year | CE | Year | CE | Year | CE | |
| Relative Ranking (Highest CE to lowest CE) | 2007 | 17,659.84 | 2008 | 14,813.99 | 2007 | 12,533.47 | 2007 | 12,093.28 |
| 2008 | 17,542.67 | 2007 | 14,800.69 | 2004 | 12,322.17 | 2004 | 11,732.4 | |
| 2006 | 17,137.34 | 2009 | 14,417.06 | 2008 | 12,245.98 | 2008 | 11,582.56 | |
| 2004 | 16,809.37 | 2006 | 14,352.22 | 2005 | 11,934.75 | 2005 | 11,340.41 | |
| 2009 | 16,787.76 | 2004 | 14,333.36 | 2006 | 11,931.7 | 2006 | 11,314.56 | |
| 2005 | 16,631.94 | 2005 | 14,057.14 | 2009 | 11,873.27 | 2009 | 11,231.65 | |
| 2003 | 16,291.63 | 2003 | 14,003.74 | 2003 | 11,828.24 | 2003 | 11,196.92 | |
| 2002 | 15,376.83 | 2002 | 13,435.91 | 2002 | 11,274.53 | 2001 | 10,747.86 | |
| 2010 | 15,320.1 | 2010 | 13,404.54 | 2001 | 11,238.18 | 2010 | 10,606.76 | |
| 2001 | 15,158.41 | 2001 | 13,102.38 | 2010 | 11,184.2 | 2002 | 10,576.36 | |
| 2000 | 14,634.23 | 2000 | 12,647.96 | 2000 | 10,842.83 | 2000 | 10,232.82 | |
| 2011 | 13,590.86 | 2011 | 12,072.27 | 2011 | 10,053.99 | 2011 | 9571.74 | |
| 2017 | 12,549.77 | 2012 | 11,188.88 | 2016 | 9786.26 | 2016 | 9425.32 | |
| 2012 | 12,512.22 | 2016 | 11,106.82 | 2017 | 9744.41 | 2017 | 9266.36 | |
| 2016 | 12,465.45 | 2017 | 11,096.45 | 2015 | 9484.19 | 2015 | 9118 | |
| 2015 | 12,410.19 | 2015 | 10,945.67 | 2012 | 9451 | 2012 | 8977.79 | |
| 2014 | 12,193.98 | 2014 | 10,799.06 | 2014 | 9324.56 | 2013 | 8839.01 | |
| 2013 | 12,023.28 | 2013 | 10,794.56 | 2013 | 9280.59 | 2014 | 8803.96 | |
| ARIAC = 0 | ARIAC = 0.00089 | ARIAC = 0.0092 | ARIAC = +∞ | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Year | CE | Δ (%) | CE | Δ (%) | CE | Δ (%) | CE | Δ (%) | |
| Annual change of CEs level | 2000 | 14,634 | - | 12,648 | - | 10,843 | - | 10,233 | - |
| 2001 | 15,158 | 3.6% | 13,102 | 3.6% | 11,238 | 3.6% | 10,748 | 5.0% | |
| 2002 | 15,377 | 1.4% | 13,436 | 2.5% | 11,275 | 0.3% | 10,576 | –1.6% | |
| 2003 | 16,292 | 5.9% | 14,004 | 4.2% | 11,828 | 4.9% | 11,197 | 5.9% | |
| 2004 | 16,809 | 3.2% | 14,333 | 2.4% | 12,322 | 4.2% | 11,732 | 4.8% | |
| 2005 | 16,632 | –1.1% | 14,057 | −1.9% | 11,935 | –3.1% | 11,340 | –3.3% | |
| 2006 | 17,137 | 3.0% | 14,352 | 2.1% | 11,932 | 0.0% | 11,315 | –0.2% | |
| 2007 | 17,660 | 3.0% | 14,801 | 3.1% | 12,533 | 5.0% | 12,093 | 6.9% | |
| 2008 | 17,543 | –0.7% | 14,814 | 0.1% | 12,246 | –2.3% | 11,583 | –4.2% | |
| 2009 | 16,788 | –4.3% | 14,417 | –2.7% | 11,873 | –3.0% | 11,232 | –3.0% | |
| 2010 | 15,320 | –8.7% | 13,405 | –7.0% | 11,184 | –5.8% | 10,607 | –5.6% | |
| 2011 | 13,591 | –11.3% | 12,072 | –9.9% | 10,054 | –10.1% | 9572 | –9.8% | |
| 2012 | 12,512 | –7.9% | 11,189 | –7.3% | 9451 | –6.0% | 8978 | –6.2% | |
| 2013 | 12,023 | –3.9% | 10,795 | –3.5% | 9281 | –1.8% | 8839 | –1.5% | |
| 2014 | 12,194 | 1.4% | 10,799 | 0.0% | 9325 | 0.5% | 8804 | –0.4% | |
| 2015 | 12,410 | 1.8% | 10,946 | 1.4% | 9484 | 1.7% | 9118 | 3.6% | |
| 2016 | 12,465 | 0.4% | 11,107 | 1.5% | 9786 | 3.2% | 9425 | 3.4% | |
| 2017 | 12,550 | 0.7% | 11,096 | –0.1% | 9744 | –0.4% | 9266 | –1.7% | |
| 2000–2017 | 2000–2008 | 2009–2017 | |
|---|---|---|---|
| ln (initial GDP/cap) | –0.041 | –0.11 1 | –0.24 2 |
| R 2 | 1.2% | 23.0% | 47.0% |
| Half-life 3 | 49.9 | 25.9 |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liontakis, A. How Does a Policymaker Rank Regional Income Distributions across Years? A Study on the Evolution of Greek Regional per Capita Income. Economies 2020, 8, 40. https://doi.org/10.3390/economies8020040
Liontakis A. How Does a Policymaker Rank Regional Income Distributions across Years? A Study on the Evolution of Greek Regional per Capita Income. Economies. 2020; 8(2):40. https://doi.org/10.3390/economies8020040
Chicago/Turabian StyleLiontakis, Angelos. 2020. "How Does a Policymaker Rank Regional Income Distributions across Years? A Study on the Evolution of Greek Regional per Capita Income" Economies 8, no. 2: 40. https://doi.org/10.3390/economies8020040
APA StyleLiontakis, A. (2020). How Does a Policymaker Rank Regional Income Distributions across Years? A Study on the Evolution of Greek Regional per Capita Income. Economies, 8(2), 40. https://doi.org/10.3390/economies8020040





