Comparing Sentiment- and Behavioral-Based Leading Indexes for Industrial Production: When Does Each Fail?
Abstract
1. Introduction
1.1. Identifying Leading Indexes
1.2. LL Categories
1.3. Hypotheses
2. Data
2.1. Time Series and German Economy Characteristics
2.2. Methodology
2.2.1. The Rolling Average Leading–Lagging Method
2.2.2. We Explain the LL Method in Four Steps
2.3. Principal Component Analysis (PCA)
2.4. Power Spectral Analysis
3. Results
3.1. Smoothing Macroeconomic Series
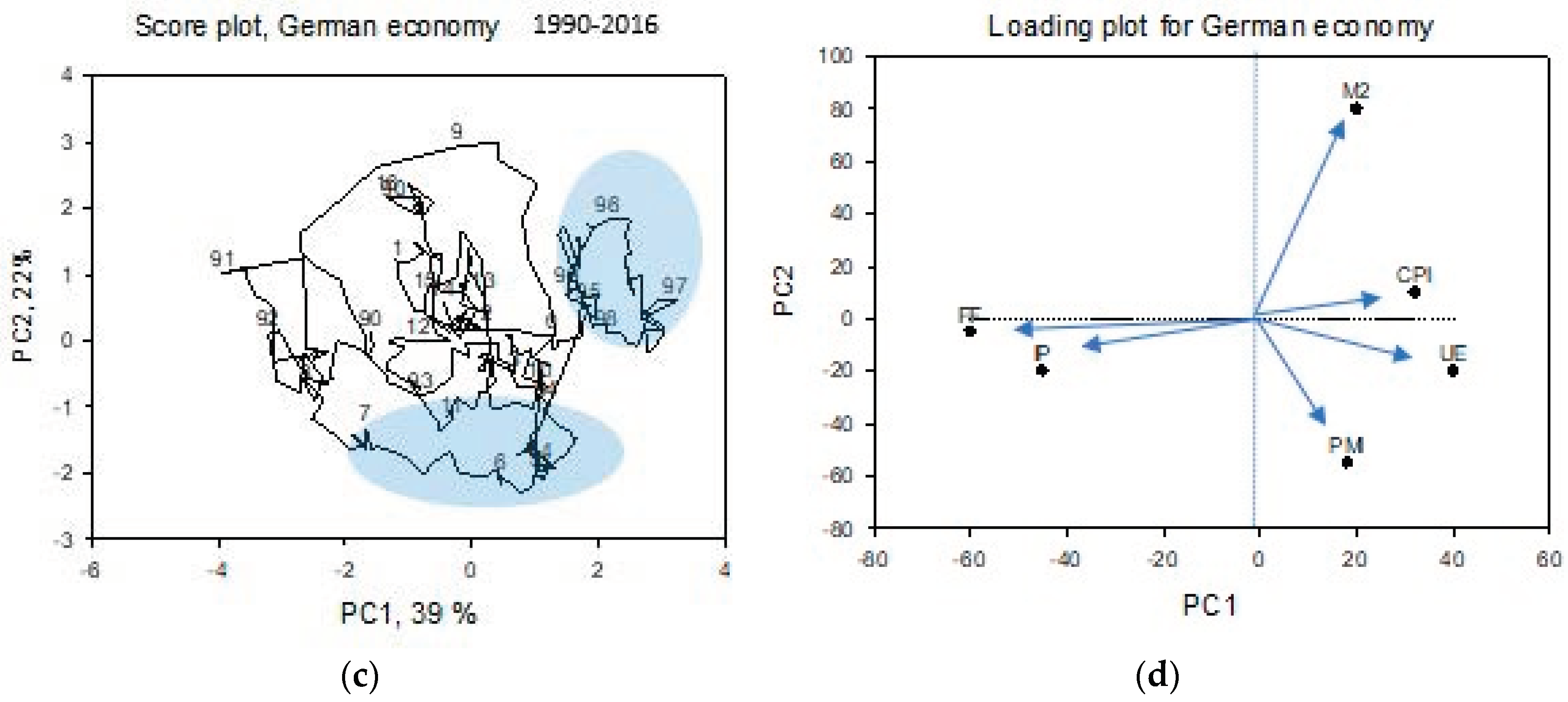
3.2. Leading–Lagging Relations
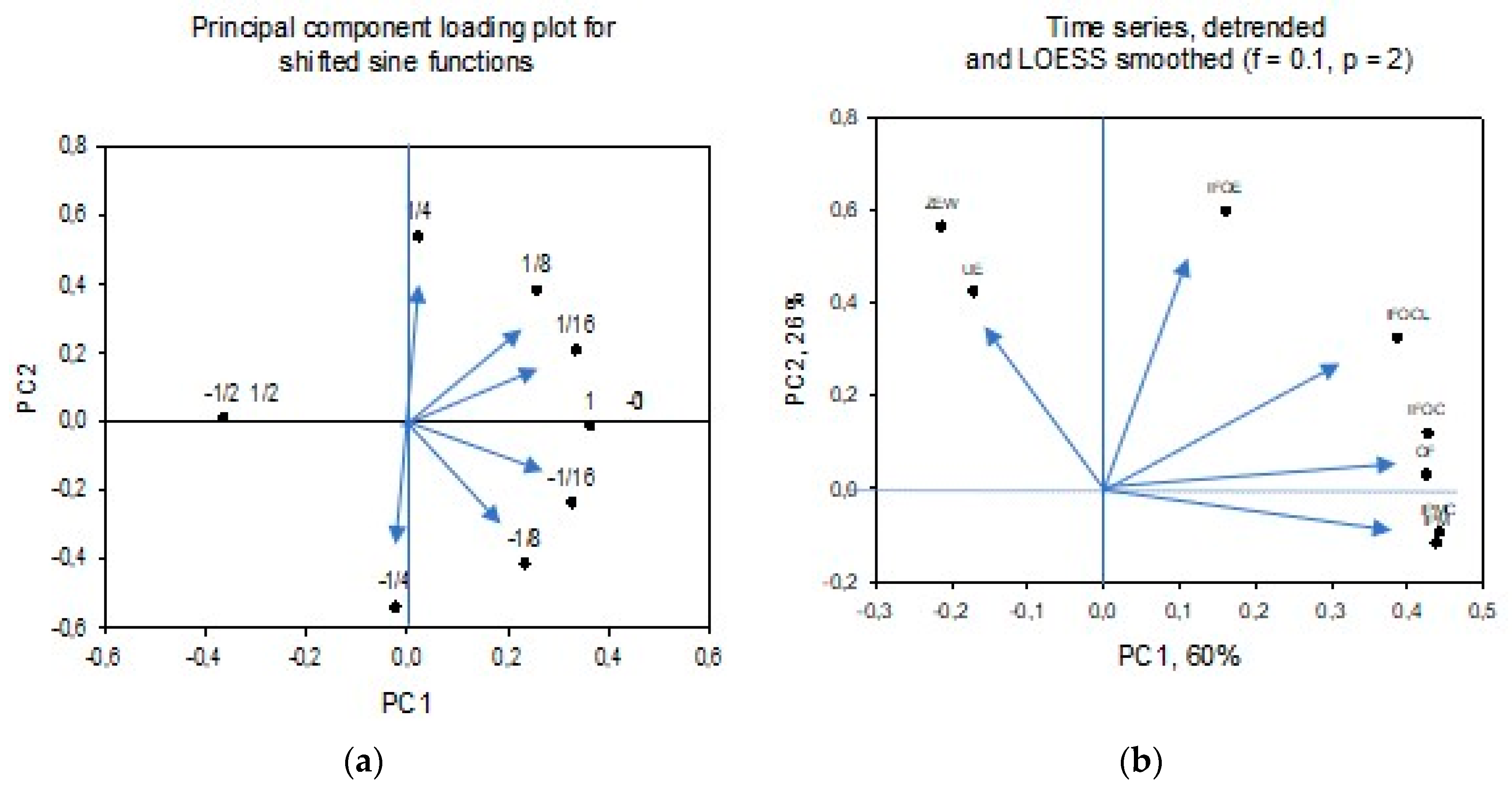
3.3. Relations among Detrended Time Series
4. Discussion
4.1. Comparing ifo and ZEW to the Behavioral-Based Index, OF
4.2. Periods: Recession, Recoveries, Index Volatilities
4.3. Time Windows with Anomaly Predictions
4.4. Cycle Times and Leading Times
4.5. Smoothing and Outlier Removals
4.6. Further Work
4.7. Policy Implications
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Abberger, K., M. Graff, B. Siliverstovs, and J. E. Sturm. 2018. Using rule-based updating procedures to improve the performance of composite indicators. Economic Modelling 68: 127–44. [Google Scholar] [CrossRef]
- Abel, A., B. Bernanke, and R. McNabb. 1998. Macroeconomics. Harlow: Addison-Wesley. [Google Scholar]
- Angelini, E., G. Camba-Mendez, D. Giannone, L. Reichlin, and G. Runstler. 2011. Short-term forecasts of euro area GDP growth. Econometrics Journal 14: C25–C44. [Google Scholar] [CrossRef]
- Balcilar, M., R. Gupta, A. Majumdar, and S. M. Miller. 2013. Forecasting Nevada gross gaming revenue and taxable sales using coincident and leading employment indexes. Empirical Economics 44: 387–417. [Google Scholar] [CrossRef][Green Version]
- Ball, L., J. T. Jalles, and P. Loungani. 2015. Do forecasters believe in Okun’s Law? An assessment of unemployment and output forecasts. International Journal of Forecasting 31: 176–84. [Google Scholar] [CrossRef]
- Banerji, A., P. Dua, and S. M. Miller. 2006. Performance evaluation of the new Connecticut leading employment index using lead profiles and BVAR models. Journal of Forecasting 25: 415–37. [Google Scholar] [CrossRef]
- Caglayan, M., and B. Xu. 2016. Sentiment volatility and bank lending behavior. International Review of Financial Analysis 45: 107–20. [Google Scholar] [CrossRef]
- Camba-Mendez, G., G. Kapetanios, R. J. Smith, and M. R. Weale. 2001. An autmoatic leading indicator of economic activity: forecasting growth for European countries. Econometrics Journal 4: S56–S90. [Google Scholar] [CrossRef]
- Carstensen, K., K. Wohlrabe, and C. Ziegler. 2011. Predictive Ability of Business Cycle Indicators under Test A Case Study for the Euro Area Industrial Production. Jahrbucher Fur Nationalokonomie Und Statistik 231: 82–106. [Google Scholar]
- Chakraborty, I., R. Hai, H. Holter, and S. Stepanchuk. 2016. A mulit-country equilibrium analysis of Europe. Carnegie-Rochhester-NYU Conference on public policy. Journal of Monetary Economics 85: 28–45. [Google Scholar] [CrossRef]
- Christiansen, C., J. N. Eriksen, and S. V. Moller. 2014. Forecasting US recessions: The role of sentiment. Journal of Banking & Finance 49: 459–68. [Google Scholar]
- CNNmoney. 2018. Fear & Greed Index—Investor sentiment. Available online: https://money.cnn.com/data/fear-and-greed/ (accessed on 15 October 2019).
- D’Amuri, F., and J. Marcucci. 2017. The predictive power of Google searches in forecasting US unemployment. International Journal of Forecasting 33: 801–16. [Google Scholar] [CrossRef]
- De Bondt, G. J., and E. Hahn. 2014. Introducing the Euro Area-wide Leading Indicator (ALI): Real-Time Signals of Turning Points in the Growth Cycle from 2007 to 2011. Journal of Forecasting 33: 47–68. [Google Scholar] [CrossRef]
- De Bondt, G. J., H. C. Dieden, S. Muzikarova, and I. Vincze. 2014. Modelling industrial new orders. Economic Modelling 41: 46–54. [Google Scholar] [CrossRef]
- Enders, W. 2010. Applied Econometric Time Series, 3rd ed. Hoboken: John Wiley & Sons. [Google Scholar]
- Fernandez, A., M. W. Klein, A. Rebucci, M. Schindler, and M. Uribe. 2016. Capital Control Measures: A New Dataset. IMF Economic Review 64: 548–74. [Google Scholar] [CrossRef]
- Ferrara, L., M. Marcellino, and M. Mogliani. 2015. Macroeconomic forecasting during the Great Recession: The return of non-linearity? International Journal of Forecasting 31: 664–79. [Google Scholar] [CrossRef]
- Filardo, A. J., and S. F. Gordon. 1998. Business cycle durations. Journal of Econometrics 85: 99–123. [Google Scholar] [CrossRef]
- FinancialTimes. 2018. German Economic Sentiment on the Rebound—ZEW. Available online: https://www.ft.com/content/1e3ddf54-b58a-11e8-b3ef-799c8613f4a1 (accessed on 15 October 2019).
- Forni, M., M. Hallin, M. Lippi, and L. Reichlin. 2001. Coincident and leading indicators for the EURO area. Economic Journal 111: C62–C85. [Google Scholar] [CrossRef]
- Granger, C. W. J. 1989. Forecasting in Business Economics. Boston: Academic Press. [Google Scholar]
- Heij, C., D. van Dijk, and P. J. F. Groenen. 2011. Real-time macroeconomic forecasting with leading indicators: An empirical comparison. International Journal of Forecasting 27: 466–81. [Google Scholar] [CrossRef]
- Hsieh, Hsiu-Fang, and Sarah Shannon. 2005. Three Approaches to Qualitative Content Analysis. Qualitative Health Research 15: 1277–88. [Google Scholar] [CrossRef]
- Huefner, F. P., and M. Schroeder. 2002. Forecasting Economic Activity in Germany—How Useful Are Sentiment Indicators? Mannheim: ZEW institute, Centre for European Economic Research. [Google Scholar]
- IFO. 2016. German IFO Business Survey. Available online: https://books.google.no/books?id=wj79gd3m8cUC&pg=PA330&lpg=PA330&dq=ifo+institute+for+economic+research+ifo+index&source=bl&ots=td1PeV-QHz&sig=qqaaphAxdC_DWwMZh39R3O4uPaY&hl=no&sa=X&ved=0ahUKEwjortKk2JfKAhXh73IKHZkdBoIQ6AEITzAH#v=onepage&q=ifo%20institute%20for%20economic%20research%20ifo%20index&f=false (accessed on 7 January 2016).
- Levanon, G., J. C. Manini, A. Ozyildirim, B. Schaitkin, and J. Tanchua. 2015. Using financial indicators to predict turning points in the business cycle: The case of the leading economic index for the United States. International Journal of Forecasting 31: 426–45. [Google Scholar] [CrossRef]
- Lisi, G., and M. Pugno. 2015. A matching model of endogenous growth and underground firms. International Journal of Economic Theory 11: 347–69. [Google Scholar] [CrossRef][Green Version]
- McNown, R., and K. L. Seip. 2011. Periods and structural breaks in US economic history 1959–2007: A data driven identification. Journal of Policy Modelling 33: 169–82. [Google Scholar] [CrossRef]
- OECD. 2012. OECD System of Composite Leading Indicators. Paris: OECD. [Google Scholar]
- OECD. 2016. OECD Based Recession Indicators for Germany. Available online: https://research.stlouisfed.org/fred2/series/DEUREC (accessed on 21 January 2016).
- Ozyildirim, A., B. Schaitkin, and V. Zarnowitz. 2010. Business Cycles in the Euro Area Defined with Coincident Economic Indicators and Predicted with Leading Economic Indicators. Journal of Forecasting 29: 6–28. [Google Scholar] [CrossRef]
- Schöler, K. 1994. Business climate as a leading indicator? An empirical investigation for West Germany from 1978 to 1990. Empirical Economics 19: 165–69. [Google Scholar] [CrossRef]
- Schrimpf, A., and Q. W. Wang. 2010. A reappraisal of the leading indicator properties of the yield curve under structural instability. International Journal of Forecasting 26: 836–57. [Google Scholar] [CrossRef]
- Seip, K. L., and O. Grøn. 2016. Leading the Game, Losing the Competition: Identifying Leaders and Followers in a Repeated Game. PLoS ONE 11: e0150398. [Google Scholar] [CrossRef]
- Seip, K. L., and Ø. Grøn. 2017. A new method for identifying possible causal relationships between CO2, total solar irradiance and global temperature change. Theoretical and Applied Climatology 127: 923–38. [Google Scholar] [CrossRef]
- Seip, K. L., and R. McNown. 2007. The timing and accuracy of leading and lagging business cycle indicators: A new approach. International Journal of Forecasting 22: 277–87. [Google Scholar] [CrossRef]
- Seip, K. L., Ø. Grøn, and H. Wang. 2018. Carbon dioxide precedes temperature change during short-term pauses in multi-millennial palaeoclimate records. Palaeogeography Palaeoclimatology Palaeoecology 506: 101–11. [Google Scholar] [CrossRef]
- Steckler, H. O., and T. Ye. 2017. Evaluating a leading indicator:an application-the term spread. Empirical Economics 53: 183–94. [Google Scholar] [CrossRef][Green Version]
- Sugihara, G., and R. M. May. 1990. Nonlinear forecasting as a way of distinguishing chaos from measurement errors in time series. Nature 344: 731–41. [Google Scholar] [CrossRef]
- Tang, B., and C. Bethencourt. 2017. Asymmetric unemployment-output tradeoff in the Eurozone. Journal of Policy Modeling 39: 461–81. [Google Scholar] [CrossRef]
- Tømte, O., K. L. Seip, and N. Christophersen. 1998. Evidence That Loss in Predictability Increases with Weakening of (Metabolic) Links to Physical Forcing Functions in Aquatic Ecosystems. Oikos 82: 325–32. [Google Scholar] [CrossRef]
- Ulbricht, D., K. A. Kholodilin, and T. Thomas. 2017. Do Media Data Help to Predict German Industrial Production? Journal of Forecasting 36: 483–96. [Google Scholar] [CrossRef]
- Xu, H.-C., and Wei-Xing Zhou. 2018. A weekly sentiment index and the cross-section of stock returns. Finance Research Letters 27: 135–39. [Google Scholar] [CrossRef]
- Zarnowitz, V., and A. Ozyildirim. 2006. Time series decomposition and measurement of business cycles, trends and growth cycles. Journal of Monetary Economics 53: 1717–39. [Google Scholar] [CrossRef]
- ZEW. 2016. ZEW Economic Sentiment Index. Available online: http://www.tradingeconomics.com/germany/zew-economic-sentiment-index (accessed on 15 October 2019).
- Zhang, Z. C., Y. J. Zhang, D. H. Shen, and W. Zhang. 2018. The cross-correlations between online sentiment proxies: Evidence from Google Trends and Twitter. Physica A-Statistical Mechanics and Its Applications 508: 67–75. [Google Scholar] [CrossRef]
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | It can be implemented in Excel format: With v1 = (A1, A2, A3) and v2 = (B1, B2, B3) in an Excel spread sheet, the angle is calculated by pasting the following Excel expression into C2: =SIGN((A2-A1)*(B3-B2)-(B2-B1)*(A3-A2))*ACOS(((A2-A1)*(A3-A2) + (B2-B1)*(B3-B2))/(SQRT((A2-A1)^2+(B2-B1)^2)*SQRT((A3-A2)^2+(B3-B2)^2))). |
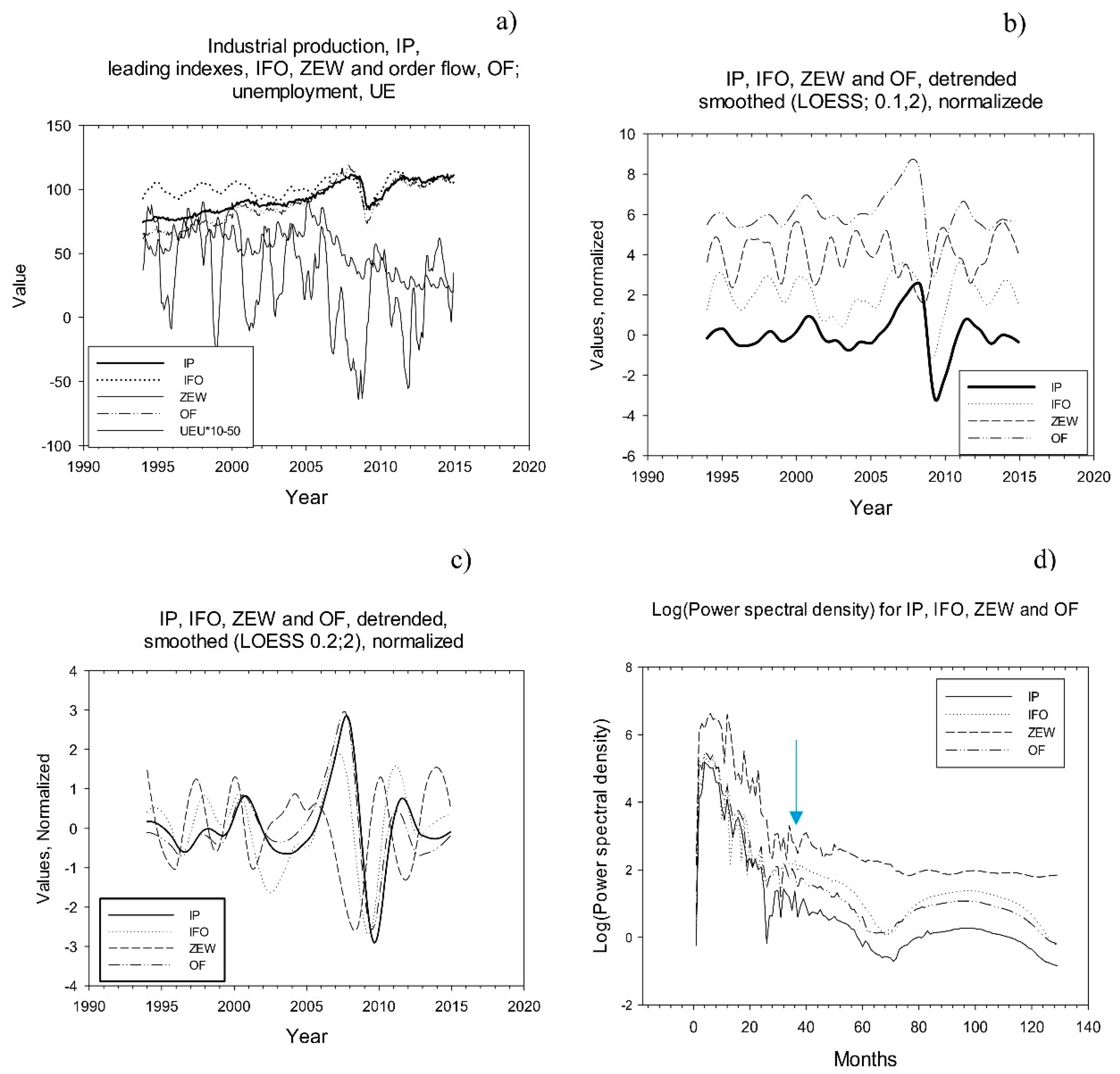
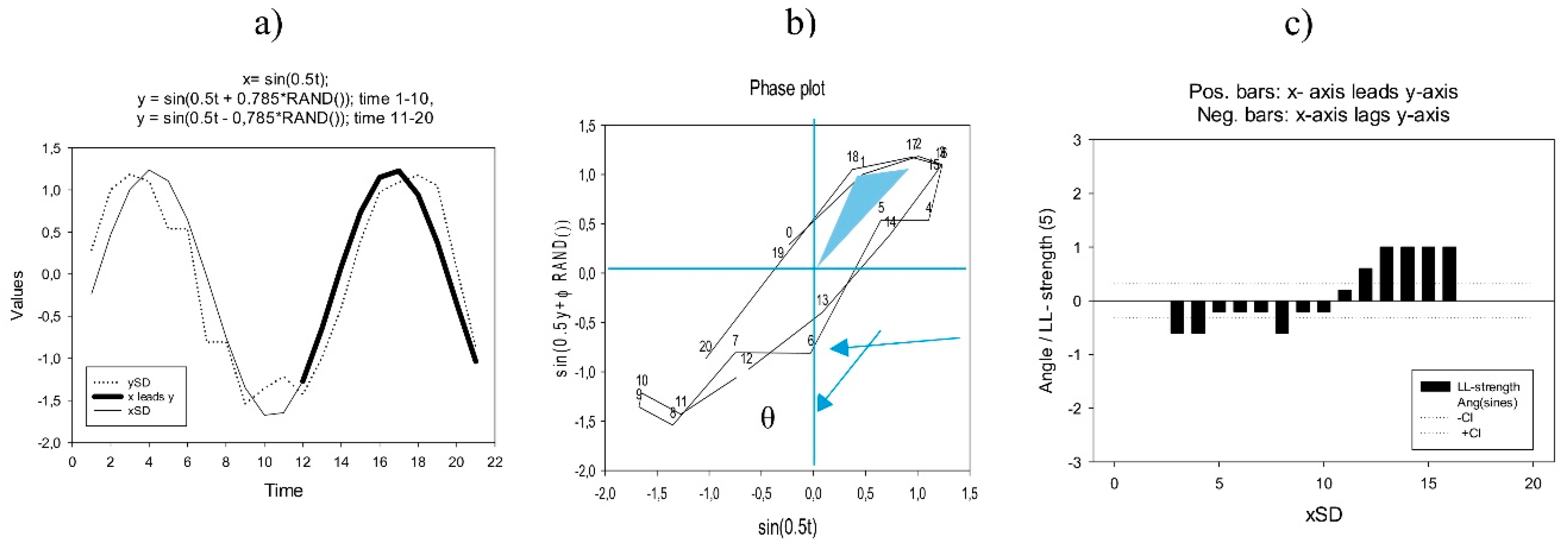
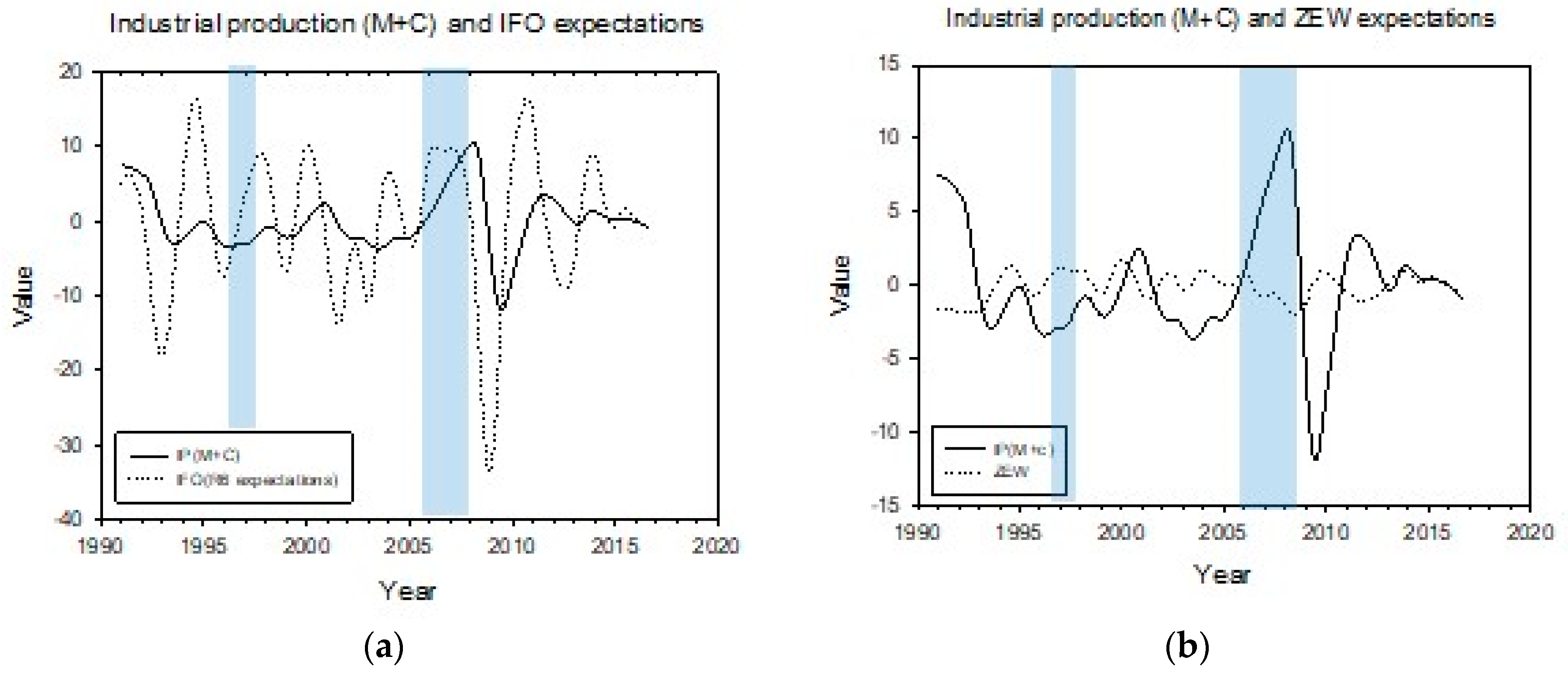
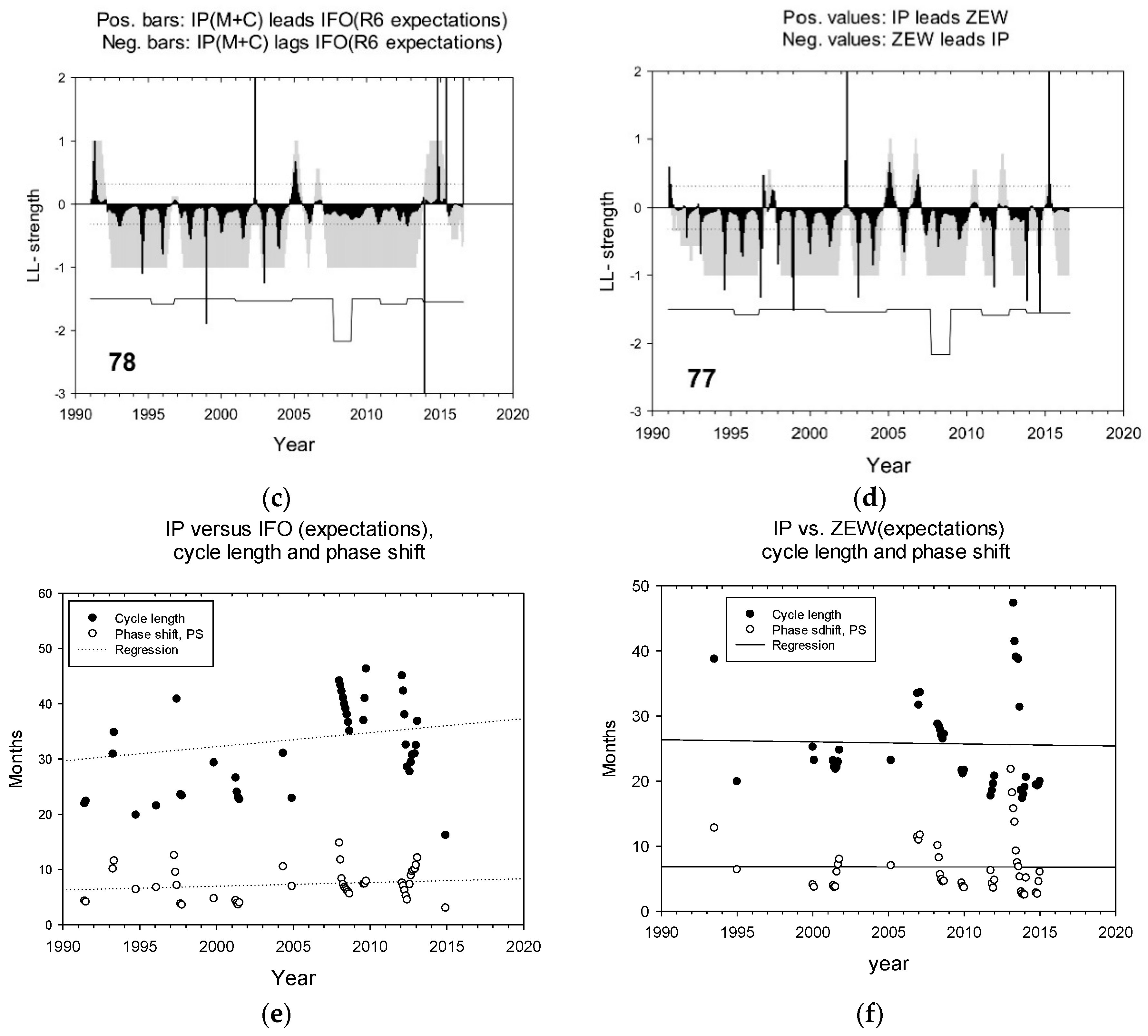
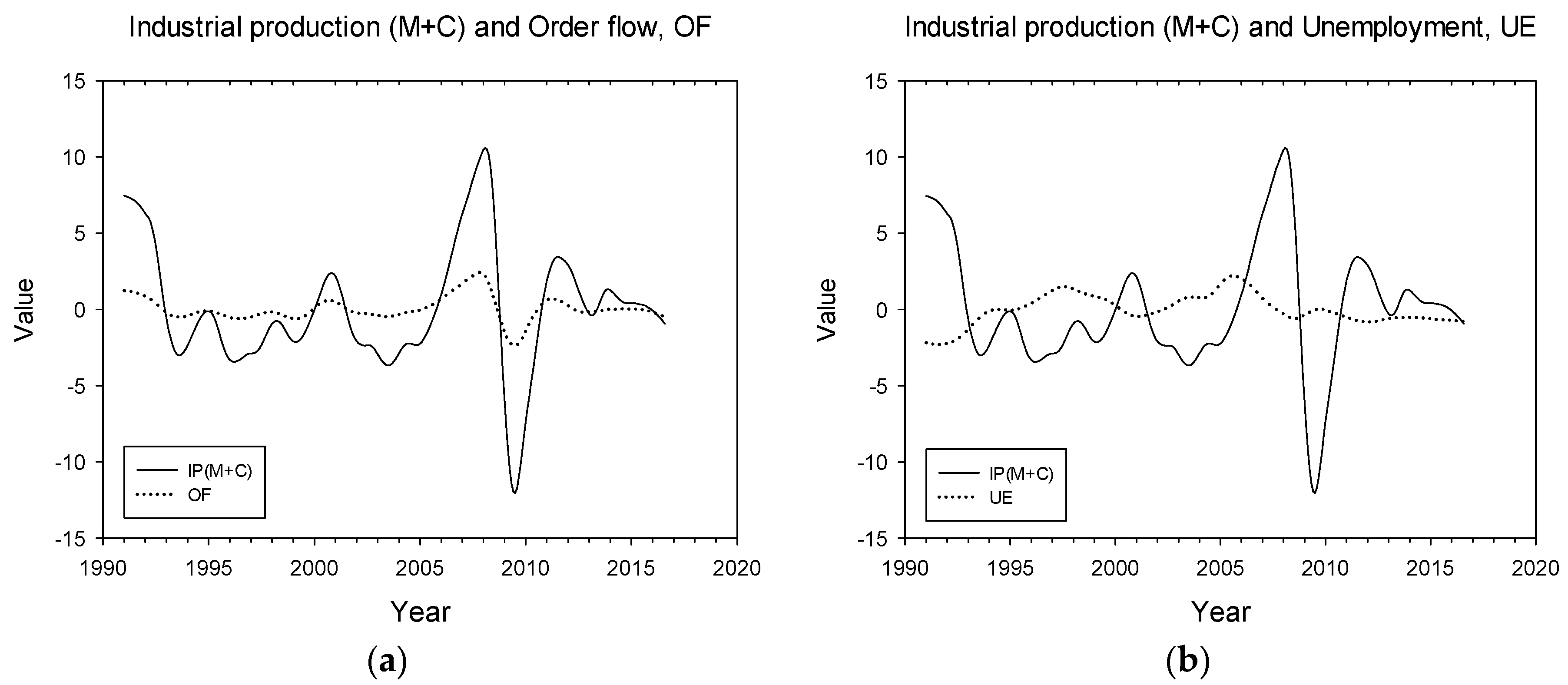
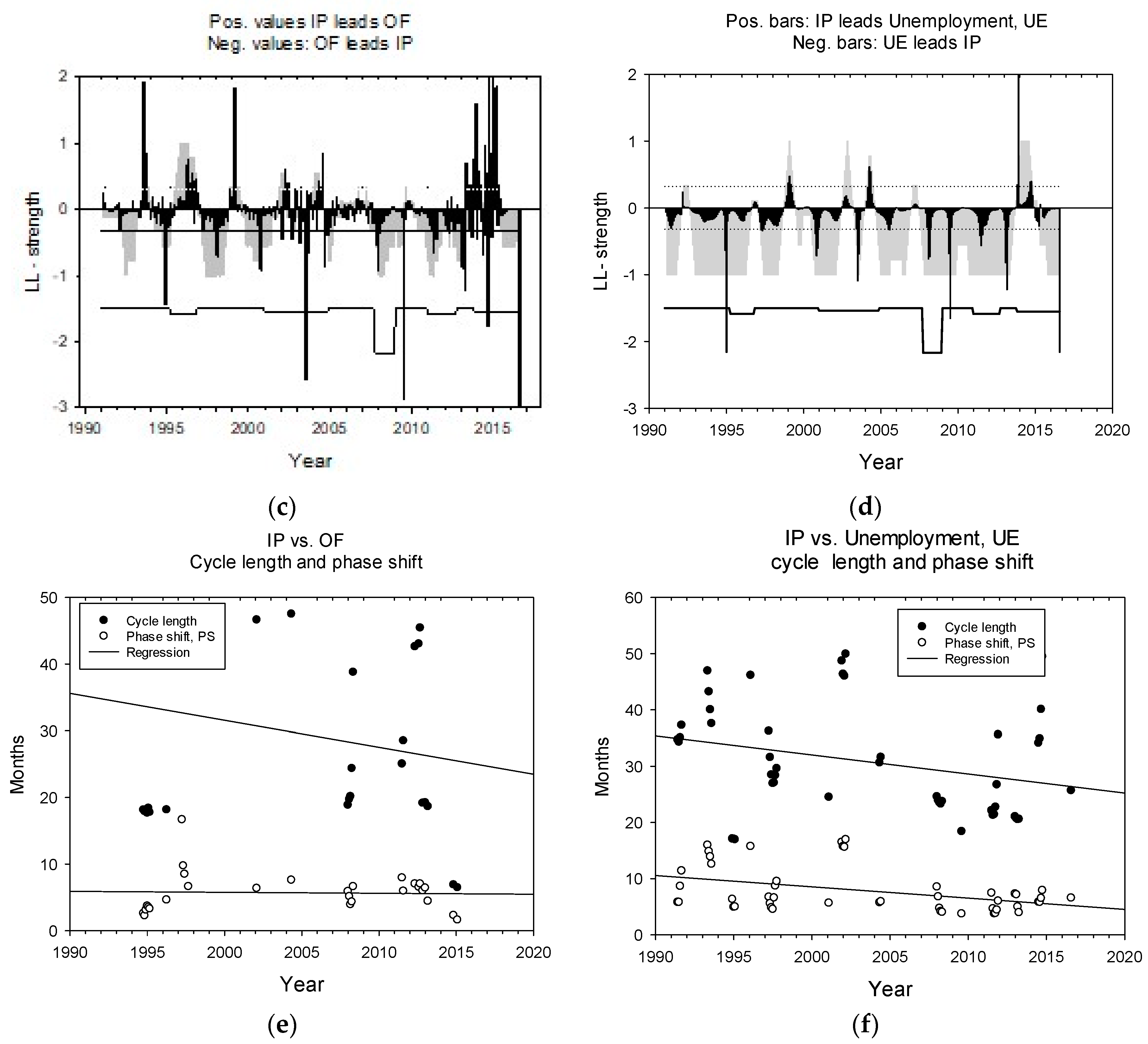
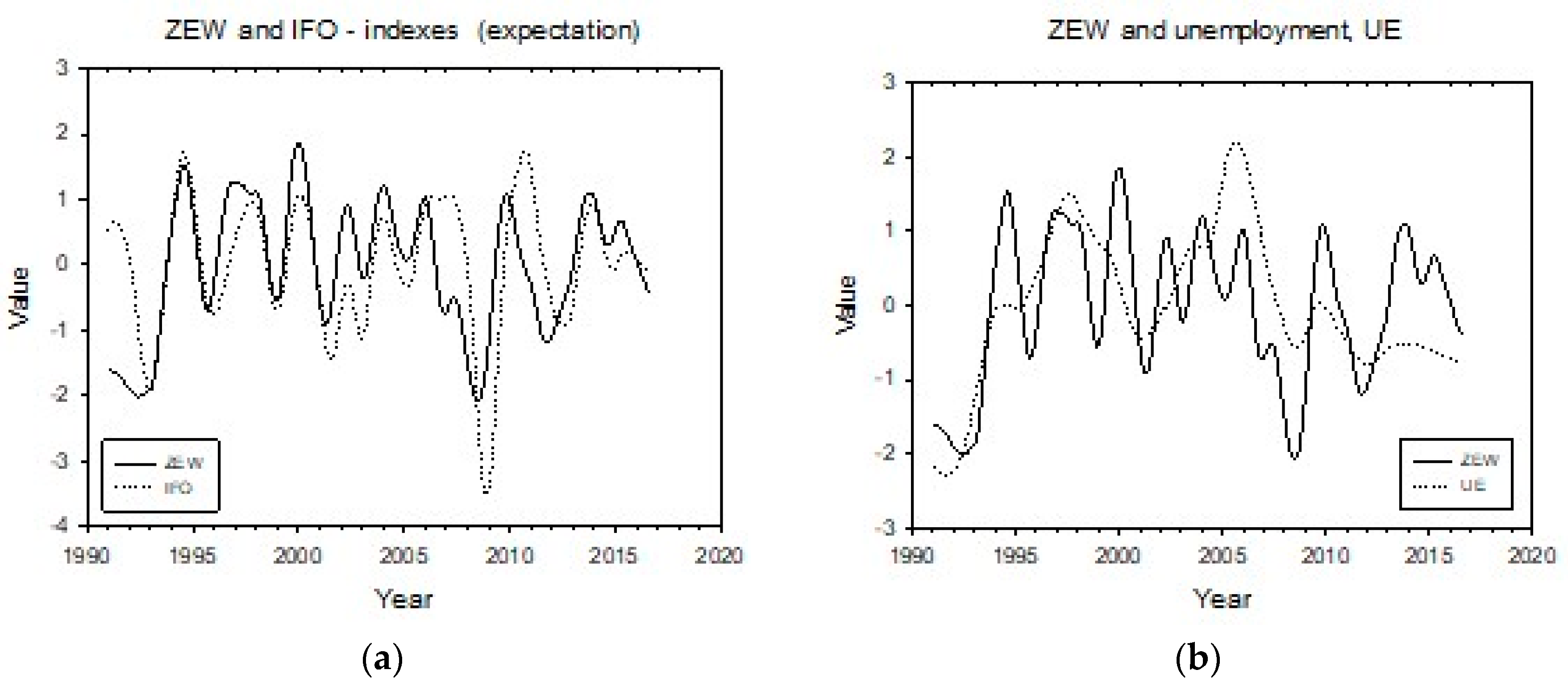
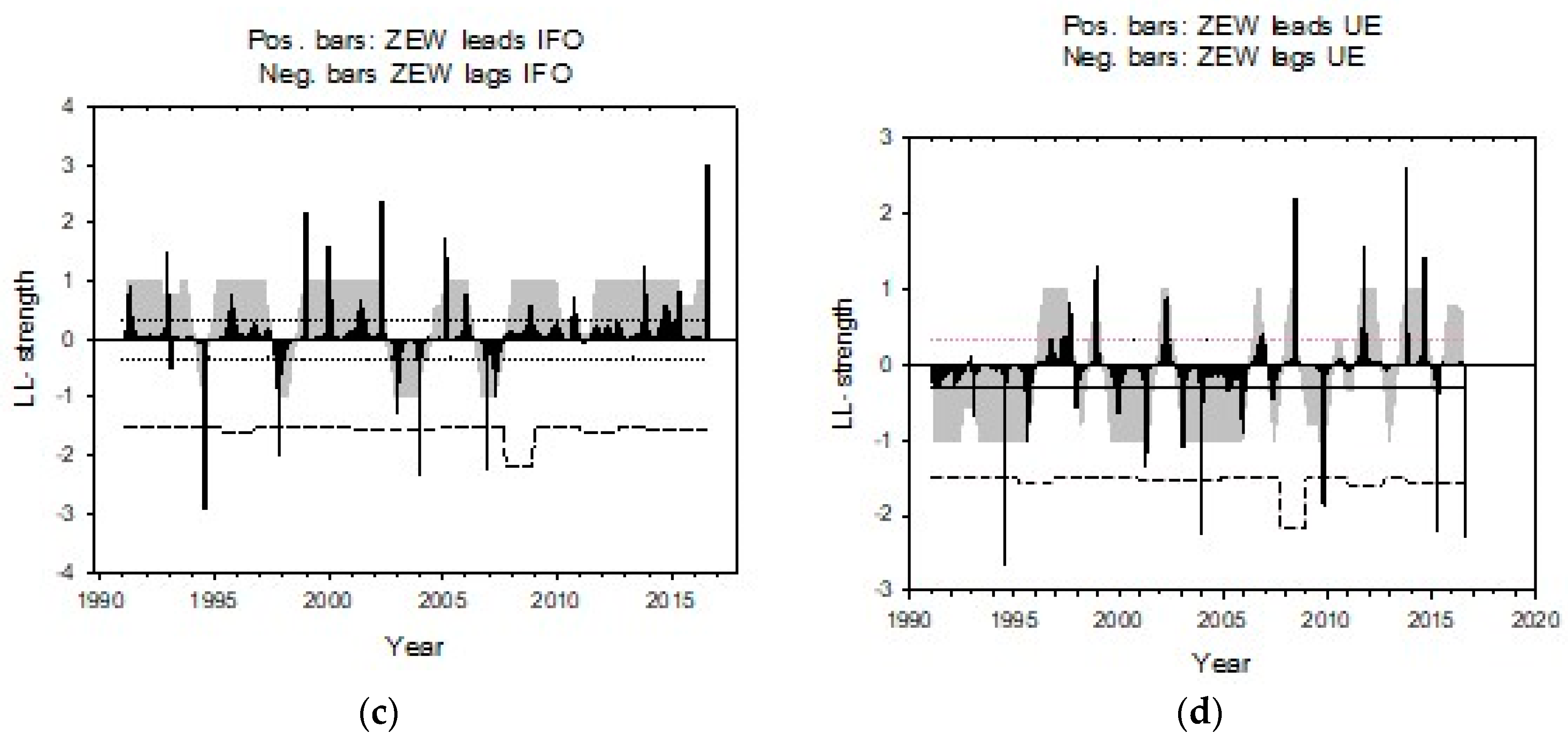
| Period | Dates | ||||
|---|---|---|---|---|---|
| Start period/peak | 1995:7 | 2001:6 | 2008:3 | 2011:6 | 2014:3 |
| End period/Trough | 1997:3 | 2005:4 | 2009:5 | 2013:3 | - |
| Recession seriousness | −1.69 | −0.76 | −13.4 | −1.77 | −1.05 |
| Index | LL Strength | Leading Time | |||||
|---|---|---|---|---|---|---|---|
| 1 | 1991–2016 | recession | recovery | cycle time, months | timing months | Leading, % | |
| 2 | ifo (managers) | −0.596 | −0.778 | −0.156 | 33.6 | 7.3 (2) | 78 |
| 3 | ZEW (financial experts) | −0.583 | −0.867 | −0.289 | 27.3 | 6.8 (5) | 77 |
| 4 | Unemployment (behavioral) | −0.564 | −0.733 | −0.556 | 32.3 | 8.0 | 73 |
| 5 | Order flow, OF | −0.186 | −0.422 | −0.289 | 29.7 | 5.7 | 46 |
| Average | −0.48 | −0.70 | −0.32 | 30.73 | 6.95 | 68.5 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Seip, K.L.; Yilmaz, Y.; Schröder, M. Comparing Sentiment- and Behavioral-Based Leading Indexes for Industrial Production: When Does Each Fail? Economies 2019, 7, 104. https://doi.org/10.3390/economies7040104
Seip KL, Yilmaz Y, Schröder M. Comparing Sentiment- and Behavioral-Based Leading Indexes for Industrial Production: When Does Each Fail? Economies. 2019; 7(4):104. https://doi.org/10.3390/economies7040104
Chicago/Turabian StyleSeip, Knut Lehre, Yunus Yilmaz, and Michael Schröder. 2019. "Comparing Sentiment- and Behavioral-Based Leading Indexes for Industrial Production: When Does Each Fail?" Economies 7, no. 4: 104. https://doi.org/10.3390/economies7040104
APA StyleSeip, K. L., Yilmaz, Y., & Schröder, M. (2019). Comparing Sentiment- and Behavioral-Based Leading Indexes for Industrial Production: When Does Each Fail? Economies, 7(4), 104. https://doi.org/10.3390/economies7040104






