Value Premium and Technical Analysis: Evidence from the China Stock Market

Abstract

We find value premium in the Chinese stock market using a conventional buy-and-hold approach which longs the portfolio with the highest BM ratio and shorts the one with the lowest BM ratio. Based on the finding, we test a new strategy by combining the value premium effect and technical analysis. During the sample period (1995 to 2015), we trade the objective portfolio or risk-free asset according to the moving average timing signals, and we find excess return from such a zero-cost trading strategy. We perform various robustness tests and find that the excess returns remain significantly positive after adjusting for risks (on three factor models) and transaction costs. In general, we find that the combined trading strategy can generate significant positive risk-adjusted returns after the transaction costs.

1. Introduction

In this paper, we investigate whether technical analysis can add additional value to investments in the Chinese stock market. In particular, we try to answer the research question of whether technical strategies can enhance conventional value investment (high BM-minus-low BM) in the Chinese market. For this purpose, we propose and examine the performance of a zero-cost strategy that combines technical analysis and value premium investing. The results show that the combined strategy can generate superior performance compared to simple buy-and-hold value investment. The excess profits made from the proposed strategy remain prominent after transaction costs are taken into consideration.

The value premium refers to the excess average return on stocks with high book-to-market (BM) ratios over those with low BM ratios. The positive relationship between BM ratio and average return are first documented in the 1980s (e.g., Rosenberg et al. 1985). Numerous studies have since confirmed the value premium effect using U.S. (Lakonishok et al. 1994; Fama and French 1992, 1996) or global data (Fama and French 1998; Bauman et al. 1998). Two main theories have been proposed to explain why the value premium exists. The first theory links the value premium with the financial distress risk of high BM firms (Fama and French 1992, 1996). The second theory claims that overreacting investors underprice the distressed firms, which leads to higher returns on high BM stocks (Daniel and Titman 1997).

The value premium has also been found to be prevalent in China’s financial market. Wang (2004) shows that there is a significant value premium in China using different investment portfolios. Su and Xu (2006) argue that the value premium exists generally in China and has a greater influence on small-size stocks. Xie and Qu (2016) study the period after the non-tradable share reform and find that the significant value premium exists from 2005 to 2012. However, these papers focus on the value premium generated from the conventional buy-and-hold returns on BM portfolios; none of them extend the research scope to the influence of technical analysis on value investing.

Technical analysis, which encompasses trading strategies using past price or volume information to predict future asset prices, has been shown to be a useful tool in the stock market. For example, Brock et al. (1992) and Lo et al. (2000) suggest that technical analysis strategy can add value to investment and is helpful for making better decisions. Zhu and Zhou (2009) explore the usefulness of moving average analysis and propose that technical analysis strategy becomes more remarkable in an incomplete information environment. Han et al. (2013) find that moving average timing strategy outperforms simple buy-and-hold strategy and has a greater effect on portfolios with higher information uncertainty. Wong et al. (2003) show that technical analysis tools such as moving average and relative strength index generate considerable profits in Singapore’s market, and Du and Wong (2018) find the simple moving average trading rule significantly outperform the buy-and-hold strategy on the Singapore Straits Times Index.

Menkhoff (2010) uses an international survey with fund managers and finds that technical analysis is prevalently used in the industry, which has a great relation with the belief of fund managers that psychological influences on stock prices are substantial. Han et al. (2016) use the moving average indicator to construct a new equity pricing factor, the trend factor, which can capture three types of trend related anomalies (short-, intermediate-, and long-term trends) and outperform other well-known reversal and momentum related factors. Technical analysis tools can also be used in forecasting market level equity risk premium (Neely et al. 2014).

According to research conducted by Lim and Luo (2012), who examine 14 Asian stock markets, including China’s, none of the stock returns follow a martingale difference sequence. This indicates that in the Chinese market, the stock price does not reflect information immediately; therefore, the application of technical analysis should be meaningful and useful in this information-asymmetric environment. A number of studies support this idea. For instance, Wong et al. (2005) find a group of moving average indicators can generate positive excess returns in Chinese stock markets. Wang et al. (2011) find that there is significant predictability of technical analysis in price changes in China.

However, the usefulness of technical analysis is debatable. Shynkevich (2012) find that, using four families of technical indicators, the performance of technical indicators deteriorated substantially in the second half of 2010s due to the improvement of efficiency in the US market. Chen and Li (2006) study the application of technical analysis in China and do not find it to be superior to passive trading strategies, as they conclude that the past price or volume cannot provide extra information in China. Zhu et al. (2015) investigate the profitability of technical trading strategies, including the moving average and trading range break, on the Shanghai Composite Index, and they show that these strategies cannot beat the buy-and-hold strategy if transaction fees are taken into consideration.

Our study is motivated by at least three causes. First, although the value premium generated from buy-and-hold strategy has been proven to be existent in China’s stock market, no study has explored whether technical analysis can further enhance the value investment in China. Our paper attempts to fill this gap. Second, a study by Ko et al. (2014) finds that in the Taiwan stock market, a market with no value premium, a combined strategy with value investment and moving average based trading can generate a better average return than the simple buy-and-hold value investment strategy. Because our sample is from a market with a positive value premium, our findings help determine whether the profitability of the combined strategy is independent of the existence of the value premium. Third, the mixed results on the usefulness of technical analysis in the Chinese market give us an incentive to provide additional evidence on this issue that can contribute to the literature on technical analysis-based trading in China.

Zhu and Zhou (2009) provide theoretical support for the rationale of our proposed approach. They utilize an asset allocation perspective to demonstrate that rational risk-averse investors would purposely adopt the moving average strategy combined with fixed wealth allocation rules, which can improve their expected utility substantially. This explains why the moving average strategy is widely used in practice among both institutional and individual investors.

We first construct decile portfolios from the sample according to the BM ratio of shares each year, with portfolio one consisting of stocks with the lowest BM ratios and portfolio ten consisting of the highest BM ratios. We then construct a zero-cost arbitrage portfolio by longing the highest BM portfolio and shorting the smallest BM portfolio at the same time. The return from such a portfolio is called the value premium. We then impose technical analysis on each BM portfolio with 20-day moving average timing signals. Based on the signals, we choose to hold either the stock portfolio or the risk-free asset.

We then form a new trading strategy by integrating the value premium effect and the moving average timing indicator into one. Under this combined strategy, we use the technical analysis based on the conventional buy-and-hold trading portfolio sorted by BM ratio. We further investigate whether the positive excess returns generated by the strategy are risk-driven. We compute the risk-adjusted excess returns by considering the risk from the capital asset pricing model (CAPM), Fama and French’s (1993) three-factor and liquidity-augmented four-factor models (Datar et al. 1998; Lam and Tam 2011). Moreover, we try different lag lengths of the moving average, such as 5, 10, 20, 50, 100, and 200 days of lag on the technical analysis portfolios. We also examine whether transactional costs eliminate the risk-adjusted excess returns.

We also perform robustness tests to ensure that the excess returns generated from the new strategy are reliable. First, we investigate the sub-period performance of the strategy by testing the risk-adjusted excess returns of these two sub-periods. Second, we use regression tests to check whether business cycles can affect the excess return. Third, we examine the timing ability of the strategy. Lastly, we perform tests on a subsample containing stocks that can be short sold.

The remainder of this paper is organized as follows. Section 2 describes the sample data and the details of the combined zero-cost trading strategy. Section 3 presents the empirical results. Section 4 discusses the robustness tests. Section 5 concludes the paper.

2. Data and Methodology

2.1. Data

China’s two main stock exchanges are the Shanghai and Shenzhen Stock Exchanges. On these two exchanges, two types of shares are listed: A-shares, which are priced and traded in RMB, and B-shares, which are priced in foreign currencies. We obtain stock-level data for all the A-shares from the China Stock Market and Accounting Research (CSMAR) database. We exclude financial companies from our sample because their BM ratios could have very different interpretations from those of companies in other industries. The China stock market was established in 1991, but until 1995, the number of stocks listed was very small. Hence, we examine the trading strategy for the period from 1 July 1995 to 30 June 2015.

Before executing the proposed strategy, we conduct a data-clearing procedure to delete stocks with negative BM ratios and remove stocks with no trading for three consecutive months. We remove 535,685 observations, about 9% of the sample, in this clearing step. We use the daily returns calculated from the stock prices adjusted for capital changes such as dividend payout, share repurchases, and stock splits. We use the daily interest rate for the one-year fixed time deposit as the proxy for the risk-free rate.

2.2. Zero-Cost Trading Strategy

The zero-cost trading strategy is constructed as follows. For the period from 1 July 1995 to 30 June 1996, we compute the end of the 1994 book-to-market (BM) ratios of stocks. We sort the stocks in ascending order by their BM ratios and assign them into decile portfolios. Portfolio 1 consists of stocks with the lowest BM ratios while Portfolio 10 consists of stocks with the highest BM ratios. We repeat this procedure for the next 20 years with annual rebalancing.

We then impose technical analysis on each BM portfolio with moving average timing signals rather than the passive buy-and-hold approach. First, we calculate the moving average (MA) indicator with L days of lag length as

$$A_{j,t,L}=\frac{P_{j,t-\left(L-1\right)}+P_{j,t-\left(L-2\right)}+\dots +P_{j,t-1}+P_{j,t}}{L},$$

(1)

where P_j,t is the average price for portfolio j on day t, L is the length in days of the moving average window, and A_j,t.L is the L-day MA indicator for portfolio j on day t.

The trading strategy is as follows. For each BM portfolio, we either buy or continue to hold the portfolio for today if the past price index P_j,t−1 is higher than the past MA indicator A_j,t−1,_L on t−1. Otherwise, we invest in the risk-free asset to protect our capital. We then compute the daily average return, ${\tilde{R}}_{j,t,L}$ or R_f,t,L, for the decile portfolios as below. For comparison, we also compute the return of the traditional buy-and-hold strategy for the deciles.

$${\tilde{R}}_{j,t,L}=\{\begin{array}{cc}{R}_{j,t},\hfill & if P_{j,t-i}>A_{j,t-1,L},\\ R_{f,t},\hfill & otherwise,\end{array}$$

(2)

Through comparisons between the returns of the moving average strategy and the traditional buy-and-hold strategy, we can study the differing effects of these two strategies on the BM premium. We expect that the portfolio returns will be higher after the application of technical analysis. Therefore, we compute the difference between the two strategies, $MA{P}_{j,t,L}$, by subtracting the return of the buy-and-hold strategy, $R_{j,t}$, from the return of the MA timing strategy, ${\tilde{R}}_{j,t,L}$. If $MA{P}_{j,t,L}$ is significantly greater than zero, this indicates that the MA timing strategy outperforms the traditional buy-and-hold strategy.

$$MA{P}_{j,t,L}={\tilde{R}}_{j,t,L}-R_{j,t}, j=1,2,\dots ,10,$$

(3)

After studying the difference between the two strategies, we investigate whether the return difference, if significant, is driven by exposure to alternative risk factors. We perform regressions on $MA{P}_{j,t,L}$ with three well-known asset pricing models in the literature: the CAPM, Fama, and French three-factor (FF3F), and liquidity augmented four-factor (LIQ4F) models, which are

$$MA{P}_{j,t,L}={\alpha }_{j,L}+{\beta }_{j,L,MKT}{R}_{MKT,t}+{\epsilon }_{j,t,L}, j=1,2,\dots ,10,$$

(4)

$$MA{P}_{j,t,L}={\alpha }_{j,L}+{\beta }_{j,L,MKT}{R}_{MKT,t}+{\beta }_{j,L,SMB}{R}_{SMB,t}+{\beta }_{j,L,HML}{R}_{HML,t}+{\epsilon }_{j,t,L}, j=1,2,\dots ,10,$$

(5)

$$MA{P}_{j,t,L}={\alpha }_{j,L}+{\beta }_{j,L,MKT}{R}_{MKT,t}+{\beta }_{j,L,SMB}{R}_{SMB,t}+{\beta }_{j,L,HML}{R}_{HML,t}+{\beta }_{j,L,LIQ}{R}_{LIQ,t}+{\epsilon }_{j,t,L}, j=1,2,\dots ,10,$$

(6)

where $R_{MKT,t}$ is market excess returns; $R_{SMB,t}$ is the size factor; $R_{HML,t}$ is the book-to-market factor; $R_{LIQ,t}$ is the liquidity risk factor proxied by turnover ratio; ${\epsilon }_{j,t,L}$ is the error term assumed to have a zero mean and to be uncorrelated with all other explanatory variables; and the factor sensitivities or loadings ${\beta }_{j,L,MKT}$, ${\beta }_{j,L,SMB}$, ${\beta }_{j,L,HML}$, and ${\beta }_{j,L,LIQ}$ are the slope coefficients for the factors, respectively. ${\alpha }_{j,L}$ is the intercept of the regression.

Our new technical analysis enhanced BM strategy is implemented as follows. We start with the traditional BM strategy, in which we long the highest BM portfolio and short the lowest BM portfolio. Next, we apply the moving average indicator trading strategy to the two extreme BM portfolios. If the previous index price of portfolio 10 is higher (lower) than the previous moving average indicator, it indicates that the portfolio value is about to rise (fall). Therefore, we will long portfolio 10 (risk-free asset). In the same month, if the previous index price of portfolio 1 falls below (rises above) its previous MA indicator, the portfolio value is expected to drop (increase), and we will short portfolio one (risk-free asset). The return of such a trend-following strategy is denoted by $TL{S}_{MA,t,L}$ and is shown as follows.

$$TL{S}_{MAP,t,L}=\{\begin{array}{cc}{R}_{10,t}-R_{1,t},\hfill & if P_{10,t-1}>A_{10,t-1,L} and P_{1,t-1}<A_{1,t-1,L};\hfill \\ R_{10,t}-R_{f,t},\hfill & if P_{10,t-1}>A_{10,t-1,L} and P_{1,t-1}>A_{1,t-1,L};\hfill \\ R_{f,t}-R_{1,t},\hfill & if P_{10,t-1}<A_{10,t-1,L} and P_{1,t-1}<A_{1,t-1,L};\hfill \\ 0,& otherwise,\hfill \end{array}$$

(7)

$$TL{S}_{MAP,t,L}=\{\begin{array}{cc}0,& if P_{10,t-1}>A_{10,t-1,L} and P_{1,t-1}<A_{1,t-1,L};\hfill \\ R_{1,t}-R_{f,t},\hfill & if P_{10,t-1}>A_{10,t-1,L} and P_{1,t-1}>A_{1,t-1,L};\hfill \\ R_{f,t}-R_{10,t},\hfill & if P_{10,t-1}<A_{10,t-1,L} and P_{1,t-1}<A_{1,t-1,L};\hfill \\ R_{1,t}-R_{10,t},\hfill & otherwise,\hfill \end{array}$$

(8)

$TL{S}_{MAP,t,L}$ is the result of subtracting the return of the proposed trading strategy from the return of a traditional BM strategy. It measures the difference between the proposed trading strategy, combining the value premium effect and technical analysis with the simple buy-and-hold strategy.

3. Empirical Findings

3.1. Summary Statistics

Table 1. Descriptive statistics for BM, MA(20), and MAP ranked portfolios.

Rank	BM Ratio	BM Decile Portfolios				MA(20) Timing Portfolios				MAP
		Ave Ret	Std Dev	Skew	t	Ave Ret	Std Dev	Skew	t	Ave Ret	Std Dev	Skew	t
Panel A: Equally-weighted portfolios
Low	0.12	5.51	15.97	0.55	1.54	11.88	12.80	1.02	4.15	5.57	8.39	0.52	2.97
2	0.20	5.88	15.58	0.41	1.69	11.06	14.68	0.09	3.37	4.28	8.50	1.74	2.25
3	0.26	6.75	16.05	0.61	1.88	10.73	13.82	0.97	3.47	3.11	7.16	−0.02	1.94
4	0.31	7.82	15.97	0.62	2.19	13.23	12.56	0.55	4.71	4.44	8.12	0.75	2.45
5	0.35	8.06	16.22	0.33	2.22	12.71	13.49	0.39	4.21	3.64	8.28	0.24	1.97
6	0.40	9.39	16.94	0.41	2.48	13.18	13.72	0.94	4.29	2.84	6.46	0.29	1.96
7	0.45	9.46	16.65	0.40	2.54	13.81	13.55	0.61	4.56	3.36	8.25	0.31	1.82
8	0.52	9.45	17.35	0.42	2.43	14.40	16.46	0.90	3.91	3.89	8.64	0.26	2.02
9	0.62	9.78	17.69	0.43	2.47	13.58	14.70	0.76	4.13	2.85	5.51	0.04	2.31
High	0.85	10.28	17.78	0.77	2.59	13.03	15.85	0.79	3.68	1.77	7.15	0.21	1.11
High–Low		4.77	8.32	1.22	2.56	0.86	9.12	2.10	0.42	−4.21	7.22	0.49	−2.61
		(2.07)				(0.40)				(−2.87)
TLS						16.43	14.92	0.28	4.92	11.23	12.40	0.99	4.05
						(4.85)				(4.12)
Panel B: Value-weighted portfolios
Low	0.12	5.78	16.13	0.41	1.60	11.22	13.12	1.02	3.82	4.62	8.88	0.40	2.33
2	0.20	5.44	14.80	0.52	1.64	10.36	14.42	0.12	3.21	4.02	8.84	1.61	2.04
3	0.26	5.34	16.42	0.87	1.45	9.76	14.26	1.14	3.06	3.49	7.29	0.24	2.14
4	0.31	8.78	16.79	0.63	2.34	12.11	12.32	0.46	4.40	2.26	7.30	−0.05	1.38
5	0.35	7.28	17.78	0.58	1.83	11.86	14.03	0.54	3.78	3.55	9.00	0.73	1.76
6	0.40	7.13	18.43	0.01	1.73	12.33	14.06	0.78	3.92	4.19	6.85	0.76	2.73
7	0.45	9.49	16.60	0.41	2.56	13.21	13.42	0.72	4.40	2.74	8.09	0.24	1.51
8	0.52	8.31	17.79	0.58	2.09	13.02	17.48	1.02	3.33	3.61	8.81	0.44	1.83
9	0.62	10.35	19.24	0.84	2.41	13.41	15.59	0.95	3.85	2.12	6.65	0.11	1.42
High	0.85	10.79	18.43	0.85	2.62	13.03	17.01	0.80	3.42	1.24	6.80	0.28	0.82
High–Low		4.78	8.46	0.58	2.53	1.39	10.32	1.44	0.60	−3.87	8.16	0.16	−2.12
		(2.15)				(0.60)				(−2.12)
TLS						15.34	15.97	0.42	4.30	9.94	12.06	0.87	3.68
						(4.50)				(3.95)

The sample stocks are sorted in ascending order by their BM ratios and assigned into decile portfolios each year. The equally-weighted and value-weighted portfolio daily returns are then obtained, for which the summary statistics are reported in Panels A and B, respectively. The average returns, standard deviation, skewness, and t-test statistics of these portfolios are reported. MA(20) represents the technical analysis with 20-day moving average timing signals imposed on the BM portfolios. MAP represents the difference between the MA(20) strategy and the buy-and-hold strategy. High–Low represents the return difference between the highest and lowest BM portfolios, the highest MA(20) and lowest MA(20) portfolios, and the highest and lowest MAP, respectively. TLS_MA represents the proposed technical analysis enhanced BM strategy. TLS_MAP represents the difference between the prosed strategy and the buy-and-hold strategy. Simple t-statistics are reported in column t and Newey and West (1987) t-statistics are reported in the parentheses.

shows the summary statistics of the returns of the buy-and-hold strategy, $R_{j,t}$, the returns of the 20-day moving average timing strategy, ${\tilde{R}}_{j,t,L}$, and the difference between the two, $MA{P}_{j,t,L}$. The average return of our proposed trading strategy, $TL{S}_{MA,t,L}$, and the difference between the new strategy and the traditional BM strategy, $TL{S}_{MAP,t,L}$, are also reported at the bottom.

The average BM ratios for all 10 portfolios are less than one and range from 0.12 (portfolio 1) to 0.85 (portfolio 10), suggesting that the average book values of the sample stocks are smaller than their average market values in the China market. We further investigate the change of sample stocks’ BM ratios over time and find that there exist stocks with BM ratios bigger than one after 2008, but the proportion is very small.

In panel A, we present the results for equally-weighted portfolios. For the decile BM portfolios, the simple average returns range from 5.51 basis points to 10.28 basis points (we use “points” to refer to basis points hereafter) and increase monotonically as a whole except for the return of portfolio 8 (9.45 points), which is slightly smaller than that of portfolio 7 (9.46 points). Seven (two) of the average returns are significant at the 5% (1%) level. The average high-minus-low return is 4.77 point with a t-value of 2.071, which is significant at the 5% level. This provides preliminary evidence that BM effect exists in China market. The values of the standard deviations are increasing monotonically, which indicates that portfolios with higher average returns tend to have higher standard deviations in China. The standard deviation for the high-minus-low portfolio is about half of the value of the other BM portfolios, which is consistent with the nature of a zero-cost hedging portfolio. The skewness of the portfolios is very small, with most of the values lower than 0.6.

For the 20-day moving average (MA(20)) timing portfolios, we find that the average returns of MA20 portfolios range from 10.73 to 14.40 points and there is no obvious trend in the returns. We find that the average returns of MA timing portfolios are at least double those of the buy-and-hold portfolios. However, we observe that the standard deviations are smaller than those of the BM portfolios, which demonstrates that when we apply MA(20) strategy to the BM portfolios, we receive higher returns but lower total risks, which is a promising result. We check whether these profits (higher returns) are due to risk exposure or not in our later tests.

The differences between MA(20) and BM portfolios, MAPs, are all positive and range from 1.77 to 5.57 points. Interestingly, we observe the special pattern that the average MAPs are generally decreasing as portfolio BM ratios increase, which indicates that the moving average technical analysis is more successful for portfolios with lower BM ratios.

For the proposed trading strategy, we can see that the average high-minus-low return of the MA(20) portfolios is very small (0.86 points) and insignificant (t = 0.40), much smaller than that of the BM portfolios (4.77 points). We conjecture that the small and insignificant result is caused by the misuse of the moving average timing signals. The high-minus-low return of MA(20) can be regarded as longing the highest MA(20) and shorting the lowest MA(20) portfolios. Shorting the lowest portfolio means that we will sell the assets when the last trading price $P_{j,t-1}$ is higher than the last 20-day moving average indicator $A_{j,t-1,L}$, whose signal indicates that the price will increase. In other words, we will sell the assets that we think will grow, which is logically wrong. Therefore, we conduct our trading strategy with the correct use of the moving average indicator for the lowest BM portfolio, which we discussed in the methodology section. The $TS{L}_{MA,t,L}$ is 16.43 points, which is substantially higher than that of the buy-and-hold strategy (4.77 points). The average significant difference between the two strategies ($TS{L}_{MAP,t,L}$) is 11.23 points, which represents the additional profits from the new TLS strategy, which is 2.36 times the buy-and-hold strategy.

In panel B, we present the performance of the value-weighted portfolios to check the size effect on the result. We find that the magnitude of the portfolio average returns is only slightly bigger than the return of the corresponding equally-weighted portfolios. The simple average return of the buy-and-hold strategy ranges from 5.34 to 10.79 points, with portfolio 10 (3) getting the highest (lowest) average return. In addition, all deciles with the MA(20) strategy have higher returns than the BM portfolios, ranging from 9.76 to 13.03 points. All of the MAP returns are positive and have lower standard deviations. The daily average return of the new trading strategy, $TS{L}_{MA,t,L}$, is 15.34 points (t = 4.50), which is 221.13% higher than the high-minus-low return of the BM portfolio (4.78 points) but lower than the corresponding equally-weighted portfolios. The difference between MA(20) and buy-and-hold strategies, $TS{L}_{MAP,t,L}$, is 9.94 points (t = 3.95), which is also slightly lower than that of the corresponding equally-weighted portfolios.

Overall, Table 1 shows that the value premium effect exists in the China stock market and that the moving average technical analysis strategy is useful in producing positive and significant excess returns. In addition, the proposed strategy, $TS{L}_{MA,t,L}$, clearly outperforms the traditional buy-and-hold BM strategy.

3.2. Risk-Adjusted Performances

The MAP results show that the MA timing strategy outperforms the buy-and-hold strategy. However, we observe that generally, portfolios with higher returns have higher standard deviations, which suggests that their risk (or total risk) levels are different. Therefore, a natural research question is whether the return differences are due to exposure to risks. In this sub-section, we concentrate on the risk-adjusted profitability of MAP and TLS using three asset pricing models: the CAPM, FF3F, and LIQ4F models. We use MAP and $TL{S}_{MAP,t,L}$ as dependent variables and run time-series regressions against the risk factors. The results are presented in

Table 2. Time-series regressions with the CAPM and LIQ4F models.

Rank	CAPM			LIQ4F Model
	α	βmkt	Adj. R2	α	βmkt	βsmb	βhml	βliq	Adj. R2
Low	8.18	−0.45	0.40	9.08	−0.46	−0.59	0.20	0.15	0.45
	(5.41)	(−18.52)		(6.26)	(−18.38)	(−9.45)	(6.21)	(4.13)
2	7.13	−0.49	0.42	8.10	−0.49	−0.53	0.15	0.17	0.46
	(4.73)	(−18.38)		(5.59)	(−18.35)	(−8.92)	(5.03)	(4.99)
3	5.77	−0.46	0.39	6.70	−0.47	−0.51	0.15	0.16	0.42
	(3.75)	(−16.98)		(4.48)	(−16.78)	(−7.97)	(4.84)	(4.36)
4	7.42	−0.52	0.43	8.53	−0.51	−0.43	0.07	0.19	0.46
	(4.76)	(−18.50)		(5.58)	(−18.30)	(−6.95)	(2.24)	(5.39)
5	6.69	−0.53	0.44	8.12	−0.52	−0.53	0.05	0.15	0.47
	(4.20)	(−18.79)		(5.33)	(−18.59)	(−8.19)	(1.54)	(4.21)
6	5.64	−0.49	0.40	7.12	−0.48	−0.44	−0.01	0.19	0.44
	(3.48)	(−17.45)		(4.60)	(−17.56)	(−7.33)	(−0.28)	(5.41)
7	5.64	−0.49	0.40	8.00	−0.49	−0.47	−0.04	0.18	0.45
	(3.48)	(−17.45)		(5.12)	(−18.31)	(−7.44)	(−1.23)	(5.14)
8	6.98	−0.54	0.41	8.98	−0.51	−0.43	−0.12	0.19	0.48
	(4.10)	(−18.26)		(5.61)	(−18.34)	(−6.82)	(−3.20)	(5.18)
9	5.63	−0.49	0.39	7.30	−0.47	−0.37	−0.09	0.18	0.43
	(3.45)	(−17.32)		(4.69)	(−17.41)	(−6.29)	(−2.46)	(5.36)
High	4.65	−0.50	0.40	6.57	−0.48	−0.40	−0.14	0.15	0.45
	(2.86)	(−17.57)		(4.25)	(−17.92)	(−6.57)	(−3.56)	(4.20)
High–Low	−3.53	−0.05	0.01	−2.51	−0.02	0.19	−0.33	0.00	0.08
	(−2.49)	(−3.27)		(−1.82)	(−1.24)	(3.71)	(−8.34)	(−0.08)
TLSMAP	13.24	−0.09	0.01	15.14	−0.04	0.14	−0.46	0.12	0.06
	(5.24)	(−1.88)		(6.08)	(−0.86)	(1.39)	(−7.99)	(1.90)

The sample stocks are sorted in ascending order by their BM ratios and assigned into decile portfolios each year. The equally-weighted portfolio daily returns are then obtained. MAP is the difference between the MA(20) strategy and the buy-and-hold strategy. The regression models are $MA{P}_{j,t,L}={\alpha }_{j.L}+{\beta }_{j,L,MKT}{R}_{MKT,t}+{\epsilon }_{j,t,L}$ and $MA{P}_{j,t,L}={\alpha }_{j.L}+{\beta }_{j,L,MKT}{R}_{MKT,t}+{\beta }_{j,L,SMB}{R}_{SMB,t}+{\beta }_{j,L,HML}{R}_{HML,t}+{\beta }_{j,L,LIQ}{R}_{LIQ,t}+{\epsilon }_{j,t,L}$, where $R_{MKT,t}$ is market excess returns; $R_{SMB,t}$ is the size factor; $R_{HML,t}$ is the book-to-market factor; $R_{LIQ,t}$. is the liquidity risk factor proxied by turnover ratio; ${\epsilon }_{j,t,L}$ is an error term assumed to have a zero mean and to be uncorrelated with all other explanatory variables; and the factor sensitivities or loadings, ${\beta }_{j,L,MKT}$, ${\beta }_{j,L,SMB}$, ${\beta }_{j,L,HML}$, and ${\beta }_{j,L,LIQ}$, are the slope coefficients for the factors, respectively. ${\alpha }_{j.L}$ is the intercept of the regression. t-test statistics are presented in the parentheses.

.

If the portfolio average return, $MA{P}_{j,t,L}$ is not fully explained by the risk factors, we expect ${\alpha }_{j,L}$ to be significantly different from zero. Otherwise, it suggests that the positive additional return found in the MA strategy is artificial after taking exposure to well-documented risk factors into consideration.

Table 2 provides the results of the equally-weighted portfolios on the CAPM and LIQ4F models. Because the results of FF3F are similar to those from the LIQ4F model, we do not report them to save space. All of the alphas of the 10 portfolios in the two models are significantly different from zero at the 5% level, which suggests that the profits generated from the timing strategy are not fully captured by these well-known risk factors. The alphas of the CAPM model range from 4.65 to 8.18 points, while the alphas of the LIQ4F model range from 6.57 to 9.08 points.

The betas of the market excess return and size factors are all negative and highly significant, which can partially explain why the alpha becomes larger than the unadjusted return of the MAPs. Half of the coefficients of the HML factor are positive and half are negative. The coefficients of the LIQ factor are all significantly positive.

The alphas of the $TS{L}_{MAP}$ in the CAPM and LIQ4F models are 13.24 and 15.14 points, respectively, which are larger than the unadjusted $TS{L}_{MAP}$ (11.23 points). Interestingly, while the adjusted R² for most of the deciles in the two models are larger than 40%, the adjusted R² for the $TS{L}_{MAP}$ is extremely low. Overall, the low R² and significant alphas indicate that the CAPM and LIQ4F models cannot explain the excess profit from the new BM strategy.

3.3. Components of Strategies

We now establish that the moving average technical analysis can help us obtain better returns than the buy-and-hold strategy. We are curious about how exactly the excess returns are created. To answer this question, we consider the operation of the MA timing strategy. We know that we hold the underlying portfolio when the signal $P_{j,t-1}>A_{j,t-1,L}$ appears and hold the risk-free asset otherwise. Comparing this with the buy-and-hold strategy, a difference appears only when $P_{j,t-1}<A_{j,t-1,L}$. This difference is between the return generated from the underlying portfolio and the risk-free asset. Therefore, we can express the MAP return in another way:

$$MA{P}_{j,t,L}=\{\begin{array}{cc}0,\hfill & if P_{j,t-1}>A_{j,t-1,L};\\ R_{f,t}-R_{j,t},\hfill & otherwise,\end{array}$$

(9)

To examine the difference, we separate the sample into two parts: when $P_{j,t-1}>A_{j,t-1,L}$ (buy signal) and when $P_{j,t-1}\le A_{j,t-1,L}$ (sell signal). We calculate the proportion of days when R_j is higher (or lower) than R_f for the buying and selling signal states. The results are shown in

Table 3. Components of strategies.

Rank	Condition	Position	Equally-Weighted Portfolio
			Rp > Rf	Rp ≤ Rf
Low	Pi,t−1 > Ai,t−1,L	BM portfolio	58.8	41.2
	Pi,t−1 ≤ Ai,t−1,L	Risk-free asset	47.83	52.17
2	Pi,t−1 > Ai,t−1,L	BM portfolio	56.71	43.29
	Pi,t−1 ≤ Ai,t−1,L	Risk-free asset	49.35	50.65
3	Pi,t−1 > Ai,t−1,L	BM portfolio	56.96	43.04
	Pi,t−1 ≤ Ai,t−1,L	Risk-free asset	46.8	53.2
4	Pi,t−1 > Ai,t−1,L	BM portfolio	59.29	40.71
	Pi,t−1 ≤ Ai,t−1,L	Risk-free asset	48.82	51.18
5	Pi,t−1 > Ai,t−1,L	BM portfolio	59.71	40.29
	Pi,t−1 ≤ Ai,t−1,L	Risk-free asset	47.85	52.15
6	Pi,t−1 > Ai,t−1,L	BM portfolio	59.85	40.15
	Pi,t−1 ≤ Ai,t−1,L	Risk-free asset	46.03	53.97
7	Pi,t−1 > Ai,t−1,L	BM portfolio	60.02	39.98
	Pi,t−1 ≤ Ai,t−1,L	Risk-free asset	48.46	51.54
8	Pi,t−1 > Ai,t−1,L	BM portfolio	59.66	40.34
	Pi,t−1 ≤ Ai,t−1,L	Risk-free asset	49.38	50.62
9	Pi,t−1 > Ai,t−1,L	BM portfolio	60.15	39.85
	Pi,t−1 ≤ Ai,t−1,L	Risk-free asset	48.97	51.03
High	Pi,t−1 > Ai,t−1,L	BM portfolio	58.83	41.17
	Pi,t−1 ≤ Ai,t−1,L	Risk-free asset	49.82	50.18

We separate the MA(20) portfolio sample into two parts. One is when $P_{j,t-1}>A_{j,t-1,L}$ which indicates a buy signal and the other is when $P_{j,t-1}\le A_{j,t-1,L}$ which suggests a sell signal. We then compare the return of the BM portfolio and the risk-free rate. We calculate the proportion of each situation for buying and selling signal states.

.

We find that the proportions of the state in which $R_{j,t}>R_{f,t}$ are all bigger than 50%, ranging from 56.71% to 60.15%, when $P_{j,t-1}>A_{j,t-1,L}$. However, this does not affect the MAP. In addition, the proportions of the state in which $R_{j,t}<R_{f,t}$ are also all bigger than 50% when $P_{j,t-1}\le A_{j,t-1,L}$. The highest is 53.97% in decile 6 and the lowest is 50.18% in decile 10. Although the successful rates are not very high (mostly between 50% and 60%), all of them are bigger than 50%, which leads to better performance by MA strategy when a selling signal emerges. These results show that the MA signal is useful in generating positive excess returns and help explain why the moving average can outperform the buy-and-hold strategy.

3.4. Alternative Lag Lengths

In this sub-section, we investigate how the returns of the MAP and TLS change with the lag lengths. We conduct the moving average timing strategy with 5-day, 10-day, 20-day, 50-day, 100-day, and 200-day timing signals. The results are illustrated in Figure 1.

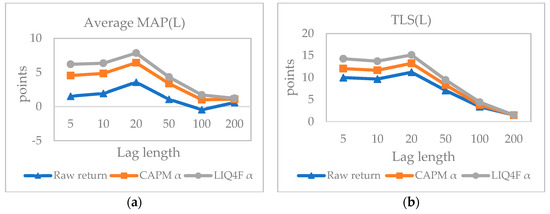
Figure 1a plots the average return of MAPs across the decile portfolios with different lag lengths. The 20-day average MAP return is the highest (in fact, although it is not plotted, the 20-day MAP is the highest for each decile portfolio). The 5-day MAP and 10-day MAP are also significantly positive but are slightly smaller than that of the 20-day signals. The returns with signals that are longer than 20 days start to decline and become progressively smaller, and the results of the 100-day lag even become negative. The CAPM and LIQ4F model-adjusted MAP alphas present similar patterns to that of the unadjusted returns.

The returns of the proposed trading strategy, TLS, are plotted in Figure 1b. Again, the 20-day lag strategy generates the highest raw and risk-adjusted profits. The MA(5) and MA(10) strategies also perform well, as their returns are close to that of MA(20). However, when lags longer than 50 days are used, the strategy return drops sharply, almost reaching zero. We conjecture that this is because the Chinese stock market is highly volatile. A shorter moving average signal can capture the fluctuations in information more accurately than a longer moving average signal. The signals with long lag length may miss important information changes, and so the abnormal return produced by these signals becomes flat and small.

The results seem to suggest that a shorter moving average of up to 50 days can produce significant and meaningful positive returns. However, the 20-day lag signal provides the best result by capturing the most information regarding past prices. To sum up, lag length can influence the performance of the moving average timing strategy, and we need to choose the best one for China’s stock market.

3.5. Transaction Operations

In the real market, the utilization of the moving average timing strategy would induce more transaction operations, resulting in higher transaction costs. In this section, we examine the effect of trading costs on the earlier results.

Table 4. Transaction operations.

Rank	MAP(5)			MAP(10)			MAP(20)			MAP(50)			MAP(100)			MAP(200)
	Holding	Freq	BETC	Holding	Freq	BETC	Holding	Freq	BETC	Holding	Freq	BETC	Holding	Freq	BETC	Holding	Freq	BETC
Low	3.80	0.29	38.77	5.56	0.20	41.20	9.35	0.13	83.35	19.37	0.07	81.28	50.06	0.04	−7.51	168.65	0.02	87.36
2	3.81	0.29	8.50	5.76	0.20	17.49	10.34	0.13	64.09	16.06	0.09	−8.96	51.74	0.04	16.88	150.48	0.02	41.78
3	3.92	0.29	11.84	6.34	0.19	15.16	9.90	0.13	47.22	25.57	0.07	24.41	43.17	0.05	−41.89	130.99	0.02	28.16
4	3.87	0.28	13.58	6.14	0.19	23.75	10.54	0.12	76.79	19.94	0.08	8.84	50.81	0.05	−25.54	137.26	0.02	0.30
5	3.95	0.28	8.28	6.16	0.19	18.48	9.59	0.13	58.54	21.51	0.07	33.90	48.25	0.04	−2.14	176.57	0.02	121.70
6	4.07	0.28	3.56	6.26	0.19	10.09	10.95	0.12	48.74	25.31	0.07	45.19	67.41	0.04	−10.50	183.08	0.02	126.02
7	3.92	0.28	4.66	6.40	0.18	28.86	11.45	0.11	61.02	22.11	0.07	22.78	46.50	0.05	−22.12	141.55	0.02	65.13
8	4.07	0.27	16.91	6.63	0.18	13.19	11.04	0.11	69.38	27.90	0.07	78.57	47.64	0.05	−9.26	146.77	0.02	81.68
9	4.00	0.28	4.42	6.37	0.18	22.56	10.80	0.12	48.92	20.48	0.07	33.73	46.56	0.05	−18.22	156.47	0.02	120.17
High	4.01	0.28	−3.00	6.72	0.18	10.80	10.45	0.12	28.91	21.22	0.08	−9.39	48.86	0.06	−60.33	141.45	0.02	52.11
High–Low		0.45			0.32			0.22			0.13			0.09			0.03
TLS		0.45			0.32			0.22			0.13			0.09			0.03
Transaction Cost for TLS			7.09			5.24			3.95			2.99			2.68			2.58
MAP for TLS			9.99			9.67			11.23			7.08			3.39			1.51
Return after Transaction Cost			2.91			4.43			7.28			4.08			0.70			−1.08

We calculate the average holding days, trading frequency of MA and TLS portfolios, break-even transaction cost and after transaction cost returns of TLS. The average holding days represent the average number of days during which the portfolio is held before it is sold out. The trading frequency of the portfolios is the fraction of the number of trading days to the number of days in the whole sample period. Break-even transaction cost (BETC) is the fee which is required in each round-trip transaction for the portfolios if the final profit is zero. Transactions Cost for TLS consists commission, transfer fee, stamp tax, and interest fee for stock borrow. MAP for TLS is the return difference between the proposed technical analysis enhanced BM strategy and the traditional buy-and-hold BM strategy.

reports the statistics that address this issue.

The average holding days is the average number of days that we hold the portfolio. Longer average holding days suggest that the trading portfolio is more stable. From Table 4, we can tell that the average holding days becomes longer as the moving average lag length increases. The average holding days of the 5-day MAP is around 4 days, while that of the 20-day MAP is around 10 days. Moreover, the average holding days for 200-day MAP ranges from 130.99 days to 183.08 days. We do not report those of the two zero-cost trading strategies because it is difficult to define the holding period while investors hold two portfolios simultaneously.

Next, we calculate the trading frequency of the MAP and TLS portfolios, which is the fraction of the number of trading days of the number of days in the whole period. A shorter (longer) lag length strategy implies that the portfolios will be traded more (less) and that the trading frequency should be higher (smaller). For the 20-day lag length, the trading frequency ranges from 0.11 to 0.13 for the 10 deciles and is 0.22 for the High–Low and TLS strategies. The trading frequency for all of the deciles with lag lengths longer than 20 days is lower than 0.10. Apparently, the MA timing strategies incur higher transaction fees if a shorter lag length is chosen for the MA indicator.

According to the China Securities Regulatory Commission, the Securities Association of China and notices of securities companies, the cost for trading A-shares consists of a commission, transfer fee, and stamp tax. The commission fee should be lower than 30 basis points of the transaction amount and is determined by securities companies in the allowable interval. Because securities companies in China use low price strategies to attract customers, according to the Eastmoney Choice Database, the average commission fee for trading stocks in 2015 is just 5.1 basis points. The amounts of the other two kinds of fees are fixed. The transfer fee for A-shares is 0.2 basis points of the transaction amount, and the stamp tax is 10 basis points only on the sell side. To sum up, we need to pay 20.6 ((5.1 + 0.2)*2 + 10) basis points on average for a round trip of transactions. Following Balduzzi and Lynch (1999), we assume that we pay the transaction fee when we trade BM portfolios but not when we trade the risk-free asset.

Following Han et al. (2013) and Ko et al. (2014), we use break-even transaction costs (BETCs) to evaluate the profit versus cost for the MAP returns. BETC here is the fee that we can afford in each round-trip transaction for the deciles if the final profit is zero. We report the results in Table 4, where we label BETCs with n.a. when the MAP return is negative, as BETCs are meaningless in such a situation. Overall, the BETCs are mostly higher than 20.6 basis points. The MAP(5) and MAP(10) strategies in general have lower BETCs because transaction operations are too frequent, thus incurring higher transaction fees. The BETCs of MAP(20) are higher than 20.6 for all deciles, indicating positive after-cost profitability. The BETCs start to decline after the MAP(20) strategy. This pattern is similar to the results in Figure 1.

In our new proposed zero-cost trading strategy, TLS, we need to borrow stocks when receiving short signals and pay interest for stock borrowing. In China, most interest rates for short-selling are lower than 9% annually, which is 2.4658 points daily (9%/365). To compute the after-cost returns of TLS, in addition to the normal transaction fee, we need to subtract the interest fee. We calculate the interest fee by multiplying the short-selling interest rate by the number of days that we borrow stocks. From Table 4, we can see that transaction costs for TLS decrease monotonically from 7.09 to 2.58 points as the lag length increases. We obtain a positive final return for all of the portfolios except for the MAP(200) strategy. Again, the MAP(20) strategy generates the highest after-transaction-cost TLS returns, which is consistent with the findings in Figure 1. Therefore, MA timing strategy with 20-day lag seems to be the best choice both before and after transaction costs.2

4. Robustness Tests

This section presents the tests of the robustness of the MA and TLS trading strategies. First, we examine whether there is a difference in the trading results in the sub-periods before and after the non-tradable stock reform in China. Second, we investigate whether business cycles affect returns. Third, we study the impact of market timing ability on the strategies. Lastly, we use an alternative sample that contains stocks for which short-selling is permitted in China’s market.

4.1. Sub-Period Analysis

Since China’s market underwent non-tradable stock reform in 2005, market conditions, such as market regulations, rules, trading mechanisms, participants, and trading volume, have changed drastically. To investigate the effect of the policy change on our strategy, we conduct tests on sub-periods, dividing our whole sample period at mid-2005 into two periods of nearly equal length. We repeat our analysis and obtain the daily average return data for the two sub-periods, 1 July 1995 to 30 June 2005 and 1 July 2005 to 30 June 2015. To examine the difference between the two subsamples, we conduct a two-sample mean test. First, we check the normality of the two subsamples using the Kolmogorov–Smirnov test, which is suitable for big data like ours. Panel A of

Table 5. Sub-period analysis.

Panel A: Normality Check (Kolmogorov–Smirnov)								Panel B: Wilcoxon Two-Sample Test
Rank			First Sub-Period		Second Sub-Period			Rank	Statistic		Normal Approximation Z	Two-Sided Pr > |Z|
			Statistic D	p-Value	Statistic D	p-Value
Low			0.2586	<0.0100	0.3258	<0.0100		Low	6021507		3.50	0.0005
2			0.2884	<0.0100	0.3415	<0.0100		2	5905501		0.91	0.3607
3			0.2925	<0.0100	0.3346	<0.0100		3	5967378		2.36	0.0184
4			0.2687	<0.0100	0.3349	<0.0100		4	5992645		2.89	0.0038
5			0.2741	<0.0100	0.3203	<0.0100		5	5956286		2.06	0.0399
6			0.2917	<0.0100	0.3289	<0.0100		6	5992566		2.93	0.0034
7			0.285	<0.0100	0.3341	<0.0100		7	5942272		1.76	0.0781
8			0.2857	<0.0100	0.3285	<0.0100		8	5956512		2.08	0.0375
9			0.2863	<0.0100	0.3307	<0.0100		9	5982790		2.69	0.0071
High			0.2883	<0.0100	0.3223	<0.0100		High	5924624		1.35	0.1766
High–Low			0.2286	<0.0100	0.2402	<0.0100		High–Low	5818216		−1.03	0.3020
TLS			0.1373	<0.0100	0.1305	<0.0100		TLS	5744009		−2.52	0.0118
Panel C: Time-series regressions with LIQ4F model
Rank	First Sub-Period						Second Sub-Period
	α	βmkt	βsmb	βhml	βliq	Adj. R2	α	βmkt	βsmb	βhml	βliq	Adj. R2
Low	7.24	−0.43	−0.56	0.22	0.14	0.44	10.96	−0.48	−0.53	0.09	0.20	0.46
	(4.01)	(−11.98)	(−6.95)	(5.61)	(2.82)		(4.86)	(−14.38)	(−6.15)	(1.67)	(3.84)
2	3.95	−0.49	−0.52	0.15	0.11	0.48	12.07	−0.49	−0.43	0.08	0.28	0.45
	(2.13)	(−11.99)	(−6.18)	(3.94)	(2.35)		(5.47)	(−14.29)	(−5.23)	(1.35)	(5.37)
3	6.07	−0.44	−0.54	0.13	0.08	0.43	7.16	−0.48	−0.38	0.09	0.30	0.42
	(3.43)	(−10.85)	(−6.56)	(3.67)	(1.69)		(2.97)	(−13.11)	(−4.16)	(1.54)	(5.11)
4	6.92	−0.49	−0.45	0.04	0.11	0.49	10.02	−0.52	−0.33	0.04	0.31	0.45
	(3.81)	(−12.09)	(−5.74)	(1.11)	(2.37)		(4.06)	(−14.01)	(−3.72)	(0.69)	(5.49)
5	6.45	−0.49	−0.44	0.02	0.06	0.47	9.86	−0.55	−0.44	−0.04	0.32	0.48
	(3.41)	(−11.56)	(−5.42)	(0.65)	(1.19)		(4.19)	(−15.19)	(−4.77)	(−0.71)	(5.34)
6	5.75	−0.44	−0.39	−0.03	0.13	0.43	8.73	−0.51	−0.42	−0.03	0.26	0.44
	(3.07)	(−11.45)	(−4.98)	(−0.89)	(3.10)		(3.57)	(−13.69)	(−4.82)	(−0.48)	(4.47)
7	5.43	−0.44	−0.45	−0.07	0.10	0.44	10.83	−0.54	−0.41	−0.08	0.29	0.48
	(2.88)	(−11.79)	(−5.91)	(−1.77)	(2.48)		(4.43)	(−14.70)	(−4.43)	(−1.30)	(4.94)
8	7.63	−0.48	−0.40	−0.13	0.17	0.49	10.58	−0.55	−0.43	−0.15	0.22	0.48
	(3.83)	(−11.48)	(−4.93)	(−2.87)	(3.83)		(4.24)	(−14.84)	(−4.77)	(−2.20)	(3.58)
9	5.81	−0.44	−0.40	−0.10	0.12	0.43	8.71	−0.49	−0.25	−0.17	0.29	0.44
	(2.94)	(−11.57)	(−5.15)	(−2.19)	(2.85)		(3.64)	(−13.22)	(−2.98)	(−2.77)	(5.22)
High	3.83	−0.41	−0.33	−0.13	0.14	0.42	9.73	−0.54	−0.39	−0.21	0.18	0.48
	(1.94)	(−10.87)	(−4.39)	(−2.84)	(3.06)		(4.23)	(−15.22)	(−4.60)	(−3.34)	(3.18)
High–Low	−3.41	0.02	0.22	−0.35	0.00	0.12	−1.22	−0.05	0.14	−0.30	−0.02	0.04
	(−1.83)	(1.09)	(3.05)	(−7.28)	(−0.03)		(−0.60)	(−2.46)	(1.90)	(−6.23)	(−0.45)
TLS	11.12	0.04	−0.05	−0.41	0.19	0.09	19.32	−0.11	0.22	−0.52	0.06	0.05
	(3.42)	(0.52)	(−0.31)	(−5.62)	(2.25)		(5.20)	(−1.81)	(1.61)	(−5.35)	(0.70)

The two sub-periods are before and after the non-tradable stock reform. The first sub-period is from 1 July 1995 to 30 June 2005 and the second sub-period is from 1 July 2005 to 30 June 2015. Panel A presents the results of the Kolmogorov–Smirnov test which checks the normality of the two subsamples. Panel B presents the results of the Wilcoxon rank-sum test which checks the difference between the two sample periods after knowing they do not follow normal distributions. Panel C presents results of the time-series regressions with the LIQ4F model for the two sub-periods. t-test statistics are presented in the parentheses.

shows that all of the p-values for the sample differences are smaller than 0.01, which indicates that the samples do not follow a normal distribution.

We then conduct the Wilcoxon rank-sum test to check the difference between the two sub-periods after determining that they do not follow a normal distribution. Panel B of Table 5 reports the test results. Most of the p-values are smaller than 0.1, ranging from 0.0005 to 0.3607. The p-value of the TLS portfolio is 0.0118, which is very small and rejects the null hypothesis. The two sub-samples are significantly different from each other in the TLS strategy.

Next, we run regressions with the CAPM, FF3F, and LIQ4F models to check the robustness of the risk-adjusted returns. Because the results are similar, we only report the LIQ4F model alphas and betas in the sub-periods in Table 5 to save space.

Overall, we find that the two sub-periods’ results are similar to those for the whole period. All of the alphas of the deciles are positive, and almost all of them are significant (portfolio 10 is marginally significant at 10%). As in the previous findings, the coefficients of market excess return and SMB are negative. The TLS strategy alphas are large and highly significant for both sub-periods; however, the result for the latter sub-period is better than the former for both the deciles and the TLS. Specifically, the second sub-period alpha of the TLS is 19.32 points, while that of the former period is 11.12. The results suggest that the MA and TLS strategies work better in the most recent period, which has undergone non-tradable share reform to push more non-tradable shares to become tradable shares in the market. As many more shares are traded in the market, the market becomes more efficient, which suggests that technical analysis should become less profitable in the market. However, our results seem to contradict this inference. These results are interesting and need further investigation, which is beyond the scope of our study.

4.2. Business Cycles

We now come to the question of whether there is any relation between the moving average signals and business cycles. Here, we use two methods to test the influence of business cycles. First, Liew and Vassalou (2000) construct the following model, which uses the GDP growth rate as a proxy for good and bad business states

$$\begin{array}{cc}MA{P}_{j,t,L}& ={\alpha }_{j.L}+{\beta }_{j,L,MKT}{R}_{MKT,t}+{\beta }_{j,L,SMB}{R}_{SMB,t}+{\beta }_{j,L,HML}{R}_{HML,t}+{\beta }_{j,L,Good}{D}_{Good,t}^{GDP}+\hfill \\ & {\beta }_{j,L,Bad}{D}_{Bad,t}^{GDP}+{\epsilon }_{j,t,L}, j=1,\dots ,10,\hfill \end{array}$$

(10)

$$\begin{array}{cc}TL{S}_{t,L}=& {\alpha }_L+{\beta }_{L,MKT}{R}_{MKT,t}+{\beta }_{L,SMB}{R}_{SMB,t}+{\beta }_{L,HML}{R}_{HML,t}+{\beta }_{L,Good}{D}_{Good,t}^{GDP}+{\beta }_{L,Bad}{D}_{Bad,t}^{GDP}+\hfill \\ & {\epsilon }_{t,L},\hfill \end{array}$$

(11)

In the model, $D_{Good,t}^{GDP}$ and $D_{Bad,t}^{GDP}$ are the dummy variables for good and bad business states. When the GDP growth rate in the quarter is in the top 25% of the whole sample period, $D_{Good,t}^{GDP}$ will be one, which indicates that business cycles are in a good period. $D_{Bad,t}^{GDP}$ indicates the bad state when the quarterly GDP growth rate is in the bottom 25% of the overall sample. We can determine the contribution of both expansionary (good business state) and recessionary (bad business state) periods from their coefficients. If they are significantly positive, the predictability is strong, and the strategy works in the state.

The other model from Cooper et al. (2004) uses a dummy variable for bad market performance. We follow them and perform the following regression using market return data:

$$\begin{array}{cc}MA{P}_{j,t,L}& ={\alpha }_{j.L}+{\beta }_{j,L,MKT}{R}_{MKT,t}+{\beta }_{j,L,SMB}{R}_{SMB,t}+{\beta }_{j,L,HML}{R}_{HML,t}+{\beta }_{j,L,Bad}{D}_{Bad,t}^{Market}+{\epsilon }_{j,t,L}, \hfill \\ & j=1,\dots ,10,\hfill \end{array}$$

(12)

$$TL{S}_{t,L}={\alpha }_L+{\beta }_{L,MKT}{R}_{MKT,t}+{\beta }_{L,SMB}{R}_{SMB,t}+{\beta }_{L,HML}{R}_{HML,t}+{\beta }_{L,Bad}{D}_{Bad,t}^{Market}+{\epsilon }_{t,L},$$

(13)

$D_{Bad,t}^{Market}$ is the dummy variable that denotes the bad state of the business cycle. We calculate the market return of the past three years before every yearly holding period. If the result is negative, $D_{Bad,t}^{Market}$ will be one, and zero otherwise. We can determine the effect of a bad market environment on our excess return from its coefficients. If the coefficients on $D_{Bad,t}^{Market}$ are significantly positive, our strategy works in the bad market state.

Panels A and B of

Table 6. Business cycle.

Rank	Good and Bad States Are Identified by GDP Growth (Past 20 Years)								Good and Bad States Are Identified by Past Three-Year Market Returns
	α	βmkt	βsmb	βhml	βliq	βGood	βBad	Adj. R2	α	βmkt	βsmb	βhml	βliq	βBad	Adj. R2
Low	9.74	−0.46	−0.59	0.20	0.15	1.91	−4.45	0.45	9.60	−0.46	−0.59	0.20	0.15	−1.29	0.45
	(4.93)	(−18.36)	(−9.43)	(6.16)	(4.13)	(0.50)	(−1.46)		(4.88)	(−18.38)	(−9.46)	(6.21)	(4.13)	(−0.47)
2	7.55	−0.49	−0.52	0.15	0.17	6.48	−3.94	0.46	8.68	−0.49	−0.53	0.15	0.17	−1.45	0.46
	(3.78)	(−18.33)	(−8.89)	(4.99)	(4.98)	(1.79)	(−1.21)		(4.53)	(−18.35)	(−8.93)	(5.03)	(4.99)	(−0.52)
3	7.27	−0.47	−0.51	0.15	0.16	1.69	−3.88	0.42	7.19	−0.47	−0.51	0.15	0.16	−1.22	0.42
	(3.61)	(−16.77)	(−7.93)	(4.81)	(4.36)	(0.44)	(−1.20)		(3.48)	(−16.79)	(−7.96)	(4.84)	(4.37)	(−0.44)
4	8.77	−0.51	−0.43	0.07	0.19	2.01	−2.85	0.46	10.33	−0.51	−0.43	0.07	0.19	−4.49	0.47
	(4.29)	(−18.28)	(−6.92)	(2.21)	(5.39)	(0.50)	(−0.89)		(4.97)	(−18.30)	(−6.96)	(2.24)	(5.40)	(−1.56)
5	8.49	−0.52	−0.53	0.05	0.15	2.00	−3.36	0.47	9.59	−0.52	−0.53	0.05	0.15	−3.65	0.47
	(4.14)	(−18.58)	(−8.17)	(1.52)	(4.21)	(0.51)	(−1.03)		(4.57)	(−18.60)	(−8.21)	(1.55)	(4.21)	(−1.28)
6	7.67	−0.48	−0.43	−0.01	0.19	1.29	−3.42	0.44	8.59	−0.48	−0.44	−0.01	0.19	−3.66	0.44
	(3.66)	(−17.55)	(−7.32)	(−0.31)	(5.42)	(0.32)	(−1.06)		(4.00)	(−17.56)	(−7.35)	(−0.28)	(5.42)	(−1.27)
7	8.31	−0.49	−0.47	−0.04	0.18	5.03	−6.01	0.45	9.56	−0.49	−0.48	−0.04	0.18	−3.90	0.45
	(3.99)	(−18.31)	(−7.42)	(−1.29)	(5.14)	(1.28)	(−1.75)		(4.47)	(−18.31)	(−7.47)	(−1.23)	(5.15)	(−1.33)
8	9.63	−0.51	−0.43	−0.12	0.19	1.65	−4.18	0.48	11.75	−0.51	−0.43	−0.12	0.19	−6.91	0.48
	(4.46)	(−18.33)	(−6.78)	(−3.24)	(5.19)	(0.41)	(−1.21)		(5.27)	(−18.35)	(−6.86)	(−3.20)	(5.19)	(−2.33)
9	8.26	−0.47	−0.37	−0.09	0.18	0.05	−3.89	0.43	7.94	−0.47	−0.37	−0.09	0.18	−1.60	0.43
	(3.95)	(−17.39)	(−6.25)	(−2.49)	(5.36)	(0.01)	(−1.18)		(3.63)	(−17.40)	(−6.29)	(−2.46)	(5.36)	(−0.55)
High	6.04	−0.48	−0.39	−0.14	0.15	3.46	−1.15	0.45	8.74	−0.48	−0.40	−0.14	0.15	−5.41	0.45
	(2.90)	(−17.92)	(−6.57)	(−3.57)	(4.20)	(0.84)	(−0.37)		(3.98)	(−17.93)	(−6.60)	(−3.56)	(4.21)	(−1.91)
High–Low	−3.70	−0.02	0.19	−0.33	0.00	1.55	3.30	0.08	−0.85	−0.02	0.19	−0.33	0.00	−4.12	0.08
	(−1.95)	(−1.25)	(3.67)	(−8.31)	(−0.09)	(0.43)	(1.11)		(−0.49)	(−1.23)	(3.68)	(−8.35)	(−0.08)	(−1.50)
TLS	14.84	−0.04	0.15	−0.46	0.12	5.53	−4.02	0.06	18.04	−0.04	0.14	−0.46	0.12	−7.22	0.06
	(4.30)	(−0.86)	(1.42)	(−8.01)	(1.90)	(0.84)	(−0.77)		(5.05)	(−0.86)	(1.37)	(−8.00)	(1.91)	(−1.57)

Two models are used to test the influence of business cycle. One is $MA{P}_{j,t,L}={\alpha }_{j.L}+{\beta }_{j,L,MKT}{R}_{MKT,t}+{\beta }_{j,L,SMB}{R}_{SMB,t}+{\beta }_{j,L,HML}{R}_{HML,t}+{\beta }_{j,L,Good}{D}_{Good,t}^{GDP}+{\beta }_{j,L,Bad}{D}_{Bad,t}^{GDP}+{\epsilon }_{j,t,L}$. In the model, $D_{Good,t}^{GDP}$ and $D_{Bad,t}^{GDP}$ are the dummy variables for good and bad business states. When the GDP growth rate in the quarter is in the top 25% of the whole sample period, $D_{Good,t}^{GDP}$ will be one, which indicate the business cycle is in good period. On the other hand, $D_{Bad,t}^{GDP}$ indicates the bad state when the quarterly GDP growth rate is in the bottom 25% of the overall sample. The other model is $MA{P}_{j,t,L}={\alpha }_{j.L}+{\beta }_{j,L,MKT}{R}_{MKT,t}+{\beta }_{j,L,SMB}{R}_{SMB,t}+{\beta }_{j,L,HML}{R}_{HML,t}+{\beta }_{j,L,Bad}{D}_{Bad,t}^{Market}+{\epsilon }_{j,t,L}$. We use $D_{Bad,t}^{Market}$ as the dummy variable to denote the bad state of the business cycle. We calculate the market return of past three years before the yearly holding period. If the result is negative, $D_{Bad,t}^{Market}$ will be one and zero otherwise. t-test statistics are presented in the parentheses.

show the results of these two regressions. We find that the pattern of the alphas in the two models changes only slightly from before. However, the coefficients on most of the dummy variables are insignificant. For the first model, 9 of the 10 portfolio coefficients are insignificant at the 10% level. For the second model, only two of the coefficients of the dummy variable $D_{Bad,t}^{Market}$ are significant at either the 5% or 10% level. These results clearly show that business cycles have a very weak influence on the average returns of MA strategy.3

4.3. Market Timing Ability

To find out more about how the moving average and TLS strategies can outperform the buy-and-hold strategy, we also investigate their timing ability, which may drive the performance. We take use approaches proposed by Treynor and Mazuy (1966) and Henriksson and Merton (1981) to test the market timing ability of the two strategies in our paper.

Treynor and Mazuy (1966)’s model is

$$MA{P}_{j,t,L}={\alpha }_{j.L}+{\beta }_{j,L,MKT}{R}_{MKT,t}+{\beta }_{j,L,MK{T}^2}{R}_{MKT,t}^2+{\epsilon }_{j,t,L}, j=1,\dots ,10,$$

(14)

$$TL{S}_{t,L}={\alpha }_L+{\beta }_{L,MKT}{R}_{MKT,t}+{\beta }_{L,MK{T}^2}{R}_{MKT,t}^2+{\epsilon }_{t,L},$$

(15)

These is a quadratic model where $R_{MKT,t}^2$ is the squared market excess return. If the coefficients are significantly positive, it indicates that the strategies may have some market timing ability.

Henriksson and Merton (1981) propose the following model to test market timing ability:

$$MA{P}_{j,t,L}={\alpha }_{j.L}+{\beta }_{j,L,MKT}{R}_{MKT,t}+{\gamma }_{j,L,MKT}{R}_{MKT,t}{I}_{r_{MKT,t}>0}+{\epsilon }_{j,t,L}, j=1,\dots ,10,$$

(16)

$$TL{S}_{t,L}={\alpha }_L+{\beta }_{L,MKT}{R}_{MKT,t}+{\gamma }_{L,MKT}{R}_{MKT,t}{I}_{r_{MKT,t}>0}+{\epsilon }_{t,L},$$

(17)

In these regressions, the value of the indicator function, $I_{r_{MKT}}$, will be one if the market excess return is positive and zero otherwise. If the parameter ${\gamma }_{L,MKT}$ is significantly positive, it suggests that there is market timing ability.

The regression results of these two tests are shown in

Table 7. Market timing ability.

Rank	TM Regression				HM Regression
	α	βmkt	βmkt2	Adj. R2	α	βmkt	γmkt	Adj. R2
Low	7.22	−0.45	0.30	0.40	3.39	−0.49	0.08	0.40
	(3.93)	(−18.54)	(0.50)		(1.23)	(−13.02)	(1.41)
2	3.88	−0.49	1.03	0.43	−1.46	−0.56	0.14	0.43
	(2.01)	(−18.82)	(1.55)		(−0.50)	(−13.55)	(2.40)
3	4.14	−0.46	0.52	0.39	0.21	−0.51	0.09	0.39
	(2.05)	(−17.14)	(0.73)		(0.07)	(−11.84)	(1.48)
4	6.13	−0.51	0.41	0.43	1.51	−0.56	0.10	0.44
	(3.05)	(−18.65)	(0.57)		(0.49)	(−12.74)	(1.53)
5	4.29	−0.53	0.76	0.44	−0.20	−0.58	0.11	0.44
	(2.18)	(−19.11)	(1.09)		(−0.07)	(−13.19)	(1.82)
6	5.86	−0.49	−0.07	0.40	2.56	−0.51	0.05	0.40
	(3.14)	(−17.54)	(−0.10)		(0.86)	(−11.55)	(0.81)
7	4.72	−0.51	0.49	0.41	−0.43	−0.56	0.11	0.41
	(2.44)	(−18.15)	(0.72)		(−0.14)	(−12.77)	(1.76)
8	3.22	−0.53	1.20	0.43	−3.06	−0.61	0.16	0.43
	(1.61)	(−18.61)	(1.65)		(−0.99)	(−13.30)	(2.51)
9	4.92	−0.49	0.23	0.39	0.93	−0.52	0.08	0.39
	(2.61)	(−17.38)	(0.33)		(0.31)	(−11.72)	(1.21)
High	2.73	−0.50	0.61	0.40	−2.15	−0.55	0.11	0.40
	(1.45)	(−17.70)	(0.88)		(−0.72)	(−12.29)	(1.74)
High–Low	−4.49	−0.05	0.31	0.01	−5.53	−0.06	0.03	0.01
	(−3.61)	(−3.22)	(1.15)		(−3.29)	(−2.77)	(0.94)
TLS	11.88	−0.09	0.43	0.01	7.52	−0.14	0.09	0.01
	(3.58)	(−1.86)	(0.35)		(1.42)	(−1.85)	(0.86)

Two methods are used to test the market timing ability. One is $MA{P}_{j,t,L}={\alpha }_{j.L}+{\beta }_{j,L,MKT}{R}_{MKT,t}+{\beta }_{j,L,MK{T}^2}{R}_{MKT,t}^2+{\epsilon }_{j,t,L}$. These are quadratic models, where $R_{MKT,t}^2$ the squared market excess return. The other model is $MA{P}_{j,t,L}={\alpha }_{j.L}+{\beta }_{j,L,MKT}{R}_{MKT,t}+{\gamma }_{j,L,MKT}{R}_{MKT,t}{I}_{r_{MKT,t}>0}+{\epsilon }_{j,t,L}$. In these regressions, we have $I_{r_{MKT,t}>0}$. The value of this indicator function will be one if the market excess return is positive and will be zero otherwise. t-test statistics are presented in the parentheses.

. Different from the results of Han et al. (2013) and Ko et al. (2014), most of the coefficients on ${\beta }_{j,L,MK{T}^2}$ and ${\gamma }_{j,L,MKT}$ in our regressions are insignificant. In particular, both of the market timing coefficients for the TLS strategy are insignificant. In addition, the alpha values do not change substantially from our main findings. The overall results suggest that the profits generated by our strategy are not due to market timing ability.

4.4. Subsample of Short-Selling

As China’s stock market is very young, the government and stock exchanges have implemented a number of regulations to stabilize investors’ trading behaviors and control risks. On 31 March 2010, China lifted the restriction on short-selling and allowed certain large cap stocks to be short-sold by qualified investors. The list quickly expanded in the following years, and short-selling activities in China developed rapidly.

Because short-selling was not allowed before 2010, it may not be possible to implement the MA and TLS strategies for our whole sample period. To check whether the profits generated from our strategies are realistic, we re-ran our tests in the period after 2010, when short-selling was flexible. Because not all stocks can be short-sold, when we conduct the TLS strategy, some stocks in the low BM portfolio cannot be shorted in the real market. We exclude those stocks and perform a subsample test from 31 March 2010 to 30 June 2015. We repeat the method used in Section 4.1 to obtain the summary statistics of the average returns of BM deciles, MA(20), and MAP(20) strategy.

From the summary statistics in

Table 8. Subsample of short-selling.

Rank	BM Decile Portfolios				MA(20) Timing Portfolios		MAPs
	Ave Ret	Std Dev	Skew	t	Ave Ret	Std Dev	Skew	t	Ave Ret	Std Dev	Skew	t
Low	−0.53	20.78	−0.45	−0.06	4.31	16.94	0.01	0.62	4.22	7.02	0.33	1.47
2	1.68	21.79	−0.30	0.19	10.07	10.94	1.74	2.25	7.57	13.07	1.74	1.42
3	2.10	26.75	−0.25	0.19	2.44	24.12	−0.58	0.25	−0.25	5.58	0.92	−0.11
4	2.41	25.37	−0.24	0.23	10.17	14.66	1.67	1.70	6.93	14.02	1.69	1.21
5	0.48	27.54	−0.62	0.04	7.44	13.93	0.47	1.31	6.01	14.94	1.45	0.99
6	1.80	28.38	−0.49	0.16	9.07	15.86	1.16	1.40	6.47	15.42	1.41	1.03
7	0.48	29.43	−0.45	0.04	4.70	16.32	0.08	0.71	3.39	13.41	0.92	0.62
8	0.52	30.35	−0.59	0.04	5.97	19.34	0.77	0.76	4.63	13.11	1.16	0.87
9	0.67	31.17	−0.57	0.05	7.78	19.22	1.03	0.99	6.17	13.88	1.80	1.09
High	−0.81	32.97	−0.53	−0.06	6.77	16.41	1.63	1.01	6.84	19.27	1.99	0.87
High–Low	−0.94	12.81	−0.55	−0.18	1.76	7.90	−0.28	0.55	2.25	15.05	2.15	0.37
	(−0.18)				(0.99)				(0.45)
TLS					10.50	14.12	1.61	1.82	10.86	15.62	0.43	1.70
					(3.25)				(2.81)

Stocks that cannot be shorted are excluded from the lowest BM portfolio and a subsample test is performed for the period from 31 March 2010 to 30 June 2015. Summary statistics of average return of BM decile portfolios, MA(20) strategy and MAP returns. t-test statistics are presented in the parentheses.

, we find that the moving average strategy still outperforms the tradition buy-and-hold strategy, with higher returns on all portfolios. Almost all of the MAPs are positive. The result of the zero-cost trading strategy (TLS) for MA(20) is 10.50 points (t = 3.25), which is much bigger than the result from the high-minus-low with buy-and-hold strategy. Obviously, the moving average indicator is useful, and the TLS strategy is profitable.

In conclusion, excluding stocks that cannot be shorted in the lowest BM portfolio, the moving average technical analysis indicator and proposed TLS strategy work well and still contribute impressive and significant excess returns. This subsample test provides further evidence for the validity and usefulness of our two trading strategies.

5. Conclusions

In this paper, we first use the buy-and-hold strategy to confirm the existence of value premium in China’s stock market. We then use a technical analysis tool, the moving average indicator, to conduct trade on the decile BM portfolios. The results suggest that technical analysis is workable and has superior performance compared to the buy-and-hold strategy. Next we construct a zero-cost trading strategy by longing the high BM portfolio and shorting the low BM portfolio at the same time using the moving average indicator and find a much higher average excess return. Using the CAPM, FF3F, and LIQ4F models, the returns of our strategy are still positive and significant. In addition, the profits remain positive and significant after tests are conducted using different lag length moving average indicators and considering transaction costs.

Robustness tests are essential in our study. We discover that non-tradable share reforms and business cycles do not affect the predictability of technical analysis, and market-timing ability cannot explain it either. Finally, we conduct tests in the period in which short-selling is allowed and find that significant positive profits still exist in the subsample.

This study makes an initial attempt to unveil the profitability of combined trading strategies in China’s stock market. Extensions of our combined strategies would include other technical analysis, such as candlestick analysis and relative strength index, and firm characteristics, such as size and liquidity. Another direct extension would be to identify more drivers of profitability by investigating more macroeconomic and risk factors, such as investment and profitability.