Export–Output Growth Nexus Using Threshold VAR and VEC Models: Empirical Evidence from Thailand
Abstract
1. Introduction
2. Background
Relationship between Export and Economic Growth
3. Methodology
3.1. Threshold Vector Autoregression Model (TVAR)
3.2. Threshold Vector Error Correction Model (TVECM)
3.3. Generalized Impulse Response Function (GIRF)
3.4. Econometric Methodology
4. Data and Empirical Results
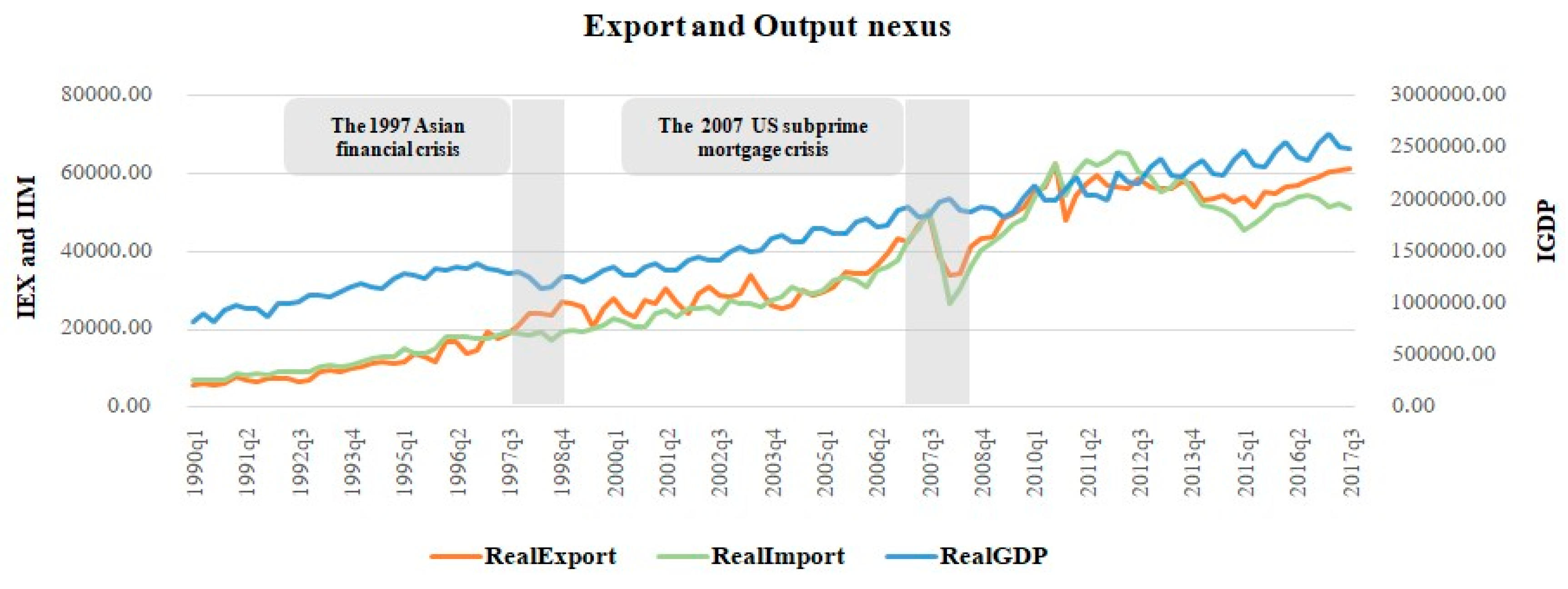
4.1. Dataset
4.2. Empirical Results
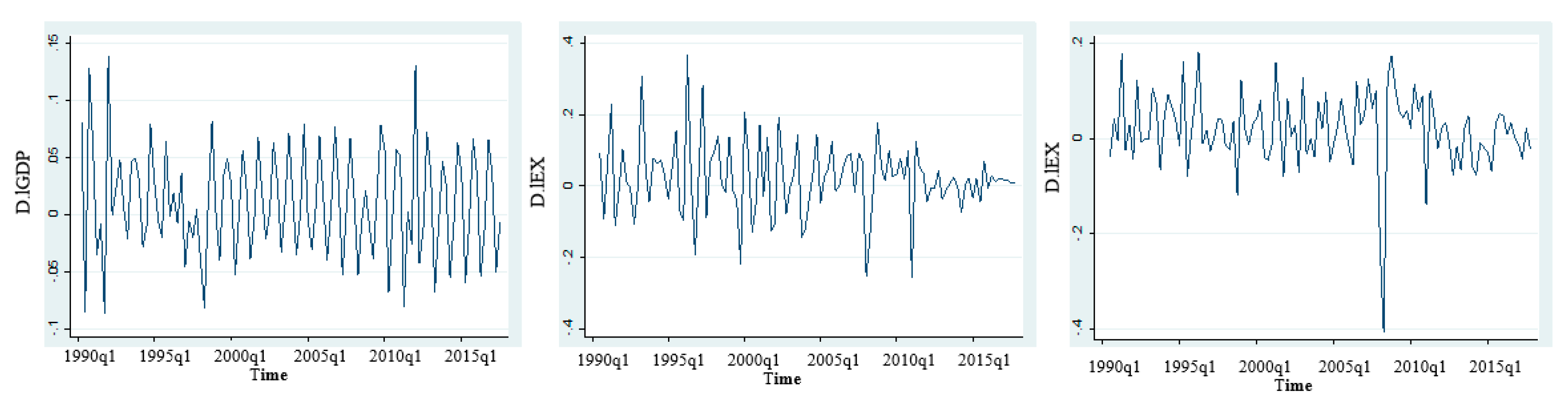
4.2.1. Unit Root and Cointegration
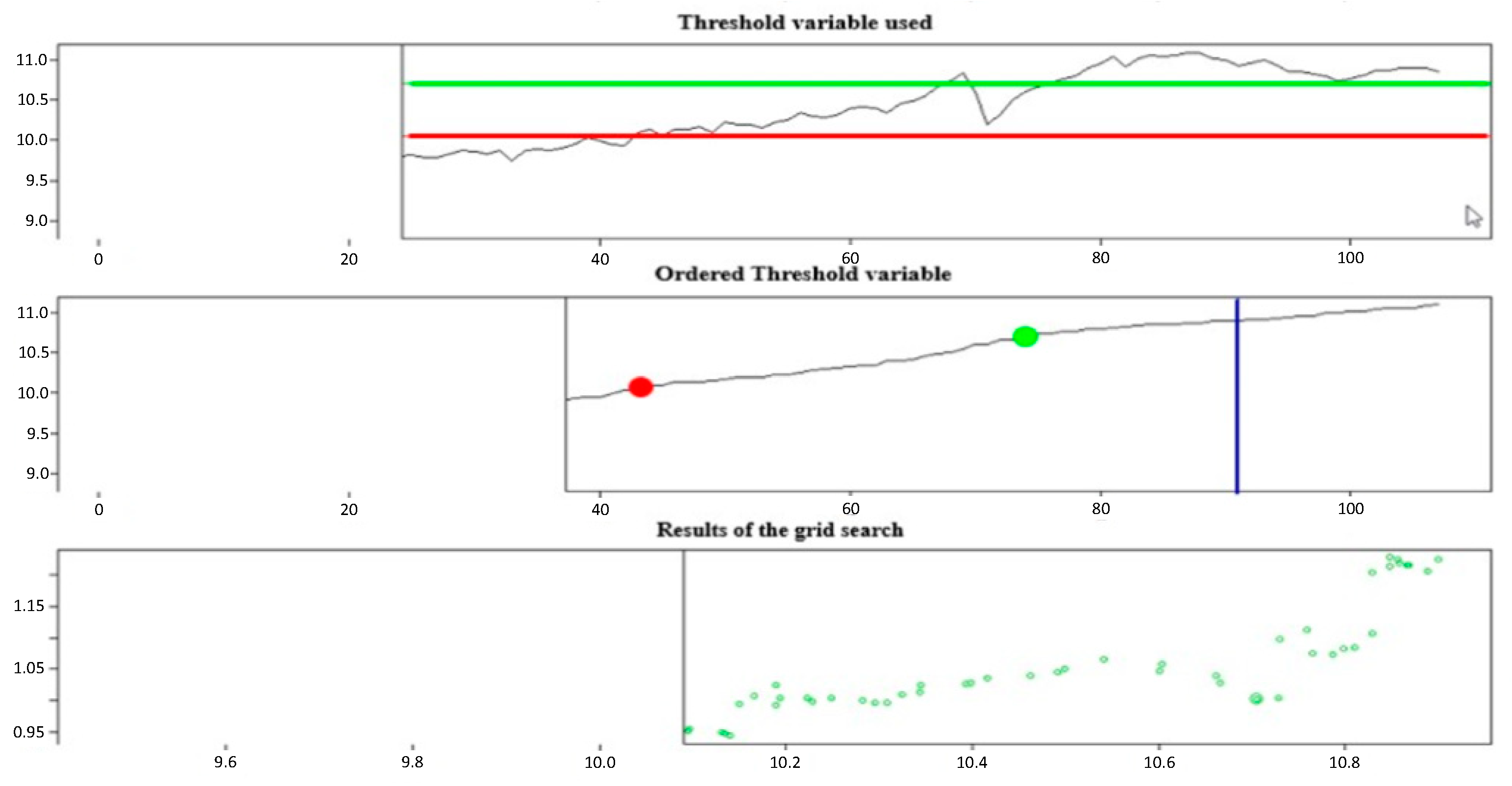
4.2.2. Threshold VAR (TVAR) Model
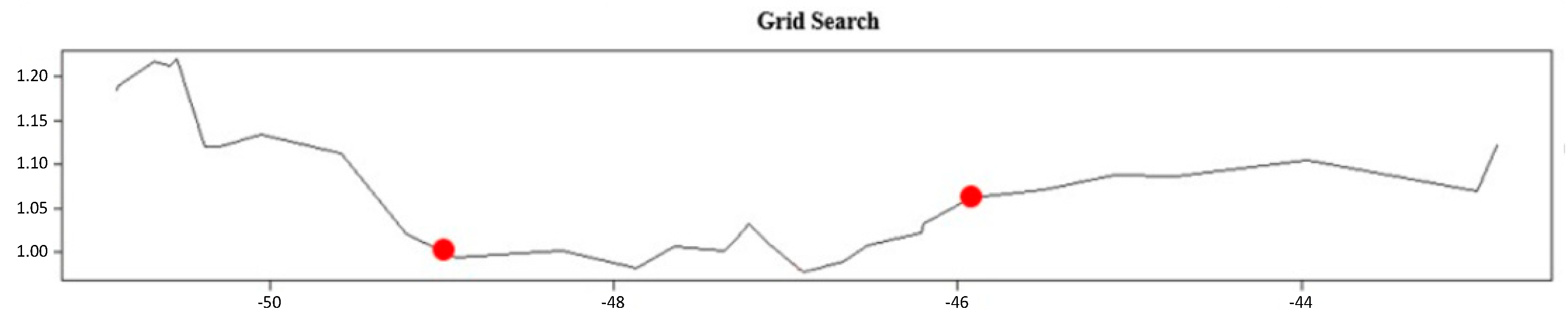
4.2.3. Threshold Vector Error Correction (TVEC) Model
4.2.4. Linear Cointegration and Threshold Cointegration Models
4.2.5. Five-Year Forecasting of TVAR
4.2.6. Generalized Impulse Response Function (GIRF)
5. Conclusions and Policy Recommendations
- The export–output behavior responding to economic crises can be reasonably characterized by the two-threshold VAR model (the threshold values were 10.05 and 10.71) and the two-threshold VEC model (the threshold values were −49.20 and −45.93). These export–output scenarios are distorted because of the long-term equilibrium. The empirical findings convey that the export, import, and output pass-throughs at the lower, medium, and upper regimes react to changes in the structure. Those structural breaks have a significant effect on the different regimes. Consequently, for Thailand, this phenomenon supports the ELG hypothesis with regard to business cycle asymmetry.
- According to threshold cointegration, the GDP associated with the export adjusts the long-term equilibrium relationship; however, export and import do not exist with regard to the long-term equilibrium relationship when business cycles take place.
- As for the evaluation of the performance of the prediction models, the two-threshold VAR model has a better goodness-of-fit measurement because of the smaller RMSE and MPE values than the VEC model. Thereafter, the five-year forecast (2018–2022) was predicted. The export–output growth nexus scenarios seem to undergo a consistent upswing.
- The regime IRFs allowed us to explicitly identify the reactions of the whole system at stake within each regime (up, medium, and down) in response to structure breaks. These dynamics are quite different across regimes.
Author Contributions
Funding
Conflicts of Interest
References
- Andrews, Donald Wilfrid Kao, and Werner Ploberger. 1994. Optimal Tests when a Nuisance parameter is Present Only under the 257 Alternative. Econometrica 62: 1383–414. [Google Scholar] [CrossRef]
- Arnade, Carlos, and Utpal Vasavada. 1995. Causality between productivity and exports in agriculture: Evidence from Asia 259 and Latin America. Journal of Agricultural Economics 46: 174–86. [Google Scholar] [CrossRef]
- Awokuse, Titus Ogundari, and Dimitris K. Christopoulosb. 2009. Nonlinear dynamics and the export-output growth nexus. Economic Modelling 26: 184–90. [Google Scholar] [CrossRef]
- Balassa, Bela. 1971. Regional integration and trade liberalization in Latin. Journal of Common Market Studies 10: 58–77. [Google Scholar] [CrossRef]
- Balke, S. Nathan, and Thomas B. Fomby. 1997. Threshold Cointegration. Economic Modelling. International Economic Review 38: 627–45. [Google Scholar]
- Edwards, Sebastian. 1993. Openness, trade liberalization, and growth in developing countries. Journal of Economic Literature 31: 1358–93. [Google Scholar]
- Elliott, Graham, Thomas J. Rothenberg, and J. H. Stock. 1996. Efficient Tests for an Autoregressive Unit Root. Econometrica 64: 813–36. [Google Scholar] [CrossRef]
- Haddad, Hedi Ben. 2010. The Export-Output Nexus: A Markov-Switching Approach. The Empirical Economics Letters 9: 257–64. [Google Scholar]
- Hansen, Bruce E. 1999. Testing for linearity. Journal of Economic Surveys 13: 551–76. [Google Scholar] [CrossRef]
- Hansen, Bruce E. 2000. Sample Splitting and Threshold Estimation. Econometrica 68: 575–603. [Google Scholar] [CrossRef]
- Hansen, Bruce E., and Byeongseon Seo. 2002. Testing for two-regime Threshold Cointegration in vector error-correction models. Journal of Econometrics 110: 293–318. [Google Scholar] [CrossRef]
- Hubrich, Kirstin, and Timo Teräsvirta. 2013. Thresholds and smooth transitions in vector autoregressive models. Advances in Econometrics 32: 273–326. [Google Scholar]
- Huck, Schuyler W., Tracey L. Cross, and Sheldon B. Clark. 1986. Overcoming misconceptions about z-scores. Teaching Statistics 8: 38–40. [Google Scholar] [CrossRef]
- Koop, Gary, M. Hashem Pesaran, and Simon M. Potter. 1996. Impulse Response Analysis in Nonlinear Multivariate Models. Journal of Econometrics 74: 119–47. [Google Scholar] [CrossRef]
- Krolzig, Hans-Martin. 1997. Markov-Switching Vector Autoregression. Berlin: Springer. [Google Scholar]
- Krueger, Anne O. 1978. Foreign Trade Regimes and Economic Development: Liberalization Attempts and Consequence. Cambridge: Balinger. [Google Scholar]
- Kugler, Peter, and Jomâa Dridi. 1993. Growth and Exports in LDCs: A Multivariate Time Series Study. Revista Internazionale Di Scienze Economiche e Commerciali 40: 759–67. [Google Scholar]
- Lee, Chien-Hui, and Bwo-Nung Huang. 2002. The relationship between exports and economic growth in East Asian countries: A multivariate threshold autoregressive approach. Journal of Economic Development 27: 45–68. [Google Scholar]
- Liu, Yi, and Ning Zhang. 2015. Sustainability of Trade Liberalization and Antidumping: Evidence from Mexico’s Trade Liberalization toward China. Sustainability 7: 11484–503. [Google Scholar] [CrossRef]
- Ram, Rati. 1985. Export and economic growth: Some additional evidence. Economic Development and Cultural Change 33: 415–25. [Google Scholar] [CrossRef]
- Reppas, Panayiotis A., and Dimitris K. Christopoulos. 2005. The export-output growth: Evidence from African and Asian countries. Journal of Policy Modeling 27: 929–40. [Google Scholar] [CrossRef]
- Richards, Donald G. 2001. Exports as a determinant of long-run growth in Paraguay. Journal of Development Studies 38: 128–46. [Google Scholar] [CrossRef]
- Salvatore, Dominick, and Thomas Hatcher. 1991. Inward and outward oriented trade strategies. Journal of Development Studies 27: 7–25. [Google Scholar] [CrossRef]
- Sengupta, Jati K. 1993. Growth in NICs in Asia: Some tests of new growth theory. Journal of Development Studies 29: 342–57. [Google Scholar] [CrossRef]
- Tsay, Ruey. 1998. Testing and modeling multivariate threshold models. Journal of the American Statistical Association 93: 1188–202. [Google Scholar] [CrossRef]
- Ulrich, Anne. 2014. Export-Oriented Horticultural Production in Laikipia, Kenya: Assessing the Implications for Rural Livelihoods. Sustainability 6: 336–47. [Google Scholar] [CrossRef]
- Xu, Zhenhui. 1996. On the causality between export growth and GDP growth: An empirical reinvestigation. Review of International Economics 4: 172–84. [Google Scholar] [CrossRef]
- Yamada, Hiroshi. 1998. A note on the causality between export and productivity. Economics Letter 61: 111–14. [Google Scholar] [CrossRef]


| Measurements | GDP | RealEX | RealIM |
|---|---|---|---|
| Mean | 1.653 | 0.033 | 0.032 |
| Median | 1.596 | 0.029 | 0.028 |
| Maximum | 2.639 | 0.062 | 0.066 |
| Minimum | 0.823 | 0.006 | 0.007 |
| Standard Deviation | 0.492 | 0.018 | 0.018 |
| Skewness | 0.251 | 0.084 | 0.317 |
| Kurtosis | 1.866 | 1.651 | 1.753 |
| Jarque–Bera Test | 7.100 | 8.551 | 9.047 |
| Probability | 0.028 | 0.013 | 0.011 |
| Variables | Levels | First Different | ||
|---|---|---|---|---|
| DF-GLS tau a | DF-GLS tau b | DF-GLS tau a | DF-GLS tau b | |
| lGDP | −2.141(5) | 1.531 | −5.035 (2) *** | −5.092 (2) *** |
| lEX | −0.735 (7) | 1.032 | −3.621(7) *** | −2.760 (3) *** |
| lIM | −0.951 (8) | 0.939 | −3.095 (6) *** | −2.760 (5) *** |
| Model Selection | Lag = 1 | Lag = 2 | Lag = 3 | Lag = 4 | Lag = 5 |
|---|---|---|---|---|---|
| AIC | −15.982 | −16.494 | −16.590 | −16.681 | −16.601 |
| HO | −15.853 | −16.271 | −16.272 | −16.282 | −16.112 |
| SC | −15.670 | −15.962 | −15.834 | −15.693 | −15.394 |
| FPE | 1.151 | 6.879 | 6.269 | 5.738 | 6.223 |
| Series | Hypothesis | Eigen Test | 0.05 Critical Values | Test Statistic | 0.05 Critical Values |
|---|---|---|---|---|---|
| lGDP, lEX, lIM | r = 0 | 14.51 ** | 9.24 | 73.59 | 34.91 |
| r ≤ 1 | 19.31 ** | 15.67 | 33.81 | 19.96 | |
| r ≤ 2 | 39.78 ** | 22.00 | 14.51 | 9.24 |
| LR test for Linearity vs. 1 Threshold | |
| LR statistic | 103.72 |
| p-Value | 0.00 |
| Estimated threshold | 10.13 (Percentage of Observations: 44.9% and 55.1%) |
| LR test for Linearity vs. 2 Thresholds | |
| LR statistic | 206.94 |
| p-Value | 0.00 |
| Estimated threshold | 10.05; 10.71 (Percentage of Observations: 40.2%, 29%, and 30.8%) |
| LR test for 1 Threshold vs. 2 Thresholds | |
| LR statistic | 103.23 |
| p-Value | 0.00 |
| Estimated threshold | 10.13; [10.05, 10.71] |
| Variables | Regime 1 Percentage of Observations of 40.2% | Regime 2 Percentage of Observations of 29.0% | Regime 3 Percentage of Observations of 30.8% |
|---|---|---|---|
| lGDP | |||
| Intercept | −0.627 (1.945) | 3.246 (1.691) | 2.609 (1.741) |
| lGDP-1 | 0.753 (0.151) *** | 0.779 (0.464) | 0.325 (0.197) |
| lEX-1 | −0.139 (0.068) * | −0.016 (0.108) | 0.166 (0.192) |
| lIM-1 | −0.080 (0.121) | 0.056 (0.096) | −0.168 (0.202) |
| lGDP-2 | −0.102 (0.174) | −0.945 (0.476) | −0.314 (0.207) |
| lEX-2 | 0.067 (0.072) | −0.035 (0.124) | 0.119 (0.195) |
| lIM-2 | 0.139 (0.132) | 0.054 (0.115) | −0.019 (0.211) |
| lGDP-3 | 0.039 (0.172) | 0.698 (0.526) | 0.122 (0.201) |
| lEX-3 | 0.001 (0.068) | −0.008 (0.112) | −0.090 (0.184) |
| lIM-3 | −0.095 (0.129) | 0.048 (0.106) | 0.017 (0.210) |
| lGDP-4 | 0.433 (0.161) ** | 0.122 (0.441) | 0.545 (0.185) ** |
| lEX-4 | 0.147 (0.073) * | −0.018 (0.080) | 0.226 (0.209) |
| lIM-4 | −0.152 (0.108) | 0.091 (0.100) | −0.056 (0.163) |
| lEX | |||
| Intercept | −5.167 (3.944) | −1.568 (3.428) | 5.558 (3.528) |
| lGDP-1 | 0.277 (0.305) | −0.281 (0.940) | 0.205 (0.399) |
| lEX-1 | 0.502 (0.138) *** | 0.638 (0.218) ** | 0.348 (0.389) |
| lIM-1 | 0.299 (0.245) | 0.433 (0.194) * | 0.658 (0.409) |
| lGDP-2 | −0.745 (0.351) * | 0.818 (0.964) | 0.566 (0.419) |
| lEX-2 | −0.214 (0.145) | 0.020 (0.251) | 0.619 (0.396) |
| lIM-2 | −0.477 (0.266) | −0.029 (0.232) | −0.431 (0.426) |
| lGDP-3 | 0.928 (0.348) ** | −0.797 (1.066) | −0.471 (0.408) |
| lEX-3 | 0.539 (0.137) *** | −0.132 (0.227) | 0.432 (0.372) |
| lIM-3 | −0.729 (0.260) ** | −0.103 (0.214) | −0.684 (0.424) |
| lGDP-4 | −0.007 (0.325) | 0.208 (0.893) | −0.116 (0.375) |
| lEX-4 | −0.048 (0.147) | 0.152 (0.163) | −0.205 (0.423) |
| lIM-4 | 1.015 (0.219) *** | 0.248 (0.204) | 0.524 (0.329) |
| lIM | |||
| Intercept | 0.017 (0.022) | −0.065 (0.324) | 0.419 (0.155) |
| lGDP-1 | −8.819 (3.761) * | −2.826 (3.270) | −4.241 (3.366) |
| lEX-1 | 0.754 (0.291) * | −0.744 (0.897) | 0.056 (0.381) |
| lIM-1 | 0.210 (0.234) | 0.846 (0.185) *** | 1.315 (0.390) ** |
| lGDP-2 | −0.281 (0.335) | 1.022 (0.920) | 0.158 (0.400) |
| lEX-2 | 0.076 (0.138) | 0.0206 (0.251) | 0.661 (0.377) |
| lIM-2 | 0.012 (0.254) | 0.040 (0.221) | −0.666 (0.407) |
| lGDP-3 | 0.204 (0.332) | −0.896 (1.017) | −0.411 (0.389) |
| lEX-3 | 0.044 (0.131) | −0.004 (0.217) | −0.602 (0.404) |
| lIM-3 | −0.268 (0.248) | −0.219 (0.204) | 0.727 (0.355) * |
| lGDP-4 | 0.289 (0.310) | 0.774 (0.852) | −0.299 (0.357) |
| lEX-4 | 0.161 (0.140) | 0.040 (0.156) | 0.524 (0.329) |
| lIM-4 | 0.256 (0.209) | 0.230 (0.194) | 0.440 (0.314) |
| Variables | Regime 1 Percentage of Observations of 36.8% | Regime 2 Percentage of Observations of 33.0% | Regime 3 Percentage of Observations of 30.2% |
|---|---|---|---|
| lGDP | |||
| ECT | −0.002 (0.906) | −0.004 (0.647) | −0.008 (0.021) * |
| Intercept | −0.054 (0.924) | 0.191 (0.629) | 0.391 (0.015) * |
| lGDP-1 | −0.270 (0.134) | 0.0192 (0.955) | 0.513 (0.008) ** |
| lEX-1 | 0.105 (0.462) | 0.042 (0.579) | −0.228 (0.007) ** |
| lIM-1 | −0.151 (0.279) | 0.006 (0.938) | 0.042 (0.727) |
| lGDP-2 | −0.600 (0.002) ** | −0.400 (0.320) | −0.389 (0.037) * |
| lEX-2 | 0.120 (0.500) | −0.012 (0.900) | 0.030 (0.763) |
| lIM-2 | −0.035 (0.791) | 0.040 (0.593) | 0.164 (0.267) |
| lGDP-3 | −0.300 (0.130) | −0.044 (0.904) | 0.551 (0.005) ** |
| lEX-3 | 0.016 (0.921) | 0.013 (0.853) | −0.136 (0.131) |
| lIM-3 | −0.047 (0.733) | 0.041 (0.632) | 0.095 (0.539) |
| lGDP-4 | 0.336 (0.083)8 | 0.549 (0.153) | −0.071 (0.671) |
| lEX-4 | 0.226 (0.131) | 0.040 (0.576) | 0.077 (0.380) |
| lIM-4 | 0.191 (0.500) | −0.300 (0.194) | −0.073 (0.735) |
| lEX | |||
| ECT | −0.011 (0.158) | −0.039 (0.032) * | −0.038 (0.110) |
| Intercept | −0.418 (0.220) | −1.851 (0.033) * | 1.987 (0.107) |
| lGDP-1 | 0.533 (0.194 | −0.420 (0.568) | −0.326 (0.400) |
| lEX-1 | −0.092 (0.608) | −0.194 (0.237) | −0.635 (0.042) * |
| lIM-1 | 0.210 (0.421) | 0.534 (0.002) ** | 0.364 (0.228) |
| lGDP-2 | −0.261 (0.512) | −0.331 (0.702) | 0.422 (0.280) |
| lEX-2 | −0.288 (0.186) | −0.442 (0.010) * | −0.344 (0.328) |
| lIM-2 | −0.449 (0.162) | 0.039 (0.807 | 0.358 (0.214) |
| lGDP-3 | 0.987 (0.019) * | −0.502 (0.527) | −0.224 (0.599) |
| lEX-3 | −0.226 (0.152) | −0.227 (0.152) | 0.016 (0.929) |
| lIM-3 | 0.095 (0.538) | 0.041 (0.632) | −0.283 (0.343) |
| lGDP-4 | −0.071 (0.671) | −0.786 (0.345) | −0.201 (0.629) |
| lEX-4 | 0.203 (0.286) | −0.172 (0.266) | −0.377 (0.243) |
| lIM-4 | 0.309 (0.291) | 0.498 (0.038) * | 0.248 (0.268) |
| lIM | |||
| ECT | −0.161 (0.542) | −0.531 (0.202) | −0.322 (0.282) |
| Intercept | −0.188 (0.136) | −0.242 (0.310) * | −0.144 (01328) |
| lGDP-1 | 0.335 (0.399) | 1.062 (0.146) | −0.054 (0.885) |
| lEX-1 | 0.110 (0.599) | 0.401 (0.014) * | −0.132 (0.659) |
| lIM-1 | −0.445 (0.081) | −0.301 (0.063) | −0.007 (0.980) |
| lGDP-2 | −0.002 (0.994) | 1.895 (0.027) * | 0.227 (0.547) |
| lEX-2 | 0.110 (0.599) | −0.442 (0.010) * | 0.024 (0.941) |
| lIM-2 | −0.349 (0.260) | −0.574 (0.000) *** | 0.202 (0.468) |
| lGDP-3 | 0.049 (0.901) | 1.232 (0.113) | 0.096 (0.815) |
| lEX-3 | 0.030 (0.869) | 0.209 (0.172) | 0.520 (0.129) |
| lIM-3 | −0.448 (0.167) | −0.657 (0.000) *** | −0.353 (0.222) |
| lGDP-4 | 0.245 (0.482) | 2.380 (0.004) ** | −0.258 (0.521) |
| lEX-4 | −0.015 (0.932) | 0.354 (0.019) * | 0.103 (0.741) |
| lIM-4 | 0.191 (0.500) | −0.300 (0.193) | −0.073 (0.735) |
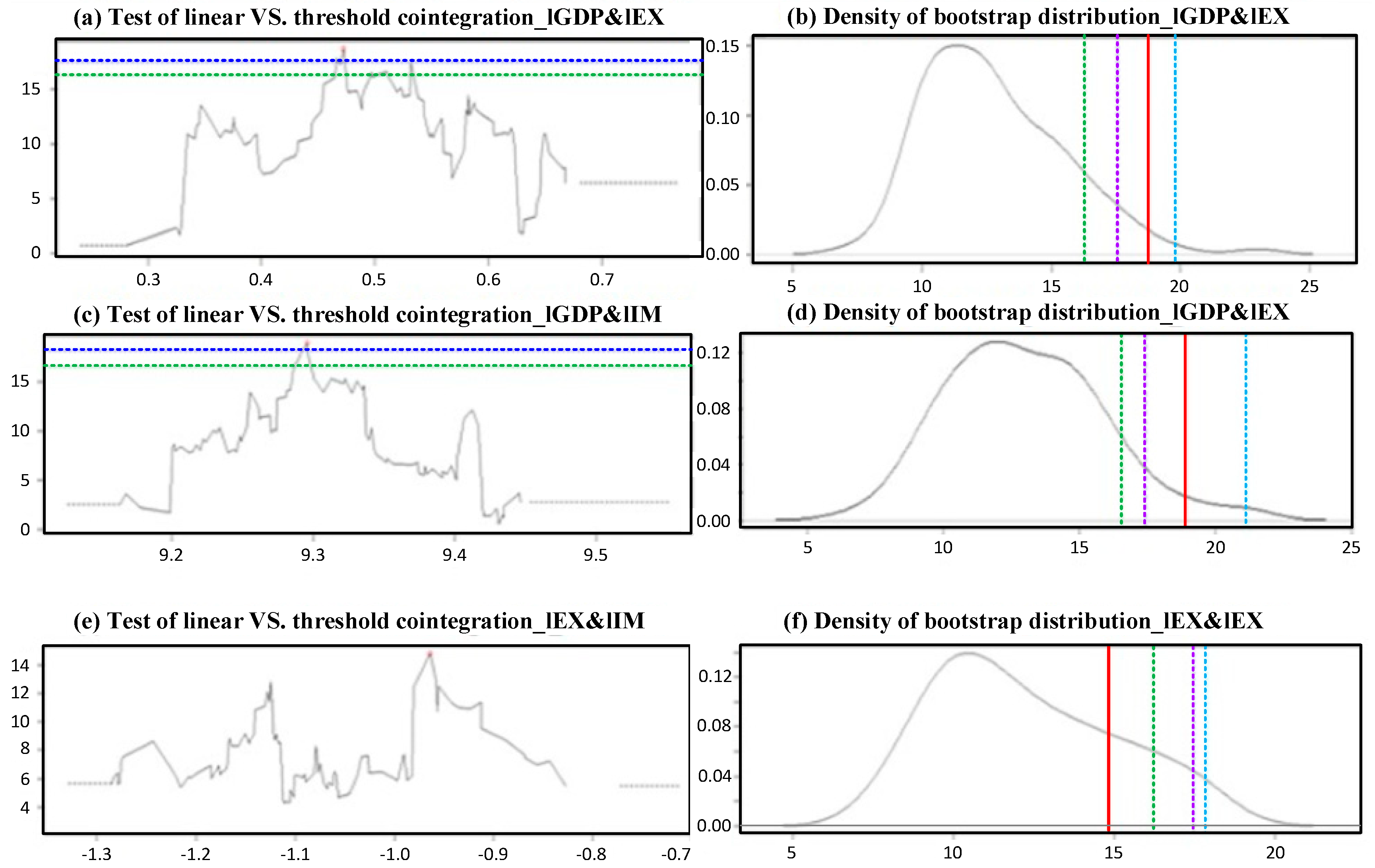
| Test | lGDP & lEX | lGDP & lIM | lEX & lIM | |||
|---|---|---|---|---|---|---|
| Sup-LM test (p-Value) | Critical value | Critical value | Critical value | |||
| 18.763 * (0.002) | 16.311 (90%) 17.545 (95%) 19.838 (99%) | 18.927 * (0.004) | 16.481 (90%) 18.164 (95%) 23.209 (99%) | 14.826 * (0.21) | 16.212 (90%) 17.470 (95%) 17.870 (99%) | |
| Maximized threshold value | 9.472 | 9.296 | −0.964 | |||
| Cointegrating value | −0.467 | −0.487 | −1.107 | |||
| Number of bootstrap replications: 100 (fixed-repressor bootstrap) | ||||||
| Model Selection | Linearity | Nonlinearity | |||
|---|---|---|---|---|---|
| VECM | TVAR (1 Threshold) | TVAR (2 Thresholds) | TVEC (1 Threshold) | TVEC (2 Thresholds) | |
| AIC | −1566.586 | −1792.417 | −1801.531 | −1786.440 | −1790.023 |
| BIC | −1496.851 | −1628.807 | −1483.465 | −1560.048 | −1449.103 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Romyen, A.; Liu, J.; Sriboonchitta, S. Export–Output Growth Nexus Using Threshold VAR and VEC Models: Empirical Evidence from Thailand. Economies 2019, 7, 60. https://doi.org/10.3390/economies7020060
Romyen A, Liu J, Sriboonchitta S. Export–Output Growth Nexus Using Threshold VAR and VEC Models: Empirical Evidence from Thailand. Economies. 2019; 7(2):60. https://doi.org/10.3390/economies7020060
Chicago/Turabian StyleRomyen, Arisara, Jianxu Liu, and Songsak Sriboonchitta. 2019. "Export–Output Growth Nexus Using Threshold VAR and VEC Models: Empirical Evidence from Thailand" Economies 7, no. 2: 60. https://doi.org/10.3390/economies7020060
APA StyleRomyen, A., Liu, J., & Sriboonchitta, S. (2019). Export–Output Growth Nexus Using Threshold VAR and VEC Models: Empirical Evidence from Thailand. Economies, 7(2), 60. https://doi.org/10.3390/economies7020060





