Asymmetry in Exchange Rate Pass-Through to Consumer Prices: New Perspective from Sub-Saharan African Countries
Abstract
1. Introduction
2. Literature Review
2.1. Theoretical Review
2.2. Empirical Review
3. Data and Methodology
3.1. Data and Model Specification
3.2. Exchange Rate Pass-Through Estimation Per Country
3.3. Panel Pass-Through Estimation
4. Empirical Results and Discussion
4.1. Results of Pass-Through Estimations per Country
4.2. Results of Dynamic Panel ERPT Estimations
4.2.1. Robustness Tests under Cross-Sectional Dependence Analysis
4.2.2. Results of Panel Pass-Through Estimations
4.2.3. Estimations of Pass-Through with Respect to Size and Direction of Exchange Rates
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
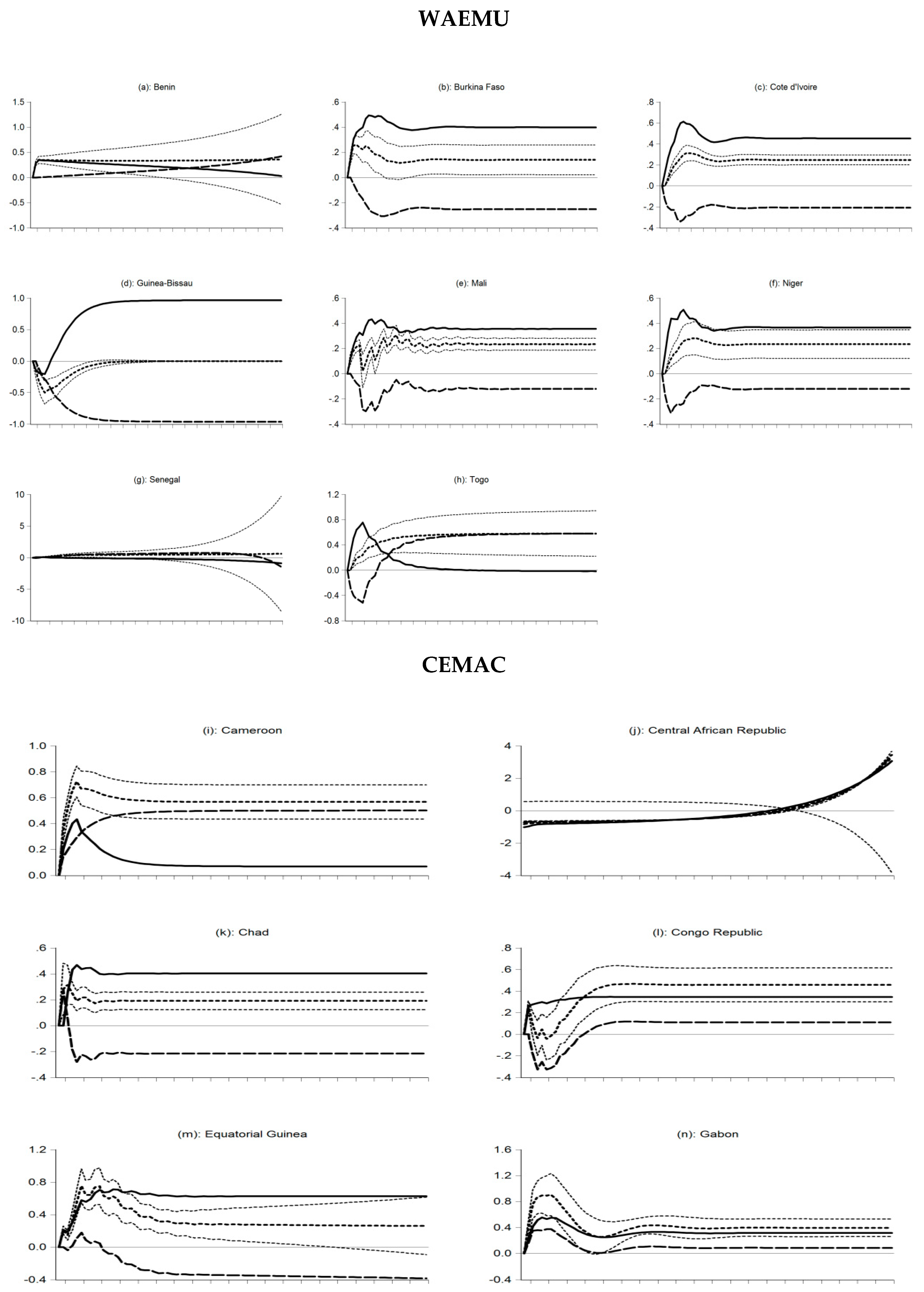

Appendix B
Appendix B.1
| Obs. | 40 | 45 | 50 | 55 | 60 | 65 | 70 | 75 | 80 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1% | k = 4 | I(0) | 4.428 | 4.394 | 4.306 | 4.244 | 4.176 | 4.188 | 4.098 | 4.168 | 4.096 |
| I(1) | 6.250 | 5.914 | 5.874 | 5.726 | 5.676 | 5.694 | 5.570 | 5.548 | 5.512 | ||
| k = 5 | I(0) | 4.045 | 4.030 | 3.955 | 3.928 | 3.783 | 3.783 | 3.747 | 3.772 | 3.725 | |
| I(1) | 5.898 | 5.598 | 5.583 | 5.408 | 5.338 | 5.300 | 5.285 | 5.213 | 5.163 | ||
| 5% | k = 4 | I(0) | 3.202 | 3.178 | 3.136 | 3.068 | 3.062 | 3.068 | 3.022 | 3.042 | 3.010 |
| I(1) | 4.544 | 4.450 | 4.416 | 4.334 | 4.314 | 4.274 | 4.256 | 4.244 | 4.216 | ||
| k = 5 | I(0) | 2.962 | 2.922 | 2.900 | 2.848 | 2.817 | 2.835 | 2.788 | 2.802 | 2.787 | |
| I(1) | 4.338 | 4.268 | 4.218 | 4.160 | 4.097 | 4.090 | 4.073 | 4.065 | 4.015 | ||
| 10% | k = 4 | I(0) | 2.660 | 2.638 | 2.614 | 2.578 | 2.568 | 2.574 | 2.552 | 2.558 | 2.548 |
| I(1) | 3.838 | 3.772 | 3.746 | 3.710 | 3.712 | 3.682 | 3.648 | 3.654 | 3.644 | ||
| k = 5 | I(0) | 2.483 | 2.458 | 2.435 | 2.393 | 2.385 | 2.397 | 2.363 | 2.380 | 2.355 | |
| I(1) | 3.708 | 3.647 | 3.600 | 3.583 | 3.565 | 3.543 | 3.510 | 3.515 | 3.500 |
Appendix B.2
| Countries with High Inflation (K = 13) (Average Inflation Above 2.33%) | Countries with Hyperinflation (K = 7) (Average Inflation Above 3.5%) | Countries with Low Inflation (K = 27) (Average-Inflation Below 2.33%) |
|---|---|---|
| Guinea-Bissau, Angola, Congo Democratic Republic, Ghana, Guinea, Kenya, Liberia, Madagascar, Malawi, Nigeria, Sao Tome and Principe, Tanzania and Zambia | Angola, Congo Democratic Republic, Ghana, Guinea, Malawi, Nigeria and Zambia | Benin, Burkina Faso, Cote d’Ivoire, Mali, Niger, Senegal, Togo, Cameroon, Central African Republic, Chad, Congo Republic, Equatorial Guinea, Gabon, Botswana, Cabo Verde, Comoros, Ethiopia, Gambia, Lesotho, Mauritius, Mozambique, Namibia, Rwanda, Seychelles, South Africa, Swaziland and Uganda. |
References
- Akofio-Sowah, Naa Anyeley. 2009. Is There a Link Between Exchange Rate Pass-Through and the Monetary Regime: Evidence from Sub-Saharan Africa and Latin America. International Advances in Economic Research 15: 296–309. [Google Scholar] [CrossRef]
- An, Lian, and Jian Wang. 2011. Exchange Rate Pass-Through: Evidence Based on Vector Autoregression with Sign Restrictions. Open Economies Review 23: 359–80. [Google Scholar] [CrossRef]
- Bada, Abiodun, Ajibola Olufemi, Inuwa Tata, Idowu Peters, Sani Bawa, Anigwe Onwubiko, and Udoko Onyowo. 2016. Exchange rate pass-through to inflation in Nigeria. CBN Journal of Applied Statistics 7: 49–70. [Google Scholar]
- Baharumshah, Ahmad Zubaidi, Abdalla Sirag, and Siew-Voon Soon. 2017. Asymmetric exchange rate pass-through in an emerging market economy: The case of Mexico. Research in International Business and Finance 41: 247–59. [Google Scholar] [CrossRef]
- Bahmani-Oskooee, Mohsen, and Amirhossein Mohammadian. 2017. Asymmetry Effects of Exchange Rate Changes on Domestic Production in Emerging Countries. Emerging Markets Finance and Trade 54: 1442–59. [Google Scholar] [CrossRef]
- Banerjee, Anindya, Juan Dolado, and Ricardo Mestre. 1998. Error-correction Mechanism Tests for Cointegration in a Single-equation Framework. Journal of Time Series Analysis 19: 267–83. [Google Scholar] [CrossRef]
- Beck, Nathaniel, and Jonathan N. Katz. 1995. What to Do (and Not to Do) with Time-Series Cross-Section Data. American Political Science Review 89: 634–47. [Google Scholar] [CrossRef]
- Ben Cheikh, Nidhaleddine. 2012. Asymmetric Exchange Rate Pass-Through in the Euro Area: New Evidence from Smooth Transition Models. Economics: The Open-Access, Open-Assessment E-Journal 6: 1. [Google Scholar] [CrossRef]
- Berner, Eike. 2010. Exchange rate pass-through: New evidence from German micro data. International Economics 124: 75–100. [Google Scholar] [CrossRef]
- Bhundia, Ashok. 2002. An Empirical Investigation of Exchange Rate Pass-Through in South Africa. IMF Working Papers. Washington, DC: International Monetary Fund. [Google Scholar] [CrossRef]
- Breusch, Trevor, and Pagan Adrian. 1980. The Lagrange Multiplier Test and its Applications to Model Specification in Econometrics. The Review of Economic Studies. [Google Scholar] [CrossRef]
- Brun-Aguerre, Raphael, Ana-Maria Fuertes, and Kate Phylaktis. 2012. Exchange rate pass-through into import prices revisited: What drives it? Journal of International Money and Finance 31: 818–44. [Google Scholar] [CrossRef]
- Brun-Aguerre, Raphael, Ana-Maria Fuertes, and Matthew Greenwood-Nimmo. 2016. Heads I win; tails you lose: Asymmetry in exchange rate pass-through into import prices. Journal of the Royal Statistical Society: Series A (Statistics in Society) 180: 587–612. [Google Scholar] [CrossRef]
- Bui, Minh Tam. 2018. Causality in Vietnam’s Parallel Exchange Rate System during 2005–2011: Policy Implications for Macroeconomic Stability. Economies 6: 68. [Google Scholar] [CrossRef]
- Bussière, Matthieu, Simona Delle Chiaie, and Tuomas Peltonen. 2014. Exchange Rate Pass-Through in the Global Economy: The Role of Emerging Market Economies. IMF Economic Review 62: 146–78. [Google Scholar] [CrossRef]
- Campa, Jose Manuel, and Linda Goldberg. 2002. Exchange Rate Pass-Through into Import Prices: A Macro or Micro Phenomenon? SSRN Electronic Journal. [Google Scholar] [CrossRef]
- Campa, Jose Manuel, and Linda Goldberg. 2005. Exchange Rate Pass-Through into Import Prices. Review of Economics and Statistics 87: 679–90. [Google Scholar] [CrossRef]
- Choudhri, Ehsan U., and Dalia S. Hakura. 2015. The exchange rate pass-through to import and export prices: The role of nominal rigidities and currency choice. Journal of International Money and Finance 51: 1–25. [Google Scholar] [CrossRef]
- Choudhri, Ehsan U., Hamid Faruqee, and Dalia S. Hakura. 2005. Explaining the exchange rate pass-through in different prices. Journal of International Economics 65: 349–74. [Google Scholar] [CrossRef]
- Conrad, Daren, and Jaymieon Jagessar. 2018. Real Exchange Rate Misalignment and Economic Growth: The Case of Trinidad and Tobago. Economies 6: 52. [Google Scholar] [CrossRef]
- Delatte, Anne-Laure, and Antonia Lòpez-Villavicencio. 2012. Asymmetric exchange rate pass-through: Evidence from major countries. Journal of Macroeconomics 34: 833–44. [Google Scholar] [CrossRef]
- Dickey, David, and Wayne Fuller. 1981. Likelihood Ratio Statistics for Autoregressive Time Series with a Unit Root. Econometrica. [Google Scholar] [CrossRef]
- Dornbusch, Rudiger. 1985. Exchange Rates and Prices. NBER Working Paper No. 1769. Cambridge: National Bureau of Economic Research. [Google Scholar] [CrossRef]
- Driscoll, John, and Aart Kraay. 1998. Consistent Covariance Matrix Estimation with Spatially Dependent Panel Data. Review of Economics and Statistics 80: 549–60. [Google Scholar] [CrossRef]
- Frankel, Jeffrey, David Parsley, and Shang-Jin Wei. 2011. Slow Pass-through Around the World: A New Import for Developing Countries? Open Economies Review 23: 213–51. [Google Scholar] [CrossRef]
- Frees, Edward W. 1995. Assessing cross-sectional correlation in panel data. Journal of Econometrics 69: 393–414. [Google Scholar] [CrossRef]
- Friedman, Milton. 1937. The Use of Ranks to Avoid the Assumption of Normality Implicit in the Analysis of Variance. Journal of the American Statistical Association. [Google Scholar] [CrossRef]
- Frimpong, Siaw, and Anokye Adam. 2010. Exchange Rate Pass-Through in Ghana. International Business Research. [Google Scholar] [CrossRef]
- Goldberg, Linda S., and Jose Manuel Campa. 2010. The Sensitivity of the CPI to Exchange Rates: Distribution Margins, Imported Inputs, and Trade Exposure. The Review of Economics and Statistics 2: 392–407. [Google Scholar] [CrossRef]
- Goldberg, Pinelopi, and Michael Knetter. 1996. Goods Prices and Exchange Rates: What Have We Learned? Cambridge: National Bureau of Economic Research. [Google Scholar] [CrossRef]
- Hoechle, Daniel. 2007. Robust Standard Errors for Panel Regressions with Cross-Sectional Dependence. The Stata Journal 7: 281–312. [Google Scholar] [CrossRef]
- International Monetary Fund. 2012. Exchange Rate Pass-Through in Sub-Saharan African Economies and its Determinants. IMF Working Papers. Washington, DC: International Monetary Fund. [Google Scholar] [CrossRef]
- Jombo, Wytone, Kisu Simwaka, and Austin Chiumia. 2014. Exchange Rate Pass-Through in Malawi: Evidence from Augmented Phillips Curve and Vector Autoregressive Approaches. Standard Global Journal of Business Management 1: 34–40. [Google Scholar]
- Jooste, Charl, and Yaseen Jhaveri. 2014. The Determinants of Time-Varying Exchange Rate Pass-Through in South Africa. South African Journal of Economics 82: 603–15. [Google Scholar] [CrossRef]
- Karoro, Tapiwa D., Meshach J. Aziakpono, and Nicolette Cattaneo. 2009. Exchange Rate Pass-Through to Import Prices in South Africa: Is There Asymmetry? South African Journal of Economics 77: 380–98. [Google Scholar] [CrossRef]
- Kassi, Diby François, Gang Sun, Ning Ding, Dilesha Nawadali Rathnayake, and Guy Roland Assamoi. 2018. Asymmetry in exchange rate pass-through to consumer prices: Evidence from emerging and developing Asian countries. Economic Analysis and Policy. [Google Scholar] [CrossRef]
- Kmenta, Jan. 1986. Elements of Econometrics, 2nd ed. New York: Macmillan. [Google Scholar]
- Knetter, Michael. 1994. Is export price adjustment asymmetric?: Evaluating the market share and marketing bottlenecks hypotheses. Journal of International Money and Finance 13: 55–70. [Google Scholar] [CrossRef]
- Krugman, Paul. 1986. Pricing to Market when the Exchange Rate Changes. Cambridge: National Bureau of Economic Research. [Google Scholar] [CrossRef]
- Kwiatkowski, Denis, Peter C. B. Phillips, Peter Schmidt, and Yongcheol Shin. 1992. Testing the null hypothesis of stationarity against the alternative of a unit root. Journal of Econometrics 54: 159–78. [Google Scholar] [CrossRef]
- Maka, Evans Darnor. 2013. Asymmetric Pass-Through of Exchange Rate Changes to CPI Inflation in Ghana. International Journal of Economics, Finance and Management 2: 338–50. [Google Scholar]
- Marston, Richard C. 1990. Pricing to market in Japanese manufacturing. Journal of International Economics 29: 217–36. [Google Scholar] [CrossRef]
- Mwase, Nkunde. 2006. An Empirical Investigation of the Exchange Rate Pass-Through to Inflation in Tanzania. IMF Working Papers. Washington, DC: International Monetary Fund. [Google Scholar] [CrossRef]
- Narayan, Paresh Kumar. 2005. The saving and investment nexus for China: Evidence from cointegration tests. Applied Economics 37: 1979–90. [Google Scholar] [CrossRef]
- Newey, Whitney K., and Kenneth West. 1987. A Simple, Positive Semi-Definite, Heteroskedasticity and Autocorrelation Consistent Covariance Matrix. Econometrica 55: 703–8. [Google Scholar] [CrossRef]
- Olivei, Giovanni P. 2002. Exchange rates and the prices of manufacturing products imported into the United States. New England Economic Review, 3–18. [Google Scholar]
- Otani, Akira, Shigenori Shiratsuka, and Toyoichiro Shirota. 2003. The Decline in the Exchange Rate Pass-Through: Evidence from Japanese Import Prices. Institute for Monetary and Economic Studies 21: 53–81. [Google Scholar]
- Ozkan, Ibrahim, and Luffi Erden. 2015. Time-varying nature and macroeconomic determinants of exchange rate pass-through. International Review of Economics & Finance 38: 56–66. [Google Scholar] [CrossRef]
- Parks, Richard W. 1967. Efficient Estimation of a System of Regression Equations when Disturbances are Both Serially and Contemporaneously Correlated. Journal of the American Statistical Association. [Google Scholar] [CrossRef]
- Pesaran, Hashem M. 2004. General Diagnostic Tests for Cross Section Dependence in Panels. CESifo Working Paper Series No. 1229; IZA Discussion Paper No. 1240. Cambridge, UK: University of Cambridge. [Google Scholar]
- Pesaran, Hashem M., Yongcheol Shin, and Richard J. Smith. 2001. Bounds testing approaches to the analysis of level relationships. Journal of Applied Econometrics 16: 289–326. [Google Scholar] [CrossRef]
- Phillips, Peter C. B., and Pierre Perron. 1988. Testing for a Unit Root in Time Series Regression. Biometrika 75: 335–46. [Google Scholar] [CrossRef]
- Pollard, Patricia S., and Cletus Coughlin. 2004. Size Matters: Asymmetric Exchange Rate Pass-Through at the Industry Level. SSRN Electronic Journal. [Google Scholar] [CrossRef]
- Savoie-Chabot, Laurence, and Mikael Khan. 2015. Exchange Rate Pass-Through to Consumer Prices: Theory and Recent Evidence. Discussion Paper 2015-9. Ottawa: Bank of Canada. [Google Scholar]
- Sbia Rashid, Muhammad Shahbaz, and Helmi Hamdi. 2014. A contribution of foreign direct investment, clean energy, trade openness, carbon emissions and economic growth to energy demand in UAE. Economic Modelling 36: 191–97. [Google Scholar] [CrossRef]
- Shahbaz, Muhammad, Thi Hong Van Hoang, Mantu Kumar Mahalik, and David Roubaud. 2017. Energy consumption, financial development and economic growth in India: New evidence from a nonlinear and asymmetric analysis. Energy Economics 63: 199–212. [Google Scholar] [CrossRef]
- Shin, Yongcheol, Byungchul Yu, and Matthew Greenwood-Nimmo. 2014. Modelling Asymmetric Cointegration and Dynamic Multipliers in a Nonlinear ARDL Framework. In Festschrift in Honor of Peter Schmidt. New York: Springer, pp. 281–314. [Google Scholar] [CrossRef]
- Takhtamanova, Yelena F. 2010. Understanding changes in exchange rate pass-through. Journal of Macroeconomics 32: 1118–30. [Google Scholar] [CrossRef]
- Taylor, John Bernard. 2000. Low inflation, pass-through, and the pricing power of firms. European Economic Review 44: 1389–408. [Google Scholar] [CrossRef]
- Usman, Ojonugwa, and Osama Mohammed Elsalih. 2018. Testing the Effects of Real Exchange Rate Pass-Through to Unemployment in Brazil. Economies 6: 49. [Google Scholar] [CrossRef]
- Utku Özmen, Mustafa, and Fatih Akçelik. 2017. Asymmetric exchange rate and oil price pass-through in motor fuel market: A microeconometric approach. The Journal of Economic Asymmetries 15: 64–75. [Google Scholar] [CrossRef]
- Ware, Roger, and Ralph Winter. 1988. Forward markets, currency options and the hedging of foreign exchange risk. Journal of International Economics 25: 291–302. [Google Scholar] [CrossRef]
- Yanamandra, Venkataramana. 2015. Exchange rate changes and inflation in India: What is the extent of exchange rate pass-through to imports? Economic Analysis and Policy 47: 57–68. [Google Scholar] [CrossRef]
- Yellen, Janet Louise. 2015. Inflation Dynamics and Monetary Policy. Paper presented at the Philip Gamble Memorial Lecture, University of Massachusetts, Amherst, MA, USA, September 24. [Google Scholar]
| 1 | World Trade Organization, International Trade Statistics 2015. |
| Nominal Exchange Rate (ler) | Consumer Price Index (lcpi) | Output Gap (gap) | Money Supply (lmon) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| dlert (%) | dlcpit (%) | gapt (%) | dlmont (%) | ||||||||
| Country | Period | Mean | Std. Dev | Depr (+) | Appr (−) | Mean | Std. Dev | Mean | Std. Dev | Mean | Std. Dev |
| CFA franc zone (14) | 1990Q2–2017Q4 | 0.630 | 8.249 | 51.98 | 48.02 | 1.047 | 3.539 | −2.548 | 56.625 | 0.231 | 6.795 |
| WAEMU (KW = 8) | 1990Q2–2017Q4 | 0.595 | 8.197 | 51.48 | 48.52 | 1.067 | 3.664 | −3.451 | 40.905 | 0.185 | 7.601 |
| Benin | 1992Q1–2017Q4 | 0.655 | 8.280 | 52.43 | 47.57 | 1.037 | 2.943 | −0.099 | 8.627 | 0.191 | 3.946 |
| Burkina Faso | 1990Q1–2017Q4 | 0.587 | 8.224 | 51.35 | 48.65 | 0.719 | 2.241 | −0.118 | 8.419 | 0.839 | 4.099 |
| Cote d’Ivoire | 1990Q1–2017Q4 | 0.587 | 8.224 | 51.35 | 48.65 | 0.886 | 2.027 | −0.012 | 2.840 | 0.201 | 4.067 |
| Guinea-Bissau | 1990Q1–2017Q4 | 0.587 | 8.224 | 51.35 | 48.65 | 2.994 | 6.314 | −26.854 | 111.282 | −1.312 | 18.486 |
| Mali | 1990Q1–2017Q4 | 0.587 | 8.224 | 51.35 | 48.65 | 0.691 | 2.770 | −0.052 | 4.843 | 0.164 | 4.038 |
| Niger | 1990Q1–2017Q4 | 0.587 | 8.224 | 51.35 | 48.65 | 0.679 | 3.234 | −0.194 | 9.586 | 0.243 | 5.730 |
| Senegal | 1990Q1–2017Q4 | 0.587 | 8.224 | 51.35 | 48.65 | 0.627 | 2.522 | −0.042 | 4.232 | 0.726 | 2.392 |
| Togo | 1990Q1–2017Q4 | 0.587 | 8.224 | 51.35 | 48.65 | 0.896 | 4.646 | −0.000 | 8.556 | 0.434 | 3.768 |
| CEMAC (KC = 6) | 1990Q2–2017Q4 | 0.679 | 8.326 | 52.66 | 47.34 | 1.018 | 3.361 | −1.303 | 72.963 | 0.295 | 5.498 |
| Cameroon | 1990Q1–2017Q4 | 0.587 | 8.224 | 51.35 | 48.65 | 0.808 | 2.173 | −0.025 | 2.820 | 0.000 | 3.463 |
| Central African Rep. | 1990Q1–2015Q4 | 0.727 | 8.463 | 53.40 | 46.60 | 1.404 | 3.285 | −8.599 | 180.258 | 0.501 | 4.888 |
| Chad | 1990Q1–2015Q4 | 0.727 | 8.463 | 53.40 | 46.60 | 0.961 | 4.902 | −0.369 | 13.719 | -0.000 | 4.807 |
| Congo Rep. | 1990Q1–2015Q4 | 0.727 | 8.463 | 53.40 | 46.60 | 1.085 | 3.248 | −0.181 | 11.021 | 0.736 | 4.067 |
| Equatorial Guinea | 1990Q1–2017Q4 | 0.587 | 8.224 | 51.35 | 48.65 | 1.332 | 3.214 | 1.085 | 17.733 | 0.104 | 9.688 |
| Gabon | 1990Q1–2016Q4 | 0.730 | 8.334 | 53.27 | 46.73 | 0.532 | 2.837 | −0.058 | 4.248 | 0.456 | 3.192 |
| Oil price (dloilt (%)) | 1990Q1–2017Q4 | 0.793 | 8.326 | ||||||||
| Nominal Exchange Rate (ler) | Consumer Price Index (lcpi) | Output Gap (gap) | Money Supply (lmon) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| dlert (%) | dlcpit (%) | gapt (%) | dlmont (%) | ||||||||
| Country | Period | Mean | Std.Dev | Depr (+) | Appr (−) | Mean | Std. Dev | Mean | Std. Dev | Mean | Std. Dev |
| Other SSA (KO = 26) | 2.61 | 10.919 | 67.78 | 32.22 | 3.135 | 6.327 | −2.157 | 114.791 | 0.502 | 4.208 | |
| Angola | 1996Q1–2017Q4 | 9.575 | 23.576 | 87.36 | 12.64 | 11.872 | 14.491 | −0.062 | 3.777 | −0.15 | 5.775 |
| Botswana | 1990Q1–2017Q4 | 1.484 | 4.996 | 66.67 | 33.33 | 1.99 | 1.045 | −0.022 | 3.243 | 0.691 | 5.07 |
| Cabo Verde | 1990Q1–2017Q4 | 0.196 | 5.217 | 52.25 | 47.75 | 0.776 | 1.789 | −6.168 | 56.87 | 0.99 | 2.489 |
| Comoros | 2000Q1–2013Q4 | −0.667 | 5.188 | 45.45 | 54.55 | 0.799 | 3.659 | 0.03 | 5.457 | 1.615 | 3.677 |
| Congo, D. Rep | 1995Q1–2016Q4 | 11.864 | 28.785 | 77.01 | 22.99 | 11.203 | 19.856 | −0.14 | 5.218 | 0.837 | 5.129 |
| Ethiopia | 1990Q1–2008Q4 | 2.094 | 10.249 | 97.33 | 2.67 | 2.127 | 4.69 | −0.054 | 3.771 | 0.131 | 3.381 |
| Gambia | 1990Q1–2014Q4 | 1.708 | 6.41 | 69.7 | 30.3 | 1.373 | 1.684 | −2.022 | 22.038 | 0.748 | 5.737 |
| Ghana | 1990Q1–2017Q4 | 4.497 | 6.545 | 96.4 | 3.6 | 4.341 | 3.588 | −0.05 | 3.903 | 0.701 | 3.737 |
| Guinea | 2004Q1–2016Q4 | 2.997 | 8.574 | 79.39 | 19.61 | 3.822 | 2.933 | −0.027 | 5.971 | 0.506 | 5.907 |
| Kenya | 1990Q1–2017Q4 | 1.353 | 6.414 | 59.46 | 40.54 | 2.758 | 3.334 | −0.036 | 3.076 | 0.26 | 2.424 |
| Lesotho | 1990Q1–2017Q4 | 1.385 | 7.069 | 60.36 | 39.64 | 1.867 | 2.975 | −36.104 | 452.383 | −0.098 | 3.014 |
| Liberia | 2001Q1–2015Q4 | 1.127 | 7.538 | 72.88 | 27.12 | 2.411 | 3.246 | 40.344 | 312.087 | 1.72 | 5.73 |
| Madagascar | 1990Q1–2017Q4 | 2.117 | 8.882 | 57.66 | 42.34 | 2.726 | 3.415 | −0.03 | 5.431 | 0.646 | 3.136 |
| Malawi | 1990Q1–2016Q4 | 5.158 | 11.082 | 76.64 | 23.36 | 4.733 | 7.091 | −0.179 | 12.304 | 0.157 | 6.208 |
| Mauritius | 1990Q1–2017Q4 | 0.72 | 4.247 | 61.26 | 38.74 | 1.335 | 1.24 | −0.028 | 2.638 | 0.574 | 1.444 |
| Mozambique | 2007Q1–2017Q4 | 1.885 | 7.272 | 60.47 | 39.53 | 1.99 | 2.408 | −0.043 | 4.029 | 1.286 | 2.901 |
| Namibia | 2002Q1–2015Q4 | 0.133 | 7.704 | 49.21 | 50.79 | 1.432 | 0.931 | −61.524 | 3.719 | 0.6 | 3.986 |
| Nigeria | 1990Q1–2016Q4 | 3.409 | 15.658 | 71.03 | 28.97 | 4.117 | 4.544 | −0.091 | 4.9 | 0.132 | 7.624 |
| Rwanda | 1990Q1–2016Q4 | 2.187 | 7.755 | 67.29 | 32.71 | 1.891 | 2.594 | −1.113 | 20.016 | 0.254 | 4.436 |
| Sao T. and Prin. | 2001Q1–2017Q4 | 1.264 | 4.147 | 64.18 | 35.82 | 2.989 | 2.061 | −0.002 | 3.482 | 0.379 | 3.395 |
| Seychelles | 1990Q1–2017Q4 | 0.82 | 8.297 | 65.77 | 34.23 | 0.934 | 3.384 | 10.771 | 160.238 | 0.695 | 3.484 |
| South Africa | 1990Q1–2017Q4 | 1.385 | 7.069 | 60.36 | 39.64 | 1.63 | 1.075 | −0.012 | 1.601 | 0.322 | 1.431 |
| Swaziland | 1990Q1–2016Q4 | 1.534 | 7.108 | 61.68 | 38.32 | 1.912 | 2.057 | −0.577 | 11.681 | 0.401 | 3.158 |
| Tanzania | 1990Q1–2016Q4 | 2.258 | 4.61 | 73.83 | 26.17 | 2.946 | 4.583 | −0.091 | 4.079 | 0 | 2.363 |
| Uganda | 1993Q1–2017Q4 | 1.102 | 4.946 | 59.6 | 40.4 | 1.574 | 2.046 | −0.116 | 3.694 | 0.941 | 3.477 |
| Zambia | 1990Q1–2017Q4 | 5.226 | 15.458 | 67.57 | 32.43 | 6.35 | 7.394 | −0.103 | 4.264 | 0.136 | 4.439 |
| All SSA countries | 1990Q1–2017Q4 | 1.849 | 10.023 | 61.7 | 38.3 | 2.331 | 5.52 | −2.307 | 96.65 | 0.398 | 5.353 |
| Oil price (dloilt (%)) | 1990Q1–2017Q4 | 0.793 | 8.326 | ||||||||
| Nominal Exchange Rate (ler) | Consumer Price Index (lcpi) | Output Gap (gap) | Money Supply (lmon) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| lert | lcpit | gapt | lmont | |||||||||
| Country | ADF: | PP | KPSS | ADF: | PP | KPSS | ADF: | PP | KPSS | ADF: | PP | KPSS |
| H0 = I(1) | H0 = I(1) | H0 = I(0) | H0 = I(1) | H0 = I(1) | H0 = I(0) | H0 = I(1) | H0 = I(1) | H0 = I(0) | H0 = I(1) | H0 = I(1) | H0 = I(0) | |
| Benin | −2.916 ** | −2.874 *** | 0.201 | −3.352 ** | −3.242 ** | 1.152 * | −5.434 * | −3.225 ** | 0.025 | −1.173 | −0.79 | 0.843 * |
| Burkina Faso | −2.235 | −2.21 | 0.357 *** | −1.935 | −1.693 | 1.140 * | −4.687 * | −3.841 * | 0.025 | 0.87 | 0.22 | 0.923 * |
| Cote d’Ivoire | −2.235 | −2.21 | 0.357 *** | −3.045 ** | −2.344 | 1.127 * | −4.369 * | −3.575 * | 0.026 | −1.06 | −0.812 | 0.559 ** |
| Guinea-Bissau | −2.235 | −2.21 | 0.357 *** | −3.383 ** | 7.297 * | 0.911 * | −4.937 * | −4.412 * | 0.263 | −1.623 | −3.692 * | 0.512 ** |
| Mali | −2.235 | −2.21 | 0.357 *** | −2.785 *** | −1.465 | 1.122 * | −3.060 ** | −2.746 *** | 0.029 | −2.395 | −2.4 | 0.749 |
| Niger | −2.235 | −2.21 | 0.357 *** | −2.585 *** | −1.221 | 1.081 * | −4.739 * | −3.786 * | 0.027 | −1.104 | −0.665 | 0.520 ** |
| Senegal | −2.235 | −2.21 | 0.357 *** | −1.763 | −1.697 | 1.081 * | −4.345 * | −3.846 * | 0.027 | 1.72 | 0.624 | 1.093 * |
| Togo | −2.235 | −2.21 | 0.357 *** | −2.023 | −1.655 | 1.063 * | −4.924 * | −3.434 * | 0.025 | 0.074 | −0.125 | 0.772 * |
| Cameroon | −2.235 | −2.21 | 0.357 *** | −1.93 | −1.661 | 1.121 | −5.832 * | −3.877 * | 0.028 | −1.644 | −1.237 | 0.518 ** |
| Central African Rep. | −2.076 | −2.048 | 0.374 *** | 1.496 | 1.532 | 1.17 | −9.055 * | −9.014 * | 0.045 | −1.938 | −1.3 | 0.234 |
| Chad | −2.076 | −2.048 | 0.374 *** | −1.904 | −1.452 | 1.141 | −4.718 * | −2.950 ** | 0.038 | −1.252 | −2.236 | 0.191 |
| Congo Rep. | −2.076 | −2.048 | 0.374 *** | −1.165 | −1.124 | 1.108 | −3.486 ** | −3.435 ** | 0.022 | 0.252 | 2.611 | 0.62 |
| Equatorial Guinea | −2.076 | −2.048 | 0.374 *** | −5.251 * | −1.577 | 1.177 | −7.638 * | −7.638 * | 0.041 | −0.299 | −1.648 | 0.344 |
| Gabon | −2.094 | −2.062 | 0.382 *** | −0.842 | −0.898 | 1.014 | −2.697 *** | −3.259 ** | 0.03 | −0.569 | −0.983 | 0.828 |
| Angola | −6.989 * | −5.277 * | 0.843 * | −2.464 | −7.545 * | 1.000 * | −3.496 ** | −3.398 ** | 0.049 | −1.919 | −1.333 | 0.766 * |
| Botswana | −1.488 | −1.468 | 1.140 * | −1.241 | −4.866 * | 1.220 * | −2.445 | −3.375 ** | 0.029 | −1.02 | −1.895 | 0.891 * |
| Cabo Verde | −1.935 | −1.951 | 0.193 | −1.853 | −3.923 * | 1.156 * | −5.907 * | −9.570 * | 0.445 | −2.089 | −2.077 | 1.008 * |
| Comoros | −1.547 | −1.547 | 0.649 ** | −1.779 | −1.453 | 0.896 * | −4.281 * | −2.779 *** | 0.05 | −0.82 | −2.837 *** | 0.889 |
| Congo Dem. Rep. | −2.121 | −4.526 * | 0.948 * | −4.518 * | −4.265 * | 0.943 * | −2.695 *** | −3.438 ** | 0.056 | −0.824 | 0.078 | 0.852 |
| Ethiopia | −1.124 | −2.178 | 0.909 * | 0.138 | 0.565 | 0.996 * | −3.856 * | −3.134 ** | 0.042 | −1.555 | −1.497 | 0.887 * |
| Gambia | −0.462 | −0.109 | 1.130 * | −0.075 | −0.358 | 1.209 * | −2.48 | −3.341 ** | 0.076 | −2.045 | −0.283 | 1.120 * |
| Ghana | −2.052 | −1.922 | 1.163 * | −2.918 ** | −2.626 *** | 1.192 * | −3.845 * | −3.461 ** | 0.033 | −1.973 | −2.504 | 0.917 * |
| Guinea | −0.369 | −2.656 *** | 0.902 * | −4.525 * | −4.274 * | 0.953 * | −3.899 * | −2.59 | 0.047 | −1.96 | −1.437 | 0.568 |
| Kenya | −2.974 ** | −3.070 ** | 1.029 * | −1.999 | −2.779 ** | 1.205 * | −4.165 * | −3.204 ** | 0.036 | −2.614 *** | −2.742 *** | 0.628 ** |
| Lesotho | −1.697 | −1.329 | 1.025 * | −1.862 | −2.690 ** | 1.052 * | −11.187 * | −12.343 * | 0.129 | −1.435 | −2.547 | 0.243 * |
| Liberia | −0.899 | −2.024 | 0.908 * | −0.911 | −2.596 *** | 0.970 * | −7.664 * | −7.665 * | 0.136 | −3.930 * | −1.02 | 0.805 * |
| Madagascar | −1.767 | −1.776 | 1.106 * | −2.088 | −2.137 | 1.184 * | −3.741 * | −4.648 * | 0.023 | −1.006 | −3.317 ** | 1.001 * |
| Malawi | −2.185 | −1.053 | 1.119 * | −2.424 | −1.56 | 1.136 * | −5.075 * | −3.872 * | 0.025 | −1.737 | −1.049 | 0.299 |
| Mauritius | −1.696 | −1.696 | 1.059 * | −3.320 ** | −3.222 ** | 1.217 * | −2.31 | −3.670 * | 0.029 | −1.146 | −1.486 | 1.165 * |
| Mozambique | −0.859 | −0.368 | 0.626 ** | −0.323 | −0.343 | 0.823 * | −3.682 * | −2.561 | 0.076 | −1.172 | −1.916 | 0.763 * |
| Namibia | −0.95 | −1.161 | 0.654 ** | −0.088 | −0.841 | 1.023 | −5.108 * | −4.446 * | 0.615 ** | −1.711 | −1.393 | 0.684 ** |
| Nigeria | −1.606 | −1.606 | 1.053 * | −1.984 | −3.039 ** | 1.105 * | −3.624 * | −3.084 ** | 0.038 | −3.168 ** | −2.617 *** | 0.11 |
| Rwanda | −2.827 *** | −3.379 ** | 1.054 * | −0.849 | −1.72 | 1.200 * | −3.588 * | −3.059 ** | 0.041 | −3.109 ** | −1.995 | 0.575 ** |
| Sao Tome & Prin. | −1.286 | −1.292 | 1.024 * | −1.843 | −1.827 | 1.051 * | −4.318 * | −3.111 ** | 0.042 | −2.565 | −2.397 | 0.611 ** |
| Seychelles | −0.25 | −0.374 | 1.018 * | 0.047 | 0.219 | 1.108 * | −5.102 * | −5.132 * | 0.059 | −2.451 | −2.212 | 0.248 |
| South Africa | −1.697 | −1.329 | 1.025 * | −2.679 *** | −3.577 * | 1.214 * | −3.591 * | −3.008 ** | 0.036 | −1.394 | −0.957 | 1.040 * |
| Swaziland | −0.99 | −1.019 | 0.991 * | −2.334 | −2.434 | 1.180 * | −3.564 * | −3.298 ** | 0.043 | −0.706 | −0.567 | 0.371 *** |
| Tanzania | −3.460 ** | −3.020 ** | 1.122 * | −2.626 *** | −4.070 * | 1.104 * | −3.699 * | −3.945 * | 0.044 | −3.365 ** | −2.054 | 0.308 |
| Uganda | −0.512 | 0.116 | 1.095 * | 0.081 | 0.252 | 1.195 * | −2.507 | −7.135 * | 0.058 | −2.071 | −0.125 | 0.772 * |
| Zambia | −5.974 * | 5.648 * | 0.976 * | −5.107 * | −8.642 * | 1.102 * | −3.561 * | −3.236 ** | 0.045 | −2.071 | −2.761 *** | 1.125 * |
| Oil price | ADF: | PP | KPSS | |||||||||
| loilt | −1.174 | −1.011 | 0.973 * | |||||||||
| Countries | Unrestricted NARDL | Restricted NARDLs | ||||||
|---|---|---|---|---|---|---|---|---|
| NARDL Model (2] | NARDL Model (3] | NARDL Model (4] | NARDL Model (5] | |||||
| STA & LTA | STA & LTS | STS & LTA | STS & LTS | |||||
| tBDM | FPSS | tBDM | FPSS | tBDM | FPSS | tBDM | FPSS | |
| Unrestricted NARDL | Restricted NARDLs | |||||||
| WAEMU (KW = 8) | ||||||||
| Benin | −1.682 | 4.252 ** | −1.463 | 6.070 * | −1.198 | 7.016 * | −3.743 *** | 3.092 |
| Burkina Faso | −4.314 ** | 3.346 | −3.856 *** | 3.213 | −4.573 ** | 3.754 *** | −3.743 *** | 3.092 |
| Cote d’Ivoire | −1.917 | 2.123 | 0.285 | 1.880 | −5.515 * | 5.934 * | −1.308 | 2.254 |
| Guinea-Bissau | −5.637 * | 8.895 * | −6.024 * | 10.935 * | −5.333 * | 8.164 * | −5.718 * | 9.898 * |
| Mali | −7.187 * | 10.217 * | −3.215 | 2.900 | −5.593 * | 7.371 * | −2.148 | 3.479 |
| Niger | −5.422 * | 5.552 * | −5.167 * | 5.805 * | −5.786 * | 6.128 * | −5.302 * | 6.018 * |
| Senegal | −4.277 ** | 3.365 | −4.153 ** | 5.085 ** | −1.956 | 5.563 * | −1.090 | 6.178 * |
| Togo | −3.521 | 3.782 *** | −2.978 | 4.232 ** | −3.473 | 5.395 * | −2.828 | 4.346 ** |
| CEMAC (KC = 6) | ||||||||
| Cameroon | −4.370 ** | 6.517 * | 1.154 | 0.567 | −5.299 * | 10.009 * | −1.749 | 2.564 |
| Central African Rep. | −0.532 | 3.399 | 0.838 | 4.377 ** | −1.133 | 1.592 | 0.328 | 2.444 |
| Chad | −6.597 * | 8.501 * | −5.337 * | 7.000 * | −6.057 * | 8.832 * | −5.080 * | 6.460 * |
| Congo Rep. | −4.355 ** | 6.594 * | −2.719 | 4.540 ** | −2.787 | 2.443 | −1.650 | 2.748 |
| Equatorial Guinea | −5.902 * | 7.451 * | −2.203 | 3.412 | −4.915 * | 5.845 * | −1.384 | 1.576 |
| Gabon | −4.602 ** | 6.210 * | −2.029 | 1.318 | −3.544 | 3.004 | −2.866 | 2.178 |
| Unrestricted NARDL | Restricted NARDLs | |||||||
|---|---|---|---|---|---|---|---|---|
| NARDL Model (2) | NARDL Model (3) | NARDL Model (4) | NARDL Model (5) | |||||
| STA & LTA | STA & LTS | STS & LTA | STS & LTS | |||||
| tBDM | FPSS | tBDM | FPSS | tBDM | FPSS | tBDM | FPSS | |
| Other (KO = 26) | ||||||||
| Angola | −0.797 | 14.627 * | −0.769 | 17.781 * | −2.674 | 9.344 * | −1.622 | 11.470 * |
| Botswana | −2.145 | 6.572 * | −2.840 | 14.743 * | −2.334 | 4.082 ** | −1.938 | 14.237 * |
| Cabo Verde | −4.602 ** | 7.592 * | −5.504 * | 9.469 * | −4.393 ** | 7.897 * | −5.157 ** | 9.452 * |
| Comoros | −7.058 * | 10.040 * | −5.265 * | 6.001 * | −8.238 * | 11.705 * | −6.497 * | 8.901 * |
| Congo, Dem. Rep. | −3.246 | 16.544 * | −1.823 | 24.557 * | −0.226 | 4.757 * | 1.681 | 3.307 |
| Ethiopia | −1.454 | 4.752 ** | 2.776 | 9.477 * | −1.588 | 4.257 ** | −1.806 | 3.781 *** |
| Gambia | −5.105 * | 8.456 * | −3.547 | 6.682 * | −5.617 * | 8.874 * | −2.865 | 5.082 * |
| Ghana | −2.051 | 1.850 | −2.072 | 2.196 | −1.618 | 1.485 | −1.633 | 1.800 |
| Guinea | 4.273 ** | 27.936 * | −1.776 | 18.369 * | 0.460 | 6.912 * | 0.800 | 11.365 * |
| Kenya | 2.595 | 10.845 * | −0.746 | 4.973 ** | 2.865 | 10.538 * | −0.789 | 4.423 ** |
| Lesotho | −0.419 | 3.763 *** | −1.178 | 4.529 ** | −0.608 | 5.090 ** | −2.072 | 5.999 * |
| Liberia | −4.362 ** | 6.276 * | −3.714 | 4.010 *** | −4.137 ** | 4.104 *** | 0.471 | 1.159 |
| Madagascar | −0.524 | 5.870 * | −1.910 | 7.069 * | −3.301 | 5.745 * | −3.002 | 7.793 * |
| Malawi | −3.672 | 7.609 * | −3.686 *** | 9.085 * | −2.363 | 4.740 ** | −2.293 | 5.571 * |
| Mauritius | −2.683 | 2.801 | −2.223 | 2.325 | −2.751 | 2.792 | −1.802 | 2.438 |
| Mozambique | −2.688 | 8.900 * | −4.503 *** | 11.843 * | −1.845 | 11.138 * | 0.565 | 6.294 * |
| Namibia | −3.144 | 3.703 *** | −0.978 | 1.449 | −1.735 | 4.289 ** | −0.401 | 1.392 |
| Nigeria | −6.595 * | 8.916 * | −2.039 | 6.912 * | −2.075 | 5.492 *** | −2.154 | 6.189 * |
| Rwanda | −2.981 | 3.501 *** | −4.612 ** | 5.470 ** | −4.412 ** | 4.509 ** | −4.612 ** | 5.470 ** |
| Sao Tome and Prin. | −3.151 | 3.547 *** | −3.681 *** | 4.355 ** | −4.356 ** | 6.041 * | −5.478 * | 7.374 * |
| Seychelles | −1.719 | 6.984 * | −3.240 | 7.859 * | −7.373 * | 15.031 * | −7.098 * | 12.491 * |
| South Africa | −3.345 | 3.561 *** | −1.470 | 2.800 | −3.419 | 5.073 ** | −1.326 | 3.296 |
| Swaziland | −1.922 | 2.293 | −1.759 | 2.478 | −1.922 | 2.293 | −1.759 | 2.478 |
| Tanzania | −1.645 | 5.296 ** | 0.553 | 5.472 * | −2.721 | 5.935 * | 0.402 | 4.453 ** |
| Uganda | −2.952 | 3.070 | −1.023 | 1.626 | −4.163 *** | 4.538 ** | −1.575 | 2.316 |
| Zambia | −2.708 | 4.153 ** | −2.852 | 4.407 ** | −3.767 | 9.404 * | −2.492 | 6.644 * |
| Country | Short-Term Tests (WST): | Long-Term Tests (WLT): | Unrestricted & Restricted NARDL Models |
|---|---|---|---|
| WAEMU (KW = 8) | |||
| Benin (a) | 66.787 * | 6.121 ** | Rest. NARDL model (2) |
| Burkina Faso (a) | 12.752 * | 4.921 ** | Unr. NARDL model (2) |
| Cote d’Ivoire (c) | - | 81.428 * | Rest. NARDL model (4) |
| Guinea-Bissau (a) | 11.648 * | 0.001 | Rest. NARDL model (3) |
| Mali (a) | 4.105 ** | 78.592 * | Rest. NARDL model (2) |
| Niger (a) | 1.348 | 0.213 * | Rest. NARDL model (4) |
| Senegal (a) | −0.034 | 0.248 * | Unr. NARDL model (4) |
| Togo (a) | 1.613 | 7.754 * | Unr NARDL model (4) |
| CEMAC (KC = 6) | |||
| Cameroon (a) | 66.843 * | 74.393 * | Unr. NARDL model (2) |
| Central Afr. Rep (b) | 24.061 * | - | Rest. NARDL model (3) |
| Chad (a) | 20.088 * | 18.444 * | Rest. NARDL model (2) |
| Congo Rep (a) | 6.035 ** | 28.834 * | Rest. NARDL model (2) |
| Equatorial Guinea (a) | 4.864 ** | 134.545 * | Unr. NARDL model (2) |
| Gabon (a) | 22.314 * | 27.315 * | Rest. NARDL model (2) |
| Country | Short-Term Tests (WST): | Long-Term Tests (WLT): | Unrestricted & Restricted NARDL Models |
|---|---|---|---|
| Other SSA (KO = 26) | |||
| Angola (c) | - | 5.268 ** | Rest. NARDL model (4) |
| Botswana (a) | - | 12.604 * | Rest. NARDL model (4) |
| Cabo Verde (a) | 0.000 | 1.578 | Rest. NARDL model (5) |
| Comoros (a) | 10.231 * | 19.186 * | Unr. NARDL model (2) |
| Congo, Dem. Rep. (a) | 89.649 * | 18.103 * | Unr. NARDL model (2) |
| Ethiopia (a) | 4.735 ** | 2.021 | Rest. NARDL model (3) |
| Gambia (a) | 3.386 *** | 31.198 * | Unr. NARDL model (2) |
| Ghana (a) | 6.008 ** | 0.201 | Rest. NARDL model (3) |
| Guinea (a) | 0.533 * | 9.784 * | Unr. NARDL model (2) |
| Kenya (a) | 1.749 | 55.533 * | Rest. NARDL model (4) |
| Lesotho (a) | 6.786 ** | 0.046 | Rest. NARDL model (3) |
| Liberia (a) | 1.336 | 15.238 * | Rest. NARDL model (4) |
| Madagascar (a) | 15.562 * | 10.967 * | Unr. NARDL model (2) |
| Malawi (b) | 3.007 *** | - | Rest. NARDL model (3) |
| Mauritius (a) | 0.022 | 52.450 * | Rest. NARDL model (4) |
| Mozambique (a) | 5.109 *** | 0.017 | Rest. NARDL model (3) |
| Namibia (a) | 1.117 | 31.412 * | Rest. NARDL model (4) |
| Nigeria (a) | 17.208 * | 482.010 * | Unr. NARDL model (2) |
| Rwanda (a) | 8.007 * | 2.303 | Rest. NARDL model (3) |
| Sao Tome & Prin.(a) | 9.692 * | 0.001 | Rest. NARDL model (3) |
| Seychelles (c) | - | 97.620 * | Rest NARDL model (4) |
| South Africa (a) | 5.793 ** | 23.204 * | Unr. NARDL model (2) |
| Swaziland (a) | - | 3.777 *** | Rest. NARDL model (4) |
| Tanzania (a) | 1.086 | 5.463 ** | Rest. NARDL model (4) |
| Uganda (c) | - | 90.710 * | Rest. NARDL model (4) |
| Zambia (a) | 1.479 | 4.405 ** | Rest. NARDL model (4) |
| Asymmetric Exchange Rate Pass-Through (ERPT) | Symmetric Exchange Rate Pass-Through (ERPT) | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Long-Term ERPT | Short-Term ERPT | Diagnostics | Long-Term ERPT | Short-Term ERPT | Diagnostics | |||||||||
| Countries | Adj. | Appr(−) | Depr(+) | LTS | Appr(−) | Depr(+) | STS | χ2SC | Adj. | LTS | STS | χ2SC | ||
| WAEMU (KW = 8) | ||||||||||||||
| Benin | −0.072 *** | −0.034 | 0.282 | - | 0.347 * | 0.638 | 0.459 | −0.025 | −0.711 | 0.131 * | 0.655 | 0.157 | ||
| Burkina Faso | −0.194 * | 0.251 ** | 0.396 * | - | 0.166 * | 0.545 | 2.706 *** | −0.154 * | 0.463 * | 0.173 * | 0.467 | 1.823 | ||
| Cote d’Ivoire | −0.264 * | 0.207 * | 0.455 * | - | - | 0.184 * | 0.635 | 0.401 | −0.029 | 0.353 | 0.219 * | 0.591 | 3.332 ** | |
| Guinea-Bissau | −0.118 * | - | - | 0.990 * | - | −0.643 * | 0.599 | 0.404 | −0.096 * | 1.151 * | −0.218 ** | 0.548 | 0.905 | |
| Mali | −0.322 * | 0.122 ** | 0.356 * | 0.176 * | 0.011 | 0.658 | 0.368 | −0.061 ** | 0.426 * | 0.180 * | 0.599 | 0.304 | ||
| Niger | −0.277 * | 0.132 | 0.363 * | - | - | 0.272 * | 0.688 | 0.881 | −0.218 * | 0.699 * | 0.162 * | 0.650 | 0.243 | |
| Senegal | −0.085 *** | −0.372 | 0.019 | - | - | −0.011 | 0.624 | 0.937 | −0.038 | −0.074 | −0.010 | 0.622 | 1.186 | |
| Togo | −0.188 * | −0.508 | 0.045 | - | - | 1.310 * | 0.632 | 0.200 | −0.142 * | 0.641 * | 0.739 * | 0.585 | 0.759 | |
| CEMAC (KC = 6) | ||||||||||||||
| Cameroon | −0.165 * | −0.474 * | 0.077 | −0.142 * | 0.472 * | 0.854 | 0.831 | −0.036 *** | 0.090 | 0.367 * | 0.720 | 4.074 | ||
| Cent. African R. | 0.019 | - | - | −0.088 | −0.200 ** | 0.325 * | 0.583 | 0.131 | 0.007 | 0.295 | 0.117 * | 0.516 | 0.273 | |
| Chad | −0.458 * | 0.390 * | 0.601 * | −0.249 ** | 0.447 * | 0.616 | 0.646 | −0.290 * | 0.708 * | 0.260 * | 0.555 | 0.139 | ||
| Congo Rep. | −0.161 * | −0.105 | 0.351 | 0.517 * | 0.164 * | 0.721 | 1.805 | −0.051 | 0.479 *** | 0.162 * | 0.576 | 0.864 | ||
| Eq. Guinea | −0.224 * | 0.035 | 0.518 * | −0.123 | 0.216 * | 0.748 | 0.375 | −0.026 | 0.530 | 0.289 * | 0.580 | 0.897 | ||
| Gabon | −0.175 * | −0.070 | 0.317 * | −0.311 * | 0.304 * | 0.725 | 0.778 | −0.097 * | 0.404 * | −0.005 | 0.615 | 0.250 | ||
| Asymmetric Exchange Rate Pass-Through (ERPT) | Symmetric Exchange Rate Pass-Through (ERPT) | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Long-Term ERPT | Short-Term ERPT | Diagnostics | Long-Term ERPT | Short-Term ERPT | Diagnostics | |||||||||
| Countries | Adj. | Appr(−) | Depr(+) | LTS | Appr(−) | Depr(+) | STS | χ2SC | Adj. | LTS | STS | χ2SC | ||
| Other SSA (KO = 26) | ||||||||||||||
| Angola | −0.072 * | −4.121 *** | 0.934 * | - | - | - | 0.506 * | 0.938 | 0.084 | −0.034 | 0.878 * | 0.562 * | 0.935 | 0.570 |
| Botswana | −0.021 | −0.748 | −0.129 | - | - | - | - | 0.601 | 0.529 | −0.015 | −0.607 | - | 0.598 | 0.782 |
| Cabo Verde | - | - | - | - | - | - | - | - | - | −0.134 * | 0.183 *** | 0.105 ** | 0.320 | 1.182 |
| Comoros | −0.859 * | −0.830 * | −0.356 * | - | 0.272 | −1.265 * | - | 0.852 | 3.987 ** | −0.872 * | −0.466 * | 0.913 * | 0.584 | 0.242 |
| Congo, Dem. Rep. | −0.207 * | −1.784 * | 0.719 * | - | 4.400 * | −0.089 *** | - | 0.901 | 0.799 | 0.142 *** | 1.075 * | 1.010 * | 0.781 | 0.766 |
| Ethiopia | 0.144 * | - | - | 0.556 * | −5.978 ** | −0.232 * | 0.272 * | 0.626 | 1.554 | −0.133 *** | 0.131 | −0.114 ** | 0.626 | 2.234 |
| Gambia | −0.172 * | 0.038 | 0.399 * | - | −0.069 *** | - | - | 0.354 | 1.127 | −0.058 * | 0.826 * | - | 0.183 | 0.283 |
| Ghana | −0.056 ** | - | - | 0.853 * | −0.573 *** | 0.246 * | - | 0.622 | 2.576 *** | −0.044 | 0.871 * | 0.251 * | 0.617 | 2.767 *** |
| Guinea | 0.169 * | 1.703 * | 2.172 * | - | 0.533 * | −0.000 | - | 0.938 | 3.238 *** | 0.032 | 3.597 | 0.193 * | 0.656 | 2.792 *** |
| Kenya | 0.096 * | −1.556 * | 0.674 ** | - | - | - | - | 0.476 | 0.127 | −0.009 | −5.014 | 0.247 * | 0.471 | 1.173 |
| Lesotho | −0.015 | - | - | −0.887 | −0.125 *** | 0.164 * | - | 0.415 | 0.973 | −0.027 ** | −0.324 | - | 0.373 | 1.673 |
| Liberia | −0.230 * | 0.771 * | 1.549 * | - | −0.193 * | 0.205 ** | - | 0.645 | 1.362 | 0.033 | 1.634 | 0.425 ** | 0.481 | 1.253 |
| Madagascar | −0.161 * | 0.149 | 0.699 * | - | - | - | - | 0.426 | 0.578 | −0.071 * | 0.806 * | - | 0.410 | 1.067 |
| Malawi | −0.108 * | - | - | 0.851 * | 0.276 | 0.102 * | - | 0.860 | 1.455 | −0.077 ** | 0.830 * | 0.172 | 0.862 | 1.296 |
| Mauritius | −2.751 * | 0.226 ** | 0.765 * | - | - | - | −0.135 * | 0.222 | 0.359 | −0.020 *** | 0.618 | −0.121 * | 0.201 | 0.672 |
| Mozambique | −0.643 * | - | - | 0.747 * | 0.747 *** | −0.558 * | - | 0.932 | 6.233 ** | 0.060 | 4.137 | 0.995 * | 0.894 | 4.724 ** |
| Namibia | −0.118 *** | −1.067 | 0.011 | - | - | - | 0.082 | 0.349 | 0.654 | −0.013 | 0.642 | 0.047 | 0.082 | 0.265 |
| Nigeria | −0.235 * | −5.750 * | 0.561 * | - | 2.625 * | 0.107 * | - | 0.713 | 0.072 | −0.021 ** | 0.316 | 0.040 ** | 0.630 | 0.843 |
| Rwanda | −0.086 * | - | - | 0.655 * | - | - | - | 0.264 | 2.114 | −0.086 * | 0.655 * | - | 0.264 | 2.114 |
| Sao Tome and Prin | −0.126 * | - | - | 1.878 * | 0.379 * | −0.140 | - | 0.700 | 1.135 | −0.209 * | 1.983 * | −0.137 | 0.690 | 0.975 |
| Seychelles | −0.526 * | 0.302 * | 0.632 * | - | - | - | 0.347 * | 0.606 | 4.575 ** | −0.243 * | 0.974 * | 0.221 * | 0.527 | 0.764 |
| South Africa | −0.050 * | 0.103 | 0.416 * | - | - | −0.055 ** | - | 0.536 | 1.121 | −0.012 | −0.033 | 0.004 | 0.522 | 0.857 |
| Swaziland | −0.061 *** | 0.257 | 0.595 * | - | - | - | - | 0.458 | 0.184 | −0.030 *** | 0.714 * | - | 0.456 | 0.170 |
| Tanzania | −0.125 * | −1.554 *** | 0.368 | - | - | - | −0.254 * | 0.546 | 1.892 | 0.014 | 5.901 | 0.438 * | 0.524 | 1.320 |
| Uganda | −0.277 * | −0.801 * | 0.238 ** | - | - | - | 0.278 * | 0.295 | 1.667 | −0.040 | 0.888 ** | 0.085 ** | 0.223 | 4.131 ** |
| Zambia | −0.125 * | 0.547 * | 0.775 * | - | - | - | 0.114 ** | 0.749 | 0.260 | −0.065 ** | 0.658 * | 0.173 * | 0.754 | 1.454 |
| Cross Dependence Tests | CD | FT | Rave | CDLM | ||||
|---|---|---|---|---|---|---|---|---|
| Coef | p-Value | Coef | p-Value | Coef | p-Value | Coef | p-Value | |
| Fixed effect (WAEMU) | 24.262 | 0.000 | 3.368 | 0.000 | 519.615 | 0.000 | 1559.421 | 0.000 |
| Random effect (WAEMU) | 24.116 | 0.000 | 3.409 | 0.000 | 528.953 | 0.000 | 1553.25 | 0.000 |
| Fixed effect (CEMAC) | 6.21 | 0.000 | 1.207 | 0.000 | 165.836 | 0.000 | 314.531 | 0.000 |
| Random effect (CEMAC) | 5.787 | 0.000 | 0.982 | 0.000 | 180.469 | 0.000 | 271.852 | 0.000 |
| Fixed effect (Other countries) | 25.842 | 0.000 | 7.046 | 0.000 | 162.692 | 0.000 | 5647.464 | 0.000 |
| Random effect (Other countries) | 13.113 | 0.000 | 7.704 | 0.000 | 159.692 | 0.000 | 8331.561 | 0.000 |
| Fixed effect (All countries) | 61.443 | 0.000 | 12.345 | 0.000 | 423.375 | 0.000 | 18,037.34 | 0.000 |
| Random effect (All countries) | 29.254 | 0.000 | 9.441 | 0.000 | 186.45 | 0.000 | 23,452.55 | 0.000 |
| Country | Long-Term Relationship | Short-Term Relationship | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Asym. Adjust. | Sym. Adjust. | Long-Term ERPT | Wald Test Long-Term | Cumulative ERPT | Wald Test Cumulative | |||||
| Depr(+): | Appr(−) | Depr(+) | STERPT | |||||||
| FGLS estimator | ||||||||||
| CFA Franc zone (K = 14) | −0.049 * | −0.046 * | 0.447 * | 0.637 * | 0.648 * | 16.530 * | −0.118 * | 0.265 * | 0.183 * | 106.530 * |
| WAEMU (KW =08) | −0.064 * | −0.058 * | 0.387 * | 0.544 * | 0.563 * | 11.410 * | −0.115 * | 0.258 * | 0.177 * | 60.240 * |
| CEMAC (KC = 06) | −0.033 * | −0.032 * | 0.574 ** | 0.845 * | 0.839 * | 4.860 ** | −0.130 * | 0.277 * | 0.187 * | 46.840 * |
| Other SSA (KO = 26) | −0.016 * | −0.016 * | 0.410 * | 0.195 * | 0.032 ** | 8.290 * | −0.012 | 0.118 * | 0.087 * | 29.350 * |
| All SSA countries (K = 40) | −0.015 * | −0.015 * | 0.420 * | 0.244 * | 0.011 | 9.570 * | −0.030 ** | 0.176 * | 0.127 * | 114.440 * |
| POLS_DK estimator | ||||||||||
| CFA Franc zone (K = 14) | −0.050 * | −0.049 * | 0.438 ** | 0.640 * | 0.673 * | 6.290 ** | −0.091 | 0.244 * | 0.175 * | 10.220 * |
| WAEMU (KW = 08) | −0.057 * | −0.056 * | 0.401 ** | 0.553 * | 0.581 * | 3.480 *** | −0.058 | 0.222 * | 0.165 * | 6.040 ** |
| CEMAC (KC = 06) | −0.038 * | −0.036 * | 0.552 *** | 0.858 * | 0.878 * | 5.040 ** | −0.147 ** | 0.283 * | 0.193 * | 16280 * |
| Other SSA (KO = 26) | −0.020 * | −0.018 * | 0.181 | 0.125 * | 0.040 * | 0.270 | 0.105 | 0.196 * | 0.187 * | 1.520 |
| All SSA countries (K = 40) | −0.020 * | −0.019 * | 0.174 *** | 0.140 * | 0.027 | 0.130 | 0.057 | 0.210 * | 0.191 * | 7.460 * |
| Behavior of the Exchange Rate: 1990Q1–2017Q4 (Percent of Total Changes) | ||||||
|---|---|---|---|---|---|---|
| Sub-Regions | Overall | Appreciations | Depreciations | |||
| Large Change | Small Change | Large Change | Small Change | Large Change | Small Change | |
| CFA Franc zone (K = 14) | 58.63 | 41.37 | 29.18 | 70.82 | 28.85 | 71.15 |
| WAEMU (KW = 08) | 58.41 | 41.59 | 29.82 | 70.18 | 29.01 | 70.99 |
| CEMAC (KC = 06) | 58.93 | 41.07 | 28.33 | 71.67 | 28.64 | 71.36 |
| Other SSA (KO = 26) | 45.10 | 54.90 | 13.42 | 86.58 | 30.15 | 69.85 |
| All SSA countries (K = 40) | 50.27 | 49.73 | 19.37 | 80.63 | 29.63 | 70.37 |
| Sub-Regions | Overall | Appreciations | Depreciations | Asymmetry Tests | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Large | Small | H0: | Large | Small | H0: | Large | Small | H0: | H0: | H0: | |
| L | S | L = S | LA | SA | LA = SA | LD | SD | LD = SD | LA = LD | SA = SD | |
| FGLS estimator | |||||||||||
| CFA Franc zone (K = 14) | 0.102 * | −0.047 | 5.740 ** | −0.127 * | −0.344 * | 4.460 ** | 0.170 * | 0.228 ** | 0.380 | 120.060 * | 11.750 * |
| WAEMU (KW = 08) | 0.101 * | −0.061 | 4.050 ** | −0.125 * | −0.289 ** | 1.500 | 0.169 * | 0.150 | 0.020 | 68.720 * | 4.100 ** |
| CEMAC (KC = 06) | 0.099 * | −0.029 | 1.780 | −0.128 * | −0.415 ** | 3.240 *** | 0.166 * | 0.330 ** | 1.220 | 49.670 * | 8.230 * |
| Other SSA (KO = 26) | 0.008 *** | 0.017 | 0.040 | −0.026 | −0.089 | 0.500 | 0.064 * | −0.009 | 1.040 | 14.740 * | 0.340 |
| All SSA countries (K= 40) | 0.067 * | −0.043 | 8.590 * | −0.055 * | −0.214 * | 6.010 ** | 0.112 * | 0.124 ** | 0.040 | 96.710 * | 11.270 * |
| POLS_DK estimator | |||||||||||
| CFA Franc zone (N = 14) | 0.102 *** | 0.012 | 0.810 | −0.157 * | −0.203 | 0.090 | 0.173 * | 0.264 | 0.330 | 16.130 * | 2.750 *** |
| WAEMU (KW = 08) | 0.101 *** | 0.027 | 0.390 | −0.142 ** | −0.062 | 0.170 | 0.167 * | 0.165 | 0.000 | 13.510 * | 0.410 |
| CEMAC (KC = 06) | 0.101 | −0.010 | 1.270 | −0.169 * | −0.359 ** | 1.530 | 0.177 * | 0.366 ** | 1.510 | 14.870 * | 7.400 * |
| Other SSA (KO = 26) | 0.101 * | −0.155 | 5.580 ** | −0.045 | 0.062 | 0.50 | 0.291 * | 0.037 | 2.530 | 20.750 * | 0.010 |
| All SSA countries (K = 40) | 0.226 * | 0.041 | 4.370 ** | −0.060 *** | 0.002 | 0.320 | 0.269 * | 0.170 | 0.830 | 34.160 * | 0.600 |
| Long-Term Relationship | Short-Term Relationship | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Country | Asym. Adjust. | Sym. Adjust. | Long-Term ERPT | Wald Test Long-Term | Cumulative ERPT | Wald Test Cumulative | ||||
| Depr(+): | LTERPT | Appr(−) | Depr(+) | STERPT | ||||||
| FGLS estimator | ||||||||||
| High inflation (K = 13) | −0.029 * | −0.029 * | 0.402 * | 0.157 * | 0.025 | 5.420 ** | −0.037 | 0.052 * | 0.045 * | 5.950 ** |
| Hyperinflation (K = 7) | −0.031 * | −0.032 * | 0.395 ** | 0.166 * | 0.079 * | 1.970 | −0.020 | 0.061 * | 0.059 * | 2.820 *** |
| Low inflation (K = 27) | −0.016 * | −0.014 * | 0.546 * | 0.351 * | −0.057 ** | 4.590 ** | −0.064 * | 0.106 * | 0.042 * | 119.200 * |
| POLS_DK estimator | ||||||||||
| High inflation (K = 13) | −0.033 * | −0.032 * | 0.293 ** | 0.119 * | 0.031 | 3.130 ** | 0.0002 | 0.171 * | 0.166 * | 4.210 ** |
| Hyperinflation (K = 7) | −0.034 * | −0.034 * | 0.442 * | 0.152 * | 0.091 * | 4.770 ** | 0.069 | 0.185 * | 0.185 * | 1.060 |
| Low inflation (K = 27) | −0.014 * | −0.012 * | 0.771 * | 0.496 * | −0.051 | 2.270 | −0.095 ** | 0.145 ** | 0.079 | 7.710 * |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kassi, D.F.; Rathnayake, D.N.; Edjoukou, A.J.R.; Gnangoin, Y.T.; Louembe, P.A.; Ding, N.; Sun, G. Asymmetry in Exchange Rate Pass-Through to Consumer Prices: New Perspective from Sub-Saharan African Countries. Economies 2019, 7, 5. https://doi.org/10.3390/economies7010005
Kassi DF, Rathnayake DN, Edjoukou AJR, Gnangoin YT, Louembe PA, Ding N, Sun G. Asymmetry in Exchange Rate Pass-Through to Consumer Prices: New Perspective from Sub-Saharan African Countries. Economies. 2019; 7(1):5. https://doi.org/10.3390/economies7010005
Chicago/Turabian StyleKassi, Diby François, Dilesha Nawadali Rathnayake, Akadje Jean Roland Edjoukou, Yobouet Thierry Gnangoin, Pierre Axel Louembe, Ning Ding, and Gang Sun. 2019. "Asymmetry in Exchange Rate Pass-Through to Consumer Prices: New Perspective from Sub-Saharan African Countries" Economies 7, no. 1: 5. https://doi.org/10.3390/economies7010005
APA StyleKassi, D. F., Rathnayake, D. N., Edjoukou, A. J. R., Gnangoin, Y. T., Louembe, P. A., Ding, N., & Sun, G. (2019). Asymmetry in Exchange Rate Pass-Through to Consumer Prices: New Perspective from Sub-Saharan African Countries. Economies, 7(1), 5. https://doi.org/10.3390/economies7010005





