China’s Bank Balance Sheet and Financing of Heterogeneous Enterprises
Abstract
1. Introduction
1.1. Increasing Attention to Financial Institutions’ Balance Sheets
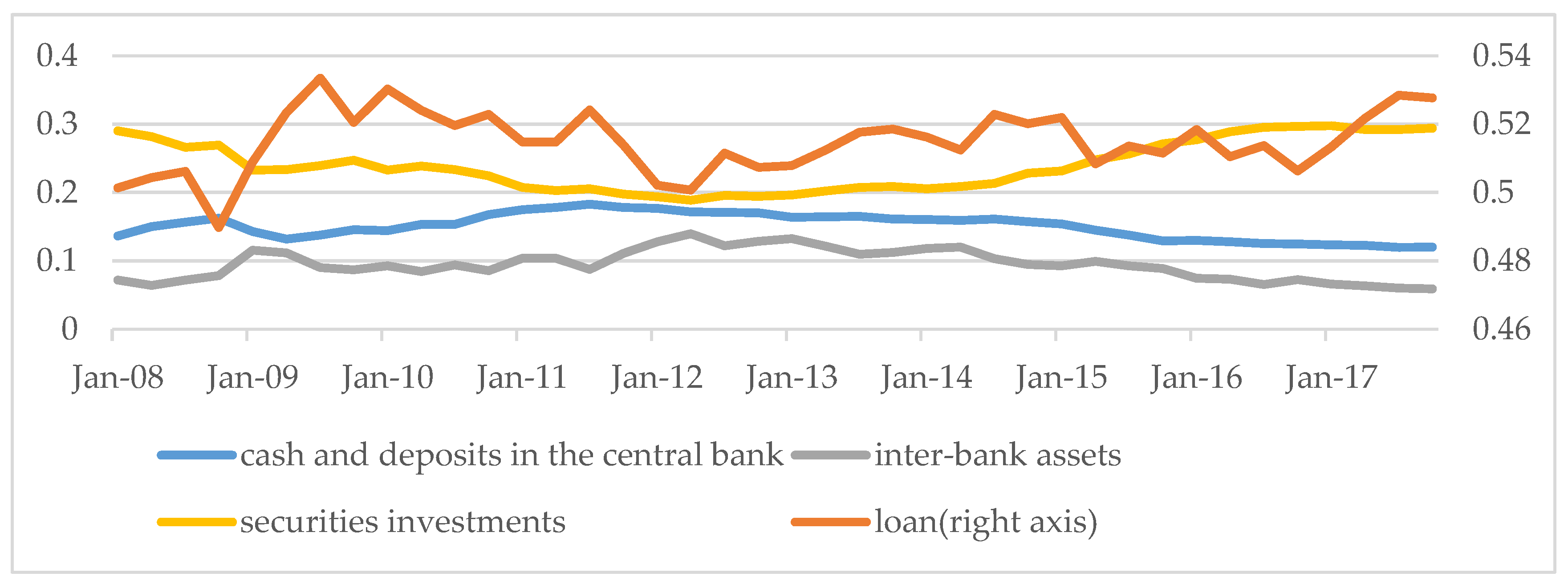
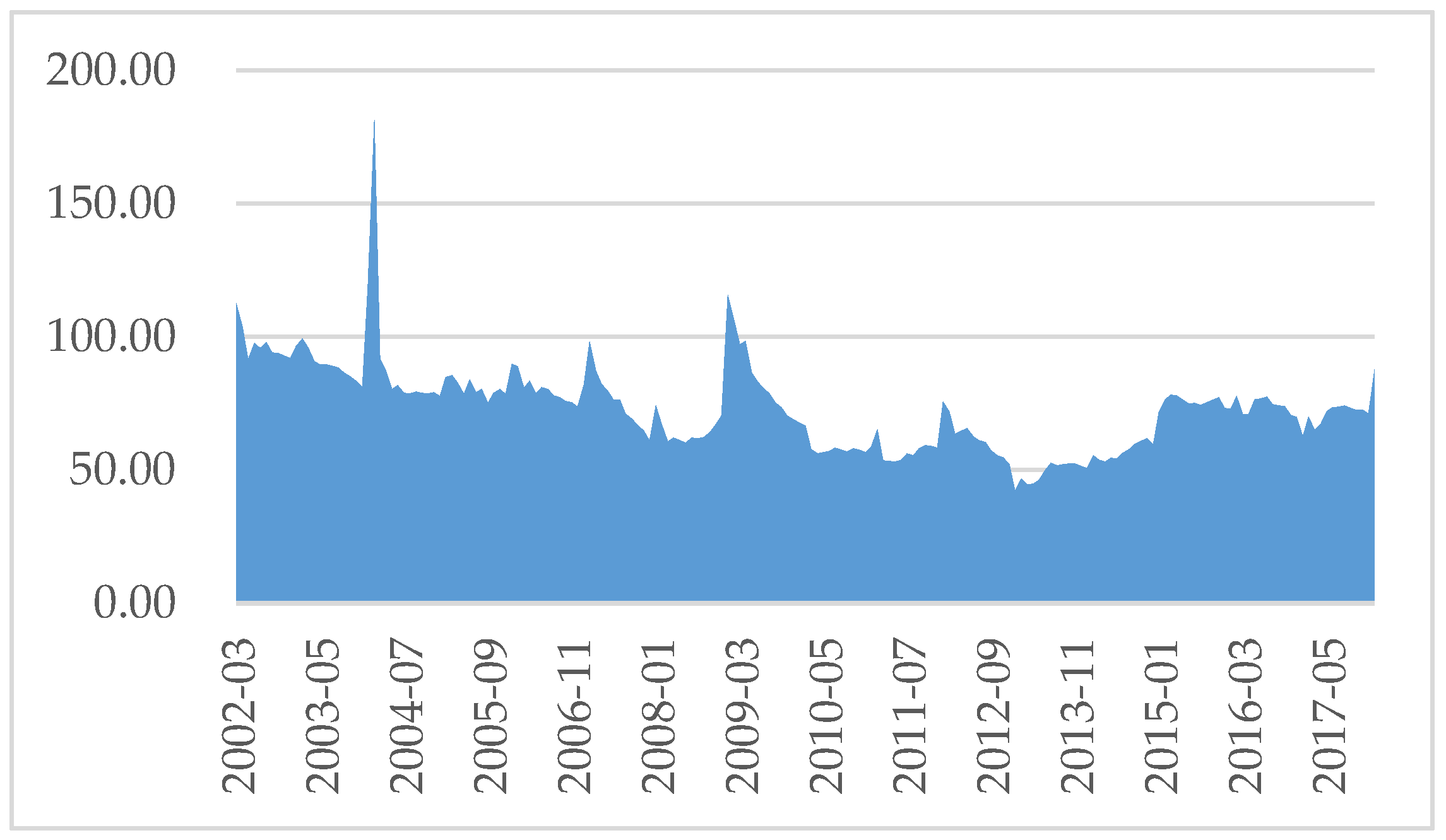
1.2. New Changes in Bank’s Balance Sheets
1.3. Reasons for Changes in Balance Sheets
1.3.1. Banks—The Supply Side of the Funds
1.3.2. Enterprises: The Demand Side of Funds
1.4. Contribution of This Paper
2. Literature Review
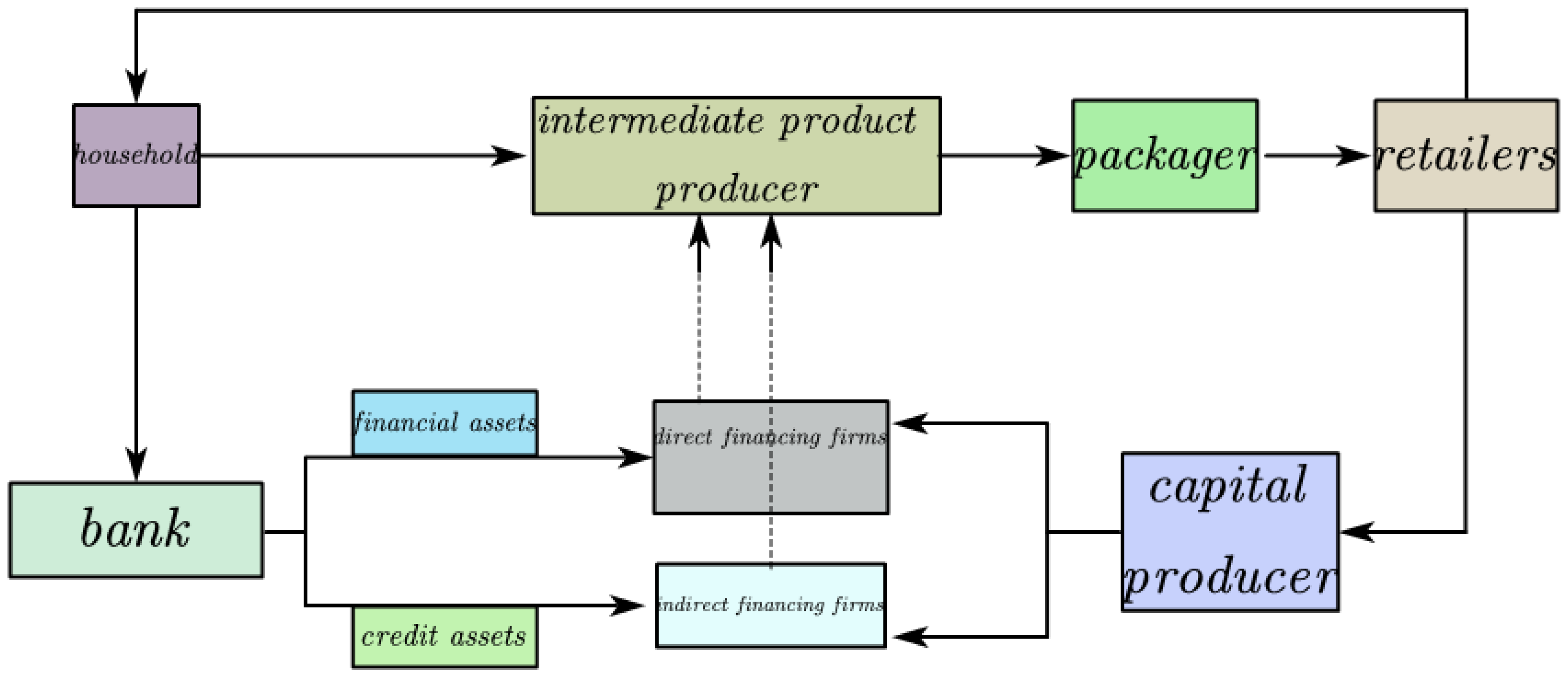
3. Theoretical Model
3.1. Household
3.2. Bank
3.2.1. Bank Balance Sheet
3.2.2. Evolution of the Bank’s Net Worth
3.2.3. Moral Hazard Problem
3.2.4. Bank Optimization
3.2.5. Motion Equation of the Total Value of the Bank
3.3. Direct Financing Enterprises: Firm A
3.4. Indirect Financing Enterprise: Firm B
3.5. Capital Producers
3.6. Packagers and Retailers
3.6.1. Packagers
3.6.2. Retailer
3.7. Central Bank
3.8. Market Clearing Conditions
4. Parameter Estimation
4.1. Calibration
4.2. Bayesian Estimation
5. Variance Decomposition and Impulse Response Analysis
5.1. Variance Decomposition
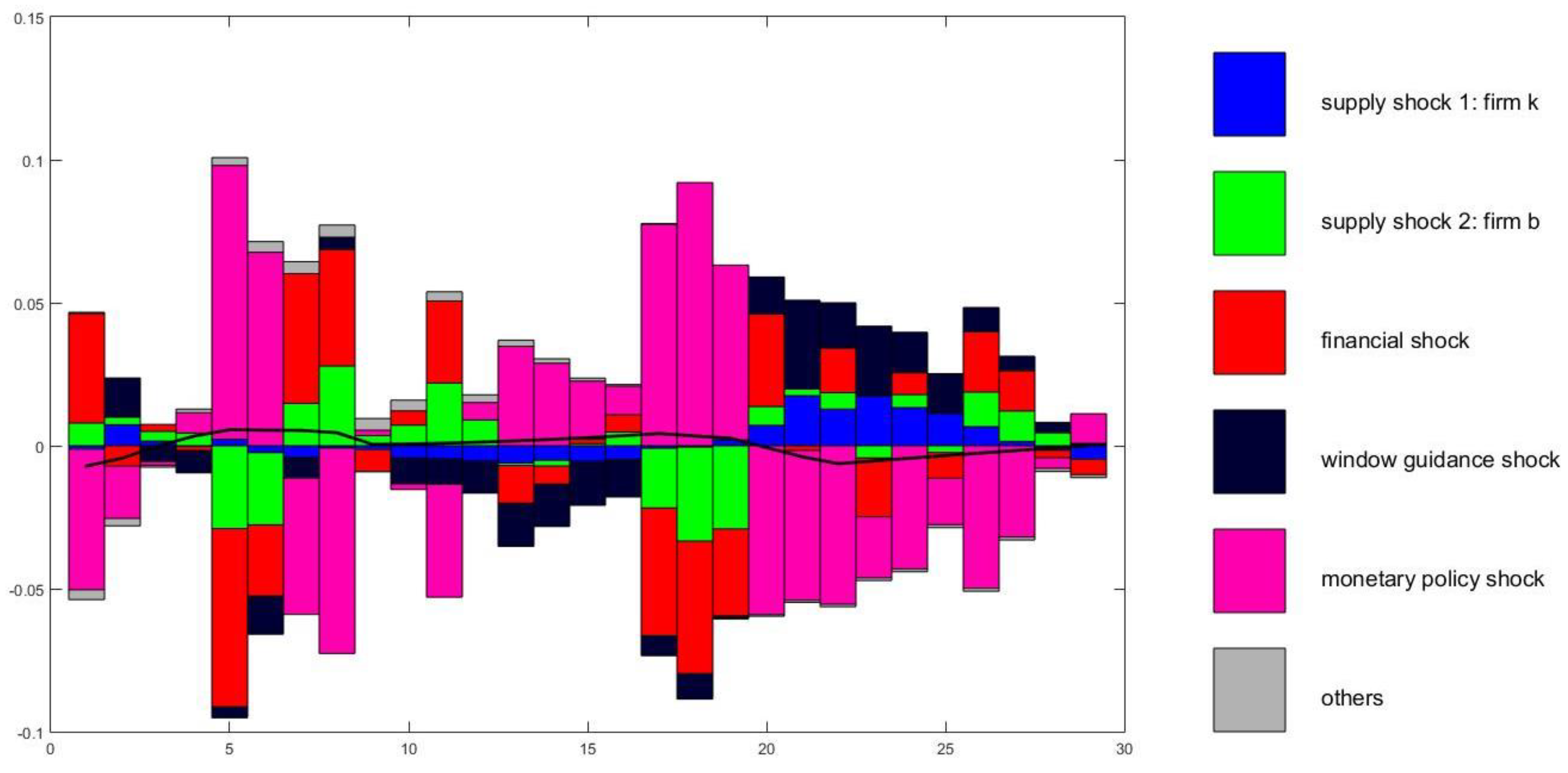
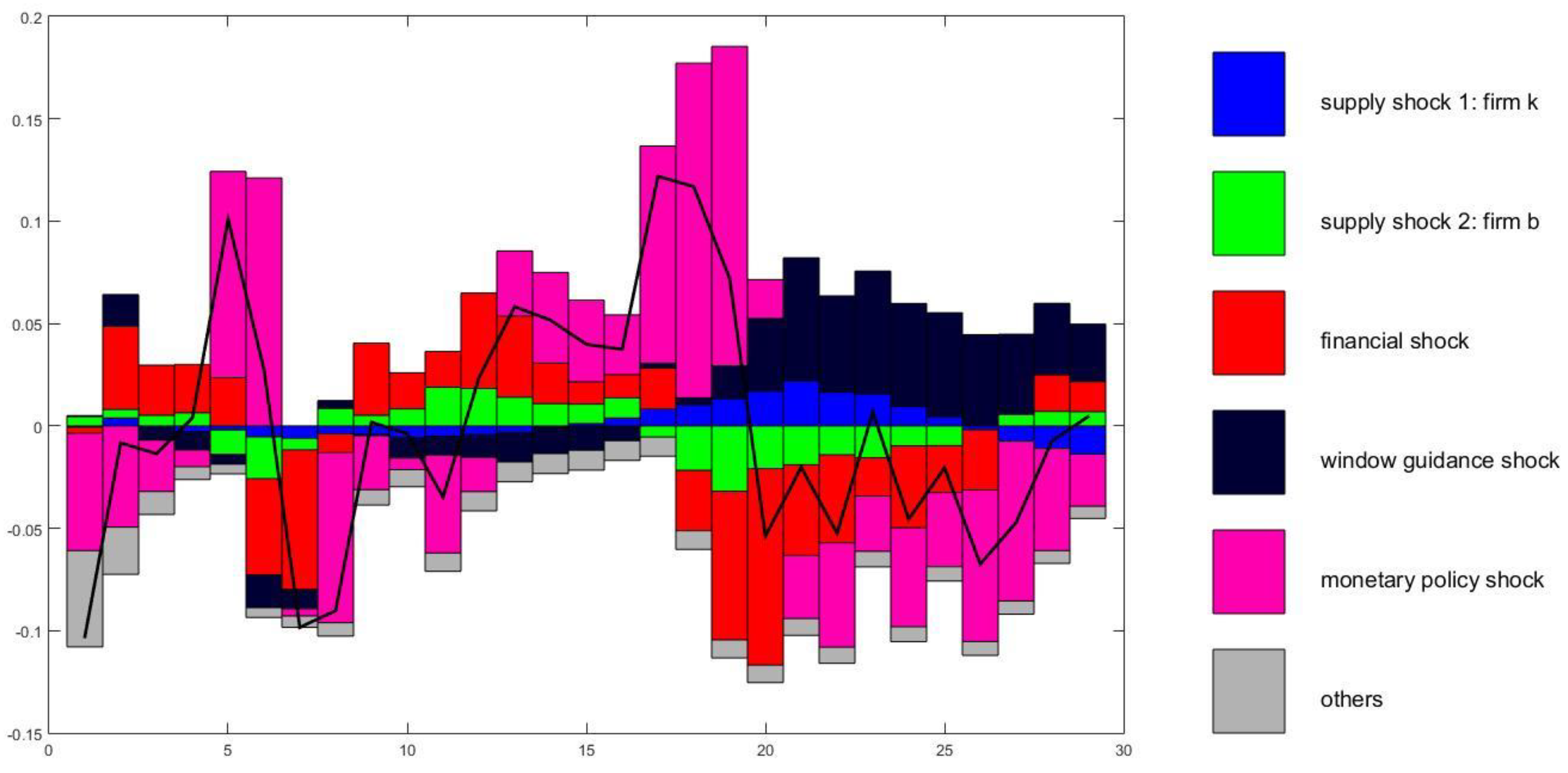
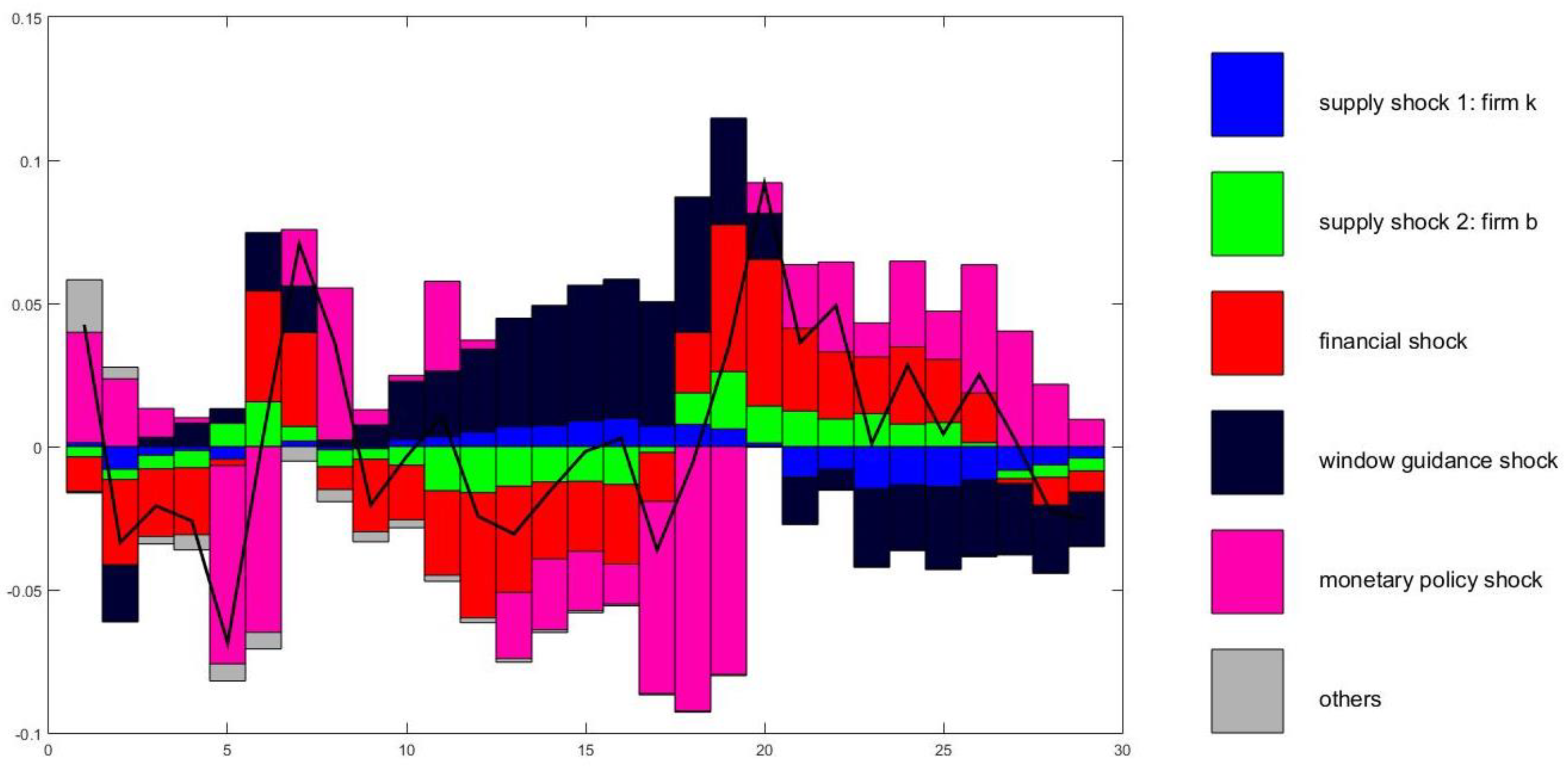
5.2. Historical Variance Decomposition
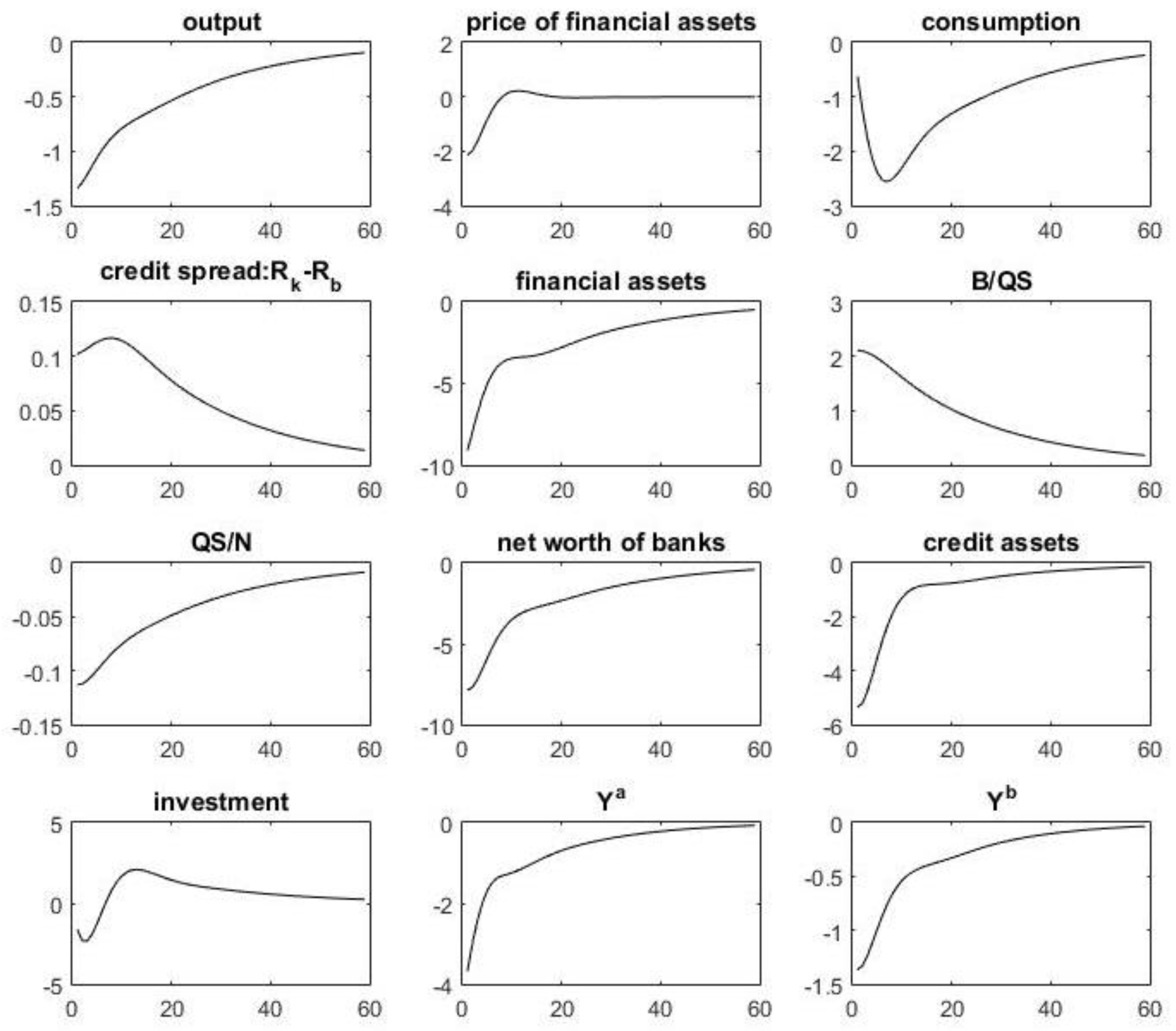
5.3. Financial Shock
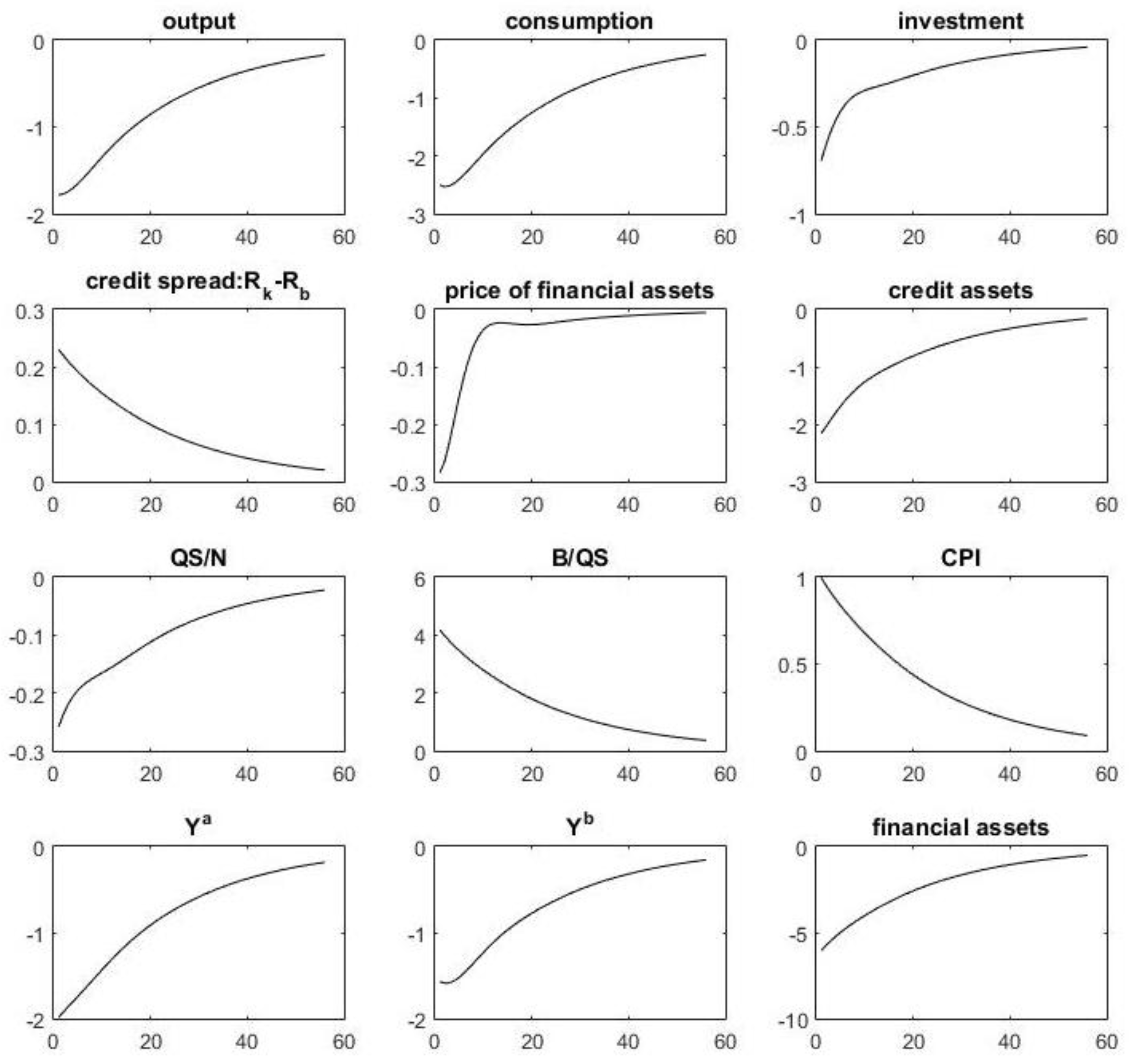
5.4. Monetary Policy Shocks
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- Angeloni, Ignazio, and Ester Faia. 2013. Capital regulation and monetary policy with fragile banks. Journal of Monetary Economics 60: 311–24. [Google Scholar] [CrossRef]
- Canova, Fabio. 1998. Detrending and business cycle facts: A user’s guide. Journal of Monetary Economics 41: 475–512. [Google Scholar] [CrossRef]
- Chen, Xiaoguang, and Yulin Zhang. 2010. Credit Constraint, Government Consumption and China’s Actual Economic Cycle. Economic Research 45: 48–59. [Google Scholar]
- Chen, Xin, Huaming Wang, and Yuchao Peng. 2017. The Causes of Social Financing Scale Fluctuation and Its Reflection on Macroeconomics—Based on DSGE Model and Its Variance Decomposition Analysis. Investment Research 36: 36–51. [Google Scholar]
- Chun, Chang, Kaiji Chen, Daniel F. Waggoner, and Tao Zha. 2015. Trends and Cycles in China’s Macroeconomy. Working paper. Atlanta: Federal Reserve Bank of Atlanta. [Google Scholar]
- Dib, Ali. 2009. Credit and Interbank Bank Markets in a New Keynesian Model. Mimeo: Bank of Canada. [Google Scholar]
- Du, Qingyuan, and Liutang Gong. 2005. A RBC Model with Financial Accelerator. Journal of Finance 4: 16–30. [Google Scholar]
- Gertler, Mark, and Peter Karadi. 2011. A model of unconventional monetary policy. Journal of Monetary Economics 58: 17–34. [Google Scholar] [CrossRef]
- Gertler, Mark, and Nobuhiro Kiyotaki. 2010. Financial Intermediation and Credit Policy in Business Cycle Analysis. In Handbook of Monetary Economics. Edited by Benjamin M. Friedman and Woodford Michael. Amsterdam: Elsevier. [Google Scholar]
- Gertler, Mark, Nobuhiro Kiyotaki, and Albert Queralto. 2012. Financial crises, bank risk exposure and government financial policy. Journal of Monetary Economics 59: S17–34. [Google Scholar] [CrossRef]
- Goodfriend, Marvin, and Bennett T. McCallum. 2007. Banking and interest rates in monetary policy analysis: A quantitative exploration. Journal of Monetary Economics 54: 1480–507. [Google Scholar] [CrossRef]
- Iacoviello, Matteo. 2005. House Prices, Borrowing Constraints, and Monetary Policy in the Business Cycle. American Economic Review 95: 739–64. [Google Scholar] [CrossRef]
- International Monetary Fund (IMF). 2008. Global Financial Stability Report: Market Development and Issues. Beijing: China Financial Publishing House. [Google Scholar]
- Kang, Li, and Liutang Gong. 2014. Financial Friction, Bank Net Assets and International Economic Crisis Transmission—Based on Multi-sector DSGE Model Analysis. Economic Research 49: 147–59. [Google Scholar]
- Li, Daokui, and Mei Song. 2009. The US dollar M_2 contraction induced the world financial crisis: The internal and external factors of the financial crisis and its test. World Economy 4: 15–26. [Google Scholar]
- Liu, Xiaoxing, and Dengbao Yao. 2016. Financial Disintermediation, Asset Price and Economic Fluctuation: Based on DNK-DSGE Model Analysis. The Journal of World Economy 39: 29–53. [Google Scholar]
- Lv, Zhaofeng, and Meibo Huang. 2011. Analysis of China’s economic cycle welfare cost. The Journal of World Economy 6: 71–83. [Google Scholar]
- Meh, Césaire A., and Kevin Moran. 2010. The role of bank capital in the propagation of shocks. Journal of Economic Dynamics & Control 34: 555–76. [Google Scholar]
- Mei, Dongzhou, and Liutang Gong. 2011. The Determinants of Exchange Rate Regime in the Emerging Economies. Economic Research Journal 11: 74–86. [Google Scholar]
- Ming, Ming, Licong Zhang, and Jingwei Yu. 2017. Commercial Banking and Bond Market: Looking at Interest Rate Changes from Subjects. Interest Rate Debt Weekly 10: 7–20. [Google Scholar]
- Nelson, Charles R., and Charles R. Plosser. 1982. Trends and random walks in macroeconomic time series: Some evidence and implications. Journal of Monetary Economics 10: 139–62. [Google Scholar] [CrossRef]
- Qiu, Xiang, and Qianglong Zhou. 2014. Transmission of shadow banking and monetary policy. Economic Research 49: 91–105. [Google Scholar]
- Shan, Haojie. 2008. Reestimating the Capital Stock of China: 1952–2006. The Journal of Quantitative & Technical Economics 10: 17–32. [Google Scholar]
- Sun, Xiaotao. 2013. The Cycle of Trend Decomposition Theory and Chinese Economy. Ph.D. Thesis, Huazhong University of Science and Technology, Wuhan, China. [Google Scholar]
- Tang, Xiaobin, and Jinquan Liu. 2012. Correlation Analysis between Inflation, Uncertainty of Inflation and Uncertainty of Money Growth. Systems Engineering 5: 17–23. [Google Scholar]
- Wang, Qing, and Jiao Tian. 2016. Bank Capital Supervision and Systematic Financial Risk Transfer—Analysis Based on DSGE Model. China Social Sciences 3: 99–122. [Google Scholar]
- Yan, Chaoming. 2008. The Great Recession: How to Survive and Develop in the Financial Crisis: Lessons from Japan’s Great Recession. Pune: Oriental Publishing House. [Google Scholar]
- Yi, Huiman. 2017. Reconstructing the bank’s balance sheet. China Finance 1: 9–13. [Google Scholar]
- Zheng, Chao. 2016. The Operation Mode and Development Strategy of China’s Commercial Banks’ Investment and Loan Linkage. Southern Finance 6: 20–25. [Google Scholar]
- Zhuang, Ziguan, Xiaoyong Cui, Liutang Gong, and Hengfu Zou. 2012. Expectations and Business Cycle: Can News Shocks Be a Major Source of China’ s Economic Fluctuations? Economic Research Journal 6: 46–59. [Google Scholar]
| Parameter | Description | Value | Parameter | Description | Value |
|---|---|---|---|---|---|
| Household intertemporal discount factor | 0.994 | Capital output elasticity of indirect financing enterprise | 0.55 | ||
| Consumption inertia | 0.815 | Mortgage rate for loans | 0.7 | ||
| Labor weighting | 3.409 | Credit rate mark up | 1.5 | ||
| Frisch elasticity of labor supply | 0.33 | Proportion of direct financing enterprises’ products in the portfolio | 0.4 | ||
| Bank survival probability | 0.972 | Substitution elasticity of the two types of enterprises | 2 | ||
| Proportion of funds diverted by banker | 0.381 | Substitution elasticity of retails | 4.167 | ||
| Moral hazard coefficient | −0.294 | Combination ratio of two types of labor | 0.5 | ||
| Moral hazard coefficient | 6.361 | Price stickiness | 0.75 | ||
| Proportion of assets retained by the exited bankers | 0.026 | Price index’s weight for inflation steady state | 0.241 | ||
| Capital output elasticity of direct financing enterprise | 0.35 | Interest rate smoothing | 0.589 | ||
| Capital depreciation rate | 0.025 | Weight of expected inflation in Taylor rule | 1.216 | ||
| Entrepreneur intertemporal discount factor | 0.95 | Weight of output gap in Taylor rule | 0.870 |
| Parameter | Prior Distribution | Prior Mean | Prior 90% Confidence Interval | Posterior Distribution | Posterior 90% Confidence Interval | ||
|---|---|---|---|---|---|---|---|
| Uniform | 28 | −30.80 | 86.80 | 70.900 | 61.442 | 79.957 | |
| Beta | 0.500 | 0.171 | 0.829 | 0.485 | 0.392 | 0.585 | |
| Beta | 0.500 | 0.171 | 0.829 | 0.263 | 0.031 | 0.519 | |
| Beta | 0.500 | 0.171 | 0.829 | 0.289 | 0.103 | 0.462 | |
| Beta | 0.500 | 0.171 | 0.829 | 0.931 | 0.908 | 0.953 | |
| Beta | 0.500 | 0.171 | 0.829 | 0.350 | 0.318 | 0.380 | |
| Inv-gamma | 0.050 | −1.562 | 1.695 | 0.020 | 0.011 | 0.030 | |
| Inv-gamma | 0.050 | −1.562 | 1.695 | 0.013 | 0.009 | 0.016 | |
| Inv-gamma | 0.050 | −1.562 | 1.695 | 0.073 | 0.014 | 0.155 | |
| Inv-gamma | 0.050 | −1.562 | 1.695 | 0.883 | 0.542 | 1.193 | |
| Inv-gamma | 0.050 | −1.562 | 1.695 | 0.037 | 0.029 | 0.045 | |
| Supply Shock | Supply Shock | Financial Shock | Window Guidance | Monetary Shock |
|---|---|---|---|---|
| 3.64 | 0.17 | 28.34 | 14.12 | 53.73 |
| 20.54 | 9.18 | 9.09 | 3.26 | 57.94 |
| 3.53 | 3.05 | 28.71 | 13.46 | 51.25 |
| 6.93 | 2.36 | 42.87 | 22.93 | 24.91 |
| 8.71 | 5.31 | 13.25 | 52.96 | 19.76 |
| 7.41 | 5.80 | 23.32 | 3.24 | 60.22 |
| 5.80 | 13.25 | 10.38 | 41.69 | 28.88 |
| 7.75 | 1.84 | 33.58 | 21.08 | 35.74 |
| 2.37 | 2.46 | 48.92 | 17.59 | 28.66 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, K.; Yao, Q. China’s Bank Balance Sheet and Financing of Heterogeneous Enterprises. Economies 2018, 6, 65. https://doi.org/10.3390/economies6040065
Huang K, Yao Q. China’s Bank Balance Sheet and Financing of Heterogeneous Enterprises. Economies. 2018; 6(4):65. https://doi.org/10.3390/economies6040065
Chicago/Turabian StyleHuang, Kun, and Qiuge Yao. 2018. "China’s Bank Balance Sheet and Financing of Heterogeneous Enterprises" Economies 6, no. 4: 65. https://doi.org/10.3390/economies6040065
APA StyleHuang, K., & Yao, Q. (2018). China’s Bank Balance Sheet and Financing of Heterogeneous Enterprises. Economies, 6(4), 65. https://doi.org/10.3390/economies6040065




