Changes in Natural Disaster Risk: Macroeconomic Responses in Selected Latin American Countries
Abstract
:1. Introduction
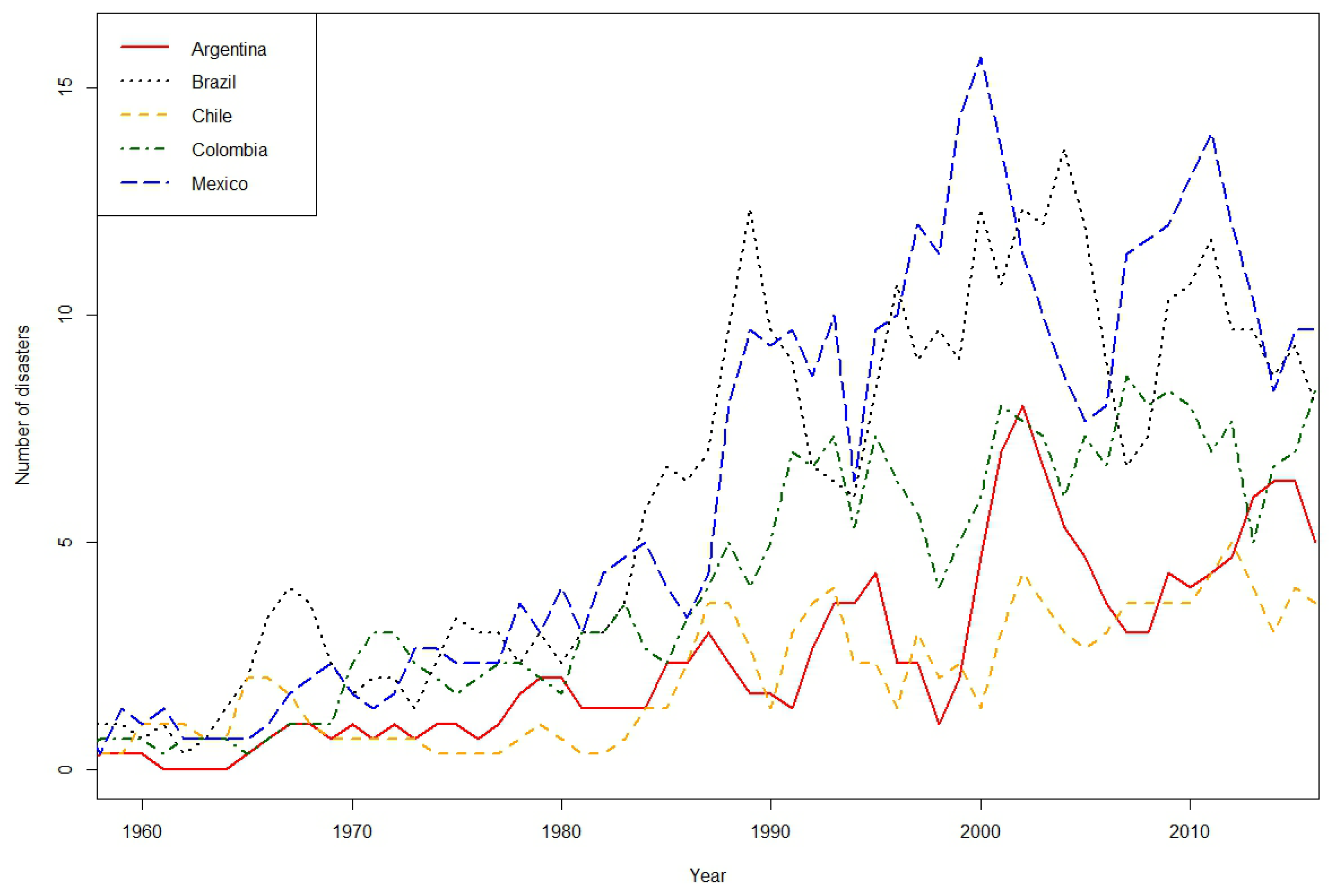
2. Evidence on Natural Disasters in Latin America
3. Model Overview
3.1. Households
3.2. Firms
3.3. Public Authority
4. Simulations
4.1. Calibration
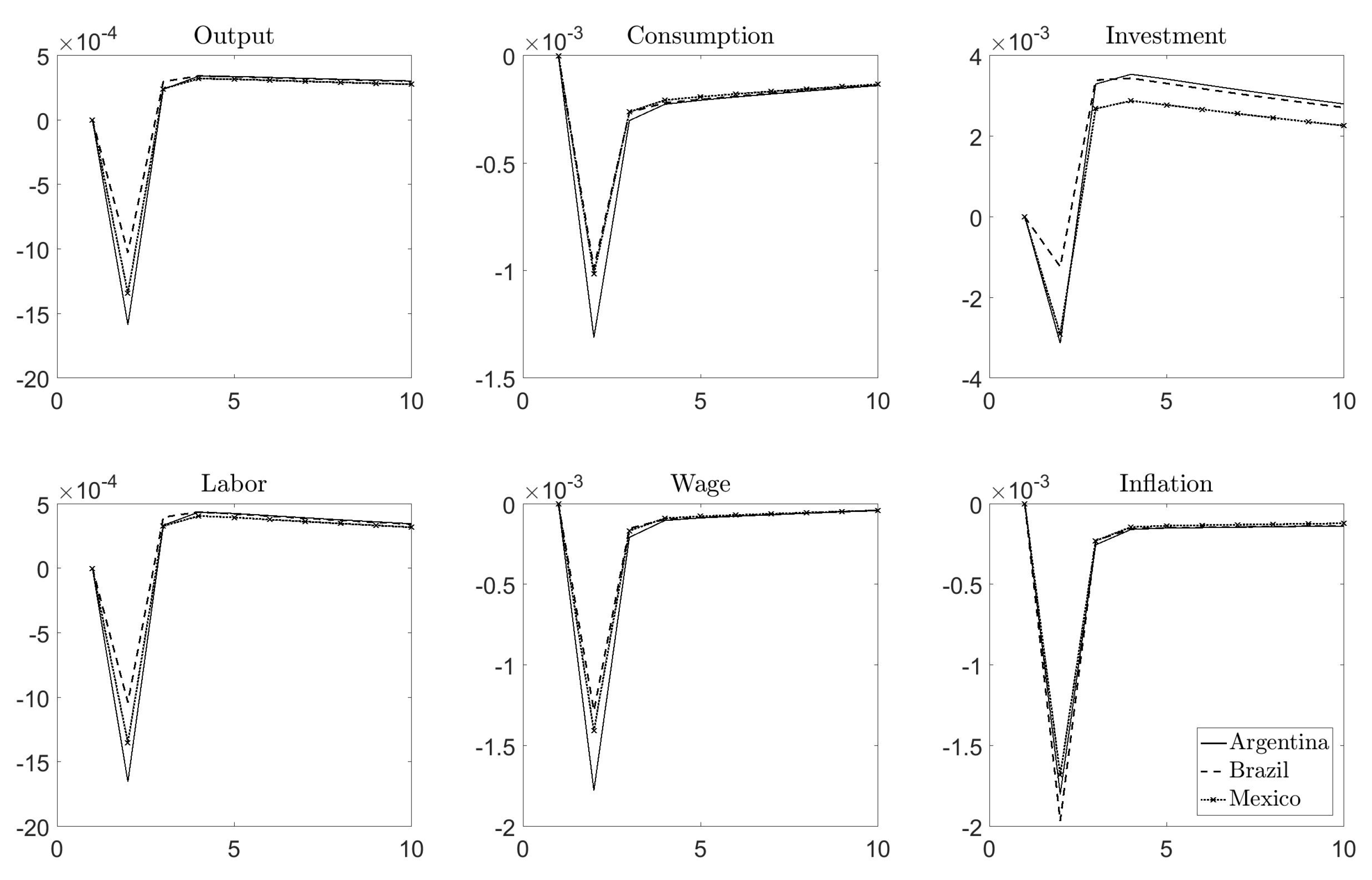
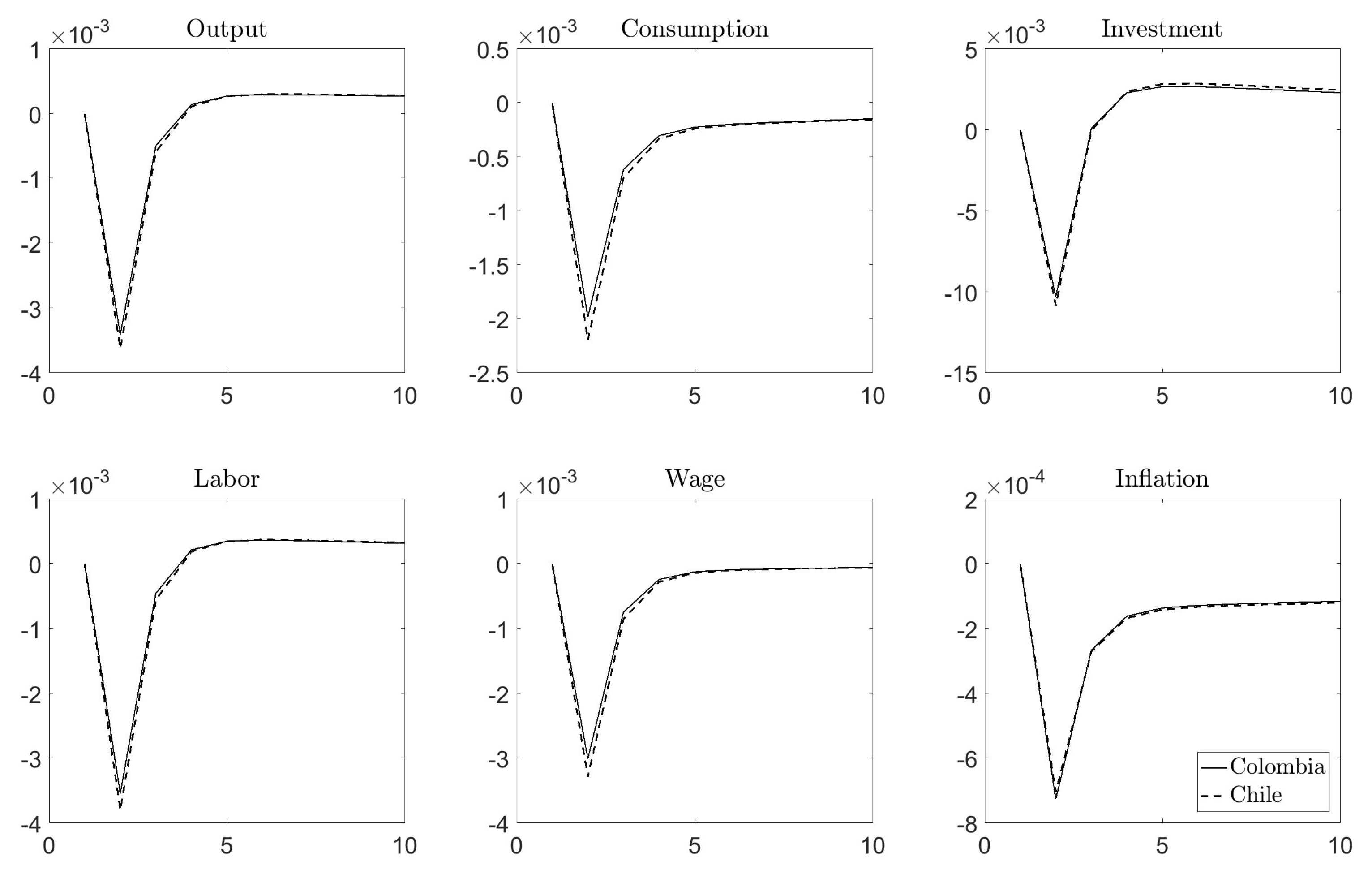
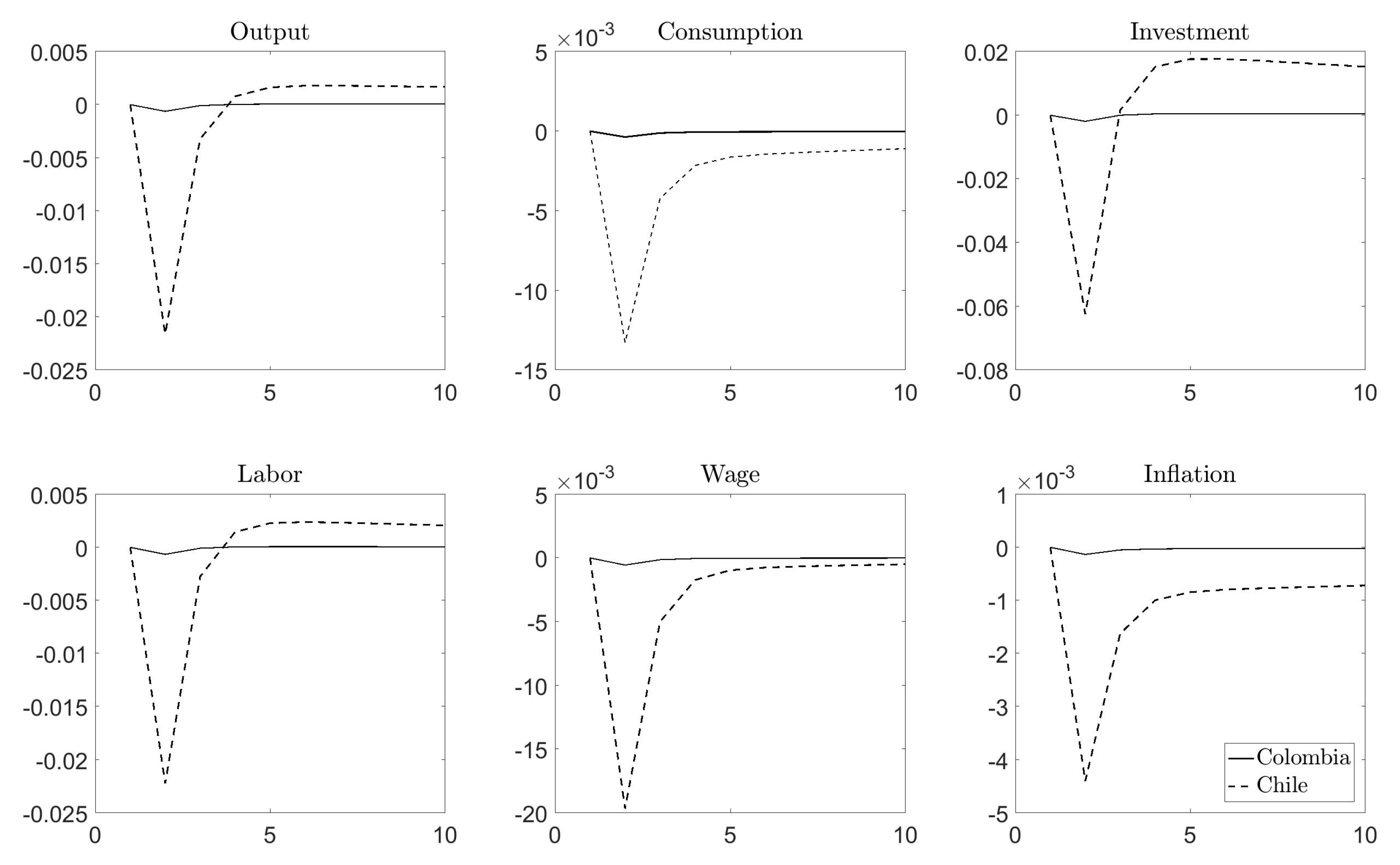
4.2. Response to a Disaster Risk Shock: Country-Specific EIS and Price Stickiness Only
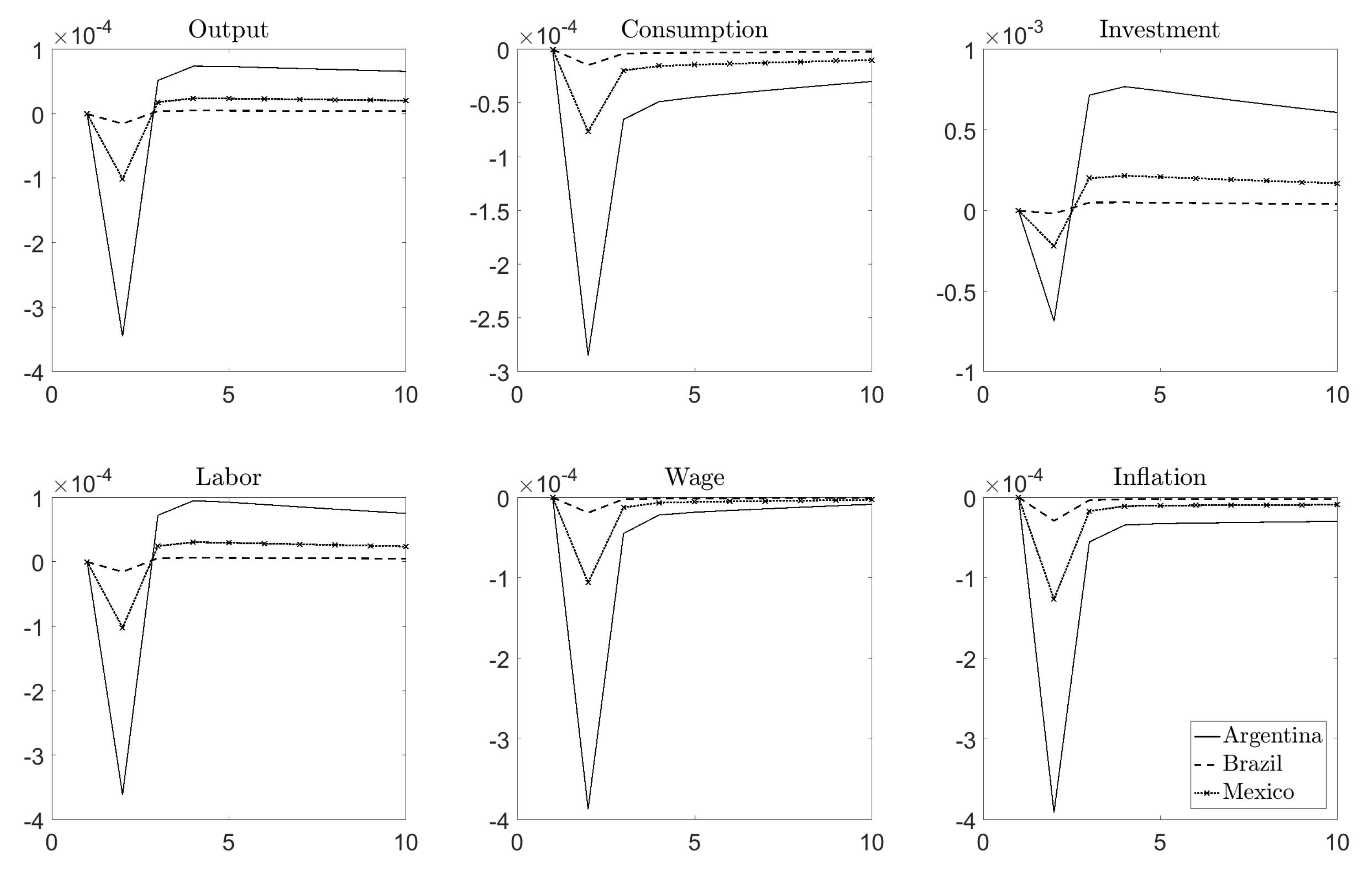
4.3. Response to a Disaster Risk Shock: Country-Specific Disaster Size and Probability
5. Conclusions
Acknowledgments
Conflicts of Interest
Abbreviations
| DSGE | Dynamic Stochastic General Equilibrium |
Appendix A
| Argentina | |||||
|---|---|---|---|---|---|
| Type | Date | Damage | Capital Stock | Deflator | |
| Flood | October 1985 | 1,300,000 | 894440000 | 0.5650 | 0.002572431 |
| Flood | 1 April 2013 | 1,300,000 | 2017062625 | 1.0560 | 0.000610323 |
| Flood | 11 April1998 | 1,100,000 | 1206780125 | 0.7790 | 0.001170111 |
| Flood | 28 April 2003 | 1,028,210 | 1282971250 | 0.8570 | 0.000935156 |
| Flood | May 1983 | 1,000,000 | 874513312.5 | 0.5290 | 0.002161613 |
| Flood | 4 April 2016 | 1,000,000 | na | ||
| Flood | August 1983 | 800,000 | 874513312.5 | 0.5290 | 0.00172929 |
| Flood | 1 October 2001 | 750,000 | 1284127375 | 0.8270 | 0.000706232 |
| Flood | September 1993 | 600,000 | 1009387687.5 | 0.7140 | 0.000832521 |
| Flood | 23 March 1988 | 490,000 | 937870750 | 0.6120 | 0.000853693 |
| Average : | 0.001285708 | ||||
| Nb. obs. > 0.001 | 4 | ||||
| Annual prob. | 0.0597 | ||||
| Brazil | |||||
| Type | Date | Damage | Capital Stock | Deflator | |
| Drought | January 2014 | 5,000,000 | 13311434000 | 1.0750 | 0.000349411 |
| Drought | 1978 | 2,300,000 | 3732019500 | 0.3710 | 0.001661154 |
| Drought | December 2004 | 1,650,000 | 8978346000 | 0.8800 | 0.000208836 |
| Drought | May 2012 | 1,460,000 | 12151692000 | 1.0390 | 0.000115638 |
| Flood | June 1984 | 1,000,000 | 5157555500 | 0.5480 | 0.000353814 |
| Flood | June 1984 | 1,000,000 | 5157555500 | 0.5480 | 0.000353814 |
| Flood | 2 February 1988 | 1,000,000 | 6099374000 | 0.6120 | 0.000267894 |
| Flood | 11 January 2011 | 1,000,000 | 11662182000 | 1.0210 | 0.0000839836 |
| Flood | 22 November 2008 | 750,000 | 9948994000 | 0.9800 | 0.00007.6923 |
| Drought | November 1985 | 651,000 | 5341811500 | 0.5650 | 0.000215697 |
| Average : | 0.000368717 | ||||
| Nb. obs. > 0.001 | 1 | ||||
| Annual prob. | 0.0149 | ||||
| Chile | |||||
| Type | Date | Damage | Capital Stock | Deflator | |
| Earthquake | 27 February 2010 | 30,000,000 | 906230500 | 1.0000 | 0.033104161 |
| Flood | 25 March 2015 | 1,500,000 | na | ||
| Earthquake | 3 March 1985 | 1,500,000 | 203282750 | 0.5650 | 0.013059973 |
| Extreme temp. | 10 September 2013 | 1,000,000 | 1087604125 | 1.0560 | 0.000870693 |
| Earthquake | 24 January 1939 | 920,000 | na | ||
| Wildfire | 15 January 2017 | 870,000 | na | ||
| Earthquake | 16 September 2015 | 800,000 | na | ||
| Volcanic activity | 24 April 2015 | 600,000 | na | ||
| Earthquake | 21 May 1960 | 550,000 | 57127410.156 | 0.1730 | 0.055650882 |
| Earthquake | 6 May 1953 | 500,000 | 42003230.469 | 0.1515 | 0.078573243 |
| Average : | 0.03625179 | ||||
| Nb. obs. > 0.001 | 4 | ||||
| Annual prob. | 0.0597 | ||||
| Colombia | |||||
| Type | Date | Damage | Capital Stock | Deflator | |
| Earthquake | 25 January 1999 | 1,857,366 | 963227750 | 0.7910 | 0.002437766 |
| Flood | 1 September 2011 | 1,290,000 | 1567348875 | 1.0210 | 0.000806117 |
| Flood | April 2011 | 1,030,000 | 1567348875 | 1.0210 | 0.000643644 |
| Volcanic activity | 13 November 1985 | 1,000,000 | 581150875 | 0.5650 | 0.003045528 |
| Flood | 6 April 2010 | 1,000,000 | 1488079250 | 1,0000 | 0.000672007 |
| Earthquake | 31 March 1983 | 410,900 | 538144687.5 | 0.5290 | 0.001443382 |
| Flood | November 1970 | 138,800 | 293590625 | 0.2250 | 0.002101187 |
| Insect infestation | 17 May 1995 | 104,000 | 855184437.5 | 0.7440 | 0.000163456 |
| Flood | 15 March 2012 | 62,000 | 1646414750 | 1.0390 | 0.0000362441 |
| Storm | 17 October 1988 | 50,000 | 658900687.5 | 0.6120 | 0.000123993 |
| Average : | 0.001147333 | ||||
| Nb. obs. > 0.001 | 4 | ||||
| Annual prob. | 0.0597 | ||||
| Mexico | |||||
| Type | Date | Damage | Capital Stock | Deflator | |
| Storm | 19 October 2005 | 5,000,000 | 4645159500 | 0.9090 | 0.001184147 |
| Storm | 13 September 2013 | 4,200,000 | 6297161000 | 1.0560 | 0.000631598 |
| Earthquake | 19 September 1985 | 4,104,000 | 2321685000 | 0.5650 | 0.00312864 |
| Storm | 15 September 2010 | 3,900,000 | 5671746000 | 1.0000 | 0.000687619 |
| Flood | 28 October 2007 | 3,000,000 | 5074071000 | 0.9620 | 0.000614596 |
| Storm | 10 September 2014 | 2,500,000 | 6498113500 | 1.0750 | 0.000357886 |
| Storm | 1 October 2005 | 2,500,000 | 4645159500 | 0.9090 | 0.000592073 |
| Storm | 30 June 2010 | 2,000,000 | 5671746000 | 1.0000 | 0.000352625 |
| Storm | 22 June 1993 | 1,670,000 | 2988199500 | 0.7140 | 0.000782724 |
| Storm | 12 September 2013 | 1,500,000 | 6297161000 | 1.0560 | 0.000225571 |
| Average : | 0.000855748 | ||||
| Nb. obs. > 0.001 | 2 | ||||
| Annual prob. | 0.0299 |
References
- Barro, Robert J. 2006. Rare disasters and asset markets in the twentieth century. The Quarterly Journal of Economics 121: 823–66. [Google Scholar] [CrossRef]
- Burstein, Ariel, Martin Eichenbaum, and Sergio Rebelo. 2005. Large devaluations and the real exchange rate. Journal of political Economy 113: 742–84. [Google Scholar] [CrossRef]
- Caruso, German, and Sebastian Miller. 2015. Long run effects and intergenerational transmission of natural disasters: A case study on the 1970 Ancash Earthquake. Journal of Development Economics 117(SC): 134–50. [Google Scholar] [CrossRef]
- Caruso, German Daniel. 2017. The legacy of natural disasters: The intergenerational impact of 100 years of disasters in Latin America. Journal of Development Economics 127(SC): 209–33. [Google Scholar] [CrossRef]
- Cavallo, Eduardo, Sebastian Galiani, Ilan Noy, and Juan Pantano. 2013. Catastrophic natural disasters and economic growth. Review of Economics and Statistics 95: 1549–61. [Google Scholar] [CrossRef]
- Cavallo, Eduardo, Andrew Powell, and Oscar Becerra. 2010. Estimating the direct economic damages of the earthquake in haiti. The Economic Journal 120: F298–312. [Google Scholar] [CrossRef]
- Gabaix, Xavier. 2011. Disasterization: A Simple Way to Fix the Asset Pricing Properties of Macroeconomic Models. American Economic Review 101: 406–9. [Google Scholar] [CrossRef]
- Gabaix, Xavier. 2012. Variable Rare Disasters: An Exactly Solved Framework for Ten Puzzles in Macro-Finance. The Quarterly Journal of Economics 127: 645–700. [Google Scholar] [CrossRef]
- Gagnon, Etienne. 2009. Price setting during low and high inflation: Evidence from mexico. The Quarterly Journal of Economics 124: 1221–63. [Google Scholar] [CrossRef]
- Gourio, Francois. 2012. Disaster Risk and Business Cycles. American Economic Review 102: 2734–66. [Google Scholar] [CrossRef]
- Havranek, Tomas, Roman Horvath, Zuzana Irsova, and Marek Rusnak. 2015. Cross-country heterogeneity in intertemporal substitution. Journal of International Economics 96: 100–18. [Google Scholar] [CrossRef]
- Hsiang, Solomon M., and Amir S. Jina. 2014. The Causal Effect of Environmental Catastrophe on Long-Run Economic Growth: Evidence From 6700 Cyclones. NBER Working Papers 20352. Cambridge: National Bureau of Economic Research, Inc. [Google Scholar]
- Isoré, Marlène, and Urszula Szczerbowicz. 2017. Disaster risk and preference shifts in a New Keynesian model. Journal of Economic Dynamics and Control 79: 97–125. [Google Scholar] [CrossRef]
- Lazzaroni, Sara, and Peter A van Bergeijk. 2014. Natural disasters’ impact, factors of resilience and development: A meta-analysis of the macroeconomic literature. Ecological Economics 107: 333–46. [Google Scholar] [CrossRef]
- Marfè, Roberto, and Julien Penasse. 2017. The Time-Varying Risk of Macroeconomic Disasters (10 April 2017). Technical report. Paris: Finance Meeting EUROFIDAI-AFFI. [Google Scholar]
- Morandé, Felipe, and Mauricio Tejada. 2008. Price Stickiness in Emerging Economies: Empirical Evidence for Four Latin-American Countries. Technical report, Documentos de Trabajo 286. Santiago: Universidad de Chile. [Google Scholar]
- Siriwardane, Emil N. 2015. The Probability of Rare Disasters: Estimation and Implications. Technical report, Harvard Business School Working Paper. Boston: Harvard Business School. [Google Scholar]
- Skidmore, Mark, and Hideki Toya. 2002. Do natural disasters promote long-run growth? Economic Inquiry 40: 664–87. [Google Scholar] [CrossRef]
- Toya, Hideki, and Mark Skidmore. 2007. Economic development and the impacts of natural disasters. Economics Letters 94: 20–25. [Google Scholar] [CrossRef]
| 1. | The opinions expressed in this paper are those of the authors and do not necessarily reflect the views of the Bank of Finland. |
| 2. | Caruso and Miller (2015) and Caruso (2017) argue that other long run welfare consequences exist, such as negative health effects, impacts on labor markets, and losses of human capital accumulation, even without clear effects in terms of growth. |
| 3. | The depreciation rate is a function of the utilization rate u of capital as , and the capital adjustment costs given by the function . |
| 4. | This assumption follows Gourio (2012) and its role is further discussed in Isoré and Szczerbowicz (2017). |
| 5. | This does not mean that other parameters are not country-specific, but that their importance for the simulations of this particular model is negligible, such keeping them identical across countries favor the ease of comparison. |
| 6. | Argentina’s estimate from Havranek et al. (2015) is negative and therefore here replaced by an arbitrarily small but positive value, such that the model runs consistently. |
| 7. | As for comparison, prices change every 7.5 months on average in the US. |
| Disaster risk | ||
| probability of disaster | 0.0037 | |
| size of disaster | 0.0078 | |
| persistence of (log) disaster risk | 0.965 | |
| st. dev. of innovations to (log) disaster risk | 0.2 | |
| Utility function | ||
| discount factor | 0.9976 | |
| risk aversion coefficient | 3.8 | |
| leisure preference | 2.33 | |
| (Country-specific) EIS | ||
| Argentina | 0.1 | |
| Brazil | 0.107 | |
| Chile | 0.137 | |
| Colombia | 0.158 | |
| Mexico | 0.158 | |
| Investment | ||
| capital depreciation rate | 0.0067 | |
| capital adjustment cost | 2 | |
| steady-state utilization rate of capital | 1 | |
| Production | ||
| capital share of production | 0.33 | |
| elasticity of substitution among goods | 6 | |
| trend growth of productivity | 0.0017 | |
| (Country-specific) Calvo probability | ||
| Argentina | 0.41 | |
| Brazil | 0.33 | |
| Chile | 0.7 | |
| Colombia | 0.68 | |
| Mexico | 0.375 | |
| Public authority | ||
| Taylor rule inflation weight | 1.6 | |
| Taylor rule output weight | 0.4 | |
| target (gross) inflation rate | 1.0017 | |
| interest rate smoothing parameter | 0.947 |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Isoré, M. Changes in Natural Disaster Risk: Macroeconomic Responses in Selected Latin American Countries. Economies 2018, 6, 13. https://doi.org/10.3390/economies6010013
Isoré M. Changes in Natural Disaster Risk: Macroeconomic Responses in Selected Latin American Countries. Economies. 2018; 6(1):13. https://doi.org/10.3390/economies6010013
Chicago/Turabian StyleIsoré, Marlène. 2018. "Changes in Natural Disaster Risk: Macroeconomic Responses in Selected Latin American Countries" Economies 6, no. 1: 13. https://doi.org/10.3390/economies6010013
APA StyleIsoré, M. (2018). Changes in Natural Disaster Risk: Macroeconomic Responses in Selected Latin American Countries. Economies, 6(1), 13. https://doi.org/10.3390/economies6010013





