Regional Economic Convergence in Turkey: Does the Government Really Matter for? †
Abstract
1. Introduction
2. Theoretical Background of Convergence Approach
3. Convergence Studies in Turkey
4. Data and Model
5. Empirical Findings
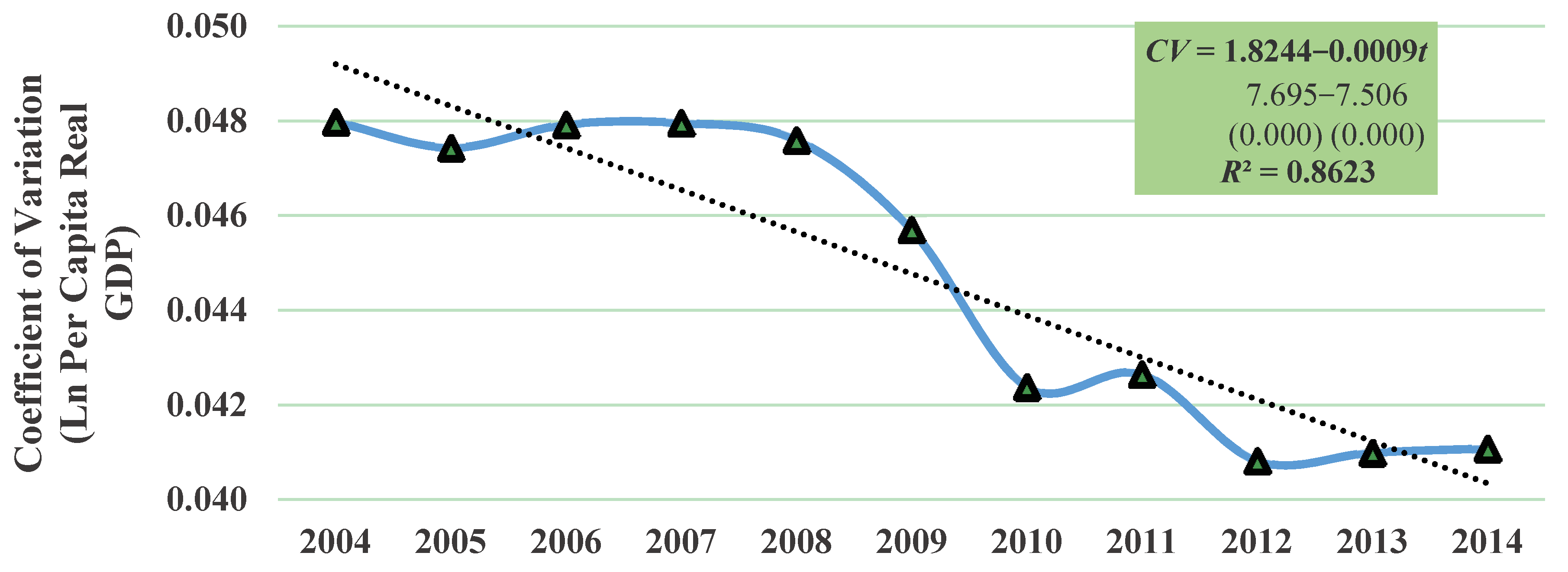
5.1. σ-Convergence of NUTS 2 Regions
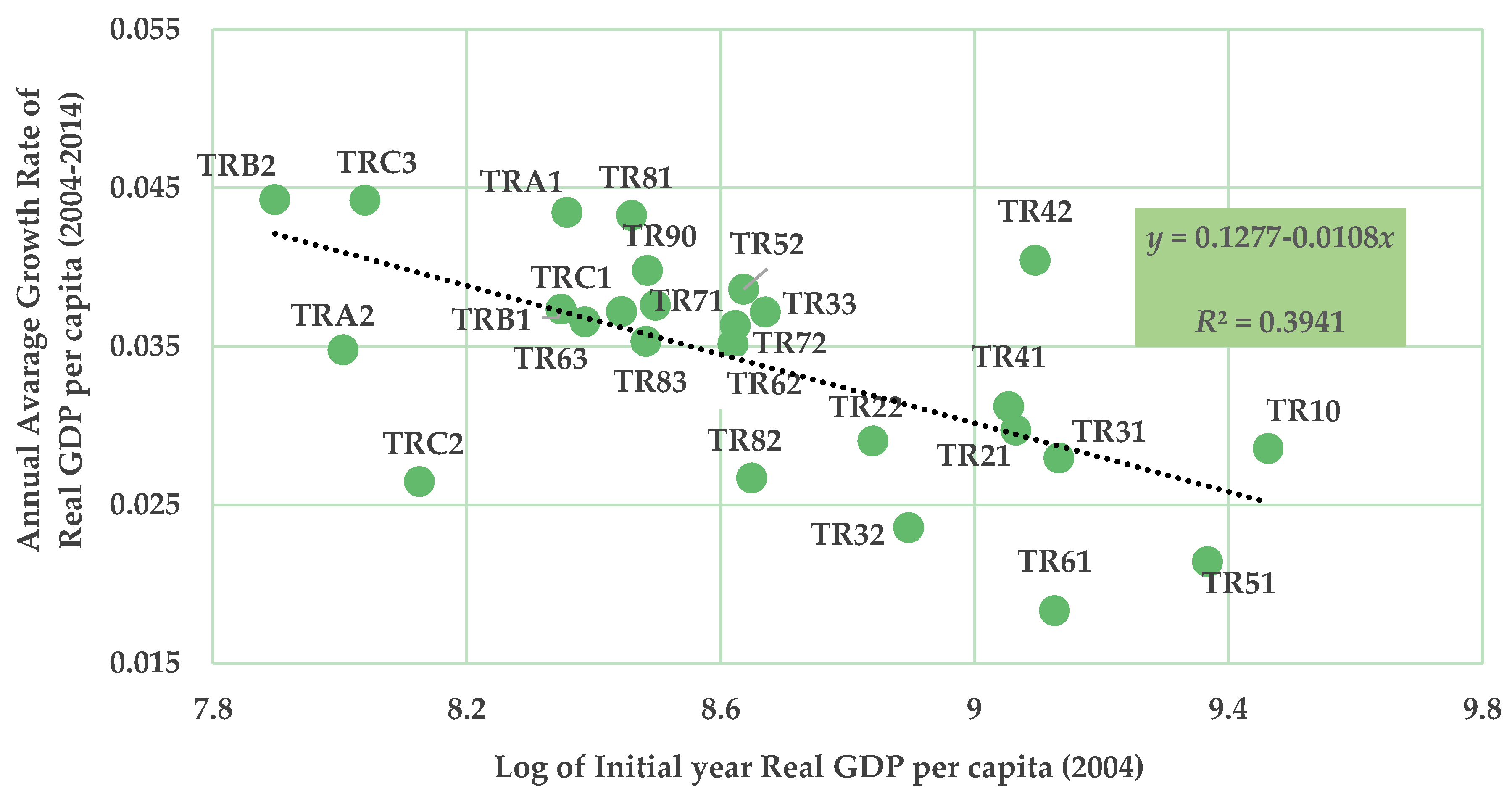
5.2. Absolute and Conditional β-Convergence of NUTS 2 Regions
5.3. Panel Data Analysis of the Convergence Approach
6. Conclusions
Author Contributions
Conflicts of Interest
Appendix A
| NUTS Code | Provinces | NUTS Code | Provinces |
|---|---|---|---|
| TR10 | İstanbul | TR71 | Kırıkkale, Aksaray, Niğde, Nevşehir, Kırşehir |
| TR21 | Tekirdağ, Edirne, Kırklareli | TR72 | Kayseri, Sivas, Yozgat |
| TR22 | Balıkesir, Çanakkale | TR81 | Zonguldak, Karabük, Bartın |
| TR31 | İzmir | TR82 | Kastamonu, Çankırı, Sinop |
| TR32 | Aydın, Denizli Muğla | TR83 | Samsun, Tokat, Çorum, Amasya |
| TR33 | Manisa, Afyonkarahisar, Kütahya, Uşak | TR90 | Trabzon, Ordu, Giresun, Rize, Artvin, Gümüşhane |
| TR41 | Bursa, Eskişehir, Bilecik | TRA1 | Erzurum, Erzincan, Bayburt |
| TR42 | Kocaeli, Sakarya, Düzce, Bolu, Yalova | TRA2 | Ağrı, Kars, Iğdır, Ardahan |
| TR51 | Ankara | TRB1 | Malatya, Elazığ, Bingöl, Tunceli |
| TR52 | Konya, Karaman | TRB2 | Van, Muş, Bitlis, Hakkari |
| TR61 | Antalya, Isparta, Burdur | TRC1 | Gaziantep, Adıyaman, Kilis |
| TR62 | Adana, Mersin | TRC2 | Şanlıurfa, Diyarbakır |
| TR63 | Hatay, Kahramanmaraş, Osmaniye | TRC3 | Mardin, Batman, Şırnak, Siirt |
References
- Arbia, Giuseppe, and Gianfranco Piras. 2005. Convergence in Per-capita GDP across European Regions Using Panel Data Models Extended to Spatial Autocorrelation Effects. Available online: https://ssrn.com/abstract=936327 (accessed on 11 January 2017).
- Aslan, Alper, and Ferit Kula. 2011. Is there Really Divergence across Turkish Provinces? Evidence from the Lagrange Multiplier Unit Root Tests. European Planning Studies 19: 539–49. [Google Scholar] [CrossRef]
- Baltagi, Badi. 2005. Econometric Analysis of Panel Data, 3rd ed. Chichester: John Wiley & Sons Ltd. [Google Scholar]
- Barro, Robert J., and Xavier X. Sala-i-Martin. 1991. Convergence across states and regions. Brookings Papers on Economic Activity 1: 107–58. [Google Scholar] [CrossRef]
- Barro, Robert J., and Xavier X. Sala-i-Martin. 1992. Convergence. Journal of Political Economy 100: 223–51. [Google Scholar] [CrossRef]
- Barro, Robert J., and Xavier X. Sala-i-Martin. 1995. Economic Growth. New York: McGraw-Hill. [Google Scholar]
- Barro, Robert J., and Xavier X. Sala-i-Martin. 2004. Economic Growth, 2nd ed. Cambridge: The MIT Press. [Google Scholar]
- Baumol, William J. 1986. Productivity growth, convergence, and welfare: What the long-run data show. American Economic Review 76: 1072–85. [Google Scholar]
- Berber, Metin, Rahmi Yamak, and Seyfettin Artan. 2000. Türkiye’de Yakınlaşma Hipotezinin Bölgeler Bazında Geçerliligi Üzerine bir Çalışma: 1975–1997. 9. Ulusal Bölge Bilimi/Bölge Planlama Kongresi Bildirileri. Paper presented at 9. Ulusal Bölge Bilimi ve Bölge Planlama Kongresi, Trabzon, 5–6 October 2000. [Google Scholar]
- Bonnefond, Céline. 2014. Growth Dynamics and Conditional Convergence among Chinese Provinces: A Panel Data Investigation Using System GMM Estimator. Journal of Economic Development 39: 1–25. [Google Scholar]
- Button, Kenneth. 1998. Infrastructure investment, endogenous growth, and economic convergence. Annals of Regional Science 32: 145–62. [Google Scholar] [CrossRef]
- Canova, Fabio, and Albert Marcet. 1995. The Poor Stay Poor: Non-Convergence across Countries and Regions. Available online: https://ssrn.com/abstract=289497 (accessed on 13 February 2017).
- Chaudhuri, Jayasri Ray. 2001. An Introduction to Development and Regional Planning: With Special Reference to India. New Delhi: Orient BlackSwan. [Google Scholar]
- Cuaresma, Jesus Crespo, Doris Ritzberger-Grünwald, and Maria Antoinette Silgoner. 2008. Growth, convergence and EU membership. Applied Economics 40: 643–56. [Google Scholar] [CrossRef]
- Durlauf, Steven, and Danny T. Quah. 1999. The new Empirics of Economic Growth. In Handbooks of Macroeconomics. Edited by John B. Taylor and Michael Woodford. Cornwall: North-Holland, vol. 1A, pp. 235–308. [Google Scholar]
- Erk, Nejat, Sanli Ateş, and Tuba Direkçi. 2000. Convergence and growth within GAP region (South Eastern Anatolia Project) and overall Turkey’s regions. Proceedings of the METU International Conference in Economics IV, Ankara, Turkey, 13–16 September 2000. [Google Scholar]
- Erlat, Haluk. 2005. Türkiye’de Bölgesel Yakınsama Sorununa Zaman Dizisi Yaklaşımı. In Bölgesel Gelişme Stratejileri ve Akdeniz Ekonomisi. Edited by Haluk Erlat. Ankara: Türkiye Ekonomi Kurumu, pp. 251–76. [Google Scholar]
- Ersungur, Ş. Mustafa, and Özgür Polat. 2010. Türkiye’de Bölgeler Arasında Yakınsama Analizi. Atatürk Üniversitesi Sosyal Bilimler Enstitüsü Dergisi 8: 335–43. [Google Scholar]
- Filiztekin, Alpay. 1999. Convergence across Turkish Provinces and Sectoral Dynamics. Available online: http://myweb.sabanciuniv.edu/alpayf/files/2010/04/provconv.pdf (accessed on 13 February 2017).
- Filiztekin, Alpay. 2009. Türkiye’de Bölgesel Farklar. Available online: http://research.sabanciuniv.edu/11643/1/BolgeselFarklar_YKY.pdf (accessed on 13 February 2017).
- Friedman, Milton. 1992. Do Old Fallacies Ever Die? Journal of Economic Literature 30: 2129–32. [Google Scholar]
- Gaulier, Guillaume, Christophe Hurlin, and Philippe Jean-Pierre. 1999. Testing Convergence: A Panel Data Approach. Annales d’Économie et de Statistique 55/56: 411–27. [Google Scholar] [CrossRef]
- Gerni, Cevat, Selahattin Sarı, Haktan Sevinç, and Ömer Selçuk Emsen. 2015. Bölgesel Dengesizliklerin Giderilmesinde Yatırım Teşviklerinin Rolü ve Başarı Kriteri Olarak Yakınsama Analizleri: Türkiye Örneği. Proceedings of the International Conference on Eurasian Economies, Kazan, Russia, 9–11 September 2015. [Google Scholar]
- Gezici, Ferhan, and Geoffrey J. D. Hewings. 2004. Regional Convergence and Economic Performance of Peripheral Areas in Turkey. Review of Urban and Regional Development Studies 16: 113–32. [Google Scholar] [CrossRef]
- Ginevičius, Romualdas, and Agnė Šimelytė. 2011. Government incentives directed towards foreign direct investment: A case of central and eastern Europe. Journal of Business Economics and Management 12: 435–50. [Google Scholar] [CrossRef]
- Greene, William H. 2003. Econometric Analysis, 5th ed. New Jersey: Prentice Hall. [Google Scholar]
- Hirschman, Albert O. 1958. The Strategy of Economic Development. New Haven: Yale University. [Google Scholar]
- Islam, Nazrul. 1995. Growth empirics: A panel data approach. Quarterly Journal of Economics, 110: 1127–70. [Google Scholar] [CrossRef]
- Karaalp, Hacer Simay, and Fuat Erdal. 2012. Sanayileşmenin Bölgesel Yığılması ve Komşu İllerin Büyümesi Gelir Farklılıklarını Artırır mı? Türkiye için Bir Beta Yakınsama Analizi. Ege Akademik Bakış 12: 475–86. [Google Scholar]
- Lall, Somik, and Serdar Yilmaz. 2000. Regional Economic Convergence: Do Policy Instruments Make a Difference? Available online: http://siteresources.worldbank.org/WBI/Resources/wbi37161.pdf (accessed on 10 January 2017).
- Lee, Michael, Ritchard Longmire, Laszlo Matyas, and Mark Harris. 1998. Growth convergence: Some panel data evidence. Applied Economics 30: 907–12. [Google Scholar] [CrossRef]
- Lopez-Rodriguez, Jesus. 2008. Regional Convergence in the European Union: Results from a Panel Data Model. Economics Bulletin 18: 1–7. [Google Scholar]
- Magrini, Stefano. 2004. Regional (di)convergence. In Handbook of Regional and Urban Economics. Edited by J. Vernon Henderson and Jacques-François Thisse. Amsterdam: Elsevier B. V., vol. 4, pp. 2741–96. [Google Scholar]
- Mankiw, N. Gregory, David Romer, and David N. Weil. 1992. A Contribution to the Empirics of Economic Growth. The Quarterly Journal of Economics 107: 407–37. [Google Scholar] [CrossRef]
- Michelis, Leo, and Simon Neaime. 2004. Income Convergence in the Asia-Pacific Region. Journal of Economic Integration 19: 470–98. [Google Scholar] [CrossRef]
- Michelis, Leo, Athanasios P. Papadopoulos, and Gregory T. Papanikos. 2004. Regional convergence in Greece in the 1980s: an econometric investigation. Applied Economics 36: 881–88. [Google Scholar] [CrossRef]
- Myrdal, Gunnar. 1957. Economic Theory and Underdeveloped Regions. London: University Paperbacks, Methuen & Co Ltd. [Google Scholar]
- Önder, A. Özlem, Ertuğrul Deliktaş, and Metin Karadağ. 2010. The Impact of Public Capital Stock on Regional Convergence in Turkey. European Planning Studies 18: 1041–55. [Google Scholar] [CrossRef]
- Özgül, Seda, and Metin Karadağ. 2015. Regional Convergence in Turkey Regarding Welfare Indicators. Sosyoekonomi 23: 38–50. [Google Scholar]
- Piras, Gianfranco, and Giuseppe Arbia. 2007. Convergence in per-capita GDP across EU-NUTS 2 regions using panel data models extended to spatial Autocorrelations Effects. Statistica 67: 157–72. [Google Scholar]
- Quah, Danny T. 1996. Empirics for economic growth and convergence. European Economic Review 40: 1353–75. [Google Scholar] [CrossRef]
- Ranjpour, Reza, and Zahra Karimi Takanlou. 2008. Evaluation of the income convergence hypothesis in ten new members of the European union: A panel unit root approach. Panoeconomicus 55: 157–66. [Google Scholar] [CrossRef]
- Republic of Turkey Ministry of Development. 2015. Available online: http://www2.kalkinma.gov.tr/kamuyat/il.html?2015_0 (accessed on 20 December 2016).
- Republic of Turkey Ministry of Economy. 2014. Investment Incentives. Available online: http://www.economy.gov.tr/portal/faces/home/invest-incent/invest-incentives? (accessed on 17 February 2017).
- Republic of Turkey Ministry of Economy. 2016. İstatistikler ve Yayınlar. Available online: http://www.ekonomi.gov.tr/portal/content/conn/UCM/uuid/dDocName:EK-229074 (accessed on 10 October 2016).
- Republic of Turkey Official Gazette. 2012. Yatirimlarda Devlet Yardimi Hakkinda Karar. Available online: http://www.resmigazete.gov.tr/main.aspx?home=http://www.resmigazete.gov.tr/eskiler/2012/06/20120619.htm&main=http://www.resmigazete.gov.tr/eskiler/2012/06/20120619.htm (accessed on 9 January 2017).
- Romer, David. 1996. Advanced Macroeconomics. New York: McGraw-Hill. [Google Scholar]
- Sağbaş, İsa. 2002. Türkiye’de Kamu Harcamalarının Yakınsama Üzerindeki Etkisi. Afyon Kocatepe Üniversitesi İ.İ.B.F. Dergisi 4: 137–48. [Google Scholar]
- Sala-i-Martin, Xavier X. 1996a. The Classical Approach to Convergence Analysis. The Economic Journal 106: 1019–36. [Google Scholar] [CrossRef]
- Sala-i-Martin, Xavier X. 1996b. Regional Cohesion: Evidence and Theories of Regional Growth and Convergence. European Economic Review 40: 1325–52. [Google Scholar] [CrossRef]
- Shen, Daqing, Ruiqiang Wang, and Nan Yi. 2008. Analysis of the Convergence of Regional Economic Growth in Beijing. International Journal of Business and Management 3: 52–58. [Google Scholar] [CrossRef]
- Solow, Robert M. 1956. A contribution to the theory of economic growth. Quarterly Journal of Economics 70: 65–94. [Google Scholar] [CrossRef]
- Studenmund, A. H. 1992. Using Eonometrics: A Practical Guide, 2nd ed. New York: Harper Collins Publishers. [Google Scholar]
- Tansel, Aysit, and Nil Demet Gungor. 1998. Economic growth and convergence: An application to the provinces of Turkey, 1975–1995. Available online: https://www.academia.edu/7142026/Economic_Growth_and_Convergence_An_Application_to_the_Provinces_of_Turkey_1975-1995 (accessed on 10 January 2017).
- Temple, Jonathan. 1999. The New Growth Evidence. Journal of Economic Literature 37: 112–56. [Google Scholar] [CrossRef]
- Turkish Statistical Institute. 2017a. Regional Statistics. Available online: https://biruni.tuik.gov.tr/bolgeselistatistik/anaSayfa.do?dil=en (accessed on 12 February 2017).
- Turkish Statistical Institute. 2017b. Population Estimates, 2000–2006, Address Based Population Registration System (ABPRS), 2007–2016. Available online: www.tuik.gov.tr/PreIstatistikTablo.do?istab_id=1590 (accessed on 20 February 2017).
- Varblane, Urmas, and Priit Vahter. 2005. An Analysis of the Economic Convergence Process in the Transition Countries. Available online: https://ssrn.com/abstract=757204 (accessed on 21 December 2016).
- Wallace, T. Dudley, and J. Lew Silver. 1988. Econometrics: An Introduction. Reading: Addison-Wesley Publishing Company. [Google Scholar]
- Wooldridge, Jeffrey M. 2010. Econometric Analysis of Cross Section and Panel Data, 2nd ed. Cambridge: MIT Press. [Google Scholar]
- Yildirim, Julide, Nadir Öcal, and Süheyla Özyildirim. 2009. Income Inequality and Economic Convergence in Turkey: A Spatial Effect Analysis. International Regional Science Review 32: 221–54. [Google Scholar] [CrossRef]
- Zeren, Fatma, and Veli Yilanci. 2011. Türkiye’de Bölgeler Arası Gelir Yakınsaması: Rassal Katsayılı Panel Veri Analizi Uygulaması. Business and Economics Research Journal 2: 143–51. [Google Scholar]
| 1 | The NUTS classification (Nomenclature of territorial units for statistics) is a hierarchical system for dividing up the economic territory of the EU. |
| 2 | The implementation period of the Incentive Law No. 5084 was finalized on 31.12.2009. However, the period of benefiting from the incentives was extended until 2012 with the Law No. 5568 and the amendment made in Article 7 of Law No. 5084. Finally, the last investment incentive program, which put into effect in June 2012, is still ongoing (Republic of Turkey Ministry of Economy 2014). |
| 3 | Also see the Appendix for regional context and region codes. |
| 4 | Barro and Sala-i-Martin (2004, pp. 466–67) estimate the speed of convergence for the U.S. states by an univariate regression model, , where and are final and initial year per capita GDP, is a constant, is the length of the period, and is the coefficient of convergence speed. In this equation, the coefficient of initial income, , also equals to in Equations (4) and (5), and then . In order to obtain equation, we take the log of both sides of this equation . Thus, we reach the coefficient as given in Equation (6). |
| 5 | According to Wallace and Silver (1988, p. 123), when studying on cross-sectional data, it is often seen that the value of R-square is 0.3 or less than this value. Also, Studenmund (1992, p. 47) argues that an R-square value of around 0.50 in a cross-sectional analysis is adequate for goodness of fit. |
| Author/s | Period/Sample | Dependent Variable | Method 1 | Some of the Findings |
|---|---|---|---|---|
| Tansel and Gungor (1998) | 1975–1995 | Labor productivity level and productivity growth | NLS, OLS and panel FE |
|
| 67 provinces | ||||
| Filiztekin (1999) | 1975–1995 | GDP and GDP per capita | NLS and panel FE |
|
| 65 provinces | ||||
| Berber et al. (2000) | 1975–1997 | GDP per capita | OLS |
|
| 7 geographical regions | ||||
| Erk et al. (2000) | 1979–1997 | Real GDP per capita | OLS and NLS |
|
| 67 provinces | ||||
| Sağbaş (2002) | 1986–1997 | Real GDP per capita | OLS |
|
| 67 provinces | ||||
| Gezici and Hewings (2004) | 1980–1997 | GDP per capita | OLS |
|
| 16 functional regions and 67 provinces | ||||
| Erlat (2005) | 1975–2001 | Real GDP per capita | IPS, ADF and CADF panel unit root tests |
|
| 7 geographical regions and 65 provinces | ||||
| Yildirim et al. (2009) | 1987–2001 | Real GDP per capita | OLS, SEM, SAR, and GWR |
|
| 67 provinces | ||||
| Önder et al. (2010) | 1980–2001 | Real GDP per capita | Pooled panel, FE, GMM-DIF, GMM-SYS |
|
| 26 NUTS 2 regions | ||||
| Ersungur and Polat (2010) | 1987–2000 | GDP per capita | OLS |
|
| 12 NUTS 1 regions | ||||
| Aslan and Kula (2011) | 1975–2001 | GDP per capita | Univariate and panel LM |
|
| 67 provinces | ||||
| Zeren and Yilanci (2011) | 1991–2000 | GDP per capita | Panel FE and RE |
|
| 26 NUTS 2 regions | ||||
| Karaalp and Erdal (2012) | 1993–2001 | GDP per capita | Panel FE and GMM |
|
| 73 provinces | ||||
| Gerni et al. (2015) | 2004–2012 | Regional tax revenue per capita | OLS |
|
| 81 provinces | ||||
| 26 NUTS 2 regions | ||||
| Özgül and Karadağ (2015) | 1990–2001 | GDP per capita and per person employed | OLS |
|
| Year | Ln Per Capita Real GDP | Standard Deviation | Coefficient of Variation |
|---|---|---|---|
| 2004 | 8.6448 | 0.4148 | 0.0480 |
| 2005 | 8.7124 | 0.4132 | 0.0474 |
| 2006 | 8.7571 | 0.4197 | 0.0479 |
| 2007 | 8.7703 | 0.4206 | 0.0480 |
| 2008 | 8.7857 | 0.4182 | 0.0476 |
| 2009 | 8.7273 | 0.3988 | 0.0457 |
| 2010 | 8.8198 | 0.3738 | 0.0424 |
| 2011 | 8.8857 | 0.3789 | 0.0426 |
| 2012 | 8.9355 | 0.3647 | 0.0408 |
| 2013 | 8.9877 | 0.3684 | 0.0410 |
| 2014 | 9.0189 | 0.3704 | 0.0411 |
| Method: OLS | |||
|---|---|---|---|
| Included Observations: 26 | |||
| Coefficient | Std. Error | Prob. | |
| Constant | 0.1277 | 0.0237 | 0.000 *** |
| Log of Initial Year Real GDP per capita | −0.0108 | 0.0027 | 0.001 *** |
| R-square | 0.3941 | ||
| F-statistic | 15.6101 | ||
| Prob. (F-statistic) | 0.001 | ||
| Speed of Convergence (β) | 1.15 % | ||
| Method: OLS | |||
|---|---|---|---|
| Included observations: 26 | |||
| Coefficient | Std. Error | Prob. | |
| Constant | 0.1663 | 0.0287 | 0.000 *** |
| Log of Initial Year Real GDP per capita | −0.0175 | 0.0040 | 0.000 *** |
| Log of per capita Government Investments | 0.0014 | 0.0025 | 0.579 |
| Log of per capita Fixed Investment Incentives | 0.0028 | 0.0012 | 0.033 ** |
| R-square | 0.5091 | ||
| F-statistic | 7.6054 | ||
| Prob. (F-statistic) | 0.001 | ||
| Speed of Convergence (β) | 1.94 % | ||
| MODEL I | MODEL II | MODEL III | MODEL IV | |||||
|---|---|---|---|---|---|---|---|---|
| Pooled | FE Two-Way | Pooled | FE Two-Way | Pooled | FE Two-Way | Pooled | FE Two-Way | |
| Constant | 0.212 | 2.331 | 0.275 | 2.303 | 0.086 | 2.230 | 0.166 | 2.189 |
| [2.876] | [6.043] | [4.285] | [5.960] | [1.202] | [5.765] | [2.633] | [5.645] | |
| (0.004) | (0.000) | (0.000) | (0.000) | (0.230) | (0.000) | (0.009) | (0.000) | |
| Ln per capita real GDP (t−1) | −0.035 | −0.269 | −0.036 | −0.261 | −0.015 | −0.255 | −0.015 | −0.244 |
| [−4.348] | [−6.071] | [−4.475] | [−5.919] | [−2.062] | [−5.754] | [−2.040] | [−5.548] | |
| (0.000) | (0.000) | (0.000) | (0.000) | (0.040) | (0.000) | (0.042) | (0.000) | |
| Ln Per capita Investment Incentives | 0.015 | 0.006 | 0.016 | 0.006 | ||||
| [4.686] | [2.296] | [4.965] | [2.454] | |||||
| (0.000) | (0.022) | (0.000) | (0.015) | |||||
| Ln Per Capita Government Investments | 0.012 | 0.008 | 0.016 | 0.010 | ||||
| [1.722] | [1.490] | [2.325] | [1.717] | |||||
| (0.086) | (0.137) | (0.021) | (0.087) | |||||
| F-statistics (p-value) | 10.793 | 21.444 | 14.596 | 21.858 | 4.819 | 21.482 | 4.162 | 21.821 |
| (0.000) | (0.000) | (0.000) | (0.000) | (0.001) | (0.000) | (0.042) | (0.000) | |
| Number of obs. | 260 | 260 | 260 | 260 | 260 | 260 | 260 | 260 |
| Number of period | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 |
| Number of cross. | 26 | 26 | 26 | 26 | 26 | 26 | 26 | 26 |
| R-square | 0.112 | 0.781 | 0.102 | 0.779 | 0.036 | 0.776 | 0.016 | 0.773 |
| Hausman Test * (p-value) | χ2 (3): | χ2 (2): | χ2 (2): | χ2 (1): | ||||
| 33.346 | 30.867 | 30.248 | 27.806 | |||||
| (0.000) | (0.000) | (0.000) | (0.000) | |||||
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gömleksiz, M.; Şahbaz, A.; Mercan, B. Regional Economic Convergence in Turkey: Does the Government Really Matter for? Economies 2017, 5, 27. https://doi.org/10.3390/economies5030027
Gömleksiz M, Şahbaz A, Mercan B. Regional Economic Convergence in Turkey: Does the Government Really Matter for? Economies. 2017; 5(3):27. https://doi.org/10.3390/economies5030027
Chicago/Turabian StyleGömleksiz, Mustafa, Ahmet Şahbaz, and Birol Mercan. 2017. "Regional Economic Convergence in Turkey: Does the Government Really Matter for?" Economies 5, no. 3: 27. https://doi.org/10.3390/economies5030027
APA StyleGömleksiz, M., Şahbaz, A., & Mercan, B. (2017). Regional Economic Convergence in Turkey: Does the Government Really Matter for? Economies, 5(3), 27. https://doi.org/10.3390/economies5030027





