Fréchet Distribution Applied to Salary Incomes in Spain from 1999 to 2014. An Engineering Approach to Changes in Salaries’ Distribution
Abstract
:1. Introduction
- (1)
- The data from Table 1 and Table 2 was post-processed in order to obtain an estimation of the salaries earned in brackets of half minimum wage from 5 to 7.5 times the minimum wage and from 7.5 to 10 times the minimum wage. To do this, the evolution of the minimum wage in Spain from 1999 to 2014 is required (see Table 3).
- (2)
- The data (salaries paid) was made non-dimensional in order to directly compare the distributions from different years.
- (3)
- A corrected Fréchet distribution was fitted to the data (once post-processed), the evolution from 1999 to 2014 of this distribution being analyzed in order to detect changes in their main parameters and study the data through them.
2. Methodology
- the number of salaried people depends linearly on the salary, and
- the average salary corresponding to each new sub-bracket of half minimum wage is centered in relation to the aforementioned bracket.
The Fréchet Distribution Fitted to the Data
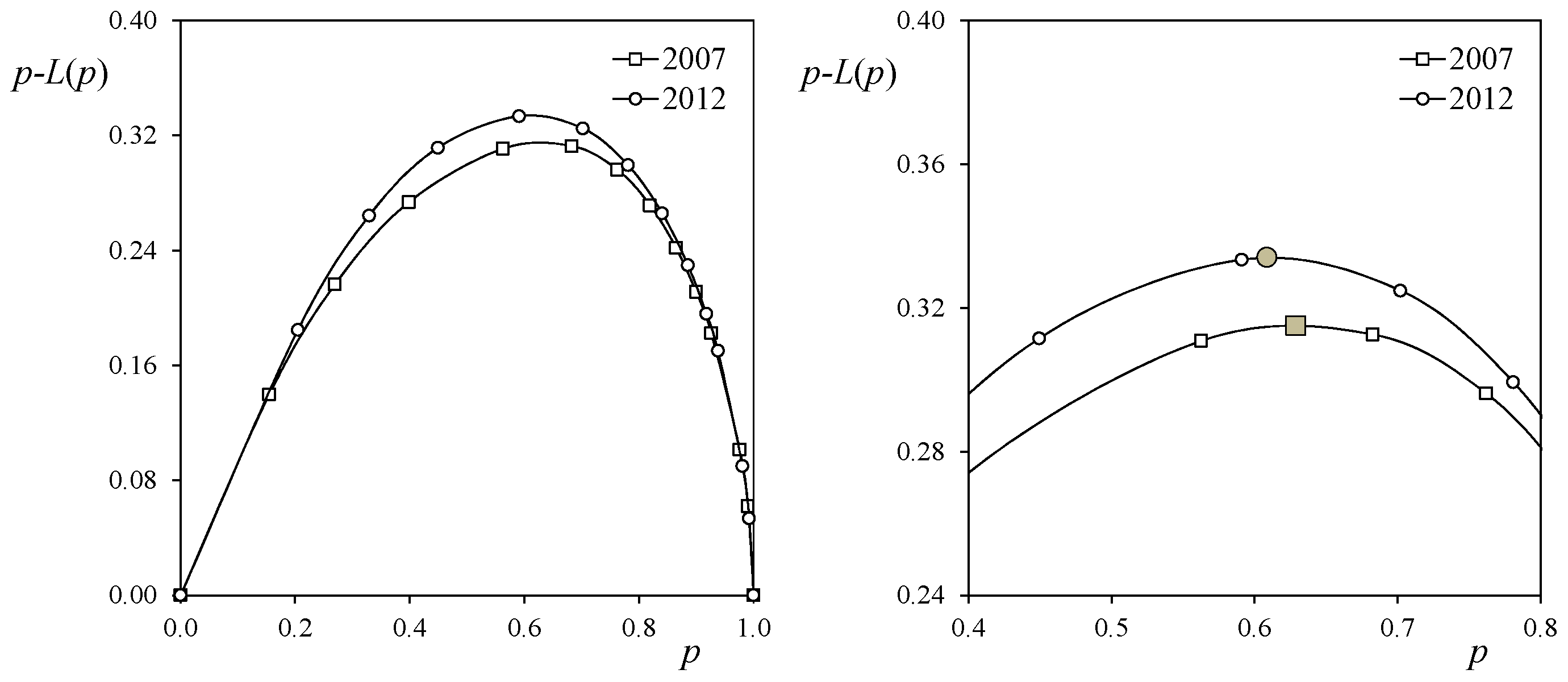
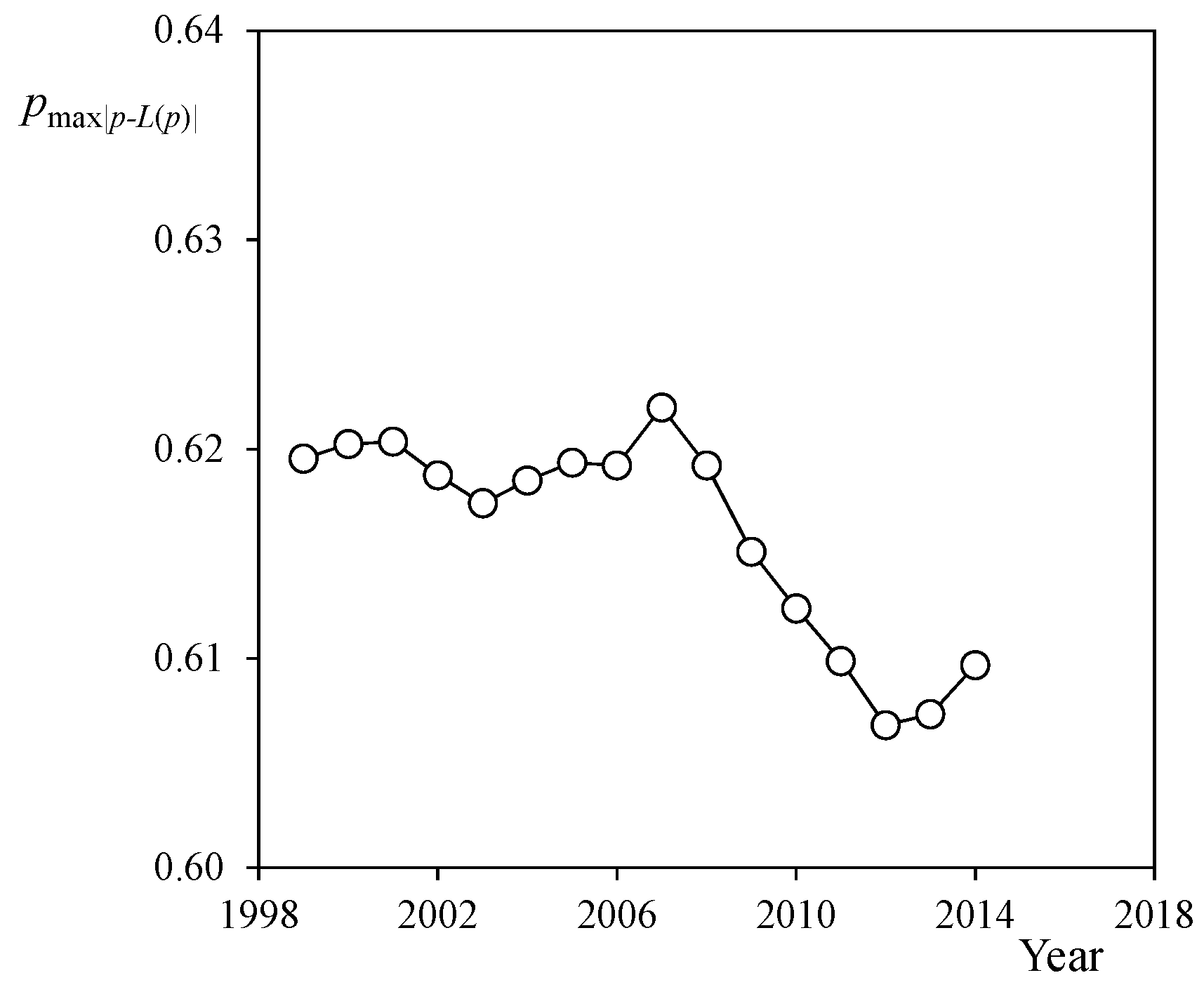
3. Results and Discussion
4. Conclusions
- The Fréchet distribution has proven to fit the studied salaries’ distributions well, having a similar accuracy in relation to the data when compared to other distributions (Log-Normal, Gamma, Dagum, GB2) that can be considered more complex.
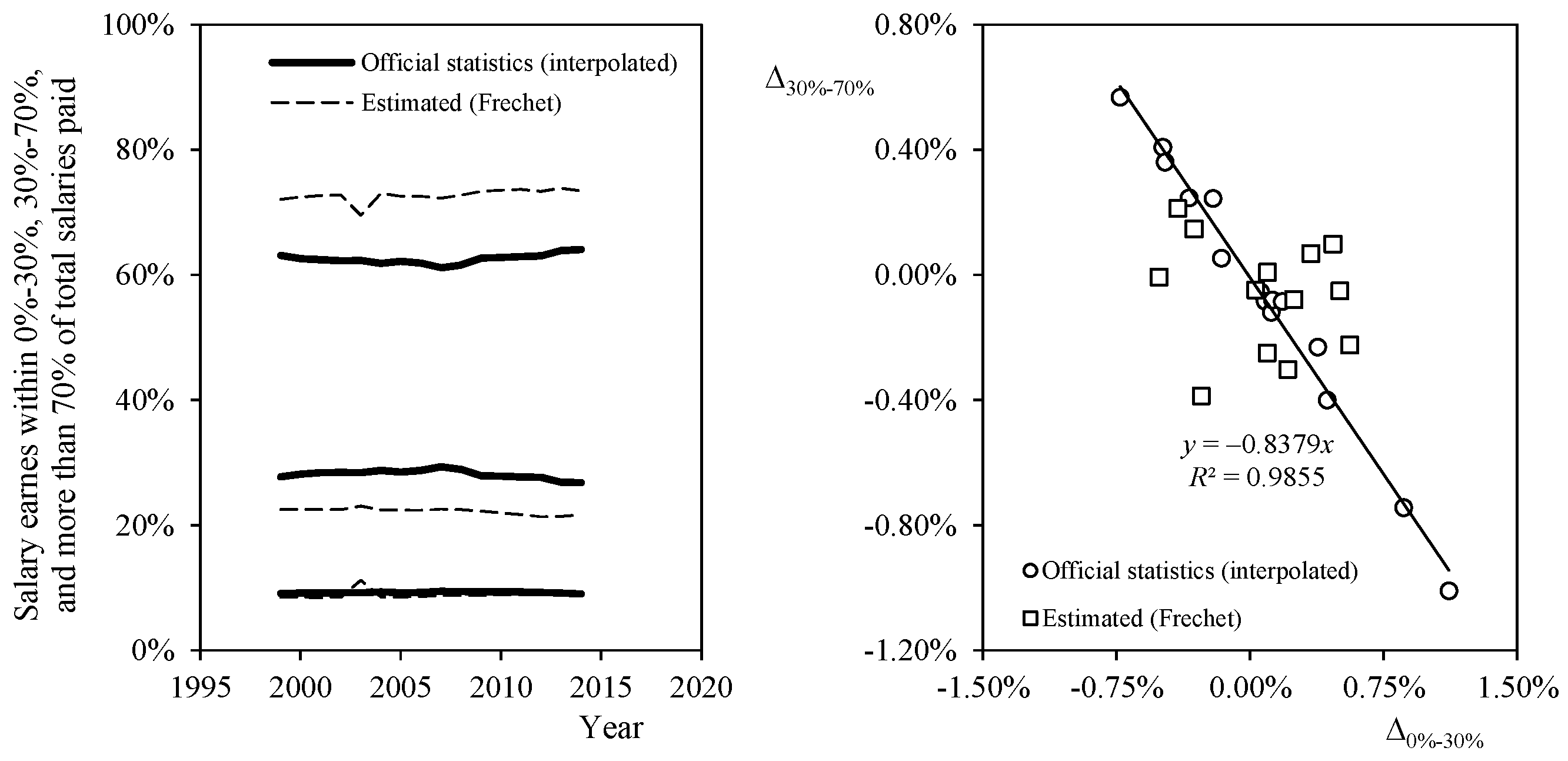
- The analysis of the results showed that changes in the salary distribution as a result of the economy evolution are reflected in the 0%–30% and 30%–70% brackets of the total salaries paid, the top 30% (affecting 9% of the salaried people) being quite resilient to those changes from 2002 to 2014 in Spain.
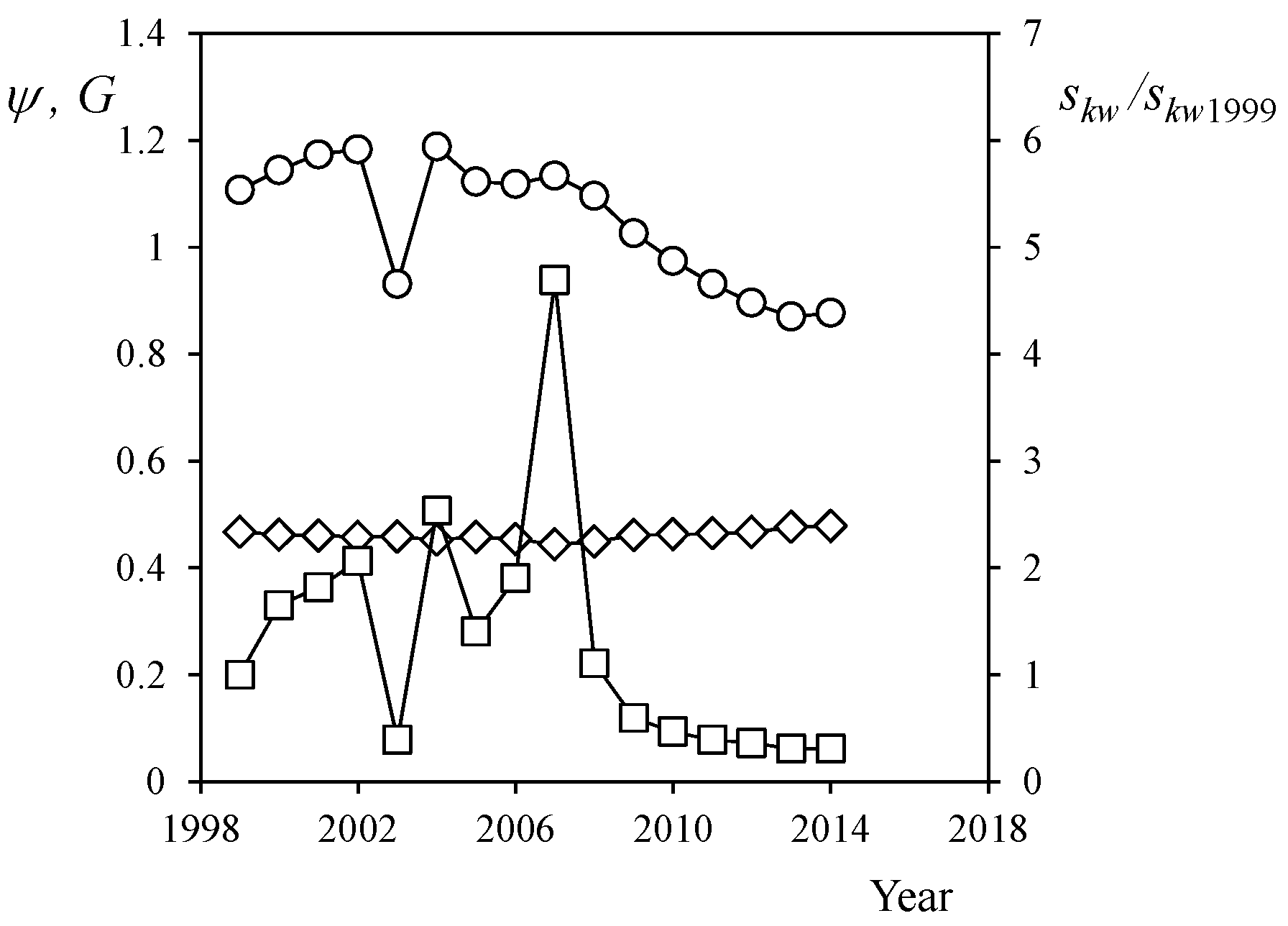
- Finally, the results based on the distributions’ asymmetry (skewness) indicate an increasingly more balanced salaries distribution (i.e., less skewed) starting in 2007. However, this seems to be in contrast with the evolution of the Gini coefficient.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Abbas, Kamran, and Yincai Tang. 2012. Comparison of Estimation Methods for Frechet Distribution with Known Shape. Caspian Journal of Applied Sciences Research 1: 58–64. [Google Scholar]
- Alonso, Mario. 2016. El sector público en España está poco auditado. El País, January 3. Available online: http://economia.elpais.com/economia/2015/12/29/actualidad/1451383564_744232.html (accessed on 21 April 2017).
- Argimón, Isabel, and Ángel Luis Gómez. 2006. Empleo y salarios en las AAPP : Una perspectiva macroeconómica. Revistas. Presupuesto Y Gasto Público 41: 73–92. [Google Scholar]
- Asplund, Rita, and Erling Barth, eds. 2005. Education and Wage Inequality in Europe. A literature Review. Helsinki: ETLA. [Google Scholar]
- Atkinson, Anthony B., and François Bourguignon. 2015. Handbook of Income Distribution. Amsterdam: Elsevier B.V. [Google Scholar]
- Azad, Abul Kalam, Mohammad Golam Rasul, and Talal Yusaf. 2014. Statistical Diagnosis of the Best Weibull Methods for Wind Power Assessment for Agricultural Applications. Energies 7: 3056–85. [Google Scholar] [CrossRef]
- Banerjee, Anand, Victor M. Yakovenko, and T. Di Matteo. 2006. A study of the personal income distribution in Australia. Physica A: Statistical Mechanics and its Applications 370: 54–59. [Google Scholar] [CrossRef]
- Botella, Marta, Pablo Hernández de Cos, and Javier J. Pérez. 2009. Algunas consideraciones sobre los efectos macroeconómicos de los salarios y del empleo de las Administraciones Públicas. Boletín Económico. Banco de España 9: 57–74. [Google Scholar]
- Burkhauser, Richard V., and Kenneth A. Couch. 2009. Intragenerational inequality and intertemporal mobility. In The Oxford Handbook of Economic Inequality. Edited by Wiemer Salverda, Brian Nolan and Timothy M. Smeeding. New York: Oxford University Press, pp. 522–45. [Google Scholar]
- Carmona, René. 2014. Statistical Analysis of Financial Data in R. New York: Springer. [Google Scholar]
- Carrasco, Raquel, Juan F. Jimeno, and A. Ortega. 2015. Returns to Skills and the Distribution of Wages: Spain 1995–2010. Oxford Bulletin of Economics and Statistics 77: 542–65. [Google Scholar] [CrossRef]
- Chotikapanich, Duangkamon, D. S. Rao, and Kam Ki Tang. 2007. Estimating income inequality in China using grouped data and the generalized beta distribution. Review of Income and Wealth 53: 127–47. [Google Scholar] [CrossRef]
- Cran, G.W. 1988. Moment estimators for the 3-parameter Weibull distribution. IEEE Transactions on Reliability 37: 360–63. [Google Scholar] [CrossRef]
- Cubas, Javier, Santiago Pindado, and Marta Victoria. 2014. On the analytical approach for modeling photovoltaic systems behavior. Journal of Power Sources 247: 467–74. [Google Scholar] [CrossRef]
- Cubas, Javier, Santiago Pindado, and Carlos de Manuel. 2014. Explicit Expressions for Solar Panel Equivalent Circuit Parameters Based on Analytical Formulation and the Lambert W-Function. Energies 7: 4098–115. [Google Scholar] [CrossRef]
- De Gusmão, Felipe R. S., and Edwin M. M. Ortega. 2011. The generalized inverse Weibull distribution. Statistical Papers 52: 591–619. [Google Scholar] [CrossRef]
- Dorvlo, Atsu S. S. 2002. Estimating wind speed distribution. Energy Conversion & Management 43: 2311–18. [Google Scholar]
- Espejo, Isabel García, and Marta Ibáñez Pascual. 2007. Los trabajadores pobres y los bajos salarios en España: Un análisis de los factores familiares y laborales asociados a las distintas situaciones de pobreza. Empiria. Revista de Metodología de Ciencias Sociales 14: 41–67. [Google Scholar] [CrossRef]
- Febrer, Antonia, and Juan Mora López. 2004. Wage Distribution in Spain, 1994-1999: An Application of a Flexible Estimator of Conditional Distributions. Alicante: University of Alicante, pp. 1–38. [Google Scholar]
- Fisher, Ronald Aylmer, and Leonard Henry Caleb Tippett. 1928. Limiting forms of the frequency distribution of the largest or smallest member of a sample. Mathematical Proceedings of the Cambridge Philosophical Society 24: 180–90. [Google Scholar] [CrossRef]
- Galindo, Cristina. 2015. Lo que aprendimos de la crisis. El País, December 6. Available online: http://economia.elpais.com/economia/2015/12/03/actualidad/1449157907_637737.html (accessed on 21 April 2017).
- García, Carmelo, Mercedes Prieto, and Hipólito Simón. 2014. La modelización paramétrica de las distribuciones salariales. Revista de Economía Aplicada 22: 5–38. [Google Scholar]
- Goda, Yoshimi, Masanobu Kudaka, and Hiroyasu Kawai. 2010. Incorporating of Weibull distribution in L-moments method for Regional Frequency Analysis of Peak over Threshold wave heights. Paper presented at the 32nd International Conference on Coastal Engineering (ICCE 2010), Shangai, China, June 30–July 5; pp. 1–11. [Google Scholar]
- Jagielski, Maciej, and Ryszard Kutner. 2013. Modelling of income distribution in the European Union with the Fokker–Planck equation. Physica A Statistical Mechanics & Its Applications 392: 2130–38. [Google Scholar]
- Jiménez, Miguel. 2015. El Sueldo Medio Declarado a Hacienda Cae al Nivel Más Bajo Desde 2007. El País, November 18. Available online: http://economia.elpais.com/economia/2015/11/17/actualidad/1447782510_551814.html (accessed on 21 April 2017).
- Jiménez, Miguel. 2015. Los Hombres Acaparan el 82% de los Sueldos Más Altos, Según Hacienda. El País, November 19. Available online: http://economia.elpais.com/economia/2015/11/18/actualidad/1447872182_528635.html (accessed on 21 April 2017).
- Justus, C.G., W. R. Hargraves, Amir Mikhail, and Densie Graber. 1978. Methods for Estimating Wind Speed Frequency Distributions. Journal of Applied Meteorology 17: 350–53. [Google Scholar] [CrossRef]
- Khan, M. Shuaib, G. R. Pasha, and Ahmed Hesham Pasha. 2008. Theoretical analysis of inverse weibull distribution. Wseas Transactions on Mathematics 7: 30–38. [Google Scholar]
- Kleiber, Christian. 2008. A guide to the Dagum distributions. In Modeling Income Distributions and Lorenz Curves. New York: Springer, pp. 97–117. [Google Scholar]
- Kleiber, Christian, and Samuel Kotz. 2003. Statistical Size Distributions in Economics and Actuarial Sciences. Hoboken: John Wiley and Sons. [Google Scholar]
- Klein, Nadja, Thomas Kneib, Stefan Lang, and Alexander Sohn. 2015. Bayesian structured additive distributional regression with an application to regional income inequality in Germany. The Annals of Applied Statistics 9: 1024–52. [Google Scholar] [CrossRef]
- Krause, Melanie. 2014. Parametric Lorenz Curves and the Modality of the Income Density Function. The Review of Income Wealth 60: 905–29. [Google Scholar] [CrossRef]
- Krugman, Paul. 2016. On Invincible Ignorance. The New York Times, March 21. Available online: https://www.nytimes.com/2016/03/21/opinion/on-invincible-ignorance.html?_r=0 (accessed on 21 April 2017).
- Krugman, Paul. 2016. La irreductible ignorancia. El País, March 26. Available online: http://economia.elpais.com/economia/2016/03/23/actualidad/1458724332_015099.html (accessed on 21 April 2017).
- Lubrano, Michel. 2016. The Econometrics of Inequality and Poverty. In Lecture 4: Lorenz Curves and Parametric Distributions. Marseille: Centre National de la Recherche Scientifique, Groupement de Recherche en Économie Quantitative d’Aix-Marseille (GREQAM). [Google Scholar]
- Lun, Isaac Y. F., and Joseph C. Lam. 2000. A study of Weibull parameters using long-term wind observations. Renewable Energy 20: 145–53. [Google Scholar] [CrossRef]
- Machado, José AF, and José Mata. 2005. Counterfactual decomposition of changes in wage distributions using quantile regression. Journal of applied Econometrics 20: 445–65. [Google Scholar] [CrossRef]
- Mandelbrot, Benoit. 1962. Paretian Distributions and Income Maximization. Quarterly Journal of Economics 76: 57–85. [Google Scholar] [CrossRef]
- Mann, Nancy R. 1984. Statistical estimation of parameters of the Weibull and Frechet distributions. In Statistical Extremes and Applications. Dordrecht: Springer, pp. 81–89. [Google Scholar]
- Marek, Luboš, and Michal Vrabec. 2013. Model wage distribution—Mixture Density Functions. International Journal of Economics and Statistics 1: 113–121. [Google Scholar]
- McDonald, James B., and Michael R. Ransom. 1979. Functional forms, estimation techniques and the distribution of income. Econometrica: Journal of the Econometric Society 47: 1513–25. [Google Scholar] [CrossRef]
- McDonald, James B., and Michael Ransom. 2008. The generalized beta distribution as a model for the distribution of income: Estimation of related measures of inequality. In Modeling Income Distributions and Lorenz Curves. New York: Springer, pp. 147–66. [Google Scholar]
- Mendaña Saavedra, Felipe, and Carlos Pindado Carrión. 2013. Relleno con bicomponente del gap de los anillos de dovelas en los escudos no presurizados. Revista de Obras Públicas 160: 21–35. [Google Scholar]
- Orsini, Kristian. 2014. Wage adjustment in Spain: Slow, inefficient and unfair? ECFIN Country Focus 11: 1–8. [Google Scholar]
- Pijoan-Mas, Josep, and Virginia Sánchez-Marcos. 2010. Spain is different: Falling trends of inequality. Review of Economic Dynamics 13: 154–78. [Google Scholar] [CrossRef]
- Piketty, Thomas. 2014. El capital en el siglo XXI. Mexico: Fondo de Cultura Económica. [Google Scholar]
- Pindado, Santiago, Imanol Pérez, and Maite Aguado. 2013. Fourier analysis of the aerodynamic behavior of cup anemometers. Measurement Science and Technology 24: 065802. [Google Scholar] [CrossRef]
- Pindado, Santiago, Javier Cubas, and Felix Sorribes-Palmer. 2015. On the harmonic analysis of cup anemometer rotation speed: A principle to monitor performance and maintenance status of rotating meteorological sensors. Measurement 73: 401–418. [Google Scholar] [CrossRef]
- Rehman, Shafiqur, T. O. Halawani, and Tahir Husain. 1994. Weibull parameters for wind speed distribution in Saudi Arabia. Solar Energy 53: 473–79. [Google Scholar] [CrossRef]
- Rigby, Robert A., and D. Mikis Stasinopoulos. 2015. The Generalized Additive Models for Location, Scale and Shape. Journal of the Royal Statistical Society: Series C (Applied Statistics) 54: 1–2. [Google Scholar] [CrossRef]
- Seguro, J. V., and T.W. Lambert. 2000. Modern estimation of the parameters of the Weibull wind speed distribution for wind energy analysis. Journal of Wind Engineering & Industrial Aerodynamics 85: 75–84. [Google Scholar]
- Selezneva, Ekaterina, and Philippe Van Kerm. 2016. A distribution-sensitive examination of the gender wage gap in Germany. Journal of Economic Inequality 14: 21–40. [Google Scholar] [CrossRef]
- Shatnawi, Dina, Ronald L. Oaxaca, and Michael R. Ransom. 2013. Movin’ on up: Hierarchical occupational segmentation and gender wage gaps. Journal of Economic Inequality 12: 315–38. [Google Scholar] [CrossRef]
- Shittu, Olanrewaju I., and K. A. Adepoju. 2014. On the Exponentiated Weibull Distribution for Modeling Wind Speed in South Western Nigeria. Journal of Modern Applied Statistical Methods Jmasm 13: 431–45. [Google Scholar]
- Sohn, Alexander, Nadja Klein, and Thomas Kneib. 2014. A New Semiparametric Approach to Analysing Conditional Income Distributions. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=2404335 (accessed on 21 April 2017).
- Sohn, Alexander, Nadja Klein, and Thomas Kneib. 2015. A Semiparametric Analysis of Conditional Income Distributions. Schmollers Jahrbuch 135: 13–22. [Google Scholar] [CrossRef]
- Ulgen, Koray, and Arif Hepbasli. 2002. Determination of Weibull parameters for wind energy analysis of Izmir. Turkey. International Journal of Energy Research 26: 495–506. [Google Scholar] [CrossRef]
- Weibull, Waloddi. 1951. A statistical distribution function of wide applicability. Journal of Applied Mechanics 18: 293–97. [Google Scholar]
| 1 | Agencia Tributaria de España. Mercado de Trabajo y Pensiones en las Fuentes Tributarias. http://www.agenciatributaria.es/AEAT.internet/datosabiertos/catalogo/hacienda/Mercado_de_Trabajo_y_Pensiones_en_las_Fuentes_Tributarias.shtml. |
| 2 | Average annual Spanish salary falls to lowest level since 2007 (Jiménez 2015a). |
| 3 | Men account for 82% of highest salaries in Spain, says new report (Jiménez 2015b). |
| 4 | According to Kleiber and Kotz (2003), the Weibull distribution is surrounded by some controversy as the “French would argue that this is nothing else but Fréchet distribution”. |
| 5 | Selezneva and Van Kerm, published another interesting work on gender discrimination in wage distribution in Germany, showing a larger gender gap at the bottom of the distribution (Selezneva and Van Kerm 2016). |
| 6 | This work was dedicated by B. Mandelbrot to Maurice Fréchet, who proposed in 1927 the distribution selected in the present work to study the wages distribution in Spain. |
| 7 | This work by Sohn et al. is the 2014 working version of the 2015 paper ‘A Semiparametric Analysis of Conditional Income Distributions’ (Sohn et al. 2015). |
| 8 | This work, published initially in 2013 in French (and in 2014 in English), was cited more than 4700 times by the end of 2016, according to Google Scholar. |
| 9 | MacDonald and Ransom claim that the GB2 distribution fits the income distributions better than other simpler distributions such as log-normal or Weibull (McDonald and Ransom 2008). |
| 10 | Mario Alonso. President of the Institute of Auditors and the Spanish Accounting (Instituto de Censores Jurados de Cuentas) (Alonso 2016). |
| 11 | The change of the labor market law in 2010 started to be studied in 2008. During two years the government of President Rodríguez Zapatero tried to reach a wide agreement that could include both the employers’ association and the trade unions. |
| 12 | This fact agrees with what Paul Krugman said, quoting a work by Burkhauser and Couch (2009); ‘The majority of economic mobility occurs over fairly small spans of the distribution’. On Invincible Ignorance (Krugman 2016a). Also: La irreductible ignorancia (Krugman 2016b). |
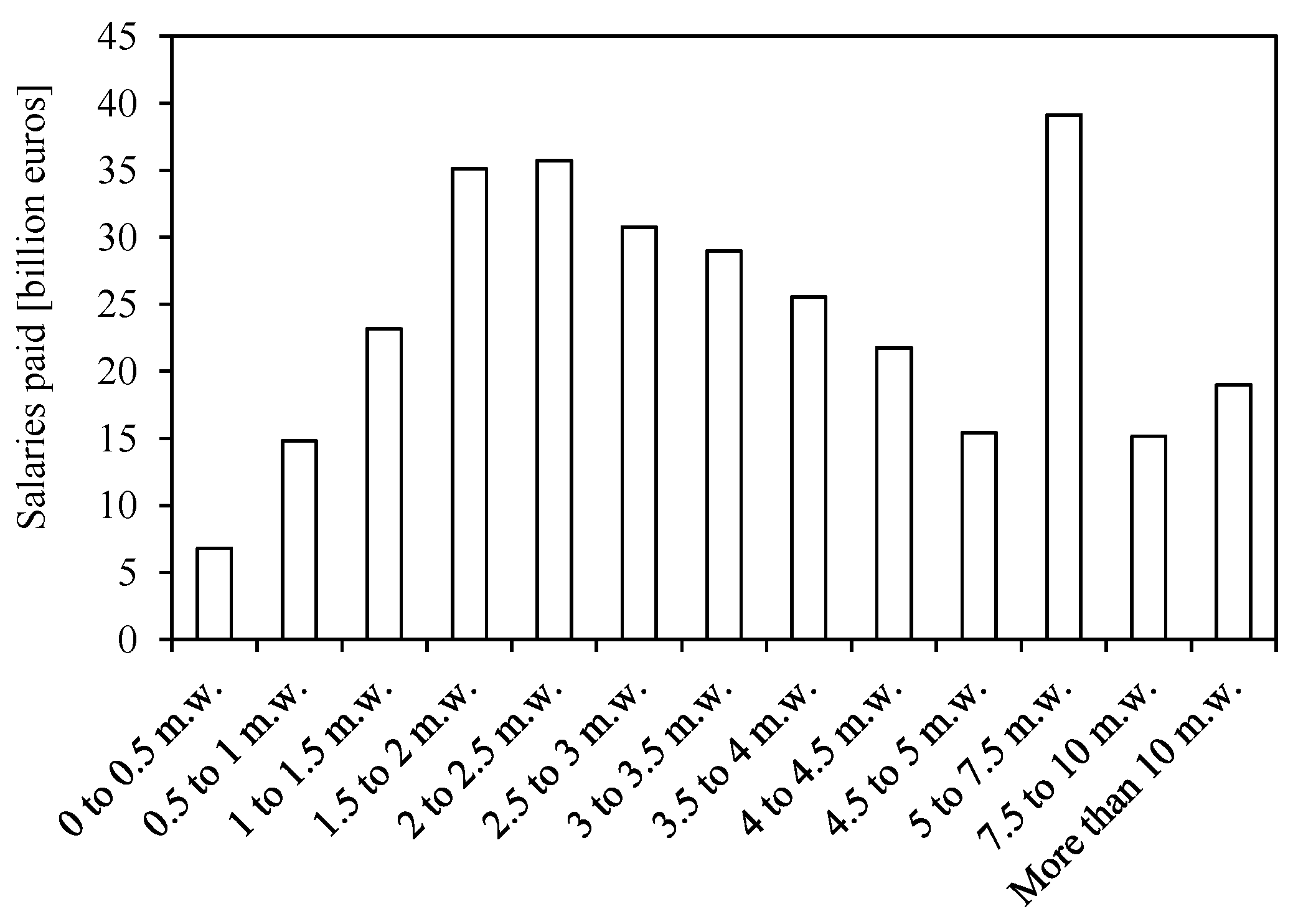
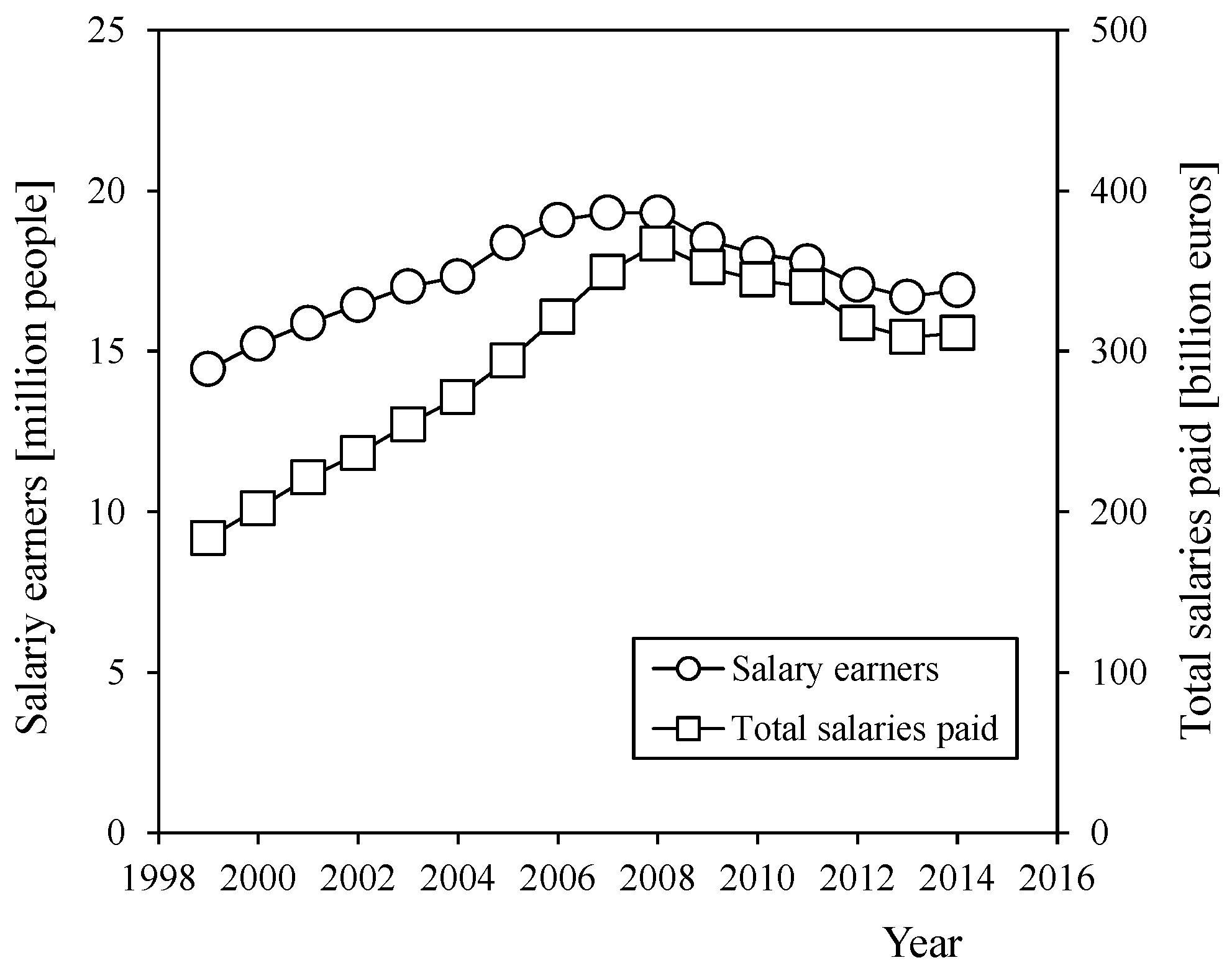

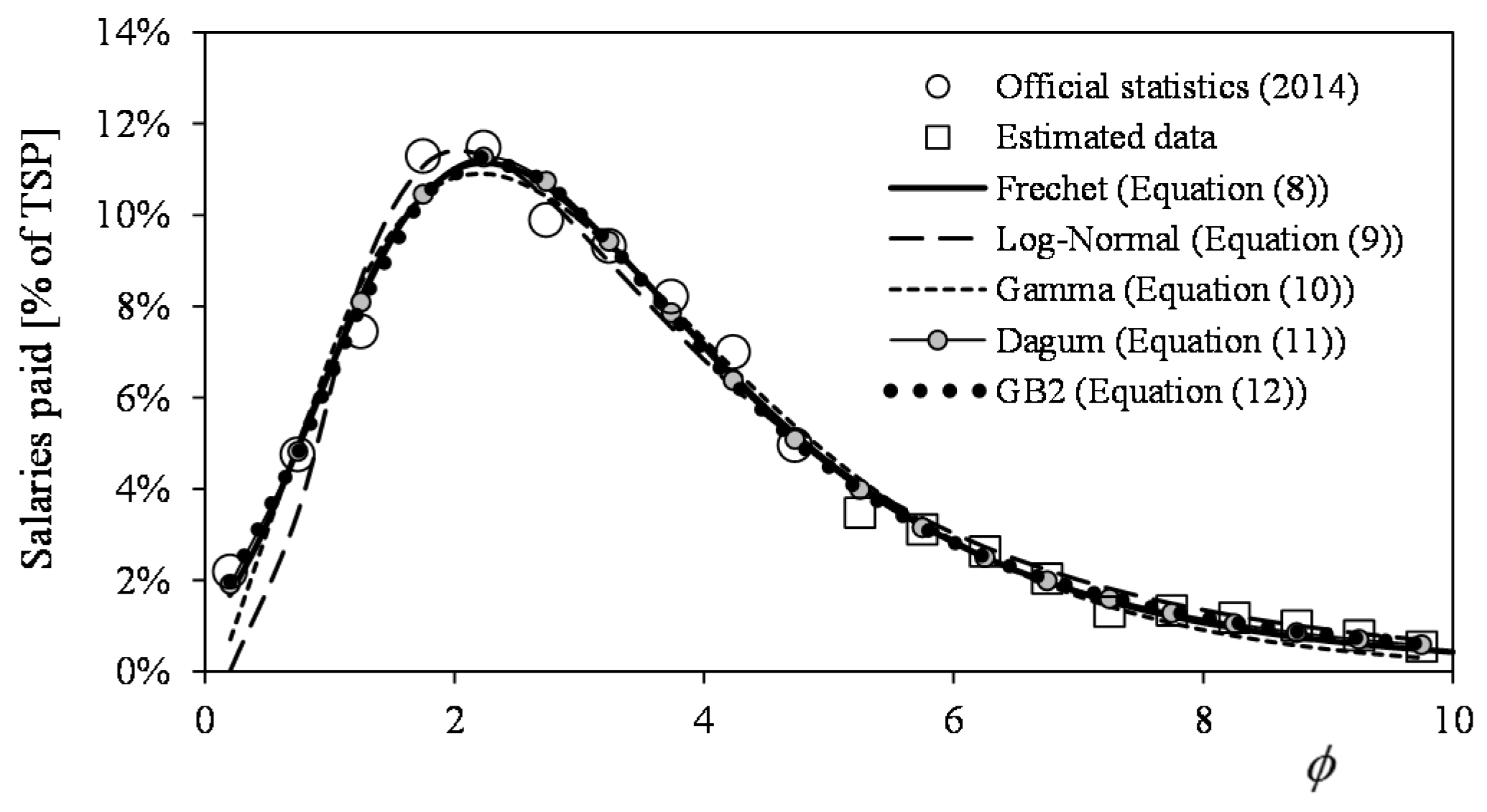

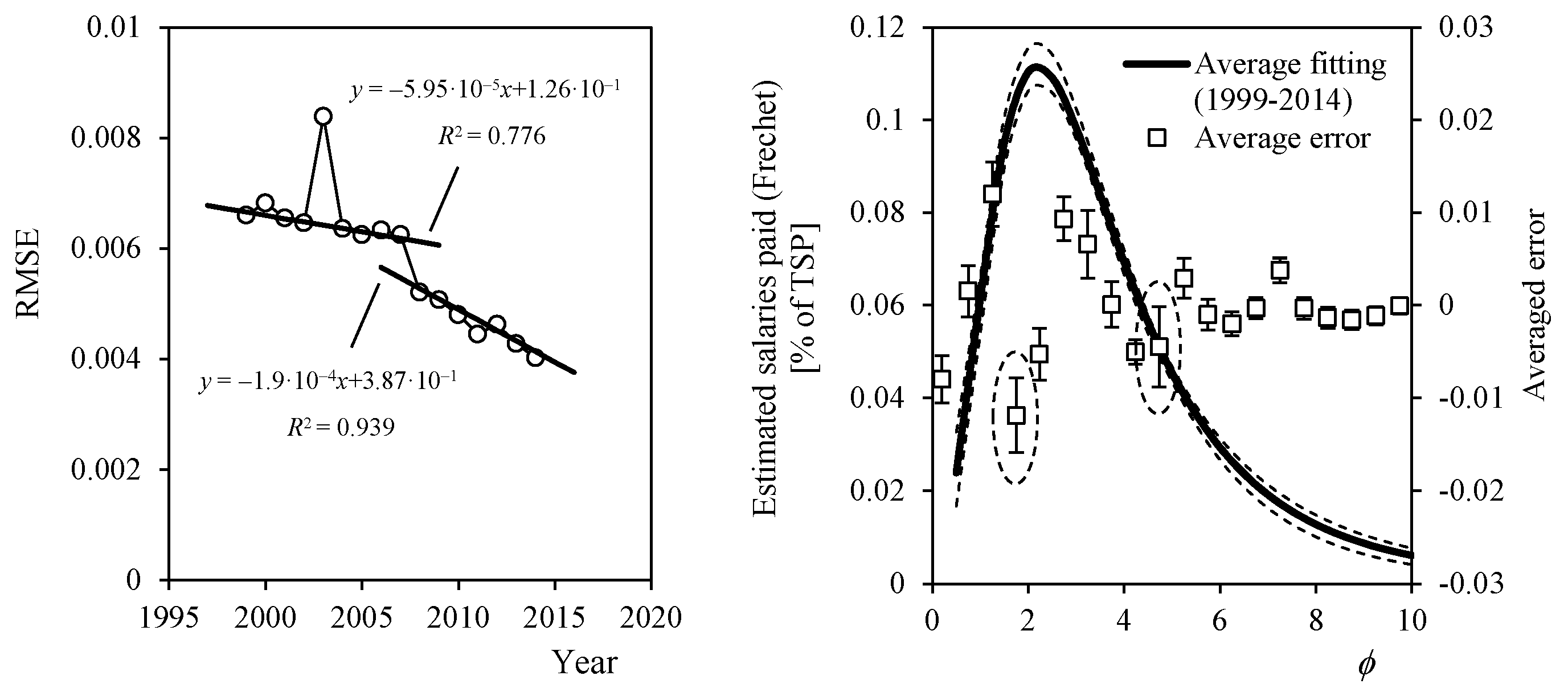

| Income | 1999 | 2000 | 2001 | 2002 | 2003 | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 to 0.5 min. wage | 2.784 | 2.774 | 2.795 | 2.833 | 2.911 | 2.851 | 3.232 | 3.286 | 2.988 | 3.090 | 3.405 | 3.420 | 3.466 | 3.494 | 3.642 | 3.695 |
| 0.5 to 1 min. wage | 1.688 | 1.739 | 1.760 | 1.817 | 1.829 | 1.887 | 2.145 | 2.187 | 2.214 | 2.284 | 2.251 | 2.207 | 2.211 | 2.122 | 2.110 | 2.197 |
| 1 to 1.5 min. wage | 1.743 | 1.819 | 1.839 | 1.870 | 1.872 | 1.970 | 2.211 | 2.359 | 2.492 | 2.481 | 2.284 | 2.215 | 2.175 | 2.051 | 1.982 | 2.047 |
| 1.5 to 2 min. wage | 2.182 | 2.341 | 2.388 | 2.440 | 2.418 | 2.583 | 2.824 | 3.010 | 3.169 | 2.966 | 2.678 | 2.592 | 2.500 | 2.417 | 2.224 | 2.220 |
| 2 to 2.5 min. wage | 1.595 | 1.760 | 1.926 | 2.024 | 2.144 | 2.174 | 2.188 | 2.281 | 2.318 | 2.281 | 2.038 | 1.979 | 1.956 | 1.896 | 1.762 | 1.769 |
| 2.5 to 3 min. wage | 1.033 | 1.114 | 1.215 | 1.282 | 1.374 | 1.399 | 1.411 | 1.467 | 1.528 | 1.548 | 1.430 | 1.389 | 1.373 | 1.344 | 1.251 | 1.244 |
| 3 to 3.5 min. wage | 0.799 | 0.848 | 0.899 | 0.950 | 0.982 | 1.013 | 1.035 | 1.081 | 1.109 | 1.122 | 1.048 | 1.059 | 1.073 | 1.017 | 0.984 | 0.990 |
| 3.5 to 4 min. wage | 0.642 | 0.689 | 0.727 | 0.746 | 0.785 | 0.793 | 0.809 | 0.847 | 0.875 | 0.879 | 0.831 | 0.823 | 0.807 | 0.768 | 0.761 | 0.756 |
| 4 to 4.5 min. wage | 0.524 | 0.548 | 0.579 | 0.605 | 0.641 | 0.643 | 0.639 | 0.657 | 0.677 | 0.689 | 0.654 | 0.641 | 0.630 | 0.553 | 0.567 | 0.569 |
| 4.5 to 5 min. wage | 0.374 | 0.417 | 0.454 | 0.484 | 0.521 | 0.522 | 0.480 | 0.491 | 0.511 | 0.521 | 0.498 | 0.456 | 0.419 | 0.342 | 0.357 | 0.361 |
| 5 to 7.5 min. wage | 0.718 | 0.791 | 0.866 | 0.935 | 1.030 | 1.003 | 0.936 | 0.953 | 0.958 | 0.979 | 0.916 | 0.851 | 0.803 | 0.727 | 0.722 | 0.726 |
| 7.5 to 10 min. wage | 0.205 | 0.224 | 0.247 | 0.265 | 0.290 | 0.282 | 0.263 | 0.267 | 0.276 | 0.277 | 0.250 | 0.236 | 0.225 | 0.201 | 0.195 | 0.197 |
| More than 10 min. wage | 0.143 | 0.156 | 0.177 | 0.187 | 0.204 | 0.199 | 0.187 | 0.185 | 0.194 | 0.194 | 0.168 | 0.156 | 0.149 | 0.133 | 0.125 | 0.128 |
| Total amount | 14.431 | 15.220 | 15.871 | 16.438 | 17.001 | 17.321 | 18.360 | 19.070 | 19.309 | 19.311 | 18.452 | 18.025 | 17.788 | 17.063 | 16.682 | 16.899 |
| Income | 1999 | 2000 | 2001 | 2002 | 2003 | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 to 0.5 min. wage | 3.428 | 3.499 | 3.615 | 3.733 | 3.856 | 4.122 | 4.991 | 5.303 | 5.221 | 5.632 | 6.371 | 6.392 | 6.513 | 6.407 | 6.586 | 6.797 |
| 0.5 to 1 min. wage | 7.363 | 7.746 | 8.002 | 8.424 | 8.659 | 9.420 | 11.542 | 12.440 | 13.320 | 14.420 | 14.684 | 14.571 | 14.789 | 14.203 | 14.216 | 14.791 |
| 1 to 1.5 min. wage | 12.778 | 13.601 | 14.031 | 14.534 | 14.831 | 16.453 | 19.914 | 22.471 | 25.085 | 26.241 | 25.107 | 24.716 | 24.544 | 23.128 | 22.464 | 23.172 |
| 1.5 to 2 min. wage | 22.269 | 24.417 | 25.470 | 26.584 | 26.922 | 30.288 | 35.597 | 39.996 | 44.331 | 43.662 | 40.927 | 40.203 | 39.278 | 37.991 | 35.191 | 35.111 |
| 2 to 2.5 min. wage | 20.731 | 23.326 | 26.059 | 27.944 | 30.219 | 32.280 | 34.993 | 38.500 | 41.291 | 42.758 | 39.756 | 39.181 | 39.223 | 38.002 | 35.558 | 35.704 |
| 2.5 to 3 min. wage | 16.480 | 18.110 | 20.168 | 21.698 | 23.731 | 25.460 | 27.674 | 30.349 | 33.338 | 35.536 | 34.118 | 33.635 | 33.707 | 33.073 | 30.925 | 30.757 |
| 3 to 3.5 min. wage | 15.097 | 16.348 | 17.707 | 19.081 | 20.113 | 21.888 | 24.105 | 26.549 | 28.721 | 30.570 | 29.697 | 30.445 | 31.226 | 29.571 | 28.807 | 28.978 |
| 3.5 to 4 min. wage | 14.007 | 15.329 | 16.516 | 17.279 | 18.533 | 19.749 | 21.738 | 24.008 | 26.151 | 27.623 | 27.164 | 27.292 | 27.099 | 25.768 | 25.710 | 25.547 |
| 4 to 4.5 min. wage | 12.931 | 13.828 | 14.899 | 15.871 | 17.152 | 18.140 | 19.458 | 21.106 | 22.943 | 24.528 | 24.203 | 24.110 | 23.975 | 20.996 | 21.671 | 21.755 |
| 4.5 to 5 min. wage | 10.305 | 11.732 | 13.052 | 14.202 | 15.600 | 16.467 | 16.299 | 17.573 | 19.310 | 20.718 | 20.581 | 19.133 | 17.779 | 14.550 | 15.258 | 15.415 |
| 5 to 7.5 min. wage | 24.948 | 28.028 | 31.311 | 34.474 | 38.690 | 39.767 | 40.058 | 42.975 | 45.575 | 48.938 | 47.509 | 44.870 | 42.974 | 38.942 | 38.911 | 39.099 |
| 7.5 to 10 min. wage | 10.173 | 11.350 | 12.779 | 13.986 | 15.623 | 16.000 | 16.109 | 17.227 | 18.786 | 19.842 | 18.658 | 17.795 | 17.218 | 15.364 | 14.955 | 15.148 |
| More than 10 min. wage | 13.049 | 14.792 | 17.513 | 18.397 | 20.460 | 21.172 | 21.600 | 22.819 | 25.165 | 26.353 | 23.370 | 22.163 | 21.463 | 19.402 | 18.443 | 19.006 |
| Total amount | 183.56 | 202.11 | 221.12 | 236.21 | 254.39 | 271.21 | 294.08 | 321.32 | 349.24 | 366.82 | 352.15 | 344.51 | 339.79 | 317.40 | 308.70 | 311.28 |
| Year | Minumum Wage [€] | Year | Minumum Wage [€] |
|---|---|---|---|
| 1998 | 5725.02 | 2007 | 7988.4 |
| 1999 | 5828.48 | 2008 | 8400 |
| 2000 | 5947.2 | 2009 | 8736 |
| 2001 | 6068.3 | 2010 | 8866.2 |
| 2002 | 6190.8 | 2011 | 8979.6 |
| 2003 | 6316.8 | 2012 | 8979.6 |
| 2004 | 6659.1 | 2013 | 9034.2 |
| 2005 | 7182 | 2014 | 9034.2 |
| 2006 | 7572.6 |
| Year | k1 | k2 | γ | c | d | λ |
|---|---|---|---|---|---|---|
| 1999 | 3.93 | 1.89 | 3.78 | 6.40 | −3.86 | 0.488 |
| 2000 | 4.11 | 1.92 | 3.42 | 5.83 | −3.25 | 0.489 |
| 2001 | 4.21 | 1.95 | 3.37 | 5.78 | −3.15 | 0.486 |
| 2002 | 4.32 | 1.97 | 3.32 | 5.76 | −3.10 | 0.488 |
| 2003 | 4.38 | 2.01 | 6.39 | 10.15 | −7.68 | 0.480 |
| 2004 | 4.55 | 1.98 | 3.25 | 5.62 | −2.95 | 0.487 |
| 2005 | 5.01 | 1.90 | 3.51 | 5.78 | −3.24 | 0.484 |
| 2006 | 5.24 | 1.89 | 3.35 | 5.44 | −2.92 | 0.485 |
| 2007 | 5.27 | 1.90 | 3.13 | 5.06 | −2.54 | 0.486 |
| 2008 | 5.29 | 1.90 | 3.68 | 6.04 | −3.51 | 0.485 |
| 2009 | 5.16 | 1.87 | 4.63 | 7.71 | −5.18 | 0.486 |
| 2010 | 5.10 | 1.84 | 5.41 | 8.78 | −6.29 | 0.483 |
| 2011 | 5.09 | 1.82 | 6.39 | 10.15 | −7.68 | 0.480 |
| 2012 | 4.95 | 1.79 | 6.93 | 10.49 | −8.08 | 0.475 |
| 2013 | 4.87 | 1.78 | 8.62 | 13.61 | −11.18 | 0.479 |
| 2014 | 4.93 | 1.78 | 8.55 | 13.60 | −11.18 | 0.479 |
| Year | φ30% | φ70% | S0%–30% [%] | S30%–70% [%] | S70%-∞ [%] | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| calc. | est. | calc. | est. | calc. | est. | calc. | est. | calc. | est. | |
| 1999 | 2.04 | 2.27 | 4.50 | 4.72 | 63.1 | 72.1 | 27.8 | 22.5 | 9.1 | 8.5 |
| 2000 | 2.07 | 2.30 | 4.56 | 4.79 | 62.6 | 72.4 | 28.2 | 22.6 | 9.2 | 8.5 |
| 2001 | 2.12 | 2.36 | 4.67 | 4.90 | 62.4 | 72.7 | 28.4 | 22.5 | 9.2 | 8.4 |
| 2002 | 2.14 | 2.38 | 4.71 | 4.93 | 62.3 | 72.8 | 28.5 | 22.5 | 9.3 | 8.5 |
| 2003 | 2.01 | 2.23 | 4.29 | 4.48 | 62.3 | 69.5 | 28.4 | 23.1 | 9.3 | 11.2 |
| 2004 | 2.15 | 2.40 | 4.72 | 4.95 | 61.8 | 73.1 | 28.8 | 22.5 | 9.4 | 8.6 |
| 2005 | 2.05 | 2.29 | 4.50 | 4.73 | 62.2 | 72.5 | 28.5 | 22.5 | 9.2 | 8.6 |
| 2006 | 2.03 | 2.27 | 4.45 | 4.69 | 61.9 | 72.6 | 28.8 | 22.4 | 9.3 | 8.7 |
| 2007 | 2.02 | 2.27 | 4.45 | 4.69 | 61.2 | 72.3 | 29.4 | 22.6 | 9.5 | 8.8 |
| 2008 | 2.04 | 2.28 | 4.46 | 4.69 | 61.6 | 72.8 | 29.0 | 22.5 | 9.5 | 8.8 |
| 2009 | 2.04 | 2.26 | 4.42 | 4.62 | 62.7 | 73.3 | 28.0 | 22.3 | 9.3 | 8.8 |
| 2010 | 2.02 | 2.25 | 4.35 | 4.54 | 62.8 | 73.5 | 27.9 | 22.0 | 9.3 | 8.9 |
| 2011 | 2.01 | 2.23 | 4.29 | 4.48 | 62.9 | 73.6 | 27.7 | 21.7 | 9.3 | 9.0 |
| 2012 | 1.97 | 2.20 | 4.18 | 4.37 | 63.0 | 73.4 | 27.7 | 21.4 | 9.3 | 9.0 |
| 2013 | 1.99 | 2.20 | 4.24 | 4.40 | 63.9 | 73.8 | 26.9 | 21.5 | 9.2 | 8.9 |
| 2014 | 1.98 | 2.19 | 4.24 | 4.40 | 64.1 | 73.4 | 26.8 | 21.7 | 9.1 | 8.8 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pindado, S.; Pindado, C.; Cubas, J. Fréchet Distribution Applied to Salary Incomes in Spain from 1999 to 2014. An Engineering Approach to Changes in Salaries’ Distribution. Economies 2017, 5, 14. https://doi.org/10.3390/economies5020014
Pindado S, Pindado C, Cubas J. Fréchet Distribution Applied to Salary Incomes in Spain from 1999 to 2014. An Engineering Approach to Changes in Salaries’ Distribution. Economies. 2017; 5(2):14. https://doi.org/10.3390/economies5020014
Chicago/Turabian StylePindado, Santiago, Carlos Pindado, and Javier Cubas. 2017. "Fréchet Distribution Applied to Salary Incomes in Spain from 1999 to 2014. An Engineering Approach to Changes in Salaries’ Distribution" Economies 5, no. 2: 14. https://doi.org/10.3390/economies5020014
APA StylePindado, S., Pindado, C., & Cubas, J. (2017). Fréchet Distribution Applied to Salary Incomes in Spain from 1999 to 2014. An Engineering Approach to Changes in Salaries’ Distribution. Economies, 5(2), 14. https://doi.org/10.3390/economies5020014






