Abstract
This study investigates the relationship between financial development and economic growth in the Ivory Coast over the period from 1961 to 2014. The final goal of this research is to develop a procedure to identify the effects of financial reforms for the Ivory Coast economic growth. Therefore, to achieve this goal, we first conducted a common component analysis (CCA) on our time series data to create: (1) a variable that would be the most appropriate proxy for the financial development; and (2) a vector of control variables for economic growth. Second, a vector autoregression model (VAR) with restriction was used as an appropriate specification of the dynamic relationship between the proxy of financial development, economic growth and other important factors of that growth (vector of control variables). Results suggest that in the Ivory Coast, growth in financial development is synonymous with the overall economic growth of the national economy. This study addresses the controversy over the appropriate proxy for the financial development in the Ivory Coast and it establishes a causal relationship between the financial development and the national economic growth.
Keywords:
financial development; economic growth; vector autoregression model; common component analysis; causality; Ivory Coast JEL Classification:
B41; C32; E63; G28; O16; O47
1. Introduction
The annual growth rate of real GDP per capita is an important statistical indicator to assess the economic performance of any economy. As a result of this evidence, a large amount of theoretical and empirical studies have attempted to identify the main drivers of economic growth and potential sources of growth. These drivers differ depending on space and time. That said, the evidence of a conclusion is not reached. The debate on the issue of financial development source or effect of economic growth is still current. Another source of debate in the literature on the finance-growth nexus is the appropriate or proper measure of financial development, Adu et al. (2013) [1].
Therefore, the research team would like to highlight the several financial reforms engaged in the Ivory Coast since 2014. The purposes of these reforms are to strengthen the stability of the financial sector and to promote its development, with the final goal to sustain the recent economic growth. The key components of these reforms include the following: (1) restructuring the public banks, (2) strengthening the transparency in financial data handling, (3) deepening the financial market by diversifying the capital market; (4) preserving and increasing the professionalism of the microfinance sector, (5) increasing small and middle-sized enterprises (SMEs) access to credit and to leasing, (6) fostering credit for mortgages, (7) regulating traditional or customary land tenure, (8) organizing producer associations, (9) rationalizing access to guaranty funds and developing a strategy to finance subsistence agriculture, and (10) strengthening the supervision of insurance and broadening insurance coverage to a larger share of the population. It seems to us that these reforms support the idea that financial development would be very important for the economic growth in the Ivory Coast. Based on this assumption, the research team has conducted this study to test the relationship between financial reforms, financial development and economic growth in the Ivory Coast and identify the channels of transition.
In our study, we use techniques of time series. This is the most common approach of the finance-growth nexus in the literature. Furthermore, we have first conducted a common component analysis (CCA) on our time series data of the different financial development proxies, to create a variable that would be the most appropriate proxy for the financial development. In addition, another CCA has been conducted on the other explanatory variables of economic growth, to create a vector of control variables for the economic growth. Secondly, a vector autoregression model (VAR) with restriction was used as an appropriate specification of the dynamic relationship between the proxy of financial development, economic growth and other important factors of that growth (vector of control variables).
The first challenges were encountered early in the research, which has used a variety of Granger causality tests. Most of them support the hypothesis of finance leading to growth. Our study is based on the estimated effects between growths on a large number of indicators of financial development. We do this to solve the problem of appropriate and proper financial development measures. Existing studies have identified several transmission channels through which financial development could affect economic growth through their effects on savings and investment. According to Levine (2002) [2], if given prior information on investment opportunities, monitoring investments and the implementation of corporate governance, trade diversification and risk management, mobilization and accumulation of savings, and the exchange of goods and services; then financial development causes an improvement in production. Each of these financial functions could influence the decisions of savings and investment and thus economic growth.
Since several market frictions and regulatory laws exist, and there are remarkably different policies around the world and through time, improvements in each of the specific situations or dimensions can have different implications for resource allocation and spending for the welfare of others types of frictions involved in the economy. That said, empirical studies show that the hypothesis which states that financial development is an important driver of economic growth, is not popular in empirical research on growth.
The role of the financial market and financial intermediation in economic growth varies significantly from one country to another. It is based on the level of political freedom, protection laws, property rights, and regulations. According to Aghion and Hawitt (2009) [3], the population is willing to save more, allowing access to resources by investors in a country where there are efficient and trustworthy banks rather than in countries where there are banks that waste deposits or cause losses for investors, by granting bad credit or defrauding investors.
Markets and financial institutions help by sharing risks, as well as promoting optimal allocation of risk and return. For example, by collecting the savings of a significant number of the population and the accumulated savings by investing in a wide range of diverse projects. A Deposit Institution (DTI) also allows small savings to take advantage of the law of large numbers and to have a reasonable and safe rate of return. The proper functioning of financial institutions can also help to be an alternative to the agency problem; by monitoring investors and ensuring that they will make productive use of their loans, rather than using them fraudulently or for private consumption. There is virtually a consensus showing that financial development is good for economic growth in exogenous growth prospects and in the endogenous growth perspective. However, there is a large disagreement regarding the indicators of financial development. Besides, what is remarkable for each transmission channel is the specificity of the country, which depends on the difference in policy, legislation and other institutional differences in space and time. The above implication for a respective country yields the use of a large number of financial development indicators, increasing the potential significance of the finance-growth nexus.
This study proposes a time series approach to study the finance-growth nexus in the Ivory Coast. To do this, we first measured a common component of proxies of financial development for a reference proxy. Then, we evaluated the dynamic relationship between the common component and economic growth in the context of a VAR. Several studies of countries using time series were based on one or two indicators of financial development. A study on Ghana (Quartey and Prah, 2008 [4]) examined a causal link that bi-varied between financial development and economic growth using four alternative indicators of financial development. These indicators included the ratio of broad money to GDP, domestic credit to GDP ratio, private credit ratio on GDP, and the ratio of private credit to the domestic credit. Also, in studies of the finance-growth nexus for Ivory Coast, Keho (2005) [5] and Esso (2010) [6] use the ratio of private credit to GDP as the sole indicator of financial development.
However, we believe as other studies in the literature suggest, that a single financial indicator cannot allow us to identify the appropriate proxy for financial development for any given country. The level of financial development in a country must be considered as a composite index derived as many proxies of financial development as possible. Also, in the estimation of our model, we used each indicator one after another to control each of them. Also, we derived a composite index using each proxy information, and then as an indicator of financial development, the common components analysis (CCA) method. As in Adu et al. (2013) [1], we support that the effect of financial development on economic growth is only meaningful with choosing the appropriate proxy. In Adu et al. (2013) [1] study on Ghana, using the ratio of private credit to GDP or sector credit ratio on total private credit. They found a positive and significant effect of financial development on economic growth in Ghana. It is important to note that they are not the same result by using the ratio of the supply of broad money to GDP as a proxy for financial development and that the coefficient of this variable is significantly negative. Thus, the indexes they have created through the principal components analysis method confirm the meaning of the choice of proxy. We believe that the common components analysis is more indicated. This helps us to understand the controversial results in the literature, and therefore studies using a single indicator are not able to identify financial sector variables that produce a positive effect on the improvement of economic growth.
This research highlight that the common component has a significant long run relationship with economic growth in Ivory Coast. The findings indicate that both the deposit ratio of liabilities and the common component cause the economic growth. In other words, the causal link between economic growth and financial development is unidirectional. Furthermore, this study finding addresses the identification of the appropriate proxy for the financial development in Ivory Coast, which is the deposit ratio of liabilities. The structure of this paper is divided as follows: Section 2 presents a literature review; Section 3 describes the methods used in the study; Section 4 presents the results; and finally, Section 5 presents the discussion, conclusions, and policy implications.
2. Literature Review
Schumpeter’s pioneering work in 1911 [7], and the most recent work by Patrick (1966) [8], Goldsmith (1969) [9], MacKinnon (1973) [10], and Shaw (1973) [11], indicate that the relationship between financial development and economic growth remain an important topic in the economic literature. Through cross-sectional data sets, temporal and dynamic panel techniques, several aspects of this relationship have been extensively analyzed in theoretical and empirical work on either a single country or a set of cross-nations, as well as industry and business. Schumpeter (1911) [7] emphasizes the role of financial intermediaries in capital accumulation, evaluation and selection of projects, risk management, monitoring contractors, and facilitating transactions and trade; therefore, they are essential to the promotion of technical innovation and economic growth. Assuming that the size of a financial system is positively correlated with the supply and quality of financial services, Goldsmith (1969) [9] finds a positive correlation between financial development and economic performance in a sample of 35 developed countries. MacKinnon (1973) [10] and Shaw (1973) [11] suggest that government intervention on the development of financial systems is an obstacle in the process of economic growth; then it should be noted that these studies provide the basis for the liberalization of the financial sector in several developing countries, especially the Ivory Coast in the Structural Adjustment Programs (SAPs) impulses by the IMF and the World Bank. In this paradigm, one is tempted to argue that financial development is considered to exert positive effects on economic growth. However, some economists remain skeptical about the decisive role of financial development in the economic growth process. Robinson (1952 [12], p. 52) asks about the unidirectional causality; stating that “it seems for the most part until the enterprise leads, finance follows”. Lucas (1988) [13] estimates that economists insist too badly about the importance of finance, in the overestimating. Chandavarkar (1992 [14], p. 134) noted that "none of the pioneers of development economics have lists finance as a factor of development". In this paradigm, we are tempted to suggest that finance is of very little importance and does not respond passively to economic growth. This criticism argues that the importance of growth in the financial sector is more pronounced in developed countries, with the efficiency and orderly functioning of financial markets than in developing countries where there is dysfunction of the financial sphere.
Instead, Lewis (1955) [15] posits that economic growth initially facilitates the formation of financial markets and then mature financial markets promote economic growth and assuming a two-way relationship between financial development and economic growth exists. Lewis (1955) [15] and Patrick (1966) [8] concluded that the relationship of supply leads are in the early stage of economic development and that also, causality runs from financial development to economic growth, or if the relationship demand leads prevail in the later stage, the causality is reversed. Obviously, there is no consensus from economists regarding the relationship between financial development and economic growth. Therefore, a convenient way to try to resolve these theoretical controversies is the need for empirical study.
Several empirical studies that focus on cross-cutting approaches, have found that the level of financial development is a good predictor of economic growth (e.g., Beck, Levine, and Loayza, 2000 [16]; Gregorio and Guidotti, 1995 [17]; King and Levine, 1993 [18]; Levine, 2002 [2]). A number of works in the recent literature on endogenous growth also promote the positive role that financial intermediaries have played in economic growth (e.g., Amable and Chatelain, 2001 [19]; Bencivenga and Smith, 1991 [20]; Bencivenga, Smith and Starr, 1995 [21]; Benhabib and Spiegel, 2000 [22]). These researchers support the view that financial development may increase the savings rate, stimulate investment, avoid premature capital liquidations, reduce the cost of external financing, improve the efficiency of the allocation capital and ensure more productive technology choices. Each of these factors in their own respect led to strong economic growth.
Alternatively, different models of joint determination of real and financial sectors (e.g., Deidda and Fattouh, 2002 [23]; Odedokun 1996 [24]; Rioja and Valev, 2004 [25]) present a nonlinear relationship between financial development and economic growth, indicating that the financial development is not associated with higher growth rates at all levels of economic development. Although the existence of a positive relationship between financial development and economic growth (Choong and Chan, 2011 [26]), even after taking into account other determinants of growth, has been recognized, the empirical results do not address the issue of direction of causality between finance and growth. Most cross-sectional studies and panel data argue that financial development has a positive influence on growth, even after controlling for other growth variables and the potential biases induced by simultaneous, variables omitted and unobserved country-specific effects on the finance-growth nexus (Khan, 2008 [27]; Gelb, 1989 [28]; Khan and Senhadji, 2003 [29]; King and Levine, 1993 [18]; Levine et al., 2000 [30]).
Levine et al. (2000) [30], for example, in a study of 71 countries, for a period from 1960 to 1995, using the financial development indicators as the ratio of liquid liabilities to GDP, the ratio of deposit money bank assets, the sum of monetary assets, deposit banks and domestic assets of the central banks, and the ratio of loans to the private sector on nominal GDP. They found a positive relationship between financial development and economic growth in these 71 countries. Esso (2010) [6], in a study on Economic Community of West African States (ECOWAS), use a single financial development indicator that is the ratio of credit to private sector to GDP. It concludes for some countries of ECOWAS that financial development leads to growth and, for other countries, the inverse relationship was found. Unlike cross-sectional studies, time series approaches using VAR framework offer the ability to analyze the model of causality and its evolution over time between financial development and economic growth. Most of the time series studies found either unidirectional causality from finance to growth (e.g., Bell and Rousseau, 2001 [31]; Christopoulos and Tsionas 2004 [32]; Fase and Abma, 2003 [33]) or bidirectional causality (e.g., Caldern and Liu, 2003 [34]; Demetriades and Hussein, 1996 [35]; Luintel and Khan, 1999 [36]). These studies also show that causal models vary by country; and therefore, highlight the dangers of statistical inference based on cross-country studies. They warn against the acceptance of the generalization that finance leads the growth and warn against the consequences of bias from economic policies, especially for developing countries. Similar criticism has been advanced by Neusser and Kugler (1998) [37]. Similarly, many endogenous growth models also support a bidirectional relationship between financial development and economic growth (e.g., Berthelemy and Varoudakis, 1996 [38]; Greenwood and Jovanovic, 1990 [39]; Greenwood and Smith, 1997 [40]). Kargbo and Adamu (2009) [41] examine the relationship between financial development and economic growth in Sierra Leone for the period 1970 to 2008. Their results support the hypothesis of finance leading growth in Sierra Leone with the fact that financial development has a significantly positive effect on growth. More importantly, they show that the investment is an important driver via financial development that fuels economic growth. Keho Y. (2005) [5] in a study on the finance-growth nexus in the Ivory Coast only uses the ratio of credit to the private sector as a proxy for financial development in a VAR model, and finds that the credit has no significant effect on growth.
In general, theoretical models and empirical analysis have provided conflicting predictions and implications on the impact of financial development on economic growth and the impact of the global financial development on economic performance. Given the achievement of extraordinary economic performance in recent years in the Ivory Coast, we have a great opportunity to test the hypothesis of Schumpeter empirically; we believe that this study could be informative and complementary to the existing literature on the finance-growth nexus.
3. Methods
Annual data time series are used for this study covering the period from 1961 to 2013, capturing the ante- and post-economic reform and periods of structural adjustment programs for the Ivory Coast. Our data comes from sources, including very recent statistics from the Central Bank of West African States (BCEAO), the West African Economic and Monetary Union (WAEMU), and the World Bank (2012 and 2013) databases.
Following our literature review on the finance-growth link, the empirical specification to capture the impact of financial development on growth in this study is based on the endogenous growth model , where the output variable, real growth, is a function of the real capital stock (a compound of human and physical capital), the savings rate and efficiency of financial intermediation (see Rebelo, 1991 [42]; Pagano, 1993 [43]; Jalil and Ferdun, 2011 [44]). In the context of Jalil and Ferdun (2011) [44], Luintel and Khan (1999) [36], Khan (2008) [27], Keho (2005) [5] and Liang and Teng (2005) [45], we postulate the specific relationship of the next economic growth:
Our indicator for economic growth is , the natural logarithm of real GDP per capita, as in Luintel and Khan (1999) [36] and Levine et al. (2000) [30]. Real GDP per capita is measured by the ratio of real GDP to total population, real GDP is measured by nominal GDP divided by the GDP deflator (1961 = 100). Since the data sources do not provide the GDP deflator, we must estimate through a new construction of implicit deflator, which is calculated using the current value of GDP and GDP index. is a vector of control variables of growth, which includes, (labor force employment), (capital stock with proxy for the gross fixed capital formation of real GDP), (real gross government spending with proxy for the general government final consumption expenditure on GDP), (the level of trade openness of the economy, with proxy total exports and imports to GDP). denotes the real interest rate (with the proxy for the interest rate of deposits deflated the annual inflation rate in %, using the Consumption Price Index as the measure of the price level). is a dummy variable that is 1 in 1993 and 1994. We use this variable to control for the effect of the devaluation of the local currency XOF on the economic aggregates. is a common component of proxies of financial development. It is common in the literature to use ratios for some measure of money stock to GDP as a proxy for financial development. However, the proxy poses significant problems of interpretation because of monetary aggregates: (1) they are over the extent of monetization of financial development, especially in developing countries such as the Ivory Coast; (2) they do not make a differentiation in liability amounts for financial institutions, and (3) they may not represent the current volume of funds channeled to productive sectors (see, Demetriades and Hussein, 1996 [35]; Gregorio and Guidotti, 1995 [17]; Luintel and Khan, 1999 [36]). However, we assume that the size of financial intermediaries is positively related to the availability and quality of financial services. We use the following financial development proxies: , ratio of bank credit (domestic credit of the banking institutions on GDP), , deposit ratio of liabilities (total deposits of the banking institutions’ liabilities to GDP) , credit ratio of private sector (private sector credit to GDP) and , (credits to the private sector on total domestic credit). All our variables are in logarithm, except and .
In terms of prior expectations, literature growth predicted a positive relationship between real output, financial development and the real interest rate (King and Levine, 1993 [18]). The school expressionist represented by MacKinnon (1973) [10] and Shaw (1973) [11] indicates that financial intermediation improves investment; that is the result of an increase in the level of output and a positive real interest rate that deepens financial intermediation through the increase in the volume and value of savings which leads to the increase in output by improving the productivity of capital (Khan 2008 [27]). The expected relationship between real output and the control variables of growth follow from the growth literature and also an empirical issue. We examine each series for the presence of a potential unit root using three tests; the Augmented Dickey and Fuller (1979) (ADF) test [46], the Phillips and Perron (1988) (PP) test [47], and the Kwiatkowski-Phillips-Schmidt-Shin (1992) (KPSS) test [48].
For the estimation of the common component of financial development proxies , we follow the methodology proposed by Lumsdaine and Prasad (2003) [49]. This procedure takes place in three stages.
The first step begins with the measurement of a conditional variance, using a univariate , which is performed as follows:
Equation (1) shows the average specializations with financial development proxy i at time t, the average financial development proxy , is the term of the error, and corresponds to the available information at time t.
Equation (2) that ascends conditional variance is a function of the constant , the term of the ARCH (), and the term of GARCH ().
From each model univariate GARCH (1, 1), we estimate the different conditional variances . We derive the conditional standard deviations , which could be interpreted as a measure of the contribution of temporal variations on fluctuations in the financial development proxies i, on the fluctuations in the common component of the same proxies.
The second step is the construction of the points of the temporal variations , using the conditional standard deviations , as follows,
Finally, in the third step we calculate the common component of financial development proxies, giving
Consistent with Lumsdaine and Prasad (2003) [49], the capital assumption of the methodology is the conditional relative standard deviation in the measure of the degree of commonality of shared fluctuations between different proxies. In other words, the methodology implicitly shows that the shock between the proxies can propagate without restriction in the same directions as the initial shock.
To identify which proxies are most sensitive to the common component of proxies, we calculate individual regressions. Regressing two variables expressed in levels when they are integrated of order one I(1) and they are not co-integrated leads to false results. However, in agreement with Engle and Granger (1987) [50], if a linear combination of integrated series of order one I(1) is stationary (i.e., that the error terms from the long-run equation estimated by OLS is integrated of order zero I(0), then series are co-integrated. In order to conduct this test procedure, we use cointegration tests of Johansen (1988) [51] and with the restriction proposed by Pesaran and Shin (2002) [52].
To examine the direction of causality and the dynamic impact of shocks on the system, we use a VAR. Suppose that the level of may be represented as a non-stationary VAR to p-th order:
According to Hamilton (1994) [53], the VAR (p) can be parameter as:
with a vector (4 × 1) integrated variables of order one I(1); for and ; are matrices of coefficients (5 × 5); are the iid vector of error terms.
From the above, Johansen (1988) [51] and Johansen and Juselius (1992) [54] extracted a trace test and maximum eigenvalue test to identify the existence and the number of co-integrating vectors in the context of a VAR model and Osterwald-Lenum (1992) [55] display the appropriate critical values based on the response surface coefficients from MacKinnon-Haug-Michelis (1999) [56]. If there are co-integrating vectors, this implies that is a rank deficient, then can be decomposed as: with a matrix (4 × ) and a matrix ( × 4). Therefore, the Equation (6) can be rewritten as:
The components are the correlation coefficients of the long-run deviations, indicating the speed of adjustment towards the long-run equilibrium, and the rows of can be interpreted as different co-integrating vectors. Pesaran and Shin (2002) [52] suggest identifying co-integrating vectors through restriction tests, with the just-identified restriction proposed by Johansen (1991) [57] and the over- identified restriction.
Each vector requires at least restrictions and one of them should be the normalization restriction. Restrictions must be based on economic theory. In fact, identified co-integrating vectors could be interpreted as having an economic significance of long-term dynamic relationships.
For illustration, we assume that in our VAR model, there are two co-integrating vectors, which are standardized respectively as the relationship of economic growth and financial development. Following Pesaran and Shin (2002) [52], we need at least four theoretically plausible restrictions on vector to reveal the long-term relationships between the variables:
Two normalization restrictions are simple here: they are the coefficients vector and the coefficients vector . In theory, financial development indirectly affects economic growth. Thus, the restriction is generated by assuming that the coefficient in the first vector of cointegration. In addition, in order to identify the most significant cointegration vector, Wickens (1996) [58] shows that the coefficients of correlation (in our case and ) should be statistically significant and their signs must be negative.
After identifying co-integrating vectors, we test the causality between financial development and economic growth. Johansen and Juselius (1992) [54] show that the test in which there is a restriction on zero is the test of weak exogeneity, while Hall and Milne (1994) [59] also show that the weak exogeneity in a co-integrated system matches a long-term causality. Indeed, if the null hypothesis is rejected, then the vector of economic growth is not weakly exogenous to the vector of financial development. This implies that financial development causes economic growth in the long term. Similarly, if the null hypothesis is rejected, then the vector of the financial development is not weakly exogenous to the vector of economic growth. This means that economic growth causes financial development over the long term. If the null hypothesis is rejected, it means a two-way causal relationship between financial development and economic growth in the long term will prevail.
4. Results
The examination of long-run relationships among financial development, economic growth, and other key growth factors in the Ivory Coast is carried out in four steps. We use a VAR framework depending on the time series characteristics of the dataset. Indeed, we first investigated the order of integration of the variables using standard tests for the presence of unit roots. Next, we extracted the common component of the financial development’s proxies. At the third step, the number of cointegrating vectors is tested using the Johansen maximum likelihood approach while the economically meaningful co-integrating vector is identified through tests of over-identifying restrictions. Finally, the causal relationship between the common component of the financial development’s proxies and economic growth is evaluated through tests of weak exogeneity.
4.1. Summary Statistics, Correlation, and Unit Root Tests
This study uses annual data covering the period 1961–2013. It is well known that the span of the data is more important than the number of observations and there is no interest in the VAR framework by switching from low frequency to high frequency data (see Campbell and Perron, 1991 [60]).
Appendix Table A1 presents the summary statistics of the data. Only LNQC and LNL have increased steadily during the past 53 years. Data also indicates that LNQc correlates positively with LNG (0.5022), LNK (0.5844), LNRCB (0.2751), LNRCSP (0.6508), LNRCSPD (0.6777), and LNRDP (0.2943). However, the correlation between LNQC and both LNL (−0.4803) and LNTR (−0.2889) are negative (see Table A2).
Table A3 summarizes the results of three unit roots tests (ADF, PP, and KPSS) on each of the interested variable. The t-statistics indicate that all of the variables contain unit root except R. However, differencing (LNQC, FD, and Z) once reveals that all the variables are stationary at 1% level of significance. Thus, we have concluded that all series are integrated of order one, or I(1).
4.2. Extraction of the Common Component
The series representing the common component on Equation (4) is shown in Figure 1. The general finding is that the common component of financial development proxies remains negative throughout the time period of the study. However, we notice two phases in the common component of financial development in the Ivory Coast. A first phase from 1961 to the late 1983s is marked by a relative strong financial development. The second phase marked by a drop in the financial development from the 1980s until now. The time periodsfrom the 1980s is known as the period of multiple economic and financial policies implementations in the Ivory Coast. Among these policies are the devaluation of the country’s currency and the different SAPs implementation. The civil war, from 2002 through 2011, may have also been a cause of the decrease in financial development. However, we must remark that the common component contains only two proxies of financial development. We had opted for four flights in our methodology. The common component with four proxies does not theoretically provide significant results. The common component constructed with two proxies (INRDP and LNRCB) provided much better results both theoretically and empirically.
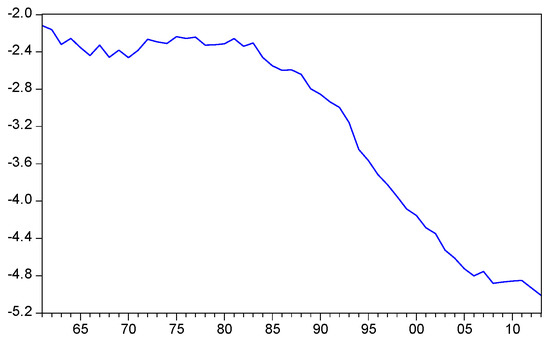
Figure 1.
Series representing the common component (The vertical line for the Financial Development and the horizontal line for the time horizon).
4.3. Common Component and Proxies of Financial Development
Regression results show that the proxy LNRDP and LNRCB are the most responsive to the common component of the financial development’s proxies; whereas, the other financial development’s proxies are least responsive with the common component. Furthermore, the proxies LNRDP and LNRCB are the best proxies’ followers of the common component in contrast with other proxies of financial development.
4.4. Common Component of Financial Development Proxies and Economic Growth
For the estimation purpose of a Vector Error Correction (VEC) model, two approaches are available. The first one is the Johansen (1988) [51] approach which is used when all variables in the endogenous vector are integrated of the same order. The second approach that we can use is the Pesaran et al. (2001) [61] approach. This is better when the variables of the endogenous vector do not have the same integration order. We then focus on the Johansen method. Our endogenous vector components are all integrated of one order I(1). The first step of this approach is to estimate a VAR model on the endogenous vector without differentiation.
where , is a set of exogenous variables (Dum9394, and ). This estimation aims to calculate the optimal lag (order of the VAR). Thus the VEC order is . After the estimation of the optimal order of the VAR, we should run the trace and maximum eigenvalue tests (Johansen, 1988 [51] and Johansen and Juselius, 1992 [54]). These two tests allow us to conclude about the existence and the number () of long run relationships in the endogenous vector. Once we estimate this number of long run relationships (, where 3 denotes the dimension of our endogenous vector), we can estimate the following VEC:
where denotes the residual of the j-th long run equation.
The last step is to test the stability of the VEC, the non-serial correlation (Breusch-Godfrey Lagrange Multiplier “LM” test), the homoscedasticity of residuals (the White homoscedasticity test with and without cross-terms), and the normality (Jarque Bera multivariate normality test based on Cholesky decomposition). This last test is useful but not compulsory (Gonzalo, 1994 [62]).
4.5. Empirical Results
The estimations are done following the steps described in the section above. The lag length test on the models allows us to conclude to a Vector Error Correction Model (VECM) with lag two for the models with common component, lag one for the model with “LNRDP”, and lag four for the models with “LNRCB” (see Appendix Table A4, Table A5 and Table A6). The cointegration test, with the right lag, leads to the conclusion that there is one long run relationship in each model (see Appendix Table A7). The selected models are (1) a VECM with intercept and no trend in the long run equation, and no intercept in the short term equation for the VECM with the common component, (2) a VECM with trend and intercept in the long run equation and short term equation for the VECM with “LNRDP”, and (3) a VECM with trend and intercept in the long run equation, and intercept with no trend in the short term equation for the VECM with “LNRCB”. Note that all estimated models fulfill the hypothesis of stability (see Appendix Table A5) and the independent and identically distributed assumption on residuals (see Appendix Table A4).
Table 1 summarizes the long run equations estimates. Financial development variables coefficients are used as normalization coefficients (see Table 1). These estimates highlight a significant long run relationship between economic growth and all selected financial development indicators.

Table 1.
Long-run equations (three models).
Table 2 contains estimations of all VECM. The long run residuals coefficients are negative and significantly different from 0 for at least one component of the endogenous vector in each VECM. That is consistent with the theory on VECM. It confirms that the VECM specification is well suited for our purpose. Due to identification problems, estimated coefficients in the short term equations cannot be interpreted directly. Thus, we compute Granger causality tests, impulsive responses to shocks and variances decomposition to discuss our results.

Table 2.
VECM estimated coefficients (three models).
4.6. Causality Tests
Granger (1969) [63] lag causality refers to the predictability. X is causal for Y if taking into account the lag values (history) of the variable X helps to predict the value of the variable Y. Table 3 gives the results of the Granger causality test from economic growth to financial development indicators and Table 4 gives the results of the Granger causality test from financial development indicators to economic growth.

Table 3.
Causality tests for LNQC to financial development indicators

Table 4.
Causality tests from financial development indicators to growth.
As we can see from Table 3, the only one indicator of financial development that is caused by growth is “LNRCB”. Both “LNRDP” and the common component cause economic growth, and “LNRCB” does not cause economic growth. This means that the causal links between economic growth and each financial development indicator are unidirectional. Economic growth causes “LNRCB” and “LNRCB” is not causal for economic growth. The common component and “LNRDP” cause economic growth but are not caused by economic growth. This finding is consistent with the literature (e.g., Beck, Levine, and Loayza, 2000 [16]; Gregorio and Guidotti, 1995 [17]; King and Levine, 1993 [18]; Levine, 2002 [2]; Adu et al., 2013 [1]).
4.7. Variances Decomposition and Impulsive Responses Analysis
Variances decomposition is related to standard errors of prediction. For each variable of the endogenous vector, we decompose standard errors of prediction into three parts due to each variable of the endogenous vector. For the VECM with the common component as a financial development indicator, the standard errors of the prediction of the common component are mostly (up to 60%) due to the common component to the 10th period. After that, around half of the standard errors are due to both common component and economic growth. However, standard errors of predictions of economic growth are due to economic growth (around 80% all over prediction period), see Table 5.

Table 5.
Variances decomposition in VECM with the common component (FD).
For the VECM with “LNRCB” as financial development indicator; standard errors of prediction of “LNRCB” are mostly due to “LNRCB” until the 8th period of projection and to economic growth from the 8th to the 15th period of projection. However, the standard errors of prediction of economic growth are mostly due to the financial indicator “LNRCB” (over around 60% on the prediction period), see Table 6.

Table 6.
Variances decomposition in VECM with the LNRCB.
When we take “LNRDP” as the financial indicator, the financial indicator prediction of standard errors are mostly due to the indicator itself. In this model, we can see that the standard errors of the economic growth prediction are due to variation in economic growth to the 10th period of prediction and after that, it is the indicator “Z” for which impact is more important on prediction of standard errors (see Table 7).

Table 7.
Variances decomposition in VECM with the LNRDP.
The impulse responses analysis focuses on the effect of an external shock on one of the endogenous variables of the vector on the others over time, using the generalized impulse decomposition procedure developed by Pesaran and Shin (1998) [64]. We chose to analyze these impulses responses on 15 periods since the shock occurs. As we can see in the first column of graphs in Figure 2, an external positive shock on the financial indicator (common component) increases economic growth during the first three years. After these years, the growth declines to reach its initial level two years after. However, its impacts on financial development have a J-curve trend but remain stable after 8 years. However, an external positive shock on economic growth produces positive effects on financial development that continues increasing after the shock. This finding remains slightly consistent if we focus on the VECM with “Lnrcb” as a financial indicator (see Figure 3). However, a positive shock on the financial development indicator leads to an increasing effect of this indicator.
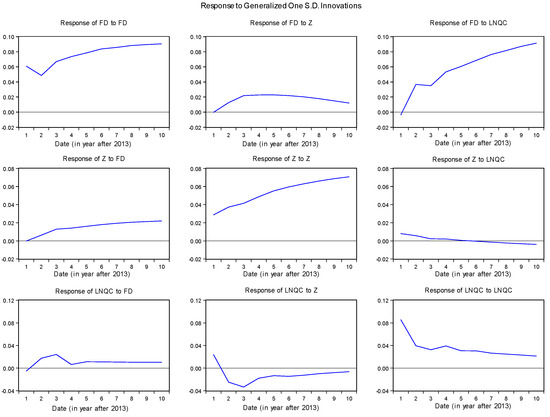
Figure 2.
Impulse responses on the VECM with common component.
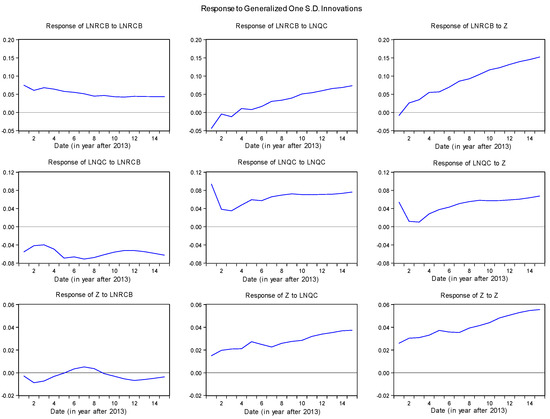
Figure 3.
Impulse responses on the VECM with LNRCB.
In contrast, when we focus on the VECM with “Lnrdp” as the financial indicator (see Figure 4), we can see that a positive shock on the economic growth leads to a decrease of the financial indicator, while a positive shock on the financial development indicator leads to the same impact on the economic growth as in the first two models, i.e., an increase of economic growth.
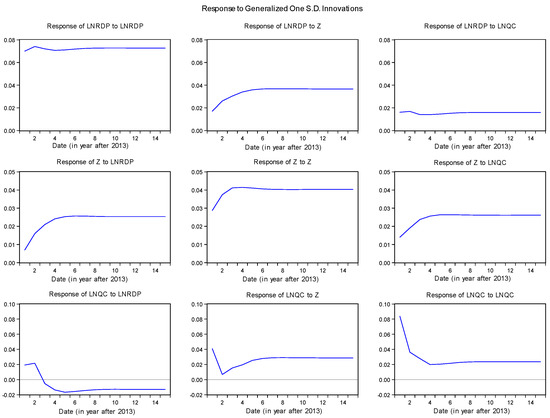
Figure 4.
Impulse responses on the VECM with LNRDP.
5. Conclusions and Policy Implications
This paper analyzes the relationship between the financial development and the economic growth in the Ivory Coast, using annual data from 1961 to 2013. We constructed the common component of four financial indicators to represent the financial development, of which only two were retained: the ratio of bank credit (domestic credit of the banking institutions on GDP) and the deposit ratio of liabilities (total deposits of the banking institutions’ liabilities to GDP). The common component procedure used in this work was developed by Lumsdaine and Prasad (2003) [49]. The dynamic relationships between the common component of the financial development and the economic growth in Ivory Coast, which are of significant concern to policy makers, were also established.
The common component has a significant long run relationship with economic growth in the Ivory Coast. The results indicate that both the deposit ratio of liabilities and the common component cause the economic growth in that country. In other words, the causal link between economic growth and financial development is unidirectional. In addition, our results address the identification of the appropriate proxy for the financial development in the Ivory Coast, which is the deposit ratio of liabilities.
The findings of this study help to understand the conflicting results in the literature as many studies rely on single indicators, and hence are unable to identify which financial sector variables have positive growth-enhancing effects and which do not. Accounting for the structural break in the model did not significantly change the results, implying robustness of our estimates. Furthermore, these findings have implications on the program of the Ivorian government in terms of the development of a sustainable economic growth program.
A number of recommendations can be drawn from this work. Firstly, we recommend caution in the choice of financial development indicators as policy instruments, particularly an emphasis on the deposit ratio of liabilities in the design and implementation of growth policies. On the basis of the evidence in this study, policies that improve access to affordable credit by the private sector, including small and medium enterprises (SMEs), would spur the needed innovation, expansion in the capacity of the agricultural sector, the industry and manufacturing companies to generate the expected employment levels, household incomes and the overall economic growth. Secondly, our findings also indicate that expansionary fiscal results could be inimical to economic growth. The Ivorian government should reduce macroeconomic uncertainty by taming inflation towards growth-enhancing targets while promoting policies to reduce high lending interest rates on credit as well. Finally, the Ivorian government should adopt to the following course of actions to protect the Ivorian from an abrupt increase in prices: (1) enact or expand conditional cash transfer programs, (2) provide short to long-term employment opportunities to marginalized Ivorian people (such as the youth), and (3) intensify the monitoring of prices of certain goods and services and impose stiffer penalties on violators.
Since the temporal framework of this study does not cover the recent years (2015−2016), we need to highlight that the Ivory Coast is engaged in several financial reforms. The authorities started to implement these reforms in 2014, in order to strengthen the stability of the financial sector and to promote its development. The key components of these reforms include the following: (1) restructuring the public banks, (2) strengthening the transparency in financial data handling, (3) deepening the financial market by diversifying the capital market; (4) preserving and increasing the professionalism of the microfinance sector, (5) increasing small and middle-sized enterprises (SMEs) access to credit and to leasing, (6) fostering credit for mortgages, (7) regulating traditional or customary land tenure, (8) organizing producer associations, (9) rationalizing access to guaranty funds and developing a strategy to finance subsistence agriculture, and (10) strengthening the supervision of insurance and broadening insurance coverage to a larger share of the population. It seems to us that these reforms support the idea that financial development would be very important for the economic growth in the Ivory Coast. Conclusions reveal that the points 1, 2, 3, and 5 among the reforms undertaken, are in line with the findings of this paper.
Acknowledgments
The authors would like to express their sincere thanks to the Florida State University Center for Economic Forecasting and Analysis (CEFA), the University Alassane Ouattara (Bouake-Ivory Coast), and the University of Cergy-Pontoise (France), and the ENSEA (Côte d’Ivoire) for their support on this portion of the project. The authors would also like to express their gratitude to Julie Harrington and Vakaramoko Diaby for their guidance and advices in the development of this paper.
Author Contributions
The paper is a joint contribution of all co-authors.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
I Descriptive Statistics on Key Variables

Table A1.
Summary statistics.
| LNQC | LNG | LNK | LNL | LNRCB | LNRCSP | LNRCSPD | LNRDP | LNTR | R | |
|---|---|---|---|---|---|---|---|---|---|---|
| Mean | 6.19 | −2.12 | −8.01 | 3.81 | −1. 3 | −1.44 | −0.14 | −8.44 | −0.3 | 1.03 |
| Median | 6.19 | −2.10 | −8.42 | 3.98 | −1.36 | −1.58 | −0.21 | −8.44 | −0.31 | 0.75 |
| Max | 6.61 | −1.70 | −5.83 | 4.22 | −0.67 | −0.86 | 0.19 | −8.14 | 0.36 | 9.67 |
| Min | 5.70 | −2.74 | −9.66 | 2.99 | −1.82 | −1.99 | −0.49 | −8.7 | −0.59 | −8.69 |
| Std. dev | 0.19 | 0.32 | 1.22 | 0.39 | 0.35 | 0.38 | 0.22 | 0.13 | 0.20 | 2.49 |
| Skew. | 0.09 | −0.35 | 0.36 | −0.68 | 0.28 | 0.17 | 0.19 | 0.20 | 1.17 | −0.61 |
| Kurtosis | 2.73 | 1.79 | 1.59 | 1.99 | 1.71 | 1.46 | 1.55 | 2.97 | 4.60 | 9.75 |

Table A2.
Data correlation summary.
| LNQC | LNG | LNK | LNL | LNRCB | LNRCSP | LNRCSPD | LNRDP | LNTR | R | |
|---|---|---|---|---|---|---|---|---|---|---|
| LNQC | 1.00 | |||||||||
| LNG | 0.50 | 1.00 | ||||||||
| LNK | 0.58 | 0.32 | 1.00 | |||||||
| LNL | −0.48 | −0.18 | −0.98 | 1.00 | ||||||
| LNRCB | 0.28 | 0.74 | −0.19 | 0.33 | 1.00 | |||||
| LNRCSP | 0.65 | 0.91 | 0.35 | −0.22 | 0.82 | 1.00 | ||||
| LNRCSPD | 0.68 | 0.37 | 0.90 | −0.89 | −0.19 | 0.40 | 1.00 | |||
| LNRDP | 0.29 | 0.66 | 0.24 | −0.15 | 0.42 | 0.54 | 0.25 | 1.00 | ||
| LNTR | −0.29 | −0.22 | −0.50 | 0.47 | −0.15 | −0.36 | −0.39 | 0.18 | 1.00 | |
| R | −0.15 | −0.05 | −0.23 | 0.24 | 0.08 | −0.07 | −0.26 | −0.03 | 0.23 | 1.00 |
II Unit Root Tests
The values are the t-statistics and we use the Mackinnon (1996) [65] one-sided p-values. ADF and PP tests have null hypotheses of unit root in the series while KPSS test has null hypothesis of no unit root in series. The test equations included trend and intercept. Lag lengths were based on Schwarz’s (1978) [66] Information Criterion. For the PP test, the optimal bandwidth using Newey-West was applied.

Table A3.
Unit root tests on variables.
| Variable | ADF Test Statistic | PP Test Statistic | KPSS Test Statistic | Variable Type |
|---|---|---|---|---|
| LNQ | −3.09 | −3.09 | 0.15 | Not I(0) |
| FD | −1.63 | −1.77 | 0.19 | Not I(0) |
| Z | −1.71 | −1.69 | 0.18 | Not I(0) |
| R | −7.82 | −17.99 | 0.16 | I(0) |
| ΔLNQ | −7.91 | −8.05 | 0.08 | I(1) |
| ΔFD | −5.63 | −5.70 | 0.15 | I(1) |
| ΔZ | −4.57 | −4.61 | 0.18 | I(1) |
III Lag Length Test
The rows that contain values with maximum stars (*) indicate the significance levels of lag to be considered in a VAR model. Note that for a VECM, the optimal lag will be that of the VAR minus one.

Table A4.
Lag length for the VECM with LNRCB.
| Lag | LogL | LR | FPE | AIC | SC | HQ |
|---|---|---|---|---|---|---|
| 0 | 63.42372 | NA | 2.08 × 10−5 | −2.267655 | −1.916805 | −2.135068 |
| 1 | 221.2801 | 276.2487 | 4.22 × 10−8 | −8.470004 | −7.768304 * | −8.204831 * |
| 2 | 228.3431 | 11.47743 | 4.62 × 10−8 | −8.389298 | −7.336747 | −7.991537 |
| 3 | 235.5617 | 10.82785 | 5.08 × 10−8 | −8.315071 | −6.911670 | −7.784724 |
| 4 | 243.8667 | 11.41940 | 5.40 × 10−8 | −8.286113 | −6.531863 | −7.623179 |
| 5 | 260.1987 | 20.41492 * | 4.18 × 10−8 * | −8.591611 * | −6.486510 | −7.796090 |
Notes: LogL, Log likelihood; LR, Log Likelihood Ratio test statistic; FPE, Final Prediction Error; AIC, Akaike Information Criterion; SC, Schwarz Information Criterion; HQ, Hannan Quinn Information Criterion.

Table A5.
Lag length for the VECM with lnrdp.
| Lag | LogL | LR | FPE | AIC | SC | HQ |
|---|---|---|---|---|---|---|
| 0 | 97.71034 | NA | 5.37 × 10−6 | −3.620830 | −3.273353 | −3.488998 |
| 1 | 225.7382 | 224.7019 | 4.19 × 10−8 | −8.479110 | −7.784155 * | −8.215445 * |
| 2 | 236.6028 | 17.73819 * | 3.91 × 10−8 * | −8.555217 * | −7.512786 | −8.159720 |
| 3 | 245.2953 | 13.12739 | 4.03 × 10−8 | −8.542665 | −7.152756 | −8.015335 |
| 4 | 251.7642 | 8.977282 | 4.61 × 10−8 | −8.439356 | −6.701970 | −7.780194 |

Table A6.
Lag length for the VECM with common component
| Lag | LogL | LR | FPE | AIC | SC | HQ |
|---|---|---|---|---|---|---|
| 0 | 19.42776 | NA | 0.000131 | −0.425623 | −0.078146 | −0.293791 |
| 1 | 226.4512 | 363.3473 | 4.07 × 10−8 | −8.508214 | −7.813260 * | −8.244549 * |
| 2 | 238.0555 | 18.94565 | 3.69 × 10−8 | −8.614509 | −7.572077 | −8.219011 |
| 3 | 249.8621 | 17.83048 * | 3.35 × 10−8 * | −8.729066 * | −7.339158 | −8.201737 |
| 4 | 257.7135 | 10.89584 | 3.62 × 10−8 | −8.682185 | −6.944799 | −8.023023 |
IV Cointegration Tests
In the three models below, we reject the hypothesis of no cointegration and cannot reject the hypothesis of one cointegration. Thus we can estimate, for each of these three models, one long run relationship.

Table A7.
Cointegration tests (three models).
| Models | Hypothesized No. of CE(s) | Eigenvalue | Trace Statistic | 0.05 Critical Value | Prob.** |
|---|---|---|---|---|---|
| VECM with common component (FD) | None * | 0.428183 | 46.91313 | 35.19275 | 0.0018 |
| At most 1 | 0.195912 | 18.96635 | 20.26184 | 0.0746 | |
| At most 2 | 0.148947 | 8.064019 | 9.164546 | 0.0806 | |
| VECM with LNCRB | None * | 0.452736 | 52.75848 | 42.91525 | 0.0039 |
| At most 1 | 0.321921 | 23.82291 | 25.87211 | 0.0881 | |
| At most 2 | 0.102210 | 5.175296 | 12.51798 | 0.5714 | |
| VECM with LNRDP | None * | 0.353990 | 38.32457 | 35.01090 | 0.0213 |
| At most 1 | 0.252693 | 16.04059 | 18.39771 | 0.1036 | |
| At most 2 | 0.022974 | 1.185364 | 3.841466 | 0.2763 |
Notes: * number of cointegration relationship selected. We reject the hypothesis of no cointegration relationship but we do not reject the hypothesis of “at most 1”; ** p-value.
V Models Validation
There are two major tests to conduct: the residuals test and the stability test. Residuals tests are summarized in Table A4. The white heteroscedasticity test on the three estimated models reveals that residuals are homoscedastic in all models. The Breusch-Godfrey LM test for non-autocorrelation on the residuals leads to the conclusion that there are no serial correlations in residuals. For the normality test, the applied Jarque Bera test reveals that a part of the model with “LNRDP”, the other two estimated models meet the normality hypothesis. However, the model with “LNRDP” has no normally distributed residuals and is not weak for estimated coefficients or post estimation tests (Gonzalo, 1994 [62]). Thus, the residuals series for the estimated models have good properties.

Table A8.
Hypothesis tests on residuals (three models).
| Residual Tests ** | VEC with “LNRCB” | VEC with “LNRDP” | VEC with the Common Component |
|---|---|---|---|
| Normality test * | 0.9985 | 0.0451 | 0.3295 |
| Homoscedasticity + | 0.3493 | 0.2770 | 0.3112 |
| Non autocorrelation ++ | 0.1720 | 0.7061 | 0.3837 |
** p-values are reported in table * Null hypothesis of normality is rejected if the p-value is under 0.05 + Null hypothesis of homoscedasticity is rejected if the p-value is under 0.05. ++ Null hypothesis of non-autocorrelation is rejected if the p-value is under 0.05
The stability test consists of a comparison of all modulus of the roots of the VECM with the number one (1). Note that all modulus, apart from the first two larger moduli, must be less than one (1). The results in Table 12 show that, except for the first two roots, the other AR roots moduli are lower than one. That insures the VECM stability.

Table A9.
Stability of VECM: AR roots modulus (three models).
| Root Number | AR Roots Modulus | ||
|---|---|---|---|
| VECM with FD | VECM with LNRCB | VECM with LNRDP | |
| 1 | 1.000000 | 1.000000 | 1.000000 |
| 2 | 1.000000 | 1.000000 | 1.000000 |
| 3 | 0.876871 | 0.942626 | 0.499015 |
| 4 | 0.766738 | 0.889582 | 0.499015 |
| 5 | 0.524532 | 0.889582 | 0.316225 |
| 6 | 0.524532 | 0.751982 | 0.263769 |
| 7 | 0.486266 | 0.751982 | |
| 8 | 0.486266 | 0.619958 | |
| 9 | 0.008034 | 0.619958 | |
| 10 | 0.605491 | ||
| 11 | 0.605491 | ||
| 12 | 0.589958 | ||
| 13 | 0.589958 | ||
| 14 | 0.588532 | ||
| 15 | 0.013849 | ||
Notes: 1451st test is useful but not compulsory (Gonzalo, 1994 [62]).
References
- G. Adu, G. Marbuah, and J.T. Meansah. “Financial development and economic growth in Ghana: Does the measure of financial development matter? ” Rev. Dev. Financ. 3 (2013): 192–203. [Google Scholar] [CrossRef]
- R. Levine. “Bank-based or market-based financial systems: Which is better? ” J. Financ. Intermed. 11 (2002): 398–428. [Google Scholar] [CrossRef]
- P. Aghion, R. Blundell, R. Griffith, P. Howitt, and S. Prantl. “The effects of entry on incumbent innovation and productivity.” Rev. Econ. Stat. 91 (2009): 20–32. [Google Scholar] [CrossRef]
- P. Quartey, and F. Prah. “Financial development and economic growth in Ghana: Is there a causal link? ” Afr. Financ. J. 10 (2008): 28–54. [Google Scholar]
- Y. Keho. “Efficacité Macroéconomique du Crédit en Côte d’Ivoire: Une Approche en termes de Causalité.” Revue Ivoirienne des Sciences Economiques et de Gestion (RISEG) 11 (2007): 38. [Google Scholar]
- L.J. Esso. “Cointegrating and causal relationship between financial development and economic growth in ECOWAS countries.” J. Econ. Int. Financ. 2 (2010): 36–48. [Google Scholar]
- J.A. Schumpeter. The Theory of Economic Development. Cambridge, MA, USA: Harvard University Press, 1911. [Google Scholar]
- H.T. Patrick. “Financial development and economic growth in undeveloped countries.” Econ. Dev. Cult. Chang. 14 (1966): 174–189. [Google Scholar] [CrossRef]
- R.W. Goldsmith. Financial Structure and Development. New Haven, CT, USA: Yale University Press, 1969. [Google Scholar]
- R.I. MacKinnon. Money and Capital in Economic Development. Washington, DC, USA: Brookings Institution, 1973. [Google Scholar]
- E.S. Shaw. Financial Deepening in Economic Development. New York, NY, USA: Oxford University Press, 1973. [Google Scholar]
- J. Robinson. The Rate of Interest and Other Essays. London, UK: Macmillan, 1952. [Google Scholar]
- R.E. Lucas Jr. “On the mechanics of economic development.” J. Monet. Econ. 22 (1988): 3–42. [Google Scholar] [CrossRef]
- A. Chandavarkar. “Of finance and development: Neglected and unsettled questions.” World Dev. 22 (1992): 133–142. [Google Scholar] [CrossRef]
- R.E. Lewis Jr. The Theory of Economic Growth. London, UK: George Allen and Unwin, 1955. [Google Scholar]
- T. Beck, R. Levine, and N. Loayza. “Finance and the sources of growth.” J. Financ. Econ. 58 (2000): 261–300. [Google Scholar] [CrossRef]
- J. Gregorio, and P.E. Guidotti. “Financial development and economic growth.” World Dev. 23 (1995): 433–448. [Google Scholar] [CrossRef]
- R.G. King, and R. Levine. “Finance and growth: Schumpeter might be right.” Q. J. Econ. 108 (1993): 717–737. [Google Scholar] [CrossRef]
- B. Amable, and J.B. Chatelain. “Can financial infrastructures foster economic development? ” J. Dev. Econ. 64 (2001): 481–498. [Google Scholar] [CrossRef]
- V.R. Bencivenga, and B.D. Smith. “Financial intermediation and endogenous growth.” Rev. Econ. Stud. 58 (1991): 195–209. [Google Scholar] [CrossRef]
- V. Bencivenga, B. Smith, and R. Starr. “Transaction costs, technological choice and endogenous growth.” J. Econ. Theory 67 (1995): 153–177. [Google Scholar] [CrossRef]
- J. Benhabib, and M.M. Spiegel. “The role of financial development in growth and investment.” J. Econ. Growth 5 (2000): 341–360. [Google Scholar] [CrossRef]
- L. Deidda, and B. Fattouh. “Non−linearity between finance and growth.” Econ. Lett. 74 (2002): 339–345. [Google Scholar] [CrossRef]
- M.O. Odedokun. “Alternative econometric approaches for analyzing the role of the financial sector in economic growth: Time-series evidence from LDCs.” J. Dev. Econ. 50 (1996): 119–146. [Google Scholar] [CrossRef]
- F. Rioja, and N. Valev. “Does one size fit all? A reexamination of the finance and growth relationship.” J. Dev. Econ. 74 (2004): 429–447. [Google Scholar] [CrossRef]
- C.K. Choong, and S.G. Chan. “Financial development and Economic growth: A review.” Afr. J. Bus. Manag. 5 (2011): 2017–2027. [Google Scholar]
- M.A. Khan. “Financial development and economic growth in Pakistan: Evidence based on autoregressive distributed lag (ARDL) approach.” South Asia Econ. J. 9 (2008): 375–390. [Google Scholar] [CrossRef]
- A.H. Gelb. Financial Policies, Growth, and Efficiency. Washington, DC, USA: The World Bank, 1989. [Google Scholar]
- M.S. Khan, and A.S. Senhadji. “Financial development and economic growth: A review and new evidence.” J. Afr. Econ. 12 (2003): ii89–ii110. [Google Scholar] [CrossRef]
- R. Levine, N. Loayza, and T. Beck. “Financial intermediation and growth: Causality and causes.” J. Monet. Econ. 46 (2000): 31–77. [Google Scholar] [CrossRef]
- C. Bell, and P.L. Rousseau. “Post−independence India: A case of finance−led industrialization? ” J. Dev. Econ. 65 (2001): 153–175. [Google Scholar] [CrossRef]
- D.K. Christopoulos, and E.G. Tsionas. “Financial development and economic growth: Evidence from panel unit root and cointegration tests.” J. Dev. Econ. 73 (2004): 55–74. [Google Scholar] [CrossRef]
- M. Fase, and R. Abma. “Financial environment and economic growth in selected Asian countries.” J. Asian Econ. 14 (2003): 11–21. [Google Scholar] [CrossRef]
- C. Calderón, and L. Liu. “The direction of causality between financial development and economic growth.” J. Dev. Econ. 72 (2003): 321–334. [Google Scholar] [CrossRef]
- P.O. Demetriades, and K.A. Hussein. “Does financial development cause economic growth? Time-series evidence from 16 countries.” J. Dev. Econ. 51 (1996): 387–411. [Google Scholar] [CrossRef]
- K.B. Luintel, and M. Khan. “A quantitative reassessment of the finance–growth nexus: Evidence from a multivariate VAR.” J. Dev. Econ. 60 (1999): 381–405. [Google Scholar] [CrossRef]
- K. Neusser, and M. Kugler. “Manufacturing growth and financial development: Evidence from OECD countries.” Rev. Econ. Stat. 80 (1998): 638–646. [Google Scholar] [CrossRef]
- J.C. Berthelemy, and A. Varoudakis. “Economic growth, convergence clubs, and the role of financial development.” Oxf. Econ. Pap. 48 (1996): 300–328. [Google Scholar] [CrossRef]
- J. Greenwood, and B. Jovanovic. “Financial development, growth, and the distribution of income.” J. Political Econ. 98 (1990): 1076–1107. [Google Scholar] [CrossRef]
- J. Greenwood, and B. Smith. “Financial markets in development and the development of financial market.” J. Econ. Dyn. Control 21 (1997): 145–181. [Google Scholar] [CrossRef]
- S.M. Kargbo, and P.A. Adamu. “Financial development and economic growth in Sierra Leone.” J. Monet. Econ. Integr. 9 (2009): 30–61. [Google Scholar]
- S. Rebelo. “Long-run policy analysis and long-run growth.” J. Polit. Econ. 99 (1991): 500–521. [Google Scholar] [CrossRef]
- M. Pagano. “Financial markets and growth: an overview.” Eur. Econ. Rev. 37 (1993): 613–622. [Google Scholar] [CrossRef]
- A. Jalil, and M. Feridun. “Impact of financial development on economic growth: Empirical evidence from Pakistan.” J. Asia Pac. Econ. 16 (2011): 71–80. [Google Scholar] [CrossRef]
- Q. Liang, and T. Jian-Zhou. “Financial development and economic growth: Evidence from China.” China Econ. Rev. 17 (2006): 395–411. [Google Scholar] [CrossRef]
- D.A. Dickey, and W.A. Fuller. “Distribution of the estimators for autoregressive time series with a unit root.” J. Am. Stat. Assoc. 74 (1979): 427–431. [Google Scholar] [CrossRef]
- P.C. Phillips, and P. Perron. “Testing for a unit root in time series regression.” Biometrika 75 (1988): 335–346. [Google Scholar] [CrossRef]
- D. Kwiatkowski, P. Phillips, P. Schmidt, and Y. Shin. “Testing null of stationarity of against the alternative of a unit root.” J. Econ. 54 (1992): 159–178. [Google Scholar] [CrossRef]
- R.L. Lumsdaine, and E.S. Prasad. “Identifying the common component of international economic fluctuations: A new approach.” Econ. J. 113 (2003): 101–127. [Google Scholar] [CrossRef]
- R.F. Engle, and C.W. Granger. “Co-integration and error correction: Representation, estimation, and testing.” Econometrica 55 (1987): 251–276. [Google Scholar] [CrossRef]
- S. Johansen. “Statistical analysis of Cointegration Vector.” J. Econ. Dyn. Control 12 (1988): 231–254. [Google Scholar] [CrossRef]
- M.H. Pesaran, and Y. Shin. “Long−Run structural modeling.” Econ. Rev. 21 (2002): 49–87. [Google Scholar] [CrossRef]
- J.D. Hamilton. Time Series Analysis. Princeton, NJ, USA: Princeton University Press, 1994. [Google Scholar]
- S. Johansen, and K. Juselius. “Testing structural hypothesis in a multivariate cointegration analysis of the PPP and UIP for UK.” J. Econ. 53 (1992): 211–244. [Google Scholar] [CrossRef]
- M. Osterwald−Lenum. “A note with quantiles of the asymptotic distribution of the ML cointegration rank tests statistics.” Oxf. Bull. Econ. Stat. 54 (1992): 461–472. [Google Scholar] [CrossRef]
- J.G. MacKinnon, A.A. Haug, and L. Michelis. “Numerical distribution functions of likelihood ratio tests for cointegration.” J. Appl. Econom. 14 (1999): 563–577. [Google Scholar] [CrossRef]
- S. Johansen. “Estimation and hypothesis testing of cointegration vectors in Gaussian vector autoregressive models.” Econometrica 59 (1991): 1551–1580. [Google Scholar] [CrossRef]
- R.W. Wickens. “Interpreting cointegrating vectors and common stochastic trends.” J. Econom. 74 (1996): 255–271. [Google Scholar] [CrossRef]
- S.G. Hall, and A. Milne. “The relevance of p−star analysis to UK monetary policy.” Econ. J. 104 (1994): 597–604. [Google Scholar] [CrossRef]
- J.Y. Campbell, and P. Perron. “Pitfalls and opportunities: What macroeconomists should know about unit roots.” Natl. Bur. Econ. Res. 6 (1991). [Google Scholar] [CrossRef]
- M.H. Pesaran, Y. Shin, and J.R. Smith. “Bounds testing approaches to the analysis of level relationships.” J. Appl. Econom. 3 (2001): 289–326. [Google Scholar] [CrossRef]
- J. Gonzalo. “Five alternative methods of estimating long-run equilibrium relationships.” J. Econom. 60 (1994): 203–233. [Google Scholar] [CrossRef]
- C.W.J. Granger. “Investigating causal relations by econometric models and cross-spectral methods.” Econometrica 37 (1969): 424–438. [Google Scholar] [CrossRef]
- H.H. Pesaran, and Y. Shin. “Generalized impulse response analysis in linear multivariate models.” Econ. Lett. 58 (1998): 17–29. [Google Scholar] [CrossRef]
- J.G. MacKinnon. “Numerical distribution functions for unit root and cointegration tests.” J. Appl. Econom. 11 (1996): 601–618. [Google Scholar] [CrossRef]
- G. Schwarz. “Estimating the dimension of a model.” Ann. Stat. 6 (1978): 461–464. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).