Short-Term Forecasting of the JSE All-Share Index Using Gradient Boosting Machines
Abstract
1. Introduction
1.1. Overview
1.2. Literature Review
1.2.1. Traditional vs. Machine Learning Methods
1.2.2. Short-Term Forecasting of the Stock Market Indices
1.2.3. Principal Component Regression
1.2.4. Stock Market Indices Forecasting Using Gradient Boosting Machines
1.3. Contribution and Research Highlights
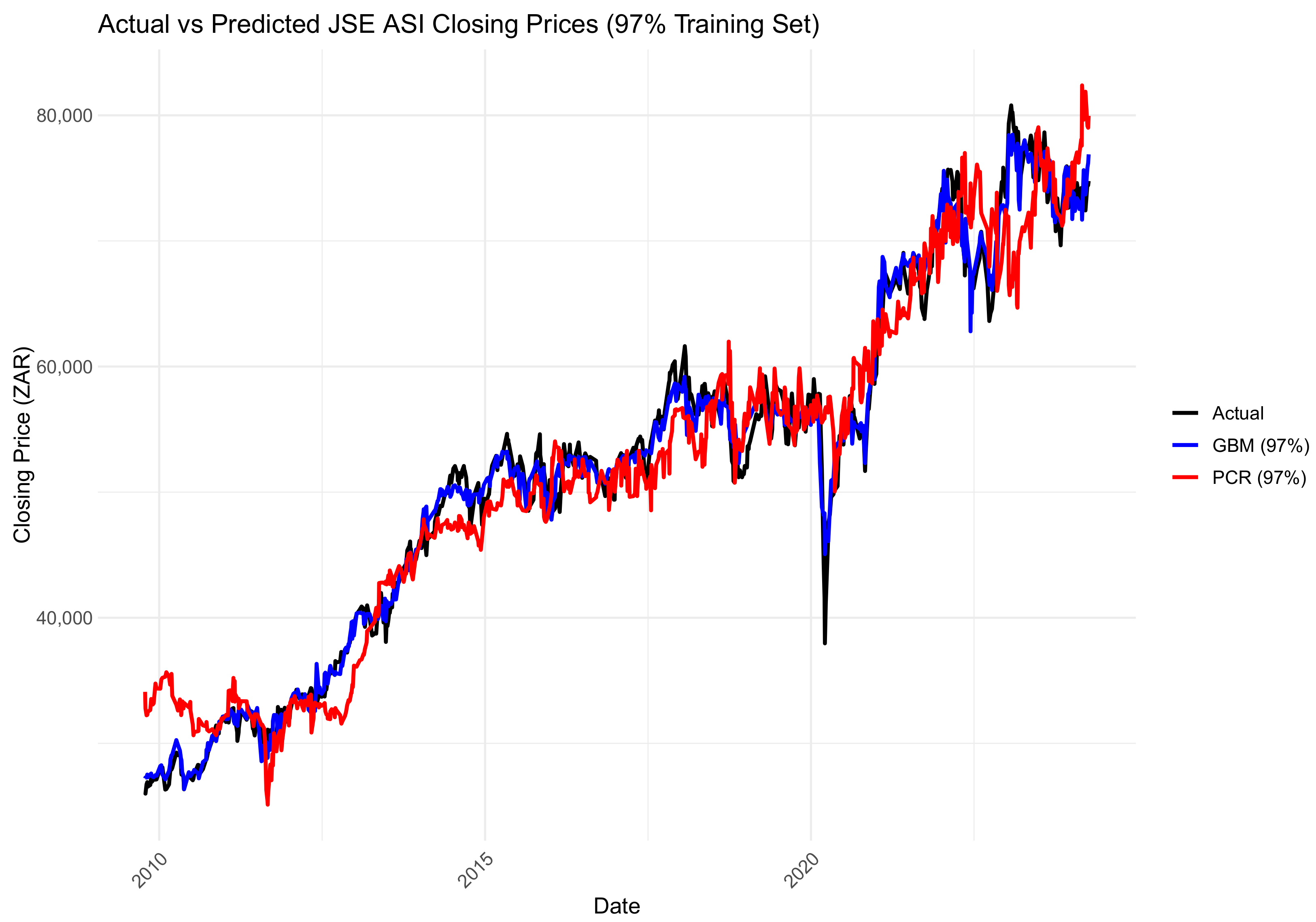
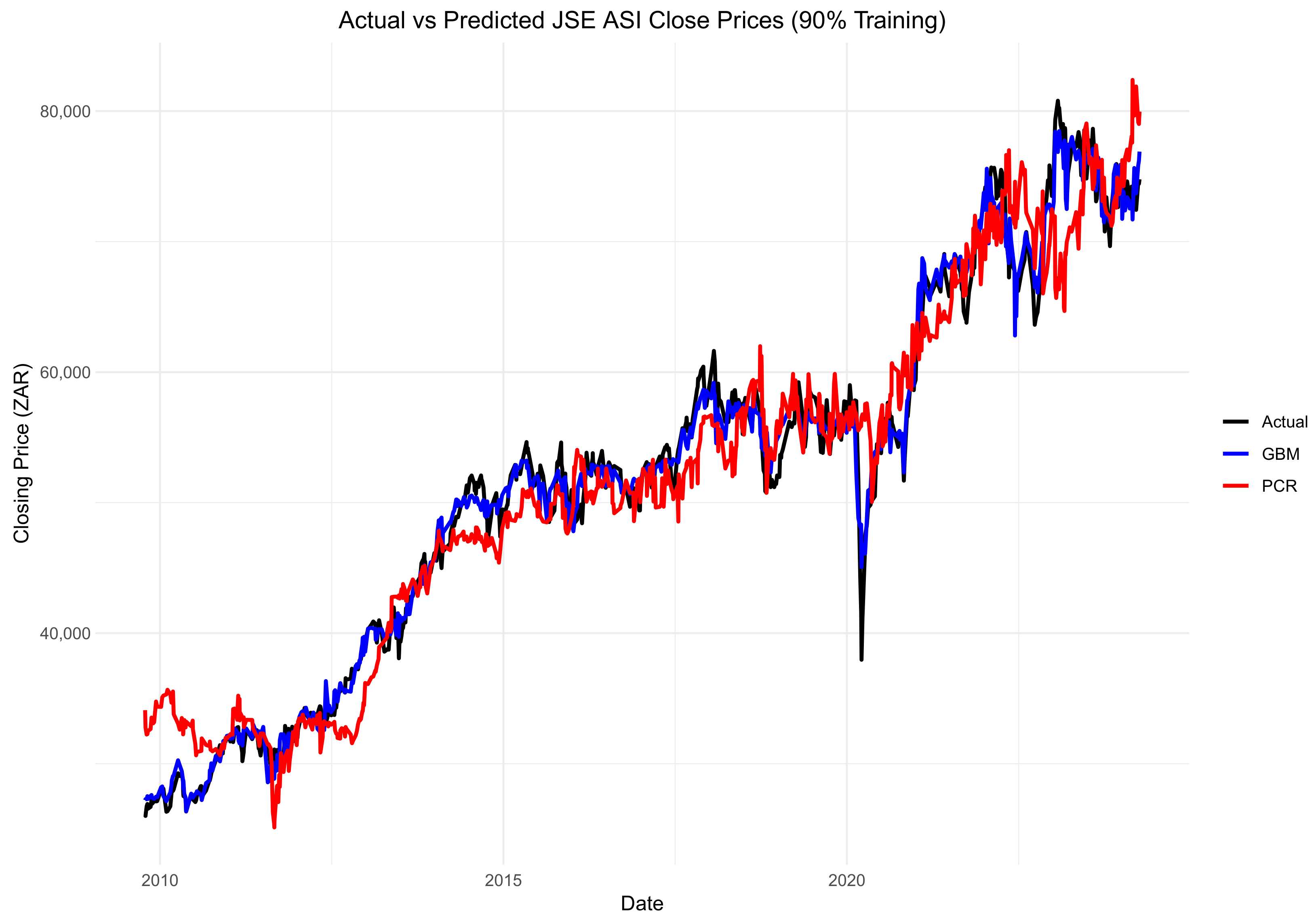
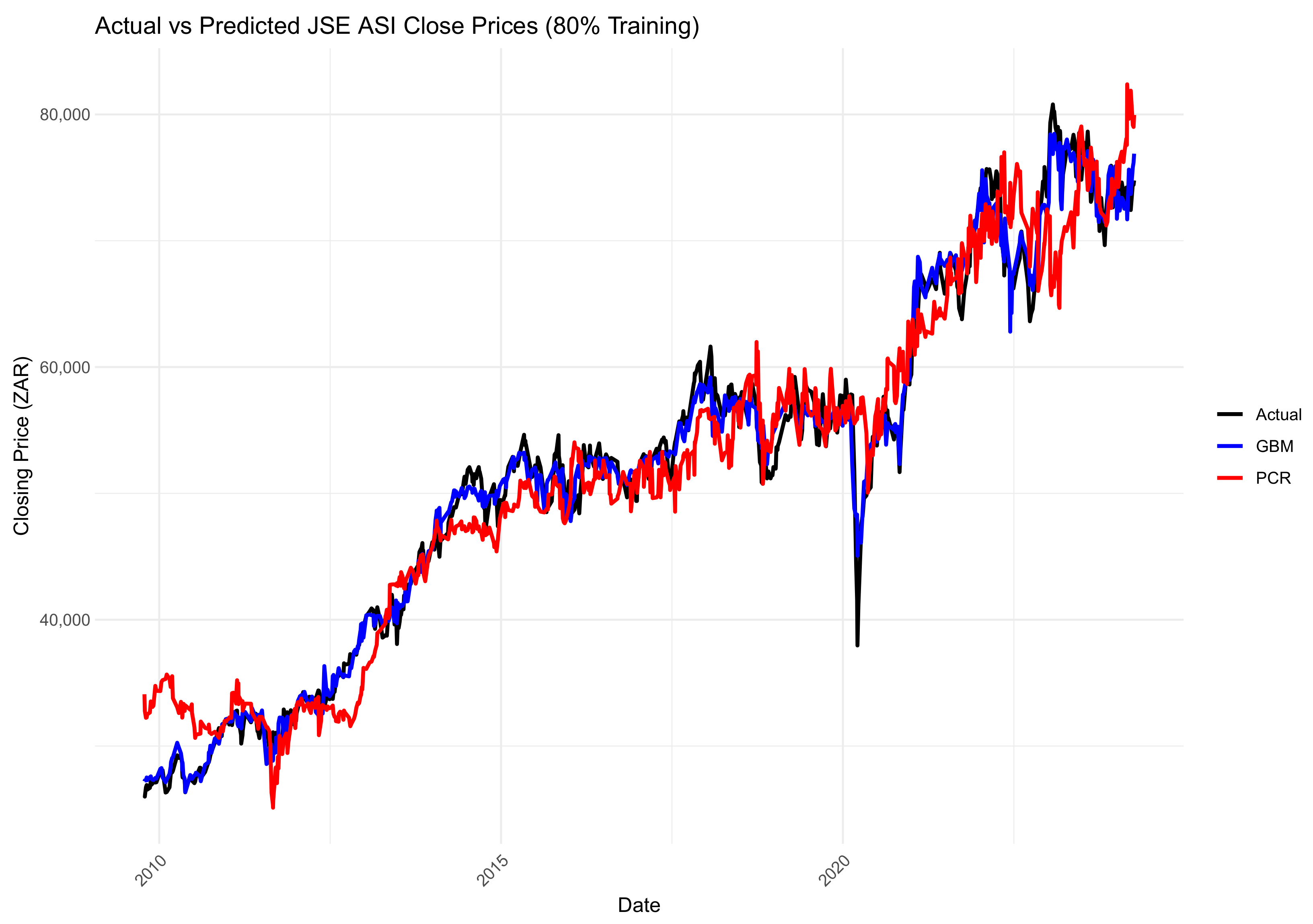
- The GBM performed better than PCR in all train–test splits with significantly better forecasting accuracy.
- The performance gap between PCR and the GBM reduced with larger training sets, particularly at the 97% split, indicating that PCR is competitive as more data are available.
- The ability of the GBM to exploit nonlinearities and interactions makes it well-suited to capture complex financial time series.
2. Models
2.1. Gradient Boosting Machines
2.1.1. Bagging and Boosting
2.1.2. Base Learner
2.1.3. Loss Function
Squared-Error
Absolute Error
2.1.4. Gradient Boosting
- : Initial prediction model, set to minimise the overall error in the beginning.
- : Loss function measuring the error between the actual target and the model prediction .
- Loop to M: Iterative loop where a new tree is added at each iteration to improve the model step-by-step.
- : Pseudo-residuals, representing the errors (negative gradients) from the previous model’s predictions, used as targets for the next tree.
- : Terminal nodes in the new L-leaf tree, grouping data points based on residuals.
- : Optimal weight for each terminal node, minimising the error within each region of the new tree.
- Update : The new model prediction is obtained by adding the weighted contribution of the new tree.
- is the shrinkage factor that controls the learning rate. A small reduces overfitting (Qin et al., 2013).
- Learning rate (): This controls the contribution of each tree to the final model. A smaller learning rate generally improves performance but requires more trees.
- Tree depth (interaction depth): Controls the maximum depth of each decision tree, which determines how complex the model can become by allowing the capture of higher-order interactions.
- Number of trees (M): Refers to the total number of boosting iterations and must be chosen carefully to balance underfitting and overfitting.
- Minimum number of observations in a node (n.minobsinnode): Ensures that splits occur only if a node contains enough data, helping to regularise the model.
| Algorithm 1: Gradient_TreeBoost |
|
1: 2: for to M 3: 4: 5: 6: 7: end for |
2.2. Principal Component Regression
2.3. Forecast Evaluation Metrics
2.3.1. Mean Absolute Error
2.3.2. Root Mean Squared Error
2.3.3. Mean Absolute Percentage Error
2.3.4. Mean Absolute Scaled Error
3. Empirical Results
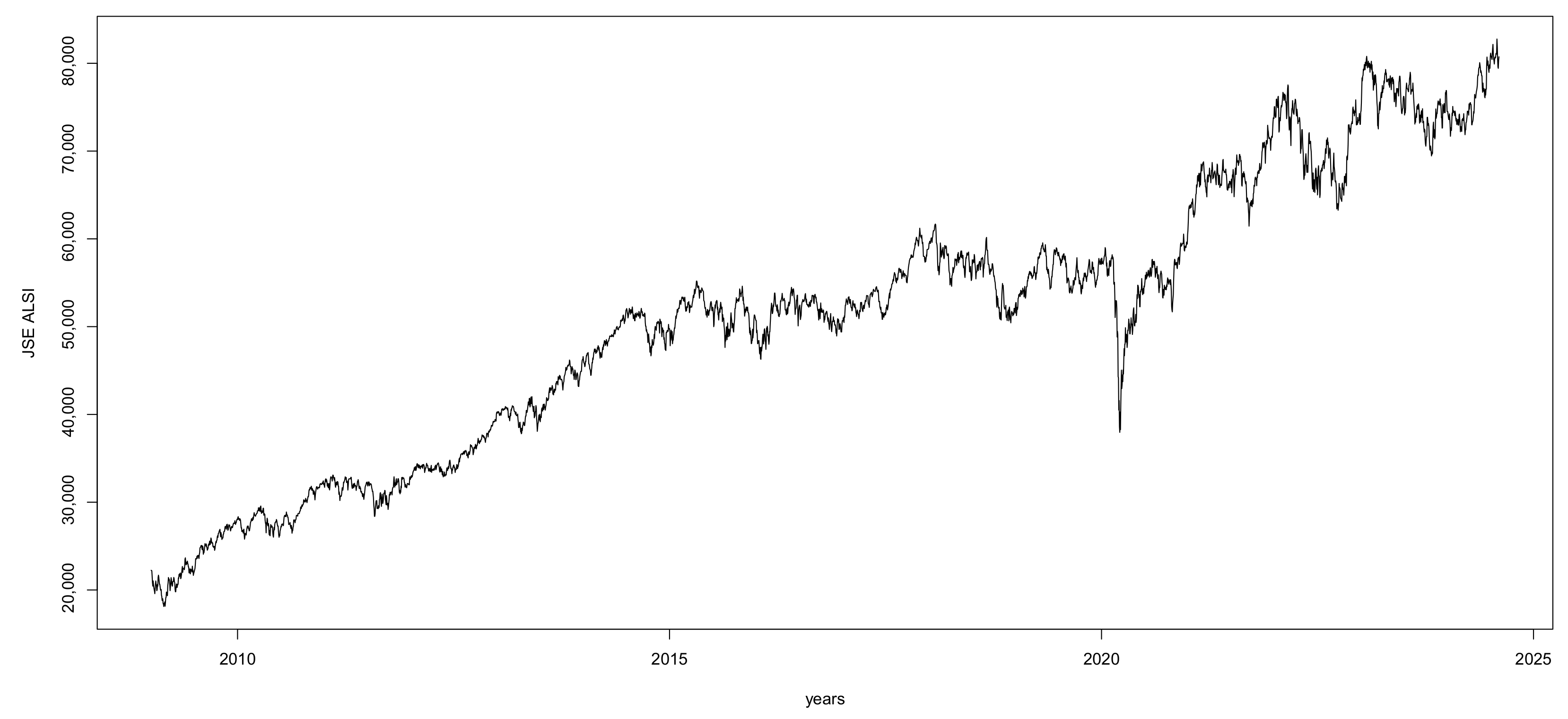
3.1. Exploratory Data Analysis
3.1.1. Data Source
3.1.2. Data Characteristics
- diff1—the logarithmic difference between the closing price of the JSE ASI at time t and .
- diff2—the logarithmic difference between the closing price of the JSE ASI at time t and .
- diff5—the logarithmic difference between the closing price of the JSE ASI at time t and .
- UsdZar—the exchange rate between the US dollar and South African rand.
- Oilprice(WTI)—the price of West Texas Intermediate crude oil.
- Platprice—the international market price of platinum.
- Goldprice—the international market price of gold.
- S&P500—the closing price of the S&P 500 index.
- Month—represents the months of the year.
- Day—represents the day of the week.
- Gold: https://www.investing.com/commodities/gold-historical-data (accessed on 7 October 2024)
- Platinum: https://www.investing.com/commodities/platinum-historical-data (accessed on 7 October 2024)
- Crude Oil (WTI/Brent): https://www.investing.com/commodities/crude-oil-historical-data (accessed on 7 October 2024)
- USD/ZAR exchange rate: https://www.investing.com/currencies/usd-zar (accessed on 7 October 2024)
3.1.3. Summary Statistics
3.2. Data Processing
Dataset Description
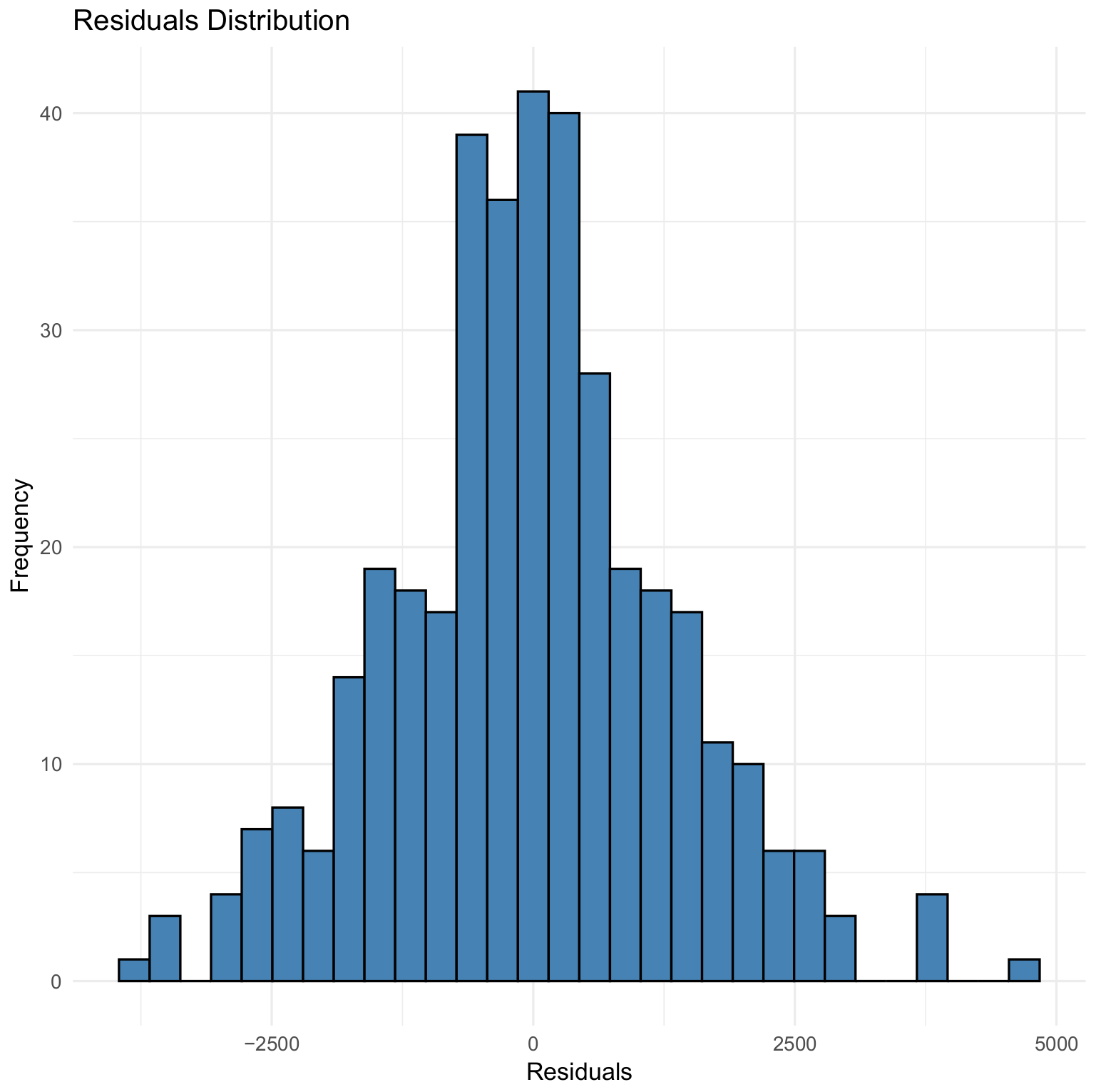
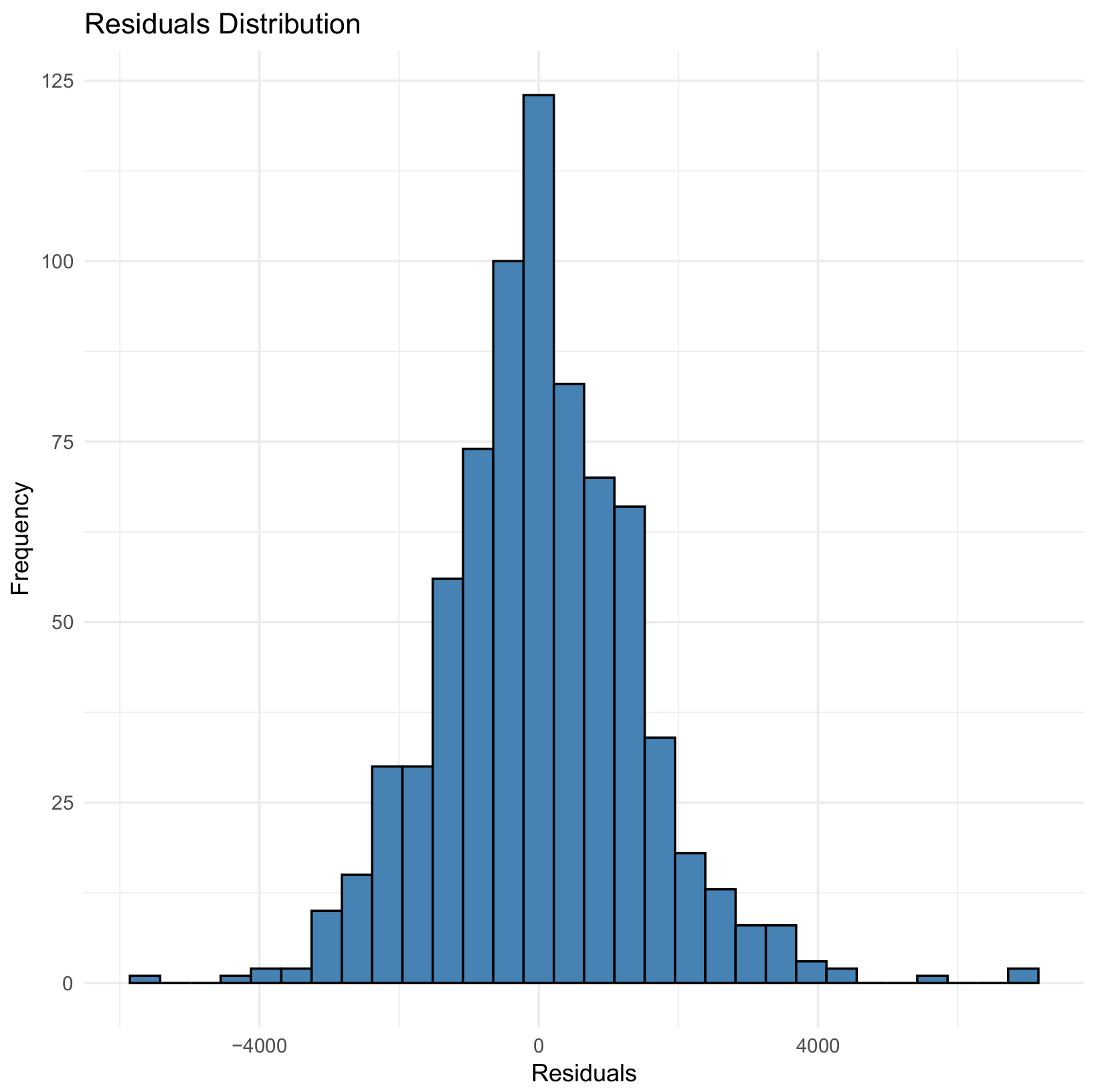
3.3. Results
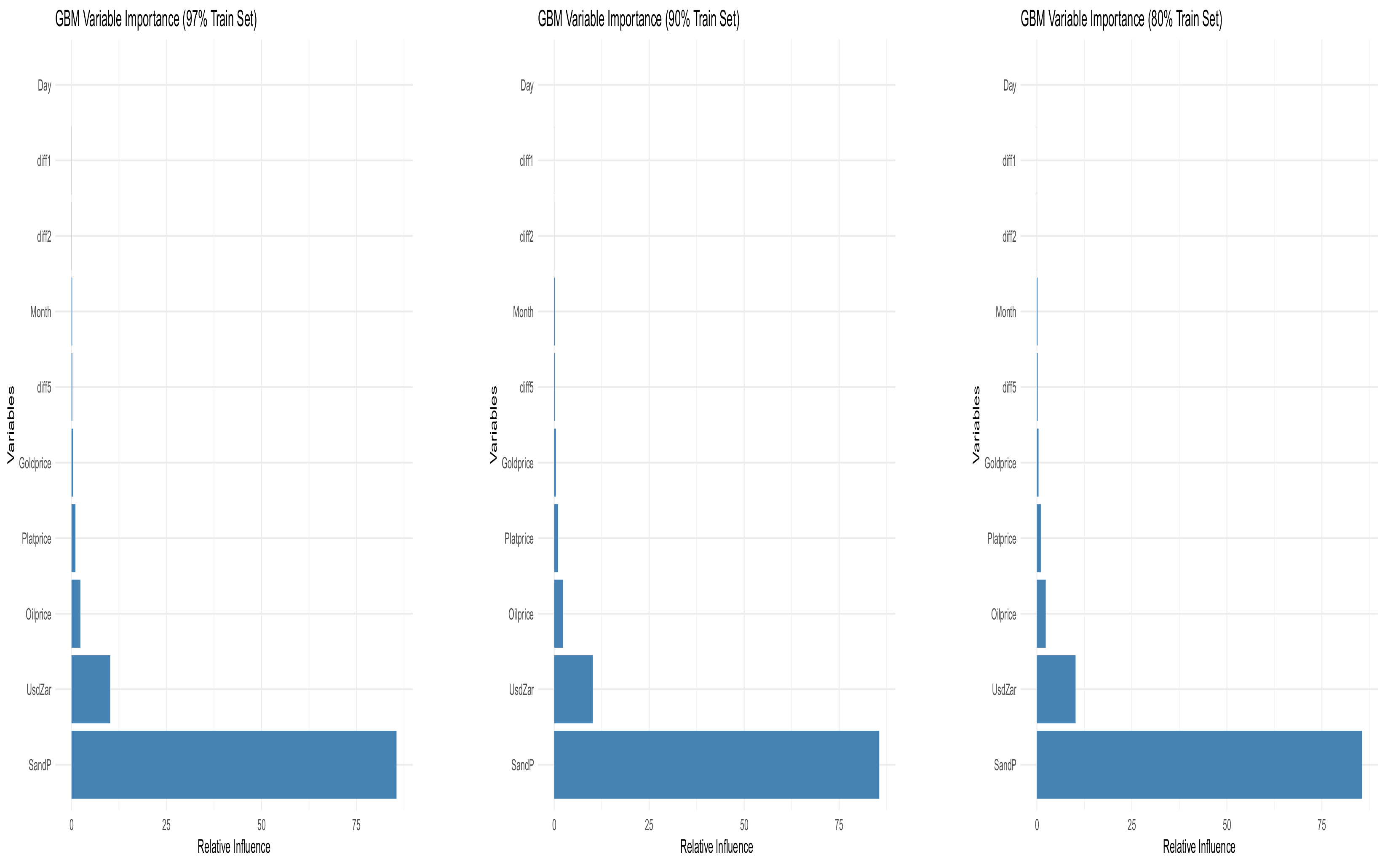
Variables Importance
3.4. Principal Component Regression
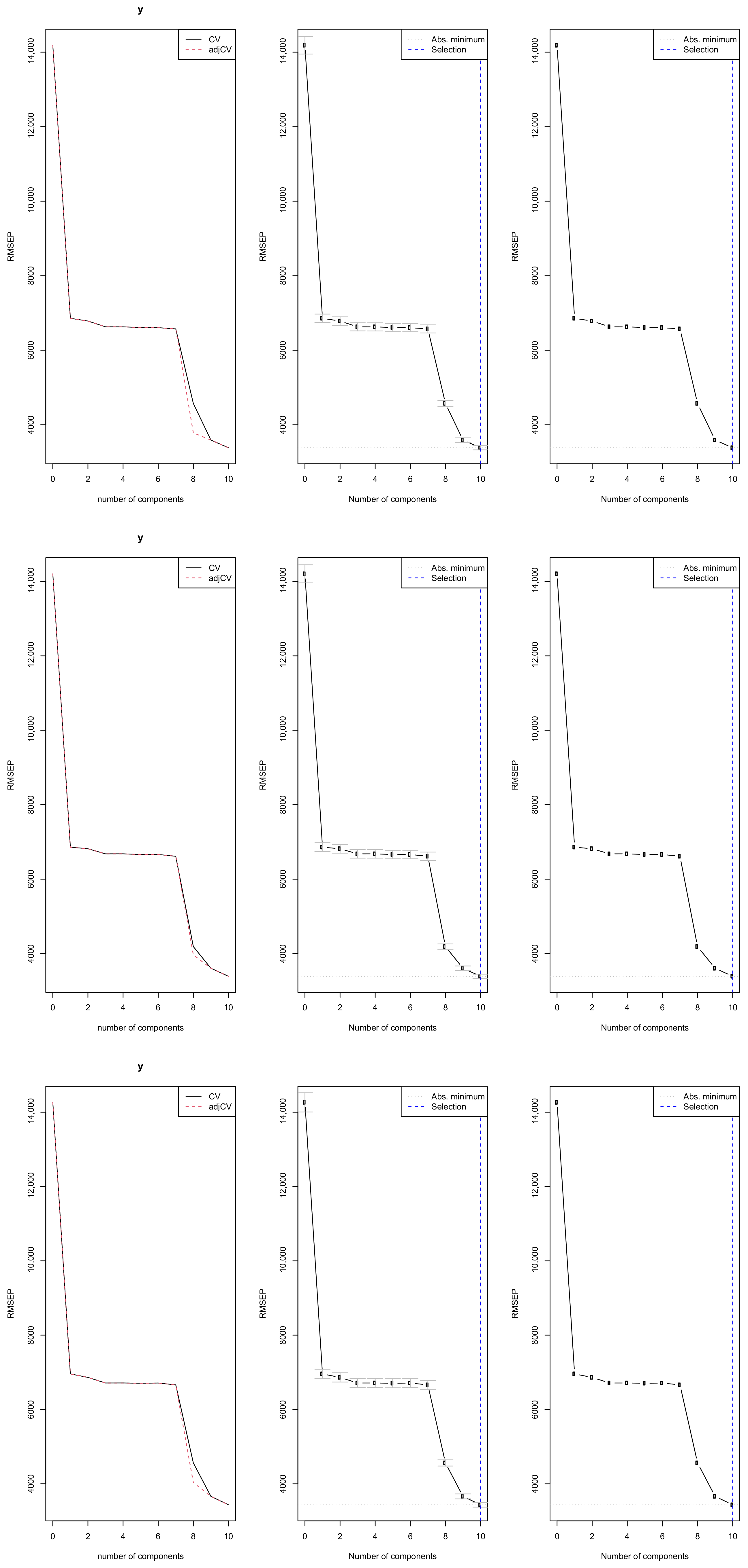
Selection of Number of Components
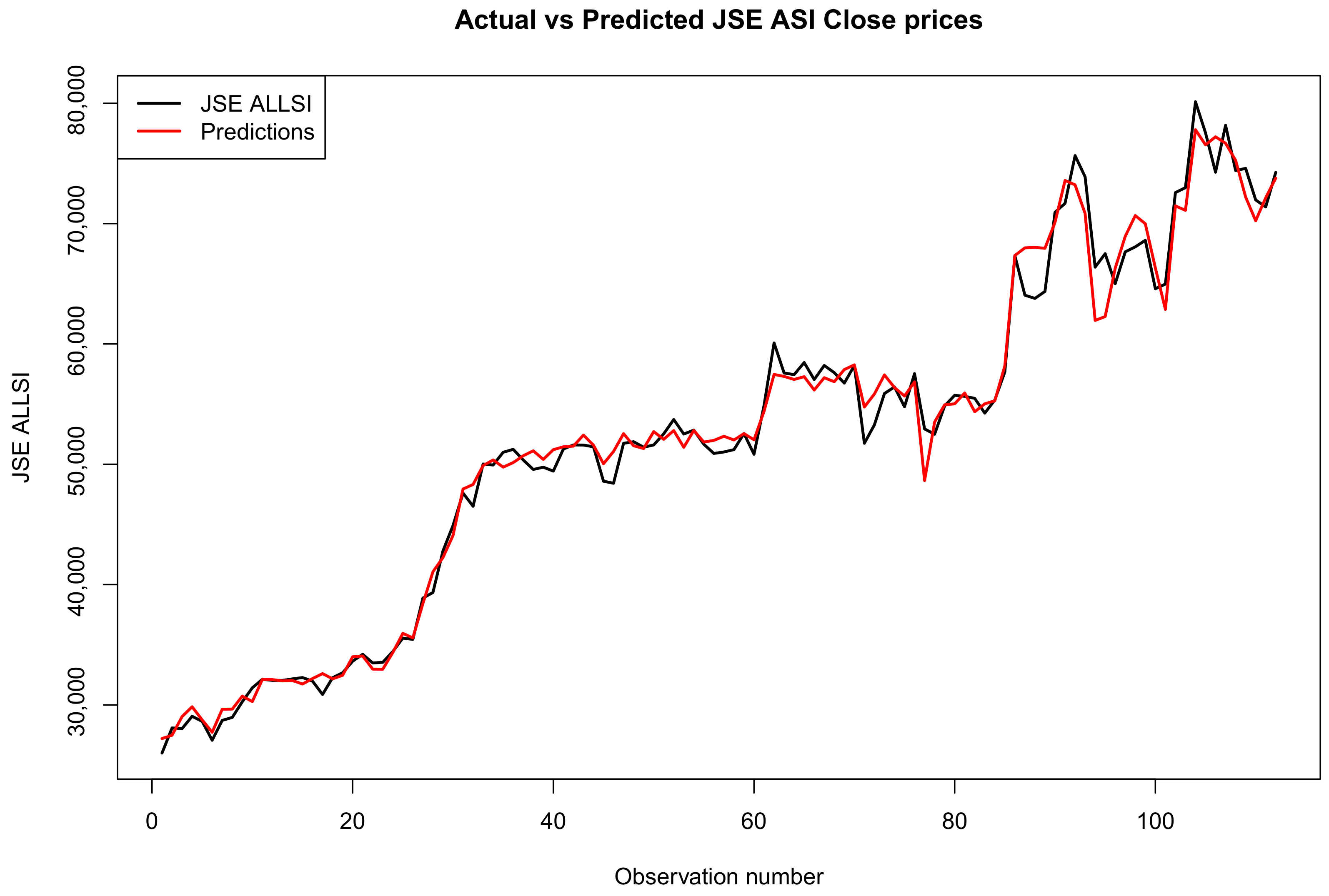
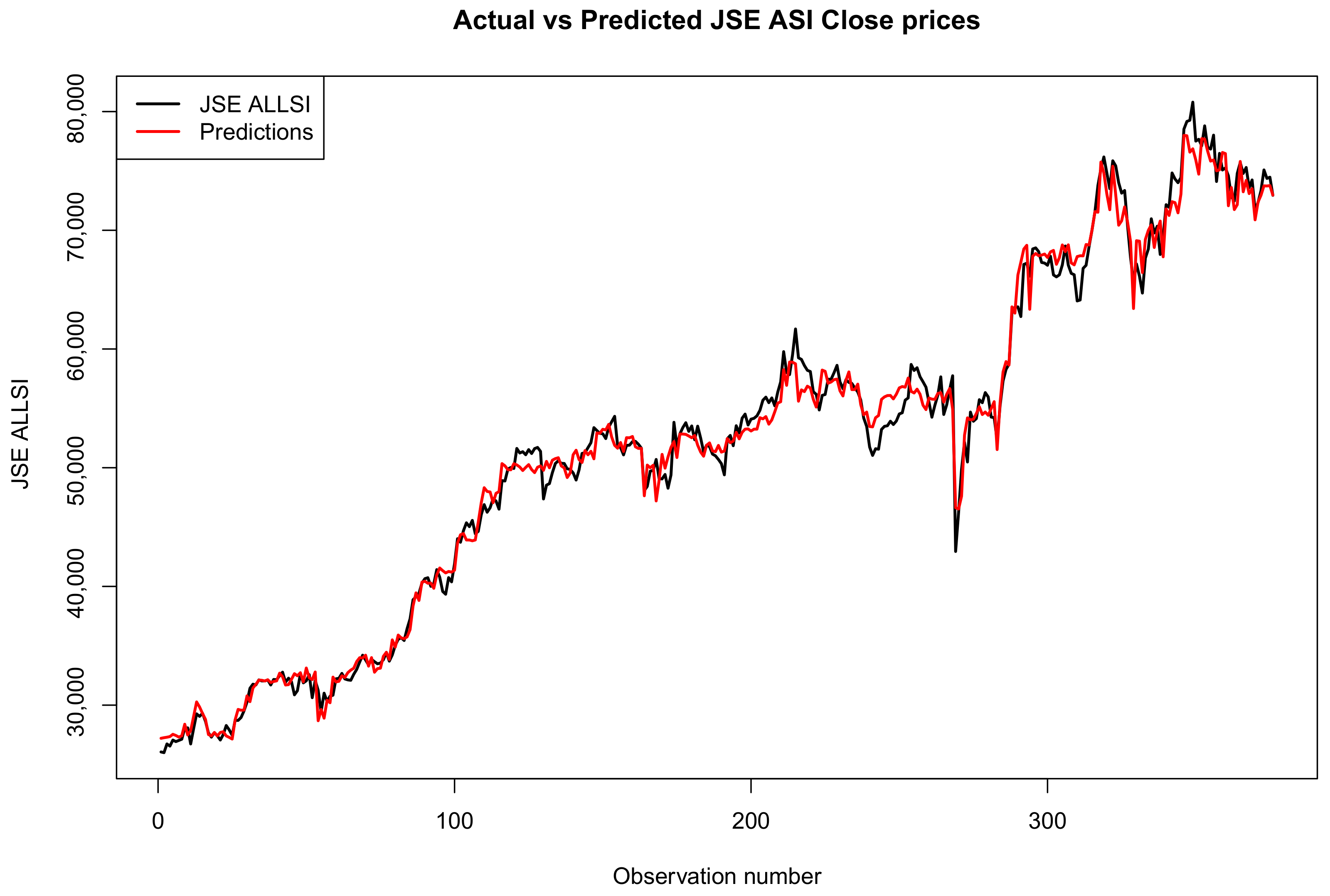
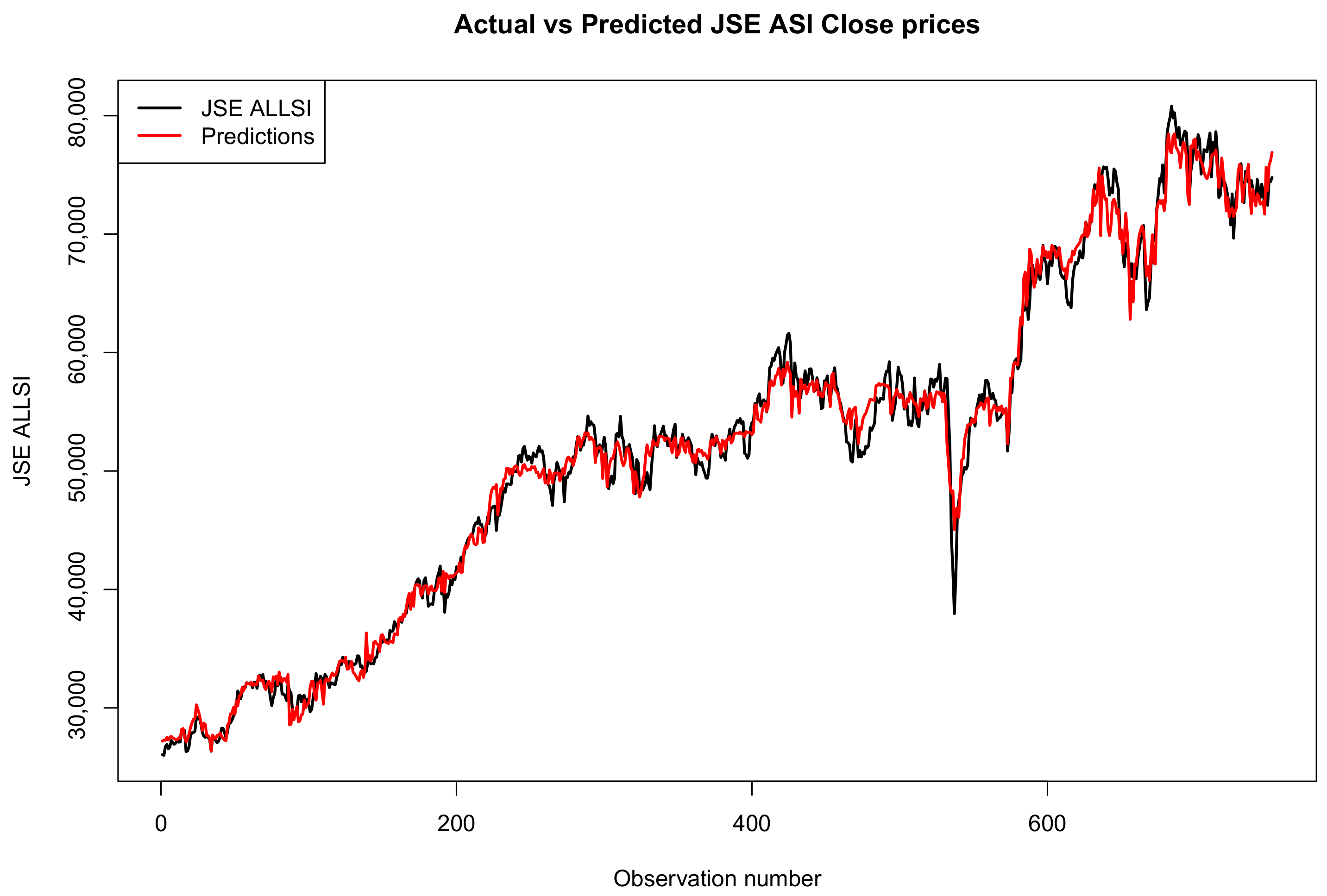
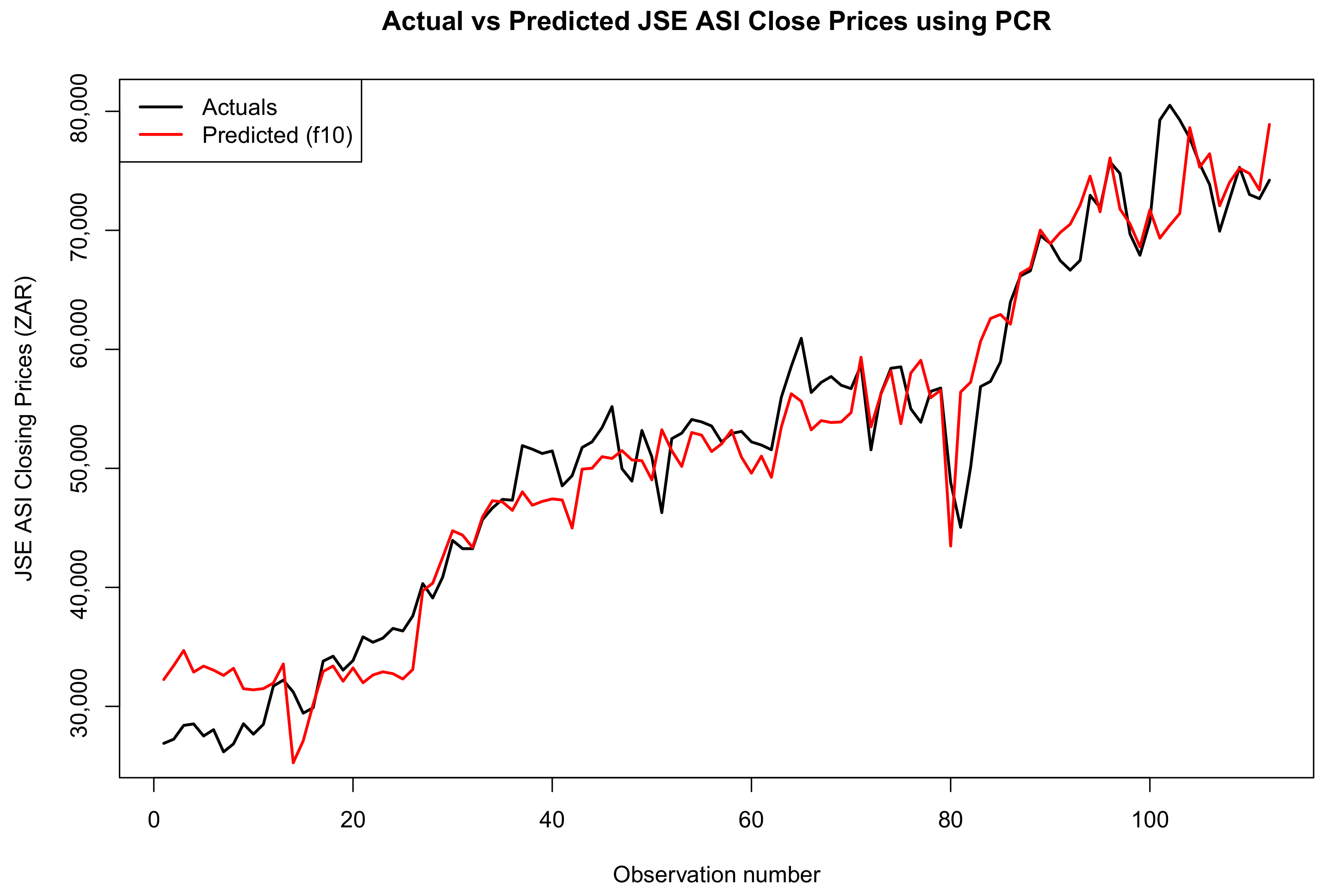
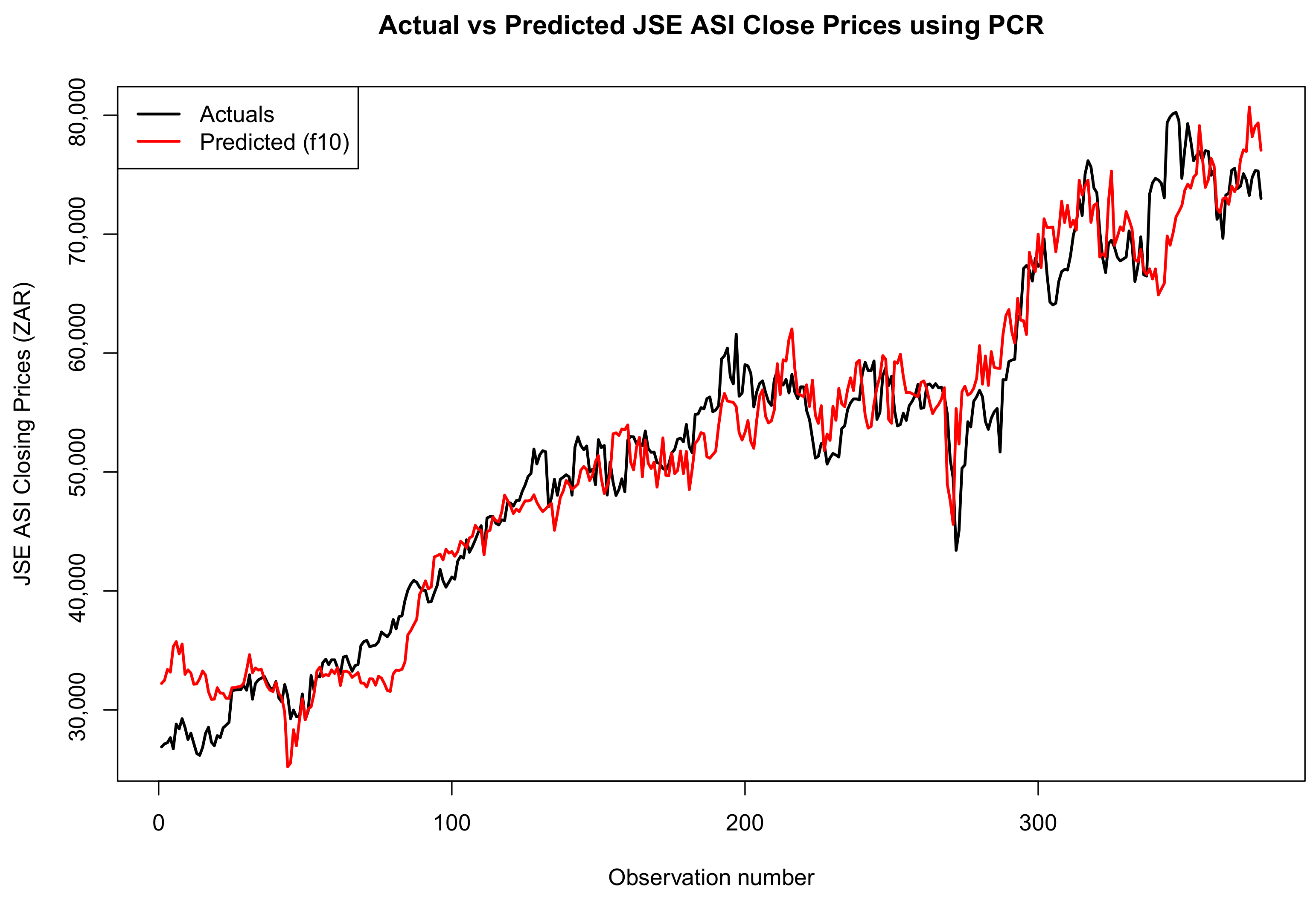
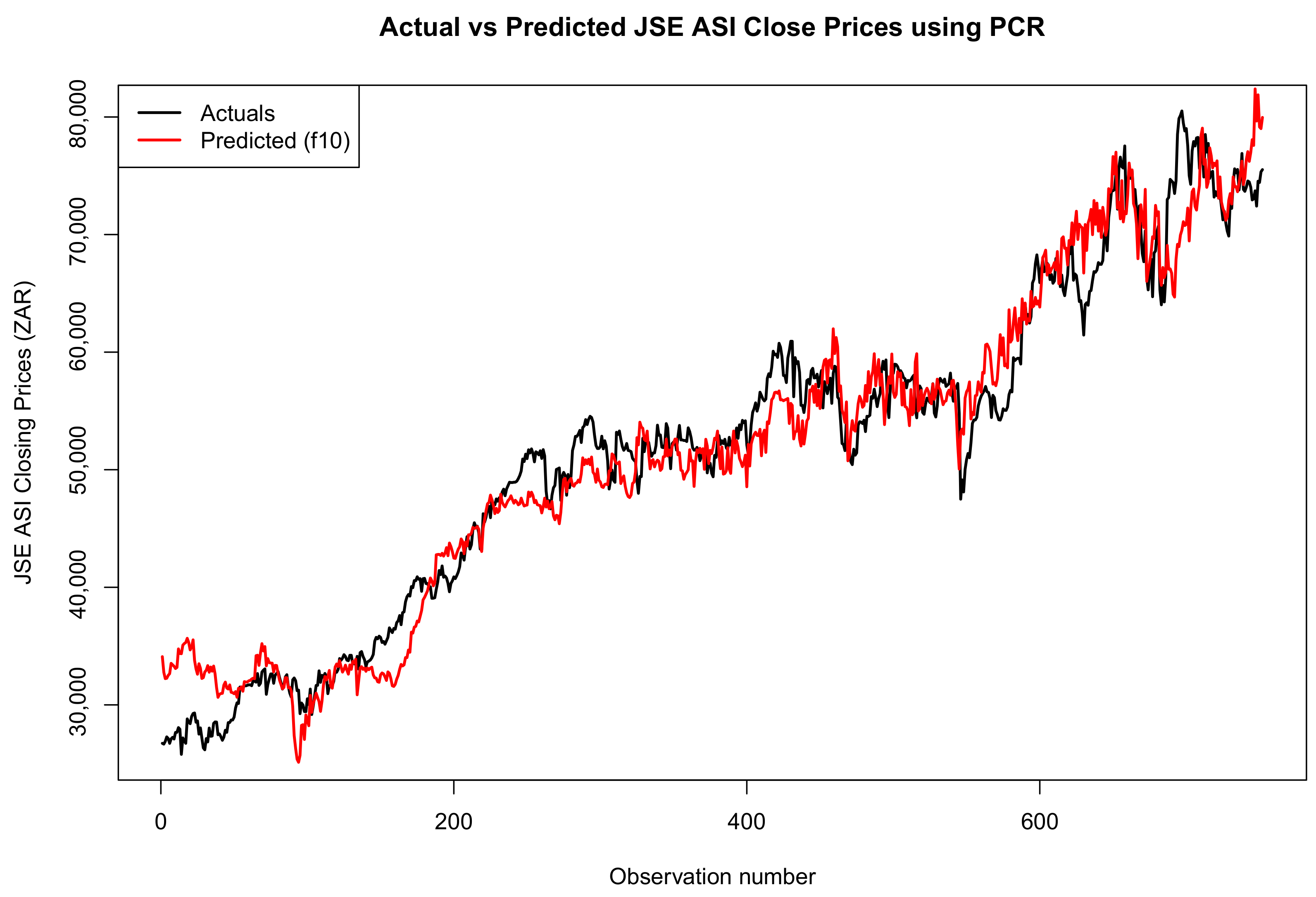
3.5. Forecast Comparison of the Two Models
Forecast Accuracy
4. Discussion
4.1. General Discussion
4.2. Limitations of This Study
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ALSI | All-Share Index |
| ANN | Artificial Neural Network |
| CNN | Convolutional Neural Networs |
| DM | Diebold–Mariano |
| GBM | Gradient Boosting Machine |
| GAN | Genetic Adversarial Network |
| JSE | Johannesburg Stock Exchange |
| LSTM | Long Short-Term Memory |
| MAE | Mean Absolute Error |
| MAPE | Mean Absolute Percentage Error |
| MASE | Mean Absolute Scaled Error |
| PCA | Principal Component Analysis |
| RMSEP | Root Mean Square Error of Prediction |
| PCR | Principal Component Regression |
| RMSE | Root Mean Square Error |
| SVR | Support Vector Regression |
References
- Balusik, A., de Magalhaes, J., & Mbuvha, R. (2021). Forecasting the JSE top 40 using long short-term memory networks. arXiv, arXiv:2104.09855. [Google Scholar] [CrossRef]
- Breiman, L. (1996). Bagging predictors. Machine Learning, 24, 123–140. [Google Scholar] [CrossRef]
- Carte, D. (2009). The all-share index: Investing 101. Personal Finance, 2009(341), 9–10. Available online: https://hdl.handle.net/10520/EJC77651 (accessed on 13 June 2024).
- Castro, S. A. B. D., & Silva, A. C. (2024). Evaluation of PCA with variable selection for cluster typological domains. REM-International Engineering Journal, 77(2), e230071. [Google Scholar] [CrossRef]
- Chowdhury, M. S., Nabi, N., Rana, M. N. U., Shaima, M., Esa, H., Mitra, A., Mozumder, M. A. S., Liza, I. A., Sweet, M. M. R., & Naznin, R. (2024). Deep learning models for stock market forecasting: A comprehensive comparative analysis. Journal of Business and Management Studies, 6(2), 95–99. [Google Scholar] [CrossRef]
- Demirel, U., Çam, H., & Ünlü, R. (2021). Predicting stock prices using machine learning methods and deep learning algorithms: The sample of the istanbul stock exchange. Gazi University Journal of Science, 34(1), 63–82. [Google Scholar] [CrossRef]
- Dey, S., Kumar, Y., Saha, S., & Basak, S. (2016). Forecasting to classification: Predicting the direction of stock market price using Xtreme Gradient Boosting. PESIT South Campus, 1, 1–10. [Google Scholar] [CrossRef]
- El-Shal, A. M., & Ibrahim, M. M. (2020). Forecasting EGX 30 index using principal component regression and dimensionality reduction techniques. International Journal of Intelligent Computing and Information Sciences, 20(2), 1–10. [Google Scholar]
- Friedman, J. H. (2001). Greedy function approximation: A gradient boosting machine. Annals of Statistics, 29(5), 1189–1232. [Google Scholar] [CrossRef]
- Friedman, J. H. (2002). Stochastic gradient boosting. Computational Statistics & Data Analysis, 38(4), 367–378. [Google Scholar] [CrossRef]
- Green, A., & Romanov, E. (2024). The high-dimensional asymptotics of principal component regression. arXiv, arXiv:2405.11676. [Google Scholar] [CrossRef]
- Hargreaves, C. A., & Leran, C. (2020). Stock prediction using deep learning with long-short-term-memory networks. International Journal of Electronic Engineering and Computer Science, 5(3), 22–32. [Google Scholar]
- Kumar, D., Sarangi, P. K., & Verma, R. (2022). A systematic review of stock market prediction using machine learning and statistical techniques. Materials Today: Proceedings, 49, 3187–3191. [Google Scholar] [CrossRef]
- Kumar, G., Jain, S., & Singh, U. P. (2021). Stock market forecasting using computational intelligence: A survey. Archives of Computational Methods in Engineering, 28(3), 1069–1101. [Google Scholar] [CrossRef]
- Liu, R. X., Kuang, J., Gong, Q., & Hou, X. L. (2003). Principal component regression analysis with SPSS. Computer Methods and Programs in Biomedicine, 71(2), 141–147. [Google Scholar] [CrossRef] [PubMed]
- Mevik, B. H., & Wehrens, R. (2015). Introduction to the pls package. Help section of the “Pls” package of R studio software (pp. 1–23). Available online: https://cran.r-project.org/web/packages/pls/vignettes/pls-manual.pdf (accessed on 27 July 2025).
- Mokoaleli-Mokoteli, T., Ramsumar, S., & Vadapalli, H. (2019). The efficiency of ensemble classifiers in predicting the johannesburg stock exchange all-share index direction. Journal of Financial Management, Markets and Institutions, 7(02), 1950001. [Google Scholar] [CrossRef]
- Nabipour, M., Nayyeri, P., Jabani, H., Mosavi, A., & Salwana, E. (2020). Deep learning for stock market prediction. Entropy, 22(8), 840. [Google Scholar] [CrossRef]
- Natekin, A., & Knoll, A. (2013). Gradient boosting machines, a tutorial. Frontiers in Neurorobotics, 7, 21. [Google Scholar] [CrossRef]
- Nevasalmi, L. (2020). Forecasting multinomial stock returns using machine learning methods. The Journal of Finance and Data Science, 6, 86–106. [Google Scholar] [CrossRef]
- Olorunnimbe, K., & Viktor, H. (2023). Deep learning in the stock market—A systematic survey of practice, backtesting, and applications. Artificial Intelligence Review, 56, 2057–109. [Google Scholar] [CrossRef]
- Park, S., Jung, S., Lee, J., & Hur, J. (2023). A short-term forecasting of wind power outputs based on gradient boosting regression tree algorithms. Energies, 16(3), 1132. [Google Scholar] [CrossRef]
- Pashankar, S. S., Shendage, J. D., & Pawar, J. (2024). A comparative analysis of traditional and machine learning methods in forecasting the stock markets of China and the US. Forecasting, 4(1), 58–72. [Google Scholar] [CrossRef]
- Patel, J., Shah, S., Thakkar, P., & Kotecha, K. (2015). Predicting stock market index using a fusion of machine learning techniques. Expert Systems with Applications, 42(4), 2162–2172. [Google Scholar] [CrossRef]
- Peng, Y., & de Moraes Souza, J. G. (2024). Machine learning methods for financial forecasting and trading profitability: Evidence during the Russia–Ukraine war. Revista de Gestão, 31(2), 152–165. [Google Scholar] [CrossRef]
- Qin, Q., Wang, Q. G., Li, J., & Ge, S. S. (2013). Linear and non-linear trading models with gradient boosted random forests and application to Singapore stock market. Journal of Intelligent Learning Systems and Applications, 5(01), 1–10. [Google Scholar] [CrossRef]
- Quinlan, J. R. (1996). Bagging, boosting, and C4.5. AAAI/IAAI, 1, 725–730. [Google Scholar]
- Russell, F. T. S. E. (2017). FTSE/JSE all-share index. Health Care, 7(228,485), 3–50. [Google Scholar]
- Sadorsky, P. (2023). Machine learning techniques and data for stock market forecasting: A literature review. Expert Systems with Applications, 197, 116659. [Google Scholar] [CrossRef]
- Shen, J., & Shafiq, M. O. (2020). Short-term stock market price trend prediction using a comprehensive deep learning system. Journal of Big Data, 7, 1–33. [Google Scholar] [CrossRef]
- Shrivastav, L. K., & Kumar, R. (2022a). An ensemble of random forest gradient boosting machine and deep learning methods for stock price prediction. Journal of Information Technology Research (JITR), 15(1), 1–19. [Google Scholar] [CrossRef]
- Shrivastav, L. K., & Kumar, R. (2022b). Gradient boosting machine and deep learning approach in big data analysis: A case study of the stock market. Journal of Information Technology Research (JITR), 15(1), 1–20. [Google Scholar] [CrossRef]
- Soni, P., Tewari, Y., & Krishnan, D. (2022). Machine learning approaches in stock market prediction: A systematic review. Journal of Physics: Conference Series, 2161, 012065. [Google Scholar] [CrossRef]
- Thomas, J., Mayr, A., Bischl, B., Schmid, M., Smith, A., & Hofner, B. (2018). Gradient boosting for distributional regression: Faster tuning and improved variable selection via noncyclical updates. Statistics and Computing, 28, 673–687. [Google Scholar] [CrossRef]
- Vaisla, K. S., Bhatt, A. K., & Kumar, S. (2010). Stock market forecasting using artificial neural network and statistical technique: A comparison report. International Journal of Computer and Network Security, 2(8), 50–55. [Google Scholar]
- Yaroshchyk, P., Death, D. L., & Spencer, S. J. (2012). Comparison of principal components regression, partial least squares regression, multi-block partial least squares regression, and serial partial least squares regression algorithms for the analysis of Fe in iron ore using LIBS. Journal of Analytical Atomic Spectrometry, 27(1), 92–98. [Google Scholar] [CrossRef]

| Summary | Raw Data |
|---|---|
| Min | 25,756 |
| Q1 | 40,594 |
| Median | 52,485 |
| Mean | 51,792 |
| Q3 | 58,965 |
| Max | 80,791 |
| Kurtosis | −0.7891 |
| Skewness | −0.0245 |
| Variables | Relative Influence (%) |
|---|---|
| SandP | 85.5441 |
| UsdZar | 10.1830 |
| Oilprice | 2.3295 |
| Platprice | 1.0330 |
| Goldprice | 0.4385 |
| diff5 | 0.2161 |
| Month | 0.1827 |
| diff2 | 0.0393 |
| diff1 | 0.0338 |
| Day | 0.0000 |
| Variables | Relative Influence (%) |
|---|---|
| SandP | 84.6832 |
| UsdZar | 10.9973 |
| Oilprice | 2.3395 |
| Platprice | 1.0695 |
| Goldprice | 0.4244 |
| diff5 | 0.2149 |
| Month | 0.1879 |
| diff2 | 0.0463 |
| diff1 | 0.0369 |
| Day | 0.0000 |
| Variables | Relative Influence (%) |
|---|---|
| SandP | 83.4090 |
| UsdZar | 12.3171 |
| Oilprice | 2.3035 |
| Platprice | 1.0012 |
| Goldprice | 0.5212 |
| diff5 | 0.1823 |
| Month | 0.1676 |
| diff1 | 0.0537 |
| diff2 | 0.0442 |
| Day | 0.0000 |
| Test Set Size | CV Folds | Trees | MAE | RMSE | MAPE | MASE | Bias |
|---|---|---|---|---|---|---|---|
| 3% | 5 | 1000 | 1106.497 | 1538.417 | 0.02051 | 0.66410 | −98.6148 |
| 10% | 5 | 1000 | 1029.339 | 1343.929 | 0.01970 | 1.10292 | 22.4083 |
| 20% | 5 | 1000 | 1069.544 | 1428.005 | 0.02092 | 1.35021 | −14.6764 |
| Training Split | Components (Best) | CV RMSEP (Best) | Explained Variance in X (%) | Explained Variance in Y (%) |
|---|---|---|---|---|
| 97% (n = 3663) | 10 | 3345 | 100.00 | 94.22 |
| 90% (n = 3398) | 10 | 3390 | 100.00 | 94.35 |
| 80% (n = 3015) | 10 | 3383 | 100.00 | 94.34 |
| Test Split | MAE | RMSE | MAPE | MASE | Bias (ME) |
|---|---|---|---|---|---|
| 20% | 2727.49 | 3579.78 | 0.0608 | 1.40 | 108.63 |
| 10% | 2663.51 | 3411.96 | 0.0555 | 2.49 | −30.68 |
| 3% | 2551.56 | 3231.95 | 0.0543 | 3.23 | 64.91 |
| Model | Test Set Size | MAE | RMSE | MAPE | MASE | Bias |
|---|---|---|---|---|---|---|
| GBM | 3% | 1106.50 | 1538.42 | 0.02051 | 0.66410 | −98.61 |
| GBM | 10% | 1029.34 | 1343.93 | 0.01970 | 1.10292 | 22.41 |
| GBM | 20% | 1069.54 | 1428.01 | 0.02092 | 1.35021 | −14.68 |
| PCR | 3% | 2551.56 | 3231.95 | 0.05430 | 3.23 | 64.91 |
| PCR | 10% | 2663.51 | 3411.96 | 0.05549 | 2.49 | −30.68 |
| PCR | 20% | 2727.49 | 3579.78 | 0.06076 | 1.40 | 108.63 |
| Training Split | DM Statistic | p-Value | Significance |
|---|---|---|---|
| 97% | −5.845 | 5.15 × 10−8 | Significant |
| 90% | −11.520 | 2.2 × 10−16 | Significant |
| 80% | −16.361 | 2.2 × 10−16 | Significant |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mukhaninga, M.; Ravele, T.; Sigauke, C. Short-Term Forecasting of the JSE All-Share Index Using Gradient Boosting Machines. Economies 2025, 13, 219. https://doi.org/10.3390/economies13080219
Mukhaninga M, Ravele T, Sigauke C. Short-Term Forecasting of the JSE All-Share Index Using Gradient Boosting Machines. Economies. 2025; 13(8):219. https://doi.org/10.3390/economies13080219
Chicago/Turabian StyleMukhaninga, Mueletshedzi, Thakhani Ravele, and Caston Sigauke. 2025. "Short-Term Forecasting of the JSE All-Share Index Using Gradient Boosting Machines" Economies 13, no. 8: 219. https://doi.org/10.3390/economies13080219
APA StyleMukhaninga, M., Ravele, T., & Sigauke, C. (2025). Short-Term Forecasting of the JSE All-Share Index Using Gradient Boosting Machines. Economies, 13(8), 219. https://doi.org/10.3390/economies13080219







