Assessing the Impact of the Real Exchange Rate on Okun’s Misery Index in Mexico
Abstract
1. Introduction
2. Literature Review
2.1. Okun’s Misery Index
2.2. Misery Index and Exchange Rate
3. Data and Model Design
3.1. Variables and Sources
3.2. Empirical Design
4. Econometric Results and Discussion
4.1. Long-Run Analysis
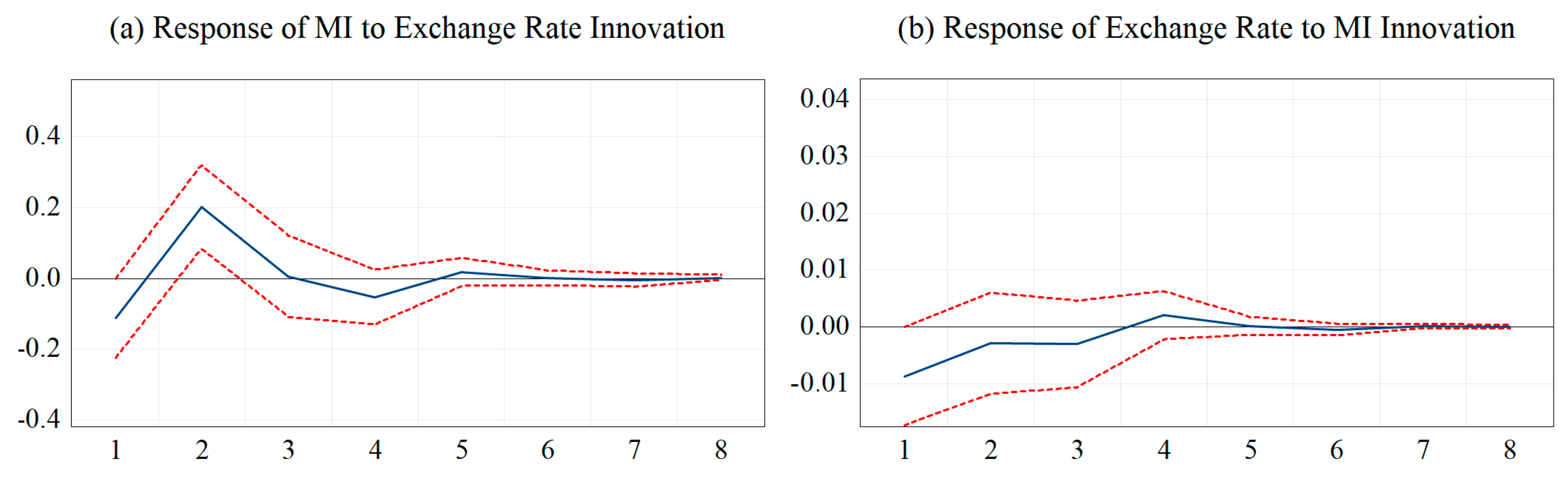
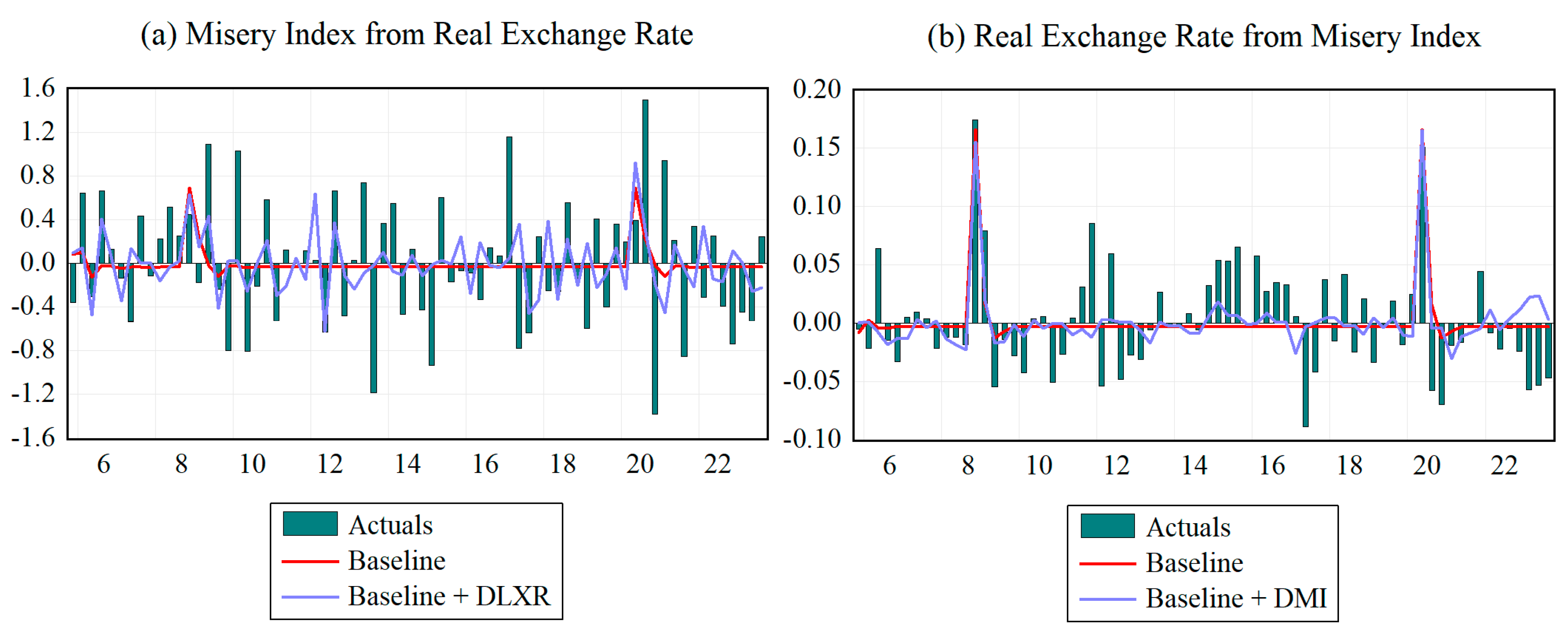
4.2. Short-Run Analysis
5. Conclusions and Recommendations
Limitations
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| * No Serial Correlation at Lag h | * No Serial Correlation at Lags 1 to h | |||||||
|---|---|---|---|---|---|---|---|---|
| Lag | LRE Statistic | p-Value | Rao F-Statistic | p-Value | LRE Statistic | p-Value | Rao F-Statistic | p-Value |
| 1 | 5.362173 | 0.2521 | 1.358754 | 0.2521 | 5.362173 | 0.2521 | 1.358754 | 0.2521 |
| 2 | 8.017090 | 0.0910 | 2.053383 | 0.0910 | 11.99129 | 0.1516 | 1.536009 | 0.1518 |
| 3 | 5.963363 | 0.2019 | 1.514759 | 0.2019 | 14.65726 | 0.2607 | 1.244841 | 0.2614 |
| 4 | 3.297755 | 0.5093 | 0.828727 | 0.5093 | 18.96221 | 0.2706 | 1.209208 | 0.2721 |
| 5 | 6.116185 | 0.1906 | 1.554535 | 0.1907 | 22.59555 | 0.3091 | 1.150382 | 0.3119 |
| 6 | 2.125974 | 0.7126 | 0.531751 | 0.7126 | 22.70972 | 0.5370 | 0.946069 | 0.5415 |
| 7 | 0.118539 | 0.9983 | 0.029412 | 0.9983 | 22.92288 | 0.7369 | 0.803206 | 0.7420 |
| 8 | 5.578133 | 0.2329 | 1.414708 | 0.2330 | 30.56466 | 0.5392 | 0.951003 | 0.5495 |
| 9 | 5.762430 | 0.2176 | 1.462535 | 0.2176 | 32.53910 | 0.6340 | 0.888995 | 0.6469 |
| 10 | 1.102395 | 0.8939 | 0.274603 | 0.8939 | 35.64930 | 0.6664 | 0.869849 | 0.6831 |
| 11 | 3.605337 | 0.4620 | 0.907143 | 0.4621 | 37.50537 | 0.7446 | 0.819598 | 0.7633 |
| 12 | 3.554283 | 0.4697 | 0.894114 | 0.4697 | 43.08476 | 0.6741 | 0.865624 | 0.7025 |
| Null Hypothesis: No Residual Autocorrelations Up to Lag h | |||||
|---|---|---|---|---|---|
| Lags | Q-Statistic | p-Value * | Adj Q-Statistic | p-Value * | d.f. |
| 1 | 0.392710 | --- | 0.398241 | --- | --- |
| 2 | 1.400316 | --- | 1.434635 | --- | --- |
| 3 | 4.833822 | 0.3048 | 5.017424 | 0.2855 | 4 |
| 4 | 8.001211 | 0.4334 | 8.371131 | 0.3981 | 8 |
| 5 | 12.48405 | 0.4076 | 13.18852 | 0.3555 | 12 |
| 6 | 13.76411 | 0.6163 | 14.58494 | 0.5552 | 16 |
| 7 | 13.99566 | 0.8307 | 14.84143 | 0.7854 | 20 |
| 8 | 17.76590 | 0.8142 | 19.08294 | 0.7476 | 24 |
| 9 | 24.21756 | 0.6700 | 26.45627 | 0.5480 | 28 |
| 10 | 25.02663 | 0.8049 | 27.39584 | 0.6989 | 32 |
| 11 | 27.25165 | 0.8528 | 30.02208 | 0.7479 | 36 |
| 12 | 28.40836 | 0.9148 | 31.41014 | 0.8323 | 40 |
| * No Serial Correlation at Lag h | * No Serial Correlation at Lags 1 to h | |||||||
|---|---|---|---|---|---|---|---|---|
| Lag | LRE Statistic | p-Value | Rao F-Statistic | p-Value | LRE Statistic | p-Value | Rao F-Statistic | p-Value |
| 1 | 4.703049 | 0.3191 | 1.188372 | 0.3192 | 4.703049 | 0.3191 | 1.188372 | 0.3192 |
| 2 | 8.283749 | 0.0817 | 2.123120 | 0.0817 | 10.79898 | 0.2134 | 1.376061 | 0.2136 |
| 3 | 3.307509 | 0.5077 | 0.831142 | 0.5078 | 14.37428 | 0.2774 | 1.219006 | 0.2781 |
| 4 | 2.899300 | 0.5748 | 0.727389 | 0.5748 | 19.10525 | 0.2632 | 1.218680 | 0.2647 |
| 5 | 4.038284 | 0.4008 | 1.017716 | 0.4009 | 23.16568 | 0.2807 | 1.182002 | 0.2834 |
| 6 | 0.811291 | 0.9369 | 0.201870 | 0.9369 | 23.32726 | 0.5006 | 0.974510 | 0.5051 |
| 7 | 2.691945 | 0.6106 | 0.674814 | 0.6106 | 25.56886 | 0.5967 | 0.907047 | 0.6031 |
| 8 | 7.014688 | 0.1351 | 1.788810 | 0.1351 | 34.43723 | 0.3519 | 1.091143 | 0.3622 |
| 9 | 9.182917 | 0.0567 | 2.362018 | 0.0567 | 41.82470 | 0.2326 | 1.194874 | 0.2454 |
| 10 | 0.905700 | 0.9237 | 0.225445 | 0.9237 | 43.54280 | 0.3231 | 1.104845 | 0.3423 |
| 11 | 4.360221 | 0.3594 | 1.100251 | 0.3595 | 48.28636 | 0.3038 | 1.114701 | 0.3288 |
| 12 | 1.232252 | 0.8728 | 0.307125 | 0.8728 | 49.33318 | 0.4197 | 1.024552 | 0.4536 |
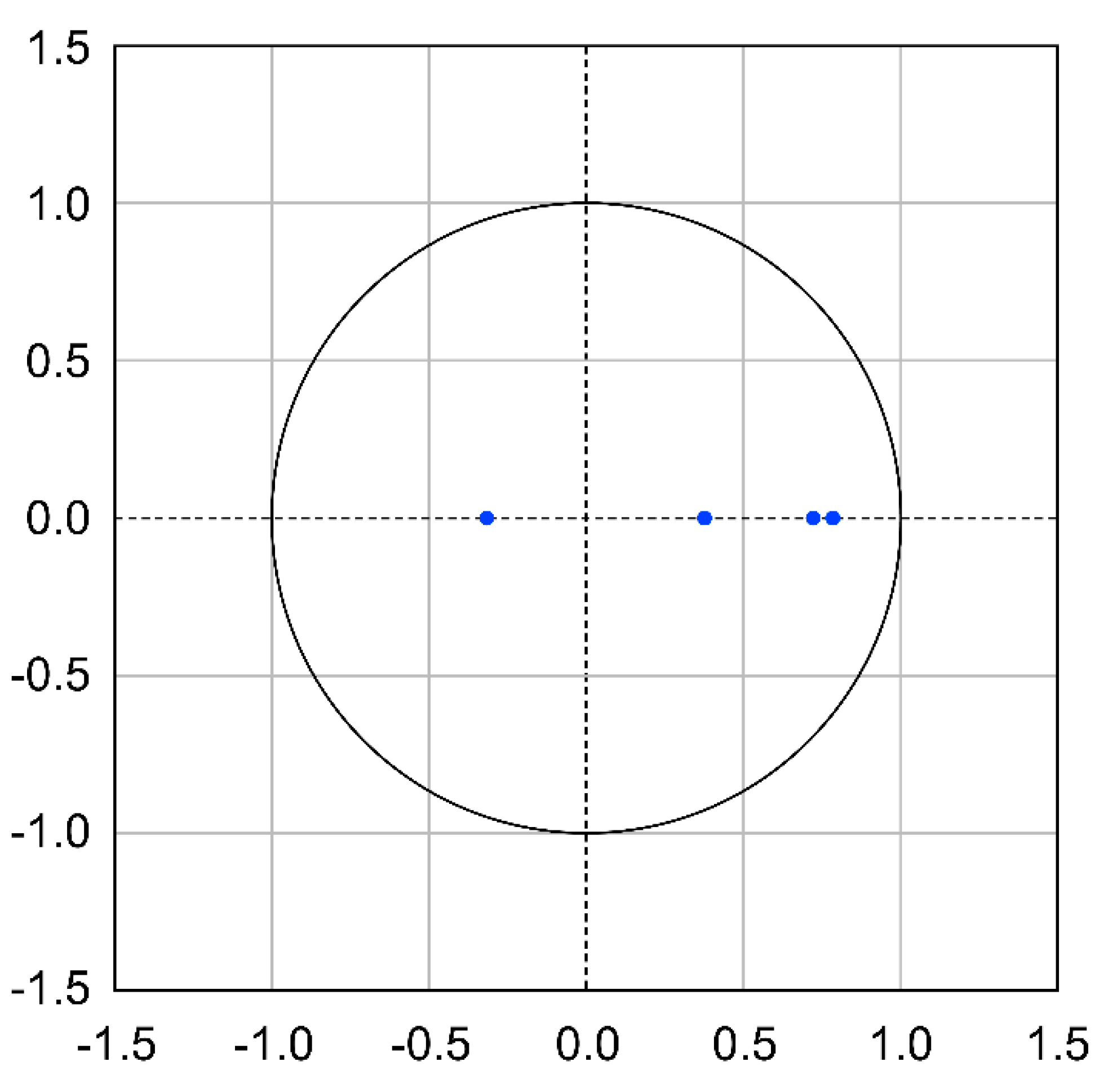
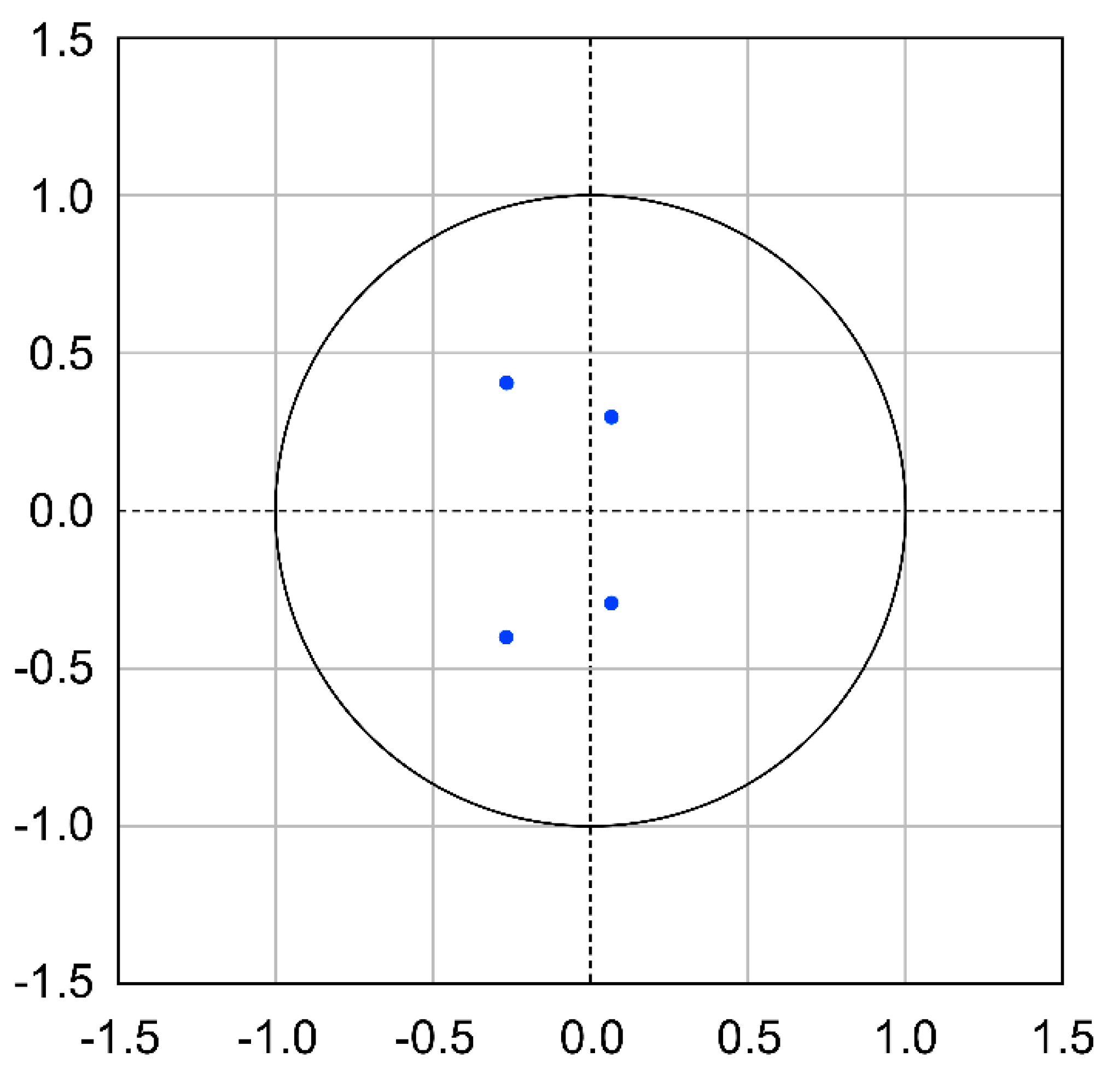
| Statistic | Equation | Equation | ||
|---|---|---|---|---|
| Value | p-Value | Value | p-Value | |
| Maximum LR F-statistic | 1.722261 | 0.6065 | 2.314556 | 0.2738 |
| Maximum Wald F-statistic | 10.33356 | 0.6065 | 13.88734 | 0.2738 |
| Exponential LR F-statistic | 0.635868 | 0.4158 | 0.713582 | 0.3154 |
| Exponential Wald F-statistic | 4.115641 | 0.3489 | 4.983755 | 0.2003 |
| Average LR F-statistic | 1.249985 | 0.2285 | 1.380411 | 0.1579 |
| Average Wald F-statistic | 7.499911 | 0.2285 | 8.282463 | 0.1579 |
| Variable | VIFs |
|---|---|
| 1.013801 | |
| 1.174215 | |
| 1.379386 | |
| 1.232990 | |
| 1.050168 | |
| NA |
References
- Açcı, R. C., & Çuhadar, P. (2021). Unemployment or inflation? What does the misery index say about the causes of crime? METU Studies in Development, 48, 185–200. [Google Scholar]
- Adrangi, B., & Macri, J. (2019). Does the misery index influence a U.S. President’s political re-election prospects? Journal of Risk and Financial Management, 12(1), 22. [Google Scholar] [CrossRef]
- Akarsu, G. (2020). Unemployment, exchange rate and exchange rate volatility relation: Analysis for Turkey. Çankırı Karatekin Üniversitesi İktisadi ve İdari Bilimler Fakültesi Dergisi, 10(1), 179–209. [Google Scholar] [CrossRef]
- Alam, M. S., Shahbaz, M., & Paramati, S. R. (2016). The role of financial development and economic misery on life expectancy: Evidence from post financial reforms in India. Social Indicators Research, 128, 481–497. [Google Scholar] [CrossRef]
- Amiri, A., & Ventelou, B. (2012). Granger causality between total expenditure on health and GDP in OECD: Evidence from the Toda–Yamamoto approach. Economics Letters, 116(3), 541–544. [Google Scholar] [CrossRef]
- Ani, E. C., Joel, E., & Baajon, M. A. (2019). Exchange rate and unemployment in Nigeria: An analysis. International Journal of Family Business and Management, 3(2), 1–7. [Google Scholar] [CrossRef]
- Ayala, D. (2025). Tipo de cambio se dispara tras confirmación de aranceles de Donald Trump. El Economista. Available online: https://www.eleconomista.com.mx/mercados/peso-mexicano-dispara-confirmacion-aranceles-20250131-744495.html (accessed on 13 March 2025).
- Bakhshi, Z., & Ebrahimi, M. (2016). The effect of real exchange rate on unemployment. Marketing and Branding Research, 3(1), 4–13. [Google Scholar] [CrossRef]
- Banco de México. (2023). Índice de tipo de cambio real bilateral con precios consumidor y con respecto a los Estados Unidos de América-(CR183). Sistema de Información Económica. Available online: https://www.banxico.org.mx/SieInternet/consultarDirectorioInternetAction.do?sector=2&accion=consultarCuadro&idCuadro=CR183&locale=es (accessed on 8 March 2025).
- Banerjee, R., Hofmann, B., & Mehrotra, A. (2022). Corporate investment and the exchange rate: The financial channel. International Finance, 25(3), 296–312. [Google Scholar] [CrossRef]
- Bayar, Y., & Aytemiz, L. (2019). The misery index, corruption and income inequality in Latin American countries: A panel cointegration and causality analysis. Scientific Annals of Economics and Business, 66(3), 309–319. [Google Scholar] [CrossRef]
- Burbidge, J., & Harrison, A. (1985). A historical decomposition of The Great Depression to determine the role of money. Journal of Monetary Economics, 16(1), 45–54. [Google Scholar] [CrossRef]
- Bush, G., & López Noria, G. (2021). Uncertainty and exchange rate volatility: Evidence from Mexico. International Review of Economics and Finance, 75, 704–722. [Google Scholar] [CrossRef]
- Büyüksarıkulak, A. M., & Suluk, S. (2022). The misery index: An evaluation on fragile five countries. Abant Sosyal Bilimler Dergisi, 22(3), 1108–1123. [Google Scholar] [CrossRef]
- Camhaji, E. (2025). El nuevo campo de negociación entre Sheinbaum y Trump: Aranceles, migración y fentanilo. El País. Available online: https://elpais.com/mexico/2025-02-04/el-nuevo-campo-de-negociacion-entre-sheinbaum-y-trump-aranceles-migracion-y-fentanilo.html (accessed on 16 March 2025).
- Chafetz, J. (2024). Is Mexico safe? An intel analyst’s guide to traveling in Mexico. Global Guardian. Available online: https://www.globalguardian.com/global-digest/is-mexico-safe (accessed on 13 March 2025).
- Chang, S. (2011). The interrelationship between exchange-rate and unemployment for South Korea and Taiwan: Evidence from a vector autoregressive approach. International Economics, 125, 65–82. [Google Scholar] [CrossRef]
- Charemza, W. W., & Deadman, D. F. (1997). New directions in econometric practice: General to specific modelling, cointegration, and vector autoregression. Edward Elgar Publishing. [Google Scholar]
- Clemens, J., Palacios, M., & Li, N. (2022). The misery index returns. Fraser Research Bulletin. [Google Scholar]
- Cohen, I. K., Ferretti, F., & McIntosh, B. (2014). Decomposing the misery index: A dynamic approach. Cogent Economics and Finance, 2(1), 991089. [Google Scholar] [CrossRef]
- Djivre, J., & Ribon, S. (2003). Inflation, unemployment, the exchange rate, and monetary policy in Israel, 1990–99: A SVAR approach. Israel Economic Review, 1(2), 71–99. [Google Scholar]
- Dornbusch, R., Fischer, S., & Startz, R. (2002). Macroeconomía. McGraw-Hill. [Google Scholar]
- Enders, W. (2015). Applied econometric time series. John Wiley & Sons. [Google Scholar]
- Expansión. (2025). Aranceles e inflación de EU moverán al tipo de cambio esta semana. Expansión. Available online: https://expansion.mx/mercados/2025/02/10/tipo-de-cambio-dolar-peso-se-movera-aranceles-inflacion-eu (accessed on 1 March 2025).
- Faintuch, Z., & Chafetz, J. (2024). The most dangerous countries in the world by region. Global Guardian. Available online: https://www.globalguardian.com/global-digest/most-dangerous-countries (accessed on 13 March 2025).
- Feldmann, H. (2011). The unemployment effect of exchange rate volatility in industrial countries. Economics Letters, 111(3), 268–271. [Google Scholar] [CrossRef]
- Gaddo, F. (2011). An international analysis of the misery index. Fondazione Magna Carta. [Google Scholar]
- Gaite, P., & Marturet, T. N. (2022). Enseñanzas del modelo de Krugman y Taylor (1978). Cuadernos de Economía Crítica, 8(15), 165–176. [Google Scholar]
- Gakuru, E., & Yang, S. (2024). Misery index improvement: A review based on theoretical and empirical evidence. Journal of the Knowledge Economy, 16, 3970–3995. [Google Scholar] [CrossRef]
- Galindo, A., Izquierdo, A., & Montero, J. M. (2007). Real exchange rates, dollarization and industrial employment in Latin America. Emerging Markets Review, 8(4), 284–298. [Google Scholar] [CrossRef]
- Grabia, T. (2012). The Okun misery index in the European Union countries from 2000 to 2009. Comparative Economic Research. Central and Eastern Europe, 14(4), 97–115. [Google Scholar] [CrossRef]
- Gujarati, D. N., & Porter, D. C. (2009). Econometría. McGraw-Hill. [Google Scholar]
- Guzmán, M., & García, P. (2008). El modelo VAR y sus principales problemas. Panorama Económico, 3(26), 95–117. [Google Scholar] [CrossRef][Green Version]
- Hortalà i Arau, J., & Rey Miró, D. (2011). Relevancia del índice de malestar económico. Cuadernos de Economía, 34(96), 162–169. [Google Scholar] [CrossRef]
- INEGI. (2023). Banco de información económica. Available online: https://www.inegi.org.mx/app/indicadores/?tm=0 (accessed on 4 December 2023).
- Jaramillo, P. G. (2009). Estimación de VAR bayesianos para la economía chilena. Revista de Análisis Económico, 24(1), 101–126. [Google Scholar]
- Johnson, O. E. G. (1987). Currency depreciation and imports: The many ways in which depreciation can affect imports. Finance & Development, 24(2), 18–21. [Google Scholar] [CrossRef]
- Krugman, P., Obstfeld, M., & Melitz, M. J. (2023). International economics: Theory and policy. Pearson. [Google Scholar]
- Krugman, P., & Taylor, L. (1978). Contractionary effects of devaluation. Journal of International Economics, 8(3), 445–456. [Google Scholar] [CrossRef]
- Lizondo, J. S., & Montiel, P. J. (1989). Contractionary devaluation in developing countries: An analytical overview. Staff Papers (International Monetary Fund), 36(1), 182–227. [Google Scholar] [CrossRef]
- Lovell, M. C., & Tien, P. (2000). Economic discomfort and consumer sentiment. Eastern Economic Journal, 26(1), 1–8. [Google Scholar] [CrossRef]
- Melgoza, R. (2025). Tipo de cambio podría superar los 24 pesos por dólar por aranceles de Trump: BBVA. El Economista. Available online: https://www.eleconomista.com.mx/mercados/peso-mexicano-superar-24-pesos-dolar-aranceles-trump-bbva-20250201-744602.html (accessed on 15 March 2025).
- Muhammad, A., D’Souza, A., & Amponsah, W. (2013). Violence, instability, and trade: Evidence from Kenya’s cut flower sector. World Development, 51, 20–31. [Google Scholar] [CrossRef]
- Murphy, R. H. (2016). A short empirical note on state misery indexes. Journal of Regional Analysis & Policy, 46(2), 186–189. [Google Scholar]
- Okun, A. M. (1962). Potential GNP: Its measurement and significance (Cowles foundation paper 190). Cowles Foundation for Research in Economics, Yale University. [Google Scholar]
- Ouliaris, S., & Rochon, C. (2018). The U.S. personal saving rate (Working paper: WP/18/128). International Monetary Fund. [Google Scholar] [CrossRef]
- Ramoni-Perazzi, J., & Orlandoni-Merli, G. (2013). El índice de miseria corregido por informalidad: Una aplicación al caso de Venezuela. Ecos de Economía, 17(36), 29–49. [Google Scholar] [CrossRef]
- Redacción AN/MDS. (2025). Aranceles a México son por migración y fentanilo, no por el T-MEC: Trump. Aristegui Noticias. Available online: https://aristeguinoticias.com/220125/dinero-y-economia/aranceles-a-mexico-son-por-migracion-y-fentanilo-no-por-el-t-mec-trump/ (accessed on 15 March 2025).
- Riascos, J. C. (2009). El índice de malestar económico o índice de miseria de Okun: Breve análisis de casos, 2001–2008. Tendencias, 10(2), 92–124. [Google Scholar]
- Sánchez, F. (2020). Índice de miseria de Okun: Una aproximación para México. In J. N. Cruz (Ed.), Pobreza y desigualdades en México: Revisión teórica y ejercicios prácticos (pp. 155–181). Instituto de Investigaciones Económicas—UNAM. [Google Scholar] [CrossRef]
- Sánchez, F. (2022). Measuring the effect of the misery index on international tourist departures: Empirical evidence from Mexico. Economies, 10(4), 81. [Google Scholar] [CrossRef]
- Secretaría de Economía. (2023). Comercio exterior, países con tratados y acuerdos firmados con México. Gobierno de México. Available online: https://www.gob.mx/se/acciones-y-programas/comercio-exterior-paises-con-tratados-y-acuerdos-firmados-con-mexico (accessed on 15 March 2025).
- Singh, J. (2024). Does economic misery stifle human development? Empirical evidence from Asian countries. GeoJournal, 89(3), 116. [Google Scholar] [CrossRef]
- Toda, H. Y., & Yamamoto, T. (1995). Statistical inference in vector autoregressions with possibly integrated processes. Journal of Econometrics, 66(1–2), 225–250. [Google Scholar] [CrossRef]
- Topbie, J. A., Anyamaobi, G. N., & Lasisi, O. K. (2024). Implication of macroeconomic fundamentals on the twin-evil of macroeconomic phenomena: “With the focus on Nigeria”. International Journal of Humanity and Social Sciences, 3(5), 15–30. [Google Scholar] [CrossRef]
- Tule, K. M., Egbuna, E. N., Dada, E., & Ebuh, G. U. (2017). A dynamic fragmentation of the misery index in Nigeria. Cogent Economics & Finance, 5(1), 1336295. [Google Scholar] [CrossRef]
- Vélez, M. A., & Peña, D. D. (2024). Inversión extranjera y su relación con el tipo de cambio en México. Commercium Plus, 6(2), 108–116. [Google Scholar] [CrossRef]
- Wang, N., Shah, M. H., Ali, K., Abbas, S., & Ullah, S. (2019). Financial structure, misery index, and economic growth: Time series empirics from Pakistan. Journal of Risk and Financial Management, 12(2), 100. [Google Scholar] [CrossRef]
- Wiseman, C. (1992). More on misery: How consistent are alternative indices? A comment. The American Economist, 36(2), 85–88. [Google Scholar] [CrossRef]
- Yang, B., & Lester, D. (1999). The misery index and suicide. Psychological Reports, 84(3), 1086. [Google Scholar] [CrossRef]
| Series | Innovation Outlier | Additive Outlier | ||||||
|---|---|---|---|---|---|---|---|---|
| I | II | III | IV | I | II | III | IV | |
| −3.998 | −3.330 | −3.628 | −2.825 | −3.643 | −3.397 | −3.550 | −2.952 | |
| −3.281 | −4.644 * | −4.622 | −4.041 | −3.759 | −4.745 * | −4.758 | −3.218 | |
| −4.083 | −3.644 | −3.515 | −2.781 | −3.677 | −3.411 | −3.500 | −2.917 | |
| −9.274 *** | −9.225 *** | −8.910 *** | −7.886 *** | −9.313 *** | −9.331 *** | −8.834 *** | −8.026 *** | |
| −12.85 *** | −13.01 *** | −13.02 *** | −13.03 *** | −14.37 *** | −14.40 *** | −13.82 *** | −4.931 *** | |
| −8.618 *** | −8.569 *** | −8.350 *** | −7.759 *** | −8.693 *** | −8.708 *** | −8.392 *** | −7.901 *** | |
| Lag | LR | FPE | AIC | SIC | HQ |
|---|---|---|---|---|---|
| 0 | NA | 116.2548 | 10.43153 | 10.49735 | 10.45758 |
| 1 | 184.5155 | 7.331994 | 7.667882 | 7.865317 | 7.746007 |
| 2 | 16.11427 | 6.373693 * | 7.527377 * | 7.856436 * | 7.657587 * |
| 3 | 2.462904 | 6.899910 | 7.605732 | 8.066414 | 7.788025 |
| 4 | 10.55843 * | 6.492230 | 7.543093 | 8.135398 | 7.777470 |
| 5 | 1.104440 | 7.192347 | 7.642774 | 8.366703 | 7.929234 |
| 6 | 2.288530 | 7.799099 | 7.719797 | 8.575349 | 8.058341 |
| 7 | 2.379900 | 8.441051 | 7.793432 | 8.780608 | 8.184060 |
| 8 | 7.849587 | 8.188671 | 7.755844 | 8.874643 | 8.198555 |
| Data Trend | None | None | Linear | Linear | Quadratic |
|---|---|---|---|---|---|
| Test Type | No Intercept No Trend | Intercept No Trend | Intercept No Trend | Intercept Trend | Intercept Trend |
| Two Lags | |||||
| Trace | 0 | 0 | 0 | 0 | 0 |
| Max-Eig | 0 | 0 | 0 | 0 | 0 |
| Four Lags | |||||
| Trace | 0 | 0 | 0 | 0 | 0 |
| Max-Eig | 0 | 0 | 0 | 0 | 0 |
| Lag | LR | FPE | AIC | SIC | HQ |
|---|---|---|---|---|---|
| 0 | NA | 0.000497 | −1.932124 | −1.799417 | −1.879685 |
| 1 | 22.23605 * | 0.000392 | −2.169558 | −1.904145 * | −2.064680 * |
| 2 | 8.495226 | 0.000384 * | −2.189932 * | −1.791813 | −2.032617 |
| 3 | 6.810211 | 0.000386 | −2.186138 | −1.655312 | −1.976383 |
| 4 | 1.634125 | 0.000424 | −2.094106 | −1.430575 | −1.831914 |
| 5 | 1.092194 | 0.000471 | −1.993120 | −1.196882 | −1.678489 |
| 6 | 1.004325 | 0.000524 | −1.891222 | −0.962278 | −1.524152 |
| 7 | 5.577000 | 0.000533 | −1.881550 | −0.819899 | −1.462041 |
| 8 | 8.029342 | 0.000513 | −1.927616 | −0.733259 | −1.455668 |
| Variable | ||
|---|---|---|
| 0.478737 [3.98217] | 0.074604 [0.06398] | |
| 0.225245 [1.78380] | −0.573589 [−0.46833] | |
| 0.038671 [3.00923] | 1.065944 [8.55179] | |
| −0.030162 [−1.55877] | −0.225278 [−1.20033] | |
| 0.780846 [1.14093] | 11.82874 [1.78191] | |
| 0.191187 [1.67823] | −0.306813 [−0.27767] | |
| −0.011081 [−0.80242] | 0.083919 [0.62655] | |
| 0.677962 | 0.895723 | |
| Adjusted | 0.648235 | 0.886097 |
| Null Hypotheses | d.f. | p-Value | |
|---|---|---|---|
| does not Granger cause | 9.666012 | 2 | 0.0080 *** |
| does not Granger cause | 0.265825 | 2 | 0.8755 |
| Variables | ||
|---|---|---|
| 0.128823 [1.31272] | 3.819202 [3.02555] | |
| −0.030660 [−0.28781] | 1.670138 [1.21883] | |
| −0.003668 [−0.40536] | −0.530535 [−4.55862] | |
| −0.008184 [−0.96880] | −0.278505 [−2.56302] | |
| −0.003381 [−0.75140] | −0.047239 [−0.81612] | |
| 0.169423 [6.16693] | 0.723980 [2.04870] | |
| 0.382458 | 0.333405 | |
| Adjusted | 0.335675 | 0.282905 |
| Test | Value | p-Value | |
|---|---|---|---|
| Doornik–Hansen normality test | |||
| Skewness | 0.865978 | 0.6486 | |
| Kurtosis | 0.228025 | 0.8922 | |
| Jarque–Bera | 1.094002 | 0.8952 | |
| White heteroskedasticity test (no cross-terms) | 37.03463 | 0.0944 | |
| White heteroskedasticity test (cross-terms) | 55.19198 | 0.2214 | |
| Null Hypotheses | p-Value | ||
|---|---|---|---|
| does not Granger cause | 11.65146 | 2 | 0.0030 *** |
| does not Granger cause | 0.938579 | 2 | 0.6254 |
| Period | ||||
|---|---|---|---|---|
| 1 | 100.000 | 0.000 | 5.383 | 94.616 |
| 5 | 98.912 | 1.087 | 16.528 | 83.471 |
| 10 | 98.900 | 1.099 | 16.532 | 83.467 |
| 15 | 98.900 | 1.099 | 16.532 | 83.467 |
| 20 | 98.900 | 1.099 | 16.532 | 83.467 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sánchez, F.; Arias Guzmán, E.J. Assessing the Impact of the Real Exchange Rate on Okun’s Misery Index in Mexico. Economies 2025, 13, 168. https://doi.org/10.3390/economies13060168
Sánchez F, Arias Guzmán EJ. Assessing the Impact of the Real Exchange Rate on Okun’s Misery Index in Mexico. Economies. 2025; 13(6):168. https://doi.org/10.3390/economies13060168
Chicago/Turabian StyleSánchez, Fernando, and Ericka Judith Arias Guzmán. 2025. "Assessing the Impact of the Real Exchange Rate on Okun’s Misery Index in Mexico" Economies 13, no. 6: 168. https://doi.org/10.3390/economies13060168
APA StyleSánchez, F., & Arias Guzmán, E. J. (2025). Assessing the Impact of the Real Exchange Rate on Okun’s Misery Index in Mexico. Economies, 13(6), 168. https://doi.org/10.3390/economies13060168







