Abstract
In this paper, the Balassa–Samuelson–Tariffi effect is revisited. This research first aims to explain that the behaviour of the real exchange rate shows structural breaks in the short term. A partial equilibrium model “á la Rogoff” is formally formulated where there are relative prices of non-tradable goods in terms of tradable goods in the supply side. Secondly, a general equilibrium model is built after a utility function is added to the partial equilibrium model. It is presented as a mathematical mechanism that shows a stationary state in the real exchange rate considering not only non-tradable goods but also tradable goods both in the domestic market and the foreign market. It is explained that any change in a currency’s price in terms of another currency in real terms is transitory in the long run, thereby disappearing after a certain period of time. In the general equilibrium model, any price’s change in non-tradable goods will be compensated by either a price’s change in tradable goods or changes in the nominal exchange rate. Therefore, this study’s main contribution is to show theoretically that the real exchange rate is constant over time in the long run.
JEL Classification:
F31; F41
1. Introduction
Could a real exchange rate’s fluctuations be explained by structural breaks? Are those breaks in real exchange rates transitory changes or permanent changes? Is there a relationship between the real exchange rate (RER) and another real variable? Is the RER constant over time in the long run? These are some of the questions that academics and policy makers have been asking themselves when they study not only the behaviour of the main currencies’ prices around the globe but also the differences in prices of goods and services across borders.
On the one hand, empirical evidence has been found regarding the first question about the existence of structural breaks in the time series of real exchange rates. Econometric models have shown that there are permanent changes in real exchange rates (RERs). According to these models, permanent changes of RERs are explained by fluctuations in real economic variables, which have statistically significant effects over RERs. Those changes in RERs are related to significant variations in other economic variables such as tariffs on imports in the eurozone (Tariffi, 2019), or they are linked to determinants’ fluctuations in real economic activity such as productivity improvements in Brazil, Russia, and China (Tariffi, 2012).
However, it is possible that structural breaks could not be found on times series such as RER in the long run even if they are found when it is considered only in the short term. Since the short-term behaviour of the real exchange rate has been modelled—and theoretically explained—in previous papers, in this paper I am going to present a general equilibrium model with tradables and non-tradable goods for the long run. A partial equilibrium model with only the supply side has been previously published in the literature mentioned before. In this paper, there is a model of real exchange rates that includes not only the supply side but also the demand side to show the general equilibrium for both consumers and producers.
In order to model the behaviour of the real exchange rate, I have found two main theoretical models. On the one hand, structural breaks in the RER are explained by the Balassa–Samuelson effect. In the previous literature, Balassa (1964) and Samuelson (1964) criticise the purchasing power parity (PPP) theory and they highlight the relationship between productivity and currency overvaluations. Since it built a new theoretical model to show the mechanism that explains the relationship between productivity and the real exchange rate based on the Balassa–Samuelson effect (Tariffi, 2010, 2012, 2013, 2019), I am going to call this new theoretical model the Balassa–Samuelson–Tariffi effect from now on. This mechanism emphasises that those structural changes in the RER are related to fluctuations in the ratio productivity of tradable goods relative to productivity of non-tradable goods in the domestic country and productivity of tradable goods relative to productivity of non-tradable goods in the foreign country. This mechanism will bring simultaneous equilibria in both internal and external markets as in Edwards (1988a) and Edwards (1988b).
Moreover, this theory also shows that changes in foreign prices of tradable goods relative to prices of non-tradable goods in terms of domestic prices of tradable goods relative to prices of non-tradable goods cannot be offset by changes in the nominal exchange rate. Based on Obstfeld and Rogoff (1999), Tariffi (2010, 2012, 2013, 2019) shows that there is a mathematical mechanism in the relationship between productivity and the real ex-change rate. Moreover, Azcona (2017) shows the link between productivity and the RER in a specific case where there is a Cobb–Douglas production function with both tradable and non-tradable sectors, but he does not include the utility function in the partial equilibrium model in order to find a general equilibrium model. My approach is similar to the model that can be found in the baseline of the new Keynesian model in a small open economy developed by Galí and Monacelli (2016), but they do not classify consumption in both tradable and non-tradable goods as I do in this paper.
On the other hand, real exchange rate’s transitory changes have been long explained through the purchasing power parity (PPP) theory. There is a significant amount of literature related to the purchasing power parity (PPP) theory, and it has been widely debated. Cassel (1918) published an early paper in the exchange rate’s literature to introduce the concept of purchasing power parity (PPP). Mundell (1960) and Fleming (1962) specify that the fixed-exchange-rate system operates most effectively if capital is highly mobile while the flexible-exchange-rate system works best if capital is immobile. These authors also say that the expansionary effect of a given increase in money supply is greater if a country has a floating exchange rate than if it has a fixed rate. Dornbusch (1976) studies the role of capital mobility in economies with flexible exchange rate regimes to analyse the long-run equilibrium. Therefore, the PPP mechanism is able to keep the RER constant over time. This characteristic of the RER’s behaviour is a proportional result of those changes in international prices across countries that are equally compensated by fluctuations in the nominal exchange rate. The RER’s time series shows transitory changes as a consequence of compensations not only between domestic and foreign prices but also taking into account the price of one currency in terms of another. In any case, the PPP puzzle is one of the central questions in international economics and it has been largely addressed by many authors (Blanco & Cravino, 2020; Bordo et al., 2017; Carvalho & Nechio, 2011; Rogoff, 1996; Sardà & Pérez-Lacasta, 2003; Tariffi, 2024).
In the next sections, I first revisit the Balassa–Samuelson–Tariffi effect, and I write a partial equilibrium model “á la Rogoff” to explain why there are structural breaks in the real exchange rate. Secondly, I build a general equilibrium model to explain the behaviour of the real exchange rate in the long run considering both tradable and non-tradable goods. Finally, the last section concludes my work in this paper.
2. The Partial Equilibrium Model
In order to start building the model, I recall the partial equilibrium model to analyse the supply side, as in Figure 1. When there are structural breaks in real exchange rates, the technology determines levels of productivity in which economies produce tradable goods relative to non-tradable goods.
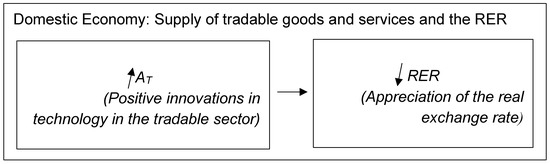
Figure 1.
Supply of tradable goods in the domestic economy. An improvement in technology in the tradable sector decreases the real exchange rate.
As a result of innovations in the tradable sector AT, if there are improvements in productivity of tradable goods relative to non-tradable goods, which are higher in the domestic economy than those in the foreign economy, the RER decreases, and it appreciates.
Formally, the partial equilibrium model is based on the Balassa–Samuelson–Tariffi effect for the short term. As in Obstfeld and Rogoff (1999), there are two economies and two types of goods, tradables T and non-tradables NT.
Production functions are given by
where Y is output, K is capital, L is labour, and A is technology or total factor productivity. Even if F denotes production functions in both tradable and non-tradable sectors, firms producing goods in the tradable sector transform inputs to outputs applying a different technology from that which is applied in the non-tradable sector. Outputs are given by constant returns to scale in F(.), and there are positive and diminishing returns in inputs. In the limit, the first derivatives of F(.) satisfy the Inada condition.
YT = AT F1(KT, LT)
YNT = ANT F2(KNT, LNT),
The firm’s maximisation problem is given by
for both tradable and non-tradable sectors such that these three beforementioned conditions are satisfied. Parameter (1/(1 + z)) ∈ [0, 1] is the discount factor, P is the price of goods and services, w is the level of labour wage for workers, r is the capital’s price, and i = 1, 2. For simplicity, it is assumed that capital depreciation is equal to zero.
(π) = Σt∞ (1/(1 + z))t [P × AFi(K, L) − wL − rK]
As shown in the Appendix A, first order conditions for both production functions are the following:
where Ə and ’ denote a derivative, and k = K/L is labour per capita. Equations (1) and (2) can be represented by the following equations:
Əπ/ƏK = 0 → P × Af’(k) − r = 0 → r = P × Af’(k)
Əπ/ƏL = 0 → P × A[f(k) − f’(k)k] − w = 0 → w = P × A[f(k) − f’(k)k]
Tradable goods sector:
r = PT × ATf’(kT)
w = PT × AT[f(kT) − f’(kT)kT]
Non-tradable sector:
r = PNT × ANTf’(kNT)
w = PNT × ANT[f(kNT) − f’(kNT)kNT]
It is assumed that the level of prices is defined in geometric averages with weights equal to γ and 1 − γ for tradable goods prices and non-tradable goods prices, respectively.
where PD is goods and services at domestic prices, and PE is goods and services at foreign prices. Assuming also perfect mobility of labour in between both tradable and non-tradable productive sectors, the following equations can be obtained:
where D is the domestic country, and E is the foreign country.
PD = PDTγ × PDNT1−γ
PE = PETγ × PENT1−γ
PDT × ADT[d(kDT) − d’(kDT)kDT] = w = PDNT × ADNT[d(kDNT) − d’(kDNT)kDNT]
PET × AET[g(kET) − g’(kET)kET] = w = PENT × AENT[g(kENT) − g’(kENT)kENT]
Note that—as has been explained by Égert et al. (2006)—there is a component of prices of tradable goods that can be considered as exogenous and determined on the international market. Without losing generalisation, tradable goods prices—for both domestic and foreign markets—can be equal to the numeraire (PDT = PET = 1).
Thus, I rewrite Equations (3) and (4) as
PD = (1)γ × PDNT1−γ = PDNT1−γ
PE = (1)γ × PENT1−γ = PENT1−γ
Real exchange rate is defined as RER = c1 × [(NER × PE)/PD], where NER is the nominal exchange rate. Assuming that the abovementioned PPP holds only for the tradable goods competitive market, the nominal exchange rate is given by
NER = c2 × (PDT/PET)
Rewriting Equation (9), that is, PDT = (NER × PET)/c2, and combining this equation with the numeraire 1 = (NER × 1)/c2, the nominal exchange rate is constant over time, as NER = c2. Thus, the real exchange rate can be written as
RER = (c1 × c2) [PE/PD]
Combining Equations (5)–(8) and the RER, the Balassa–Samuelson–Tariffi effect can be obtained as
RER = c3 × {AET[g(kET) − g’(kET)kET]/AENT[g(kENT) − g’(kENT)kENT]}1−γ/
{ADT[d(kDT) − d’(kDT)kDT]/ADNT[d(kDNT) − d’(kDNT)kDNT]}1−γ
{ADT[d(kDT) − d’(kDT)kDT]/ADNT[d(kDNT) − d’(kDNT)kDNT]}1−γ
When improvements in productivity of tradable goods relative to non-tradable goods are higher in the domestic economy than the corresponding productivity ratio in the foreign economy, the real exchange rate decreases, and it gets appreciated. Assuming a non-tradable sector intensive in labour and a tradable sector intensive in capital, the Balassa–Samuelson–Tariffi effect explains that domestic economic growth increases technological progress and improves tradable goods productivity levels relative to non-tradable goods productivity. This productivity improvement in the domestic economy—relative to the foreign economy—decreases the real exchange rate. At the same time, when an increase in the productivity of the tradable goods sector relative to the productivity of the non-tradable goods sector is greater in the domestic economy than in the foreign economy, there are both a decrease and an appreciation of the real exchange rate.
3. The General Equilibrium Model
In order to go from a partial equilibrium model to a general equilibrium one, it is necessary to include the demand side and the utility function in the model. It means that those structural breaks that can be found in real exchange rates are just transitory changes, and the real exchange rate is constant over time in the long run. An example of such a demand side is the one that can be explained through a quite simple model shown in Figure 2. When increasing levels of consumption raise imports of goods and services, there is also an increment in the level of the real exchange rate, and it depreciates, thereby compensating those changes shown in Figure 1 where there is only the supply side in the partial equilibrium model.
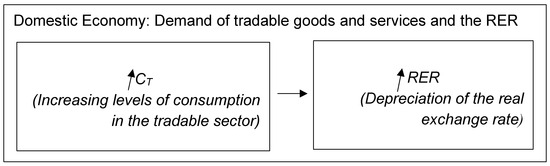
Figure 2.
Demand of tradable goods in the domestic economy.
In order to build a formal general equilibrium model with real exchange rates, it is considered a small economy with both tradable and non-tradable sectors. As in Section 2, production functions are given by
YT = AT F1(KT, LT)
YNT = ANT F2(KNT, LNT)
Notice that A is a productivity shifter in a way that the labour factor is internationally immobile across countries in the model, but workers are allowed to migrate instantaneously from one economic sector to another one within the economy.
The firm’s maximisation problems are
for the tradable and the non-tradable sectors, respectively.
(π) = Σs=t∞ (1/(1 + r))s−t [AT,S F1(KT,S, LT,S) − wSLT,S − ΔKT,S+1]
(π) = Σs=t∞ (1/(1 + r))s−t [PDNT,S × ANT,S F2(KNT,S, LNT,S) − wSLNT,S − ΔKNT,S+1]
As in Obstfeld and Rogoff (1999), r is a constant world interest rate, ΔK is the Kt+1 − Kt, (π) = Vt = Σs=t∞ (1/(1 + r))s−t ds, and PDNT is the relative price of domestic non-tradables in terms of tradables in the dynamic model. First-order conditions for capital and labour can be represented by the following equations:
Tradable goods sector:
r = ATf’(kT)
w = AT[f(kT) − f’(kT)kT]
r = ATf’(kT)
w = AT[f(kT) − f’(kT)kT]
Non-tradable goods sector:
r = PNT × ANTf’(kNT)
w = PNT × ANT[f(kNT) − f’(kNT)kNT]
r = PNT × ANTf’(kNT)
w = PNT × ANT[f(kNT) − f’(kNT)kNT]
The representative consumer maximises a lifetime utility function = (see Appendix A for more details).
If it is assumed that consumer preferences are homothetic, and the utility function is of the Cobb–Douglas form u(CT, CNT) = G(CTh CNT1−h), for some strictly concave and increasing function G(.), the optimal consumption demands will satisfy
(Əu/ƏCNT)/(Əu/ƏCT) = PDNT = (1 − h) CT/h CNT
Notice that the assumption of homothetic preferences implies that the ratio between tradable and non-tradable consumption depends on the relative price of non-tradables PDNT, and not on the spending level.
It is also assumed that the economy is in a steady state with national consumption spending equal to income in the following way:
where Q is financial wealth, and B is net foreign assets. The general equilibrium can be found—assuming a steady state à la Rogoff—as follows:
Q ≡ B + KT + KNT = B + K
The overbars denote equilibrium values associated with a steady state in consumption. The domestic supply can be written algebraically as
Since the economy has been assumed stationary with unchanging financial wealth, the steady-state consumption expenditure is written as the following:
Solving this equation for T yields the economy’s steady-state budget constraint.
If the utility function is represented by a special case of the constant-elasticity-of-substitution (CES) form, it is described as
u(CT, CNT) = [h1/θCT(θ−1)/θ + (1 − h)1/θCNT(θ−1)/θ]θ/(θ−1), γ ϵ (0,1), θ > 0
When maximising the CES utility function subject to the constraint of the total expenditure function measured as Z = CT + PDNT CNT, it yields
hCNT/(1 − h) CT = PDNT−θ
In this case, the relative demand depends not only on domestic, non-tradable prices but also on the elasticity of substitution between tradables and non-tradables θ.
In the previous Section 2, it is assumed that the level of prices is defined in geometric averages, and tradable goods prices—for both domestic and foreign markets—are equal to the numeraire (PDT = PET = 1) as follows:
PD = PDTγ × PDNT1−γ and PD = (1)γ × PDNT1−γ = PDNT1−γ
PE = PETγ × PENT1−γ and PE = (1)γ × PENT1−γ = PENT1−γ
Therefore, the law of one price holds in the long run, and the home-to-foreign price level ratio is
PD/PE = PDNT1−γ/PENT1−γ
In the above case, the nominal exchange rate is given by NER = c2 × (PDT/PET), which can be rewritten as PDT = (NER × PET)/c2. Combining last equation with the numeraire, 1 = (NER × 1)/c2 can be obtained, and the nominal exchange rate is constant over the time, as NER = c2. Finally, recalling the definition of the real exchange rate, RER = c1 × [(NER × PE)/PD], the real exchange rate can be written as RER = (c1 × c2) [PE/PD].
In this section, it is shown that the general equilibrium model allows for a utility function. Relative consumption depends on domestic, non-tradable prices when the utility function takes the Cobb–Douglas form, and it depends not only on domestic, non-tradable prices but also on the elasticity of substitution when the utility function takes the CES form.
Substituting Equations (10) and (11) in RER = (c1 × c2) [PENT1−γ/PDNT1−γ], the results are the two following equations:
RER = (c1 × c2) [PENT1−γ/[(1 − h) CT/h CNT]1−γ]
RER = (c1 × c2) [PENT1−γ/{[h CNT/(1 − h) CT]θ}1−γ]
Depending on the consumption share in tradables with respect to non-tradables and elasticity of substitution of consumption between both tradables and non-tradables, Equations (13) and (14) explain that an increase occurring in consumption of tradables is going to increase the RER, and it is going to offset any initial RER change induced by the Balassa–Samuelson–Tariffi effect in the partial equilibrium model. Therefore, the RER is constant over time in the long run in the general equilibrium model.
4. Concluding Remarks
Even if there is evidence that says that real exchange rate fluctuations are explained by structural breaks in the short term, it is shown in this paper that those changes are transitory in the long run. Shifts in real exchange rates can be explained by fundamentals as real variables, but, at the same time, the real exchange rate could be constant depending on how long the period of considered time is. Since the PPP holds for tradable goods in the long run, it was first introduced in the relationship between the RER and productivity according to the Balassa–Samuelson–Tariffi effect in Section 2. In the second section, a partial equilibrium model was presented to show such an effect, which means that improvements in productivity of tradable goods relative to non-tradable goods of the domestic economy in terms of the same productivity ratio in the foreign economy decreases the real exchange rate.
In Section 3, the ratio between consumption in tradables and consumption in non-tradables depends on the relative price of non-tradables. It means that consumption depends on the relative price of domestic non-tradables in terms of tradables when the utility function takes the Cobb–Douglas form, and it depends not only on domestic non-tradable prices but also on the corresponding elasticity of substitution when the utility function takes the CES form. In any case, initial changes in the RER, as a consequence of productivity changes—as described in Section 2—are offset by changes in consumption—as described in Section 3. The general equilibrium model shows that there is not only a supply for each demand but also consumption and production in the long run.
Main economic implications are based on the study of real exchange-rate behaviour. Changes in levels of productivity affect the real exchange rate in the short term when changes in the relative prices of tradable goods in terms of non-tradable goods are compensated by fluctuations in the nominal exchange rate in a way that keeps the real exchange rate constant in the long run. Depending on the consumption share in tradables with respect to non-tradables and the elasticity of substitution of consumption between both tradables and non-tradables, an increase occurring in consumption of tradables relative to consumption of non-tradables is going to increase the RER, and it is going to offset any initial RER change induced by the Balassa–Samuelson–Tariffi effect in the partial equilibrium model. Since the general equilibrium model allows for a utility function, the RER is constant over time in the long run. It was presented using a mathematical mechanism that shows how a partial equilibrium model is transformed into a general equilibrium one, including the real exchange rate. Adding a utility function in the Balassa–Samuelson–Tariffi effect, any appreciation of the RER—as a consequence of positive innovations in productivity in the tradable sector—is going to be reversed by increases in levels of domestic consumption in the same goods sector or industry.
Regarding the theoretical framework constructed, a constant real exchange rate in the long run is not an assumption in this research but rather one of the possible outcomes that could be obtained, given the assumptions made. Because a constant real exchange rate is just one of the possible outcomes, this model is a feasible result in between many outcomes. It means that there are no research limitations with this model, but other feasible outcomes that are not relevant when building the current model in this research are possible. However, empirical validation of the mathematical formulation presented for the general equilibrium model with the real exchange rate could be performed in further research. Policy implications could also be found when writing another more policy-oriented paper in the future.
Funding
The APC was funded by the Faculty of Economics and Business at the University of Barcelona (CEGE: 2655EC00144000). This research did not receive any other external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Conflicts of Interest
The author declare no conflict of interest.
Appendix A. Proofs
A. Firms. According to the constant returns to the scale assumption, the production function F(K, L) can be written as F(K, L) = L/L × F(K, L) = L × F(K/L, L/L) = L × F(k,1) = L × f(k), where k = K/L is the capital/labour ratio, and f(k) = F(k, 1) by definition. Note that differentiating the production function with respect to K and L, given constants L and K, respectively, the first order conditions can be derived as
Əf(k)/ƏK = f’(k)
Əf(k)/ƏL = f(k) − f’(k)k
B. Households. The consumer’s problem for a small two-period endowment economy takes the form
where . In order to find the first order condition, it is necessary to maximise the utility function such that the constraint is given by
Note that , and . When , there is not consumption. Thus, ci = 0. Two other constraints are and .
Also, can be found by rewriting Equation (A2) as
The previous Equation (A3) can be obtained taking into account the following steps:
Substituting (A3) in Equation (A1), the following can be obtained:
The first order condition (FOC) can thus be derived as
Rearranging terms, first order conditions can thus be written as and .
Finally, the intertemporal Euler equation is given by and .
The consumer’s problem for a small economy in a dynamic model is given by a finite multiperiod environment T (and no definite end time) rather than two periods. Assuming all individuals in the economy are identical and the population size is equal to 1 (a homogeneous population of size 1), Equation (A1) can be written as . Thus,
Note that = C and = Y for all individuals i where C is aggregate consumption, Y is aggregate output, and T is any number greater than zero.
With consumption occurring over T rather than two periods and between any two dates t and s, the natural generalised additive finite-horizons utility function (starting on date t but ending on date t + T) is
Taking the limit of the T-period economy (T), the infinite-horizons utility function can be written as
References
- Azcona, N. (2017). Non-traded goods and real exchange rate fluctuations: A structural VAR analysis. International Advances in Economic Research, 23, 137–148. [Google Scholar] [CrossRef]
- Balassa, B. (1964). The purchasing-power parity doctrine: A reappraisal. The Journal of Political Economy, 72(6), 584–596. [Google Scholar] [CrossRef]
- Blanco, A., & Cravino, J. (2020). Price rigidities and the relative PPP. Journal of Monetary Economics, 116, 104–116. [Google Scholar] [CrossRef]
- Bordo, M. D., Choudhri, E. U., Fazio, G., & MacDonald, R. (2017). The real exchange rate in the long run: Balassa-Samuelson effects reconsidered. Journal of International Money and Finance, 75, 69–92. [Google Scholar]
- Carvalho, C., & Nechio, F. (2011). Aggregation and the PPP puzzle in a sticky-price model. American Economic Review, 101, 2391–2424. [Google Scholar] [CrossRef]
- Cassel, G. (1918). Abnormal deviations in international exchanges. The Economic Journal, 28(112), 413–415. [Google Scholar] [CrossRef]
- Dornbusch, R. (1976). La teoría de los regímenes de tipos de cambio flexibles y la política macroeconómica. Cuadernos de Economía (Latin American Journal of Economics), 13(39), 27–50. [Google Scholar]
- Edwards, S. (1988a). Real and monetary determinants of real exchange rate behaviour: Theory and evidence from developing countries. Journal of Development Economics, 29, 311–341. [Google Scholar] [CrossRef]
- Edwards, S. (1988b). The determination of equilibrium real exchange rate (UCLA Working Paper, No. 508). UCLA Department of Economics. [Google Scholar]
- Égert, B., Halpern, L., & MacDonald, R. (2006). Equilibrium exchange rates in transition economies: Taking stock of the issues. Journal of Economic Surveys, 20(2), 257–324. [Google Scholar] [CrossRef]
- Fleming, M. (1962). Domestic financial policies under fixed and floating exchange rate. International Monetary Fund, Staff Papers, 9, 369–379. [Google Scholar] [CrossRef]
- Galí, J., & Monacelli, T. (2016). Understanding the gains from wage flexibility: The exchange rate connection. American Economic Review, 106(12), 3829–3868. [Google Scholar] [CrossRef]
- Mundell, R. (1960). The monetary dynamics of international adjustment under fixed and flexible exchange rates. The Quarterly Journal of Economics, 74(2), 227–257. [Google Scholar] [CrossRef]
- Obstfeld, M., & Rogoff, K. (1999). Foundations of international macroeconomics (p. 804). Fourth Printing. The MIT Press. [Google Scholar]
- Rogoff, K. (1996). The purchasing power parity puzzle. Journal of Economic Literature, 34(2), 647–668. [Google Scholar]
- Samuelson, P. (1964). Theoretical notes on trade problems. The Review of Economics and Statistics, 46(2), 145–154. [Google Scholar] [CrossRef]
- Sardà, J., & Pérez-Lacasta, J. (2003). Exchange rate and long run equilibrium in transition economies. International Advances in Economic Research, 9(1), 35–47. [Google Scholar]
- Tariffi, L. (2010). Euro-dollar real exchange rate misalignments: Is the euro overvalued? China-USA Business Review, 9(7), 1–21. [Google Scholar]
- Tariffi, L. (2012). Explaining real exchange rate behaviour through tariffs: The BRIC’s case. International Journal of Academic Research in Economics and Management Sciences, 1(2), 1–40. [Google Scholar]
- Tariffi, L. (2013). Ensayos sobre los determinantes reales del tipo de cambio [Ph.D. thesis, UB Economics]. Available online: http://hdl.handle.net/2445/48563 (accessed on 18 February 2025).
- Tariffi, L. (2019). Explaining the exchange rate in the euro zone through non-tradable goods and the income effect. International Journal of Development Research, 9(2), 25753–25762. [Google Scholar]
- Tariffi, L. (2024). Desalineación cambiaria del euro con respecto al dólar. CIVREF Working Paper Series, 1, 1–31. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).