Deterministic and Stochastic Macrodynamic Models for Developing Economies’ Policies: An Analysis of the Brazilian Economy

Abstract

This work verifies the interactions between fiscal and monetary policies in Brazil, involving real GDP, the Interest index, Inflation index, real Exchange rate, and actual public debt, using empirical data from January 1998 to December 2018 to calibrate the model. In the analyses, we employ macrodynamic deterministic and stochastic models of differential equations to examine the interconnection of the endogenous variables and the stability of Brazilian economic policy. In the stochastic model, we introduced stochastic perturbations in the uncontrollable coefficients and additive random walks affecting the endogenous variables. Shocks imposed on the structured dynamic model showed that stochastic innovations propagate more strongly in the monetary variables: inflation, interest rates, and exchange rates. We have also established forecasts for endogenous variables from January 2019 to December 2026 and conducted backtest analyses using the empirical data observed for the endogenous variables from January 2019 to December 2023. The forecast estimations were demonstrated to be satisfactory.

1. Introduction

The interaction between fiscal and monetary policies in an economy influences how the economic process will develop. Both directly influence market regulation, inflation control, job creation, and economic growth. Although their mechanisms and immediate objectives are distinct, they complement each other. Therefore, establishing a process for controlling fiscal and monetary policies is essential to defining an appropriate economic policy for a country.

The interaction between fiscal and monetary policies has long been a topic of discussion, with both playing a critical role in economic stability and growth. However, this issue has become even more important today, especially after turbulent periods marked by the COVID-19 pandemic, geopolitical tensions, and financial uncertainty, as highlighted in Blinder (2021) and Chen et al. (2022).

The interrelationship among fiscal discipline, debt sustainability, and economic growth underscores the need for updated fiscal strategies that account for a given economy’s specific economic conditions and debt levels. It is common to reflect, balance, and evaluate significant economic events over the years. Particularly in developing economies, the COVID-19 pandemic crisis was accompanied by a rapid increase in sovereign debt, requiring immediate action from their monetary and fiscal authorities. The years following the COVID-19 pandemic presented new challenges, testing global resilience and recovery capabilities. Therefore, over the coming years, economies must continually adapt their policy frameworks to address these challenges.

Economic studies that simulate economic, fiscal, and monetary behavior are essential for analyzing the relationships between policies, verifying how they may interact, and improving them. Policymakers must continually improve the economic process to achieve an efficient economy, and sound monetary policy is necessary to achieve the desired objectives. Within this context, in this paper, we will study the interactions between fiscal and monetary policies in the Brazilian economy (a developing economy), showing how they are interconnected using deterministic and stochastic macrodynamic differential equations models. First, we structure a deterministic dynamic system model comprising five differential equations with the following endogenous variables: real GDP, the nominal interest rate, the nominal inflation rate, the real exchange rate, and real public debt.

Given that emerging economies (EMEs) are exposed to external and/or internal political and/or economic shocks, the proposed macrodynamic model was perturbed, rendering it a stochastic system. In this stochastic model, we impose stochastic perturbations on the levels of the model’s uncontrollable parameters using normal distributions. We also introduced additive shocks to the endogenous variables, simultaneously with shocks to the uncontrolled parameters, via one-dimensional (1-D) random walks across all five dependent variables. In addition, we conduct a comprehensive analysis of the behavior of all coefficient signs in dynamic system equations, relating them to the economic perspective. We also analyzed the interactions between fiscal and monetary policies, as detected by the dynamics of the system equations. Finally, we calibrated the model using monthly data from January 1998 to December 2018. Prior to this period, the data revealed several changes resulting from internal and external disturbances in the Brazilian economy, making it challenging to calibrate the model. However, we limited the dataset to December 2018, as one of the objectives of the study is to verify the model’s potential to predict economic behavior through backtesting, during and after the severe COVID-19 crisis and the Ukraine crisis, which severely shook the Brazilian economy, and also verify the model’s robustness to predict economic behavior for an extended period. Therefore, the longer the model can forecast the behavior of monetary and fiscal policy, the better it is, because the model is a research tool used to analyze the future behavior of the country’s economic policy process efficiency, as policymakers must continually assess the interaction between fiscal and monetary policies.

In the following, we will emphasize some economic and empirical techniques used in literature reviews that examine the relationships between macroeconomic and monetary policies, which are essential for situating the reader in the article’s context.

According to Sargent and Wallace (1981), if fiscal policy dominates monetary policy, the fiscal authorities have the premise to define their budgets, set deficits and surpluses, and thus determine the revenues from securities sales. In this sense, the monetary authorities must finance the fiscal charges through seigniorage, maximize income by selling securities in the financial market, and establish inflation control policies. Nevertheless, this control becomes problematic when the market cannot absorb the volume of securities imposed on it. Thus, monetary authorities must tolerate the additional inflation, create currency, and generate seigniorage income to complement fiscal policy goals.

On the other hand, if monetary policy dominates fiscal policy, the financial authorities define their policy by announcing the growth rates of the monetary base for current and future periods, determining the seigniorage revenue they will provide the government. So, fiscal policymakers adjust their budgets to match the market’s security sales and seigniorage revenue. The Central Bank (BACEN) can successfully and permanently control inflation in this regime of monetary dominance.

According to the International Monetary Fund’s report (IMF, 2003), fiscal dominance may become essential for EMEs, as these economies have generally experienced increased public debt, accompanied by fiscal imbalances, in recent decades. In this sense, fiscal policy has become a significant concern for monetary policy in EMEs. Unsustainable budgetary deficits and high levels of public debt create an environment of fiscal dominance in many countries, leading to inflation increases at high and volatile levels and increased risk premiums on public debt, which induces an unfavorable exchange rate and exposes EMEs to capital outflows, as summarized by Yörükoğlu and Kılınç (2012).

In addition to the aspects presented above, the economic reality of EMEs becomes even more complex, as most of them are exposed to both external and internal political and financial shocks. These shocks reduce the economic growth rate and the recovery speed in the face of any crisis. Conceptually, the EMEs absorb shocks in the IEs for a few reasons: (i) shocks in IEs can be shared by EMEs as a result of monetary policy movements that induce EMEs to absorb this type of propagation (Canova, 2005). (ii) shocks to the IEs are transmitted to EMEs through integrated goods markets (Kim, 2001), and (iii) shocks to the IEs are transmitted through integrated financial markets (Brandao-Marques et al., 2020, among others).

Shocks in the monetary policy of international economies (IEs) contribute significantly to the considerable variability in macroeconomic variables in EMEs, both in Asia and Latin America. These shocks induce movements in output and inflation, both in the IEs and in EMEs, playing a crucial destabilizing role in nominal exchange rates. However, the intensity of these effects depends on the performance of each economy’s floating exchange rate regime, which may stabilize these effects but not inhibit the transmission process (Calvo & Reinhart, 2000). Thus, it is challenging to discover the intensity of monetary shocks on real demand and supply in the IE and the monetary movements among the IEs and EMEs’ output. In this case, the price level in EMEs may increase or remain constant, depending on whether the price increases in the IE are passed through to the exchange rate and whether the increase in aggregate demand from the IE affects either prices or the economy’s structure.

According to Canova (2005), the continental movements of monetary shocks in IEs intertwine with the other two types of shocks (integrated goods and financial markets) that also generate effects on production and inflation. Thus, it is challenging to determine the impact of monetary shocks on actual demand and supply in the IEs and the monetary movements between the global economy and the output of EMEs. The transmission of shocks via trade occurs through the comovements of products. In this case, the price level in EMEs may increase or remain constant, depending on whether the increase in prices in the IEs passes through the exchange rate and whether the increase in global aggregate demand affects either the prices or the economy’s structure.

In the same way, the monetary shocks of the IEs and their intertwined effect on the integrated goods and financial markets also cause movement in the interest rate and currency of the EMEs, whose intensity depends on the details of the EMEs’s monetary policy. If it is accommodative, the currency will follow domestic production; if the goal is to control inflation, the interest rate should be increased. When IEs prices no longer induce price changes in EMEs, their exchange rates will adjust to maintain equilibrium.

Transmission via financial markets works in such a way that if there is a shock that lowers interest rates in the IEs (for example, an expansionary monetary shock), then EME currencies should appreciate, or the bond price level of EMEs is expected to rise, causing local interest rates to fall. If EMEs’ exchange rates adjust fully and instantly, there is no change in their macroeconomic variables. In this case, production and prices in the domestic economy may increase. The money supply could increase if local central banks react positively to output expansion or contract if price concerns guide monetary policy. A priori, the importance of the financial market channel depends on at least two factors: the degree of financial integration between the markets and the levels of free fluctuation of the exchange rate regimes of the EMEs.

Some shocks will have more significant international repercussions than others. The magnitude of the spillovers of each type of shock depends on the commercial and financial integration of the receiving country with the global economy, the regulation of financial openness, the exchange rate regime, the development of the financial market, the rigidity of the labor market, and structure of the industry and participation in global values’ chains (Georgiadis, 2016). In short, shocks to the IEs from monetary and structural policies (integrated goods and financial markets) affect both inflation and interest rates of the EMEs simultaneously, as well as transmission channels that play essential roles in the economic process.

The research we will propose here is a new approach to analyzing economic shocks. In this procedure, we simulate bands of exogenous economic shocks without identifying them (internal and/or external) and track their economic effects. We will address their effects on monetary and fiscal policy and identify how these shocks change the structure of the economic process. The results of our study shed light on how we can establish control procedures in the dynamics of the process via controllable parameters.

After highlighting the behavioral aspects of EMEs and the conclusions drawn, several questions can be raised in studies examining the interaction between fiscal and monetary policy in EMEs. In particular, we aim to understand the interactions between fiscal and monetary variables, including public debt, GDP, interest rates, exchange rates, and inflation. Also, we want to understand the capacity of an EMEs to absorb external and internal shocks.

Therefore, in this study, we will analyze the interactions between Brazilian macroeconomic policies, using a model similar to Kirsanova et al. (2006) and following the suggestions of Blanchard (2004), who affirmed that the macrodynamic models are an excellent way to study the relationship between fiscal and monetary variables in EMEs. He also emphasized that, due to the complexity of the EMEs’ economic realities, it would be necessary to introduce some shocks into the dynamic model to adapt it to macroeconomic reality better and establish a way to control the evolution of such surprises. Thus, we consider a macrodynamic model to identify the nature of a developing country’s responses when faced with exogenous shocks, submitted indistinctly to internal and/or external sources, and project the trajectories of Brazilian macroeconomic variables under the implemented macrodynamic policy. In this study, we used monthly data on the Brazilian economy from January 1998 to December 2018. This study focuses on Brazil, a leading developing economy and one of the world’s ten largest, providing a representative context for analyzing emerging market dynamics. It was subjected to the most diverse processes of instabilities due to internal and external crises (we can stress here that in the period analysis of this article, the Brazilian’s economy has always been characterized by instability due to the effects of economic, financial, and monetary crises, as the global financial crisis of subprime mortgage crisis, 2007–2008; and also, in 2020, under the effects of the global COVID-19 pandemic).

Based on the arguments highlighted earlier, the research’s general objective is divided into two parts. The first part involves structuring and calibrating macrodynamic models (both deterministic and stochastic), characterized by five ordinary differential equations for the Brazilian economy, and subsequently obtaining their estimates. The second part analyzes the solutions to each model equation and the behavior of Brazilian economy forecasts under parameter shocks (changes in the economy’s structure) and additional shocks to the model’s endogenous variables.

We transform the deterministic model into a stochastic one to verify the Brazilian economy’s ability to absorb shocks. To that end, we introduce generalized stochastic shocks in the parameters of uncontrollable impacts and additive stochastic innovations in the model’s endogenous variables.

Regarding the Brazilian economy, chosen as a case study, we want to examine the growth of public debt and determine whether a process of fiscal dominance governs it. Second, we want to examine the effects of the intensity of short-term interest rates on inflationary control—a proxy for inflation control in the Brazilian economy—and on GDP growth—and the effects of the exchange rate on inflationary control, despite not being a monetary control tool—and on GDP.

In addition to this introduction, the study is organized into four further sections. Section 2 presents the empirical literature review, which involves the techniques used to solve macrodynamic models. Section 3 is dedicated to the methodology by which the deterministic and stochastic macrodynamic models are structured. This section is subdivided into three subsections: the mathematical formulation of the macrodynamic deterministic model, the transformation of this dynamic model into a stochastic model, and the details of the databases used for model identification. Section 4 is dedicated to the computational procedures for solving the deterministic and stochastic models and analyzing their results, involving two subsections: parameter identification of the deterministic model and results of the deterministic model, and Calibration of the stochastic model and stochastic model results. This last subsection involves several subdivisions, which we do not discriminate against here. Finally, Section 5 presents the conclusions.

2. Empirical Literature Review

Many empirical studies analyze the vulnerability of EMEs due to internal and external shocks using the Structural Vector Autoregressive (SVAR) method and its variants. The SVAR model enables the imposition of specific hypotheses on the reactions of variables to different types of shocks, which can reveal economic information embedded in the time series model (Ranta et al., 2024). Generally, the SVAR model involves a vector of unobservable exogenous variables interpreted as stochastic perturbations (error term) in the structural equations. This error term is needed to obtain a VAR representation in the reduced form of the SVAR. According to Keating (1992) and Rickman (2010), two alternatives are commonly used to represent the dynamics of economic relations: (i) long-term neutrality constraints, established by stochastic shocks with uncorrelated temporary effects (a white noise I.I.D); (ii) contemporary homogeneity constraints, established by permanent stochastic shock, modeled as a random walk. In this last process, the stochastic components are equal to the sum of all past and present realizations in the noise term (Stock & Watson, 2001; Canova et al., 2007). In both models, a structural shock in a variable at any moment can potentially lead to shocks in all error terms, generating a contemporaneous movement in all endogenous variables. SVAR models are unidirectional models, from the IEs to the EMEs, where it is assumed, a priori, that stochastic shocks in EMEs rarely affect the IEs.

The SVAR methodology is often applied to analyze the behavior of external shocks in EMEs, utilizing financial and macroeconomic variables from the US and their effects on EMEs. Kim’s (2001) early work examined the international transmission of monetary policy shocks from the US to the G7 countries. The author found that expansionary shocks from US monetary policy drive booms in advanced economies caused by changes in the trade balance; however, the drop in world interest rates is the primary factor behind this mechanism. Canova (2005) studied how US shocks are transmitted to eight Latin American countries. The author concluded that the macroeconomic characteristics of each country and the differences in financial structures among world economies explain the asymmetric nature of developing countries’ responses to exogenous shocks. Canova (2005) also stressed that the financial channel plays a crucial role in transmission.

Still analyzing the effect of shocks on IEs over EMEs using SVAR models, Mackowiak (2007) found that output and price level shocks in Asian and Latin American EMEs affect their economies more intensely than US monetary policy shocks. Wright (2012) identified the effects of monetary shocks on long-term interest rates on six US Treasuries during the Quantitative Easing policy. The conclusion was that reduction shocks in the yields on US Treasury bonds induced reductions in the yields on its corporate bonds, the long-term sovereign bonds of other developed economies analyzed, and the appreciation of their respective currencies. Bowman et al. (2015) extended the work of Wright (2012) to an international scenario involving seventeen countries (from Asia, Latin America, Eastern Europe, and North America). The study used data on sovereign bond yields, exchange rates, and EME equity portfolio liquidity ratios. The findings showed that EMEs’ asset prices, particularly sovereign bonds, responded vigorously to announcements of US unconventional monetary policy.

Many papers have analyzed the behavior of external shocks in EMEs using different SVAR variants. Mertens and Ravn (2013) and Stock and Watson (2012) employed a Bayesian Vector Autoregression (BVAR) technique with asymmetric conjugate priors to examine the shocks and fundamentals that impact the predicted variables. The conclusion is that US policy shocks have significant real and nominal contagion effects, affecting both advanced economies and EMEs. The main channels through which the effects propagated were trade, exchange rate liquidity flows, and commodity prices. The results were asymmetric, with more significant effects in the case of contractionary US monetary policy shocks. Finally, the research identified contrasts in the behavior of transmission mechanisms across countries with different characteristics related to exchange rates, dollar exposure, and capital control regimes. Di Giovanni and Shambaugh (2008) explored the connection between interest rates in major industrialized countries and real output growth in EME economies using a random coefficient panel OLS model. They found that high interest rates in the first group (industrialized countries) have a contractionary effect on real GDP in the second group (EMEs), mainly in countries with a fixed exchange rate regime. The impact of foreign interest rates on domestic interest rates was found to be the most likely transmission channel among other channels, particularly in terms of trade effects. Canova et al. (2007), Canova and Ciccarelli (2009), and Ciccarelli et al. (2013) analyzed the transmission of monetary shocks from the US to EME economies using Bayesian panel VAR methods with random coefficients. This approach enabled us to make inferences about the average impact of an external shock on macroeconomic and financial variables in EMEs. Using this technique, Canova et al. (2007) examined the cyclical properties of G-7 countries. The study examines the interaction between inflation and the natural rate of unemployment in G-7 countries, the transmission of monetary policy shocks across various economic sectors, and the construction of asset portfolios in different geographic regions. The authors demonstrated the existence of a significant global cycle in which country-specific indicators play a less prominent role in the process. Ciccarelli et al. (2013) also employed panel VAR models to examine heterogeneity and spillovers in macrofinancial variables between G-7 countries and European economies, with a focus on the recession triggered by the European and subprime crises. The study examines several fundamental and financial variables, leading to the conclusion that the transmission of shocks tends to be faster and more pronounced across financial variables than real variables. Country-specific factors account for the heterogeneous behavior observed across the countries. Bhattarai et al. (2020) also estimated the spillover effects of uncertainty shocks in the US using Bayesian panel VAR models. They designed a Bayesian panel VAR for fifteen EMEs, involving the exogenous uncertainty variable estimated for the US and a broad set of macroeconomic and financial variables for the EMEs. They found that a monetary tightening in the US causes adverse fundamental and financial effects in the EMEs.

Bianchi’s (2012) research is situated within the realm of interaction between fiscal and monetary policies. This research examined the relationships between fiscal and monetary variables using the stochastic general equilibrium dynamic model, also known as the general stochastic dynamic equilibrium (DSGE) model.1 DSGE modeling involves an optimization process fully specified by prospective agents, with a stochastic structure of defined exogenous forces, and imposes an explicit general equilibrium structure. The author demonstrates that the temporal evolution of monetary and fiscal policies can change the dominant regime to one of the following cases: (i) active fiscal policy and passive monetary policy, (ii) passive fiscal policy and active monetary policy, and (iii) active fiscal and monetary policies. Silveira (2006) also developed a version of the new Keynesian DSGE model for two countries with a small open economy. The model uses a Bayesian approach and is applied to data from the Brazilian economy. This model considers the effects of external frictions (price stickiness) on the structural form of the transmission process of monetary shocks. Imposing a bias on household preferences allowed the model to capture empirical evidence of real exchange rate fluctuations; however, despite the structural shocks affecting endogenous variables in the right direction, the magnitudes of the effects were somewhat unrealistic. Linardi (2016) estimated a Bayesian DSGE model for a small open economy (structured, using data from the Brazilian economy for the period of inflation targeting since 1999). The model included a series of shocks important for explaining macroeconomic fluctuations in EMEs. However, the study failed to conclude that the Brazil central bank’s interest rate setting policy does not affect exchange rate volatility, a necessary factor for its exchange rate policy to float freely.

DSGE models are characterized as promising for simulating economic and financial problems, as highlighted by Kydland and Prescott (1982), who emphasize that these models provide a theoretically consistent framework for testing macroeconomic theories and evaluating quantitative policy. However, Canova and Ciccarelli (2013), on page 5, emphasize that due to their very essence, DSGE models impose many restrictions, not always by the statistical properties of the data. Thus, the policy prescriptions they provide are built into the model’s assumptions and should be considered more as a benchmark than a realistic assessment of the options and constraints faced by policymakers in real-world situations, as also highlighted above by Silveira (2006). Therefore, the results of the DSGE estimates remain highly dependent on the model’s structure. This consideration means that this model has difficulty modeling certain macroeconomic variables (Blanchard & Galí, 2007; Chung et al., 2021, among others).

Using a different methodology, Kirsanova et al. (2006) developed a five-equation macrodynamic model to illustrate the results of optimal monetary and fiscal policies applied both cooperatively and non-cooperatively to stabilize the economy against shocks. The authors used the analysis of replicating the impulse-response functions in inflation and demand as a solution technique. The numerical simulations aborded three cases of games: (i) fiscal and monetary authorities are benevolent and cooperate in setting their macroeconomic policy instruments. Therefore, the response to an inflationary shock was one in which the fiscal rule left monetary policy to bear the burden of stabilizing the economy in the face of the shock. In that case, fiscal policy controls debt slowly; (ii) a result similar to the first case occurs if fiscal authorities act as a Stackelberg leader, aiming to increase output; and (iii) if the tax authority plays the monetary authority in a Nash game, in which the social welfare will be severely impaired if it aims, possibly, to increase output.

3. Methodology

3.1. Mathematical Formulation of the Macrodynamic Model

In the model presented in this study, we assume that the analyzed economy employs an inflation-targeting regime. Then, the exchange rate may be exposed to shocks, as exchange rate flexibility is a fundamental condition in the operation of this monetary system.

Under this regime, it examines the interplay between fiscal and monetary policies, in which the level of government debt influences the behavior of fiscal policy. At the same time, the adjustment thresholds of the nominal interest rate and inflation underscore the behavior of monetary policy. Therefore, alternating these behaviors establishes a game if the fiscal authority does not stabilize its debt level and the central bank responds sluggishly to inflation. This game’s interplays determine the concepts of fiscal and monetary dominance. The concepts of fiscal dominance (FD) and monetary dominance (MD) are purely theoretical. In reality, the proper dominant regime is unobservable and unknown. Therefore, distinguishing between the two regimes is valuable for controlling the economic process.

In the debate about fiscal dominance, non-Ricardian behavior of public debt can cause the monetary authority to lose control over inflation. Therefore, a specific debt level relative to the gross domestic product can be an indicator of the success (or lack thereof) of the inflation-targeting regime, providing a means for the fiscal authority to ensure the long-term solvency of the debt, and serving as a factor in identifying fiscal dominance. Thus, it is considered in the study formulated that the existence of a high debt level is already characterized as an indicator of the need to establish fiscal adjustments to guarantee the solvency of the public debt if, at the same time, the monetary policy is conducted for a nominal interest rate at a low bound and inflation is developing trend ascendant above the inflation target threshold.

Based on the above argument, we observe that by establishing the intensities of interactions between the exchange rate, inflation, interest rates, and public debt, we have a valuable tool for determining fiscal and monetary policy procedures. Additionally, to complement the proposed model, which encompasses all the essential variables in the dynamics of the economic process, we included the GDP variable, representing the outcome of the interactive process among the other macroeconomic variables.

Relative to the interest rate, $\mathrm{i}\left(\mathrm{t}\right)$, we consider that Fisher’s rule defines its nominal intertemporal change (Fisher, 1930), that is:

$$\mathrm{i}\left(\mathrm{t}\right)=\mathrm{r}\left(\mathrm{t}\right)+\mathsf{\pi }\left(\mathrm{t}\right)$$

(1)

where $\mathsf{\pi }\left(\mathrm{t}\right)$ and $\mathrm{r}\left(\mathrm{t}\right)$ represent, respectively, the observed inflation and real interest rates, the Central Bank defines the nominal short-term interest rate for the Brazilian economy, $\mathrm{i}\left(\mathrm{t}\right)$, the SELIC rate.

In the following subsections, we describe the ordinary differential equations for the real output, nominal interest rate, inflation, real exchange rate, and real sovereign debt. We structure the dynamic model from these equations to establish the interaction between fiscal and monetary policies.

3.1.1. Sovereign Debt and Macrodynamic Model

Cafiso (2012) obtained a difference equation that allows for estimating the factors that affect the variation of public debt. Following this author, we derive the equation that describes the variation of sovereign debt, one of the intertemporal restrictions on government policy regarding the economy’s public debt. This formulation structures, in weighted terms, the deficit in national and foreign currency, and explicitly assumes that inflation and nominal interest rates are also involved in weighted terms, corresponding to the domestic and foreign effects. The exchange rate serves as a weighing instrument for comparing the units of domestic and foreign variables.

As Walsh (2017), we derive the discrete public debt equation from the identity of the consolidated budget of the government sector, as follows:

$$\underset{=\mathrm{s}\mathrm{p}\mathrm{e}\mathrm{n}\mathrm{d}\mathrm{i}\mathrm{n}\mathrm{g}}{\underbrace{\mathrm{G}\left(\mathrm{t}\right)+\mathrm{i}\left(\mathrm{t}\right)\mathrm{B}(\mathrm{t}-1)}}=\underset{=\mathrm{r}\mathrm{e}\mathrm{v}\mathrm{e}\mathrm{n}\mathrm{u}\mathrm{e}\mathrm{s}}{\underbrace{\mathrm{T}\left(\mathrm{t}\right)+\left(\mathrm{B}\left(\mathrm{t}\right)-\mathrm{B}\left(\mathrm{t}-1\right)\right)+\left(\mathrm{H}\right(\mathrm{t})-\mathrm{H}(\mathrm{t}-1\left)\right)}},$$

(2)

where $\mathrm{G}\left(\mathrm{t}\right)$ is government spending, $\mathrm{B}\left(\mathrm{t}\right)$ is public debt at time t (at level), $\mathrm{T}\left(\mathrm{t}\right)$ is government tax revenue, $\mathrm{H}\left(\mathrm{t}\right)$ is the monetary base, and $\mathrm{i}\left(\mathrm{t}\right)$ is the short-term nominal interest rate of the economy.

In Equation (2), we have that $\mathrm{i}\left(\mathrm{t}\right)\mathrm{B}(\mathrm{t}-1)$ represents debt expenses, in period $\mathrm{t}-1$, indexed to a nominal interest rate $\mathrm{i}\left(\mathrm{t}\right)$, implicit at maturity t, on $\mathrm{B}(\mathrm{t}-1)$. The government pays its expenditures with tax revenues, such as seigniorage income at time t, ${\mathrm{s}}^{*}\left(\mathrm{t}\right)=\mathrm{H}\left(\mathrm{t}\right)-\mathrm{H}(\mathrm{t}-1)$, or through the issuance of debt securities, given by $\mathrm{B}\left(\mathrm{t}\right)-\mathrm{B}\left(\mathrm{t}-1\right)$. The Equation (2) can still be manipulated, isolating $\mathrm{B}\left(\mathrm{t}\right)$ on the left side and the other terms on the right and making $\mathrm{w}\left(\mathrm{t}\right)=\mathrm{T}\left(\mathrm{t}\right)-\mathrm{G}\left(\mathrm{t}\right)$:

$$\mathrm{B}\left(\mathrm{t}\right)=\mathrm{B}\left(\mathrm{t}-1\right)+\mathrm{i}\left(\mathrm{t}\right)\mathrm{B}(\mathrm{t}-1)-\left(\mathrm{w}\right(\mathrm{t})+{\mathrm{s}}^{*}(\mathrm{t}\left)\right)$$

(3)

As public debt is usually monitored as a percentage of GDP, the debt is related to the resource available for payment, thus, being comparable across countries. Therefore, we can write the Equation (3) as follows:

$${\displaystyle \frac{\mathrm{B}\left(\mathrm{t}\right)}{\mathrm{P}\left(\mathrm{t}\right)\mathrm{Y}\left(\mathrm{t}\right)}}={\displaystyle \frac{\mathrm{B}(\mathrm{t}-1)}{\mathrm{P}\left(\mathrm{t}\right)\mathrm{Y}\left(\mathrm{t}\right)}}+{\displaystyle \frac{\mathrm{i}\left(\mathrm{t}\right)\mathrm{B}(\mathrm{t}-1)}{\mathrm{P}\left(\mathrm{t}\right)\mathrm{Y}\left(\mathrm{t}\right)}}-\left({\displaystyle \frac{\mathrm{w}\left(\mathrm{t}\right)+{\mathrm{s}}^{*}\left(\mathrm{t}\right)}{\mathrm{P}\left(\mathrm{t}\right)\mathrm{Y}\left(\mathrm{t}\right)}}\right)\to \mathrm{b}(\mathrm{t})={\displaystyle \frac{(1+\mathrm{i}(\mathrm{t}\left)\right)\mathrm{B}(\mathrm{t}-1)}{(1+\mathsf{\alpha }(\mathrm{t}\left)\right)\mathrm{P}\left(\mathrm{t}-1\right)\mathrm{Y}(\mathrm{t}-1)}}-\left({\displaystyle \frac{\mathrm{W}\left(\mathrm{t}\right)+{\mathrm{S}}^{*}\left(\mathrm{t}\right)}{\mathrm{P}\left(\mathrm{t}\right)\mathrm{Y}\left(\mathrm{t}\right)}}\right)$$

(4)

We rearranged Equation (4), considering $\mathrm{b}\left(\mathrm{t}\right)=\mathrm{B}\left(\mathrm{t}\right)/\mathrm{P}\left(\mathrm{t}\right)\mathrm{Y}\left(\mathrm{t}\right)$, $\mathrm{W}\left(\mathrm{t}\right)=\mathrm{w}\left(\mathrm{t}\right)/\mathrm{P}\left(\mathrm{t}\right)\mathrm{Y}\left(\mathrm{t}\right)$, ${\mathrm{S}}^{*}\left(\mathrm{t}\right)={\mathrm{s}}^{*}\left(\mathrm{t}\right)/\mathrm{P}\left(\mathrm{t}\right)\mathrm{Y}\left(\mathrm{t}\right)$, and the nominal GDP is $\mathrm{P}\left(\mathrm{t}\right)\mathrm{Y}\left(\mathrm{t}\right)=\left(1+\mathsf{\alpha }\left(\mathrm{t}\right)\right)\mathrm{P}\left(\mathrm{t}-1\right)\mathrm{Y}(\mathrm{t}-1)$, where $\mathsf{\alpha }\left(\mathrm{t}\right)$ represents the rate of GDP change, $\mathrm{P}\left(\mathrm{t}\right)$ is the cost price of a production unit in the economy, and $\mathrm{Y}\left(\mathrm{t}\right)$ is the output of the economy. Thus, we have

$$\mathrm{b}(\mathrm{t})={\displaystyle \frac{(1+\mathrm{i}(\mathrm{t}\left)\right)}{(1+\mathsf{\alpha }(\mathrm{t}\left)\right)}}\mathrm{b}(\mathrm{t}-1)-(\mathrm{W}(\mathrm{t})+{\mathrm{S}}^{*}(\mathrm{t}))$$

(5)

In Equation (5), public debt is represented in terms of GDP. Also, in Equation (5), $\mathrm{P}\left(\mathrm{t}\right)\mathrm{Y}\left(\mathrm{t}\right)=\left(1+\mathsf{\pi }\left(\mathrm{t}\right)\right)\mathrm{P}(\mathrm{t}-1)\left(1+\mathsf{\eta }\left(\mathrm{t}\right)\right)\mathrm{Y}(\mathrm{t}-1)$, where $\left(1+\mathsf{\pi }\left(\mathrm{t}\right)\right)$ is the current inflation index, and $(1+\mathsf{\eta }(\mathrm{t}\left)\right)$ is the GDP growth index, consequently defining $\left(1+\mathsf{\alpha }\left(\mathrm{t}\right)\right)=\left(1+\mathsf{\pi }\left(\mathrm{t}\right)\right)\left(1+\mathsf{\eta }\left(\mathrm{t}\right)\right)$. Therefore, we have

$$\mathrm{b}(\mathrm{t})={\displaystyle \frac{(1+\mathrm{i}(\mathrm{t}))}{\left(1+\mathsf{\pi }(\mathrm{t})\right)\left(1+\mathsf{\eta }(\mathrm{t})\right)}}\mathrm{b}(\mathrm{t}-1)-(\mathrm{W}(\mathrm{t})+{\mathrm{S}}^{*}(\mathrm{t}))$$

(6)

Cafiso (2012) defined the nominal interest rate and inflation as follows:

$$\mathrm{i}(\mathrm{t})=\widehat{\mathrm{i}}(\mathrm{t})+\mathsf{ϵ}(\mathrm{t}){\mathsf{\theta }}^{\mathrm{f}}\left(1+{\mathrm{i}}^{\mathrm{f}}(\mathrm{t})\right),$$

(7)

$$\mathrm{and} \mathsf{\pi }(\mathrm{t})=\widehat{\mathsf{\pi }}(\mathrm{t})+\mathsf{ϵ}(\mathrm{t}){\mathsf{\mu }}^{\mathrm{f}}\left(1+{\mathsf{\pi }}^{\mathrm{f}}(\mathrm{t})\right)$$

(8)

where $\widehat{\mathrm{i}}(\mathrm{t})={\mathsf{\theta }}^{\mathrm{h}}{\mathrm{i}}^{\mathrm{h}}(\mathrm{t})+{\mathsf{\theta }}^{\mathrm{f}}{\mathrm{i}}^{\mathrm{f}}(\mathrm{t})$ is the weighted average of domestic and foreign interest rates, and $\widehat{\mathsf{\pi }}(\mathrm{t})={\mathsf{\mu }}^{\mathrm{h}}{\mathsf{\pi }}^{\mathrm{h}}(\mathrm{t})+{\mathsf{\mu }}^{\mathrm{f}}{\mathsf{\pi }}^{\mathrm{f}}(\mathrm{t})$ is the weighted average of domestic and foreign inflation rates, where ${\mathrm{i}}^{\mathrm{h}}(\mathrm{t})$ and ${\mathrm{i}}^{\mathrm{f}}(\mathrm{t})$ are, respectively, domestic and foreign interest rates, and ${\mathsf{\pi }}^{\mathrm{h}}(\mathrm{t})$ and ${\mathsf{\pi }}^{\mathrm{f}}(\mathrm{t})$ are domestic and foreign inflation, respectively; ${\mathsf{\theta }}^{\mathrm{h}}$ and ${\mathsf{\theta }}^{\mathrm{f}}$ are, respectively, the share in the nominal interest rate of the domestic interest rate and the foreign interest rate, with ${\mathsf{\theta }}^{\mathrm{h}}+{\mathsf{\theta }}^{\mathrm{f}}=1$. Likewise, ${\mathsf{\mu }}^{\mathrm{h}}$ and ${\mathsf{\mu }}^{\mathrm{f}}$ are, respectively, the share of the domestic inflation rate and the foreign inflation rate in the nominal inflation rate, with ${\mathsf{\mu }}^{\mathrm{h}}+{\mathsf{\mu }}^{\mathrm{f}}=1$. The local currency’s depreciation (appreciation) rate is $\mathsf{ϵ}\left(\mathrm{t}\right)=∆\mathrm{E}\left(\mathrm{t}\right)/\mathrm{E}(\mathrm{t}-1)$ ($\mathrm{E}\left(\mathrm{t}\right)$ is the nominal exchange rate). If $\mathsf{ϵ}\left(\mathrm{t}\right)>0$ means depreciation; otherwise, if $\mathsf{ϵ}\left(\mathrm{t}\right)<0$ means appreciation.

Substituting (7) and (8) in (6) and diminishing $\mathrm{b}(\mathrm{t}-1)$ on both sides of the resulting equation, we have:

$$∆\mathrm{b}(\mathrm{t})=\left[{\displaystyle \frac{\left[1+\widehat{\mathrm{i}}(\mathrm{t})+\mathsf{ϵ}(\mathrm{t}){\mathsf{\theta }}^{\mathrm{f}}\left(1+{\mathrm{i}}^{\mathrm{f}}(\mathrm{t})\right)\right]}{\left(1+\mathsf{\eta }\left(\mathrm{t}\right)\right)\left[1+\widehat{\mathsf{\pi }}(\mathrm{t})+\mathsf{ϵ}(\mathrm{t}){\mathsf{\mu }}^{\mathrm{f}}\left(1+{\mathsf{\pi }}^{\mathrm{f}}(\mathrm{t})\right)\right]}}-1\right]\mathrm{b}(\mathrm{t}-1)-\left(\mathrm{W}(\mathrm{t})+{\mathrm{S}}^{*}(\mathrm{t})\right)$$

(9)

Also, according to Cafiso (2012), the real interest rate can be defined as follows:

$$\mathrm{r}(\mathrm{t})={\displaystyle \frac{\left[1+\widehat{\mathrm{i}}(\mathrm{t})+\mathsf{ϵ}(\mathrm{t}){\mathsf{\theta }}^{\mathrm{f}}\left(1+{\mathrm{i}}^{\mathrm{f}}(\mathrm{t})\right)\right]}{\left[1+\widehat{\mathsf{\pi }}(\mathrm{t})+\mathsf{ϵ}(\mathrm{t}){\mathsf{\mu }}^{\mathrm{f}}\left(1+{\mathsf{\pi }}^{\mathrm{f}}(\mathrm{t})\right)\right]}}-1,\mathrm{o}\mathrm{r} \mathrm{r}(\mathrm{t})={\displaystyle \frac{({\widehat{\mathrm{i}}}_{\mathrm{t}}-\widehat{\mathsf{\pi }}(\mathrm{t}))+\mathsf{ϵ}(\mathrm{t})\left[{\mathsf{\theta }}^{\mathrm{f}}\left(1+{\mathrm{i}}^{\mathrm{f}}(\mathrm{t})\right)-{\mathsf{\mu }}^{\mathrm{f}}\left(1+{\mathsf{\pi }}^{\mathrm{f}}(\mathrm{t})\right)\right]}{\left[1+\widehat{\mathsf{\pi }}(\mathrm{t})+\mathsf{ϵ}(\mathrm{t}){\mathsf{\mu }}^{\mathrm{f}}\left(1+{\mathsf{\pi }}^{\mathrm{f}}(\mathrm{t})\right)\right]}}$$

(10)

Replacing (10) in Equation (9) and imposing an impact parameter to each term of the resulting equation, we have:

$$∆\mathrm{b}(\mathrm{t})=\left[{\displaystyle \frac{{\mathrm{r}}_{\mathrm{t}}-\mathsf{\eta }\left(\mathrm{t}\right)}{\left(1+\mathsf{\eta }\left(\mathrm{t}\right)\right)}}\right]\mathrm{b}(\mathrm{t}-1)-\mathrm{W}(\mathrm{t})-{\mathrm{S}}^{*}(\mathrm{t})$$

(11)

According to Cafiso (2012), in the real world $∆\mathrm{b}(\mathrm{t})\ne \left[\left({\mathrm{r}}_{\mathrm{t}}-\mathsf{\eta }\left(\mathrm{t}\right)\right)/\left(1+\mathsf{\eta }\left(\mathrm{t}\right)\right)\right]\mathrm{b}(\mathrm{t}-1)-\mathrm{W}(\mathrm{t})-{\mathrm{S}}^{*}(\mathrm{t})$, but $∆\mathrm{b}\left(\mathrm{t}\right)=\left[\left({\mathrm{r}}_{\mathrm{t}}-\mathsf{\eta }\left(\mathrm{t}\right)\right)/\left(1+\mathsf{\eta }\left(\mathrm{t}\right)\right)\right]\mathrm{b}\left(\mathrm{t}-1\right)-\mathrm{W}\left(\mathrm{t}\right)+\mathrm{S}\left(\mathrm{t}\right)$. As Cafiso (2012), here we have in Equation (11), the primary balance, W(t), has a negative sign since the more significant the primary surplus ($\mathrm{T}\left(\mathrm{t}\right)>\mathrm{G}\left(\mathrm{t}\right)$), the smaller the increase in debt. Similarly to $\mathrm{W}\left(\mathrm{t}\right)$, ${\mathrm{S}}^{*}(\mathrm{t})$ is inversely related to debt creation because the government can use seigniorage to pay for goods and services. Then, Equation (11) does not hold. The terms on the right and left sides do not correspond; their difference equals the so-called stock-flow adjustment. The inventory adjustment includes all transactions that cause debt but do not generate a deficit or that cause a deficit but do not generate debt. If the value of ${\mathrm{S}}^{*}(\mathrm{t})$ is greater than that of S(t), the S(t) term is positive (in another way is negative). The main component of the S(t) is the net acquisition of financial assets, which, among other items, records the change in loans. Furthermore, the ${\mathrm{S}}^{*}(\mathrm{t})$ term can be disregarded in analyzing advanced economies. Indeed, seigniorage revenues are no longer pursued because of their inflationary consequences. Then, we can write Equation (11) with S(t) accompanied by a negative sign, and we put coefficients in each term of the left side of Equation (11) to capture the respective impacts, such as:

$$∆\mathrm{b}(\mathrm{t})={\mathsf{\theta }}_1\left[{\displaystyle \frac{\mathrm{r}\left(\mathrm{t}\right)-\mathsf{\eta }\left(\mathrm{t}\right)}{\left(1+\mathsf{\eta }\left(\mathrm{t}\right)\right)}}\right]\mathrm{b}(\mathrm{t}-1)-{\mathrm{u}}_5\mathrm{W}(\mathrm{t})-{\mathsf{\theta }}_2\mathrm{S}(\mathrm{t})$$

(12)

where ${\mathsf{\eta }}_{\mathrm{t}}$ is the real GDP growth rate. We expect a positive sign for the parameter ${\mathrm{u}}_5$ and a positive or negative sign for the parameter ${\mathsf{\theta }}_1$, which depends on the $\mathrm{r}\left(\mathrm{t}\right)$ and $\mathsf{\eta }\left(\mathrm{t}\right)$ values. We expect a positive or negative sign for the parameter ${\mathsf{\theta }}_2$ since it depends on how it is accounted for, which may change from country to country. The parameter notations in this equation are such that ${\mathsf{\theta }}_1$ and ${\mathsf{\theta }}_2$ are designated as uncontrollable parameters, and ${\mathrm{u}}_5$ is controllable.

We write Equation (11) in the continuous differential form, as follows:

$${\displaystyle \frac{\mathrm{d}\mathrm{b}\left(\mathrm{t}\right)}{\mathrm{d}\mathrm{t}}}={\mathsf{\theta }}_1\left[{\displaystyle \frac{\mathrm{r}\left(\mathrm{t}\right)-\mathsf{\eta }\left(\mathrm{t}\right)}{\left(1+\mathsf{\eta }\left(\mathrm{t}\right)\right)}}\right]\mathrm{b}(\mathrm{t}-1)-{\mathrm{u}}_5\mathrm{w}\left(\mathrm{t}\right)-{\mathsf{\theta }}_2\mathrm{s}(\mathrm{t}),$$

(13)

or, considering that $\mathrm{b}(\mathrm{t})=\left[{\displaystyle \frac{1}{(1+\mathsf{\alpha }(\mathrm{t}\left)\right)}}\right]\mathrm{b}(\mathrm{t}-1)$, we have that (13), as de Jong and van der Ploeg (1991)

$${\displaystyle \frac{\mathrm{d}\mathrm{b}\left(\mathrm{t}\right)}{\mathrm{d}\mathrm{t}}}={\mathsf{\theta }}_1\left(\mathrm{r}\left(\mathrm{t}\right)-\mathsf{\eta }\left(\mathrm{t}\right)\right)\mathrm{b}(\mathrm{t})-{\mathrm{u}}_5\mathrm{w}\left(\mathrm{t}\right)-{\mathsf{\theta }}_2\mathrm{s}(\mathrm{t})$$

(14)

It is observed in Equation (13) (or (14)) that the real interest rate, r(t), maintains a positive relationship with debt variability and a negative relationship with the GDP growth rate, η(t). Therefore, the higher the real interest rate, the more significant the impact on debt growth. Conversely, the greater the η(t), the greater the effect of debt decrease. As noted in the above equation, the compelling interest on government debt is a weighted average of domestic and foreign interest rates, and the inflation rate is also a weighted average of domestic inflation for the non-tradable sector and world inflation. The exchange rate of the tradable sector establishes the exchange relations between these domestic and foreign variables. Therefore, exchange rate movements have a direct influence on sovereign debt dynamics.

We established the coefficient of the primary surplus (or deficit), W(t), as a control parameter in Equations (13) and (14). As defined in this equation, this control parameter enables the identification of its impacts on the dynamic model and its effect on the economic system, as well as the amplitude of its impact. In summary, the parameter control effect on debt follows the same direction as the variable variability W(t), which is that when positive (primary surplus), it negatively impacts debt, and when negative (primary deficit), it positively impacts debt.

3.1.2. Inflation Targeting and Macrodynamic Model

According to Guender (2006), in small open economies, the decisions of domestic firms are affected by movements in the exchange rate. Therefore, the author introduces an open economy Phillips Curve that establishes how domestic producers react to changes, assuming that domestic firms adjust their optimal product price in concurrence with changes in the price of the foreign consumption good. A key feature of the open economy Phillips Curve is the presence of the real exchange rate. This New Keynesian open-economy model characterizes discretionary monetary policy in an open economy as differing substantially from the framework in a closed economy. Thus, the inflation rate is determined as follows (Equation (19b) in Guender (2006):

$$\pi \left(t\right)=\tau \left[y\left(t\right)-\overline{y}\left(t\right)\right]+{\pi }^e\left(t\right)+\theta e\left(t\right)$$

(15)

where $\mathrm{y}\left(\mathrm{t}\right)$ is the output and $\overline{\mathrm{y}}\left(\mathrm{t}\right)$) the potential outcome, the term ($\mathrm{y}\left(\mathrm{t}\right)-\overline{\mathrm{y}}\left(t\right)$) represents the output gap, ${\mathsf{\pi }}^{\mathrm{e}}\left(t\right)$ the expected inflation, $\mathrm{e}\left(\mathrm{t}\right)$ the real exchange rate, and $\mathsf{\tau }\gtrless 0$ and $\mathsf{\theta }\gtrless 0$,2 define the impact relationships, respectively, of the output gap and the exchange rate, on the inflation.

Correa and Minella (2010) investigated the presence of nonlinear exchange rate pass-through mechanisms for inflation in Brazil, intending to identify the Keynesian Phillips curve. The estimations indicated the presence of nonlinear mechanisms in the short-run pass-through in Brazil. The short-run pass-through is higher when the economy is booming, when the exchange rate depreciates above some threshold, and when exchange rate volatility is lower. These results are likely related to market pricing behavior, price adjustment costs, and uncertainty about the degree of persistence of exchange rate changes, demonstrating the validity of the Keynesian Phillips Curve for the Brazilian economy.

Then, subtracting the previous period’s inflation on both sides of Equation (15), we have:

$$\mathsf{\pi }\left(\mathrm{t}\right)-\mathsf{\pi }\left(\mathrm{t}-1\right)=\mathsf{\tau }\left[\mathrm{y}\left(\mathrm{t}\right)-\overline{\mathrm{y}}\left(\mathrm{t}\right)\right]+\left[{\mathsf{\pi }}^{\mathrm{e}}\left(\mathrm{t}\right)-\mathsf{\pi }\left(\mathrm{t}-1\right)\right]+\mathsf{\theta }\mathrm{e}\left(\mathrm{t}\right)$$

(16)

Finally, by adjusting the impact parameters and incorporating a control term for the inflation differential relative to the expected inflation, we rewrite Equation (16) as a continuous differential equation:3

$${\displaystyle \frac{\mathrm{d}\mathsf{\pi }\left(\mathrm{t}\right)}{\mathrm{d}\mathrm{t}}}={\mathsf{\sigma }}_1\left[\mathrm{y}\left(\mathrm{t}\right)-\overline{\mathrm{y}}\left(\mathrm{t}\right)\right]+{\mathsf{\sigma }}_2\mathrm{e}\left(\mathrm{t}\right)+{\mathrm{u}}_3\left[\mathsf{\pi }\left(\mathrm{t}\right)-{\mathsf{\pi }}^{\mathrm{e}}\left(\mathrm{t}\right)\right]$$

(17)

where ${\sigma }_1\gtrless 0$ is an uncontrolled impact parameter of the output gap on the inflation variation, which can be negative for economies in development, ${\sigma }_2\gtrless 0$ is an uncontrolled impact parameter of the exchange rate effect on the inflation variation, which can be negative for economies in development as Aghion et al. (2009); and $u_3>0$ is a controlled impact parameter of the difference between inflation and inflation target on the inflation variation.

We define the coefficient of ($\mathsf{\pi }\left(\mathrm{t}\right)-{\mathsf{\pi }}^{\mathrm{e}}\left(\mathrm{t}\right)$) as a controllable parameter that impacts inflation, as it allows interventionist actions by government managers through ${\mathrm{u}}_3$. A change in the stance of monetary policy will induce changes in individuals’ consumption patterns and companies’ investment plans, resulting in shifts in actual economic activity and, ultimately, affecting inflation. Therefore, we can observe that the expected inflation index is a key term for controlling inflation. Thus, changes in the inflation target drive, in the same direction, the change process in the inflation index (IPCA) and the nominal interest index (SELIC). This process implies that the changes in IPCA and the nominal SELIC occur through a previous shift in inflation expectations. Then, we will consider that the variable ($\mathsf{\pi }\left(\mathrm{t}\right)-{\mathsf{\pi }}^{\mathrm{e}}\left(\mathrm{t}\right)$) is a controllable variable via the control of the variable π^e(t), with significant effects on inflation and the short-run interest rate.

We define the coefficient of the output ($y\left(t\right)-\overline{y}\left(t\right)$) as ${\sigma }_1$, an uncontrollable parameter that impacts inflation. To establish the relationship between the output gap and inflation, we must emphasize the interaction between interest rates and inflation.

The short-term interest rate index evolves in the same direction as the performance of the economic process, increasing in a boom and decreasing in a recession (Maka & Holanda Barbosa, 2017). However, depending on the characteristics of the economy (developed or developing), the Central Bank’s intervention occurs differently, being more intense in developing economies. Changes in the short-term interest rate influence investment decisions, consumption, net exports, aggregate demand, and the general price level. In short, the effectiveness of monetary policy depends directly on how much short-term interest impacts consumers and investors, precisely on output.

Thus, a positive output gap (in a boom) is associated with a positive change in the nominal interest rate due to both the economic process and interventions, with a consequent retraction impact on the inflation rate. A negative output gap (in a recession) is associated with a negative change in the nominal interest rate, with a consequent positive impact on the inflation rate. Therefore, ${\sigma }_1$ can be negative in a developing economy due to the central bank’s intense intervention in exchange rates. However, ${\sigma }_1$ can be positive in a developed economy due to the Central Bank’s lack of intervention in exchange rates, where the volatility of the productivity effect prevails as a function of the exchange rate’s appreciation or depreciation.

In Equation (17), we define the impact coefficient ${\sigma }_2$, which we expect to be either positive or negative (this sign is identified during the calibration process in Section 3 below). To understand this assumption, we recall that the link between productivity and the real exchange rate induces the impact of the real exchange rate on inflation. The theoretical importance of the real exchange rate for the conduct of monetary policy under an Inflation-targeting regime is highlighted by Aizenman et al. (2011), based on the version by Ball (1999) and Aghion et al. (2009). These authors concluded that the real exchange rate depreciation reduces productivity in developing countries, attributing it to financial channels. The adverse effects of exchange rate volatility on productivity are more pronounced in the financial markets of developing countries than in those of developed countries. Productivity gains cause an increase in relative prices, contributing to the appreciation of the real exchange rate. In other words, the higher the productivity of an economy, the more appreciated its real exchange rate will be, with a consequent positive impact on inflation. This relationship between the real exchange rate and inflation is established by the Balassa-Samuelson effect (Samuelson, 1964; Balassa, 1964). The logic of this process is that higher productivity causes higher wages in the tradable goods sector of an EME, which will also lead to higher wages in the non-tradable sector (services). This concomitant price increase in economies experiencing more significant growth (developing economies) will result in more intense inflation rate increases than the corresponding effects in developed economies, which are subject to slower growth. Therefore, based on this understanding, the appreciation of the currency in developing economies induces high productivity, accompanied by a substantial increase in inflation, which, in turn, imposes a negative impact on ${\sigma }_2$, as the positive inflationary impact due to the currency appreciation predominates over the negative effect of increased productivity on inflation. High-income countries (developed economies) are more technologically advanced, operating at high levels of productivity, and therefore subject to little variability in the productivity of transactional goods, and with a small wage gap between the two sectors of goods (transactional and non-transactional), unlike what occurs in low-income countries (low productivity). In that case, the negative effect of productivity on inflation predominates over the positive inflationary impact due to currency appreciation, inducing a positive ${\sigma }_2$.

3.1.3. Policy Interest Rate and Macrodynamic Model

Taylor’s rule, as enunciated by Taylor (1993), is an exogenous interest rate estimation model. This monetary policy rule responds to the macroeconomic and monetary variables underlying the economic process, defined as follows:

$$\mathrm{i}\left(\mathrm{t}\right)-{\mathrm{r}}^{*}=\mathsf{\pi }\left(\mathrm{t}\right)+\left[\mathsf{\pi }\left(\mathrm{t}\right)-{\mathsf{\pi }}^{*}\left(\mathrm{t}\right)\right]+\mathsf{\tau }\left[\mathrm{y}\left(\mathrm{t}\right)-\overline{\mathrm{y}}\left(\mathrm{t}\right)\right]$$

(18)

where $\mathrm{i}$ is the nominal interest rate estimated by the Taylor rule, ${\mathrm{r}}^{*}$ the equilibrium real interest rate (natural interest rate), and $\mathsf{\pi }$ the observed inflation rate, ${\mathsf{\pi }}^{*}(\simeq {\mathsf{\pi }}^{\mathrm{e}})$ the Central Bank inflation target, $y-\overline{y}$ is the output gap ($\mathrm{y}$ is the Gross Domestic Product, GDP, and $\overline{y}$ is the potential product), and $\mathsf{\tau }$ is the sensitivity coefficient to product variation.

In Equation (18), we subtracted the term $i\left(\mathrm{t}-1\right)$ on both sides, which leads to:

$$∆\mathrm{i}\left(\mathrm{t}\right)=-\left(\mathrm{i}\left(\mathrm{t}-1\right)-{\mathrm{i}}^{*}\left(\mathrm{t}\right)\right)+\left[\mathsf{\pi }\left(\mathrm{t}\right)-{\mathsf{\pi }}^{\mathrm{e}}\left(\mathrm{t}\right)\right]+\mathsf{\tau }\left[\mathrm{y}\left(\mathrm{t}\right)-\overline{\mathrm{y}}\left(\mathrm{t}\right)\right]$$

(19)

where ${\mathrm{i}}^{*}\left(\mathrm{t}\right)={\mathrm{r}}^{*}+\mathsf{\pi }\left(\mathrm{t}\right)$.

Taylor’s rule holds that central banks must set an interest rate, aiming at an explicit or implicit inflation target, and keep GDP growth near its potential. Both orthodox mainstream and heterodox theories accept Taylor’s rule (Arestis & Sawyer, 2008, among others), which analyzed the dynamic structure of discretionary policies involving the interaction of macroeconomic variables by a model, reconsidering the foundations of monetary policy established in the New Consensus Macroeconomic (NCM) framework. They utilized a six-equation open economy model to summarize the NCM. Their New Keynesian model involves a monetary policy-operating rule of the Taylor rule form for exogenous interest rate determination in an open economy, as shown in Equation (18) above.

Similar to the Arestis and Sawyer (2008) framework, our dynamic model structure analyzes the dynamic macroeconomic behavior involving the New Keynesian curve and Taylor’s rule. Then, we suggest that the short-term interest rate set by Taylor’s rule, as in Equation (19), may apply to an open economy, even though in such an economy, there are different channels through which the country’s economy integrates with international financial markets. For example, securitizing foreign debts depends on the US government bond rates, country risk, and currency risk, suggesting that the domestic interest rate in the open economy depends on the international interest rate. This consideration is supported by the understanding that the exchange rate is related to interest rates and inflation (Nucu, 2011).

Then, the interaction between external and domestic economies is reflected integrally in the business cycle, where interest rates and exchange rates are positively correlated, both growing during a boom and falling during a recession. Therefore, we consider the output gap as a proxy of the exchange rate ($\mathrm{y}\left(\mathrm{t}\right)-\mathrm{y}\left(\mathrm{t}\right)\approx \mathrm{e}\left(\mathrm{t}\right)$), given by the term $\left[\mathrm{y}\left(\mathrm{t}\right)-\overline{\mathrm{y}}\left(\mathrm{t}\right)\right]$ in Equation (19), to capture fully the interaction effects between domestic and extern economies, causing the economy to evolve into a boom or to a recession; that is, respectively a positive or negative output gap. In this context, the exchange rate appreciates when the economy enters a boom (and the interest rate decreases). However, the exchange rate depreciates when the economy enters a recession (and the interest rate increases).

Now, we introduce in the Relation (19) the proportionality parameters in each of its terms, as follows:

$$∆\mathrm{i}\left(\mathrm{t}\right)={\mathrm{a}}_1\left(\mathrm{i}\left(\mathrm{t}-1\right)-{\mathrm{i}}^{*}\left(\mathrm{t}\right)\right)+{\mathrm{a}}_2\left[\mathsf{\pi }\left(\mathrm{t}\right)-{\mathsf{\pi }}^{\mathrm{e}}\left(\mathrm{t}\right)\right]+{\mathrm{a}}_3\left[\mathrm{y}\left(\mathrm{t}\right)-\overline{\mathrm{y}}\left(\mathrm{t}\right)\right]$$

(20)

where $a_1<0$, $a_2<0$ and $a_3<0$ are expected.

We write Equation (20) in differential form, as follows:

$${\displaystyle \frac{\mathrm{d}\mathrm{i}\left(\mathrm{t}\right)}{\mathrm{d}\mathrm{t}}}={\mathrm{a}}_1\left(\mathrm{i}\left(\mathrm{t}-1\right)-{\mathrm{i}}^{*}\left(\mathrm{t}\right)\right)+{\mathrm{a}}_2\left[\mathsf{\pi }\left(\mathrm{t}\right)-{\mathsf{\pi }}^{\mathrm{e}}\left(\mathrm{t}\right)\right]+{\mathrm{a}}_3\left[\mathrm{y}\left(\mathrm{t}\right)-\overline{\mathrm{y}}\left(\mathrm{t}\right)\right]$$

(21)

Equation (21) aims to establish the effects of controlling the impact of the long and short-term interest rate differential ($\mathrm{i}\left(\mathrm{t}\right)-{\mathrm{i}}^{*}\left(\mathrm{t}\right)$) on the nominal interest rate, setting future targets for the nominal long-term interest index, which in Brazilian economy (${\mathrm{i}}^{*}\left(\mathrm{t}\right)\approx$ TJLP, the economy focus of our study. This consideration is consistent because the TJLP index must comply with the criteria established in Law 10183 of 12 February 2001. According to this law, the BACEN (Brazil’s central Bank) fixes the TJLP index equal to the inflation target plus a risk premium, thereby serving as a control parameter. This behavior enables the coefficient ${\mathrm{u}}_2$ to be a controllable parameter.

Still based on Relation (21), we define an ordinary differential equation for the evolution of the changing nominal interest rate. In this case, we consider that the interest rate of the past period is strongly connected with the interest rate of the present period when the time increment $dt$ is short. Thus, we can replace $\mathrm{i}\left(\mathrm{t}-1\right)$ by a fraction of $\mathrm{i}\left(\mathrm{t}\right)$, and applying a control term, ${\mathrm{u}}_2$, to the exchange rate, as following:

$${\displaystyle \frac{\mathrm{d}\mathrm{i}\left(\mathrm{t}\right)}{\mathrm{d}\mathrm{t}}}={\mathrm{u}}_2\left(\mathrm{i}\left(\mathrm{t}\right)-\mathrm{T}\mathrm{J}\mathrm{L}\mathrm{P}\left(\mathrm{t}\right)\right)+{\mathsf{\mu }}_1\left[\mathrm{y}\left(\mathrm{t}\right)-\overline{\mathrm{y}}\left(\mathrm{t}\right)\right]+{\mathsf{\mu }}_2[\mathsf{\pi }(\mathrm{t})-{\mathsf{\pi }}^{\mathrm{e}}(\mathrm{t})]$$

(22)

where the parameters ${\mu }_1<0, {\mu }_2<0$, and $u_2<0$.

3.1.4. Exchange Rate and Macrodynamic Model

Now, we consider the relation of variation of the real exchange rate established in Ball (1999):

$$\mathrm{e}\left(\mathrm{t}\right)={\mathsf{\omega }}_1\mathrm{r}\left(\mathrm{t}\right)+\mathsf{\vartheta }\left(\mathrm{t}\right)$$

(23)

where $e$ is the real exchange rate, $r$ the real interest rate, with the coefficient ${\omega }_1>0$ and $\vartheta$ a stochastic disturbance behaving like white noise.

As Ball (1999), the Equation (23) establishes a link between interest and exchange rates. It captures the idea that an increase in the interest rate makes domestic assets more attractive, leading to appreciation. The $\vartheta \left(t\right)$ shock captures other influences on the exchange rate, such as expectations, investor confidence, and foreign interest rates. The central bank chooses the real interest rate $\mathrm{r}\left(\mathrm{t}\right)$, which, together with Equation (23), constitutes a rule for defining $\mathrm{e}\left(\mathrm{t}\right)$ or some combination of $\mathrm{e}\left(\mathrm{t}\right)$ and $\mathrm{r}\left(\mathrm{t}\right)$.

Adding and subtracting in Equation (23), the term $\mathrm{e}(\mathrm{t}-1)$, and, at this moment, ignoring the stochastic term that will be considered later in the stochastic model. Then, we get:

$$∆\mathrm{e}\left(\mathrm{t}\right)={\mathsf{\delta }}_1\mathrm{e}(\mathrm{t}-1)+{\mathsf{\delta }}_2\mathrm{r}\left(\mathrm{t}\right)$$

(24)

where ${\delta }_1>0$ and ${\delta }_2\lessgtr 0$.

Based on the relationship (24), we assume one continuous ordinary differential equation to describe the development of the real exchange rate. Then, without loss of generality, it can be assumed that $\mathrm{e}\left(\mathrm{t}-1\right)\approx \mathrm{e}\left(\mathrm{t}\right)$, considering that the integration time is tiny (order ${10}^{-8}$) in a continuous differential equation. Thus, we have:

$${\displaystyle \frac{\mathrm{d}\mathrm{e}\left(\mathrm{t}\right)}{\mathrm{d}\mathrm{t}}}={\mathsf{\delta }}_1\mathrm{e}(\mathrm{t})+{\mathrm{u}}_4\mathrm{r}(\mathrm{t})$$

(25)

where ${\mathrm{u}}_4={\mathsf{\delta }}_2\lessgtr 0$ is a controlling factor, and we expect a positive sign, ${\mathsf{\delta }}_1>0$ is the impact of the exchange rate on itself.

In Equation (25), we established that the coefficient of the real interest rate (${\mathrm{u}}_4$) is the control parameter for the evolution of the real exchange rate. This choice is made because expansionary or contractionary monetary policies impact the exchange rate.

The short-term interest rate (in Brazil, the Selic rate) is the primary monetary policy instrument available to the Central Bank (BC) that affects the behavior of other economic variables, mainly prices and output, such as (i) the decision between consumption and investment by families and companies; (ii) the exchange rate; (iii) asset prices; (iv) credit; and (v) expectations. We are interested in analyzing the monetary policy transmission channel through the exchange rate channel, the most important one, mainly in open economies.

Although the relationship between monetary policy and the exchange rate is a widely debated topic in the economic literature, there is no consensus on the sign of this relationship. The simultaneity between these variables makes the relationship even more complex and challenging to analyze. The traditional view on the relationship between monetary policy and the exchange rate, on which the IMF position is based, establishes that the determination of the exchange rate derives from the combination of rational expectations, uncovered interest rate parity, and purchasing power parity, such as Dornbusch (1976) and Kouri (1976), among others. In this context, an increase in interest rates makes investment in the country more attractive, and the spot exchange rate appreciates, keeping future exchange rate expectations constant. The opposite would happen in the event of a reduction in the interest rate. In that case, ${\mathrm{u}}_4<0$.

However, many other authors, such as Drazen and Masson (1994), and Bensaid and Jeanne (1997), state that the proof is mixed. An increase in the interest rate can cause both an appreciation in the currency and a depreciation, which generated a great debate about the effectiveness of interest rates in periods of exchange rate crisis. In summary, Evidence is mixed not only for periods of crisis, thus creating a division in the literature on understanding the relationship between exchange rate and interest rate. Overall, findings from studies that support the mixed view conclude that some empirical results are consistent with the conventional view; however, there are also conclusions from empirical studies that support the “revisionist” view, especially studies related to periods of crisis, which show very clearly that a contractionary monetary policy (high-interest rates) impacts on exchange rate depreciation. The base argument is that raising the interest rate beyond what is necessary to offset the rising risk of premiums contributes to the collapse of exchange rates when speculation attacks them.

On the other hand, we have the so-called revisionist perspective (Stiglitz, 1999; Gertler et al., 2007, and others), or non-traditional, which postulates a positive relationship between interest rate and exchange rate that is, an increase in the interest rate causes a depreciation in the exchange rate. This fact can occur due to several factors, such as the risk of default, instability in the credit market, imbalance in the balance of payments, an inflationary environment, and other structural elements of an economy. A greater risk of foreign assets leads to the depreciation of the local currency and the need to raise interest rates to control inflation; this channel generates a positive relationship between currency depreciation and interest rates, that is, ${\mathrm{u}}_4>0$. Usually, that situation is characteristic of a developing economy.

Relative to the floating exchange rate system in developing economies (as in the case of Brazil), exchange rate fluctuations can strongly affect the price level through aggregate demand and supply. In aggregate supply, the depreciation (devaluation) of the national currency can directly and positively impact the price level through imported goods that national consumers consume. The non-direct influence of exchange rate depreciation on a country’s price level can be seen from the price of capital goods (intermediate goods) imported by the manufacturer as input. The weakening of the exchange rate will make the prices of inputs more expensive, thus contributing to a higher cost of production. Manufacturers will undoubtedly increase the prices of goods that consumers buy, with a consequent positive impact on inflation (in this case, exchange rate depreciation positively implies inflation). Thus, a higher level of inflation is accompanied by exchange rate depreciation or vice versa. This relationship is direct, as Aghion et al. (2009) showed that real exchange rate depreciation reduces productivity in developing countries with a consequent increase in inflation (effect attributed to financial channels). Those effects are more significant in developing countries’ financial markets than in developed countries. Thus, ${\mathsf{\delta }}_1>0$.

As conclusions of the analysis presented in the paragraphs above, we expect that Equation (25)’s control parameter, ${\mathrm{u}}_4$, can assume positive or negative values and, ${\mathsf{\delta }}_1>0$.

3.1.5. Output and Macrodynamic Model

Ball (1999) assumes a relation for the product in the form of a difference equation, considering the concepts of the IS curve, as follows:

$$\mathrm{y}\left(\mathrm{t}\right)={\phi }_1\mathrm{y}\left(\mathrm{t}-1\right)-{\phi }_2\mathrm{r}\left(\mathrm{t}-1\right)-{\phi }_3\mathrm{e}\left(\mathrm{t}-1\right)$$

(26)

where $\mathrm{y}\left(\mathrm{t}\right)$ is the gross domestic product, $\mathrm{r}(\mathrm{t}-1)$ is the real lagged interest rate, $\mathrm{e}(\mathrm{t}-1)$ is the real lagged exchange rate, and the constants ${\phi }_1$, ${\phi }_2$, ${\phi }_3$ are positive.

The functional relation (26) stresses the perspective characteristic of aggregate demand (the current real gross domestic product), $\mathrm{y}\left(\mathrm{t}\right)$, which depends on the lagged real output, $\mathrm{y}\left(\mathrm{t}-1\right)$, on the lagged real exchange rate $\mathrm{e}\left(\mathrm{t}\right)$, and the lagged real interest rate $\mathrm{r}\left(\mathrm{t}\right)$. In the logic of the functional relation (26), as Ball (1999) considered, ${\phi }_1$, ${\phi }_2$, ${\phi }_3$ are positives. Then, we will assume that the above equation’s exchange rate coefficient, ${\phi }_3$, has mixed sense and can be either positive or negative, as we will argue later. In this case, we consider that ${\phi }_3\lessgtr 0$. Besides, the current real gross domestic product also depends on the demand shock, which is despised at that Equations (26) since we established the formulation of the determinist model. However, it will be included in the formulation of the stochastic model later.

Adding and subtracting in Equation (26), the term $\mathrm{y}\left(\mathrm{t}-1\right)$, we get:

$$∆\mathrm{y}\left(\mathrm{t}\right)={\mathsf{\gamma }}_1\mathrm{r}\left(\mathrm{t}-1\right)+{\mathsf{\gamma }}_2\mathrm{e}\left(\mathrm{t}-1\right)+{\mathsf{\gamma }}_3\mathrm{y}\left(\mathrm{t}-1\right)$$

(27)

where the expected signs are: ${\mathsf{\gamma }}_1={-\phi }_2<0$, ${\mathsf{\gamma }}_2={\phi }_3\lessgtr 0$, and ${\mathsf{\gamma }}_3={\phi }_1-1>0$.

In summary, the lags in Equation (26) imply that small rises in and contemporaneously take a lag period to affect output. Then, remembering that we are dealing with a continuous-time equation whose integration process for its solution will occur in time increments of the order of ${10}^{-8}$, a tiny increment, we use the same procedure applied earlier; we transform Equation (27) into a deterministic continuous differential equation, written as follows:

$${\displaystyle \frac{\mathrm{d}\mathrm{y}\left(\mathrm{t}\right)}{\mathrm{d}\mathrm{t}}}={\mathrm{u}}_1\mathrm{y}\left(\mathrm{t}\right)+{\mathsf{\gamma }}_1\mathrm{r}\left(\mathrm{t}\right)+{\mathsf{\gamma }}_2\mathrm{e}\left(\mathrm{t}\right)$$

(28)

where $u_1={\gamma }_3>0$.

We will calibrate the coefficients of Equation (28) later. However, we consider ${\mathrm{u}}_1$ a control parameter impacting the Gross Domestic Product. In particular, we seek to establish economic growth rate targets by the controlling parameter induced by development policies. In a stable economic process, the control term, ${\mathrm{u}}_1$, has to assume a positive sign.

The importance of controlling the output aggregate demand is justified in establishing an analysis of aggregate income (GDP) impact on economic growth. This control can be established by analyzing the ${\mathrm{u}}_1$ evolution over time, which may induce the need to establish structural reforms to improve the aggregate product, productivity, and the reallocation of resources. In a low aggregate demand growth situation, low private investments in production occur, and the labor market unheating outcomes. In that situation, fiscal expansion can strengthen activity via public investment, especially with low long-term interest rates, which effectively increase fiscal space, at least temporarily. Almost all countries have room to reallocate public spending towards more growth-friendly items. Collective action among economies can also increase public investment in carefully selected projects with high growth impacts and increase demand without compromising fiscal sustainability. In addition, collective efforts to revive structural reform momentum would improve productivity, resource allocation, and the effects of supportive macroeconomic policies. In a weak economy and rising income inequality, structural reforms must focus on possible short-term benefits to demand and measures to promote long-term improvements in employment, productivity growth, and inclusion.

In short, economic policy managers can establish structural reforms that improve productivity and consequently impact GDP growth. These reforms involve fiscal policies, resource reallocation, and greater trade interaction with world economies.

The impact of the real exchange rate on the real output is established by the link between productivity and the real exchange rate and between productivity and inflation. Our analysis considers that inflation causes output loss since the interest rate increases and the investment decays. The productivity gains cause an increase in inflation, but it also contributes to the appreciation of the real exchange rate. In other words, the greater the productivity of an economy, the more appreciated its real exchange rate will be, with a consequent positive impact on inflation. As explained, this relationship between the real exchange rate and inflation is established by the Balassa–Samuelson effect (Samuelson, 1964; Balassa, 1964). This effect suggests that increased wages in the tradable goods sector due to increased economic productivity lead to higher wages in the non-tradable (services) sector and higher wages in the non-tradable (services) sector.

These concomitant higher wages of tradable and non-tradable sectors are more significant in the EMEs (subjected to higher growth) and cause more intense increases in inflation rates than the corresponding effects in developed economies, subject to slower growth. This fact is due to differences in productivity growth between tradable and non-tradable sectors, which are more intense in the EMEs. Therefore, product growth is associated with exchange rate appreciation and productivity growth, but larger productivity is also associated with more considerable inflation; then, we can ask the following question: how do these effects prevail on the impact on the product?

High-income countries are more technologically advanced, operating at high productivity levels, therefore, subject to small variability in the productivity of transactional goods, and with a small wage gap between the two sectors of goods (transactional and non-transactional), contrary to that occurs in low-income countries (EMEs). According to the law of one price, prices for tradable goods must be equal between countries, but not for non-tradable goods. Therefore, greater productivity in tradable goods will mean higher real wages for workers in that sector, raising their relative prices and wages and those of the local non-tradable goods they acquire. In that case, for developed economies, we understand that decreasing exchange rate (exchange rate appreciated) impacts more productivity than inflation; then, the positive productivity effect prevails over the negative inflation impact on the product, which indicates that ${\mathsf{\gamma }}_2<0$. In developed economies, the exchange rate depreciation is also associated intrinsically with productivity shrinking without altering in a significant way the inflationary process, as explained above, a condition that also induces ${\mathsf{\gamma }}_2<0$.

For developing economies (EME), the relationship between exchange rate appreciation and relative productivity growth, with consequent inflationary impact, acts more intensely than developed economies, according to the Balassa-Samuelson effect (Samuelson, 1964; Balassa, 1964). According to this effect, in developing economies, there is a greater discrepancy between wages in tradable and non-tradable goods and the more significant productivity effect in EMEs (subject to higher growth); inflationary impacts due to wage adjustments are more intense in EMEs than in developed economies. In this case, the positive effects of productivity growth on output are less significant than the effects of the inflationary impact; consequently, the inflationary impact prevails.

Also, in EMEs, the non-direct influence of exchange rate depreciation on the price level of an economy prevails, as the price of capital goods (intermediate goods) imported by the manufacturer as input. The weakening of the exchange rate will make input prices more expensive, thus contributing to a higher production cost that is passed on to consumers, with a consequent positive impact on inflation (in this case, the depreciation of the exchange rate impacts inflation more intensely than productivity (Aghion et al., 2009). This effect is attributed to financial channels.

Therefore, the increase in inflation, whether due to exchange rate appreciation or depreciation in EMEs, impacts the product on the demand and supply sides. The depreciation of the exchange rate can affect production through demand. In this case, the economy stops importing similar international products. It starts consuming more national products, and on the supply side, the economy increases its export potential due to competitive prices. Whether due to the generation of inflation due to exchange rate appreciation or depreciation. In this case, ${\mathsf{\gamma }}_2>0$.

3.1.6. Macrodynamic Model and Monetary and Fiscal Policies Mix

Considering the Equations (14), (17), (22), (25) and (28) established early, we can now set the dynamic model that allows us to obtain the evolutionary processes of the main fiscal and monetary variables of the economy. The system that describes this model is characterized by five ordinary differential equations, as described below:

$$\left\{\begin{array}{l}{\displaystyle \frac{\mathrm{d}\mathrm{y}\left(\mathrm{t}\right)}{\mathrm{d}\mathrm{t}}}={\mathrm{u}}_1\mathrm{y}\left(\mathrm{t}\right)+{\mathsf{\gamma }}_1\mathrm{r}\left(\mathrm{t}\right)+{\mathsf{\gamma }}_2\mathrm{e}\left(\mathrm{t}\right)\\ {\displaystyle \frac{\mathrm{d}\mathrm{i}\left(\mathrm{t}\right)}{\mathrm{d}\mathrm{t}}}={\mathrm{u}}_2\left(\mathrm{i}\left(\mathrm{t}\right)-{\mathrm{i}}^{*}\left(\mathrm{t}\right)\right)+{\mathsf{\mu }}_1\left[\mathrm{y}\left(\mathrm{t}\right)-\overline{\mathrm{y}}\left(\mathrm{t}\right)\right]+{\mathsf{\mu }}_2[\mathsf{\pi }(\mathrm{t})-{\mathsf{\pi }}^{\mathrm{e}} (\mathrm{t})]\\ {\displaystyle \frac{\mathrm{d}\mathsf{\pi }\left(\mathrm{t}\right)}{\mathrm{d}\mathrm{t}}}={\mathsf{\sigma }}_1\left[\mathrm{y}\left(\mathrm{t}\right)-\overline{\mathrm{y}}\left(\mathrm{t}\right)\right]+{\mathsf{\sigma }}_2\mathrm{e}\left(\mathrm{t}\right)+{\mathrm{u}}_3\left[\mathsf{\pi }\left(\mathrm{t}\right)-{\mathsf{\pi }}^{\mathrm{e}}\left(\mathrm{t}\right)\right]\\ {\displaystyle \frac{\mathrm{d}\mathrm{e}\left(\mathrm{t}\right)}{\mathrm{d}\mathrm{t}}}={\mathsf{\delta }}_1\mathrm{e}\left(\mathrm{t}\right)+{\mathrm{u}}_4\mathrm{r}\left(\mathrm{t}\right)\\ {\displaystyle \frac{\mathrm{d}{\mathrm{b}}_{\mathrm{t}}}{\mathrm{d}\mathrm{t}}}={\mathsf{\theta }}_1\left[{\mathrm{r}}_{\mathrm{t}}-{\mathsf{\eta }}_{\mathrm{t}}\right]\mathrm{b}\left(\mathrm{t}\right)-{\mathrm{u}}_5\mathrm{w}\left(\mathrm{t}\right)-{\mathsf{\theta }}_2\mathrm{s}\left(\mathrm{t}\right)\end{array}\right.$$

(29)

The dynamic model (29) involves five ordinary differential equations and five unknowns: real output, nominal interest rate, inflation, real exchange rate, and real sovereign debt. We will use this model to establish the interaction between fiscal and monetary policies and identify their effects on output and sovereign debt in an open economy.

The System (29) is deterministic since we neglected the stochastic innovations in its equations, which will be integrated into the stochastic version of the dynamic system. System (29) will be calibrated to get the resilient effects among the endogenous variables. Below, we will describe some dynamic behavior that our system must capture.

In the dynamic model structure, an interest rate decision directly impacts the exchange rate and the output, and, in the second step, the inflation rate and output via the exchange rate channel, i.e., one instrument with two targets (effects). Focusing only on domestic variables in interest rate determination may provide a combination of internal price and exchange rate instability. The effects of the exchange rate on the composition and level of demand indicate that the exchange rate should be given weight in macroeconomic policy decision-making, even though the exchange rate is not a policy instrument. Instead, it is determined in the foreign exchange market. Then, the critical feature of the dynamic model (29) is that the policy affects inflation through two channels. A monetary contraction (interest rate increase) in an open economy reduces output. It causes an exchange rate appreciation (or exchange rate depreciation, as explained earlier) that directly reduces inflation (or increases inflation) through the Phillips curve (third equation of the System (30)). The first channel involves a rise in r(t), with contemporaneous impacts in e(t), which subsequently affects the inflation and output. Moreover, in another lag period, the output gap affects inflation.

In contrast, the direct effect of an exchange-rate change on inflation takes only one period. These assumptions capture the standard view that the direct exchange rate effect is the quickest channel from policy to inflation. The impact of monetary policies in an open economy depends upon the international monetary system chosen. Then, in that argumentation, we considered a system of floating exchange rates that adjust freely to changing economic conditions.

In System (29), the Fiscal Policy impact is due to increased government spending or lower taxes to stimulate domestic spending, which only increases the exchange rate, positively impacting sovereign debt (fifth systema equation), without impacting income or output. A higher budget deficit reduces domestic savings resulting in net foreign investment (borrowing from abroad), bidding up the dollar’s value. Eventually, the higher exchange rate reduces net exports exactly enough to offset the expansionary impact of fiscal policy. However, Monetary Policy influences income in an open economy, as emphasized earlier.

3.2. Transformation of the Dynamic Model into the Stochastic Model

The System (29) has some limitations, such as the absence of variations of model parameters with time to adapt them to behavior changes; and the lack of additive stochastic terms that induce failures to model the dependent variables since some un-modeled dynamics exist. Based on these considerations, we transform the System (30) into a stochastic model to analyze the political dynamic of a developing economy facing any situation.

Therefore, to mimic the stochastic dynamics, we will introduce stochastic fluctuations on the parameters and additive chocks on the endogenous variables to capture the external and internal stochastic disturbances often suffered by developing economies over time. Thus, each System (29) differential equation becomes stochastic.

$$\left\{\begin{array}{l}{\displaystyle \frac{\mathrm{d}\mathrm{y}\left(\mathrm{t}\right)}{\mathrm{d}\mathrm{t}}}={\mathrm{u}}_1\mathrm{y}\left(\mathrm{t}\right)+\left({\mathsf{\gamma }}_1+∆{\mathsf{\gamma }}_1\right)\mathrm{r}\left(\mathrm{t}\right)+\left({\mathsf{\gamma }}_2+∆{\mathsf{\gamma }}_2\right)\mathrm{e}\left(\mathrm{t}\right)+{\mathrm{v}}_1\left(\mathrm{t}\right)\\ {\displaystyle \frac{\mathrm{d}\mathrm{i}\left(\mathrm{t}\right)}{\mathrm{d}\mathrm{t}}}={\mathrm{u}}_2\left[\mathrm{i}\left(\mathrm{t}\right)-{\mathrm{i}}^{*}\left(\mathrm{t}\right)\right]+\left({\mathsf{\mu }}_1+∆{\mathsf{\mu }}_1\right)\left[\mathrm{y}\left(\mathrm{t}\right)-\overline{\mathrm{y}}\left(\mathrm{t}\right)\right]+\left({\mathsf{\mu }}_2+∆{\mathsf{\mu }}_2\right)\left[\mathsf{\pi }\left(\mathrm{t}\right)-{\mathsf{\pi }}^{\mathrm{e}}\left(\mathrm{t}\right)\right] +{\mathrm{v}}_2\left(\mathrm{t}\right)\\ {\displaystyle \frac{\mathrm{d}\mathsf{\pi }\left(\mathrm{t}\right)}{\mathrm{d}\mathrm{t}}}=\left({\mathsf{\sigma }}_1+∆{\mathsf{\sigma }}_1\right)\left[\mathrm{y}\left(\mathrm{t}\right)-\overline{\mathrm{y}}\left(\mathrm{t}\right)\right]+\left({\mathsf{\sigma }}_2+∆{\mathsf{\sigma }}_2\right)\mathrm{e}\left(\mathrm{t}\right)+{\mathrm{u}}_3\left[\mathsf{\pi }\left(\mathrm{t}\right)-{\mathsf{\pi }}^{\mathrm{e}}\left(\mathrm{t}\right)\right]+{\mathrm{v}}_3\left(\mathrm{t}\right)\\ {\displaystyle \frac{\mathrm{d}\mathrm{e}\left(\mathrm{t}\right)}{\mathrm{d}\mathrm{t}}}=\left({\mathsf{\delta }}_1+∆{\mathsf{\delta }}_1\right)\mathrm{e}\left(\mathrm{t}\right)+{\mathrm{u}}_4\mathrm{r}\left(\mathrm{t}\right)+{\mathrm{v}}_4\left(\mathrm{t}\right)\\ {\displaystyle \frac{\mathrm{d}\mathrm{b}\left(\mathrm{t}\right)}{\mathrm{d}\mathrm{t}}}=\left({\mathsf{\theta }}_1+∆{\mathsf{\theta }}_1\right)\left[{\mathrm{r}}_{\mathrm{t}}-{\mathsf{\eta }}_{\mathrm{t}}\right]\mathrm{b}\left(\mathrm{t}\right)-{\mathrm{u}}_5\mathrm{w}\left(\mathrm{t}\right)-\left({\mathsf{\theta }}_2+∆{\mathsf{\theta }}_2\right)\mathrm{s}\left(\mathrm{t}\right)+{\mathrm{v}}_5\left(\mathrm{t}\right)\end{array}\right.$$

(30)

where the symbol $∆$ indicates parametric fluctuation of the coefficients to adapt the model to changes in behavior due to stochastic innovations that cause changes in the conduct of the economy; $v_1\left(t\right)$, $v_2 \left(t\right)$, $v_3 \left(t\right)$, $v_4 \left(t\right)$ and $v_5 \left(t\right)$ capture the external disturbances in an additive manner, which last for a certain cyclical period.

In System (31), we assume that parametric variations can be divided into two parts, a deterministic and a random: $∆{\gamma }_1={\mathsf{\omega }}_1\mathrm{n}\left(\mathrm{t}\right), ∆{\gamma }_2={\mathsf{\omega }}_2\mathrm{n}\left(\mathrm{t}\right), ∆{\mu }_1={\mathsf{\omega }}_3\mathrm{n}\left(\mathrm{t}\right), ∆{\mu }_2={\mathsf{\omega }}_4\mathrm{n}\left(\mathrm{t}\right)$, $∆{\sigma }_1={\mathsf{\omega }}_5\mathrm{n}\left(\mathrm{t}\right)$, $∆{\sigma }_2={\mathsf{\omega }}_6\mathrm{n}\left(\mathrm{t}\right)$, $∆{\delta }_1={\mathsf{\omega }}_7\mathrm{n}\left(\mathrm{t}\right)$, $∆{\theta }_1={\mathsf{\omega }}_8\mathrm{n}\left(\mathrm{t}\right)$, $∆{\theta }_2={\mathsf{\omega }}_9\mathrm{n}\left(\mathrm{t}\right)$ where ${\mathsf{\omega }}_{\mathrm{i}}$ represents the standard deviation of the stochastic parametric fluctuation, $\mathrm{n}\left(\mathrm{t}\right)$ a standard white noise with a unit variance; that is, $var(∆{\gamma }_1) ={\left({\omega }_1\right)}^2$, $var(∆{\gamma }_2) ={\left({\omega }_2\right)}^2$ and so on.

We will obtain the economic policy dynamics model involving the stochastic effects, as the definitions stressed in the paragraph above, and apply them to the System (31). Then, we split the resulting system by the sum of subsystems involving the determinist part, the control system, and the stochastic parts. Also, to establish the integration of the resulting system, we write this stochastic system as follows:

$$\begin{array}{l}\left[\begin{array}{c}dy\left(t\right)\\ di\left(t\right)\\ d\pi \left(t\right)\\ de\left(t\right)\\ db\left(t\right)\end{array}\right]=\left[\begin{array}{c}\begin{array}{c}\begin{array}{c}\begin{array}{c}{\gamma }_{1}r\left(t\right)+{\gamma }_{2}e\left(t\right)\\ {\mu }_1\left[y\left(t\right)-\overline{y}\left(t\right)\right]+{\mu }_2\left[\pi \left(t\right)-{\pi }^e \left(t\right)\right]\end{array}\end{array}\\ {\sigma }_1\left[y\left(t\right)-\overline{y}\left(t\right)\right]+{\sigma }_{2}e\left(t\right)\end{array}\\ {\delta }_{1}e\left(t\right)\\ {\theta }_1\left[{\mathrm{r}}_{\mathrm{t}}-{\mathsf{\eta }}_{\mathrm{t}}\right]b\left(t\right)-{\theta }_{2}s\left(t\right)\end{array}\right]dt+\left[\begin{array}{ccccc}y\left(t\right)& 0& 0& 0& 0\\ 0& \left[i\left(t\right)-i^{*}\left(t\right)\right]& 0& 0& 0\\ 0& 0& \left[\pi \left(t\right)-{\pi }^e\left(t\right)\right]& 0& 0\\ 0& 0& 0& r\left(t\right)& 0\\ 0& 0& 0& 0& -W\left(t\right)\end{array}\right]\left[\begin{array}{c}{u}_1\\ u_2\\ u_3\\ u_4\\ u_5\end{array}\right]dt +\\ \left[\begin{array}{c}{v}_1\left(t\right)\\ v_2\left(t\right)\\ v_3\left(t\right)\\ v_4\left(t\right)\\ v_5\left(t\right)\end{array}\right]dt+\left[\begin{array}{c}\begin{array}{c}\begin{array}{c}\begin{array}{c}{\omega }_{1}r\left(t\right)+{\omega }_{2}e\left(t\right)\\ {\omega }_3\left[y\left(t\right)-\overline{y}\left(t\right)\right]+{\omega }_4\left[\pi \left(t\right)-{\pi }^e \left(t\right)\right]\end{array}\end{array}\\ {\omega }_5\left[y\left(t\right)-\overline{y}\left(t\right)\right]+{\omega }_{6}e\left(t\right)\end{array}\\ {\omega }_{9}e\left(t\right)\\ {\omega }_7\left[{\mathrm{r}}_{\mathrm{t}}-{\mathsf{\eta }}_{\mathrm{t}}\right]b\left(t\right)-{\omega }_{8}s\left(t\right)\end{array}\right]dp\left(t\right)\end{array}$$

(31)

where $dp\left(t\right)=\eta \left(t\right)dt$ is a standard Wiener process or Brownian motion.

The stochastic system of Equation (31) can be written in a general stochastic system, as follows:

$$\mathrm{d}\mathrm{x}\left(\mathrm{t}\right)=\left[\left(\mathrm{x}\left(\mathrm{t}\right)\right)+\mathrm{g}\left(\mathrm{x}\left(\mathrm{t}\right)\right)\mathrm{u}\left(\mathrm{t}\right)+\mathrm{v}\left(\mathrm{t}\right)\right]\mathrm{d}\mathrm{t}+\mathrm{h}\left(\mathrm{x}\left(\mathrm{t}\right)\right)\mathrm{d}\mathrm{p}\left(\mathrm{t}\right),$$

(32)

with

$$\mathrm{x}\left(0\right)={\mathrm{x}}_0$$

(33)

where $\mathrm{x}\left(\mathrm{t}\right)={\left[{\mathrm{x}}_1\left(\mathrm{t}\right)\dots {\mathrm{x}}_{\mathrm{n}}\left(\mathrm{t}\right)\right]}^{\mathrm{T}}$, $\mathrm{u}\left(\mathrm{t}\right)={\left[{\mathrm{u}}_1\left(\mathrm{t}\right)\dots {\mathrm{u}}_{\mathrm{m}}\left(\mathrm{t}\right)\right]}^{\mathrm{T}}$, $\mathrm{v}\left(\mathrm{t}\right)={\left[{\mathrm{v}}_1\left(\mathrm{t}\right)\dots {\mathrm{v}}_{\mathrm{n}}\left(\mathrm{t}\right)\right]}^{\mathrm{T}}$ represent the states’ vector, control parameters’ vector, and external disturbances’ vector, respectively. $\mathrm{f}\left(\mathrm{x}\left(\mathrm{t}\right)\right)\in {\mathrm{R}}^{\mathrm{n}\ast 1}$ denotes the nonlinear interaction vector between fiscal and monetary policy variables, $\mathrm{g}\left(\mathrm{x}\left(\mathrm{t}\right)\right)\in {\mathrm{R}}^{\mathrm{n}\ast 1}$ denotes the control inputs’ matrix, and $\mathrm{h}\left(\mathrm{x}\left(\mathrm{t}\right)\right)\in {\mathrm{R}}^{\mathrm{n}\ast 1}$ represents the parametric fluctuations’ vector of the noises imposed on the dependent variables. In general, the above equation shows that ${\mathrm{x}}_1\left(\mathrm{t}\right)=\mathrm{y}\left(\mathrm{t}\right)$, ${\mathrm{x}}_2\left(\mathrm{t}\right)=\mathrm{i}\left(\mathrm{t}\right)$, ${\mathrm{x}}_3\left(\mathrm{t}\right)=\mathrm{b}\left(\mathrm{t}\right)$, ${\mathrm{x}}_4\left(\mathrm{t}\right)=\mathrm{e}\left(\mathrm{t}\right)$ and ${\mathrm{x}}_5\left(\mathrm{t}\right)=\mathsf{\pi }\left(\mathrm{t}\right)$.

3.3. Databases for Model Identification

We need to identify the impact parameters in the formulated dynamic model (System 29) through calibration. This calibration process allows us to obtain the levels of the characteristic parameters of the Brazilian economy. For thus, we will use the following databases: nominal monthly annualized interest index (SELIC index), $\mathrm{i}\left(\mathrm{t}\right)$; real Net Debt of the Public Sector, normalized by the initial real Gross Domestic Product (1998/Jan), $\mathrm{b}\left(\mathrm{t}\right)$; actual Tax Revenues, $\mathrm{T}\left(\mathrm{t}\right)$, and the real Government Financial Expenses, $\mathrm{G}\left(\mathrm{t}\right)$, both normalized by the initial real Gross Domestic Product (1998/Jan); real Exchange Rate, $\mathrm{e}\left(\mathrm{t}\right)$; nominal monthly annualized inflation index (IPCA index), $\mathsf{\pi }\left(\mathrm{t}\right)$; real Gross Domestic Product (GDP), $\mathrm{Y}(\mathrm{t}$), normalized by the initial real Gross Domestic Product (1998/Jan); nominal Brazil’s Long-Term Interest Index for monthly annualized data, ${\mathrm{i}}^{*}\left(\mathrm{t}\right)$; real seigniorage income, normalized by the initial real Gross Domestic Product (1998/Jan), $\mathrm{S}\left(\mathrm{t}\right)$; nominal monthly annualized Inflation Target Index, ${\mathsf{\pi }}^{\mathrm{e}}\left(\mathrm{t}\right)$; Nominal monthly annualized External Interest index (we consider the US interest rate as a proxy), ${\mathrm{i}}_{\mathrm{t}}^{\mathrm{f}}\left(\mathrm{t}\right)$; Nominal monthly annualized External inflation index (we assume the US CPI as a proxy), ${\mathsf{\pi }}^{\mathrm{f}}\left(\mathrm{t}\right),$ and, finally, the primary surplus (deficit), ${\mathrm{W}}_{\mathrm{t}}={\mathrm{T}}_{\mathrm{t}}-{\mathrm{G}}_{\mathrm{t}}$.

We use monthly data from January 1998 to December 2018 in the empirical analysis. As stressed before, prior to this period, the data revealed several changes resulting from internal and external disturbances in the Brazilian economy, making it challenging to calibrate the model. We extracted data from the following sources: The National Treasury Secretariat (STN), the Central Bank of Brazil (BACEN), the Brazilian Institute of Geography and Statistics (IBGE), the Institute of Applied Economic Research (IPEA), and the International Monetary Fund (IMF). A comprehensive description of these data, including the relevant sources and details on the modifications made, is provided in

Table 1. Data for the variables used in the dynamic model.

Variable	Description
$\mathrm{y}\left(\mathrm{t}\right)$	Nominal Gross Domestic Product was obtained monthly at https://www3.bcb.gov.br/sgspub/localizarseries/localizarSeries.do?method=prepararTelaLocalizarSeries (accessed on 24 October 2025), converted to real values at the price of December 2005 using the implicit deflator index, and normalized for the initial weight of the sample.
$\mathrm{i}\left(\mathrm{t}\right),\mathsf{\pi }\left(\mathrm{t}\right),{\mathrm{i}}^{*}\left(\mathrm{t}\right)$	We obtained the Nominal interest rate monthly annualized ($\mathrm{S}\mathrm{E}\mathrm{L}\mathrm{I}\mathrm{C}$), nominal monthly annualized inflation rate ($\mathrm{I}\mathrm{P}\mathrm{C}\mathrm{A}$), and nominal monthly annualized long-term interest rate ($\mathrm{T}\mathrm{J}\mathrm{L}\mathrm{P}$) at https://www.bcb.gov.br/ (accessed on 24 October 2025) and transformed them into a nominal index.
$\mathrm{T}\left(\mathrm{t}\right),\mathrm{G}\left(\mathrm{t}\right),\mathrm{b}\left(\mathrm{t}\right)$	We obtained the Tax Revenues, Government Expenditures, and Net Debt of the Public Sector (both monthly) at https://www.ipeadata.gov.br/Default.aspx (accessed on 24 October 2025). These variables were transformed into actual values at the price of December 2005 and normalized for the initial GDP value (1998/1).
$\mathrm{e}\left(\mathrm{t}\right),{\mathrm{i}}_{\mathrm{t}}^{\mathrm{f}}(\mathrm{t})$, ${\mathsf{\pi }}^{\mathrm{f}}(\mathrm{t})$	We obtained the monthly date for the exchange rate, the monthly annualized US interest rate ($i_t^f$), and the monthly annualized US inflation rate (${\pi }^f(t)$) at www.imf.org. The US inflation rate (${\pi }^f$) and US interest rate ($i_t^f$) were transformed to a moving base US-CPI and US interest indices, respectively. The standard procedure for deflating the nominal exchange rate was multiplying it by the US-CPI index and dividing it by the domestic inflation index (both monthly annualized), fixed with bases on December 2005.
$\mathrm{S}\left(\mathrm{t}\right)$	As Mankiw (1987), Friedman (1971), and Goff and Toma (1993), we average the results of the three forms of seigniorage calculation: monetary seigniorage; inflationary tax seigniorage; and opportunity cost seigniorage. Then, the results were transformed to the base in December 2005 and normalized for the initial GDP value.
$\overline{y}(\mathrm{t})$	The potential output was calculated using the Hodrick–Prescott (HP)4 filter, using different values of the filtering band, λ, such as $\lambda =400$, $\lambda =1600$ e $\lambda =6400$, $\lambda ~\infty .$ We selected the trend component of GDP as the potential output, corresponding to the $\lambda =640$.
${\mathsf{\pi }}^{\mathrm{e}}(\mathrm{t})$	We obtained the annual inflation targets from https://www3.bcb.gov.br/sgspub/consultarvalores/consultarValoresSeries.do?method=consultarGrafico (accessed on 24 October 2025), which were exposed in September 1999. Therefore, we supplemented the series from January 1998 to August 1999 with the potential inflation estimated from the HP filter, using the same procedure for the potential product explained above. Finally, we interpolated the series for monthly annualized data using the Hermite interpolation procedure.

below.

4. Computational Simulation

Next, we present the procedure for identifying the parameters of the deterministic model and the methodology for generating perturbation ranges for the stochastic models. In the subsequent subsections, we will analyze the behavior of the coefficients impacting the deterministic model, the spreading of stochastic disturbances introduced by the non-controllable coefficients, and the scattering of endogenous variables due to the variability of these parameters. Finally, we will observe how the behavior of perturbations in the control parameters and their spread across the endogenous variables of the dynamic model evolve.

4.1. Software Implemented in the Model Solution

After data collection, we developed a MATLAB program to calibrate the economic model in the study, involving a large script of about 12,000 lines. We calibrated the dynamic system in Equation (29) using the fminsearch function in MATLAB 2019a. The fourth-order Runge–Kutta method was also used (for details, see Press et al. (1992, pp. 710–723)) via the ODE45 procedure in MATLAB 2019a. This technique subdivides the segmented time ranges into smaller segments to integrate the variables accurately and achieve the specified adjustment precision. Then, to estimate the system of equations for endogenous variables at these interpoints defined by the time increments of the empirical data, it is necessary to evaluate the endogenous variable values at each subinterval. In this case, we used Hermite’s segmented interpolation.

The fminsearch procedure adjusts the impact coefficients and minimizes the error between the estimation functions and the empirical data. The fminsearch function implemented in MATLAB uses the SIMPLEX search method of Jeffrey et al. (1998). It is a direct search method that does not use numerical or analytical gradients in the calibration process of the dynamic system given by Equation (29). This subroutine enables the adjustment of coefficients for nonlinear dynamical functions or systems without restrictions, thereby minimizing the error norm between the fitted curve and the empirical data for each endogenous variation in the dynamical system.

4.2. Identification of the Parameters of the Deterministic Model

We implemented a procedure using two steps to identify the equation coefficients of the economic dynamic model, the System (29). In the first step, we applied a time integration process for the Differential Ordinary Systema Equation (29) using the fourth-order Runge–Kutta technique (Press et al., 1992, pp. 710–723). The process structure is initially mathematically described as follows:

$$\left\{\begin{array}{c}{\displaystyle \frac{dH\left(t\right)}{dt}}=f\left[X\left(t\right),t, C\left(i\right) with i=1, 2,\dots ,k\right]\\ H\left(x_0\right)=H_0\\ C\left(i\right)=C_0\end{array}\right.,$$

(34)

where $\mathrm{X}\left(\mathrm{t}\right)=\left[\begin{array}{ccc}\mathrm{y}\left(\mathrm{t}\right)& \mathrm{i}\left(\mathrm{t}\right)& \mathsf{\pi }\left(\mathrm{t}\right)\end{array}\begin{array}{cc}\mathrm{e}\left(\mathrm{t}\right)& \mathrm{b}\left(\mathrm{t}\right)\end{array}\right]$ is a vector of explaining variables that compose the function matrix $\mathrm{f}\left[\mathrm{X}\left(\mathrm{t}\right),\mathrm{C}\left(\mathrm{i}\right)\right]$, with $\mathrm{C}\left(\mathrm{i}\right)=\left[\mathrm{C}\left(1\right),\mathrm{C}\left(2\right),\dots ,\mathrm{C}\left(\mathrm{k}\right)\right]$ is the constituted parameters’ vector at the Systema (29), to be calibrated, in a total of $\mathrm{k}=14$, and ${\mathrm{C}}_0$ are the initial values admitted for these parameters at the beginning of the calibration process. $\mathrm{H}\left(\mathrm{t}\right)={\left[\begin{array}{ccc}\mathrm{y}\left(\mathrm{t}\right)& \mathrm{i}\left(\mathrm{t}\right)& \mathsf{\pi }\left(\mathrm{t}\right)\end{array}\begin{array}{cc}\mathrm{e}\left(\mathrm{t}\right)& \mathrm{b}\left(\mathrm{t}\right)\end{array}\right]}^{\prime }$ is the transposed vector of the dependent time variables, which defines the rates in which the variables included in the vector $\mathrm{H}\left(\mathrm{t}\right)$ changes, as a function of them and over time, and ${\mathrm{H}}_0$ are the vector variables’ values that makeup $\mathrm{H}\left(\mathrm{X}\left({\mathrm{t}}_0\right)\right)$ at the initial time, ${\mathrm{t}}_0$, of the integration process. In this study, $\mathrm{H}\left(\mathrm{t}\right)$ is a vector ${\mathbb{R}}^5$ and $\mathrm{f}\left(\mathrm{X}\left(\mathrm{t}\right)\right)$ is a transform function, defined as $\mathrm{f}:{\mathbb{R}}^5\times {\mathbb{R}}^5\to {\mathbb{R}}^5$.

To calibrate the parameters of the System (29), we arbitrarily established the initial values of the parameters, ${\mathrm{C}}_0$, called in this computational process $\mathrm{C}\left(\mathrm{i}\right)=\left[\begin{array}{ccc}{\mathrm{u}}_1& {\mathsf{\gamma }}_1& \dots \end{array}\begin{array}{cc}{\mathrm{u}}_5& {\mathsf{\theta }}_2\end{array}\right]$ (simply specifying here the first two and the last two), however, maintaining the expected signs for these coefficients. We also assume the initial values for ${\mathrm{H}}_0$ as the initial values (January 1998) of the empirical data series used in the study, as specified in the subsection above. With this information, we initiate the integration process of System (29) using the fourth-order Runge–Kutta method (for details, see Press et al. (1992, pp. 710–723)).

Therefore, the integration of System (29) is started via the fourth order Runge–Kutta method, with the initial values, ${\mathrm{C}}_0$, ${\mathrm{H}}_0$, and ${\mathrm{t}}_0=0$; and with the time step, h, specified, the integration process evolves until it covers the entire discretized time series; that is, for ${\mathrm{t}}_0,{\mathrm{t}}_1,\dots ,{\mathrm{t}}_{\mathrm{N}}$. In each moment, to guarantee a preset error tolerance of the order of ${10}^{-8}$, the adjustment of the time increment, h, is automatically established by the function used in the study (in this case, the Matlab function ode45). In this process, to achieve the established precision, the time series was discretized into approximately $\mathrm{N}=\mathrm{17,640}-\mathrm{t}\mathrm{i}\mathrm{m}\mathrm{e}$ points, resulting in a time increment of $\mathrm{h}=0.000057$ for the data period under analysis (252 months), with the first month referenced as ${\mathrm{t}}_0=0$.

To verify the accuracy of the solution estimated by the Runge–Kutta method for System (29), as mentioned in the above step, we need to calculate the error of the estimated solution. This error occurs when checking the deviations between each point of the estimated solution and the empirical series data. Considering that the empirical data series (from January 1998 to December 2018) contains 252 months, we need to interpolate the empirical series to constitute the empirical values for the dependent variables at all points in the time-space. This interpolation process is performed using the Hermite interpolation technique, which involves a series of orthogonal polynomials that utilize information from the function and its derivatives, resulting in high accuracy.

In every integration step, the error in estimating the solution of each equation of the System (29) is calculated through the mean squared deviation for equation j of the system, with $\mathrm{j}=1,2,\dots ,5$, determined by the square root of the variance between the estimated series with the set of coefficients assumed for the System, relative to the sample data series used in the study. The following relationship describes this squared mean deviation:

$${Erro}_j=\sqrt{{\displaystyle \frac{{\sum }_{i=1}^N{\left({\left(X_{ji}\right)}_{est}-{\left(X_{ji}\right)}_{em}\right)}^2}{N-1}}}$$

(35)

where ${Erro}_j$ represents the mean squared deviation of equation j, with $\mathrm{j}=1,2,\dots ,5$, of the system (29), ${\left(X_{ji}\right)}_{est}$ is the $X_j$ variable estimated value for each time $i=1, 2,\dots ,N$, and ${\left(X_{ji}\right)}_{em}$ is the $X_j$ variable value corresponding to the monthly empirical data time interpolated in $i$.

The global error is given by the mean squared deviation involving all system equations of the system (29), given by:

$${Erro}_G={\displaystyle \frac{{\sum }_{j=1}^5{Erro}_j}{J}}$$

(36)

where $\mathrm{J}=5$, the number of ordinary differential equations in the System (29).

The expression of the global error indicates the greater or lesser uncertainty of the average of the variables of the System (29) in rapport to a more general average, which would be the average of several averages of the variables of each equation. Therefore, we used the Global Error as the measure of uncertainty in the calibration process of the System coefficients (29).

The estimated global error is passed on to Matlab’s fminsearch function, which controls all optimization operations and applies the optimization process of the vector function $\mathrm{C}\left(\mathrm{i}\right)=\left[\mathrm{C}\left(1\right),\mathrm{C}\left(2\right),\dots ,\mathrm{C}\left(\mathrm{k}\right)\right]$, with $\mathrm{i}=1,2,\dots ,\mathrm{K}$, with $\mathrm{K}=14$, using the Nelder-Mead Simplex Method for optimization, whose details of the optimization process can be found in Appendix A. When structuring the fminsearch function, various parameters are specified, including the tolerance error in the interaction process, which in this study was set to ${10}^{-8}$. Therefore, the fminsearch function is activated after estimating the global error, establishing the calibration via the Nelder–Mead Simplex Method for optimization. Then, with the new values for vector $\mathrm{C}\left(\mathrm{i}\right)$, the integration process for the System (29) is triggered via the Runge–Kutta method and, a posteriori, triggers the estimation of the global error in the interaction ${\mathrm{m}}_{\mathrm{i}}$, say ${{\mathrm{E}\mathrm{r}\mathrm{r}\mathrm{o}}_{\mathrm{G}}}^{{\mathrm{m}}_{\mathrm{i}}}$. This process is repeated until ${{[\mathrm{E}\mathrm{r}\mathrm{r}\mathrm{o}}_{\mathrm{G}}}^{{\mathrm{m}}_{\mathrm{i}}}-{{\mathrm{E}\mathrm{r}\mathrm{r}\mathrm{o}}_{\mathrm{G}}}^{{\mathrm{m}}_{\mathrm{i}-1}}]\le {10}^{-8}$

4.3. Results of Deterministic and Stochastic Models

4.3.1. Calibration of the Deterministic Model

We carried out the calibration process of the deterministic dynamic system by using the procedure explained in Section 4.2 above. It begins by assuming a set of arbitrary initial values for the parameters of the Dynamic System (29). The initial values established for the coefficients maintained the expected signs, as described in Section 3.1.

Table 2. Parameters of the adjusted model.

Parameters	Initial Values	Calibrated Coefficients	Description
${\gamma }_1$	$-0.1142$	$-0.0738184$	Impact of the real interest rate on GDP.
${\gamma }_2$	$0.0142$	$0.0019298$	Impact of the real exchange rate on GDP.
${\mu }_1$	$-0.0103$	−0.242867	Impact of the output gap on the short-run nominal interest rate.
		−0.2428673
		−0.2428673
${\mu }_2$	$-1.6147$	$-0.0556015$	Effect of the differential between inflation and the inflation target on the short-run nominal interest rate.
${\theta }_1$	$0.0808$	$0.0008263$	Impact of the real public sector net debt on itself.
${\theta }_2$	$0.0220$	$-0.0283853$	Impact of real seigniorage income on the real public sector net debt.
${\sigma }_1$	$0.0004$	$-0.0143354$	Impact of the output gap on inflation.
${\sigma }_2$	$0.0096$	$-0.0001139$	Impact of the real exchange rate on inflation.
${\delta }_1$	$0.0820$	$0.0029517$	Impact of the real Exchange rate on itself.
$u_1$	$0.0012$	$0.0003222$	Impact of the real GDP on itself.
$u_2$	$-0.1328$	$-1.0137973$	The impact of the short- and long-term interest rate differential on the short-term nominal interest rate.
$u_3$	$-0.0198$	$0.0021355$	Impact of the differential between inflation and inflation target on inflation.
$u_4$	$0.1229$	$0.3490567$	Impact of the real interest rate on the real exchange rate.
$u_5$	$0.0049$	$0.0841699$	The effect of the real primary surplus (deficit) on the real public sector net debt.

below highlights these values in its second column.

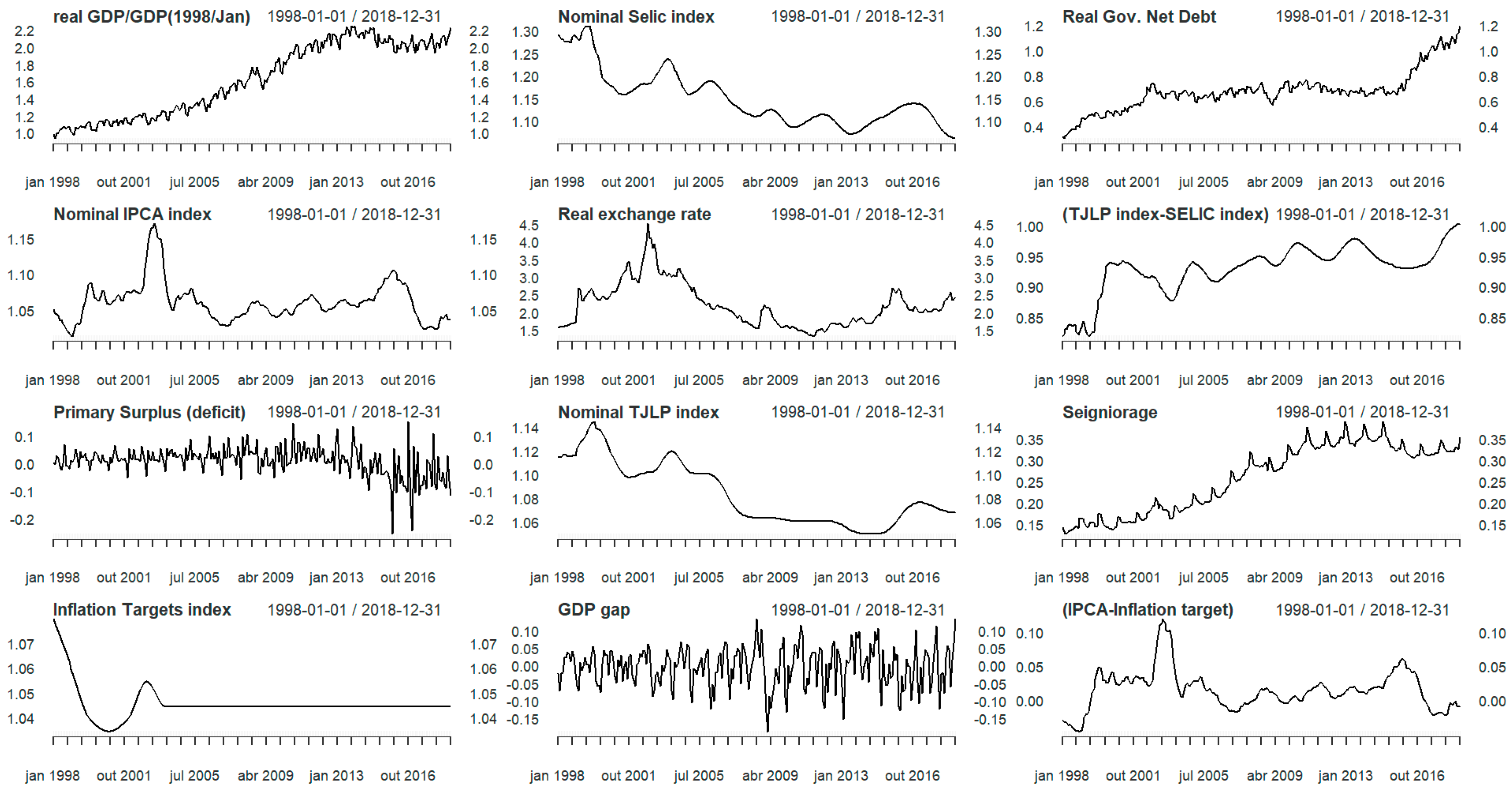
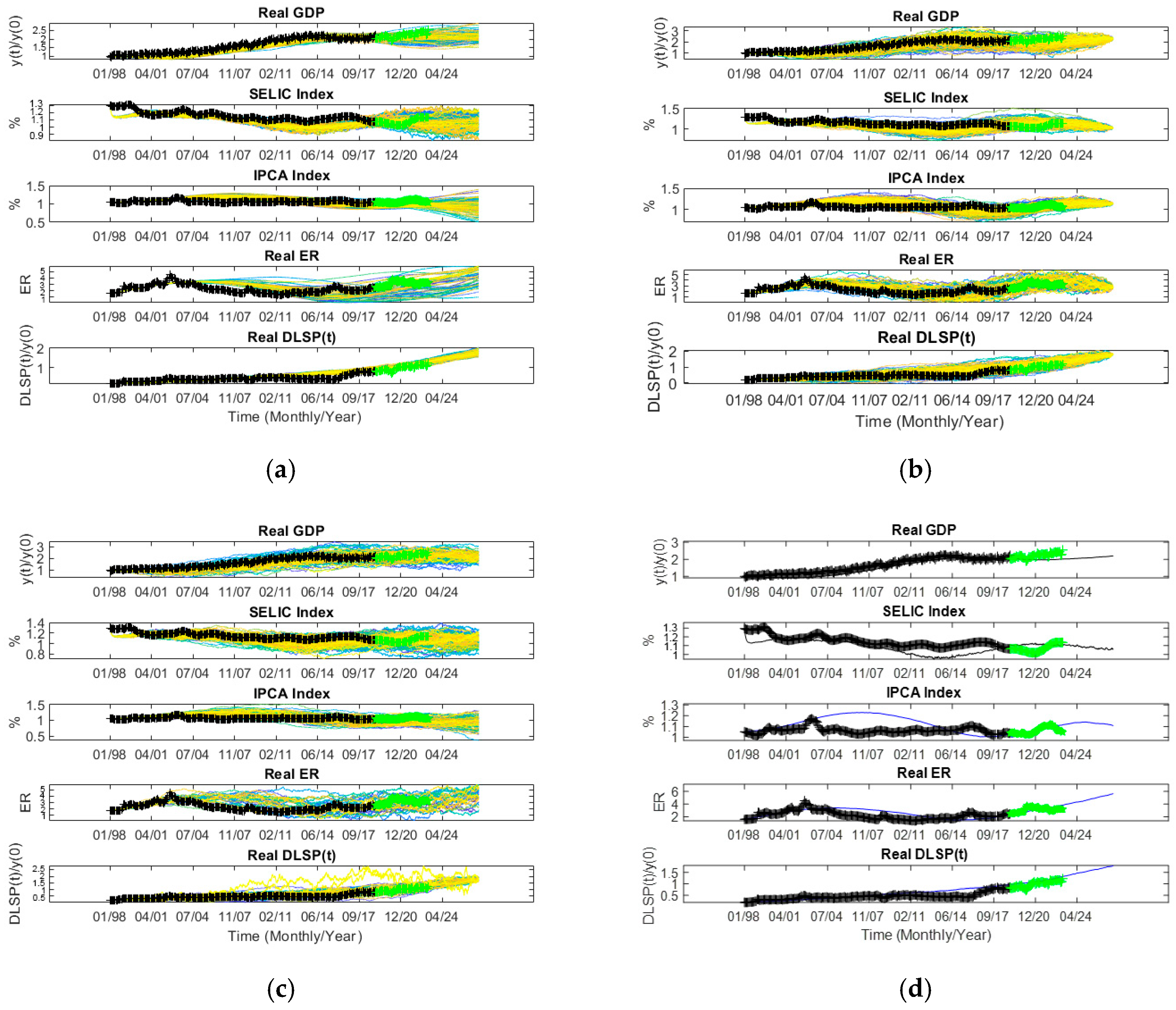
We remember that it is used the scale transformation of the variables involving values of much higher levels, in the case of real GDP, real public sector net debt, actual tax revenues, real seigniorage income, and real government expenditures, becoming them of the order of magnitude relative to a unit, similar to the others variables, which are index number with base one. This transformation was achieved by dividing all series values by the initial value of real GDP from January 1998, which facilitated the model calibration process. In the convergence process, the mean squared deviations of the System (29) equations, given by Equation (36), were, respectively, for Equations (1) to (5), were $\mathrm{E}{\mathrm{r}\mathrm{r}\mathrm{o}}_1=14.1168$, $\mathrm{E}{\mathrm{r}\mathrm{r}\mathrm{o}}_2=8.9905$, $\mathrm{E}{\mathrm{r}\mathrm{r}\mathrm{o}}_3=5.3513$, $\mathrm{E}{\mathrm{r}\mathrm{r}\mathrm{o}}_4=28.4510$, and $\mathrm{E}{\mathrm{r}\mathrm{r}\mathrm{o}}_5=5.9020$; errors estimated taking all 10042-time points discretized by the fourth order Runge–Kutta method. It can be observed that the fourth system equation, corresponding to the exchange rate variable, which exhibits a more considerable amplitude variation, presents a more significant mean error, as expected.

Table 2 above highlights in the first column the parameter symbols, in the second column the assumed initial parameter values in the calibration process, and in the third column the values of the parameters adjusted for the dynamic model system after reaching the precision specified by the error tolerance of ${10}^{-8}$. Finally, Table 2 above shows the descriptions of the parameters in the fourth column.

We will not discuss the calibration results in this section because their signs followed the typical signs for a developing economy, as explained in Section 3.1.1, Section 3.1.2, Section 3.1.3, Section 3.1.4 and Section 3.1.5 above.

Therefore, we will analyze the consistency of the short-term interest index coefficient in the first dynamic equation of System (29), having the product variation as the dependent variable. The calibration result for the real SELIC interest index coefficient (${\mathsf{\gamma }}_1$) is as expected. It showed a negative relationship between the real interest rate and Brazilian GDP, with a coefficient of $-0.0738184$. Comparing the first and second graphics in the first line at the top of Figure 1 below, we can observe that GNP has an increasing trend, and the nominal SELIC index (also the actual SELIC index) has a decreasing trend. These graphic behaviors confirm the consistency of the negative signal estimated for the coefficient ${\mathsf{\gamma }}_1$.

The value of the coefficient of the real exchange rate (${\gamma }_2$) in the first equation of the System (29) positively impacts GDP variation in the order of $0.0019298$. This result is consistent with expectations for developing economies (EMEs), as explained in detail at the end of Section 3.1.5 and in Goda and Priewe (2020). Comparing the first graphic in the first line with the second graphic in the second line of Figure 1 below, we observe that GNP has an increasing trend, and the actual exchange rate exhibits oscillations, but, on average, the real exchange rate maintained a long-run depreciation level throughout the entire period. This relationship between these two graphics emphasizes the consistency of the positive signal estimated for the coefficient ${\mathsf{\gamma }}_2$.

Some economists believe that the real exchange rate is the most critical macroeconomic price among all variables because it influences all the others (including the inflation rate) since Imports, exports, the investment rate, the savings rate, and inflation depend on the real exchange rate (Bresser-Pereira et al., 2014, p. 3). There is a clear relationship between the trend of the real exchange rate and long-term economic growth. This phenomenon is captured by the Harrod-Balassa-Samuelson effect (as explained in Section 3.1.5), in which an overvaluation of developing countries’ exchange rates for prolonged periods tends to depress their long-term economic growth rates (Dollar & Kraay, 2003; Gala, 2008).

Understanding economic growth requires focusing on what causes the initial stirrings and identifying the interacting phenomena that drive it. The effect of growth on PNP expansion is the mean rate of sustained growth of the Brazilian economy, which is proportional to the GNP slope trend during the analyzed period, as observed in the top line of the first graphic in Figure 1 above. The coefficient ${\mathrm{u}}_1$ captures, in the correct sense, this positive effect of the impact of GDP on itself in a proportion of $0.0003222$. The growth order of this effect will be analyzed later, estimating the PND growth rate in itself.

Fama (1981) indicates a negative correlation between inflation and stock returns. From this perspective, when the stock market registers advances during times of low interest rates, asset prices increase, and so does inflation. Consequently, the Central Bank of Brazil takes decisive measures to reduce inflationary pressures, acting based on its expected inflation rate. An increase in expected inflation also sustains an interest rate increase. This increase likely changes the trade-off between interest rates and stock prices, leading to inflation and interest rates moving in the same direction simultaneously. Regardless of the trade-off between stock value and interest rates, this relationship can shift significantly in response to a substantial change in inflation expectations. Therefore, we observe that the expected inflation index drives the change process in the inflation index (IPCA) and the nominal interest index (SELIC) in the same direction.

This process implies that the changes in IPCA and the nominal SELIC occur through a previous shift in inflation expectation (${\pi }^e$). Hence, we conclude that for $(\mathsf{\pi }\left(\mathrm{t}\right)-{\mathsf{\pi }}^{\mathrm{e}}\left(\mathrm{t}\right))>0$, this variable impacts positively on $\mathrm{i}\left(\mathrm{t}\right)$, tightening the economy, and for $(\mathsf{\pi }\left(\mathrm{t}\right)-{\mathsf{\pi }}^{\mathrm{e}}\left(\mathrm{t}\right))<0$, this variable impacts negatively on $\mathrm{i}\left(\mathrm{t}\right)$, releasing the economic process. This behavior was accurately captured by the coefficient ${\mathsf{\mu }}_2$, with a value of $-0.0556015$. We can observe the evolution of the variable $(\mathsf{\pi }\left(\mathrm{t}\right)-{\mathsf{\pi }}^{\mathrm{e}}\left(\mathrm{t}\right))$ over the analyzed period in the right graphic on the last line and the nominal SELIC index in the second graphic on the first line, both shown in Figure 1. As observed in the graphics, the variable $(\mathsf{\pi }\left(\mathrm{t}\right)-{\mathsf{\pi }}^{\mathrm{e}}\left(\mathrm{t}\right))$ maintains a positive trend, interrupted by oscillations, and the nominal SELIC index decreases systematically along a trend. Thus, we noticed that the oscillation of the variable $(\mathsf{\pi }\left(\mathrm{t}\right)-{\mathsf{\pi }}^{\mathrm{e}}\left(\mathrm{t}\right))$ imposes oscillation on the nominal interest index; however, the decreasing trend in the nominal SELIC index variable is due to another factor.

There is a negative bi-causality relationship between the exchange rate and interest rates, such that when the exchange rate appreciates, the interest rate decreases, and vice versa. In general, the economy can be in either a boom state (positive gap), characterized by appreciated exchange rates, or a recession (negative gap), characterized by depreciated exchange rates. These facts are because the exchange rate appreciates when the economy evolves into a boom (and the interest rate decreases). However, the exchange rate depreciates when the economy goes into recession (and the interest rate increases).

From the arguments presented above, we conjecture that ${\mathsf{\mu }}_1$ (the coefficient of the GDP gap) in the second equation has to be negative, as captured by the model’s dynamics, with a value of $-0.24286732$. We observe in the middle graphic on the last line of Figure 1, in which the signal of the GNP gap variable fluctuates constantly, shifting from negative to positive throughout the analyzed period. Nevertheless, as shown in the second graphic on the first line of Figure 1, the nominal SELIC index oscillates over a trend that decays during the analyzed period. This behavior was captured by ${\mathsf{\mu }}_1$, despite the constant oscillations of the GDP gap.

We will analyze the behavior of the controllable parameter ${\mathrm{u}}_2$ in the second equation of System (29), specifically the coefficient of the differential between the SELIC index and the nominal long-term interest index ($\mathrm{i}\left(\mathrm{t}\right)-\mathrm{T}\mathrm{J}\mathrm{L}\mathrm{P}\left(\mathrm{t}\right)$). To understand the consistency of the ${\mathrm{u}}_2$ sign, we need to determine the behavior of the TJLP index, as it complies with the criteria established in law. According to this law, the BACEN (Brazilian Central Bank) sets the TJLP index equal to the inflation target accumulated for the twelve months following the first month of the rate’s validity, plus a risk premium5.

The TJLP serves as the basis for calculating the essential cost of financing from the National Bank for Social Development (BNDES) to be granted to companies that generate employment through investments in gross fixed capital formation. Generally, the SELIC interest rate is relatively high compared to international interest rates. It is a short-term interest instrument designed to control inflation and attract foreign capital into the country or to prevent capital flight, as it serves as an index for bonds issued by the National Treasury. However, the TJLP is an interest rate subsidized by the public sector used in the long-term loans taken from the BNDES by companies selected to develop industrial and job creation projects.

The TJLP evolves as a function of the predictability of change in the expected target inflation. The TJLP index should increase if the inflation target rises, meaning that the TJLP acts in the same direction as the SELIC rate, albeit with less intensity due to a risk premium, as it is partly subsidized.

The index $\left(\mathrm{i}\left(\mathrm{t}\right)-\mathrm{T}\mathrm{J}\mathrm{L}\mathrm{P}\left(\mathrm{t}\right)\right)$ is always positive, as can be seen by comparing the second graph in the first line with the second graph in the third line, both in Figure 1. Then, a decrease in the target inflation forecast induces a shrinkage in TJLP, with a consequent increase in the variable $\left(\mathrm{i}\left(\mathrm{t}\right)-\mathrm{T}\mathrm{J}\mathrm{L}\mathrm{P}\left(\mathrm{t}\right)\right)$. An increase in the variable $\left(\mathrm{i}\left(\mathrm{t}\right)-\mathrm{T}\mathrm{J}\mathrm{L}\mathrm{P}\left(\mathrm{t}\right)\right)$, as a function of a decrease in $\mathrm{T}\mathrm{J}\mathrm{L}\mathrm{P}\left(\mathrm{t}\right)$, must cause a reduction in SELIC, which implies that its coefficient ${\mathrm{u}}_2$ (in the second equation of the System (29)) must be negative for causes a negative variation in the nominal SELIC index ($\mathrm{i}\left(\mathrm{t}\right)$), the correct sign expected. Otherwise, if at any moment the expected inflation increases, it induces an increase in the TJLP index, accompanied by a decrease in the variable $\left(\mathrm{i}\left(\mathrm{t}\right)-\mathrm{T}\mathrm{J}\mathrm{L}\mathrm{P}\left(\mathrm{t}\right)\right)$. Then, a decreasing variation in the variable $\left(\mathrm{i}\left(\mathrm{t}\right)-\mathrm{T}\mathrm{J}\mathrm{L}\mathrm{P}\left(\mathrm{t}\right)\right)$ due to an increase in the $\mathrm{T}\mathrm{J}\mathrm{L}\mathrm{P}\left(\mathrm{t}\right)$ variable must cause an increase in the SELIC interest index, which demands a negative value for ${\mathrm{u}}_2$. Thus, the coefficient ${\mathrm{u}}_2$ of the variable $\left(\mathrm{i}\left(\mathrm{t}\right)-\mathrm{T}\mathrm{J}\mathrm{L}\mathrm{P}\left(\mathrm{t}\right)\right)$ presented a negative value equal to $-1.01379732$. In summary, the coefficient ${\mathrm{u}}_2$ accurately captured the behavior of these variables.

The third equation of the system (29) has the inflation differential per unit of time as its dependent variable, and the real exchange rate, the output gap, and the difference between inflation and the inflation target are used as explanatory variables. Therefore, we will establish arguments that explain the consistency of the impacts of these variables’ coefficients on inflation variation.

Firstly, as stressed earlier, a positive output gap (in the boom) is associated with a positive variation in the nominal interest rate (SELIC increase), resulting in a consequent decrease in the inflation index (IPCA). A negative output gap (during the recession) is associated with a decrease in the nominal interest rate (as indicated by the SELIC index), resulting in a positive impact on the inflation index (as measured by the IPCA). Therefore, the output gap coefficient (${\mathsf{\sigma }}_1$) has to negatively affect the inflation variation, which was correctly estimated, in the order of $-0.01433543$. The estimative consistency of ${\mathsf{\sigma }}_1$ may be verified, comparing the IPCA index graph, the first in the second line, and the GDP gap graph, the middle graph on the last line, both in Figure 1. From these graphics, it is evident that a positive variation in the IPCA index is associated with a negative variation in the GDP, indicating a negative impact relationship.

We now analyze the consistency of the sign of the coefficient of the real exchange rate variable on the inflation variation, ${\mathsf{\sigma }}_2$. As explained in Section 3.1.2, the link between productivity and the real exchange rate establishes the impact of the real exchange rate on inflation. The theoretical importance of the real exchange rate for the conduct of monetary policy under an Inflation-targeting regime is highlighted by Aizenman et al. (2011), based on the version by Ball (1999) and Aghion et al. (2009). These authors concluded that real exchange rate depreciation reduces productivity in developing countries, attributing this to financial channels that shrink working earnings, consequently diminishing inflation. The adverse effects of exchange rate volatility on productivity are more pronounced in the financial markets of developing countries than in those of developed countries. These negative effects are significant for practically all EMEs and developing countries. However, productivity gains cause an increase in relative prices, contributing to the appreciation of the real exchange rate. In other words, the higher the productivity of an economy, the more appreciated its real exchange rate will be, with a consequent positive impact on inflation. This relationship between the real exchange rate and inflation is established by the Balassa-Samuelson effect (Samuelson, 1964; Balassa, 1964). The logic of this process is that higher productivity causes higher wages in the tradable goods sector of an EME which will also lead to higher wages in the non-tradable sector (services). This concomitant price increase in economies experiencing more significant growth (developing economies) will result in more intense inflation rate increases than the corresponding effects in developed economies, which are subject to slower growth. Therefore, it can be understood that the appreciation of the currency in developing economies induces high productivity, accompanied by a substantial increase in inflation, which in turn has a negative impact on ${\mathsf{\sigma }}_2$, as the positive inflationary impact due to the appreciation of the currency predominates over the negative effect of increased productivity on inflation. Thus, this implies a negative value for ${\mathsf{\sigma }}_2$, which was approximately $-0.00011391$, confirming the expectation.

In the following, we will analyze the behavior of the controllable coefficient ${\mathrm{u}}_3$ of the variable $\mathsf{\pi }\left(\mathrm{t}\right)-{\mathsf{\pi }}^{\mathrm{e}}\left(\mathrm{t}\right)$ on the inflation variation. As argued earlier, the changes in the expected inflation index induce changes in the same direction as the nominal interest (SELIC). Firstly, we consider $\mathsf{\pi }\left(\mathrm{t}\right)-{\mathsf{\pi }}^{\mathrm{e}}\left(\mathrm{t}\right)>0$. A positive change in ${\mathsf{\pi }}^{\mathrm{e}}\left(\mathrm{t}\right)$ causes a decrease in the variable $\mathsf{\pi }\left(\mathrm{t}\right)-{\mathsf{\pi }}^{\mathrm{e}}\left(\mathrm{t}\right)$, which implies a positive change in SELIC, with consequent decrease in inflation variation. Otherwise, if a negative change occurs in ${\mathsf{\pi }}^{\mathrm{e}}\left(\mathrm{t}\right)$, consequently growing the variable $\mathsf{\pi }\left(\mathrm{t}\right)-{\mathsf{\pi }}^{\mathrm{e}}\left(\mathrm{t}\right)$, which implies a negative change in the SELIC rate and a positive inflation rate variation due to the shrinkage in SELIC Differently, we assume now that $\mathsf{\pi }\left(\mathrm{t}\right)-{\mathsf{\pi }}^{\mathrm{e}}\left(\mathrm{t}\right)<0$. Then, a precedent shrinkage change in the ${\mathsf{\pi }}^{\mathrm{e}}\left(\mathrm{t}\right)$ implies a decrease in the negative amplitude of $\mathsf{\pi }\left(\mathrm{t}\right)-{\mathsf{\pi }}^{\mathrm{e}}\left(\mathrm{t}\right)$. Then, this positive variation $\mathsf{\pi }\left(\mathrm{t}\right)-{\mathsf{\pi }}^{\mathrm{e}}\left(\mathrm{t}\right)$ is linked to a positive inflation variation, as a negative shift in the SELIC rate occurred. However, if a positive change in ${\mathsf{\pi }}^{\mathrm{e}}\left(\mathrm{t}\right)$ occurs, increasing the negative modulus of variable $\mathsf{\pi }\left(\mathrm{t}\right)-{\mathsf{\pi }}^{\mathrm{e}}\left(\mathrm{t}\right)$ induces a positive shift in the SELIC rate. Hence, the negative variation in $\mathsf{\pi }\left(\mathrm{t}\right)-{\mathsf{\pi }}^{\mathrm{e}}\left(\mathrm{t}\right)$ is associated with a negative inflation variation.

In summary, we conclude that if the variation of the variable $\mathsf{\pi }\left(\mathrm{t}\right)-{\mathsf{\pi }}^{\mathrm{e}}\left(\mathrm{t}\right)$ is positive (negative), it is associated with a negative (positive) impact on the nominal SELIC interest index; and, as a consequence, a positive (negative) result in the inflation index. This behavior was correctly captured by ${\mathrm{u}}_3$, resulting in an inflation variation of approximately $0.00213552$. This fact can be confirmed by examining the IPCA index in the first graphic, on the second line, and the $\mathsf{\pi }\left(\mathrm{t}\right)-{\mathsf{\pi }}^{\mathrm{e}}\left(\mathrm{t}\right)$ in the last graphic, on the last line, both in Figure 1. Both variables evolve similarly and are positive. This behavior characterizes a positive impact relationship.

The fourth equation of System (29) has the exchange rate variation as its dependent variable and the real interest rate and the exchange rate as its independent variables.

Firstly, we analyze the impact of the relationship between the real interest rate and exchange rate variation. As detailed in Section 3.1.4, according to the traditional view, an increase in the interest rate leads to an appreciation of the exchange rate (Dornbusch, 1976). On the other hand, the nontraditional perspective posits a positive relationship between interest rates and exchange rates (Furman & Stiglitz, 1998). In conclusion, as presented in Section 3.1.4, the traditional view prevails in developed economies, while the nontraditional view is characteristic of developing economies, mainly because they are often in unstable situations.

In the dynamic model calibration, the coefficient of the real interest index variable with respect to the real exchange rate variation showed a positive correlation. Therefore, an increase in the real interest rate index causes a depreciation in the exchange rate, which was of the order of $0.34905671$. Some studies on the Brazilian Economy confirm this impact direction, as their findings have consistently shown a positive relationship between the interest index and the exchange rate, as noted by Blanchard (2004), among others.

In the fourth equation of the System, we have that the real exchange impacts itself. This relationship was explained in detail in Section 3.1.4, in which it was characterized that in a floating exchange rate system in developing economies, exchange rate fluctuations can significantly impact the price level through changes in aggregate demand and supply. In aggregate supply, the depreciation of the national currency can have a direct and positive impact on the price level through imported goods that national consumers purchase. The indirect influence of exchange rate depreciation on a country’s price level can be observed in the prices of capital goods (intermediate goods) imported by manufacturers as inputs, as explained in Aghion et al. (2009). The real exchange rate depreciation reduces productivity in developing countries, leading to a consequent increase in inflation, which directly impacts the exchange depreciation. Thus, for developing economies, obtaining ${\delta }_1>0$ is entirely acceptable.

Therefore, we have that the real exchange rate positively impacts the variation in the real exchange index via the coefficient ${\delta }_1$, with a value of $0.00295173$. The positive sign of the coefficient ${\delta }_1$ allows us to conclude that a depreciation of the real exchange rate induces a process of exchange rate depreciation, which can be stopped only by the induction of new perspectives in the economy or by a process of intervention by the central bank, which sometimes proves to be efficient only in the very short term. The induction of new perspectives in the economy that alter the process of evolution of the real exchange rate must occur only through changes in economic structure relating to actual wages, aggregate investment, external and internal savings, and productivity (Gala, 2008).

The fifth equation of the system (29) has as its dependent variable the debt-to-GDP differential per unit of time ($\mathrm{d}\mathrm{b}\left(\mathrm{t}\right)$) and as explanatory variables the real debt-to-GDP level ($\mathrm{b}\left(\mathrm{t}\right)$), the real primary-to-GDP balances ($\mathrm{W}\left(\mathrm{t}\right)$), and the real seigniorage-to-GDP ($\mathrm{S}\left(\mathrm{t}\right)$). Therefore, we will establish arguments that explain the consistency of the impacts of these variables’ coefficients on inflation variation.

Regarding the impact of b(t) on debt variation, the difference between the real interest rate and the real GDP growth rate, $\mathrm{r}\left(\mathrm{t}\right)-\mathsf{\eta }\left(\mathrm{t}\right)$, plays a crucial role in the debt structure. If $\mathrm{r}\left(\mathrm{t}\right)-\mathsf{\eta }\left(\mathrm{t}\right)>0$, $\mathrm{b}\left(\mathrm{t}\right)$ will become unstable because it positively impacts the $\mathrm{d}\mathrm{b}\left(\mathrm{t}\right)$. In another way, if $\mathrm{r}\left(\mathrm{t}\right)-\mathsf{\eta }\left(\mathrm{t}\right)<0$, it negatively impacts $\mathrm{d}\mathrm{b}(\mathrm{t}$), driving $\mathrm{b}\left(\mathrm{t}\right)$ towards stability.

The intensity of the impact of the amount of debt on the debt itself is a function of the intensity of the real interest rate (r(t)) and the economy’s growth rate ($\mathsf{\eta }\left(\mathrm{t}\right)$), as demonstrated in Section 3.1.1. This effect is captured in the system model (29) by the coefficient ${\mathsf{\theta }}_1$, which can be positive or negative, depending on the value of the ($\mathrm{r}\left(\mathrm{t}\right)-\mathsf{\eta }\left(\mathrm{t}\right)\lessgtr 0$). ${\mathsf{\theta }}_1$ is positive, it impacts debt growth; if ${\mathsf{\theta }}_1$ is negative, it affects the decline in debt and promotes stability. In the case of this study, the ${\mathsf{\theta }}_1$ value found was $0.0008264$. This positive coefficient value indicates that debt causes indebtedness due to the excessive amount of interest paid, leading to an unstable process.

The other variables independent of the fifth equation of the System (29), W(t) and S(t), are important in solving the economic debt (Croce, 2002). The primary difficulty in determining the solvency of the debt-to-GDP ratio lies in the fact that all relevant variables involved in this process are endogenous, including interest rates, primary balances, and seigniorage revenues. In this context, feedback from fiscal measures that generate primary balances can, in turn, affect revenues, expenses, interest rates, the behavior of private savings and government investment, and the capacity to consolidate primary balances and Seigniorage.

The government uses Seigniorage ($\mathrm{S}\left(\mathrm{t}\right)$) to balance the budget. In this case, the budget deficit will impact the current or future increase in the money supply, with a consequent rise in the inflation rate. Therefore, financial resources raised through Seigniorage are generally limited. As Sargent and Wallace (1981) note, if the primary balance ($\mathrm{W}\left(\mathrm{t}\right)$) falls into deficit, seigniorage revenues must be increased to accommodate the government’s budget constraint. The idea is that seigniorage revenue complements revenue from primary deficits. Then, the public debt will only stop growing when exogenous measures are adopted in the fiscal area so that the primary deficit is zero. These measures are of an accounting nature, as they aim to generate a primary surplus that, given a certain seigniorage supposedly under the control of the Central Bank, without incurring interest expenses and assuming exogenous growth in GDP, will enable the payment of interest on public debt.

Seigniorage is defined as the result of a monetary expansion carried out by the Central Bank, which equals the product of this expansion and real monetary balances (Rovelli, 1994; Hochreiter et al., 1996). Thus, as a monopolist in issuing paper money, the Central Bank can acquire goods and services that generate significant resources. In another way, Seigniorage can be defined as a revenue called inflationary tax (Mankiw, 1987; Hochreiter et al., 1996), which is nothing more than the compulsory transfer of income through negative real interest, paid by the monetary base, in favor of the Central Bank and against the rest of the entities that make up the economy that maintains a monetary base among their assets. In short, the Seigniorage results from mitigating the welfare effects and inflation.

Conclusively, the necessary condition for debt solvency requires only one condition: positive values for the augmented primary surplus (primary balance added to the Seigniorage). Therefore, the public debt stock is an asset with a present value equal to the augmented surplus, in which the Seigniorage is recorded as active revenue in primary balances to obtain positive operating surpluses. At the same time, Seigniorage is also accounted for as a liability, a debt security, which, at some point, must be paid off, but without any tax burden (Cukierman et al., 1992).

Regarding the impact of the primary surplus variable added to seigniorage revenue, as indicated by the efficient ${\mathrm{u}}_5$, it must necessarily be positive, considering that this term is accompanied by a negative sign in System (29). As the primary balances are positive (surplus), it has a negative impact on the debt. In this study, the calibrated ${\mathrm{u}}_5$ coefficient was $0.0841699$, confirming the equation’s expectation. Finally, the coefficient of the seigniorage variable, ${\mathsf{\theta }}_2$, accounted as a debt liability, in contrast to its use as an active revenue integrated into the primary balances, must be negative, considering that this term is accompanied by the negative sign in System (29), whose component must positively integrate the debt. Thus, ${\mathsf{\theta }}_2$ was correctly estimated in the order of $-0.0283853$.

4.3.2. Calibration of the Stochastic Model

We will analyze the stochastic dynamic model described by Systema (32), which introduces stochastic innovations. The non-controllable parameters’ impacts of the dynamic model are subject to exogenous political or economic effects, which can alter the direction and the intensity of the impact relations in the macroeconomic and monetary variables of the economy. These exogenous political and economic effects adjust the non-controllable parameters, thereby influencing the economic performance for better or worse and making the economic process more efficient or less efficient. These changes in behavior (losses or gains) are called bifurcations. We also analyzed the additive effects of stochastic innovations from domestic or IEs (or political) imposed on the macroeconomic or monetary variables.

In this study, we implement the Monte Carlo realizations to generate the stochastic effects over the non-controllable coefficients. In the Monte Carlo method, we need to specify the distribution characteristics, but we must also validate the realizations to be used in the analysis. Thus, we use the Monte Carlo method to generate the realizations, a finite sequence of arbitrary numbers whose randomness must be statistically tested. Therefore, we perform empirical statistical tests to ensure the consistency of the realizations. In our case, they were (i) the means of the realizations have to be close to the coefficient value; (ii) the distribution has to be symmetric, with a specific standard deviation (e.g., no heteroskedastic); and (iii) there must be no covariance among the realizations for any lag integers k. We proved all these conditions for all the generated realizations, classifying them as white noise.

We imposed the stochastic disturbances on the non-controllable parameters, generated through a normal probability distribution, around each calibrated value of each non-controllable parameter. For this, we assumed a given variance, the largest possible for which the stochastic achievements of the dynamic economic model converged to a stable solution.

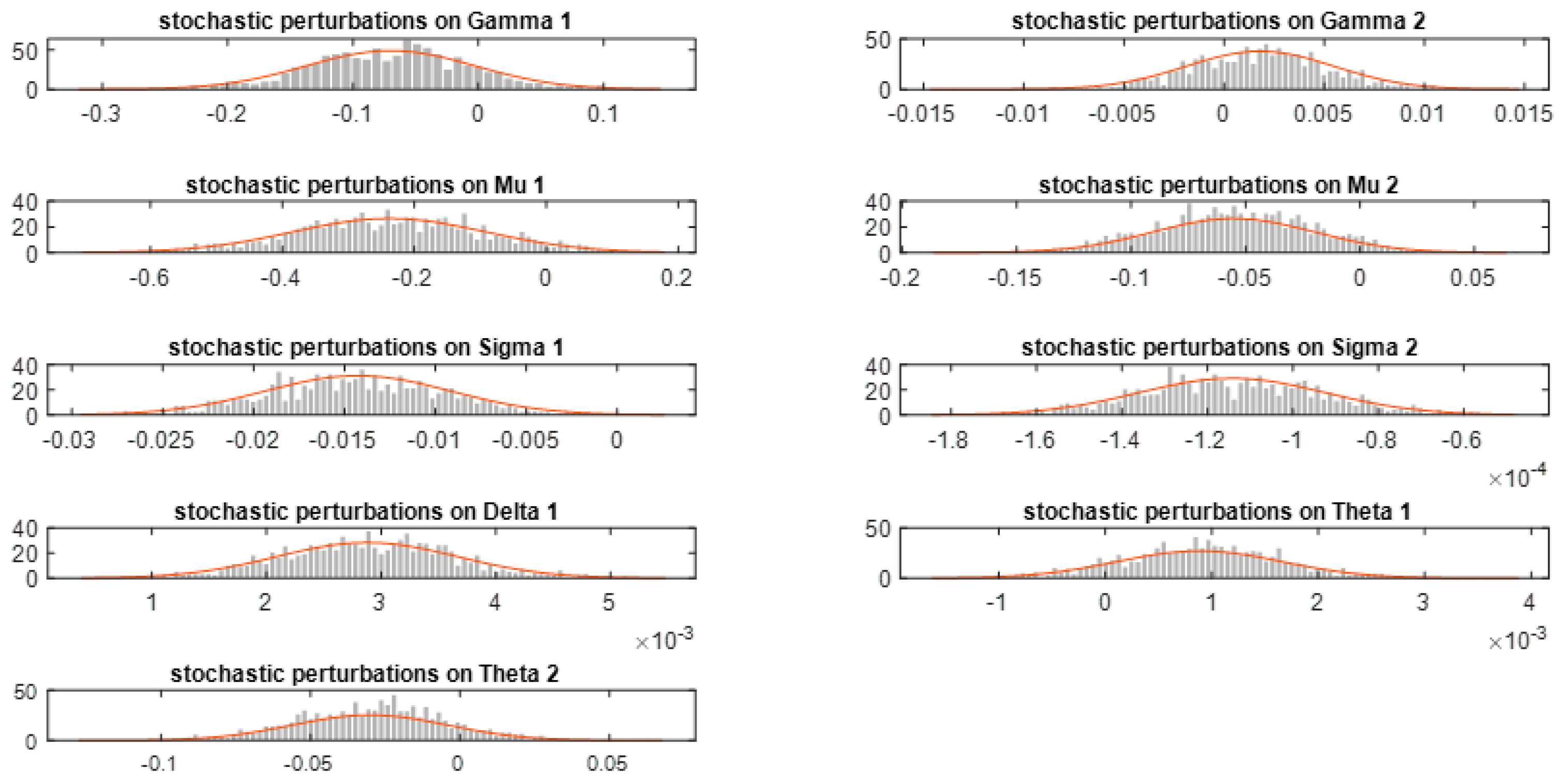
Figure 2 below shows the histograms of the stochastic shocks imposed on the calibrated coefficients of the Dynamic System (29). In each histogram of Figure 2, an overlaid red line is observed, representing the corresponding normal distribution, with an average equal to the calibrated coefficient value and a standard deviation similar to that of the spreading interval of the stochastic disturbances, highlighted in the legend of Figure 2, for each non-controllable coefficient, specified in each equation of the System (29).

Concerning the stochastic effects introduced additively, we generated them as a one-dimensional random walk, evolving over the entire forecast period, estimated through a computational subroutine, elaborated in the Matlab platform.

We generated one-dimensional random walks (1-D) to represent the stochastic disturbances described by the term $v\left(t\right)$ for all five dependent variables of the dynamic model of the System (31) by using a binomial distribution procedure as described by Feller (1968, p. 164), and by Grimmett and Stirzaker (2001, p. 202). The binomial distribution values generated are added to the corresponding variable by replacing the term $v\left(t\right)$.

From a $\mathrm{j}$ trial number established by $\mathrm{j}=1,2,\dots ,\mathrm{N}$, and assuming a probability $\mathrm{p}$ to taking the right step (positive), we generate the ${\mathrm{n}}_1$ successes by a binomial distribution choice. Then, considering that $\mathrm{q}=1-\mathrm{p}$ is the probability in j trials of taking a step to the left (negative), we have ${\mathrm{n}}_2=\mathrm{N}-{\mathrm{n}}_1$ as the success number. In that task, we generate the ${\mathrm{n}}_1$ random number sequence from the binomial distribution with $\mathrm{j}=1,2,\dots ,\mathrm{N}$, and $p=0.5$; as a function of the result, the sequence ${\mathrm{n}}_2$ was generated.

The probability density function of a binomial distribution is

$$\mathrm{P}\left(\left.{\mathrm{n}}_1\right|\mathrm{N},\mathrm{p}\right)=\left(\begin{array}{c}\mathrm{j}\\ {\mathrm{n}}_1\end{array}\right){\mathrm{p}}^{{\mathrm{n}}_1}{\mathrm{q}}^{{\mathrm{n}}_2}={\displaystyle \frac{\mathrm{j}!}{{\mathrm{n}}_1!{\mathrm{n}}_2!}}{\mathrm{p}}^{{\mathrm{n}}_1}{\mathrm{q}}^{{\mathrm{n}}_2}, \mathrm{where} {\mathrm{n}}_2=\left(\mathrm{j}-{\mathrm{n}}_1\right).$$

(37)

where the symbol $\mathrm{“}!\mathrm{”}$ represents a factorial. In a binomial distribution, the mean number of steps ${\mathrm{n}}_1$ to the right and the mean number of steps ${\mathrm{n}}_2$ to the left are, respectively, $\overline{{\mathrm{n}}_1}=\mathrm{p}\mathrm{N}$ and $\overline{{\mathrm{n}}_2}=\mathrm{q}\mathrm{N}$, and the standard deviation mean is the root-square of the variance, defined as ${\mathsf{\sigma }}_{{\mathrm{n}}_1}=\sqrt{\mathrm{p}\mathrm{q}\mathrm{N}}$.

Therefore, we now consider the distances ${\mathrm{d}}_{\mathrm{N}}$ distribution traveled after a given step number, defined as

$${\mathrm{d}}_{\mathrm{N}}={\mathrm{n}}_1-{\mathrm{n}}_2=2{\mathrm{n}}_1-\mathrm{N}$$

(38)

To formally define the one-dimensional random walk, we take the independent random variables ${\mathrm{d}}_1,{\mathrm{d}}_2,\dots ,{\mathrm{d}}_{\mathrm{N}}$, estimated by (38). Then, setting ${\mathrm{S}}_0=0$, and estimating ${\mathrm{S}}_{\mathrm{n}}={\sum }_{\mathrm{i}=0}^{\mathrm{n}}{\mathrm{d}}_{\mathrm{i}}$, with $\mathrm{n}=0,1,2,\dots ,\mathrm{N}$. The series $\left\{{\mathrm{S}}_0,{\mathrm{S}}_1,{\mathrm{S}}_2,\dots ,{\mathrm{S}}_{\mathrm{N}}\right\}$ is the simple random walk on $\mathrm{S}$, whose series gives the net distance walked. The $\mathrm{E}\left({\mathrm{S}}_{\mathrm{n}}\right)$ expectation of ${\mathrm{S}}_{\mathrm{n}}$ is zero as the trial number N increases.

Finally, since the mean of $\overline{{\mathrm{d}}_{\mathrm{N}}}$ increases as $\mathrm{N}$ increases ($\overline{{\mathrm{d}}_{\mathrm{N}}}=\sqrt{2\mathrm{N}/\mathsf{\pi }}$), we normalized the series ${\mathrm{S}}_{\mathrm{n}}$ by its maximum module to adjust the series number in a standard amplitude. In the following, we multiply it by a proportional factor ranging between the endogenous variable mean amplitude and the mean amplitude of the random walk.

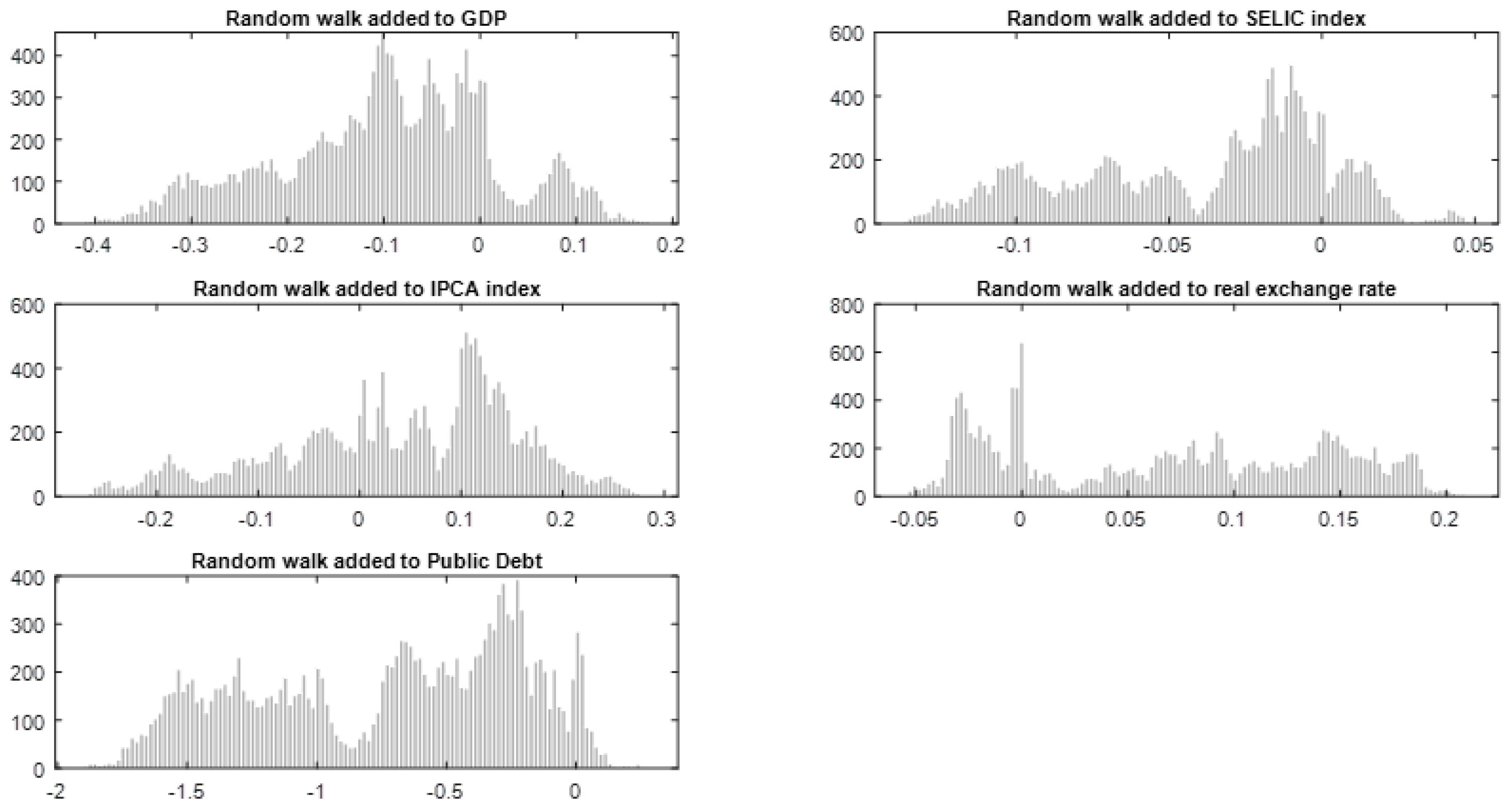
Figure 3 below shows the histograms of stochastic shocks to be added to the Model’s endogenous variables. The histograms represent the stochastic shocks for one interaction for all integration time, characterizing a one-dimensional random walk (1D) generated by binomially distributed jumps and following a $\mathrm{p}\mathrm{q}\mathrm{N}$ dispersion variance. The histograms in this figure are associated with endogenous variables in the following sequence: GDP (Ground Domestic Product), SELIC (short-term Interest rate), IPCA (Consumer Price Index), ER (actual exchange), and real DLSP (Net Public Debt). The shock bands added for these variables involve the respective ranges of stochastic variability formed by their minimum and maximum values, as shown in the Figure 3 legend, with zero means.

4.3.3. Estimation of the Deterministic Dynamic Model

In the first subsection, we examine the adjustment curves of the deterministic model (DM) and its forecasts. We will analyze both the behavior of the model calibration process during the training period and the evolution of the forecast curves, which have been established over an eight-year period. In a second subsection, we research the mean impact intensities of the variables on the variation process to identify how the variables included in the model are related and determine the intensity of each explanatory variable in the model on the corresponding dependent variable.

Adjustment Curves of the Determinist Model and Forecasts

In the first step of analyzing the deterministic dynamic model, we will focus on the adjustment curves of this model, with forecasts extending over eight years. In all graphs of Figure 4, we observe the evolution of the estimates, both for the training period (January 1998 to December 2018) and for the model forecast period (January 2019 to December 2026). We also observe in the graphics the empirical data used in the training process (represented by red crosses) and the empirical data used as backtests from January 2019 to March 2023 (represented by green crosses).

Figure 4 shows the endogenous variables of the dynamic model (29), such as real GDP per GDP of January 1998, nominal SELIC index, nominal IPCA index, Real Exchange rate (ER), and Real Debt Net of the Public Sector, per GDP of 1998/Jan (DLSP). We observe that the dynamic adjustments of all model variables were satisfactory, using the coefficients calibrated for the System (29). The System (29) is a first-order ordinary differential equations system with solid resilience, described by a rigidity relationship among variables. This deterministic System’s equations allow for defining the trend and the low-frequency components. The mean and high frequencies are characteristics of stochastic innovations, which may be better represented by a stochastic differential system, such as System (31), with perturbations in the non-controlled parameters and the model variables. The convergence of a stochastic differential system is more challenging than finding the convergence solution for deterministic systems.

The limitations presented in the dynamic model adjustments with actual data for the System (29) are mainly due to the system’s resilience effects, as we have a macrodynamic model that is mathematically closed, in which the endogenous variable evolutions follow the intrinsic relationships established by macroeconomic and monetary laws, linked by a well-defined interrelation process. Here, we performed a calibration process, followed by an integration approach to the system equations, which differs from the adjustments made by the regression models. Then, the model solution procedure enables us to determine whether the economic policies were implemented correctly in accordance with the macroeconomic rules during the training data period.

The earlier discussion about interest and inflation rates, which relate to the internal process of an economy, is linked to the country’s exchange rate. This variable establishes the price interplay between economies. A decrease in interest rates causes changes in economic activity and sustains an inflation increase. If a nation experiences significantly higher inflation, its currency tends to depreciate relative to foreign currencies. In another sense, when the economy’s exchange rate depreciates, the price level increases (inflation growth). If the exchange rate appreciates, the process occurs inversely, with a reduction in inflation.

Figure 4 shows the interaction among the SELIC index, IPCA index, and real exchange rate. Since the SELIC index was underestimated between 2002 and 2014, the IPCA index and exchange rate were overestimated in the same period. Besides these three variables being intensely volatile and absorbing diverse stochastic effects, the system model equations have resilience effects. Thus, obtaining a good calibration of a deterministic system (as System (29)) is challenging, as we do not calibrate a single independent equation but rather an equation system with its rigid interrelations. Therefore, we calibrate the tied structure in that equation’s system, interrelating the macroeconomic variables. For this reason, we conjecture that the Central Bank of Brazil (BCEN) initiated a process of establishing interest rates above the necessary level to maintain the economy’s steady state, primarily to attract international investment in domestic currency, between 2002 and 2014.

From 2015 onwards, we observed that the calibration and forecasting process estimates for the variables index SELIC, index IPCA, and real exchange rate developed, following a trajectory of average estimates that captured the low-frequency components without absorbing the effects of stochastic shocks with intermediate and high frequencies.

Between 2015 and 2019, Brazil experienced a profound political and economic crisis. This crisis resulted from supply and demand shocks resulting from monetary policy errors. These shocks led to a reduction in the Brazilian economy’s growth capacity and an increased risk of insolvency for public finances. The country experienced a significant expansion of credit and leverage between 2003 and 2013. Consumption, wages, and prices expanded greatly. The economy reached full employment, with the Brazilian currency worth much more than it should have. In 2015, the government contracted public spending, taking the SELIC (the interest rate reference) from 7.25% to 14.25%, shortly before (in 2013). This macroeconomic structure created an imbalance among the SELIC index, the IPCA index, and the exchange rate, as captured by the model described above, for the period from 2002 to 2014.

We note in Figure 4 that the calibrated model satisfactorily adjusts the trend described by the DSLP curve of the empirical data in the training period (from January 1998 to December 2018), evolving practically over the curve of empirical data and also over of the backtests’ data (from January 2019 to March 2023); that is, maintaining the growth trend slope, over the forecast period.

This growth trend in the slope of DSLP in the Brazilian economy characterizes a behavior of fiscal dominance in conditioning its economy. The frequent increase in public debt led to a budgetary imbalance during the data training period, from January 1998 to December 2018, which highlights an environment of fiscal dominance, as stressed by Yörükoğlu and Kılınç (2012).

As described, monetary governance that prevailed in the Brazilian economy, lasting more than ten years (from 2002 to 2014), resulted in fatal public sector debt growth. The explosion of uncertainty and significant exchange devaluation led to the IPCA rate reaching 10%. The implosion of tax collection added to the rigidity of spending. The tax exemption policy led to a substantial primary public deficit. In short, there was an explosion of public debt due to mismatches in monetary policy.

Finally, observing the GNP evolution graph in Figure 4, we can emphasize that the estimated GNP curve evolved satisfactorily from January 1998 to December 2018 if compared with the evolution of empirical GNP data; however, being lower over the period 2002 to 2014, a period in which the politic monetary applied by the Brazilian central bank overestimated the interest rate suggested by the dynamic system calibrated, as explained earlier.

In all the graphs in Figure 4, we observe the forecast evolutions from January 2019 to December 2026, along with the empirical data used as backtests for that period (represented by green crosses). At this point, we will analyze the forecast behaviors from a qualitative perspective. Later, in Section 4.3.5, we will explore the behavior of the forecasts from a quantitative perspective. In general, we emphasize that the endogenous variables estimated for the real GNP, nominal SELIC index, and nominal IPCA index evolve, on average, in a manner consistent with the trends in the empirical data used in the backtest analysis (green crosses). Regarding the forecast curves for the real DLSP and real Exchange rate, we observed, on average, a complete connection between the corresponding forecast curves and the empirical data used as backtests.

It is worth noting that during this period, the COVID-19 pandemic and the war in Ukraine emerged, affecting backtests. In the process of converting COVID-19 into a global pandemic, the economic crisis in the international financial system was amplified. In Brazil, this new crisis was even more severe, considering that the country’s economy was still recovering from the severe recession that occurred between 2015 and 2019. Under these circumstances, the economic effects of the crisis were strongly felt in the Brazilian economy. This new crisis led to a sharp drop in GNP and employment levels. This crisis led to a recession in the Brazilian economy. Therefore, comparing the model’s predictions for 2019 to 2023 (especially 2019 to 2021) is not feasible.

Therefore, the graphs in Figure 4 allowed us to analyze the forecast behaviors facing the observed data. From them, we could qualitatively assess how accurate the forecasted estimations of the Brazilian economy’s behavior over the next eight years are. However, we need to conduct a quantitative analysis to establish the magnitude order of these estimates relative to the backtest data. As previously emphasized, we will carry out this analysis in Section 4.3.5, which will be presented later, comparing the predictions obtained by the deterministic model analyzed here with the average predictions obtained by the stochastic model to be studied later, as well as with the data used in backtests.

The Mean Impact Intensities of the Variables on the Variation Process

The deterministic model is a valuable tool for identifying the relationships between the variables included in the model and determining the intensity of each explanatory variable on the corresponding variation in the dependent variable. To identify these interactions, we estimated the growth rates impacted (GRI)6 by each independent variable on the related variation in the dependent variable.

Table 3. Estimates of the relative impacts of the explanatory variables on the average growth monthly rate (GRI) in percentage terms.

Parameters	$\mathbf{Average} \mathbf{Growth} \mathbf{Monthly} \mathbf{Rate} \left(\mathbf{G}\mathbf{R}\mathbf{I}\right)$(%)	Description
${\gamma }_1$	$-0.0353035$	The average actual GDP growth rate is due to the actual SELIC index.
${\gamma }_2$	$0.2649742$	The average actual GDP growth rate is due to the actual exchange rate.
${\mu }_1$	$0.0000000$	The average nominal SELIC growth rate is due to the actual output gap.
${\mu }_2$	$-0.0040913$	The average nominal SELIC growth rate is due to the differential between the inflation indices and targets.
${\theta }_1$	$0.0826400$	The average real DLSP growth rate is due to the difference between the interest debt rate (mean between the SELIC index and foreign interest index), weighted by the inflation rate (mean between domestic and foreign inflation index), and the GDP rate growth.
${\theta }_2$	$-0.0890010$	$\mathrm{The} \mathrm{average} \mathrm{real} \mathrm{D}\mathrm{L}\mathrm{S}\mathrm{P}$ growth rate is due to the seigniorage.
${\sigma }_1$	$0.0000000$	The average nominal IPCA growth rate is due to the actual output gap.
${\sigma }_2$	$-0.0246871$	The average nominal IPCA growth rate is due to the real Exchange rate.
${\delta }_1$	0.29517391	The average real Exchange (ER) growth rate is due to itself.
$u_1$	$0.0322200$	The average real GDP growth rate is due to itself.
$u_2$	$-0.0786846$	The average nominal SELIC growth rate is due to the difference between the SELIC and TJLP indices.
$u_3$	$0.0170085$	The average nominal IPCA growth rate is due to the difference between the inflation indices and targets.
$u_4$	$0.1185109$	The average real Exchange (ER) growth rate is due to the real SELIC index.
$u_5$	$0.0143406$	The average real DLSP growth rate is due to the primary balance (surplus or deficit).

shows the estimates of the relative impacts of each explanatory variable over the dependent variable of each equation by using the average growth monthly rate (GRI) in percentual terms for each equation of the System (29). Economic policymakers are interested in this information to establish stable control over the country’s economy.

The first equation of the System (29) shows that the real GDP, the actual SELIC index, and real Exchange explain the GDP variation per time increment unit. Thus, based on the average growth rates in Table 3, it is observed that the Brazilian GDP has an average monthly growth of 0.265% caused by the real Exchange Rate variable, −0.0353% is due to the real SELIC index, and 0.0322% is owing to itself. The GDP average monthly growth rate is the sum of these three impact growths, totaling 0.26189%. In these detached growth rate estimates, the real Exchange Rate is the principal component impacting the Brazilian GDP growth.

The second equation of the System (29) shows that the output gap, $\mathrm{y}\left(\mathrm{t}\right)-\overline{\mathrm{y}}\left(\mathrm{t}\right)$, the $(\mathsf{\pi }\left(\mathrm{t}\right)-{\mathsf{\pi }}^{\mathrm{e}}\left(\mathrm{t}\right))$ variable, and the variable $\left(\mathrm{i}\left(\mathrm{t}\right)-\mathrm{T}\mathrm{J}\mathrm{L}\mathrm{P}\left(\mathrm{t}\right)\right)$ explain the nominal SELIC index variation per time increment unit. Table 3 stresses that the SELIC index has an average monthly growth of $-0.00409\%$ caused by the $(\mathsf{\pi }\left(\mathrm{t}\right)-{\mathsf{\pi }}^{\mathrm{e}}\left(\mathrm{t}\right))$,$-0.07868\%$ is due to the variable $\left(\mathrm{i}\left(\mathrm{t}\right)-\mathrm{T}\mathrm{J}\mathrm{L}\mathrm{P}\left(\mathrm{t}\right)\right)$, and $0.0000\%$ due to the variable $(\mathrm{y}\left(\mathrm{t}\right)-\overline{\mathrm{y}}\left(\mathrm{t}\right))$ (output gap do not causes mean changes any variable, being a cycled effect). The SELIC index average monthly growth rate is the sum of these three impact growths, totaling $-0.08277\%$. Then, we observe that the difference between the SELIC and TJLP indices is the principal component that impacts the growth of the Brazilian nominal SELIC index. Therefore, monetary authorities should be more concerned with establishing an adequate premium for the TJLP to guarantee the appropriate evolution of the short-run interest rates, which may induce stable economic growth.

The third equation of the System (29) shows that the output gap, $\mathrm{y}\left(\mathrm{t}\right)-\overline{\mathrm{y}}\left(\mathrm{t}\right)$, the variable $(\mathsf{\pi }\left(\mathrm{t}\right)-{\mathsf{\pi }}^{\mathrm{e}}\left(\mathrm{t}\right))$, and the Exchange Rate explain the nominal IPCA index variation per time increment unit. We observe that the Exchange Rate is the principal component impacting the IPCA index growth; thus, the exchange control may guarantee the appropriate evolution of inflation and induce stable economic growth. Table 3 stresses that the IPCA index has an average monthly growth of $0.0170085\%$ caused by the variable π(t) − π^e (t); $-0.0246872\%$ is due to the real Exchange Rate, and $0.0000\%$ is due to the output gap. The IPCA index average monthly growth rate is the sum of these three impact growths, totaling $-0.007678\%$. We observe that the real exchange rate was the principal factor controlling inflation.

The fourth equation of Systema (29) estimates the actual exchange rate variation per unit of time. The real interest rate causes immediate changes in public debt and economic growth and, in a second step, impacts the exchange rate, thereby reducing its direct effects on the exchange rate. Therefore, from the result stressed in Table 3, we observe that the exchange average growth rate of $0.4643\%$ is due to itself, and about $0.2151\%$ is due to the real interest rate, causing a total depreciation in the exchange rate of about $0.679471\%$. Despite the exchange rate and the real interest rate causing depreciation in the exchange, the more significant weight on exchange depreciation is due to itself, which is consistent with the expectation.

Finally, the fifth equation of Systema (29) estimates the variation in the Brazilian economy’s real public debt (DLSP) per time increment unit. In Table 3, the variable in question (DLSP) follows its growth path over the calibrated period, evolving in the function of the difference between debt interest rate and GDP rate growth, of the primary balance (surplus or deficit), and seigniorage. Therefore, according to Table 3, the total DLSP average growth rate is $0.08264\%$, caused by debt interest effects, $-0.0890\%$ due to the seigniorage, and $0.01434\%$ owing to the primary balance (surplus or deficit), totaling $0.1573\%$ per month. It is observed in these results, as expected, that debt interest positively impacts the growth of public debt, which comes from the difference between real interest debt rate and GDP rate growth, affecting the previous debt, by the relation $\left[\mathrm{r}\right(\mathrm{t})-\mathsf{\eta }(\mathrm{t}\left)\right]\mathrm{b}\left(\mathrm{t}\right)$. In the same order, the seigniorage has a positive impact on the debt.7 Despite its opposing sign, it is accompanied by a negative sign in the System (29), generating a positive impact, as explained early in the Subsection calibration of the deterministic model. The primary balance (surplus or deficit) negatively impacts the debt, and despite it having a positive sign, it is accompanied by a negative sign in the system (29).

4.3.4. Estimation of the Stochastic Dynamic Model Under Stochastic Bifurcation

We will present the analysis of stochastic solutions generated through random innovations. As we argued previously, we are dealing with a resilient equation system that offers a certain degree of rigidity but allows for some elasticity. In this context, we can identify sets of controllable and non-controllable parameters, consisting of parameters with values that differ from those that generated the primitive solution, thereby inducing an evolution process distinct from the calibrated solution. Therefore, for each set of stochastically generated parameter values, we can consider it as a generator of a new solution that we call bifurcating. In the same way, we can develop some bifurcating solutions by adding stochastic innovations to the endogenous variables, which can induce an evolution process that is different from that of the primitive solution without these perturbations. We also consider these solutions to be bifurcating solutions.

Calibration of the Stochastic Dynamic Model Under Stochastic Bifurcation

In this subsection, we will detail how the stochastic process perturbations are introduced to generate bifurcating solutions. As explained in Section 4.3.2, we simultaneously will impose the stochastic disturbances over all of the non-controllable parameters of the System Equations (31), generating them through a normal probability distribution specified for each parameter around its calibrated value. The normal distribution was determined by $\mathrm{N}({\mathrm{p}}_{\mathrm{i}},{\mathsf{\sigma }}_{\mathrm{i}}^2)$, where ${\mathrm{p}}_{\mathrm{i}}$ is the non-controllable parameter calibrated (with $\mathrm{i}=1,2,\dots ,{\mathrm{N}}_{nc}$, where ${\mathrm{N}}_{nc}$ is the non-controllable parameters number) and ${\mathsf{\sigma }}_{\mathrm{i}}^2$ is the variance for the parameter $\mathrm{i}$, chosen by test. Then, ${\mathsf{\sigma }}_{\mathrm{i}}^2$ for each parameter ${\mathrm{p}}_{\mathrm{i}}$, executing the aleatory choice of the distribution family $\mathrm{N}({\mathrm{p}}_{\mathrm{i}},{\mathsf{\sigma }}_{\mathrm{i}}^2)$, will be the new model parameters.

In the sequence, we integrate the system of differential equations by the fourth-order Runge–Kutta technique (Press et al., 1992). This process is executed exhaustively, taking into account outliers in the family distribution. Then, supposing that all parameter choices generated convergence solutions by the Runge–Kutta technique, ${\mathsf{\sigma }}_{\mathrm{i}}^2$ is enlarged until a parameter is found by random choice in the new family $\mathrm{N}({\mathrm{p}}_{\mathrm{i}},{\mathsf{\sigma }}_{\mathrm{i}}^2)$, for which the Runge–Kutta technique does not converge for a stable solution. Hence, the previous ${\mathsf{\sigma }}_{\mathrm{i}}^2$ is the larger band to choose that comprises all bifurcation solutions involving the calibrated parameter ${\mathrm{p}}_{\mathrm{i}}$. This extending process of ${\mathsf{\sigma }}_{\mathrm{i}}^2$ is repeated for all parameters ${\mathrm{p}}_{\mathrm{i}}$ up to find some non-convergent solution by the Runge–Kutta technique. By repassing this process for all parameters ${\mathsf{\sigma }}_{\mathrm{i}}^2$, we assumed the previous ${\mathsf{\sigma }}_{\mathrm{i}}^2$ as a given variance, the largest possible for which the stochastic achievements of the dynamic economic model converged to stable solutions that we called stochastic bifurcation solutions.

In a second stochastic disturbing process, we added perturbations in the model’s endogenous variables. In this procedure, we add stochastic perturbations, generating n${\mathrm{n}}_1$ and ${\mathrm{n}}_2$ sequences of random numbers from the binomial distributions, as explained in the final part of Section 4.3.2. We estimated the series $S_n$, by setting $S_0=0$, and estimating ${\mathrm{S}}_{\mathrm{n}}={\sum }_{\mathrm{i}=0}^{\mathrm{n}}{\mathrm{d}}_{\mathrm{i}}$, with $\mathrm{n}=0,1,2,\dots ,\mathrm{N}$. (where ${\mathrm{d}}_{\mathrm{i}}={\mathrm{n}}_{1\mathrm{i}}-{\mathrm{n}}_{2\mathrm{i}}$ is estimated by Equation (38)). The series $\left\{{\mathrm{S}}_0,{\mathrm{S}}_1,{\mathrm{S}}_2,\dots ,{\mathrm{S}}_{\mathrm{N}}\right\}$ is the simple random walk on $\mathrm{S}$, which gives the net distance walked. The $\mathrm{E}\left({\mathrm{S}}_{\mathrm{n}}\right)$ expectation of ${\mathrm{S}}_{\mathrm{n}}$ is zero as the trial number N increases. Following this, we normalize the series by its maximum module of ${\mathrm{d}}_{\mathrm{i}}$ to adjust the series number in a standard amplitude. We multiply the series by a proportional factor, ranging between the endogenous variable mean amplitude and the mean amplitude of the random walk. Thus, we calibrated the amplitudes of the random path, for which the solutions were obtained by the integration method of the Runge–Kutta.

Finally, we add the random walk time series generated to the corresponding endogenous variable time series. The first random walk value of the time series is added to the initial conditions of the endogenous variable (i.e., the first observed data) used by the Runge–Kutta integration method, and in each integration step, the corresponding time random walk is added to the time solutions obtained by Runge–Kutta method, and so on. If the integration process is completed successfully, we increase the multiplication factor (by raising the random walk amplitude) until a situation arises where the integration process cannot be achieved successfully. In this case, the previous integration factor is adopted as a standard to obtain bifurcating solutions.

Mathematically, the stochastic disturbances on the non-controllable coefficients are defined by $\mathrm{h}\left(\mathrm{x}\right(\mathrm{t}\left)\right)$ of the System (31), and the stochastic disturbances added to the endogenous variables are represented by the term $\mathrm{v}\left(\mathrm{t}\right)$ also in the System’s (31).

The results of the computational simulations were generated for each unit of time using the procedures earlier explained. The dynamic solutions were obtained using a fourth-order Runge–Kutta integration process with tiny time increments of ${10}^{-8}$. This procedure allowed for testing the disturbance bands and amplitudes generated for all parameters and establishing the set of all Monte Carlo’s converged realizations. For all processes, we obtained 200 Monte Carlo simulations for each case study, spanning from January 1998 to December 2018 (January 1998 to December 2018, the training period for the parameters, and January 2019 to December 2026, the forecast period). These Monte Carlo’s realizations convergent solutions are the bifurcation solutions.

Forecast Analysis of the Macrodynamic Model Under Stochastic Bifurcation

Figure 5 represents the estimates of Monte Carlo’s achievements from January 1998 to December 2018 for the training period and the eight years of the forecast period from January 2019 to December 2026.

Figure 5 makes it possible to visually highlight the effects of stochastic innovations by the scattering of Monte Carlo’s realizations’ evolution. In all graphics of this figure, the spread band of Monte Carlo’s realizations is represented in multiple colors, the empirical data used in the model training, characterized by a cross symbol in black color, from January 1998 to December 2018, and the empirical data utilized in the backtest analysis, represented by a cross symbol in green color, from January 2019 to March 2023.

Figure 5a shows the spread of solutions disturbed by stochastic innovations due only to the non-controllable parameters, Figure 5b shows the spread of solutions due to disturbances imposed by only the addition of random walk in the endogenous variables, and Figure 5c emphasizes the evolutions imposed by disturbances in the uncontrollable parameters and addition of random walk, simultaneously. Each figure shows the evolutions of the two hundred Monte Carlo realizations in similar bands for the three cases analyzed. Comparing the scales of disturbance variability for three cases, we concluded that they exhibit similar amplitudes, with little difference, which allows us to make considerations unique to all.

We introduced the stochastic disturbances in the dynamic economic system throughout the analysis period (period of the sample of the empirical data and the forecast period, from January 1998 to December 2026). It is observed in Figure 5 that the scattering bands of estimates over endogenous variables evolve in increasing ways over the all-estimation time, including the calibration data (January 1998 to December 2018) and the forecast period (from January 2019 to December 2026). At the beginning of estimation, the values for the endogenous variables stress less thick spread bands despite the stochastic disturbances introduced into the dynamic system, which, at any time, were coming from the same stochastic disturbance ranges. This behavior emphasizes that the disturbances in each system equation interact and evolve into stochastic trends, amplifying more over time. The amplification occurs due to the addition and multiplication of previous effects in each Monte Carlo simulation, increasing the uncertainties as time progresses and leading to higher levels of disturbance in the estimates in the forecast regions.

Currently, we will analyze the behavior of the forecasts from a qualitative perspective only. We highlight that the scatter bands of the endogenous variables encompass the entire empirical data used in the training process and those employed for backtesting analysis.

We observe that the resilience behavior, demonstrated when analyzing the deterministic dynamic model, is also present in the solutions of the stochastic model, regardless of the type of shocks imposed on the dynamic model. The effects presented are similar to those verified in the deterministic model solutions for the short-term interest rate equations (SELIC), the inflation index equation (IPCA), and the real exchange rate. Relative to the SELIC, there is a resistance of the interest rate to evolve entirely on the empirical data, following a long-term average dynamic trajectory, with a slight departure from the evolution of empirical data in large part of the calibration samples, as may best see in Figure 5d. Conversely, inflation is also overestimated in much of the training data evolution process, and similarly, the exchange rate is overvalued; however, with less intensity. In summary, we are executing a rigid macroeconomic model in which, as previously argued, the imposed economic process must obey the model’s equilibrium conditions, which are not broken by the stochastic shocks. Then, each solution shown in Figure 5a–c is a solution possible for the dynamic stochastic model applied in this study. They are bifurcation solutions whose usability depends on the stochastic innovations acting on the economic process at a specific moment. We analyze the spread intensity of these solutions in Section 4.3.6 below.

Figure 5d shows the evolution of the average curves of the endogenous variables of the dynamic model for the entire analysis period, from January 2019 to December 2026, with all empirical information for the training process and the analysis of backtests. In this figure, we show the evolution of the average trajectories only for that one case fed stochastic disturbances both on the uncontrollable parameters and addition of random walk simultaneously (Figure 5c) since the means curves of the three cases are completely nearby.

Considering the empirical data from backtests, we observed that the evolution processes of the averages behave satisfactorily qualitatively, showing the average growth or decrease processes for each endogenous variable over time. In the case of GDP, in the first graph, the forecasts are very close to those in the backtest data period. We can consider it a satisfactory estimate, as shown in the evolution forecast process in the first graph of Figure 5d.

In the case of interest rates, they were highly volatile during the initial forecast periods. In summary, the monetary policy implemented by the BACEN throughout the backtest period (January 2019 to March 2023) uses the SELIC interest rate as the primary instrument for controlling the general price level. Since 2019, the SELIC rate has oscillated and increased considerably. The SELIC rate went from 4.5% in December 2019 to 2% in December 2020, to 9.5% in December 2021, 13.75% in December 2022, and 13.75% in March 2023, at the end of the backtest period. Specifically, from 2021 onwards, interest rates rose significantly to contain inflation during this unstable period caused by COVID-19. Despite this, the forecast estimation was consistent, on average, as emphasized in the second graph of Figure 5d.

Concerning the accumulated inflation in 2019, it was 4.31%, 4.52% in 2020, 10.06% in 2021, and 5.79% in 2022, and the accrued inflation until March/2023 was 2.09% (but the previewed over the year, it was 4.70%). The substantial increase in inflation in the Brazilian economy was due to the crisis imposed by COVID-19, as can be observed in the IPCA index graphic of Figure 5d. In conclusion, we understand that the stochastic model implemented predicts the average inflation evolution process over the backtest forecast region satisfactorily, as seen in the third graph of Figure 5d.

The fourth graphic of Figure 5d shows the real exchange rate evolution, in which we can see that in the backtest prediction region, the model predicts the real exchange rate depreciation process satisfactorily. The real exchange rate may continue to depreciate over the forecast period and reach values close to six by 2026.

Finally, the fifth graphic of Figure 5d shows the evolution of real public debt (DLSP). From that one, the model is somewhat completely satisfactory for predicting the debt growth process in the backtest prediction region. However, we can see that the evolution of the forecast curve maintains the upward trend, indicating that Brazilian public debt is likely to continue growing at a constant rate without any prospect of decrease.

In Section 4.3.5, we will conduct a quantitative analysis to establish the order of magnitude of the average forecasts for each variable throughout the forecast period (from 2019 to 2026), as obtained by the stochastic model described here.

4.3.5. Comparison of Deterministic Model Forecasts with Stochastic Model Mean Forecasts and Backtest Data

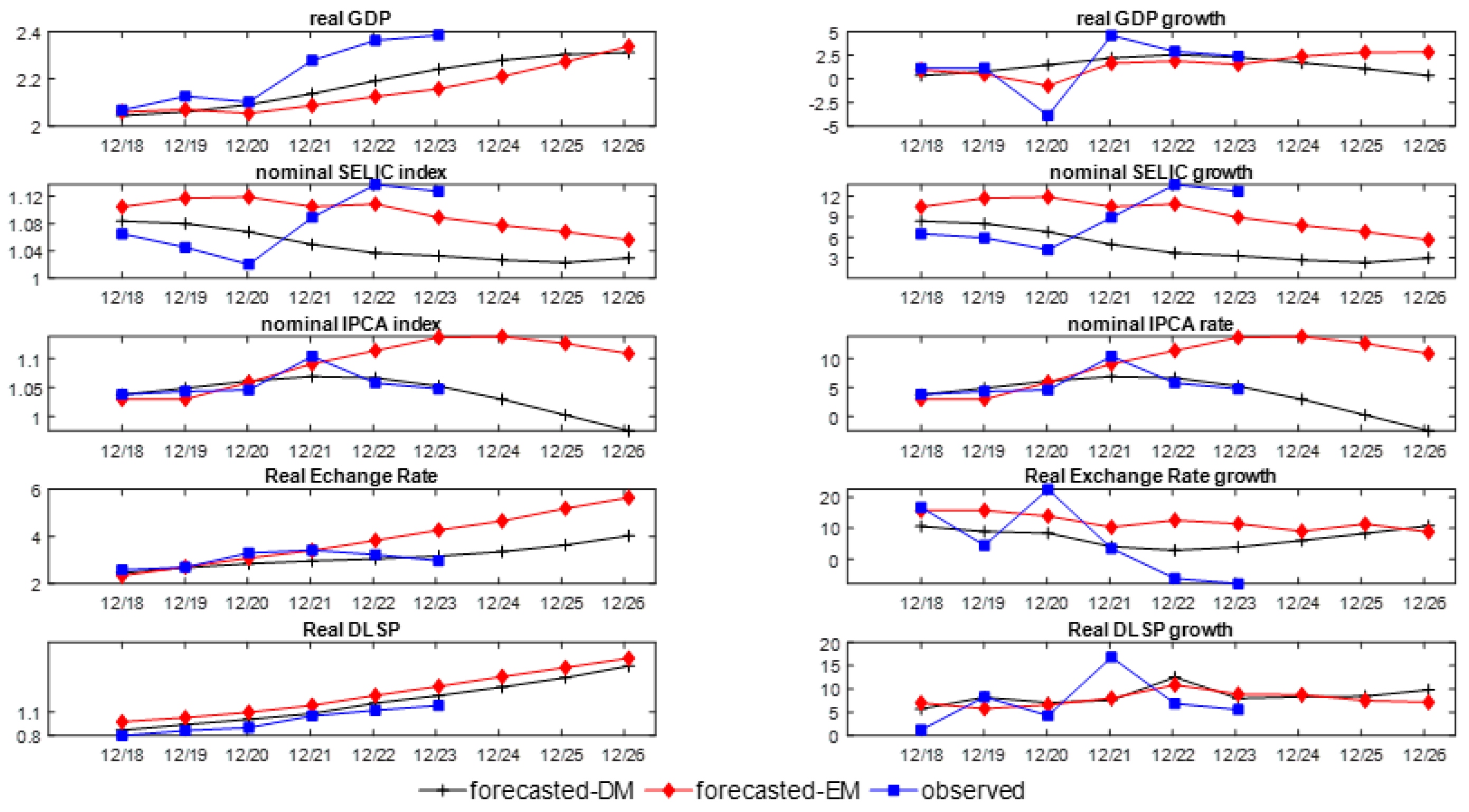
To analyze the forecast behavior of the determinist (DM) and stochastic (EM) models, we structure the mean curves’ forecast data for DM and the EM models in annual forecast data to compare them with the yearly data used as backtests. For annual data, we obtained the forecast curves estimated by the DM and EM models, for the variables real GDP, nominal SELIC index, nominal IPCA index, the real exchange rate (ER), and real DLSP from 2018 to 2026. We observe, in Figure 6, their evolution processes from 2018 to 2026.

In Figure 6, the endogenous variable levels curves are represented by the graphs in its left column, in which the backtest data are represented by a blue line overlaid by square markers, the forecasts estimated by the DM are characterized by a black line overlaid by cross markers, and the estimates calculated by the EM model are represented by a red line overlaid by diamond markers (see legend at the bottom of Figure 6).

In Figure 6, the endogenous variable growth curves are represented by the graphs in the right column. We also presented the forecasted growth rate curves for 2018 to 2026 of the endogenous variables specified in the preceding paragraph, expressed as percentages, and compared them with the backtest data for 2018 to 2023. The legend at the bottom of Figure 6 specifies the growth rates’ curves, similar to those used for the variable level.

First, we consider analyzing the variables at the level. In the left graphs of the first line, we observe the real GDP forecasts for both models, DM and EM, which maintain increasing trajectories similar to the evolution of empirical data from 2018 to 2020; however, the trajectories’ evolutions forecasted by DM and EM models present more significant discrepancy relative to backtest for the period from 2021 to 2023 but developing increasing processes overall forecast period, from 2019 to 2026, whose trajectories evolve closely over the forecast period, being the estimated levels of ME model lower than that one of the DM. Still, the evolution of the DM and EM forecasts maintains a similar slope to the backtest data.

We constate in the graphs of percentual rates, on the first figure on the right side of Figure 6, that the forecasted PND growth was accurately estimated for both models, DM and EM, in average terms, except for the years 2020 and 2021, the period under intense impact of the COVID-19 crisis, not only in Brazil but in all world (the numerical forecasts and empirical data are cataloged in

Table A2. Estimates of average predictions of the dynamical model’s endogenous variables.

Model Note	Variable	YEAR
		2018	2019	2020	2021	2022	2023	2024	2025	2026
GDP
DM	Real GDP forecasted	2.044	2.060	2.091	2.137	2.191	2.241	2.279	2.303	2.311
EM	Real GDP forecasted	2.060	2.070	2.054	2.087	2.125	2.158	2.210	2.272	2.338
Obs	Real GDP empirical	2.067	2.126	2.102	2.278	2.363	2.385
DM	Real GDP growth forecasted (%)	0.345	0.782	1.473	2.196	2.562	2.271	1.696	1.068	0.349
EM	Real GDP growth forecasted (%)	0.941	0.485	−0.737	1.645	1.894	1.536	2.381	2.811	2.831
Obs	Real GDP growth empirical (%)	1.120	1.140	−3.880	4.600	2.900	2.900
SELIC
DM	Nom. SELIC index forecasted	1.084	1.080	1.068	1.049	1.037	1.032	1.027	1.023	1.029
EM	Nom. SELIC index forecasted	1.105	1.117	1.119	1.105	1.109	1.089	1.077	1.068	1.056
Obs	Nom. SELIC index empirical	1.065	1.045	1.020	1.089	1.138	1.128
DM	Nom. SELIC rate forecasted (%)	8.356	8.004	6.789	4.926	3.668	3.241	2.655	2.255	2.947
EM	Nom. SELIC rate forecasted (%)	10.463	11.738	11.901	10.486	10.881	8.919	7.743	6.782	5.604
Obs	Nom. SELIC rate empirical (%)	6.500	5.900	4.150	8.900	13.750	12.750
IPCA
DM	Nom. IPCA index forecasted	1.038	1.049	1.061	1.069	1.066	1.052	1.029	1.002	0.975
EM	Nom. IPCA index forecasted	1.030	1.030	1.059	1.091	1.114	1.136	1.138	1.126	1.109
Obs	Nom. IPCA index empirical	1.038	1.043	1.046	1.104	1.058	1.048
DM	Nom. IPCA rate forecasted (%)	3.770	4.870	6.110	6.870	6.630	5.229	2.945	0.227	−2.495
EM	Nom. IPCA rate forecasted (%)	2.960	2.971	5.870	9.082	11.366	13.637	13.806	12.585	10.855
Obs	Nom. IPCA rate empirical (%)	3.780	4.310	4.556	10.380	5.780	4.750
EXCHANGE RATE
DM	Real ER index forecasted	2.458	2.678	2.851	2.966	3.051	3.169	3.360	3.640	4.032
EM	Real ER index rate forecasted	2.341	2.710	3.088	3.407	3.836	4.275	4.661	5.190	5.648
Obs	Real ER empirical	2.583	2,697	3.307	3.421	3.231	2.973
DM	Real ER growth forecasted (%)	10.607	8.960	8.412	4.043	2.837	3.883	6.015	8.339	10.781
EM	Real ER growth forecasted (%)	15.745	15.760	13.945	10.331	12.581	11.439	9.039	11.358	8.810
Obs	Real ER growth empirical (%)	16.778	4.437	22.597	3.445	−6.286	−7.976
Public Debt
DM	Real DLSP forecasted	0.868	0.939	1.005	1.081	1.216	1.313	1.423	1.543	1.694
EM	Real DLSP forecasted	0.973	1.029	1.097	1.186	1.314	1.431	1.557	1.673	1.793
Obs	Real DLSP empirical	0.796	0.862	0.899	1.050	1.122	1.185
DM	Real DLSP growth forecasted (%)	5.720	8.193	7.071	7.588	12.479	7.991	8.330	8.433	9.793
EM	Real DLSP growth forecasted (%)	7.019	5.791	6.599	8.032	10.872	8.905	8.743	7.498	7.137
Obs	Real DLSP growth empirical (%)	1.238	8.291	4.292	16.796	6.857	5.570

Note: DM—Deterministic model; EM—Stochastic model; Obs—Observed data.

, in Appendix A). For example, the Brazilian economy grew by 1.14% in 2019, declined by 4.1% in 2020, and expanded by 4.6% in 2021. These growth rates were atypical for the characteristics of the Brazilian economy’s macroeconomic structure, as introduced in the DM and EM models. DM forecasts are feasible during an economic stability period, a situation the Brazilian economy has not experienced since 2015. Despite that, the GPD growth rates forecasted by the DM were satisfactory for 2018 to 2023, approaching the average of the backtest points, as seen in Table A2, Appendix B. From 2019 to 2022, the DM forecasts stress increasing growths for the Brazilian economy (as the following values: 0.782; 1.473; 2.196; 2.562) and from 2024 to 2026, the DM forecasts emphasized decreasing growths for the Brazilian economy (as the following values: 2.271; 1.696; 1.098; 0.349). By contrast, the EM model is stochastic, and it can be feasible for forecasting during periods of economic instability in scenarios characterized by stochastic innovations interposed by international or domestic political and/or economic disturbances. Therefore, their forecast similarly captures the strong effects of COVID-19 in 2020, as demonstrated by the backtest points. After 2022, the EM model captures a consistent growth in the GDP, evolving from 2022 to 2026, gradually from 1.645 to 2.831, as shown in Table A2, Appendix B.

The Brazilian economy lacks consistent foundations for its growth. Industrial production stagnated due to a lack of specific technological development and investment policies. It survives due to expansionist policies caused by incentive programs that increase the economy’s liquidity. A continuous increase in labor income is a stimulus to consumption caused by programs that expand social benefits, such as the release of extraordinary withdrawals of FGTS resources by workers and the anticipation of the 13th salary for retirees and pensioners. In that scenario, the GDP growth of the Brazilian economy from 2023 to 2026 is expected to be within the forecast range, as predicted by the dynamic models applied in this study: the MD and EM forecasts.

In the graphs on the left, in the second line of Figure 6, the forecast curves for the SELIC index evolve in a decreasing trend for both forecasts, that one estimated by the deterministic model (DM) and of the one of the stochastic model (EM), throughout the entire forecast period, except for the last DM forecasted year, from 2018 to 2026. The DM forecast is close to the evolution of the sample data used as backtests from 2018 to 2020 but at a level higher than the sample curve of backtest data. From 2020, the SELIC indices used as backtests increased considerably, resulting in actions to contain the inflation increasing due to the rise of the COVID-19 crisis, inverting then the relation of the forecast curve evolution and the backtest data progression, as shown in the left graphs, on the second line of Figure 6. The EM forecasts evolved in a way entirely similar to those forecasted of the DM; however, at a level considerably higher than the DM forecasts, approaching the backtest points evolution imposed from 2022. This evolution process can also be observed in the graphs of the SELIC growth rate on the right, in the second line of Figure 6. Both SELIC level and SELIC growth are detailed numerically in Table A2, Appendix A, in which the difference between the values of the interest rates predicted by the DM and ME model and the corresponding backtest samples for the period 2018 to 2020 were, in average terms, respectively, of 2.20% and 5.85%. Already, these differences between the interest rates predicted by the DM and ME models for 2021 to 2023 were, respectively, in average terms, −7.85% and −1.70%. These differences indicate a downward trend in empirical SELIC indices for 2018 to 2020, more pronounced than those suggested by the forecast. In short, the forecasts of DM and EM models followed a systematical decrease through the forecast period (from 2019 to 2026).

In the Brazilian economy, interest rates decreased considerably from 2017 onwards, reaching a level never seen before in Brazil of 2%, even during the midst of the COVID-19 pandemic crisis. Given this context, the interest rate forecast rates by both models (DM and EM), linked with a state of stable economy, indicated a less pronounced decline than those practiced by governments until 2021. In Brazil, the impact of the COVID-19 pandemic on the economic process was intense and lasting, with a substantial effect on the production chain and labor market, and inducing a drastic increase in inflationary levels. From 2020 onwards, interest rates rose considerably (from 8.9% in 2021 to 12.75% in 2023) to contain the inflationary process and reorganize the production chain and the job market. Then, what was observed from the graphs of the nominal SELIC index level and its interest rate growth (Figure 6) was that the applied rates were lower than forecasted before 2020 and higher than estimated after 2020 by the DM and EM models. In short, the predictions established by the model evolved for all variables, always in the direction of the evolution of the samples, in such a way that the deterministic model (DM) forecasted a need to apply from 2018 to 2023 interest rates, on mean, of 5.83%, lower than that used of 8.65%. The stochastic model (EM) forecasted an average interest rate of 10.73%, higher than the average of 8.65% in the backtest data. In that context, the forecasts were consistent.

Regarding the forecasts for the evolution of the nominal inflation index (IPCA) (as for the inflation rate), we observe in the graphs of the first and second figures in the third line of Figure 6 and in Table A2, Appendix B, that the DM model forecasts, for both level and growth rate, were relatively consistent with the evolution of the sample data used as backtests, except for the year 2021, where inflation reached a very high level of 10.38%, already at the end of the intensive disruptive effects of COVID-19; caused by this epidemic and, essentially, due to the high prices of oil and its derivatives worldwide. We also observe that the forecast evolution process occurs in the direction of a deflation process, similar to the backtest indication.

We also stress in the graphs of the first and second sketches in the third line of Figure 6 and in Table A2, Appendix B, the evolutions of the nominal IPCA index levels and their growth rates predicted by the model EM, compared with the backtest values. The forecasted evolution process for the IPCA variable using the EM model aligns with the data points used as backtests from 2018 to 2021, capturing the solid inflationary impact that occurred in 2021 (10.4%). However, from that point onwards, inflation empirically established by backtest data decreases, and a process of decline begins. In contrast, the forecasts set by the EM model maintain the inflation growth forecast and reach its maximum in 2023 (inflation of the order of 13.6% against 4.8% established by the backtests), evolving with a slight inflationary decrease, such that in 2026, the end of the forecast period, the forecast inflation was 10.85%.

As emphasized, the MD model estimations align satisfactorily with the backtests (except in 2021, during the COVID-19 crisis peak), following the decreasing trajectory evolution, as indicated by the empirically established inflation in the backtest data. Unlike the EM model estimation behavior, the deterministic model (MD) indicates a stable forecast evolution.

The discrepancy between the EM model forecasts and backtests after 2021 suggests that they consistently captured the instabilities caused by COVID-19 and the oil price crises from 2021 onwards. This behavior demonstrates the presence of an inflationary process intrinsic to the macroeconomic model in the face of stochastic perturbations, which, if it does not maintain the interest rate (SELIC) higher over the forecast period, can return with force, as suggested by the SELIC forecasts from the EM model, analyzed previously.

We can also stress in the graphs on the right and left sketches, in the fourth line of Figure 6, the real exchange index and the real exchange rate forecasted (ER) by the DM and EM models from 2019 to 2026, and the backtest data. In those graphs on the right sketch, in the fourth line of Figure 6, we observe that the real ER index forecast curve obtained by the DM shows a depreciation process in the same direction as the evolution of the empirical data sample used as backtests in the sub-period from 2018 to approximately July/2023; however, at slightly lower levels, without accompanying the depreciation effects of the COVID-19 shocks, with a peak in 2021. From there, the backtest’s evolution takes an appreciative direction while the real ER index forecast curve continues its depreciation process8.

As for the graph of the evolution of the forecast established for real exchange index (ER) by the EM model (see graphs on the sketch on the left, in the fourth line of Figure 6), we observe that the predicted evolution processes for these variables coincide with data points used as backtests from 2018 to 2021, capturing the effect of the solid inflationary impact on the exchange index that occurred in 2021. From 2021 onwards, the real exchange index evolves along a path of depreciation, at levels significantly higher than those established by backtests until 2023 and well above the values predicted by the DM. In that process, we observe that the exchange rate forecasts by the EM model absorb the effects of inflation volatility expected by this model at levels much higher than those estimated by the DM.

In the fourth line of Figure 6, the graphs on the right sketch show the evolutions of the exchange rates’ growth, in percentage terms, for the forecasts and backtests. On average, the estimates for exchange rate growth using the DM between 2018 and 2021 proved satisfactory, except for 2020, which was at the center of the COVID-19 pandemic’s shocks. Nevertheless, from 2021, the backtest sample showed a decrease in the exchange rate (appreciation variation), while the exchange rate forecast by the DM showed an increase in the exchange rate (depreciation variation), with a slightly accentuated slope trend.

In the figure on the left, in the fourth line of Figure 6, we can also observe the behavior of the exchange rate growth forecast obtained by the EM model. This forecasting process evolves in a manner very similar to the evolution of the exchange rate forecast using the DM; however, at higher levels—that is, predicting a real exchange index more depreciated than those indicated by the DM—in almost the entire forecast period (from 2018 to 2026). Still, they become closer in the period from 2024 to 2026.

In the last line of Figure 6, we observe the evolution of the forecasts of real Brazilian public debt levels, normalized by the initial GDP value of January 1998 (DLSP), and compare them with the evolution of the levels of the DLSP samples used as backtests. In those graphs, we observed that the real DLSP forecasted by both DM and EM models evolves at entirely satisfactory approach levels relative to the empirical samples used as backtests. This proximity is observed across all coincidence ranges of forecast and backtest data (from 2018 to 2023), during which the public debt exhibits an upward trend. After 2023 up to 2026, the evolutions of the forecasts of DLSP for both DM and EM models maintain a growth trend with the same growth slope, similar to the backtest sample.

4.3.6. Stochastic Bifurcation Analysis

The economic reality of developing countries is much more complex than that simulated by a set of deterministic equations, such as System (29), as it is often an economic process subject to external and internal economic and political shocks. Given this context, we propose a stochastic dynamic system, System (31), to analyze the economy’s capacity to absorb shocks due to stochastic innovations. As noted in Section Forecast Analysis of the Macrodynamic Model Under Stochastic Bifurcation, in Figure 5, the resolution of this stochastic system generates a set of bifurcating solutions, all characterizing some possible stable solution for the economic process that may occur at some point in its course.

Therefore, in this context, we must estimate the ranges of oscillations of the model’s endogenous variables due both to the stochastic innovations imposed on the model’s uncontrollable coefficients and due to the stochastic innovations absolved by the model, added directly to the endogenous variables, respectively, through the terms h(x(t)) and v(t) of System (31). In that procedure, we will obtain the oscillation ranges of the endogenous variables.

Table 4. Calibrated values of parameters, shock intervals introduced in them, and in the endogenous variables.

Endogenous Variables and Model Parameters	Coefficients Identified for the System (32)	Values After Shocks
		Min	Max
$\mathrm{G}\mathrm{D}\mathrm{P}$	$0.000$	$-0.411869$	$0.175134$
$\mathrm{S}\mathrm{E}\mathrm{L}\mathrm{I}\mathrm{C}$	$0.000$	$-0.136963$	$0.048275$
$\mathrm{I}\mathrm{n}\mathrm{f}\mathrm{l}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}$	$0.000$	$-0.269705$	$0.284912$
$\mathrm{E}\mathrm{x}\mathrm{c}\mathrm{h}\mathrm{a}\mathrm{n}\mathrm{g}\mathrm{e}$	$0.000$	$-0.054736$	$0.210831$
$\mathrm{D}\mathrm{e}\mathrm{b}\mathrm{t}$	$0.000$	$-1.744465$	$0.278038$
${\gamma }_1$	$-0.0738184$	$-0.227750$	$0.072245$
${\gamma }_2$	$0.0019298$	$-0.006377$	$0.009323$
${\mu }_1$	$-0.2428670$	$-0.570900$	$0.107380$
${\mu }_2$	$-0.0556015$	$-0.124338$	$0.015622$
${\theta }_1$	$0.0008263$	$-0.000891$	$0.002599$
${\theta }_2$	$-0.0283853$	$-0.103400$	$0.023327$
${\sigma }_1$	$-0.0143354$	$-0.026240$	$-0.003324$
${\sigma }_2$	$-0.0001139$	$-0.000168$	$-0.6113\times {10}^{-4}$
${\delta }_1$	$0.0029517$	$0.001219$	$0.004710$

below shows the mean disturbances imposed on the random walk added to the endogenous variables, the calibrated noncontrollable parameters, stressed in Table 2 legend earlier, and the minimum and maximum values of the stochastic distributions applied on the noncontrollable coefficients, emphasized in Figure 2 legend, and the stochastic disturbances added to the endogenous variables, stressed in Figure 3 legend. The intervals of stochastic distributions shown in Table 4 are the maximum supported for the Monte Carlo converged solutions.

The calibrated parameters and the stochastic disturbances range introduced to the noncontrollable parameters, represented by their minimum and maximum parameters, characterize the mean tendency and the shock dispersion amplitudes, respectively. These dispensing intervals emphasize the acceptable variabilities of the uncontrollable parameters in the convergence of the Monte Carlo realizations introduced in the simulations, in which each parameter within that range generates one stable bifurcation solution. The calibrated parameter ${\mathsf{\gamma }}_1=-0.0738184$ characterizes the mean impact of the real interest rate on the GDP equation in the Dynamic System (32), its minimum is the order of ${{\mathsf{\gamma }}_1}_{min}=-0.227750$, and its maximum is the order of ${{\mathsf{\gamma }}_1}_{max}=0.072245$. Thus, we estimated the variability range for this coefficient as

$$\left[{\displaystyle \frac{(-0.227750-(-0.0738184\left)\right)}{(-0.0738184)}};{\displaystyle \frac{(0.072245-\left(-0.0738184\right))}{(-0.0738184)}}\right]{\mathsf{\gamma }}_1=\left[2.08527;-1.97860\right]{\mathsf{\gamma }}_1$$

(39)

We observe in the Relation (39) that the ranges of variation amplitudes for lower and up values acceptable for ${\mathsf{\gamma }}_1$ have to be in the following interval around the ${\mathsf{\gamma }}_1$: $\left[2.08527;-1.97860\right]{\mathsf{\gamma }}_1=\left[-0.153931;0.146057\right]$. This is the acceptable variability range for ${\mathsf{\gamma }}_1$; therefore, considering the correct economic point of view, to obtain consistent solutions, we need to impose negative values for ${\mathsf{\gamma }}_1$ within the intervals specified above. Thus, we neglect the possible interval of positive values, $[0.0; 0.146057]$, which generates a stable bifurcation solution, but this has a positive effect on real interest rates and GDP, which contradicts economic theory.

Therefore, we conjecture here that the variability of ${\mathsf{\gamma }}_1$, either below or above its calibrated value, is similar the situations to which we keep ${\mathsf{\gamma }}_1$ equal to the calibrated value, making the actual interest rate decrease or increase in the expected change proportion of ${\mathsf{\gamma }}_1$, respectively, in the ranges $[{\mathsf{\gamma }}_1-0.153931; {\mathsf{\gamma }}_1+0.0738184$]; i.e., $[{\mathsf{\gamma }}_1-0.153931; 0]$; neglecting the band of positive oscillations of ${\mathsf{\gamma }}_1$.

For example, we calculate the average actual interest index for the empirical data period (from January 1998 to December 2018), which is $1.152795$ ($15.27\%$). With this data, we can now estimate the upper and low limits of stochastic variability caused by ${\mathsf{\gamma }}_1$. A positive variability on ${\mathsf{\gamma }}_1$ (i.e., a decrease in negative module γ₁) causes a diminishing in the interest rate variability. Then, if ${\mathsf{\gamma }}_1$ trends to zero, the decrease in the average of the real interest index, taking the mean of the positive change in ${\mathsf{\gamma }}_1$, between ${\mathsf{\gamma }}_1$ and upper limit is ($0-0.0738184)/2=-0.0369092$, what produces variability in the mean real interest rate, of up to $1.152795-0.0369092\times 1.152795=1.09639958$ ($9.63\%$). Likewise, taking the average increase in negative module ${\gamma }_1$, changing from −0.0738184 up to the lower limit, $-0.153931$, i.e., ($(-0.153931+(-0.0738184\left)\right)/2=-0.1138747$) we have a mean change in the real interest rate of ($1.152795-(-0.1138747\times 1.152795))=1.02152 (2.52\%$), which may also possible, which allow stable bifurcation solutions.

Therefore, in the example above, a variability in ${\mathsf{\gamma }}_1$, ranging in $- 0.11387\le {\mathsf{\gamma }}_1\le -0.036909$, is similar to a mean variability in the real interest index ($\mathrm{R}\mathrm{I}\mathrm{I}$) of $2.52\mathrm{\%}\le \mathrm{R}\mathrm{I}\mathrm{I}\le 9.63\mathrm{\%}$, within the context of the identifications established by the estimates of Monte Carlo’s achievements.

We organized

Table 5. The negative and positive variabilities related to the respective uncontrollable parameters, as well as the probability intervals for the variabilities of stochastic disturbances, are estimated for the calibrated coefficients.

Negative and Positive VARIABILITIES for Uncontrollable Parameters	Negative Probability	Parameter Probability Between the Calibrated and Zero	Dominant Interval Probability
$\left[2.08527;-1.9786\right]{\mathsf{\gamma }}_1$	$\mathrm{P}\mathrm{r}\mathrm{o}\mathrm{b}\left\{{{\mathsf{\gamma }}_1}_{est}<{\mathsf{\gamma }}_1\right\}=42.8\mathrm{\%}$	$\mathrm{P}\mathrm{r}\mathrm{o}\mathrm{b}\left\{{\mathsf{\gamma }}_1<{{\mathsf{\gamma }}_1}_{est}<0\right\}=57.2\%$	$\mathrm{P}\mathrm{r}\mathrm{o}\mathrm{b}\left\{{{\mathsf{\gamma }}_1}_{est}<0\right\}=100\mathrm{\%}$
$\left[-4.3046; 4.8309\right]{\gamma }_2$	$\mathrm{P}\mathrm{r}\mathrm{o}\mathrm{b}\left\{{{\mathsf{\gamma }}_2}_{est}<0\right\}=21.4\%$	$\mathrm{P}\mathrm{r}\mathrm{o}\mathrm{b}\left\{0<{{\mathsf{\gamma }}_2}_{est}<{\mathsf{\gamma }}_2\right\}=20.7\%$	$\mathrm{P}\mathrm{r}\mathrm{o}\mathrm{b}\left\{0<{{\mathsf{\gamma }}_2}_{est}\right\}=78.6\%$
$\left[1.3506;-1.4421\right]{\mathsf{\mu }}_1$	$\mathrm{P}\mathrm{r}\mathrm{o}\mathrm{b}\left\{{{\mathsf{\mu }}_1}_{est}<{\mathsf{\mu }}_1\right\}=59.5\mathrm{\%}$	$\mathrm{P}\mathrm{r}\mathrm{o}\mathrm{b}\left\{{\mathsf{\mu }}_1<{{\mathsf{\mu }}_1}_{est}<0\right\}=20.0\%$	$\mathrm{P}\mathrm{r}\mathrm{o}\mathrm{b}\left\{{{\mathsf{\mu }}_1}_{est}<0\right\}=79.5\mathrm{\%}$
$\left[1.2362;-1.2809\right]{\mathsf{\mu }}_2$	$\mathrm{P}\mathrm{r}\mathrm{o}\mathrm{b}\left\{{{\mathsf{\mu }}_2}_{est}<{\mathsf{\mu }}_2\right\}=58.8\mathrm{\%}$	$\mathrm{P}\mathrm{r}\mathrm{o}\mathrm{b}\left\{{\mathsf{\mu }}_2<{{\mathsf{\mu }}_2}_{est}<0\right\}=41.2\%$	$\mathrm{P}\mathrm{r}\mathrm{o}\mathrm{b}\left\{{{\mathsf{\mu }}_2}_{est}<0\right\}=100\mathrm{\%}$
$\left[-2.0781;2.1453\right]{\mathsf{\theta }}_1$	$\mathrm{P}\mathrm{r}\mathrm{o}\mathrm{b}\left\{{{\mathsf{\theta }}_1}_{est}<0\right\}=16.4\mathrm{\%}$	$\mathrm{P}\mathrm{r}\mathrm{o}\mathrm{b}\left\{0<{{\mathsf{\theta }}_1}_{est}<{\mathsf{\theta }}_1\right\}=30\%$	$\mathrm{P}\mathrm{r}\mathrm{o}\mathrm{b}\left\{0<{{\mathsf{\theta }}_1}_{est}\right\}=83.6\mathrm{\%}$
$\left[-2.6407;-1.8217\right]{\mathsf{\theta }}_2$	$\mathrm{P}\mathrm{r}\mathrm{o}\mathrm{b}\left\{{{\mathsf{\theta }}_2}_{est}<{\mathsf{\theta }}_2\right\}=54.2\mathrm{\%}$	$\mathrm{P}\mathrm{r}\mathrm{o}\mathrm{b}\left\{{\mathsf{\theta }}_2<{{\mathsf{\theta }}_2}_{est}<0\right\}=45.8\mathrm{\%}$	$\mathrm{P}\mathrm{r}\mathrm{o}\mathrm{b}\left\{{{\mathsf{\theta }}_2}_{est}<0\right\}=100\mathrm{\%}$
$\left[0.8304;-0.7681\right]{\mathsf{\sigma }}_1$	$\mathrm{P}\mathrm{r}\mathrm{o}\mathrm{b}\left\{{{\mathsf{\sigma }}_1}_{est}<{\mathsf{\sigma }}_1\right\}=55.2\mathrm{\%}$	$\mathrm{P}\mathrm{r}\mathrm{o}\mathrm{b}\left\{{{\mathsf{\sigma }}_1<{\sigma }_1}_{est}<0\right\}=24.4\mathrm{\%}$	$\mathrm{P}\mathrm{r}\mathrm{o}\mathrm{b}\left\{0<{{\mathsf{\sigma }}_1}_{est}\right\}=79.6\mathrm{\%}$
$\left[0.4711;-0.4633\right]{\mathsf{\sigma }}_2$	$\mathrm{P}\mathrm{r}\mathrm{o}\mathrm{b}\left\{{{\mathsf{\sigma }}_2}_{est}<{\mathsf{\sigma }}_2\right\}=54.5\%$	$\mathrm{P}\mathrm{r}\mathrm{o}\mathrm{b}\left\{{{{\mathsf{\sigma }}_2<\sigma }_2}_{est}<0\right\}=45.3\mathrm{\%}$	$\mathrm{P}\mathrm{r}\mathrm{o}\mathrm{b}\left\{{{\mathsf{\sigma }}_1}_{est}<0\right\}=100\mathrm{\%}$
$\left[-0.5871;0.5955\right]{\mathsf{\delta }}_1$	$\mathrm{P}\mathrm{r}\mathrm{o}\mathrm{b}\left\{{{\mathsf{\delta }}_1}_{est}<0\right\}=28.8\%$	$\mathrm{P}\mathrm{r}\mathrm{o}\mathrm{b}\left\{0<{{\mathsf{\delta }}_1}_{est}<{\mathsf{\delta }}_1\right\}=17\%$	$\mathrm{P}\mathrm{r}\mathrm{o}\mathrm{b}\left\{0<{{\mathsf{\delta }}_1}_{est}\right\}=71.3\mathrm{\%}$

, shown below. In that table, we present in its first column the variability range estimated for all uncontrollable parameters calibrated. From there, we can analyze the variability intensity that they can accept to generate stable bifurcation solutions in a similar way to Equation (38) for ${\mathsf{\gamma }}_1$. In Table 5, we also show the probability intervals of the negative and positive variabilities related to all uncontrollable parameters generated by the stochastic disturbances estimated on the calibrated coefficients, i.e., ${{\mathsf{\gamma }}_1}_{est}$, ${{\mathsf{\gamma }}_2}_{est}$, ${{\mathsf{\mu }}_1}_{est}$, ${{\mathsf{\mu }}_2}_{est}$, ${{\mathsf{\theta }}_1}_{est}$, ${{\mathsf{\theta }}_2}_{est}$, ${{\mathsf{\sigma }}_1}_{est}$, ${{\mathsf{\sigma }}_2}_{est}$, and ${{\mathsf{\delta }}_1}_{est}$.

When imposing stochastic shocks on the coefficients of noncontrollable impacts and finding the bifurcated solutions (stable), defining the shock bands that yield the signs indicated by macroeconomic theory is convenient. Despite all stochastic noncontrollable coefficients adjusted by the procedure described in Section 4.3.2, allowing solutions to be stable and generating the convergence for the endogenous variables estimates, it is convenient to use only the one that satisfies the macroeconomic concepts. Thus, proceeding similarly to the example of the forecast, it was possible to induce the variabilities range of the uncontrollable coefficients, choose the feasible coefficients with macroeconomic theory, and associate them with the consistent variabilities for the independent variables, as designed by the macroeconomic concepts. Therefore, Table 5, in columns two to four, shows the variability band amplitudes for all uncontrollable coefficients, discriminated by positive and negative ranges. This table gives the range estimates of the coefficients’ variabilities in percentages of estimated stochastic disturbances below and above the corresponding calibration coefficients. Remember that these bands of the coefficients’ variabilities characterize the bands of the perturbations accepted in converging the stable bifurcated solutions. Most of the uncontrolled coefficients presented stabilities for feasible solutions, according to economic theory, in extensive bands within the expected signal for the coefficients, as Table 5 shows. Nevertheless, as can also be seen in this table, we have identified perturbation bands accepted in the bifurcated convergence solutions that differ from the expected signal for the coefficients; however, these bands are quite contracted. In synthesis, as the macroeconomic theory suggests, we will select only the solutions that attain the correct signs.

According to the macroeconomic theory, we consider the stochastic noncontrollable parameters included in the feasible stochastic band obtained in the perturbation process, based on the extensive argumentation stressed in Section Calibration of the Stochastic Dynamic Model Under Stochastic Bifurcation, and neglecting all uncontrollable parameters, all ranges that do not satisfy the macroeconomics argumentations presented in Section 3.1 and Section 4.3.1.

For the parameter ${\mathsf{\gamma }}_1$, we expect a negative sign. Thus, we constrain the last Table 5 column that, in the process of generating the stable bifurcations simulation, accepted only ${\mathsf{\gamma }}_1$ negative values. As can be observed, in the last Table 5 column, 100% of the stable bifurcation solutions found are in the negative range. At the same time, the parameter ${\mathsf{\gamma }}_2$ can be ${\mathsf{\gamma }}_2\lessgtr 0$. As explained in Section 3.1.5, it can be positive for developed economies but negative for developing economies (EMEs). Then, in that case, as in the last Table 5 column, 78.6% of the stable bifurcation solutions found were with negative stochastic coefficients, and only 21.4% were with positive coefficients. As we used Brazilian economy data, an EME, it is natural that its macroeconomic structure is more compatible with the behavior of other EMEs while also accepting the functional structure of a developed economy (details in Section 3.1.5).

The parameter ${\mu }_1$ is the output gap impact on the short-run nominal interest rate. Therefore, from the arguments presented in Section 3.1.3, the more probable sign for ${\mu }_1$ is negative. As shown in the last Table 5 column, 79.5% of the stable bifurcation solutions found were with negative stochastic coefficients, and only 20.4% were with positive coefficients. Thus, we discard the positive band of ${\mu }_1$ identified in Table 5. The coefficient ${\mu }_2$ captures the effect of the differential between inflation and the inflation target on the short-run nominal interest rate. In the last Table 5 column, 100% of the stable bifurcation solutions found were with ${\mu }_2$ negative stochastic coefficients, entirely consistent with the correct view.

The parameter ${\sigma }_1$ can be as ${\sigma }_1\gtrless 0$, an uncontrolled impact parameter of the output gap on the inflation variation, which probably can be negative for economies in development (EMEs), as explained in Section 3.1.2. In the last Table 5 column, 83.6% of the stable bifurcation solutions found were with negative stochastic coefficients, and only 16.4% were with positive coefficients. Thus, we discard the positive band of ${\sigma }_1$ identified in Table 5. While ${\sigma }_2$ can also be ${\sigma }_2\gtrless 0$, an uncontrolled impact parameter of the exchange rate effect on the inflation variation, which can be negative for economies for EMEs, also explained in Section 3.1.2. In the last Table 5 column, 100% of the stable bifurcation solutions found were with ${\sigma }_2$ negative stochastic coefficients, entirely consistent with the correct view.

The parameter ${\delta }_1$ positively impacts the real Exchange rate on itself, as explained in Section 3.1.4. All the stochastic coefficients generated had an oscillating range around the respective uncontrollable parameter; in a way, as in the last Table 5 column, 71.3% of the stable bifurcation solutions found were with positive stochastic coefficients (correct sign waited, and only 28.7% were with negatives coefficients. Therefore, we discard the negative band of ${\delta }_1$ identified in Table 5.

The parameter ${\mathsf{\theta }}_1$ directly affects the real public sector net debt. This uncontrollable parameter can either positively or negatively affect real public debt (DLSP), as its effect is influenced by domestic and international interest rates, inflation, both domestic and global and the economy’s growth rate, as explained in Section 3.1.1. According to the last Table 5 column, the more probable sign for ${\mathsf{\theta }}_1$ is positive, as about 83.6% of the stable bifurcation solutions found had positive stochastic coefficients, and only 16.4% had negative coefficients. However, in that case, we use all stochastic bands of ${\mathsf{\theta }}_1$ simulated, including both the positive and negative ranges, since both are possible.

Finally, the parameter ${\mathsf{\theta }}_2$ impacts real seigniorage income on the real public sector net debt. As explained in detail in Section 3.1.1, its sign depends on how it is accounted for, which may vary from country to country. Its sign must be negative in the context of the Brazilian economy. According to the last Table 5 column, the more probable sign for ${\mathsf{\theta }}_2$ is positive, involving 100% of the stable bifurcation solutions found, inducing us to use all range stochastic curves calibration.

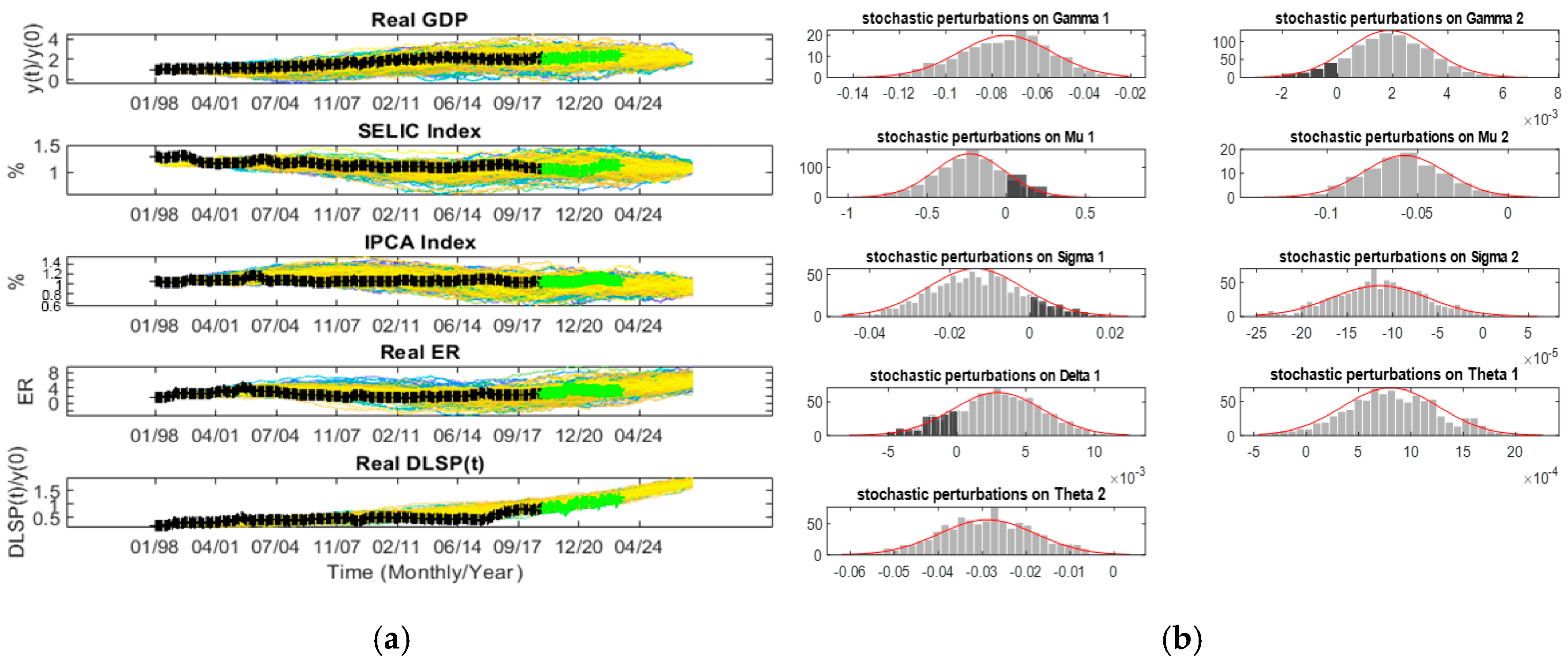
Figure 7a presents the two hundred Mont-Carlo realizations predicted for all endogenous variables, with the use of simultaneously additional shocks, in the form of random walk, in the endogenous variables and shocks in the parameters of noncontrollable impacts, maintaining just the selected ranges of perturbations feasible, discriminated by the procedure explains in the above paragraphs. Figure 7a indicates that the estimated curves simulate a wide range of curve evolutions that can cover all possible forecast processes for all endogenous variables.

It is observed in the histograms in Figure 7b that all bands of stochastic disturbances for the noncontrollable parameters followed the consistent variability intervals, as shown in Table 5. To guarantee random generations based on a normal distribution, some of the range of stochastic disturbances of some parameters overlapped small non-feasible bands (bands marked as black) according to the abovementioned criteria. However, for the case of the inconsistent stochastic coefficients, as explained above, they were not used in the estimates of the bifurcated solutions presented in Figure 7a, whose calculations were eliminated by programming flags.

From the estimations shown in Figure 7a, we will determine all annual growth rates forecasting for the endogenous variables.

Table 6. Ranges of annual GDP growth rates variability forecasted for all endogenous variables, for the period of 2019–2026.

Year	Interval of Annual Growth Rates (%)	Mean Annual Growth Rate (%)	Empirical Annual Growth Rate Used as Back Tests (%)
Real GDP
2019/January–2019/December	$\left[-7.389\%; 10.914\%\right]$	$1.865\mathrm{\%}$	$1.140\%$
2020/January–2020/December	$\left[-6.670\%; 10.206\%\right]$	$2.174\mathrm{\%}$	$-3.880\%$
2021/January–2021/December	$\left[-6.973\%; 11.978\%\right]$	$2.614\mathrm{\%}$	$4.600\%$
2022/January–2022/December	$\left[-7.409\%; 12.967\%\right]$	$2.538\mathrm{\%}$	$2.900\%$
2023/January–2023/December	$\left[-8.273\%; 11.793\%\right]$	$2.799\mathrm{\%}$	$2.900\%$
2024/January–2024/December	$\left[-7.239\%; 11.580\%\right]$	$2.517\mathrm{\%}$
2025/January–2025/December	$\left[-6.413\%; 12.339\%\right]$	$3.301\mathrm{\%}$
2026/January–2026/December	$\left[-6.887\%; 10.871\%\right]$	$2.653\mathrm{\%}$
Nominal SELIC Index
2019/January–2019/December	$\left[-3.119\%; 5.921\%\right]$	$1.380\mathrm{\%}$	$-0.600\%$
2020/January–2020/December	$\left[-3.157\%; 5.422\%\right]$	$1.174\mathrm{\%}$	$-1.750\%$
2021/January–2021/December	$\left[-2.698\%; 4.779\%\right]$	$0.949\mathrm{\%}$	$4.750\%$
2022/January–2022/December	$\left[-3.386\%; 4.898\%\right]$	$0.919\mathrm{\%}$	$4.850\%$
2023/January–2023/December	$\left[-3.473\%; 6.238\%\right]$	$1.497\mathrm{\%}$	$-1.000\%$
2024/January–2024/December	$\left[-3.207\%; 5.570\%\right]$	$1.178\mathrm{\%}$
2025/January–2025/December	$\left[-4.640\%; 7.522\%\right]$	$1.272\mathrm{\%}$
2026/January–2026/December	$\left[-4.263\%; 7.143\%\right]$	$1.602\mathrm{\%}$
Nominal IPCA Index
2019/January–2019/December	$\left[-4.382\%; 6.917\%\right]$	$0.828\mathrm{\%}$	$0.530\%$
2020/January–2020/December	$\left[-4.457\%; 6.635\%\right]$	$1.958\mathrm{\%}$	$0.246\%$
2021/January–2021/December	$\left[-2.638\%; 6.724\%\right]$	$2.318\mathrm{\%}$	$5.824\%$
2022/January–2022/December	$\left[-2.368\%; 8.221\%\right]$	$3.034\mathrm{\%}$	$-4.600\%$
2023/January–2023/December	$\left[-2.725\%; 7.961\%\right]$	$2.524\mathrm{\%}$	$-1.030\%$
2024/January–2024/December	$\left[-2.027\%; 8.021\%\right]$	$3.332\mathrm{\%}$
2025/January–2025/December	$\left[-3.320\%; 8.249\%\right]$	$2.439\mathrm{\%}$
2026/January–2026/December	$\left[-2.629\%; 5.722\%\right]$	$1.986\mathrm{\%}$
Real Exchange Rate
2019/January–2019/December	$\left[-13.709\%; 20.229\%\right]$	$3.992\%$	$4.437\%$
2020/January–2020/December	$\left[-\mathrm{14,707}\%; 22.946\%\right]$	$1.988\%$	$22.597\%$
2021/January–2021/December	$\left[-12.716\%; 18.124\%\right]$	$2.336\%$	$3.445\mathrm{\%}$
2022/January–2022/December	$\left[-14.049\%; 16.708\%\right]$	$2.016\%$	−6.286%
2023/January–2023/December	$\left[-13.140\%; 16.775\%\right]$	$1.603\%$	−7.976%
2024/January–2024/December	$\left[-14.789\%; 19.130\%\right]$	$2.114\%$
2025/January–2025/December	$\left[-13.982\%; 17.815\%\right]$	$1.985\%$
2026/January–2026/December	$\left[-15.062\%; 20.324\%\right]$	$3.168\%$
Real DSLP rate
2019/January–2019/December	$\left[-13.220\%; 17.380\%\right]$	$3.111\%$	$8.291\%$
2020/January–2020/December	$\left[-\mathrm{11,208}\%; 17.629\%\right]$	$4.770\%$	$4.292\%$
2021/January–2021/December	$\left[-7.883\%; 17.273\%\right]$	$4.188\%$	$16.796\mathrm{\%}$
2022/January–2022/December	$\left[-8.274\%; 14.801\%\right]$	$3.753\%$	6.857%
2023/January–2023/December	$\left[-10.675\%; 16.675\%\right]$	$4.046\%$	5.570%
2024/January–2024/December	$\left[-12.248\%; 18.188\%\right]$	$3.287\%$
2025/January–2025/December	$\left[-10.457\%; 15.649\%\right]$	$2.731\%$
2026/January–2026/December	$\left[-8.126\%; 16.372\%\right]$	$4.152\%$

below stresses the interval values of the variabilities for all endogenous variables, characterized by their minimum, maximum, and mean. In that table, the minimum and maximum represent the extremist values of the distribution range and the average values (the most probable value of each distribution).

The variabilities in the endogenous variables depend significantly on the positive and negative oscillations on the stochastic innovations, both on parameters and the random walks added to the endogenous variables. These stochastic innovations interfere with the economic process over time, which can cause virtuous or contractionary cycles and can change any perspective determined by the economy’s structure. Generally, these random innovations allow us to simulate an effect set due to crises in the world economy, such as, for example, COVID-19, which lasted from 2020 to 2023, the Russia-Ukraine war, which began in 2022 and continues to this day, as well as economic and/or political crises in the domestic economy. These crises exacerbate the economy’s instability and divert it from its natural process, as determined by its structure. These real-world effects may be simulated by the stochastic innovations introduced in the model and estimated by their behavior. However, we must identify the types of shocks and their intensities in the economic process to calibrate the dynamic model to establish forecasts consistent with the real economy.

Firstly, we emphasize that our primary goal in applying this dynamic stochastic model is to determine the stability conditions of the model when facing introduced stochastic innovations, both in the uncontrolled coefficients and in the addition of a random walk to the endogenous variables. Regardless of the type of stochastic innovation introduced to the model structure, it has specific effects on parameters and macroeconomic variables, which are then propagated to all other endogenous model variables. Therefore, precisely, due to this dynamic, the more important thing to do is to estimate the chocks’ ranges for which the model maintains its stability consistently with the macroeconomic theory, i.e., determine the intervals for the uncontrolled parameters and the random walk amplitudes, in which the model structure may be possible of forecasts.

We now analyze the forecasted growths for the Brazilian economy (GDP) that had a satisfactory confluence, in mean terms, with the backtests’ growth rates, except for those subjected to the intensive effect of COVID-19 (2020 and 2021). In mean terms, the GDP growth rates’ forecasts converge to the realized backtest data for 2019, 2022, and 2023, stressing a consistent evolution process over the forecast period (from 2019 to 2026), with growth rates oscillating in the forecast period in the range 1.86% to 3.30%, with a mean relatively higher than of that emphasized by the backtests, respectively, 2.55% and 1.53% per year. These forecasted results are similar to those presented by the Brazilian economy in recent years.

Relative to the nominal interest rate index (SELIC), a variable established by government agents with a base in expected inflation, the predictions evolved relatively out of alignment with the backtest data, essentially from 2020 to 2023. However, as argued previously, interest rate implementation policies in Brazil have been inappropriate since 2016, when the SELIC reached a very high level. Since 2017 (following a very high level reached by SELIC in 2016), Bacen implemented an expansionist policy to mitigate the effects of the lack of control in the productive sector of the economy due to the political crisis in the country; however, this process was conducted without harmony between the macroeconomic variables of the economic process.

The implemented expansionary monetary policies aimed at resuming economic growth, thereby sustaining an unsustainable credit and consumption expansion cycle. The interest rates decreased considerably from 2017 onwards, reaching a level never seen before in Brazil of 2%, even during the midst of the COVID-19 pandemic crisis. In this context, where economic policies aimed solely at increasing production in an expansionist process, there was an intense mismatch in the Brazilian economic process that intensified during the COVID-19 pandemic, with substantial effects on the production chain and the job market, inducing a drastic increase in inflationary levels. Starting in 2020, to contain this disjointed process, the government raised interest rates considerably (8.9% in 2021, 13.85% in 2022, and 11.75% as expected in 2023) to contain the inflationary process and reorganize the production chain and the labor market. The disjointed evolution of the SELIC context is illustrated by the fluctuations in the backtest data of growth rates from 2019 to 2023, which exhibit significant increases and decreases. However, the forecast SELIC growth rates evolve in a nearly constant manner, with a mean growth rate that is very similar to the backtest growth rates (the forecasted mean is 1.246% per year, and the backtest growth rate is 1.25% per year). The forecast results suggest that the political process governing interest rates in the Brazilian economy could be better managed, with less impact on all macroeconomic variables and fewer consequences for the country’s social and industrial processes.

This disjointed context imposed on the nominal SELIC index affects the integrated macroeconomic variables similarly, such as the IPCA index, the exchange rate (ET), the GDP growth rate, and even the public debt (DLSP), which depends heavily on the interest rates established and the exchange rate. Given this context, Table 6 shows that the forecasts for all mean of these endogenous variables evolve gradually, with almost constant growth rates with behaviors similar to the forecasted SELIC growth rates. The observed growth rates, used as backtest data, exhibit behavioral disjointed growth rates, similar to those observed regarding the SELIC growth rates, which are wholly disconnected from a process of gradual evolution.

Relative to the inflation growth rate (IPCA rate), their forecasted growth rate evolves approximately constantly, increasing to generate a mean growth rate of 2.30% per year. In contrast, the growth rates of the data backtest periods are 0.20% per year, significantly less than those forecast by the model. In the same way, the forecasted exchange growth rates also evolve similarly to the SELIC growth rates, at an almost constant rate, which has a mean depreciation rate equal to 2.29% per year, while the backtest data, in the period from 2019 to 2023, cause a depreciation of 6.43% per year. These results align with macroeconomic theory, as the Fisher effect suggests that countries’ currencies with relatively high nominal interest rates tend to depreciate, reflecting expected inflation rates and the risk premium for investors in the country. This effect links exchange rate volatility to variations in interest rates and inflation. Therefore, we can infer a relationship between exchange rate depreciation and the increase in nominal interest and inflation rates, as observed in the forecast results and the backtest data. Following the same logic as the other variables analyzed above, the public debt growth rates (DLSP) predicted for the period from 2019 to 2026 evolve with gradual growth rates, with an average rate of 3.75% per year, while the growth referring to backtest data (from 2019 to 2023), as well as for the other variables, evolves in a disjointed manner, with an average growth rate of 8.36% per year.

Finally, even in times of crisis, the imposition of interest policies with strict and inflexible values can have a negative impact on the entire economic structure, as observed through the analysis presented here. Our forecasts with the dynamic model indicated an interest rate increase since 2019, as seen in Table 6. With these results estimated by the model, we can conjecture that gradually evolving interest policies are a way to solve the negative impacts on the economic process, specifically in the social and industrial aspects. In conclusion, we observe in Table 6 that all growth rates of the endogenous variables used as backtesting (from 2019 to 2023) are included, respectively, in their forecasted intervals, for which the model demonstrated to be stables, facing all kinds of stochastic innovations. Therefore, the dynamic model implemented here demonstrated robustness in all aspects, determining all stable situations under which the dynamic model structure may prevail.

5. Final Considerations

The present work studied the interactions between fiscal and monetary policies in the Brazilian economy, showing how they are interconnected using a macrodynamic differential equations model. We structured a dynamic system comprising five differential equations, representing real GDP, the nominal interest index, the nominal inflation index, the real Exchange rate, and the real public debt. Given that EMEs are exposed to external and/or internal political and/or economic shocks, the proposed macrodynamic model was transformed into a stochastic system. In this stochastic model, we imposed stochastic disturbances on the levels of the non-controllable parameters using normal distributions within the maximum permissible ranges, thereby ensuring convergence of the solutions. We also introduced additive shocks to the endogenous variables, simultaneously with shocks to uncontrolled parameters generated by one-dimensional random walks (1-D) for all five dependent variables.

In the case study for Brazil, we use monthly data from January 1998 to December 2018 to calibrate the dynamic model and forecast the economy’s behavior from January 2019 to December 2026. The Dynamic System calibration identified that the controlled and uncontrolled coefficients of the equation system were consistent with the correct direction, as indicated by the economic analyses. The stochastic effects introduced into the equation model allowed for the identification of the variability intervals for each endogenous variable, within which the dynamic system remains stable, and the shock amplitudes that the Brazilian economy can withstand.

In the backtesting analyses of the forecast results from 2019 to 2023, although some situations occurred with a lack of accuracy confluences between the forecasted annual endogenous variables levels and the corresponding backtest data, generally, the growth rate estimations for those variables demonstrated pleasing confluences between the yearly forecasted growth rates and the backtest growth rates configured for the Brazilian economy.

The lack of confluence that occurred in some situations, among the forecasts and the backtests, due to the Brazilian economy oscillating significantly along the forecast period (from 2019 to 2023) as a function of some structural bottlenecks and due to the strong instability caused by the COVID-19 pandemic, which strongly impacted the Brazilian economy, with significant adverse effects.

The estimates showed that the Brazilian economy did not generate sufficient primary surpluses to reduce public debt significantly. On the contrary, Brazilian public debt has shown constant growth, leading to the understanding that the Brazilian economy is dominated by fiscal dominance.

We can further emphasize that, by imposing shocks on the model in question and transforming the dynamic system into a stochastic one, the effects of these disturbances propagate with greater intensity into the monetary variables: the nominal inflation index, the nominal interest rate index, and the real exchange rate.

In analyzing the impact of short-term interest rates and exchange rates on the GDP growth rate and inflation rate (as estimated in Table 3), we observed that short-term interest rates strongly affect GDP growth negatively, and exchange rate depreciation positively affects it. In contrast, exchange rate depreciation negatively affects inflation.

The stochastically disturbed dynamic model enabled us to simulate atypical economic processes within a thoroughly complex and dynamic context. These simulations enable us to understand the extent of the spreading range, which is determined by the bifurcating stable solutions. In light of that information, we can establish some control over the evolution of the economic process by adjusting the controllable parameters and, through successes and failures, making the necessary political adjustments to the economy. However, a systematic control process can be implemented in the dynamic model, using fuzzy logic, to establish controls on the evolution of the stochastic trajectories of endogenous variables, following pre-established curves defined by economic theory, and to estimate the cost of achieving that goal. We will discuss the use of fuzzy logic in control in future studies.