The Impact of COVID-19 Pandemic on the Jordanian Stock Market Returns Volatility: Evidence from ASE20

Abstract

This research examines the impact of the COVID-19 pandemic on the volatility behavior of Amman Stock Exchange (ASE) returns using ARMA–GARCH-type models for three sub-periods: pre-COVID-19, during COVID-19, and post-COVID-19. The research finds that volatility persistence is significant across all periods, with the pandemic period showing the highest impact of shocks. Bad news has no statistically significant impact on volatility in the pre-COVID-19 period or during the pandemic, while in the post-pandemic period, good news significantly influences volatility. Additionally, there exist notable changes in the autocorrelation and the shock structure of the AR and MA components. Considering these alterations in the asymmetric effects, the AR and MA components suggest significant shifts in market dynamics, investor sentiments, and economic policies in response to pandemic experiences.

1. Introduction

Modeling the volatility of stock market returns is a crucial aspect of economic and financial applications. In recent years, the significance of modeling the volatility of returns has been further highlighted by major global events, such as the COVID-19 pandemic, which brought unprecedented levels of risk and uncertainty into financial markets worldwide. As policymakers reacted to pandemic developments, the need for robust volatility models became even more evident, emphasizing their importance in both academic research and empirical applications. Modeling the volatility of returns for the periods before and after the pandemic crisis is essential to assess whether there has been a shift in stock market dynamics and investor sentiments. Recognizing these important shifts in the stock market is necessary for adapting adequate trading strategies and risk-management practices in response to new market crisis realities.

Given the unprecedented developments in the Jordanian economy during the COVID-19 pandemic, it is important to examine how this severe crisis and the aftermath of the resulting developments impacted the volatility of Amman Stock Exchange (ASE) returns. This research applies the newly established free-float Stock Price Index of the twenty active stocks of the largest companies listed on the Amman Stock Exchange (ASE20). In recent empirical studies on stock market returns volatility, ARMA–GARCH-type models have emerged as the most widely employed methodology (see Appendix A Note 1). These models are highly regarded for their ability to effectively capture periods of both high and low volatility, a common characteristic in financial markets. Indeed, their flexibility in adapting to evolving volatility patterns makes them particularly well-suited to analyzing the dynamic nature of returns volatility in ASE.

By accommodating time-varying variance, ARMA–GARCH models address the complexities associated with changing volatility behavior in times of crisis. Moreover, they are highly effective in anticipating future volatility, a critical aspect of informed financial decision making. With extensions to EGARCH, this research further captures the asymmetric effects of positive and negative shocks on volatility, providing a more accurate reflection of ASE volatility behavior.

It is worth mentioning that investigating the volatility of the returns in ASE using ARMA–GARCH-type models during crises presents several distinct advantages. Jordan’s capital market is characterized by several structural weaknesses, including underdeveloped derivative instruments, low market liquidity, modest trading in bonds, and heightened vulnerability to domestic and external shocks. Therefore, focusing on the ASE with such structural weaknesses allows for a more precise assessment of how domestic factors—such as crises, pandemic events, monetary policy shifts, and fiscal policy reforms—affect returns volatility. Understanding these dynamics is crucial for predicting market reactions to future events, providing significant insights for both domestic and international institutional investors and fund managers with an interest in frontier and emerging markets. Additionally, this research, which is based on a single market index, establishes benchmarks that facilitate comparisons with other emerging and developed markets. Such comparisons offer a deeper understanding of how domestic factors influence volatility across different financial market contexts, contributing to a more comprehensive global perspective on market behavior.

The application of ARMA–GARCH-type models entails a simultaneous estimation of the mean equation for market returns and the conditional variance equation, which captures the volatility of stock market returns. Within this context, this research aims to model the mean and volatility of stock returns in the ASE market, utilizing the ASE20 index. ARMA–GARCH-type models are employed to examine three distinct sub-periods: the pre-COVID-19 pandemic period, spanning from 1 January 2019 to 19 January 2020; the COVID-19 pandemic period, from 20 January 2020 to 4 November 2020; and the post-COVID-19 pandemic period, from 5 November 2020 to 26 March 2024.

The empirical literature on the ASE market indicates that the use of ARMA–GARCH-type models during times of crisis still underexplored. 11To the best of the authors’ knowledge, no prior study has specifically examined the mean and volatility of stock market returns in the ASE using the ASE20 index employing ARMA–GARCH-type models across three distinct sub-periods. By modeling the volatility of returns over these sub-periods, this study seeks to determine whether the policies implemented by the government in response to the pandemic have altered ASE market dynamics and investor sentiment from their historical patterns. Furthermore, it investigates whether the prolonged closure of trading activities by the government has led to shifts in the behavior of both domestic and international investors.

The rest of the paper is structured as follows. Section 2 presents a literature review. Section 3 outlines the data and details the methodology with the model-building process, and Section 4 provides a summary of the empirical results. Finally, Section 5 offers the conclusion.

2. Literature Review

Numerous earlier studies have investigated how stock markets react to various crises, with almost a consensus that stock market returns volatility tends to increase during crises. Schwert (1989, 1990) revealed that stock returns volatility increases during recessions and crises. Choudhry (1996) investigated the persistence of stock returns volatility in emerging markets before and after the 1987 crash. He employed GARCH-type models and analyzed monthly data from six emerging stock markets. His findings revealed changes in volatility patterns across these markets both before and after the October 1987 crisis. However, these changes were not uniform, suggesting that distinct market factors influenced the volatility in each country. Aggarwal et al. (1999) investigated the drivers of volatility changes in emerging stock markets by employing the GARCH model. Their focus was on understanding whether these drivers of volatility were global or country-specific events. The study revealed high volatility in emerging markets, with significant increases often corresponding to local economic and political crises.

Shin (2005) analyzed the impact of the Asian/Russian crises of the 1990s on stock market volatility in emerging markets. Employing GARCH-type models, he found that the persistence of volatility in emerging markets was significantly higher compared to developed markets. Furthermore, Shin’s research highlighted that while global crises can significantly impact volatility behavior in emerging markets, the specific changes can vary depending on individual market characteristics. Hammoudeh and Li (2008) investigated volatility behavior and persistence in Arab Gulf stock markets. They employed the GARCH model, and their findings revealed high volatility in Arab Gulf markets compared to other emerging markets, potentially explained by oil price fluctuations. In addition, most of the identified volatility spikes were linked to global events, suggesting a greater sensitivity to external factors compared to regional or local events.

Similarly, the recent literature extensively documents that the pandemic, as an unprecedented crisis, has had a profound impact on the stock market. Analyses indicate that much like in past crises, the pandemic’s effects on stock market returns and volatility differ across countries. This variation is likely due to the distinct dynamics of each country’s stock market and the prior experiences of market participants with other crises, according to Baker et al. (2020) and Milcheva (2020, 2021). For example, Yousef (2020) investigated the impact of COVID-19 on stock market volatility for the major G7 stock market indices. Using GARCH-type models, he found that the COVID-19 pandemic had a significant positive impact on the conditional variance for all seven stock indices, indicating that COVID-19 has increased market volatility. He et al. (2020) conducted an empirical analysis of daily return data from stock markets in China, Italy, South Korea, France, Spain, Germany, Japan, and the United States. Their findings indicated that COVID-19 had a negative, yet short-term, impact on these stock markets and that the pandemic led to bidirectional spill-over effects between Asian, European, and United States markets.

Açıkgöz and Günay (2020) analyzed the short- and long-term global economic impacts of the COVID-19 pandemic. They concluded that the pandemic had severe adverse effects on employees, customers, supply chains, and financial markets. These disruptions were expected to lead to a permanent shift in global dynamics. Duttilo et al. (2020), in their study on volatility modeling, examined the impact of the two waves of COVID-19 infections on stock market returns and volatility in Euro-area countries. Utilizing the Threshold GARCH-in-Mean model with exogenous dummy variables, they found that the Euro-area stock markets responded differently to the pandemic as the first wave of infections had a significant impact on the volatility of stock markets in countries with middle–large financial centers, while the second wave notably affected only Belgium’s stock market volatility. Alkayed et al. (2022) studied the impact of COVID-19 on stock market volatility for the BRICS countries using ARCH-type models. The results showed that COVID-19 had a significant positive impact on stock market volatility in Brazil, India, China, and South Africa but an insignificant impact on Russia. Anastasia et al. (2022) investigated the Nigerian stock market’s volatility response to the COVID-19 crisis. Using the EGARCH model, they found that the COVID-19 crisis did not have a leverage effect on the market, suggesting that the market responded identically to both positive and negative news about the pandemic.

From a different perspective, Ramelli and Wagner (2020) analyzed how COVID-19 affected U.S. stock market returns. They found that as news of the outbreak surfaced, returns on firms with lower cash reserves and higher leverage declined more significantly. Marsh and Chan (2020) analyzed the decline in the Dow Jones Industrial Average (DJIA) from 21 February 2020 to the end of March 2020, comparing it to declines during previous market crises. They found that the DJIA experienced a much steeper fall during the COVID-19 pandemic than in past crises. They attributed this significant drop to the widespread uncertainty surrounding the potential impacts of the pandemic. Chang et al. (2020) investigated herding behavior in renewable and fossil fuel energy stock returns across the USA, Europe, and Asia, covering periods of the Global Financial Crisis (2007–2009), the SARS outbreak (2003), and the COVID-19 pandemic (2020). They found that investors, being more sensitive to asset losses, were more exposed to herding behavior during crises, which in turn also had a spillover effect between stocks and countries.

Liu (2022) explored the vulnerabilities within the green financial market, focusing on how the green bond market responded to extreme negative shocks, such as those posed by the COVID-19 pandemic. The study highlighted that the pandemic led to significant fluctuations and negative abnormal returns in the green bond market, with volatility primarily driven by uncertainties in the traditional fixed-income market. Tan and Tuluca (2021) examined how the volatility of the U.S. stock market and its sectors behaved before, during, and after four major crises: The Mexican crisis, the Asian crisis, the Dotcom bubble burst, and the Great Recession. Interestingly, their analysis revealed that the impact of each crisis differed, even though volatility generally increased in the post-crisis period for most events. Brueckner and Vespignani (2021) used daily data from Australia and the US to estimate a vector auto-regression model that characterized the dynamic relationship between COVID-19 infections and stock market performance. Their analysis revealed a significant positive effect of COVID-19 infections on stock market performance in both markets. Jabeen et al. (2022) investigated the impact of the COVID-19 pandemic on global stock markets, emphasizing the contingent effects of both current and previous pandemics on financial markets. Their research underscored that the pandemic severely affected global markets, presenting significant challenges for economists, policymakers, heads of state, international financial institutions, regulatory authorities, and health institutions in managing the long-term effects of the outbreak.

Recent influential studies that provide significant contributions to the broader understanding of global financial markets and enrich the literature on the impacts and responses triggered by the COVID-19 pandemic include the works of Benmelech and Tzur-Ilan (2020), Eichenbaum et al. (2020), Haddad et al. (2021), Acharya et al. (2021), Cortes et al. (2022), and Govindarajan et al. (2022). These studies have provided a comprehensive framework for analyzing the pandemic’s effects on financial markets worldwide. For instance, Benmelech and Tzur-Ilan (2020) documented the behavior of key macro aggregates in the wake of the COVID-19 epidemic. They showed that a unique feature of the COVID-19 recession is that the peak-to-trough decline is roughly the same for consumption, investment, and output. They argued that COVID-19 acts like a negative shock to the demand for consumption and the supply of labor. Cortes et al. (2022) compared the Federal Reserve’s interventions during the subprime and COVID-19 crises, and they found that both reduced disaster risks in domestic equity markets; however, the subprime interventions led to negative spillovers in international markets, whereas the COVID-19 interventions had positive spillovers. The study highlighted the importance of multilateral central bank actions in mitigating global financial risks.

Acharya et al. (2021) estimated the economic value of a COVID-19 vaccine by analyzing the relationship between stock prices and vaccine progress. Their model showed that the value of a cure could represent 5–15% of total wealth, with significant implications for labor supply and asset pricing. The study emphasized the importance of understanding future pandemic risks and the potential value of resolving uncertainty about their frequency and duration. Haddad et al. (2021) investigated the disruptions in debt markets during the COVID-19 crisis. They attributed the quick recovery to the Federal Reserve’s unprecedented actions, particularly its corporate bond purchases.

It is important to mention that this research builds on the foundational work of previous studies on both the broader global level and the single ASE market level. Both this research and the earlier global studies highlight the significant impact of the COVID-19 pandemic on the heightened volatility and the critical role of external factors. While earlier studies employ various broader models and multi-market tools, this research uses ARMA–GARCH-type models to analyze volatility persistence and asymmetry within a single market, providing a micro-level analysis of the impact of the pandemic. This research offers a unique contribution to the understanding of the financial impact of COVID-19. By focusing on ASE, it provides a deeper understanding of how the pandemic altered stock market behavior in Jordan.

Additionally, this research builds on previous studies on the single market (ASE). While these studies have significantly advanced the understanding of volatility in the Jordanian stock market, certain gaps remain, particularly in examining the mean and volatility of stock returns during times of crisis. For example, Al-Rjoub (2004, 2010) and Al-Rjoub and Azzam (2012) observed fluctuating and persistent volatility behavior in the ASE during the 2008–2009 financial crisis. Al Najjar (2016) examined the volatility characteristics of the ASE using GARCH-type models, concluding that symmetric GARCH models effectively captured market characteristics and provided evidence of volatility clustering, while EGARCH results did not support the presence of a leverage effect in ASE stock returns. Similarly, Almahadin and Tuna (2016) studied the volatility behavior of the ASE with a focus on Jordanian banks and identified a positive relationship between risk and return using the GARCH-M model. More recently, Almansour et al. (2022) investigated the impact of various financial factors on companies in the real estate sector listed on the ASE during the COVID-19 pandemic, finding that the pandemic negatively affected stock returns in the real estate sector. These important studies emphasize the need for further investigation into ASE returns volatility, particularly with the application of ARMA–GARCH-type models before and after the COVID-19 pandemic. Indeed, this research provides new insights into the mean and volatility of stock returns in the ASE market utilizing the newly established ASE20 index. The findings of this study are crucial not only for enhancing the understanding of volatility in the Jordanian stock exchange but also for investigating whether the pandemic has shifted ASE market dynamics and investor sentiments from historical norms.

3. Data and Model Building

3.1. Data Definitions

This research utilizes the free-float Stock Price Index of the twenty active shares listed on the Amman Stock Exchange (ASE20) to examine the impact of the COVID-19 pandemic on the volatility behavior of ASE returns. To investigate this impact, the full data set of the ASE20 index is divided into three sub-periods: the pre-pandemic period, which starts on 1 January 2019 and ends on 19 January 2020; the pandemic period, which starts on 20 January 2020 and ends on 4 November 2020; and the post-pandemic period, which starts on 5 November 2020 and continues to 26 March 2024.

Although the COVID-19 virus first emerged in Wuhan, China in late December 2019, Jordanians did not initially perceive it as a significant threat. It was not until the pandemic sub-period began in mid-January 2020 that concerns started to develop. The situation escalated further when the World Health Organization declared COVID-19 a Public Health Emergency of International Concern in January 2020, alongside, more importantly, the emergence of the first COVID-19 cases in Jordan in mid-January 2020. These evolving developments, coupled with the Jordanian government’s enforcement of strict preventative measures, triggered widespread, real concern among Jordanians.

This phase marked an initial shift in public responses, as Jordanians began to recognize the economic, social, and health implications of the pandemic. As the virus spread, fears about its impact on public health, macroeconomic fundamentals, and corporate earnings led to significant instability in the ASE. In response to the escalating situation, the Jordanian government implemented a large-scale, strict lockdown, halting nearly all economic activities to control the virus’s spread. This lockdown resulted in sharp contractions in the economy and a decline in companies’ earnings. To further manage the situation, the ASE Board decided to suspend trading activities in the ASE from 16 March 2020 to 10 May 2020. While necessary, this decision further deepened the economic downturn and intensified market participants’ anxiety about the future performance of the ASE market.

The pandemic sub-period ended in November 2020 when the government decided to fully reopen all sectors after severe lockdowns. This decision marked a significant shift toward normality, allowing all sectors to resume operations at full capacity. It represented a turning point in Jordan’s transition from crisis management to gradual economic recovery.

The ASE20 index is a weighted index that reflects the market capitalization of the twenty most actively traded free-float shares on the ASE. The index is calculated by determining the market value of each company, which is the product of the total number of listed shares, the most recent closing price, and the percentage of free-float shares available for trading. The free-float percentage excludes shares owned by members of the board of directors who hold 5% or more of the company’s shares, as well as shares owned by the government.

The ASE20 index sample includes the following companies: the Arab Bank, the Bank of Jordan, the Housing Bank for Trade and Finance, the Jordan Petroleum Refinery/Jopetrol, the Arab Potash, the Jordan Islamic Bank, the Jordan Ahli Bank, the Cairo Amman Bank, the Etihad Bank, the Capital Bank of Jordan, Jordan Electricity, the Jordan Kuwait Bank, the Arab Jordan Investment Bank, Jordan Duty-Free Shops, Jordan Phosphate Mines, Jordan Telecom, the Safwa Islamic Bank, Alia—Royal Jordanian Airlines, Afaq Energy, and the Invest Bank.

The market capitalization of these companies accounts for approximately 78% of the total market capitalization of the 167 listed companies on the ASE. Additionally, the market value of the free-float shares of these companies represents about 83% of the total free-float value of all listed companies. The ASE20 index was sourced from the ASE market database, and daily returns were computed as continuously compounded returns, i.e., Returns = log (ASE20_t/ASE20_t−1), where the ASE20 is the closing market index at the current day (t) and the previous day (t − 1).

3.2. Data Development

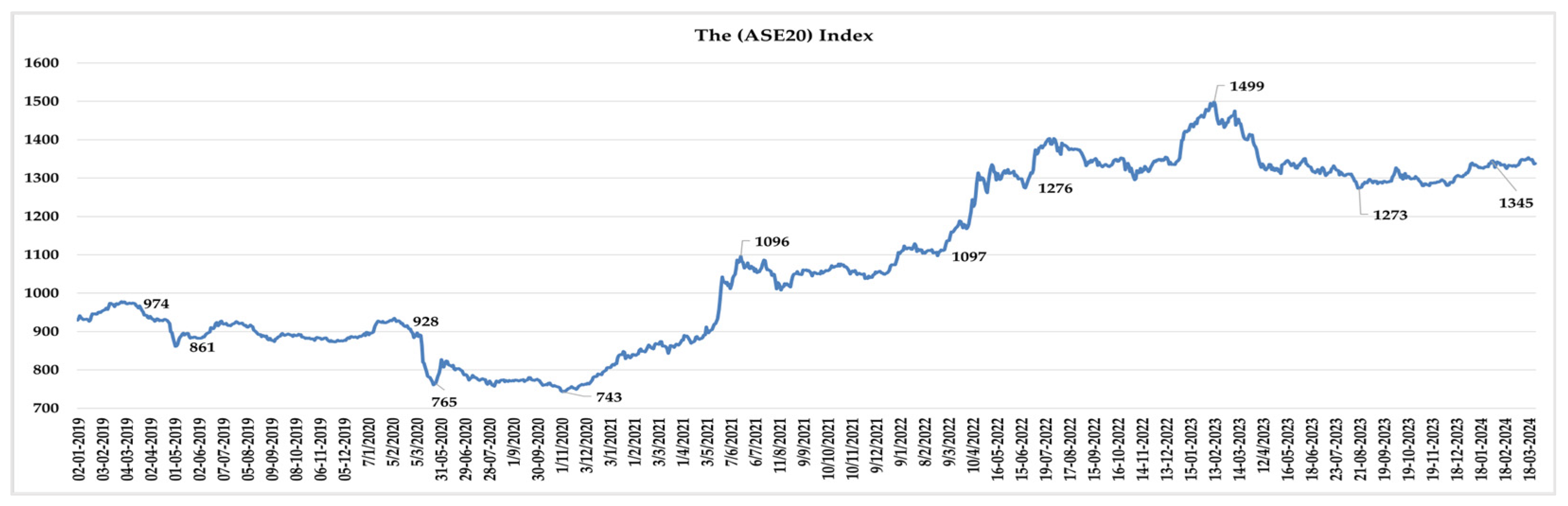
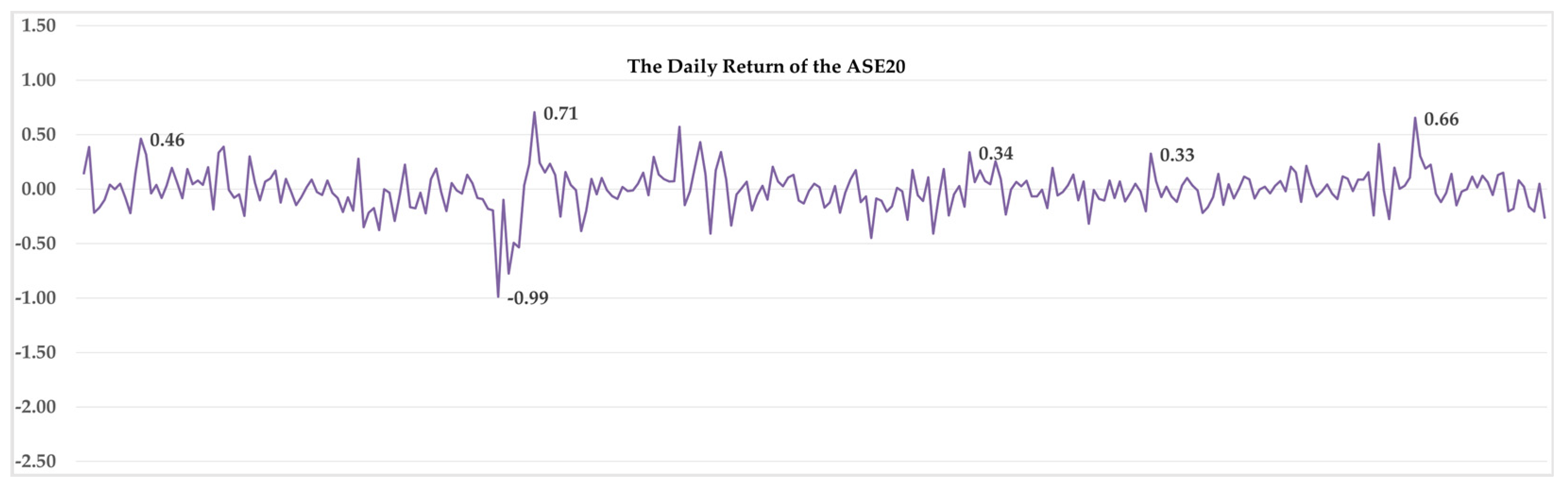
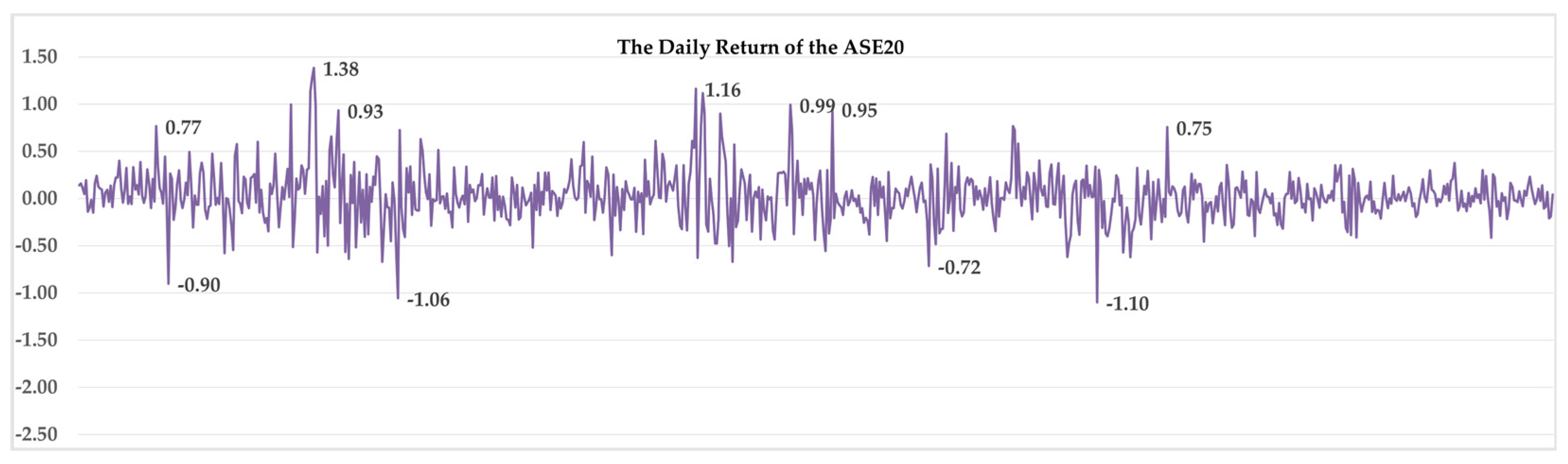
The visual inspection of the daily series of the ASE20 index and the calculated returns series for the full sample period and the three sub-periods individually, which are shown in Figure 1, Figure 2, Figure 3, and Figure 4, respectively, demonstrate the fact that the index and the returns behave differently over the three sub-periods.

As shown in Figure 1, the ASE20 index experienced a stable performance in the pre-pandemic period, with occasional fluctuations. By the beginning of the pandemic period in January 2020, a significant decline was observed in the ASE20 index. Panic and uncertainty about the pandemic’s impact on Jordan’s public health, macroeconomic fundamentals, and companies’ earnings triggered widespread instability across the ASE market. To contain the pandemic’s impacts on the economy, the Jordanian government imposed large-scale and strict lockdowns for nearly all economic sectors, which in turn led to significant Gross Domestic Product contractions and company earnings’ falls.

Following the World Health Organization’s declaration of COVID-19 as a pandemic and the increasing domestic concerns about the virus’s impact on the performance of the ASE, the ASE Board decided to hold trading activities for a long time, from 16 March 2020 to 10 May 2020. Following the closure period, a significant drop occurred in the ASE20 index, reaching new lower levels and reflecting the widespread economic downturn and investors’ anxiety about future expectations of ASE market performance.

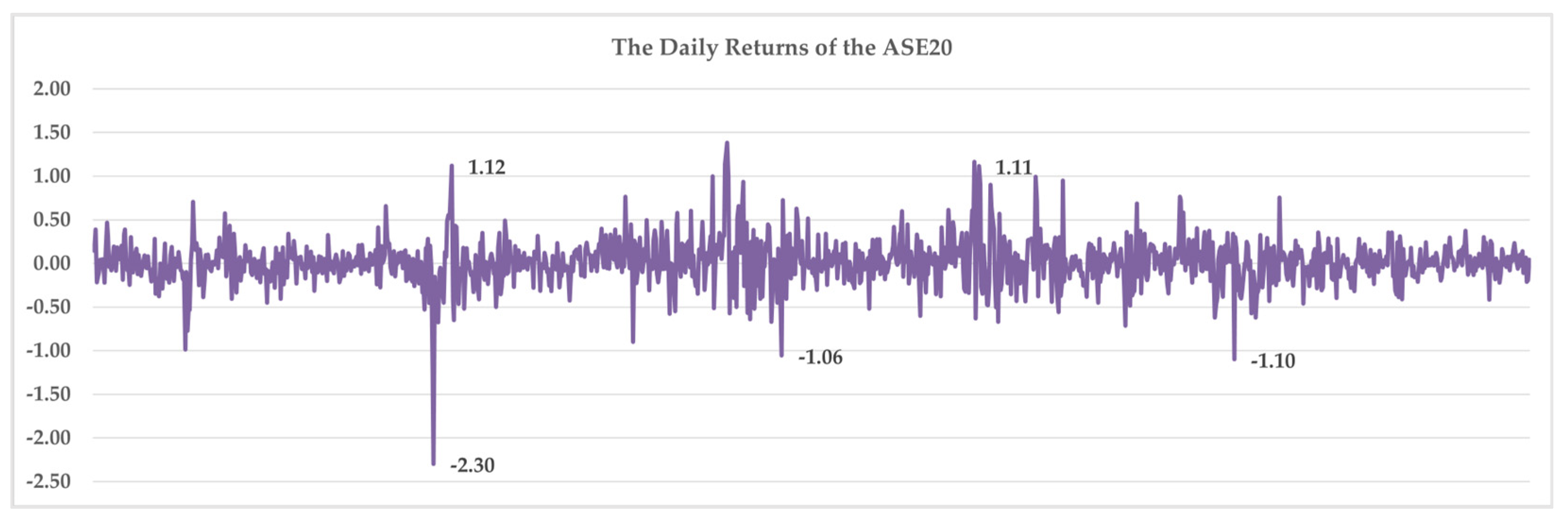
Looking at the daily ASE20 returns, as shown in Figure 2, Figure 3, Figure 4 and Figure 5, we noticed that the returns in the pre-pandemic period appeared to fluctuate within a narrow range, with occasional and minor spikes and dips as investor sentiment was stable, and the overall ASE market conditions remained calm. However, during the pandemic period, as shown in Figure 4, investors in the ASE market faced rapid and large-scale swings in the ASE20 returns. The fluctuations are more pronounced, although they still center around the zero line. This volatility in the ASE20 returns suggested behavior changes in the ASE market in response to the pandemic-related developments.

In essence, the changing pattern of volatility in the ASE20 returns was influenced not only by the uncertainty resulting from pandemic-related developments but also by the significant policy changes implemented by the Jordanian government. For example, the Central Bank of Jordan and the ASE Board had taken unprecedented stimulus measures to support the Jordanian economy and ease any economic and financial market risks. Consequently, investors in the ASE market after the pandemic period regained some confidence in the market’s prospects, driving the ASE20 index up and restraining the swings in the ASE20 returns. The index continues its upward momentum for a long time, reaching 1499 by February 2023.

Moreover, other key trends were observed in ASE market from 2019 to 2023, as shown in

Table 1. Summary of ASE market activity, 2019–2023.

Key Statistics of the ASE	2019	2020	2021	2022	2023
Number of listed companies	191	179	172	170	167
Market capitalization (JOD million)	14,914.8	12,907.8	15,495.7	18,003.8	16,939.2
Value traded (JOD million)	1585.4	1048.8	1963.3	1903.7	1457.0
Average daily trading (JOD million)	6.4	4.9	7.9	7.7	5.9
Market capitalization/GDP (%)	49.7	41.5	49.9	56.0	50.3

. The number of listed companies steadily decreased from 191 in 2019 to 167 in 2023. Market capitalization witnessed a decline in 2020 due to the economic impact of the COVID-19 pandemic. The traded value followed a similar pattern to market capitalization, with a significant drop in 2020. The market capitalization relative to GDP also dropped in 2020, followed by recovery years.

Given the unprecedented developments in Jordan during the pandemic period, it is crucial to examine how this severe crisis impacted the volatility of ASE20 returns. Additionally, it is important to assess whether there has been a shift in ASE market dynamics and investor sentiments as market participants adapt to post-pandemic realities. Equally important is testing whether the extended closure of the ASE market has caused a shift in the behavior of both domestic and international portfolio investors.

3.3. Data and Descriptive Statistics

The statistical analysis commenced by examining the distributional properties of the daily returns of the ASE20 index across the three sub-periods by utilizing the most common descriptive statistics, as presented in

Table 2. Descriptive statistics of the ASE20 return series.

Statistic	Before the Pandemic	During the Pandemic	After the Pandemic
Mean	−0.0000	−0.0014	0.0007
Standard Deviation	0.0044	0.0074	0.0060
Skewness	−0.40	−2.11	0.55
Kurtosis	7.00	18.40	6.32
Jarque–Bera (Probability)	0.000	0.000	0.000

.

The mean of ASE20 returns before the pandemic period registered a value close to zero, indicating almost no return on average for ASE market investors, while during the pandemic time a negative mean of returns (−0.0014) was observed, suggesting, on average, loss. After the pandemic period, the mean of returns switched to positive at 0.0007, indicating a substantial recovery in the ASE market. As for the standard deviation, which measures the volatility of the ASE20 returns around the mean, a low standard deviation (0.0044) was observed for the pre-pandemic period. During the pandemic period, a higher standard deviation was observed (0.0074), indicating a higher volatility in the ASE market. After the pandemic period, the standard deviation decreased to 0.0060 compared to the pandemic period and increased compared to the pre-pandemic period.

Looking at the distributional properties of the daily returns of ASE20 over the three sub-periods, a slightly negative Skewed (−0.40) was shown before the pandemic period, indicating slight asymmetry, with a longer tail on the left side. During the pandemic time, a highly negative skew (−2.11) was observed, suggesting significant asymmetry, with a much longer tail on the left side. Meanwhile, after the pandemic, a moderately positive skew (0.55) was shown, indicating moderate asymmetry, with a longer tail switched to the right side. As for Kurtosis, a high value of 7.00 before the pandemic was shown, indicating a distribution with heavy tails and more outliers. During the pandemic period, Kurtosis increased significantly to 18.40, indicating an even heavier-tailed distribution with more extreme values. Meanwhile, after the pandemic, it decreased but remained high at 6.32. The Jarque–Bera (JB) test for normality aligns with the results indicated by the Kurtosis and Skewness statistics. The JB test confirms that ASE20 returns do not follow a normal distribution.

Thus, we can assert that the ASE20 returns have exhibited the most losses and volatility during the pandemic period, followed by a recovery in the post-pandemic period. Skewness and Kurtosis indicate non-normal distribution throughout all periods, with heavier-tailed distribution and more extreme values observed during the pandemic period.

3.4. Specifications of the Suitable Models

The descriptive statistics and data trends mentioned above provide an initial indication that ARMA–GARCH-type models are well-suited for investigating the mean and volatility behavior of ASE20 returns across the specified sub-periods. This research approach begins by identifying the best-fitting conditional mean equation for the ASE20 return series, which may be an autoregressive (AR) process, a moving average (MA) process, or a combination of both, known as an ARMA process. When an ARCH effect is present, GARCH-type models are jointly estimated with the ARMA model to examine the time-varying conditional variance of the ASE20 return series, a common measure of volatility.

Within ARMA models, it is assumed that lagged values of the return series, as well as current and lagged values of error terms, may provide valuable insights into the behavior of the ASE20 return series. In the ARCH model proposed by Engle (1982), the time-varying conditional variance depends on lags of ARMA squared errors, which represent shocks. Bollerslev’s (1986) GARCH model extends the ARCH framework by allowing the conditional variance to depend on its own lags in addition to lags of ARMA squared errors. 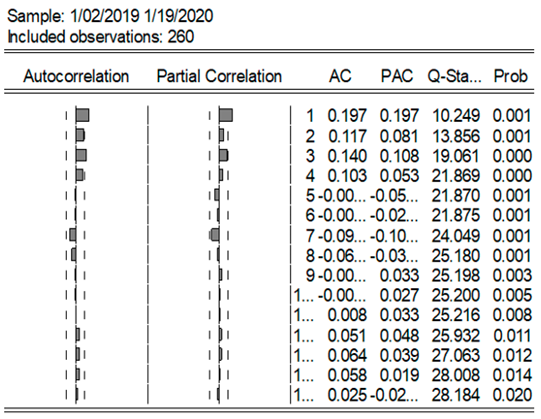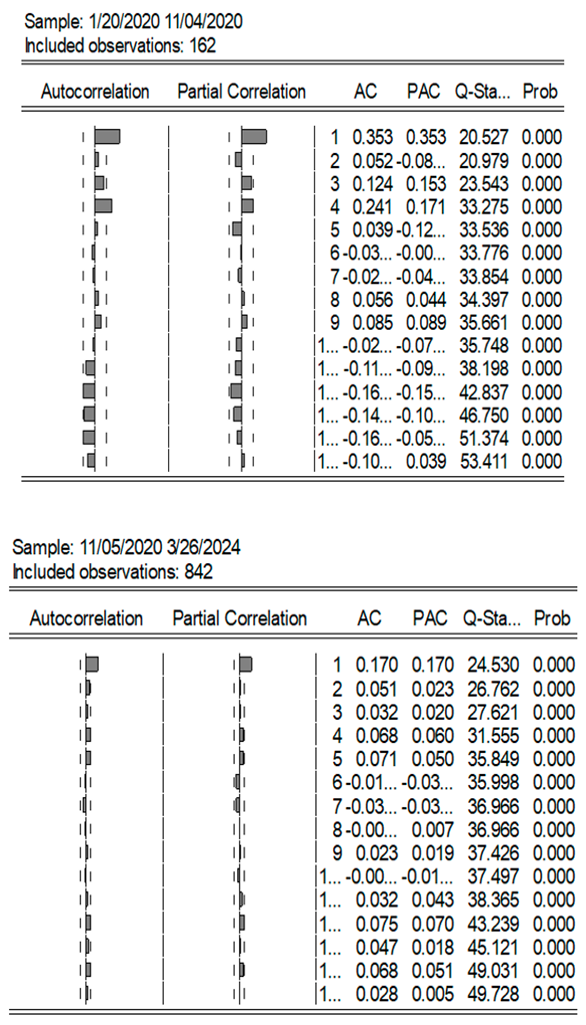To identify the best-fitting conditional mean equation for the ASE20 return series using an ARMA model, we adhered to the methodology outlined by Box and Jenkins (1976). The initial step in this process involves analyzing the Autocorrelation Coefficients (ACs) and the Partial Autocorrelation Coefficients (PACs) of both the ASE20 index and its return series. As illustrated in

Table 3. The Autocorrelation Coefficients (ACs) of the ASE20 index.

Lag	Pre-Pandemic Period	The Pandemic Period	Post-Pandemic Period
1	0.990	0.979	0.995
2	0.977	0.955	0.990
3	0.961	0.931	0.985
4	0.944	0.905	0.980
5	0.926	0.877	0.975
6	0.908	0.848	0.970
7	0.890	0.820	0.965
8	0.873	0.792	0.960
9	0.858	0.763	0.955
10	0.842	0.733	0.950

, the AC of the ASE20 index displays a distinct pattern of slow decay and persistence across all periods, with high values that decrease gradually as lag orders increase. This pattern indicates that the ASE20 index may possess a unit root and exhibit characteristics of a long memory process.

Table 4. Unit root tests for the ASE20 stock index and returns.

Period	ADF	PP
Pre-Pandemic
ASE20 Index	−1.579335	−1.554348
ASE20 Return	−6.85248 *	−17.49846 *
The Pandemic
ASE20 Index	−1.615302	−1.596591
ASE20 Return	−8.722401 *	−8.879428 *
Post-Pandemic
ASE20 Index	−2.428824	−2.402992
ASE20 Return	−30.67277 *	−31.29876 *

Note: the 1% significance levels are denoted by *.

presents the results from the Augmented Dickey–Fuller (ADF) and Phillips–Perron (PP) tests, Dickey and Fuller (1979, 1981), and Phillips and Perron (1988) which align with the findings from the Autocorrelation Coefficients. The null hypothesis of a unit root for the ASE20 index is not rejected at the 1% significance level across all periods, indicating that the ASE20 index series is non-stationary throughout the sub-periods. Conversely, for the ASE20 returns series, the same tests allow to reject the null hypothesis of a unit root at all conventional levels of significance for all sub-periods. It is crucial to ensure the stationarity of the ASE20 return series before modeling its volatility to avoid spurious results. Because the ASE20 return series is stationary, we can proceed and estimate GARCH-type models, thus fulfilling the first condition required for accurate model estimation.

The next step is to determine the best-fitting models for the conditional mean equation of the ASE20 return series for the three sub-periods through the application of an ARMA model. Selecting the appropriate orders for p and q is an essential part of building an ARMA model, and this typically involves many techniques, such as examining again the ACs and PACs, along with the well-known information criteria, like the AIC (Akaike Information Criterion), BIC (Bayesian Information Criterion), or Hannan–Quinn Information Criterion (HQC) (Akaike 1974; Hannan and Quinn 1979).

We have seen that the ASE20 return series is volatile, and the extent of this volatility varies from one period to another, with the highest in the pandemic period. As reported in

Table 5. The ACs and PACs of the ASE20 return series.

Lag	Pre-Pandemic Period		The Pandemic Period		Post-Pandemic Period
	AC	PAC	AC	PAC	AC	PAC
1	0.197	0.197	0.353	0.353	0.170	0.170
2	0.117	0.081	0.052	−0.08	0.051	0.023
3	0.140	0.108	0.124	0.153	0.032	0.020
4	0.103	0.053	0.241	0.171	0.068	0.060
5	−0.00	−0.05	0.039	−0.12	0.071	0.050
6	−0.00	−0.02	−0.03	−0.00	−0.01	−0.03
7	−0.09	−0.10	−0.02	−0.04	−0.03	−0.03
8	−0.06	−0.03	0.056	0.044	−0.00	0.007
9	−0.00	0.033	0.085	0.089	0.023	0.019
10	−0.00	0.027	−0.02	−0.07	−0.00	−0.01

, the ACs and the PACs for the ASE20 return series show a large, positive, significant spike at lag one for the pre- and post-pandemic periods, while all other autocorrelations are, in general, within the 95% confidence limit. However, within the pandemic period, the ACs and the PACs for the ASE20 return series show irregular, significant spikes for different orders (see Appendix A Note 2).

This research does not rely solely on the Autocorrelation Coefficients (ACs) and Partial Autocorrelation Coefficients (PACs) to determine the ARMA model order. Instead, we follow standard econometric procedures for identifying the ARMA model order for the ASE20 return series, incorporating both the Akaike Information Criterion (AIC) and the Hannan–Quinn Criterion (HQC). According to these criteria, the ARMA (1,1) model is chosen for both the pre- and post-pandemic periods, while the ARMA (0,4) model is selected for the pandemic period.

Consequently, for the pandemic period, the mean equation is a moving average model of order four, which implies that the current returns of the ASE20 index are significantly influenced by the recent shocks on the ASE market, i.e., the current ASE20 returns for the pandemic period are captured only by the noise shocks in the ASE market. However, for the pre- and post-pandemic periods, the ARMA (1,1) indicates that the current ASE20 returns are influenced by the immediately preceding value of returns and noise shocks.

The OLS estimation of the single ARMA models for the ASE20 return series is presented in

Table 6. Single ARMA models for the ASE20 return series for the three sub-periods.

Period	Coefficient	Prob.
The pre-pandemic period
AR (1)	0.69	0.00
MA (1)	−0.52	0.00
The pandemic period
MA (1)	0.37	0.00
MA (2)	0.06	0.35
MA (3)	0.07	0.32
MA (4)	0.25	0.00
The post-pandemic period
AR (1)	0.40	0.00
MA (1)	−0.24	0.13

. The stationary conditions associated with the ARMA models are satisfied. As reported in

Table 7. The serial correlation LM tests for the three sub-periods, respectively.

Breusch–Godfrey Serial Correlation Test	F-Statistics	Chi-Square
Pre-pandemic period	0.870	4.409
(p-value)	(0.502)	(0.490)
During the pandemic period	0.380	0.776
(p-value)	(0.684)	(0.678)
The post-pandemic period	1.437	7.195
(p-value)	(0.208)	(0.206)

, the high p-values across all periods indicate that there is no significant autocorrelation up to lag 5. This suggests that the residuals of the model are approximately white noise, implying that the model has adequately captured the ASE20 mean return series.

3.5. Combination of ARMA–GARCH-Type Model Building

Engle (1982) has shown that in the presence of the conditional heteroscedasticity (ARCH effect) of the mean equation, modeling both the mean and the variance of the time series improves the efficiency of the parameter estimates. Thus, in this empirical research, improving ARMA models for the ASE20 return series may be possible through the application of ARMA–GARCH-type models jointly.

The most important step in applying the ARMA–GARCH-type models for assessing the volatility of the ASE20 return series is to test for an ARCH effect in the residuals of the mean equations for the three specified sub-periods. To this end, we estimated the unconditional variance of the residuals from all ARMA models and then applied an ARCH test. The null hypothesis is that there are no ARCH effects up to five lags to account for one trading week. The ARCH test results in

Table 8. Heteroskedasticity tests for the three sub-periods, respectively: ARCH test.

Heteroskedasticity Test	F-Statistics	Chi-Square
Pre-pandemic period	3.585	17.128
(p-value)	(0.000)	(0.000)
During the pandemic period	6.139	26.255
(p-value)	(0.000)	(0.000)
The post-pandemic period	32.884	138.255
(p-value)	(0.000)	(0.000)

provide robust evidence for rejecting the null hypothesis for all periods. Rejecting the null hypothesis is an indication of the existence of ARCH effects in the return series of the ASE20 index for the three sub-periods, which meets the second condition for estimating GARCH-type models.

In this research, GARCH and EGARCH models are employed to study the ASE20 returns volatility in the ASE market for the three sub-periods. The specification of the GARCH model explains this period’s ASE20 return series volatility according to the variance from the last period (the GARCH term) and information about shocks observed in the previous period (the ARCH term). The Exponential GARCH (EGARCH) model introduced by Nelson (1991) enhances the traditional GARCH model by allowing for asymmetric effects of shocks on volatility through the inclusion of an asymmetric response term.

Consequently, the EGARCH model provides a more accurate representation of the response of volatility in the ASE20 return series, as it allows for differentiating between positive and negative shocks. This term is denoted by γ in the variance equation (see Appendix A Note 1). A positive γ (good news) indicates that positive shocks increase volatility more than negative shocks (bad news) of the same magnitude, while a negative γ (bad news) indicates that negative shocks increase volatility more than positive (good news) shocks of the same magnitude.

4. The Empirical Results and Discussion

After considering many specifications of GARCH-type models, this research found that E/GARCH (1,1) is an appropriate fit for the ASE20 return series. The models are estimated using the maximum likelihood method under the assumption of the Generalized Error Distribution (GED) error terms. The GED distribution is applied to account not only for the heavy tails of the ASE20 return series across the three sub-periods but also for its flexibility to adjust for the different tail heaviness of the returns. Accordingly, for the three sub-periods,

Table 9. An estimation of the ARMA–GARCH (1,1) models for the three sub-periods.

Period	Coefficient	Prob.
The Pre-Pandemic Period
AR (1)	−0.50	0.02
MA (1)	0.64	0.00
ARCH TERM	0.14	0.01
GARCH TERM	0.68	0.00
The Pandemic Period
MA (1)	0.20	0.03
MA (2)	−0.10	0.26
MA (3)	0.03	0.69
MA (4)	0.01	0.84
ARCH TERM	0.26	0.00
GARCH TERM	0.68	0.00
Post-Pandemic Period
AR (1)	0.43	0.14
MA (1)	−0.33	0.27
ARCH TERM	0.12	0.00
GARCH TERM	0.85	0.00

shows the ARMA–GARCH coefficient estimates, while

Table 10. An estimation of the ARMA–EGARCH (1,1) models for the three sub-periods.

Period	Coefficient	Prob.
The Pre-Pandemic Period
AR (1)	−0.47	0.049
MA (1)	0.61	0.00
Shocks Term	0.32	0.02
Asymmetric Term	−0.05	0.48
Volatility-Persistence Term	0.83	0.00
The Pandemic Period
MA (1)	0.16	0.05
MA (2)	0.15	0.06
MA (3)	0.03	0.67
MA (4)	0.03	0.69
Shocks Term	0.42	0.00
Asymmetric Term	−0.06	0.41
Volatility-Persistence Term	0.91	0.00
Post-Pandemic Period
AR (1)	0.60	0.00
MA (1)	−0.52	0.03
Shocks Term	0.18	0.00
Asymmetric Term	0.05	0.00
Volatility-Persistence Term	0.97	0.00

shows the ARMA–EGARCH coefficient estimates.

In the results for the variance GARCH equation reported in Table 9, the coefficients of the ARCH and GARCH terms are statistically significant in all periods. Moreover, the sum of the two estimated ARCH and GARCH coefficients for all periods is close to one, indicating that volatility shocks are quite persistent in the ASE market.

More importantly, in the results for the variance EGARCH equation reported in Table 10, this research found that across all periods, the shock terms are positive and statistically significant, with the pandemic period having the highest impact (0.42), which is the result we would expect during this uncertain time. The volatility-persistence terms across all periods are positive, significant, and close to one, confirming the persistence of volatility found from the GARCH model and indicating robust evidence of volatility clustering of the ASE20 returns, with the post-pandemic period having the highest memory process (0.97). These two patterns across all periods suggest that news about volatility from the previous periods has explanatory power for the current volatility of ASE20 return series and that volatility shocks have a long memory process.

Another important fact is that by looking at the sign and the magnitude of the asymmetric parameters in the variance equation of the EGARCH model for the three sub-periods, this research found that the coefficients for pre- and during-pandemic periods are negative, indicating that negative shocks (or bad news) tend to have a larger impact on ASE20 return volatility compared to positive shocks (or good news). However, the asymmetric parameters in these two sub-periods are not statistically significant, implying that ASE20 returns do not provide strong evidence of asymmetry in the impact of past shocks on current volatility. For the period after the pandemic, the asymmetric coefficient switched to positive, and it is statistically significant, indicating a reversal in the asymmetric effect, where positive shocks now impact ASE20 return volatility more than negative shocks.

This shift in the asymmetric component in EGARCH models can be attributed to changes in ASE market dynamics and changes in investors’ sentiments in response to the pandemic crisis. This research suggests that during the pandemic crisis, the ASE experienced high volatility regardless of the direction of market shocks, with investors reacting strongly to both positive and negative news. However, in the post-pandemic recovery phase, investors in the ASE appear to have become more optimistic, leading to a statistically significant, positive, and asymmetric effect.

This shift in market behavior may be attributed to several factors. The optimism that emerged during the recovery period could have been fueled by government stimulus packages and other CBJ interventions, such as interest rate cuts and liquidity provisions, which were implemented during the pandemic. These measures likely provided a cushion against negative shocks, stabilizing the market and encouraging increased trading activity, which in turn contributed to higher volatility. Furthermore, the pandemic may have altered investors’ risk perception. Initially, negative news was seen as a sign of more downturns, resulting in heightened volatility. However, as the markets began to stabilize, positive news started to be perceived as a signal of a strong return to stability and growth. This shift in perception likely led to a powerful impact of positive news on market volatility compared to negative news in the post-pandemic period.

The significant positive asymmetric effect observed in the post-pandemic period suggests a notable shift in investor behavior. Investors have become more sensitive to positive news, reacting more strongly to favorable developments than to negative ones. This heightened response to positive information indicates a growing sense of optimism and confidence in the market’s recovery and future growth prospects.

This shift may reflect a broader change in market sentiment, where investors are more inclined to seek out opportunities for gains, even at the risk of greater volatility. The reduced impact of negative shocks on volatility suggests that investors are less fearful of downturns, possibly because they perceive the worst effects of the pandemic as having passed. This could lead to a more resilient market where negative news is less likely to cause significant disruptions.

Another important outcome is observed in this research related to the signs of AR and MA terms in the ARMA–EGARCH models for the periods before and after the pandemic crisis. The AR (1) term is negative for the pre-pandemic period, but it switched to positive for the post-pandemic period, indicating a shift in the autocorrelation structure from a mean-reverting behavior in volatility to a persistence behavior in volatility. The MA (1) term for the pre-pandemic period is positive, but it switched to negative for the post-pandemic period, indicating a shift in the shock structure from an amplifying effect of past shocks on current volatility to a damping effect of past shocks on current volatility.

The different impacts of the AR and MA coefficients between the pre- and post-pandemic periods suggest again that the ASE20 return series has undergone a significant change in the autocorrelation and shock structures, which can be attributed to changes in ASE market dynamics, changes in investors’ sentiments, and/or changes in economic policies in response to the pandemic crisis.

It is very important to know that recognizing these important changes is crucial for adapting trading strategies and risk-management practices of ASE market participants in response to any future ASE market crises. More specifically, the movements in the estimated models can help investors, risk managers, and policymakers to better understand, forecast, and manage volatility in the ASE market.

As a diagnostic test of the ARMA–EGARCH models, it is worth mentioning that the residuals are free of an extra ARCH effect for different lags, as shown in

Table 11. Heteroskedasticity tests of the ARMA–EGARCH (1,1) models for the three sub-periods.

Heteroskedasticity Test: ARCH
Pre-pandemic period	0.240	0.242
(p-value)	(0.620)	(0.622)
During the pandemic period	1.762	5.245
(p-value)	(0.150)	(0.155)
Post- pandemic period	1.587	15.781
(p-value)	(0.105)	(0.106)

.

While this research provides valuable insights into the volatility of the ASE20 index, its focus on a single market index, the reliance on specific GARCH-type models, and the exclusion of external factors represent limitations that should be acknowledged. These constraints suggest that further research could be developed for a more comprehensive approach by incorporating multiple countries, extending the volatility models, and considering a wider range of influencing factors. The findings from Cortes et al.’s (2022) study on international spillovers can add to this research by exploring whether similar spillover effects of monetary policies to ASE were present and how they may have influenced volatility in Jordan. Moreover, insights from the Fed’s interventions in Cortes et al. (2022), Haddad et al. (2021), and Benmelech and Tzur-Ilan (2020) can be employed to discuss the potential role of international and domestic monetary and fiscal policies in shaping the volatility patterns observed by this research in the ASE. This research could also reinforce the discussion of the importance of stabilizing measures in maintaining investor confidence and reducing volatility in emerging markets like Jordan.

5. Conclusions

The impact of the COVID-19 pandemic on the volatility of the ASE20 returns for three sub-periods is investigated in this research with the application of ARMA–GARCH-type models. Such an investigation helps investors predict market dynamics and sentiment shifts. The ASE20 returns exhibited the most losses and volatility during the pandemic period, followed by a recovery in the post-pandemic period. Skewness and Kurtosis indicate non-normal distribution throughout all periods, with heavier-tailed distribution and more extreme values observed during the pandemic period. The results of the ADF and PP tests indicate that the ASE20 returns are stationary during all periods, and the results of the ARCH test confirm the existence of an ARCH effect in the residuals of ARMA mean models.

With the application of ARMA–GARCH-type models for the three specified sub-periods, this research finds that the shock terms are positive and statistically significant, with the pandemic period having the highest impact, while the volatility-persistence terms are positive, significant, and close to one, indicating robust evidence of volatility clustering of the ASE20 returns, with the post-pandemic period having the highest persistence.

More importantly, in the results for the variance EGARCH equation, this research finds that the coefficients for pre- and during-pandemic periods are negative, indicating that bad news tends to have a larger impact on ASE20 return volatility compared to good news. However, the asymmetric parameters in these two sub-periods are not statistically significant, implying that ASE20 returns do not provide strong evidence of asymmetry in the impact of past shocks on current volatility. Meanwhile, in the period after the pandemic, the asymmetric coefficient switched to positive and statistically significant, indicating a reversal in the asymmetric effect, where good news now impacts ASE20 return volatility more than bad news.

This shift in the asymmetric component in EGARCH models can be attributed to changes in ASE market dynamics and changes in investors’ sentiments in response to the pandemic crisis. This research suggests that investors have become more sensitive to positive news, reacting more strongly to favorable developments than negative ones. This heightened response to positive information indicates a growing sense of optimism and confidence in the market’s recovery and future growth prospects. The reduced impact of negative shocks on volatility suggests that investors are less fearful of downturns, possibly because they perceive the worst effects of the pandemic as having passed. This could lead to a more resilient market where negative news is less likely to cause significant disruptions.

Another important outcome is observed in this research, which is related to the signs of AR and MA terms in the ARMA–EGARCH models for pre- and post-pandemic crises. The AR (1) term indicated a shift in the autocorrelation structure from a mean-reverting behavior in volatility to a persistence behavior. The MA (1) term indicated a shift in the shock structure from an amplifying effect of past shocks on current volatility to a damping effect of past shocks. The different impacts of the AR and MA coefficients between the pre-and post-pandemic periods suggest that the ASE20 return series has undergone a significant change in the autocorrelation and shock structures, which can be attributed to changes in ASE market dynamics, changes in the sentiments of investors, and/or changes in economic policies in response to the pandemic crisis.