Abstract
This paper investigates the relationships of the Bloomberg Gender Equality Index and the MSCI World Index in global financial markets. The main objective is to analyze the degree of integration of each index from a fractional perspective for the years 2014–2021. The methodology involves fractional integration to assess the consistency and integration levels of both indices, revealing that they are remarkably consistent with integration orders close to 1 and no evidence of mean-reverting behavior. When examining potential cointegrating relationships between the two indices using the classical two-step method of Engle and Granger, the order of integration of the estimated errors is very close to 1, showing no evidence of cointegration. However, employing the more robust fractional CVAR (FCVAR) approach, the results strongly support the hypothesis of cointegration, indicating evidence of long-term co-movements between the two indices. The findings suggest that investment strategies should incorporate gender diversity criteria, as companies aligning with these benchmarks may enhance co-movements with the Bloomberg Gender Equality Index. Policymakers should promote transparency and initiatives that support gender diversity to improve market stability.
JEL Classification:
C22; G12; G15
1. Introduction
This study focuses on the Bloomberg Gender Equality Index (GEI) and the MSCI World Index to explore their potential cointegration and long-term relationships. The indices share notable similarities, including their broad representation of public companies across various sectors and the utilization of market capitalization weighting to measure performance, thereby providing comprehensive insights into global market trends and corporate behaviors (Azar and Zhou 2017). The reason for investigating the cointegration between these indices stems from the hypothesis that enhanced transparency and performance in gender equality may be increasingly valued by global investors (García-Sánchez et al. 2022). As corporations strive to meet gender diversity benchmarks, their performance might align more closely with broader market trends captured by the MSCI World Index (Fekete and Hagen 2021). Elucidating this potential alignment and co-movement can yield pivotal insights into the interconnectedness of gender equality initiatives and global financial performance (Jin et al. 2024). Such understanding has the potential to inform investment strategies and guide policy decisions aimed at fostering sustainable and inclusive market growth (Susan and Natu 2023).
Gender equality in the workplace has become a critical focus for investors, companies, and policymakers in recent years (Quinlan and VanderBrug 2016). The Bloomberg Gender Equality Index (GEI) was developed to track the performance of public companies committed to transparency in gender-related data reporting. However, the relationship between gender equality initiatives and broader market trends remains underexplored. This study aims to address this research gap by examining the long-term relationship between the Bloomberg GEI and the MSCI World Index, a benchmark for global equity markets. Previous research has demonstrated links between corporate gender diversity and financial performance (Campbell and Mínguez-Vera 2008; Galbreath 2018). However, these studies have typically focused on individual company metrics rather than market-wide indices. By analyzing the cointegration between the two indices, this paper takes a novel approach to understanding how gender equality relates to global market dynamics at a macro level.
The Global Equality Index (GEI) is a modified market capitalization-weighted index designed to monitor the progress of publicly traded companies committed to transparency in gender-related data reporting (Bloomberg 2022). By standardizing the disclosure of gender-related information, companies can attract investment and talent, empower investors to make socially conscious decisions, and allow employees and communities to hold these companies accountable for their progress (Gülsoy and Ustabaş 2019). This approach collectively strengthens the business case for gender equality. The GEI framework includes 59 questions, focusing on the disclosure of selected metrics in areas such as female leadership and career advancement, gender pay equity, inclusive policies, sexual harassment policies, and pro-women brand reputation. A company’s GEI score is determined by its transparency and data accuracy. The 380 companies featured in the 2021 index achieved a minimum GEI score of 50% and have a market capitalization exceeding USD 1 billion. By concentrating on five key pillars, the GEI provides comprehensive guidelines for measuring and tracking data essential for achieving gender equality in the workplace (Bloomberg 2022). The MSCI World Index, which includes a diverse range of large and small companies from 23 Developed Market countries, represents about 85% of the free float-adjusted market capitalization in each country, encompassing a total of 1585 companies (MSCI 2024).
The objective of this study is to assess the resilience and long-term viability of the Bloomberg GEI relative to the broader global equity markets represented by the MSCI World Index. This approach allows us to examine potential market shocks and their implications while providing flexibility in model specification (BenSaïda et al. 2018; Bonciani and Ricci 2020). Our research question asks: Are the Bloomberg GEI and MSCI World Index cointegrated, and if so, what does this reveal about the relationship between gender equality initiatives and global market trends? The findings have important implications for investors seeking diversification strategies and policymakers aiming to promote both gender equality and sustainable market growth. This study contributes to the literature by providing a macro-level analysis of how gender equality relates to global equity markets over time. The results offer insights into whether gender-focused investing can provide unique diversification benefits. Additionally, evidence of cointegration would suggest that gender equality initiatives are becoming increasingly integrated with broader market fundamentals.
To determine this potential long-term relationship between the two indices, we employed both fractional integration and cointegration methodologies. The standard approach to determine the degree of persistence in time series data is to look at unit root tests to determine if the series is stationary I(0) (with shocks having transitory effects) or nonstationary I(1) (with a unit root and the series having permanent effects of shocks). However, all classical unit root methods (e.g., Dickey and Fuller 1979; Phillips and Perron 1988; Kwiatkowski et al. 1992; Elliot et al. 1996) have very low power if the alternatives are of a fractional form (see, e.g., Diebold and Rudebusch 1991; Hassler and Wolters 1994; Lee and Schmidt 1996). This is the main motivation for using fractionally integrated methods in this paper. We aimed for our results to illuminate not only the statistical relationship but also the economic rationale and implications of such a connection. This understanding could ultimately inform investment strategies and policy decisions.
The remainder of this paper is structured as follows: Section 2 reviews the relevant literature on stock market forecasting and gender diversity. Section 3 outlines the methodological approach. Section 4 describes the data. Section 5 presents the empirical findings. Finally, Section 6 discusses the conclusions and implications of this research.
2. Literature Review
The concept of socially responsible investment (SRI) necessitates adherence to environmental, social, and governance (ESG) criteria (Hill 2020; Leventi 2022). The late 1990s marked a pivotal period for sustainable investment, epitomized by the establishment of the Dow Jones Sustainability Index, the inaugural global index to integrate sustainability criteria (Hammond and World Resources Institute 1995; Pagano et al. 2018). This momentum was further bolstered by the United Nations (UN) through the implementation of principles for responsible investment (United Nations Environment Programme Finance Initiative 2008). Sustainable products and behaviors are lauded for their role in reducing inefficiencies, optimizing resource use, and fostering innovations that yield long-term cost savings (Clark et al. 2015). These criteria serve as quality indicators for companies, enhancing their potential economic performance (Lagoarde-Segot 2011; Kocmanova et al. 2012).
The social dimension of ESG, particularly gender diversity, has gained significant prominence in recent years (Allemand et al. 2024). Gender diversity is recognized for its positive impact on financial performance, customer experience, workplace environment, and human capital management across all organizational levels (Albuquerque et al. 2018). There is a burgeoning global trend to invest in companies that lead in promoting diversity and gender equality (Keefe 2011; Chapple and Humphrey 2014). The diversity approach seeks to balance equality with the recognition of each individual’s uniqueness, focusing on two main principles: ensuring fair treatment for all and valuing individual and group differences. These principles form the foundation of diversity strategies (Barberá and Ramos 2004). Developing a robust diversity strategy has become crucial for organizations and is expected to remain a significant factor for their success. Many companies are now aligning their gender diversity initiatives with the United Nations’ Sustainable Development Goals, where Gender Equality is listed as goal number five (Cascella et al. 2022; Martínez et al. 2022; Targa et al. 2023; Mehrotra et al. 2024; etc.).
Organizations have recognized that gender diversity enhances creativity, innovation, teamwork, and flexibility within the workplace (Díaz-García et al. 2013; Jankelová et al. 2022). Effective corporate governance necessitates genuine managerial diversity, with the presence of women on boards often leading to an increased emphasis on corporate social responsibility (CSR) policies, demonstrating greater sensitivity toward these issues (Williams 2003; Bernardi et al. 2009). According to Kahreh et al. (2014), female directors exhibit a stronger orientation and greater attention to social responsibility compared to their male counterparts.
Research has elucidated a complex relationship between gender equality indices and global stock market performance (Ionascu et al. 2018; Peillex et al. 2021; Rutskiy et al. 2022). Badea et al. (2020) conducted a comparative study on the performance of gender equality indices versus overall market indices, finding that gender equality indices generally exhibited higher volatility but had distributions closer to normal compared to corresponding MSCI indices. This suggests potential differences in risk and return profiles. BlackRock’s (2023) research indicated that companies in the MSCI World Index with female CEOs outperformed those led by men by 1.0 percentage points on average in terms of the return on assets (RoA) from 2014 to 2022. Additionally, firms with higher diversity across corporate ranks tended to outperform less diverse firms by 1.2% on average between 2011 and 2022, indicating a positive relationship between gender diversity and financial performance. MSCI Inc. (2023) offers various ESG and factor indices, including those focused on gender diversity, providing tools for investors to track and compare the performance of gender-focused indices against broader market indices. These findings collectively suggest that gender equality measures may have implications for stock market performance, though the relationship is nuanced and may vary across different contexts and time periods.
The literature on financial data modeling is extensive. Since Fama’s (1970) classical random walk model testing the efficient market hypothesis, numerous studies have explored the stationarity of stock market prices using unit root methods. Early investigations include works by Groenewold and Kang (1993), Ayadi and Pyun (1994), Tabak (2007), Narayan (2008), Hasanov (2009), Gozbasi et al. (2014), Tiwari and Kyophilavong (2014), and Wang et al. (2015). Despite this, Cochrane (1991) noted that standard unit root tests have limited power in finite samples. It is now widely acknowledged that unit root testing methods also exhibit low power against various alternatives such as trend stationarity models (DeJong et al. 1992), structural breaks (Perron 1989; Campbell and Perron 1991), regime switching (Nelson et al. 2001), and fractional integration (Diebold and Rudebusch 1991; Hassler and Wolters 1994; Lee and Schmidt 1996). The literature on unit root testing has since expanded to include fractional integration, which allows the series to become stationary with a fractional differencing parameter, providing a more flexible approach to examining persistence in data. Omay and Baleanu (2021) illustrated that neglecting structural breaks and fractional integration simultaneously could lead to incorrect conclusions regarding the stochastic behavior of the COVID-19 pandemic. In another study, Omay (2015) introduced a fractional frequency flexible Fourier form DF-type unit root test, showing improved small sample properties over the integer frequency counterpart. Additional contributions to fractional integration in stock market price analysis include works by Caporale and Gil-Alana (2002), Aloy et al. (2010), and Afzal and Sibbertsen (2021).
Beltratti and Morana (2006) explored the notion of a persistent, long-term connection between international stock markets using fractional cointegration models, which incorporate shared, long-term components. Their study also examined the relationship between macroeconomic factors and stock market volatility, providing evidence of a dual connection between stock markets and macroeconomic instability. Previous research by Baur and Schulze (2005) found that standard stock index returns exhibit signs of “some” contagion, defined as crisis-specific co-exceedance unexplained by different quantile variables, which can be predicted both within and between regions. Studies investigating the relationship between financial markets and other factors, such as oil prices (Sahu et al. 2014; Guesmi et al. 2016; Hamdam and Hamdam 2019; Mokni and Youssef 2019; Hou et al. 2019; Sarwar et al. 2020; Ehouman 2020; Salisu and Gupta 2021), and macroeconomic fundamentals (Conrad and Loch 2014; Otieno et al. 2019), have been particularly significant. The results of cointegration analysis indicate the presence of a long-term equilibrium relationship.
Significant advancements have been made in understanding the relationship between various indices since the pioneering work of Beltratti and Morana (2006). Gil-Alana et al. (2014) examined the cyclical patterns of rises and declines in US, European, and Asian markets using generalized autoregressive conditional heteroskedasticity (GARCH) models. Caporale et al. (2016) analyzed the SP500 and EuroStoxx50 indices from 1986 to 2013 with fractional cointegration techniques, finding no consistent patterns of persistence, although it was more pronounced in bullish markets. They concluded that cointegration was not present over the entire period, but it did exist from 1996 to 2009. Gagnon et al. (2016) demonstrated the coherence and integration of five US and European stock indices using daily data from 2003 to 2013. During the global crisis of 2007–2009, they observed an increase in persistence and the speed of adjustment, whereas outside that period, the cointegration relationship was weaker, especially for higher-order moments.
3. Methodology
In the empirical application conducted below, a combination of partial differentiation and amalgamation methods were employed. These techniques were selected to illustrate the resilience level within the indices and its evolution over time.
The process of subtracting d-differences from a time series to render it stationary at I(0) is known as the I() method. This method can be applied for any real number d, allowing for fractional differentiation. In simpler terms, it states that follows an integrated process of order , i.e., ~I(), if it can be written as:
where is the lag operator, i.e., = − 1, and ut is I(0). If = 0 in (1), = , and , it is considered to be a short memory, compared to the situation of long memory, which is observed with > 0. It is so-named due to the strong relationships among observations that are separated by a long time. The polynomial in in (1) can be written as:
Thus, the -parameter can be interpreted as an indicator of data stability—the larger the value, the stronger the dependence within the data. Additionally, it allows for a more flexible distinction between mean reversion and non-reversion compared to traditional methods that use either 0 (for stationary series) or 1 (for nonstationary series). For real values of , convergence to its long-term projection will occur if is less than one, with a quicker return to equilibrium as approaches zero.
The estimation of is conducted via the Whittle function in the frequency domain using a parametric approach developed in Robinson (1994). This is a testing procedure based on the Lagrange multiplier (LM) principle, which considers the null hypothesis, Ho: = do, for any real value of do in the set-up given by Equation (1). This method has various advantages with respect to other procedures. Thus, for example, it is valid for all ranges of values of do, including those in the nonstationary region (do ≥ 0.5). Moreover, it has a standard N(0, 1) null limit distribution, which holds independently of the inclusion of deterministic terms in the model, such as intercepts and/or linear trends. Finally, it is the most efficient method in the Pitman sense against local departures from the null.
Next, we examined the long-term co-movements among the variables by investigating their cointegration relationships. In this analysis, we employed fractional differentiation degrees to test whether the long-term equilibrium relationship adheres to a fractional process. Here, among other methods, we used the fractional cointegration VAR approach (FCVAR) developed by Johansen and Nielsen (2010, 2012), which tests if the individual series are I() in its multivariate representation, while the long-term equilibrium relationship is I(−) with a positive , where and can be both fractional values. To introduce the FCVAR model, we first present the non-fractional CVAR model. With , being a p-dimensional I(1) time series, the CVAR model is:
where and represent the difference and the lag operator. These are utilized to derive the FCVAR model. We then find:
which is applied to , such that
where is p-dimensional-independent and identically distributed with a mean of zero, and a variance–covariance matrix . The parameters and are matrices, where . In matrix , the columns are the cointegrating relationships, and is the stationary combination, i.e., the long-term equilibrium, which is integrated to order d. The short-term parts from the long-term equilibrium are integrated to order . The coefficients in correspond to the velocity of adjustment toward equilibrium. Hence, is the long-term adjustment and represents the short-term behavior of the variables. A full description of this procedure can be found in Monge and Gil-Alana (2021).
4. Data
To determine the degree of inclusion in the global equality index, Bloomberg’s ESG database, which includes over 11,500 publicly listed companies, was evaluated based on the following criteria: (i) the current market value must be at least USD 1 billion (1,000,000,000); (ii) the average daily trading value over the past three months must exceed USD 50,000; (iii) the three-month average trading volume must be more than USD 5000. If multiple companies meet these conditions, the final selection for the index is based on liquidity, considering factors such as the average number of shares traded, the typical daily trading value, and the company’s market capitalization.
Publicly traded equities are considered for inclusion in the index if they satisfy universal criteria and achieve a GEI score above a globally established benchmark. This selection threshold is reviewed and adjusted annually. GEI assessments are conducted yearly using data from the previous fiscal year, accessible through the Bloomberg Terminal’s fundamental analysis (FA) feature. FA provides detailed financial information, including ESG data, for each company, along with a universal template for comparing firms with varied reporting formats. The index employs a modified market capitalization-weighted system, where each company’s current market cap is multiplied by its GEI score. The weightings within the GEI index are reviewed and potentially adjusted at the start of each year and quarterly thereafter, specifically on the Monday following the third Friday of the month when the New York Stock Exchange is open. The index’s constituents remain fixed throughout the year, except for companies that are delisted or acquired.
The MSCI World Index is constructed using the MSCI Global Investable Indexes (GIMI) System. This methodology is comprehensive and consistent, allowing for the comparison of global markets with various sizes, sectors, and investment styles. The index is updated quarterly—in February, May, August, and November—to promptly respond to market changes while minimizing unnecessary adjustments. In May and November, the boundaries for large and mid-cap stocks in the index are recalculated. The index is calculated using the Laspeyres’ method of a weighted arithmetic average combined with the chain-linking concept, five days a week, from Monday to Friday.
Figure 1 and Figure 2 display the two indices under examination: the Bloomberg Gender Equality Index and the MSCI World Stock Market Index. The Bloomberg Gender Equality Index demonstrates higher volatility compared to the MSCI World Stock Market Index, as the latter provides a broader and more uniform representation across all market capitalization sizes, sectors, and style categories. The charts are based on daily data series from 31 December 2014 to 5 February 2021, for both indices.
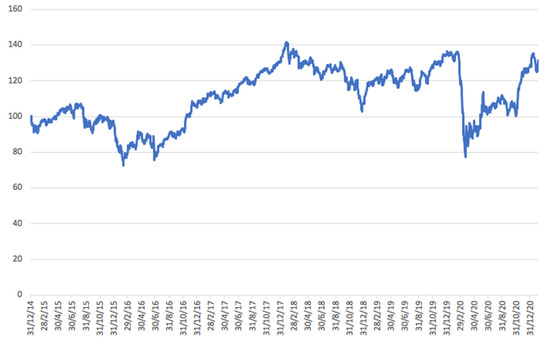
Figure 1.
Time series plot: Bloomberg Gender Equality Index.
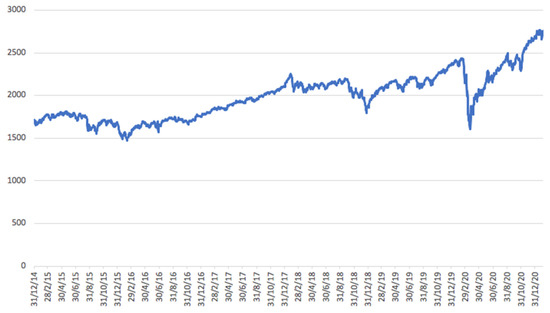
Figure 2.
Time series plot: MSCI World Stock Market Index.
5. Empirical Results
We begin this section by estimating the fractional differencing parameter, , of each individual series. To do this, we use the following model:
where is the observed time series, and and refer, respectively, to a constant and a linear time trend; is supposed to be I() so that is I(0).
Table 1 presents the estimates of d in the model described by Equation (1), along with the 95% confidence intervals for the values of . Initially, we assumed that in (1) follows a white noise process, and then we accounted for autocorrelation in the error term using Bloomfield’s (1973) exponential spectral method. This non-parametric technique implicitly determined the model for based on its spectral density function, which, in its log form, approximated an autoregressive (AR) structure. We examined three scenarios separately: first, a scenario where there are no deterministic terms (i.e., = = 0 a priori in (1)); second, a scenario involving only an intercept (i.e., = 0 a priori in (1)); and third, one including both an intercept and a linear time trend (i.e., and ≠ 0 initially in (1)). In the table, we highlight in bold the chosen model for each scenario. This selection was based on the t-values of the estimated coefficients in the -differenced processes, recognizing that the two equations in (1) can be collectively represented as follows:
with and Then, noting that is I(0) by construction, the t-values in Equation (2) remain valid. Table 2 displays the estimated coefficients for each series.

Table 1.
Estimates of the differencing parameters on the individual series.

Table 2.
Estimated coefficients based on Table 1.
We observe in Table 1 (Panels (i) and (ii)) that the intercept is sufficient to describe the deterministic part of the model since the time trend coefficients were found to be statistically insignificant in all cases. The estimates of are about 1 in all cases, (1.029 and 1.014, respectively, for and with uncorrelated errors, and 1.103 and 1.118 with serial correlation), and the unit root null hypothesis is not rejected under the assumption of white noise errors, but is rejected in favor of > 1 if autocorrelation is permitted. In the case of the logged values (panels (iii) and (iv)), the estimates of d are slightly lower (1.013 and 1.001 for the uncorrelated case and 1.073 and 1.101 with autocorrelation). The evidence of unit roots is not so clearly supported when using the spectral model of Bloomfield (1973) for the disturbance term (panel (iv)), since is slightly higher than 1, and the unit root null is now rejected in favor of > 1 in the two cases examined. Nevertheless, using standard methods that simply consider integer degrees of differentiation (i.e., 0 and 1), (e.g., Dickey and Fuller 1979; Phillips and Perron 1988; Kwiatkowski et al. 1992; Elliot et al. 1996, and Ng and Perron 2001; etc.), the I(1) hypothesis cannot be rejected in any single case.
Given the evidence supporting the I(1) hypothesis, we then explored if the two series are related in the long term using cointegration methods. Instead of assuming a classical case with an I(0) error term structure, we considered the possibility of fractional cointegration. First, we used the approach developed by Engle and Granger (1987) and further developed by Cheung and Lai (1993) and Gil-Alana (2003) for the fractional case. The idea is simple. First, we looked at the order of integration of the individual series (already carried out in Table 1 and Table 2), and based on the fact that the two series displayed statistically the same degree of integration, we next took the residuals of the OLS regression of one of the variables over the other, testing the degree of differentiation in the estimated residuals. The estimated regressions for both the original and logged data yielded the following results:
and
(t-values) in parentheses. Table 3 presents the estimates of based on these residuals, considering once again the three scenarios: no terms, an intercept, and an intercept with a linear time trend. This time, we again assumed that is a white noise process and also accounted for autocorrelation using Bloomfield’s (1973) model.

Table 3.
Estimates of the differencing parameters based on residuals on the individual series.
The first observation from Table 3 is that, according to this method, there is no evidence of any degree of cointegration between the two variables, as the order of integration of the residuals (and log-residuals) is approximately 1 in all cases. In fact, regarding the range between 0.973 and 1.002, although the values are slightly lower than those in Table 1 and Table 2, the reduction in the degree of differentiation is minimal, and the unit root null hypothesis cannot be rejected in any instance. It should be noted, however, that these results may be biased due to the estimation being performed on estimated rather than observed values. Additionally, the OLS approach may not be the most suitable method in this potential cointegration context (Robinson and Hualde 2003). Therefore, in the following analysis, we utilized the multivariate FCVAR approach developed by Johansen and Nielsen (2010, 2012), which has been widely used in recent years for cointegration analysis.
The results are presented in Table 4, where we observe that both the original and logged series exhibit a similar pattern, providing evidence for cointegration.

Table 4.
Estimated values using the FCVAR approach.
The order of integration in the bivariate representation of the two series is 0.969 for the original data and 0.975 for the log-transformed values. The reductions in the orders of integration in the cointegration relationships are exactly the same values (0.969 and 0.975), indicating that the errors in the long-term equilibrium relationships are I(0), or short memory. This finding contrasts with the results based on the previously used two-step approach, likely due to the bias introduced in the earlier method when using estimated rather than observed errors.
6. Concluding Comments
This research delved into the relationship between gender equality and the MSCI World Index, with daily data from 2014 to 2021, evaluating them first independently and then analyzing the long-term relationship between them. The methodology involved fractional integration techniques to assess the consistency and integration levels of both indices. The results show that both series are very persistent, with integration orders close to 1 and no signs of mean-reverting behavior. This absence of mean-reversion is consistent with prior research (DePenya and Gil-Alana 2004; Tabak 2007; Narayan 2008; Hasanov 2009; Gozbasi et al. 2014; Tiwari and Kyophilavong 2014). However, our findings differ from those of Adekoya (2021) and Caporale et al. (2020), who reported mean-reversion and long-term memory in different contexts.
When examining long-term equilibrium relationships, our research revealed evidence of cointegration using the multivariate approach proposed by Johansen and Nielsen (2010, 2012) via the FCVAR models. However, this cointegration was not observed when employing the two-step approach of Engle and Granger (1987), which estimates, in the second step, the order of integration in the regression errors of the two variables. This inconsistency suggests a need to further research alternative methods for estimating the relationship’s coefficients and the differencing parameters. Given the broader scope of the MSCI in comparison to the Bloomberg Gender Equality Index, it is plausible that the two series may not be cointegrated. However, the rising demand for gender diversity criteria by investors during security selection indicates a shifting dynamic. Companies aiming to be featured in the general MSCI index may increasingly strive to align with these gender diversity benchmarks. This potential alignment could result in an increasing co-movement between the two series over time.
The policy implications of these findings are significant. The evidence of cointegration, albeit inconsistent across methods, suggests that gender equality measures could be increasingly relevant to stock market performance. Policymakers and regulators might consider encouraging or mandating gender diversity disclosures and practices, as these could enhance market stability and performance. Additionally, investors and fund managers could benefit from incorporating gender equality metrics into their investment strategies, potentially leading to better risk-adjusted returns. The observed trends indicate that gender diversity is not just a social or ethical issue but also a financial one, with tangible impacts on market dynamics and corporate performance. Future research should continue to explore these relationships, using more refined methodologies and longer time frames to capture the evolving nature of gender equality’s impact on financial markets.
The limitations of this study include the relatively short time frame and the specific indices analyzed. Future research might benefit from exploring this dynamic interplay over longer periods and with different indices, further validating the findings observed with the multivariate approach of Johansen and Nielsen (2010, 2012). Additionally, policymakers should promote transparency and initiatives that support gender diversity to improve market stability, while investment strategies should incorporate gender diversity criteria to enhance co-movements with the Bloomberg Gender Equality Index.
Author Contributions
Conceptualization, J.I.; methodology, L.A.G.-A.; data curation: J.I. and M.d.R.; writing-review and editing, M.d.R. and J.I.; investigation, L.A.G.-A. and J.I. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
(MSCI Inc. 2023) MSCI Inc. 2023. Workforce Gender Diversity Data Methodology. Available online: https://www.msci.com/documents/1296102/3556282/Workforce%2BGender%2BDiversity%2BData%2BMethodology.pdf (accessed on 31 May 2023). (MSCI 2024) MSCI. 2024. MSCI ACWI IMI Index. Available online: https://www.msci.com/documents/10199/178e6643-6ae6-47b9-82be-e1fc565ededb (accessed on 31 May 2024).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Adekoya, Oluwasegun B. 2021. Persistence and efficiency of OECD stock markets: Linear and nonlinear fractional integration approaches. Empirical Economics 61: 1415–33. [Google Scholar] [CrossRef]
- Afzal, Alia, and Philipp Sibbertsen. 2021. Modelling fractional cointegration between high and low stock prices in Asian countries. Empirical Economics 60: 661–81. [Google Scholar] [CrossRef]
- Albuquerque, Rul, Yrjo Koskinen, and Chendi Zhang. 2018. Corporate Social Responsibility and Firm Risk: Theory and Empirical Evidence. European Corporate Governance Institute (ECGI)—Finance Working Paper No. 359/2013. January 15. Available online: https://ssrn.com/abstract=1961971 (accessed on 15 January 2018).
- Allemand, Isabelle, Daniela Borodak, and Xavier Hollandts. 2024. Board Gender Diversity and ESG: The Influence of the Varieties of Capitalism 1. Finance 45: 43–89. [Google Scholar] [CrossRef]
- Aloy, Marcel, Mohamed Boutahar, Karine Gente, and Anne Péguin-Feissolle. 2010. Fractional integration and cointegration in stock prices and exchange rates. Economics Bulletin 30: 115–29. [Google Scholar]
- Ayadi, O. Felix, and Chong Soo Pyun. 1994. An application of variance ratio test to the Korean securities market. Journal of Banking and Finance 18: 643–58. [Google Scholar] [CrossRef]
- Azar, Alexandre, and Heying Zhou. 2017. Do Good and Do Well: An Empirical Study of the MSCI World. Master’s thesis, Lund University School of Economics and Management, Lund, Sweden, June. [Google Scholar]
- Badea, Leonardo, Daniel Ştefan Armeanu, Dan Costin Nițescu, Valentin Murgu, Iulian Panait, and Boris Kuzman. 2020. A study of the relative stock market performance of companies recognized for supporting gender equality policies and practices. Sustainability 12: 3558. [Google Scholar] [CrossRef]
- Barberá, Esther, and Amparo Ramos. 2004. Liderazgo y discriminación de género. Revista de Psicología General y Aplicada 57: 147–60. [Google Scholar]
- Baur, DIrk, and Niels Schulze. 2005. Coexceedances in financial markets—A quantile regression analysis of contagion. Emerging Markets Review 6: 21–43. [Google Scholar] [CrossRef]
- Beltratti, Andrea, and Claudio Morana. 2006. Breaks and persistency: Macroeconomic causes of stock market volatility. Journal of Econometrics 131: 151–77. [Google Scholar] [CrossRef]
- BenSaïda, Ahmed, Sabri Boubaker, Du Khuong Nguyen, and Skander Slim. 2018. Value-at-risk under market shifts through highly flexible models. Journal of Forecasting 37: 790–804. [Google Scholar] [CrossRef]
- Bernardi, Richard A., Susan M. Bosco, and Veronica L. Columb. 2009. Does Female Representation on Boards of Directors Associate with the ‘Most Ethical Companies’ List? Corporate Reputation Review 12: 270–80. [Google Scholar] [CrossRef]
- BlackRock. 2023. Lifting Financial Performance by Investing in Women. Available online: https://www.blackrock.com/corporate/literature/whitepaper/lifting-financial-performance-by-investing-in-women.pdf (accessed on 30 November 2023).
- Bloomberg. 2022. Bloomberg Gender-Equality Index Methodology. Available online: https://assets.bbhub.io/company/sites/46/2022/01/Bloomberg-Gender-Equality-Index-Methodology.pdf (accessed on 31 January 2022).
- Bloomfield, Peter. 1973. An exponential model in the spectrum of a scalar time series. Biometrika 60: 217–26. [Google Scholar] [CrossRef]
- Bonciani, Dario, and Martino Ricci. 2020. The international effects of global financial uncertainty shocks. Journal of International Money and Finance 109: 102236. [Google Scholar] [CrossRef]
- Campbell, John Y., and Pierre Perron. 1991. Pitfalls and opportunities. What macroeconomists should know about unit roots. NBER Macroeconomic Annual 6: 1141–201. [Google Scholar] [CrossRef]
- Campbell, Kevi, and Antonio Mínguez-Vera. 2008. Gender diversity in the boardroom and firm financial performance. Journal of Business Ethics 83: 435–51. [Google Scholar] [CrossRef]
- Caporale, Guglielmo Maria, and Luis Alberiko Gil-Alana. 2002. Fractional integration and mean reversion in stock prices. The Quarterly Review of Economics and Finance 42: 599–609. [Google Scholar] [CrossRef]
- Caporale, Guglielmo Maria, Luis Alberiko Gil-Alana, and Carlos Poza. 2020. Persistence, non-linearities and structural breaks in European stock market indices. The Quarterly Review of Economics and Finance 77: 50–61. [Google Scholar] [CrossRef]
- Caporale, Guglielmo Maria, Luis Alberiko Gil-Alana, and James C. Orlando. 2016. Linkages between the US and European stock markets: A fractional cointegration approach. International Journal of Finance & Economics 21: 143–53. [Google Scholar] [CrossRef]
- Cascella, Clelia, J. Williams, and Maria Pampaka. 2022. An extended regional gender gaps index (eRGGI): Comparative measurement of gender equality at different levels of Regionality. Social Indicators Research 159: 757–800. [Google Scholar] [CrossRef]
- Chapple, Larelle, and Jacquelyn E. Humphrey. 2014. Does board gender diversity have a financial impact? Evidence using stock portfolio performance. Journal of Business Ethics 122: 709–23. [Google Scholar] [CrossRef]
- Cheung, Ying-Wong, and Kon S. Lai. 1993. A fractional cointegration analysis of purchasing power parity. Journal of Business and Economic Statistics 11: 103–12. [Google Scholar] [CrossRef]
- Clark, Gordon L., Andreas Feiner, and Michael Viehs. 2015. From the Stockholder to the Stakeholder: How Sustainability Can Drive Financial Outperformance. Available online: https://ssrn.com/abstract=2508281 (accessed on 15 January 2018).
- Cochrane, John H. 1991. A critique of the application of unit root tests. Journal of Economic Dynamics and Control 15: 275–84. [Google Scholar] [CrossRef]
- Conrad, Christian, and Karin Loch. 2014. Anticipating Long-Term Stock Market Volatility. Journal of Applied Econometrics 30: 1090–114. [Google Scholar] [CrossRef]
- DeJong, David, John Nankervis, N. E. Savin, and Charles H. Whiteman. 1992. Integration versus trend stationarity in time series. Econometrica 60: 423–33. [Google Scholar] [CrossRef]
- DePenya, Javier R., and Luis Alberiko Gil-Alana. 2004. Do Spanish stock market prices follow a random walk. European Review of Economics and Finance 3: 3–13. [Google Scholar]
- Dickey, David A., and Wayne A. Fuller. 1979. Distributions of the Estimators for Autoregressive Time Series with a Unit Root. Journal of American Statistical Association 74: 427–81. [Google Scholar]
- Diebold, Francis X., and Glenn D. Rudebusch. 1991. On the Power of Dickey-Fuller Test against Fractional Alternative. Washington: Board of Governors of the Federal Reserve System, p. 258. [Google Scholar]
- Díaz-García, Cristina, Angela González-Moreno, and Francisco Jose Sáez-Martínez. 2013. Gender diversity within R&D teams: Its impact on radicalness of innovation. Innovation 15: 149–60. [Google Scholar]
- Ehouman, Yoo Axel. 2020. Volatility transmission between oil prices and banks’ stock prices as a new source of instability: Lessons from the United States experience. Economic Modelling 91: 198–217. [Google Scholar] [CrossRef]
- Elliot, Graham, Thomas J. Rothenberg, and James H. Stock. 1996. Efficient Tests for an Autoregressive Unit Root. Econometrica 64: 813–36. [Google Scholar] [CrossRef]
- Engle, Robert, and Clive W. J. Granger. 1987. Cointegration and error correction. Representation, estimation and testing. Econometrica 55: 251–76. [Google Scholar] [CrossRef]
- Fama, Eugene. 1970. Efficient Capital Markets: A Review of Theory and Empirical Work. The Journal of Finance 25: 383–417. [Google Scholar] [CrossRef]
- Fekete, Thomas Glede, and Erik Hagen. 2021. Do Investors Reward Gender Diversity? An Event Study of the MSCI World Women’s Leadership Index. Master’s thesis, Norwegian School of Economics, Bergen, Norway, December. [Google Scholar]
- Gagnon, Marie Helene, Gabriel J. Power, and Dominique Toupin. 2016. International stock market cointegration under the risk-neutral measure. International Review of Financial Analysis 47: 243–55. [Google Scholar] [CrossRef]
- Galbreath, Jeremy. 2018. Is board gender diversity linked to financial performance? The mediating mechanism of CSR. Business & Society 57: 863–89. [Google Scholar]
- García-Sánchez, Isabel Maria, Valentina Minutiello, and Patrizia Tettamanzi. 2022. Gender disclosure: The impact of peer behavior and the firm’s equality policies. Corporate Social Responsibility and Environmental Management 29: 385–405. [Google Scholar] [CrossRef]
- Gil-Alana, Luis Alberiko. 2003. Testing of fractional cointegration in macroeconomic time series. Oxford Bulletin of Economics and Statistics 65: 517–29. [Google Scholar] [CrossRef]
- Gil-Alana, Luis Alberiko, Olanrewaju I. Shittu, and OlaOluwa S. Yaya. 2014. On the persistence and volatility in European, American and Asian stocks bull and bear markets. Journal of International Money and Finance 40: 149–62. [Google Scholar] [CrossRef]
- Gozbasi, Onur, Ilhan Kucukkaplan, and Saban Nazlioglu. 2014. Re-examining the Turikish stock market efficiency. Evidence from nonlinear unit root tests. Economic Modelling 38: 381–84. [Google Scholar] [CrossRef]
- Groenewold, Nicolaas, and Kuay Chin Kang. 1993. The semi-strong efficiency of the Australian share market. Economic Record 69: 405–10. [Google Scholar] [CrossRef]
- Guesmi, Khaled, Heni Boubaker, and Van Son Lai. 2016. From Oil to Stock Markets. Journal of Economic Integration 31: 103–33. [Google Scholar] [CrossRef][Green Version]
- Gülsoy, Tanses, and Ayfer Ustabaş. 2019. Corporate sustainability initiatives in gender equality: Organizational practices fostering inclusiveness at work in an emerging-market context. International Journal of Innovation and Technology Management 16: 1940005. [Google Scholar] [CrossRef]
- Hamdam, Reem Khamls, and Allam M. Hamdam. 2019. Linear and nonlinear sectoral response of stock markets to oil price movements: The case of Saudi Arabia. International Journal of Finance and Economics 25: 336–48. [Google Scholar] [CrossRef]
- Hammond, Allam, and World Resources Institute. 1995. Environmental Indicators: A Systematic Approach to Measuring and Reporting on Environmental Policy Performance in the Context of Sustainable Development. Washington: World Resources Institute, vol. 36. [Google Scholar]
- Hasanov, Mübariz. 2009. Is South Korea’s sotck market efficient? Evidence from a nonlinear unit root test. Applied Economics Letters 16: 163–67. [Google Scholar] [CrossRef]
- Hassler, Uwe, and Jürgen Wolters. 1994. On the power of unit root tests against fractional alternatives. Economic Letters 45: 1–5. [Google Scholar] [CrossRef]
- Hill, John. 2020. Environmental, Social, and Governance (ESG) Investing: A Balanced Analysis of the Theory and Practice of a Sustainable Portfolio. Cambridge: Academic Press. [Google Scholar]
- Hou, Yang, Steven Li, and Fenghua Wen. 2019. Time-varying volatility spillover between Chinese fuel oil and stock index futures markets based on a DCC-GARCH model with a semi-nonparametric approach. Energy Economics 83: 119–43. [Google Scholar] [CrossRef]
- Ionascu, Michaela, Ion Ionascu, Marian Sacarin, and Michaela Minu. 2018. Women on boards and financial performance: Evidence from a European emerging market. Sustainability 10: 1644. [Google Scholar] [CrossRef]
- Jankelová, Nadezda, Zuzana Joniaková, and Katarina Procházková. 2022. The way to business competitiveness: The importance of diversity management and teamwork climate in stabilizing of employees. Journal of Business economics and Management 23: 606–25. [Google Scholar] [CrossRef]
- Jin, Xing, Meng Wang, Qingyun Wang, Juan Yang, and Yi Guo. 2024. Gender diversity of senior management teams and corporate innovation efficiency: Evidence from China. Finance Research Letters 60: 104897. [Google Scholar] [CrossRef]
- Johansen, Soren, and Morten Orregaard Nielsen. 2010. Likelihood inference for a nonstationary fractional autoregressive model. Journal of Econometrics 158: 51–66. [Google Scholar] [CrossRef]
- Johansen, Soren, and Morten Orregaard Nielsen. 2012. Likelihood inference for a fractionally cointegrated vector autoregressive model. Econometrica 80: 2667–732. [Google Scholar] [CrossRef][Green Version]
- Kahreh, Mohammad Safari, Asghar Babania, Mohammad Tive, and Seyed Mehdi Mirmehdi. 2014. An examination to effects of Gender Differences on the Corporate Social Responsibility (CSR). Procedia-Social and Behavioral Sciences 109: 664–68. [Google Scholar] [CrossRef]
- Keefe, Joseph F. 2011. Gender Equality as an Investment Concept. Portsmouth: Pax World Investments. [Google Scholar]
- Kocmanova, Alena, Petr Nemecek, and Marie Docekalova. 2012. Environmental, social and governance (ESG) key performance indicators for sustainable reporting. Paper presented at the 7th International Scientific Conference, Vilnius, Lithuania, May 10–11; pp. 655–63. [Google Scholar]
- Kwiatkowski, Denis, Peter C. D. Phillips, Peter Schmidt, and Yongcheol Shin. 1992. Testing the null hypothesis of stationarity against the alternative of a unit root: How sure are we that economic time series have a unit root? Journal of Econometrics 54: 159–78. [Google Scholar] [CrossRef]
- Lagoarde-Segot, Thomas. 2011. Corporate social responsibility as a bolster for economic performance: Evidence from emerging markets. Global Business and Organizational Excellence 31: 38–53. [Google Scholar] [CrossRef]
- Lee, Dongin, and Peter Schmidt. 1996. On the power of the KPSS test of stationary against fractionally integrated alternatives. Journal of Econometrics 73: 285–302. [Google Scholar] [CrossRef]
- Leventi, Lydia. 2022. The Growing Role of Environmental, Social and Governance (ESG) Criteria in Investments. Available online: https://repository.ihu.edu.gr/xmlui/handle/11544/30045 (accessed on 7 October 2022).
- Martínez, Maria del Carmen Valls, Pedro Antonio Martín-Cervantes, and del Maria del Mar Miralles-Quirós. 2022. Sustainable development and the limits of gender policies on corporate boards in Europe. A comparative analysis between developed and emerging markets. European Research on Management and Business Economics 28: 100168. [Google Scholar] [CrossRef]
- Mehrotra, Vikas, Lukas Roth, Yusuke Tsujimoto, and Yupana Wiwattanakantang. 2024. Index Inclusion and Corporate Social Performance: Evidence from the MSCI Empowering Women Index. Available online: https://ssrn.com/abstract=4800375 (accessed on 19 April 2024).
- Mokni, Khaled, and Manel Youssef. 2019. Measuring persistence of dependence between crude oil prices and GCC stock markets: A copula approach. The Quarterly Review of Economics and Finance 72: 14–33. [Google Scholar] [CrossRef]
- Monge, Manuel, and Luis Alberiko Gil-Alana. 2021. Lithium industry and the U.S. crude oil prices. A fractional cointegration VAR and a Continuous Wavelet Transform análisis. Resources Policy 72: 102040. [Google Scholar] [CrossRef]
- MSCI Inc. 2023. Workforce Gender Diversity Data Methodology. Available online: https://www.msci.com/documents/1296102/3556282/Workforce%2BGender%2BDiversity%2BData%2BMethodology.pdf (accessed on 31 May 2023).
- MSCI. 2024. MSCI ACWI IMI Index. Available online: https://www.msci.com/documents/10199/178e6643-6ae6-47b9-82be-e1fc565ededb (accessed on 31 May 2024).
- Narayan, Paresh Kumar. 2008. Do shocks to G7 stock prices have a permanent effect? Evidence from panel unit root tests with structural change. Mathematics and Computers in Simulation 77: 369–73. [Google Scholar] [CrossRef]
- Nelson, Charles R., Jeremy Piger, and Eric Zivot. 2001. Markov regime switching and unit root tests. Journal of Business and Economic Statistics 19: 404–15. [Google Scholar] [CrossRef]
- Ng, Serena, and Pierre Perron. 2001. Lag length selection and the construction of unit root tests with good size and power. Econometrica 69: 519–1554. [Google Scholar] [CrossRef]
- Omay, Tolga. 2015. Fractional Frequency Flexible Fourier Form to approximate smooth breaks in unit root testing. Economics Letters 134: 123–26. [Google Scholar] [CrossRef]
- Omay, Tolga, and Dumitru Baleanu. 2021. Fractional unit-root tests allowing for a fractional frequency flexible Fourier form trend: Predictability of COVID-19. Advances in Differences Equations 2021: 167. [Google Scholar] [CrossRef] [PubMed]
- Otieno, Donald A., Rose W. Ngugi, and Peter W. Muriu. 2019. The impact of inflation rate on stock market returns: Evidence from Kenya. Journal of Economics and Finance 43: 73–90. [Google Scholar] [CrossRef]
- Pagano, Michael S., Graham Sinclair, and Tina Yang. 2018. Understanding ESG ratings and ESG indexes. In Research Handbook of Finance and Sustainability. Cheltenham: Edward Elgar Publishing, pp. 339–71. [Google Scholar]
- Peillex, Jonathan, Sabri Boubaker, and Breeda Comyns. 2021. Does it pay to invest in Japanese women? Evidence from the MSCI Japan empowering women index. Journal of Business Ethics 170: 595–613. [Google Scholar] [CrossRef]
- Perron, Pierre. 1989. The great crash, the oil price shock and the unit root hypothesis. Econometrica 57: 1361–401. [Google Scholar] [CrossRef]
- Phillips, Peter C., and Pierre Perron. 1988. Testing for a unit root in time series regression. Biometrika 75: 335–46. [Google Scholar] [CrossRef]
- Quinlan, Joseph, and Jackie VanderBrug. 2016. Gender Lens Investing: Uncovering Opportunities for Growth, Returns, and Impact. New York: John Wiley & Sons. [Google Scholar]
- Robinson, Peter M. 1994. Efficient tests of nonstationary hypotheses. Journal of the American Statistical Association 89: 1420–37. [Google Scholar] [CrossRef]
- Robinson, Peter M., and Javier Hualde. 2003. Cointegration in fractional, systems with unknown integration orders. Econometrica 71: 1727–66. [Google Scholar] [CrossRef]
- Rutskiy, Vladislav, Irina Yarygina, Shaida Hamoud Alshahrani, Sergei Elkin, Andrei Plotnikov, Alla Plotnikova, Oleg Ikonnikov, Valentina Everstova, Alexey Mishchenko, Ivan Seleznyov, and et al. 2022. The relationship between gender inequality and the performance of large corporations. In Proceedings of the Computational Methods in Systems and Software. Cham: Springer International Publishing, pp. 576–86. [Google Scholar]
- Sahu, Tarak Nath, Kalpataru Bandopadhyay, and Debasish Mondal. 2014. An empirical study on the dynamic relationship between oil prices and Indian stock market. Managerial Finance 40: 200–15. [Google Scholar] [CrossRef]
- Salisu, Afees A., and Rangan Gupta. 2021. Oil shocks and stock market volatility of the BRICS: A GARCH-MIDAS approach. Global Finance Journal 48: 100546. [Google Scholar] [CrossRef]
- Sarwar, Suleman, Aviral Kumar Tiwari, and Cao Tingqiu. 2020. Analyzing volatility spillovers between oil market and Asian stock markets. Resources Policy 66: 101608. [Google Scholar] [CrossRef]
- Susan, Enyan Besong, and Manases Mbengwor Natu. 2023. Re-imagining the Gender Gap in Economic Participation and Opportunities: Assessing the Link Between Sustainable Development and Gender Equality in Some African Countries. Social Indicators Research 169: 817–45. [Google Scholar] [CrossRef]
- Tabak, Benjamin M. 2007. Testing for unit root bilinearity in the Brazilian stock market. Physica A: Statistical Mechanics and Its Applications 385: 261–69. [Google Scholar] [CrossRef]
- Targa, Laya, Silvia Rueda, Jose Vicente Riera, Sergio Casas, and Cristina Portalés. 2023. Enhancing the Understanding of the EU Gender Equality Index through Spatiotemporal Visualizations. ISPRS International Journal of Geo-Information 12: 421. [Google Scholar] [CrossRef]
- Tiwari, Aviral Kumar, and Phouphet Kyophilavong. 2014. New evidence from the random walk hypothesis for BRICS stock indices. A wavelet unit root test approach. Economic Modelling 43: 38–41. [Google Scholar] [CrossRef]
- United Nations Environment Programme Finance Initiative. 2008. Making It Happen: Implementing the Principles for Responsible Investment. Available online: https://www.unepfi.org/industries/investment/making-it-happen-implementing-the-principles-for-responsible-investment/ (accessed on 31 October 2008).
- Wang, Juan, Dongxiang Zhang, and Jian Zhang. 2015. Mean reversion in stock prices of seven Asian stock markets: Unit root test and stationary test with Fourier functions. International Review of Economics & Finance 37: 157–64. [Google Scholar] [CrossRef]
- Williams, Robert J. 2003. Women on corporate boards of directors and their influence on corporate philanthropy. Journal of Business Ethics 42: 1–10. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).