Discretely Distributed Scheduled Jumps and Interest Rate Derivatives: Pricing in the Context of Central Bank Actions
Abstract
1. Introduction
1.1. Motivation
1.2. Related Literature
1.3. Contribution
- We provide analytical solutions for the characteristic function of a still broad class of models within the AJD–Skellam class of interest rate models, enabling the fast pricing of bonds and derivatives depending on overnight interest rates;
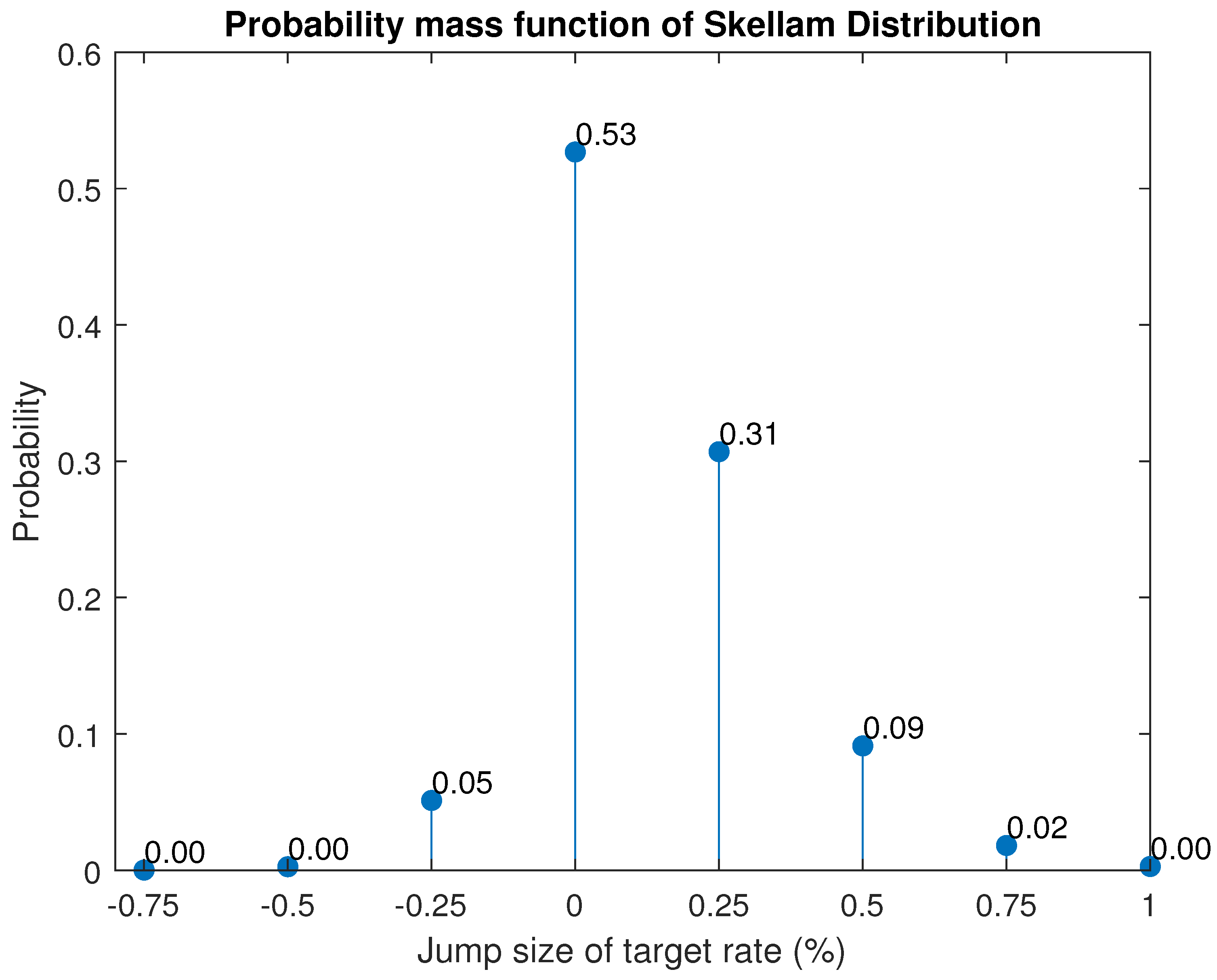
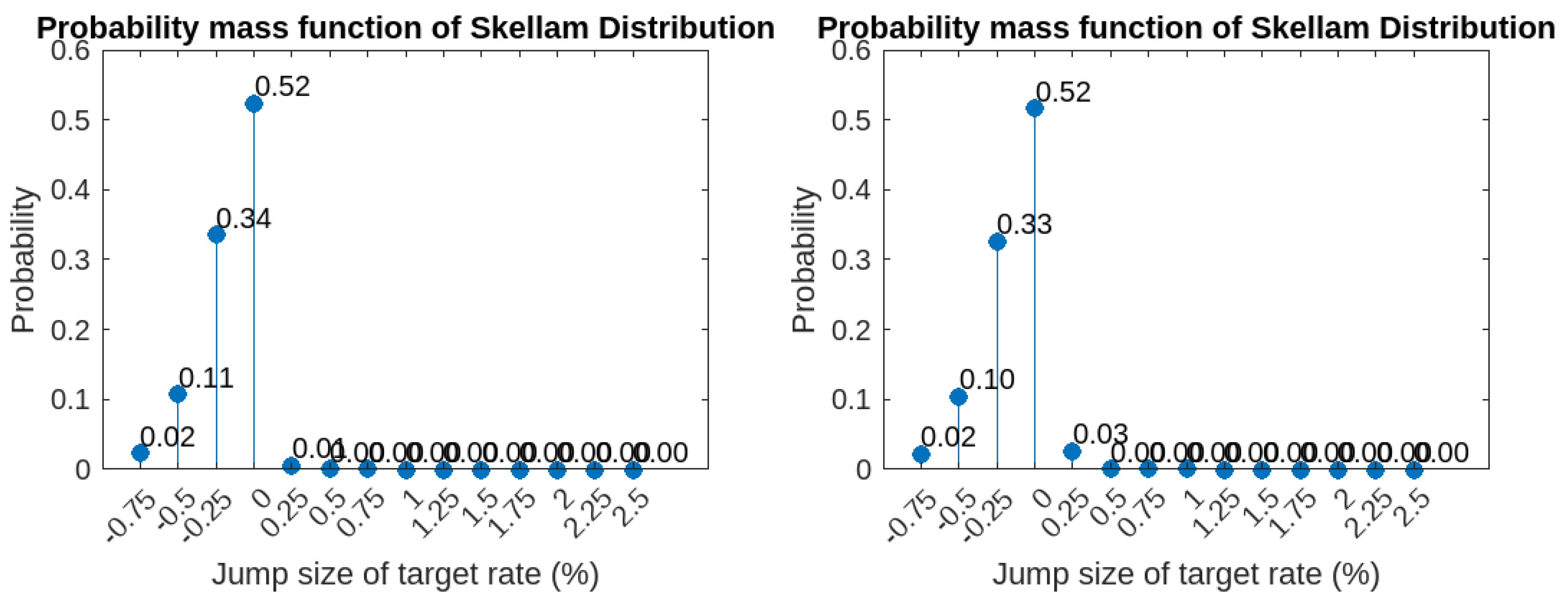
- Scheduled central bank announcements typically move the benchmark rate discretely in time and space. This class of models is consistent with this because the state space of the additive jump entry follows the modified Skellam probability distribution in discrete space. The usual distribution found in the literature for this purpose is Gaussian and, therefore, unrealistic. As far as the authors are aware, except for da Silva et al. (2023), the use of the Skellam distribution or its modifications do not exist in the context of pricing derivatives in financial markets. da Silva et al. (2023) obtained the price of an interest rate derivative of a recent vintage introduced in the Brazilian financial market, namely, the COPOM option (the acronym stands for Monetary Policy Committee);
- The model can easily allow jumps with stochastic volatility, correlations between Brownian motions, and additional random jump times. A closed-form formula exists even if the Vasicek (AJD) model is enhanced, as shown below;
- The exponential affine format of the resulting characteristic function allows us to calculate, numerically at least, via the celebrated Fourier-cosine series (COS) method (see Oosterlee and Grzelak 2019), the price of complex interest rate derivatives, and not bond prices only.Remark: The use of the COS method was confined to stock markets until recently, when da Silva et al. (2019) and da Silva et al. (2020) adapted its use to interest rate markets. A key point that permitted the authors to adapt the COS method to the needs of pricing derivatives in interest rate markets was determining that the integral of the interest rate process—and not the interest process per se—was an adequate mathematical object to achieve the pricing results. Hence, this is a supplementary contribution to this study.
1.4. Paper Outline
- We present the class of AJD–Skellam models, which connect the interest rate diffusion process with scheduled, discretely distributed jumps;
- The closed-form formula for the characteristic function of one and two-factor models, with both constant and time-dependent Skellam parameters, is provided. The particular case where the diffusion process is given by the Vasicek model is also shown;
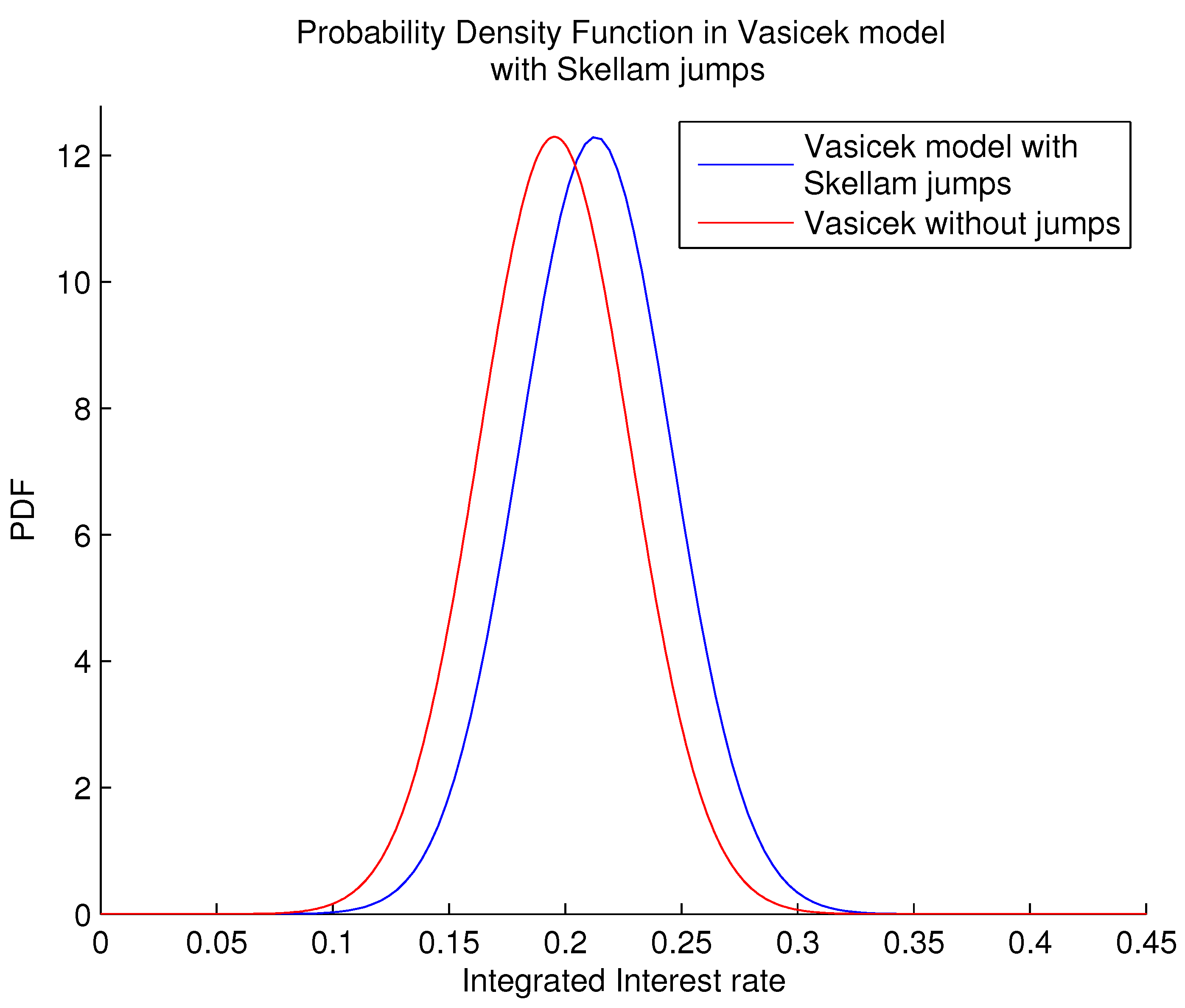
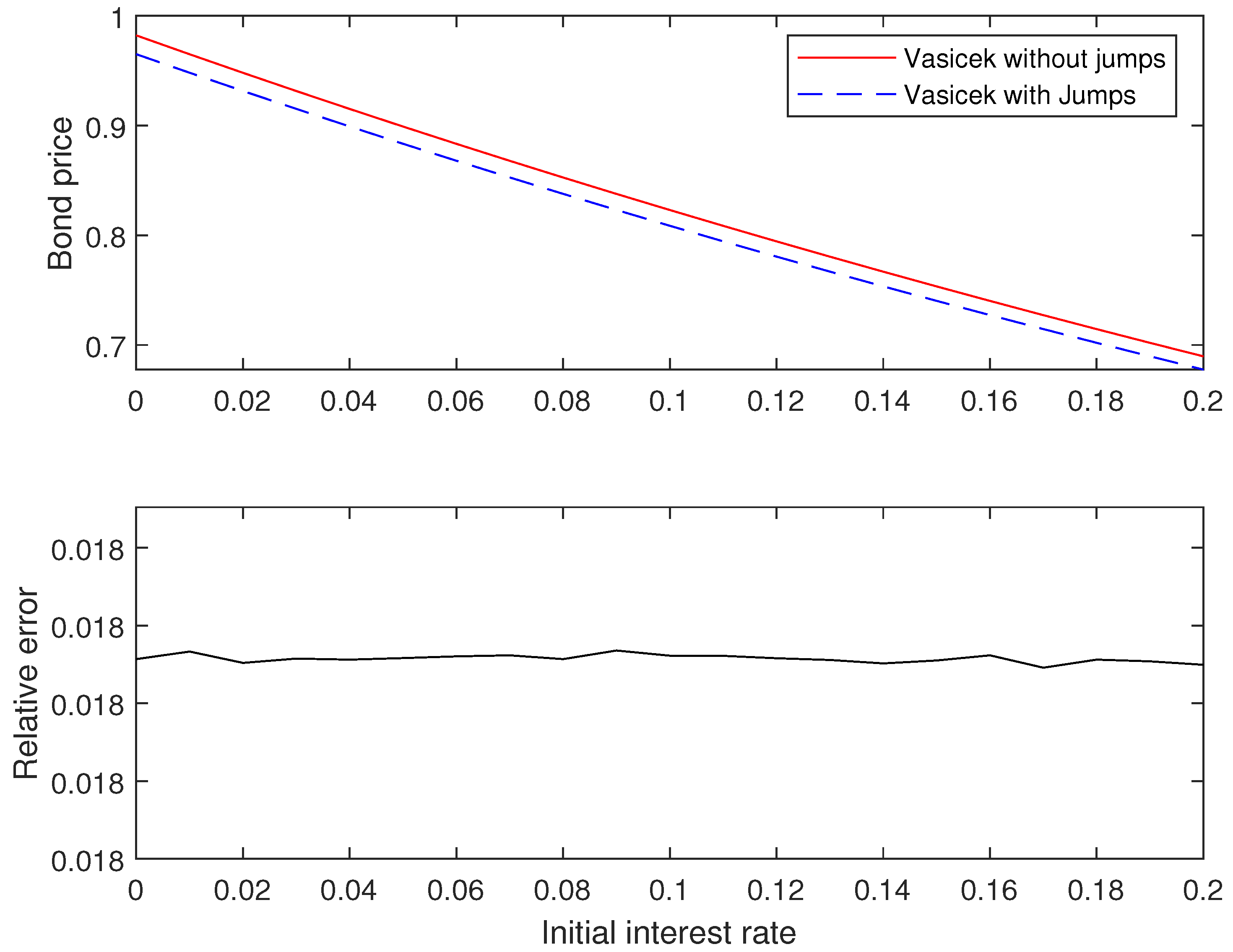
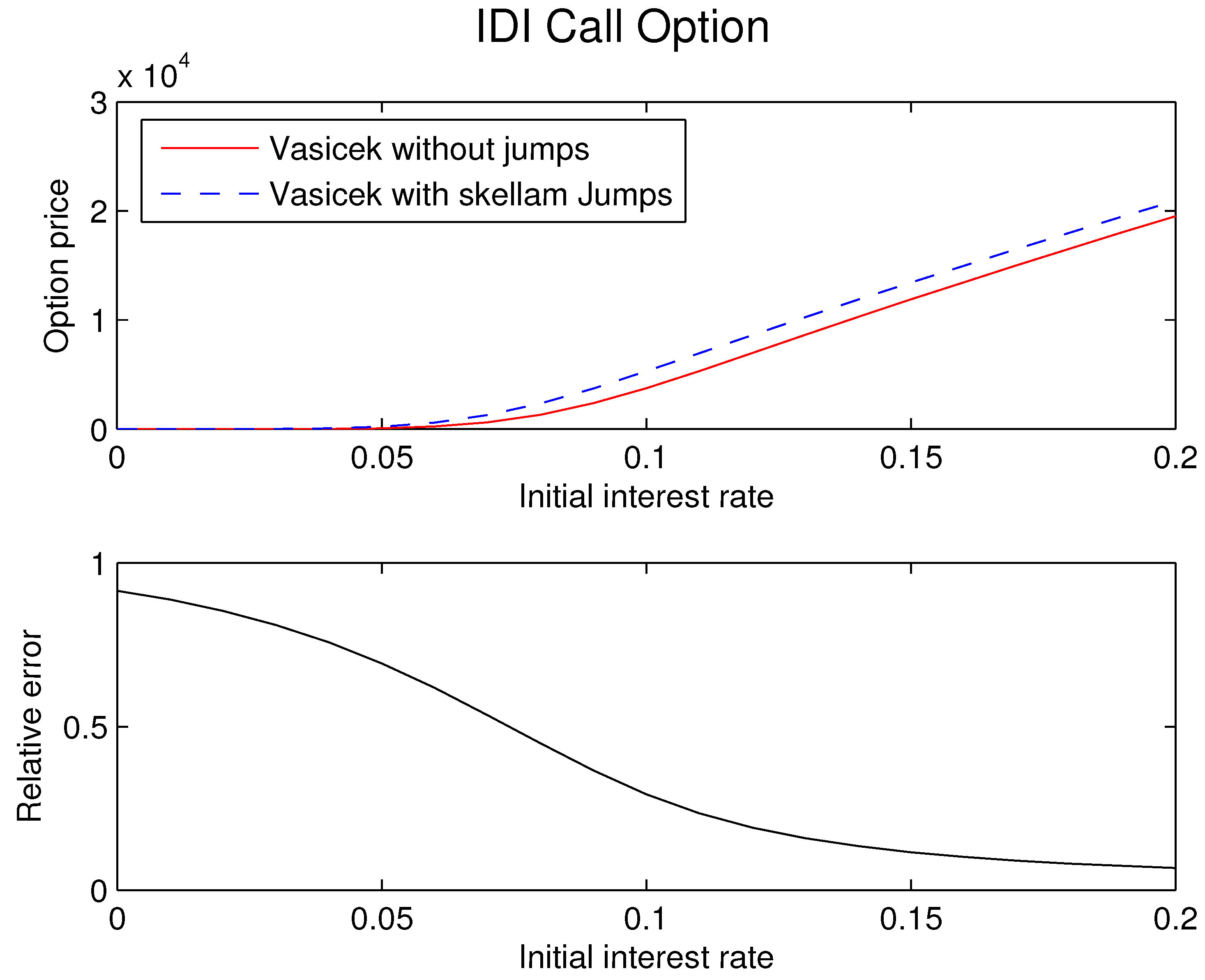
- We apply the COS method, through which we calculate the probability density functions associated with the integrated interest rate processes and, ultimately, the derivative prices. Inter alia, the Vasicek model with and without Skellam jumps was addressed, while prices referring to the (zero-coupon) bonds and the IDI call option are shown;
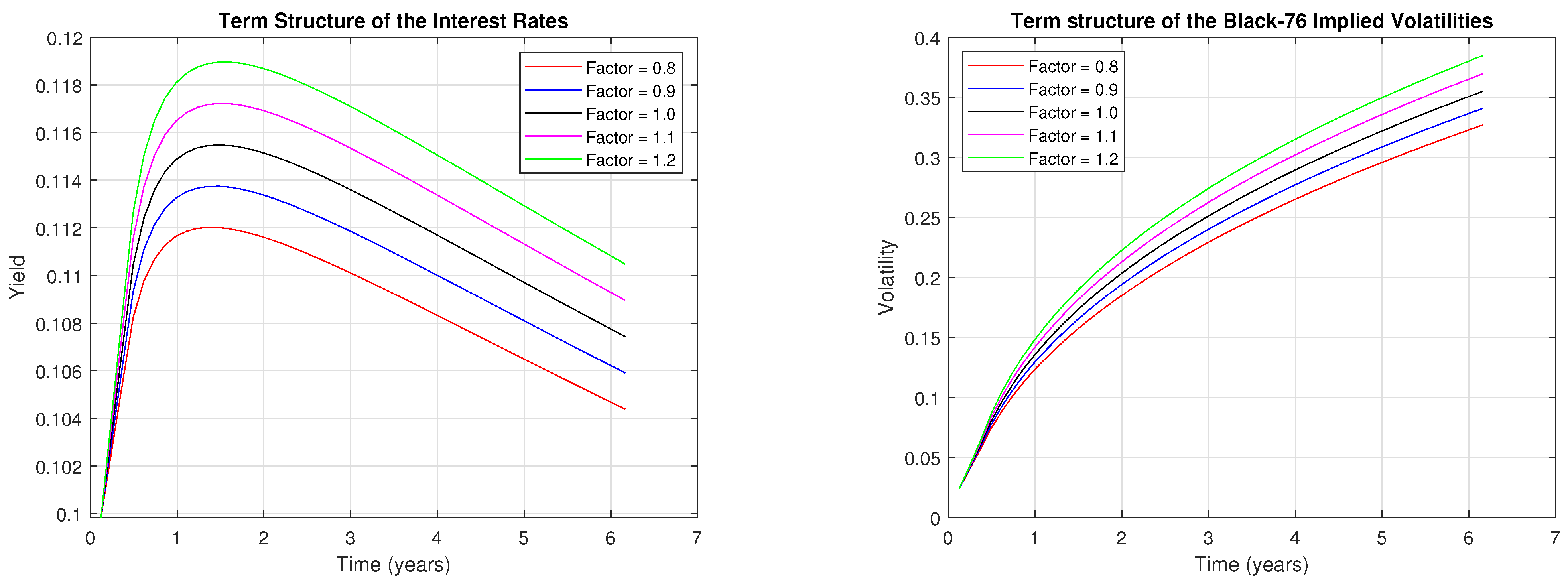
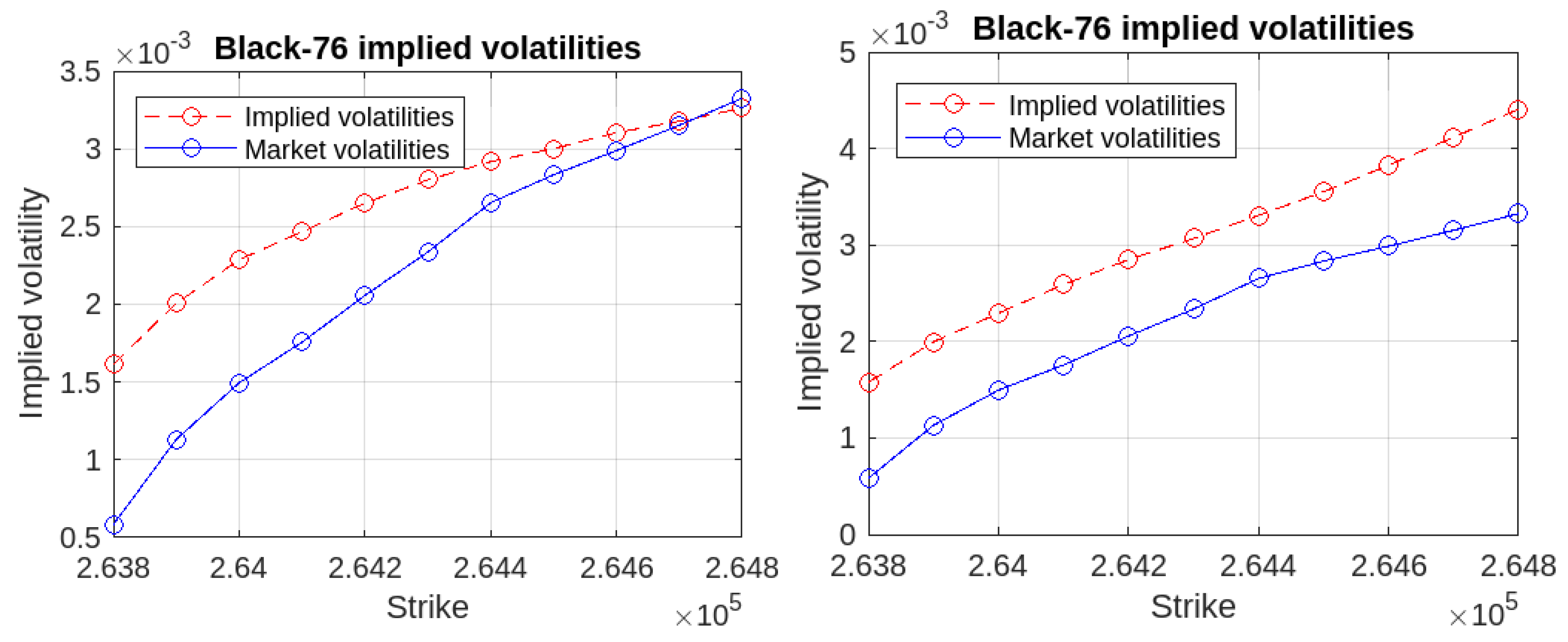
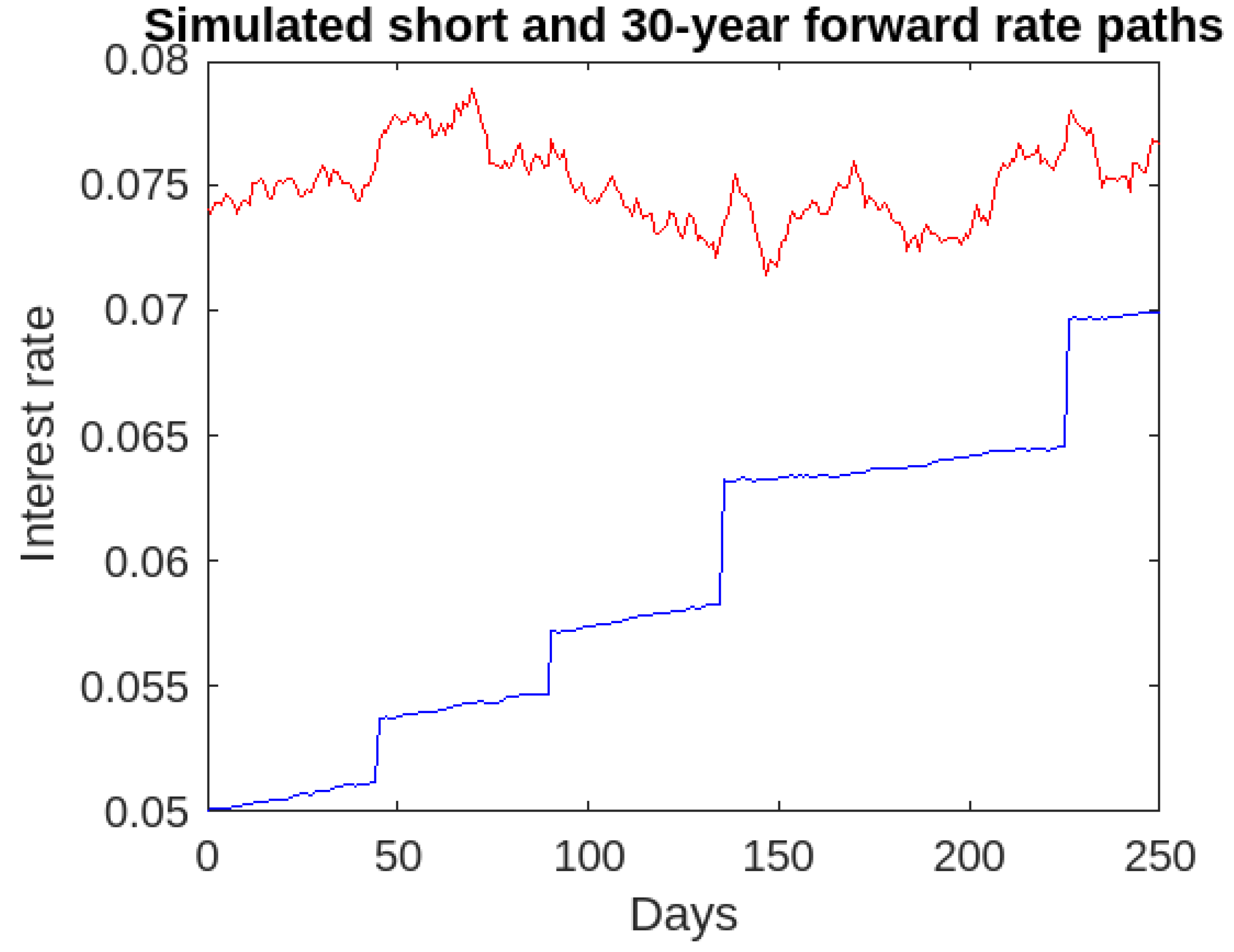
- We exhibit the term structure of interest rates under the Vasicek model equipped with Skellam jumps with time-varying parameters, as well as the Black-76 Implied Volatilities;
- We show a specific model calibration of term structure of the interest rates and the IDI option implied volatilities. We compared the performance with that of an interest rate model governed by Gaussian jumps;
- Interpretation of the model’s parameters is highlighted.
2. Methodology
2.1. The Skellam Model for Jumps
2.2. The COS Method: Representing Continuous Random Variables and Derivatives Prices via Fourier-Cosine Series
2.3. Step-by-Step Implementation
- The first step is the selection of the model, specifically the stochastic differential Equation (SDE), which governs the dynamics of interest rates between the meetings of the monetary authority. The chosen model should fall within the affine jump-diffusion (AJD) class (Duffie and Singleton 2003);
- Next, we determine the characteristic function (see, e.g., Duffie (2001) and Bouziane (2008)) for the probability distribution of the integrated interest rate under the AJD model. This function is then combined with the term associated with the model of deterministic distributed scheduled jumps, that is, the modified Skellam distribution. As detailed in the following section, if the model is AJD, the coupling of the results naturally follows;
- To compute the price of an interest rate derivative, it is necessary to find the terms and of Equation (22). The terms are associated with the interest rate model, whereas is linked to the payoff of the financial product;
- Equation (22) can be easily implemented in any spreadsheet, given that it is a simple summation. The price of the IDI option is calculated in a fraction of a second;
- To calculate the price of a zero-coupon bond, we substitute into the characteristic function.
3. Results
3.1. The Characteristic Function of the Integrated Short-Term Rate Satisfying the AJD–Skellam Model
3.2. Numerical Results
3.3. Calibration
4. Discussion
5. Conclusions
- Provide an extensive analytical framework for a significant class of interest rate models that effectively integrate discrete, scheduled jumps. This represents a substantial advancement in financial modeling, particularly in understanding and predicting the impact of central bank interventions on interest rates;
- Calculate derivative prices using the COS method. The application of this method in our model class demonstrated robustness and precision, highlighting its utility in financial computations involving complex interest rate models;
- Demonstrate the efficiency of a single-factor model within this class for calibrating the interest rate curve. Although this single-factor model has shown considerable efficacy, we anticipate that two-factor models will offer even better calibration, especially for accurately capturing the implied volatility of options;
- Appropriate interpret the model parameters.
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Yield Curve Calibration

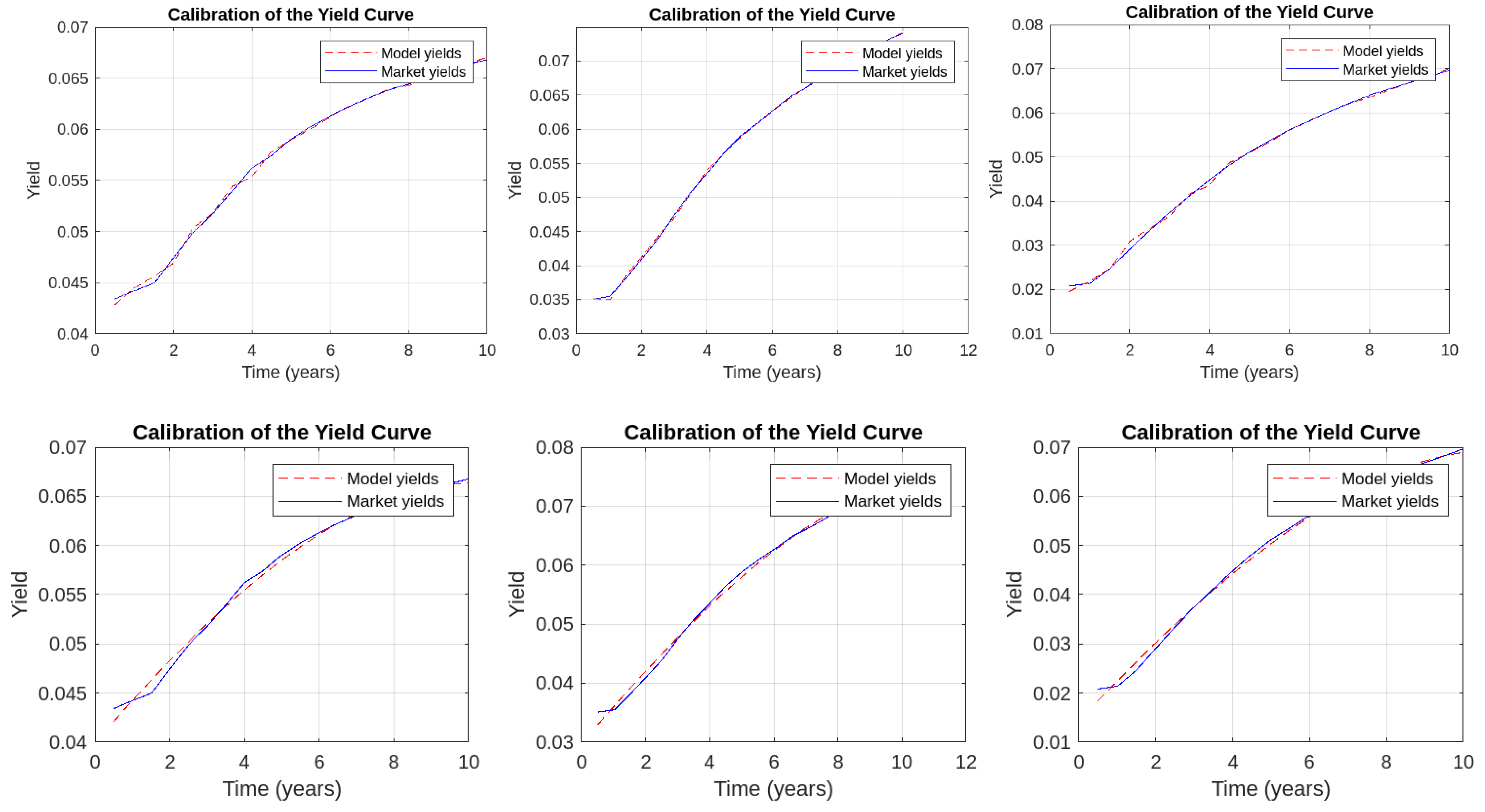
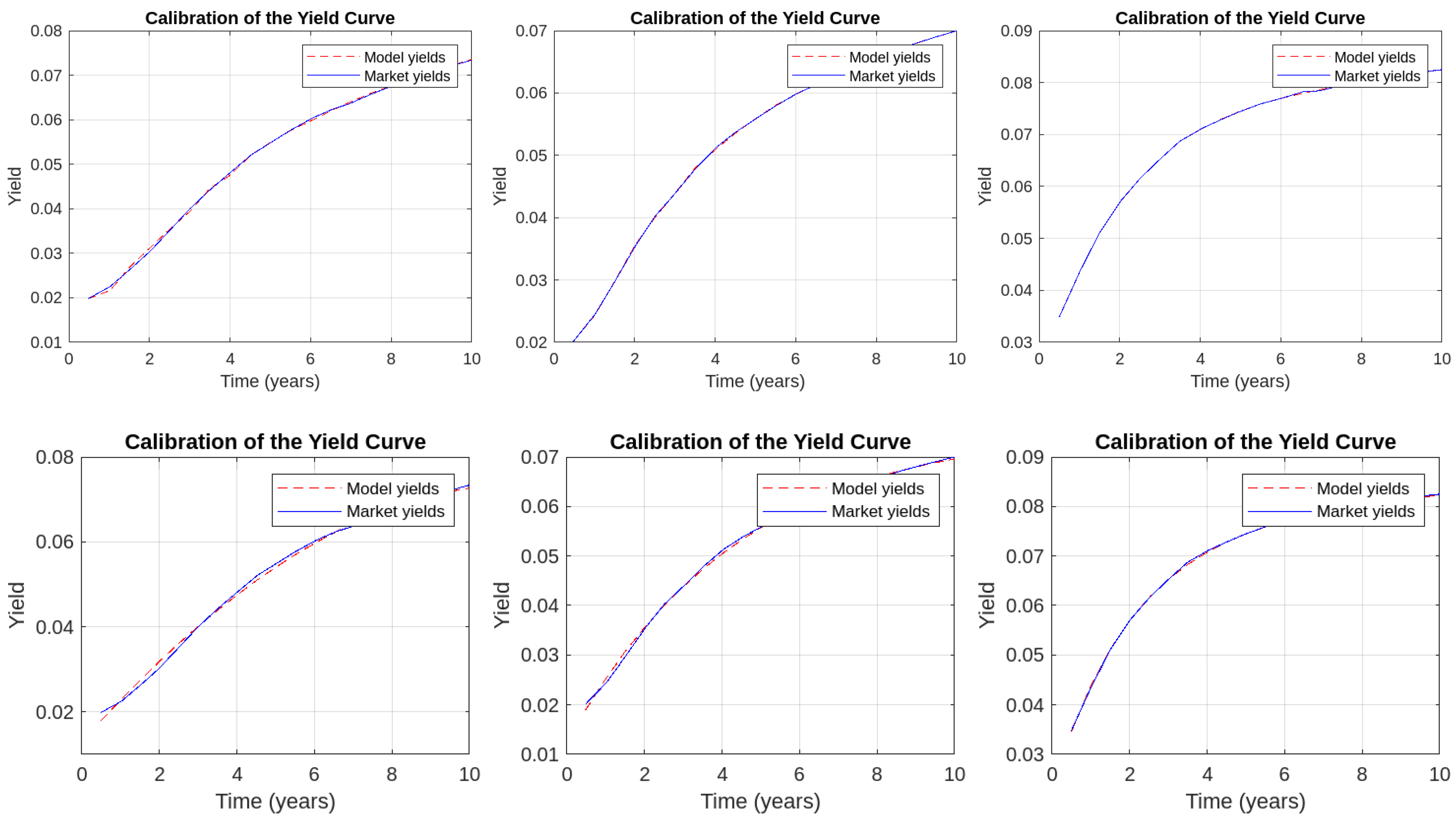
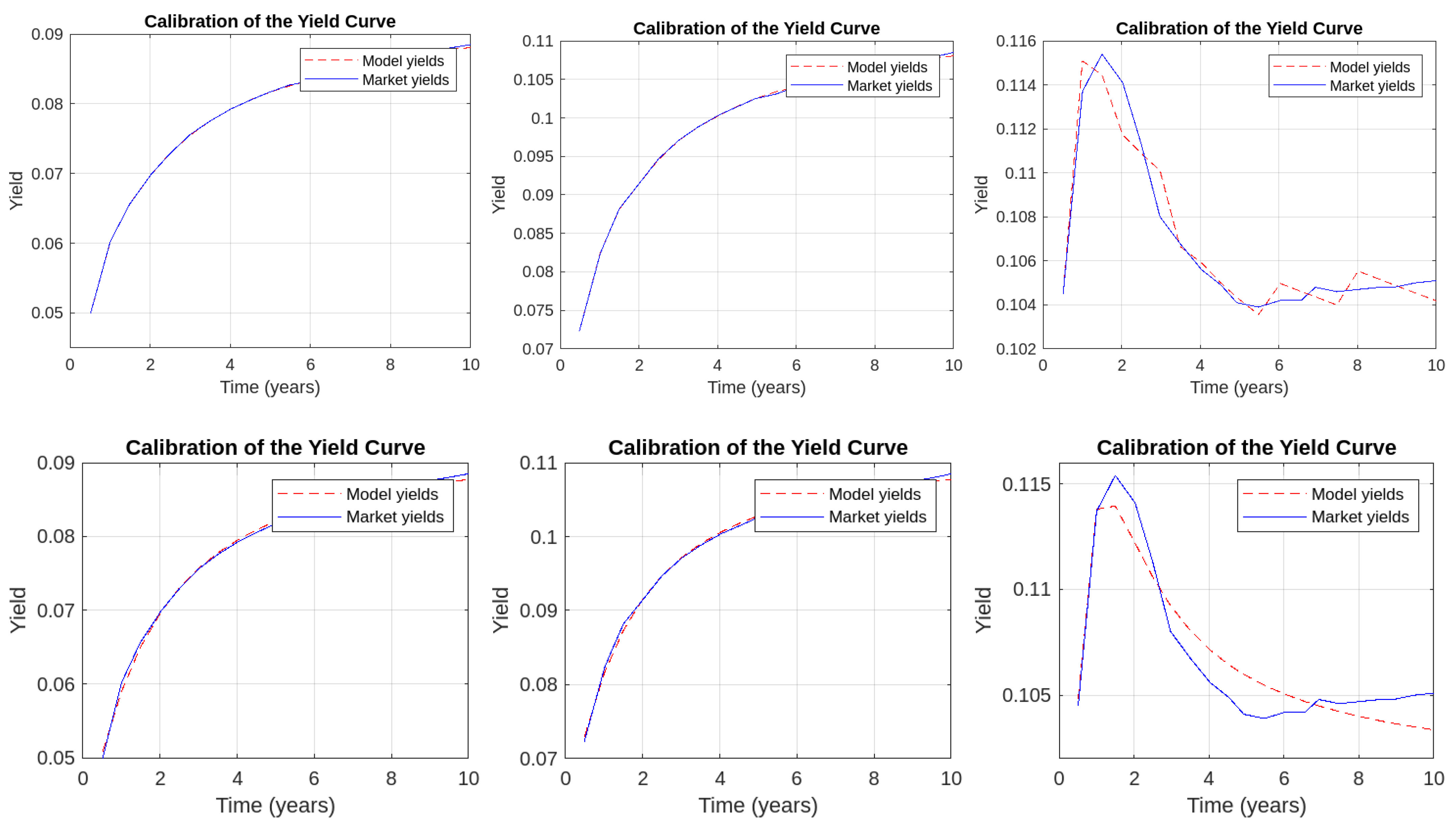

Appendix B. Characteristic Function of the Stochastic Volatility Model with Random Jumps and Stochastic Intensity
| 1 | This set of parameters are typical values found in studies involving Gaussian models with real data (see, for instance, da Silva et al. (2016)). |
References
- Almeida, Caio, and José Valentim Machado Vicente. 2012. Term structure movements implicit in Asian option prices. Quantitative Finance 12: 119–34. [Google Scholar] [CrossRef]
- Backwell, Alex, and Joshua Hayes. 2022. Expected and unexpected jumps in the overnight rate: Consistent management of the libor transition. Journal of Banking & Finance 145: 106669. [Google Scholar] [CrossRef]
- Balduzzi, Pierluigi, Edwin J. Elton, and T. Clifton Green. 2001. Economic news and bond prices: Evidence from the u.s. treasury market. Journal of Financial and Quantitative Analysis 36: 523–43. [Google Scholar] [CrossRef]
- Beber, Alessandro, and Michael W. Brandt. 2009. When it cannot get better or worse: The asymmetric impact of good and bad news on bond returns in expansions and recessions. Review of Finance 14: 119–55. [Google Scholar] [CrossRef]
- Black, Fischer. 1976. The pricing of commodity contracts. Journal of Financial Economics 3: 167–79. [Google Scholar] [CrossRef]
- Bouziane, Markus. 2008. Pricing Interest-Rate Derivatives: A Fourier-Transform Based Approach. Berlin: Springer. [Google Scholar]
- Carr, Peter, and Dilip Madan. 1999. Option valuation using the fast fourier transform. Journal of Computational Finance 2: 61–73. [Google Scholar] [CrossRef]
- Carreira, M.C.S., and R.J. Brostowicz. 2016. Brazilian Derivatives and Securities: Pricing and Risk Management of FX and Interest-Rate Portfolios for Local and Global Markets. London: Palgrave Macmillan UK. [Google Scholar]
- Coffie, Emmanuel. 2023. Delay ait-sahalia-type interest rate model with jumps and its strong approximation. Statistics & Risk Modeling 40: 67–89. [Google Scholar] [CrossRef]
- da Silva, Allan Jonathan, Jack Baczynski, and J. F. Silva Bragança. 2019. Path-dependent interest rate option pricing with jumps and stochastic intensities. Lecture Notes in Computer Science 11540: 710–16. [Google Scholar]
- da Silva, Allan Jonathan, Jack Baczynski, and José Valentim Machado Vicente. 2016. A new finite method for pricing and hedging fixed income derivatives: Comparative analysis and the case of an Asian option. Journal of Computational and Applied Mathematics 297: 98–116. [Google Scholar] [CrossRef]
- da Silva, Allan Jonathan, Jack Baczynski, and José Valentim Machado Vicente. 2020. Efficient Solutions for Pricing and Hedging Interest Rate Asian Options. Working Paper Series; Rio de Janeiro: Banco Central do Brasil. [Google Scholar]
- da Silva, Allan Jonathan, Jack Baczynski, and José Valentim Machado Vicente. 2023. Recovering probability functions with fourier series. Pesquisa Operacional 43: 1–18. [Google Scholar] [CrossRef]
- da Silva, Allan Jonathan, and Leonardo Fagundes de Mello. 2024. On the interest rate derivatives pricing with discrete probability distribution and calibration with genetic algorithm. International Journal of Economics and Finance 16: 42–56. [Google Scholar] [CrossRef]
- Duffie, D. 2001. Dynamic Asset Pricing Theory. Princeton: Princeton University Press. [Google Scholar]
- Duffie, Darrell. 2008. Financial Modeling with Affine Processes. Stanford: Stanford University. Lausanne: University of Lausanne. [Google Scholar]
- Duffie, Darrel, and Kenneth J. Singleton. 2003. Credit Risk: Pricing, Measurement, and Management. Princeton: Princeton University Press. [Google Scholar]
- Fang, F., and C. W. Oosterlee. 2008. A novel pricing method for European options based on Fourier-cosine series expansions. SIAM Journal on Scientific Computing 31: 826–48. [Google Scholar] [CrossRef]
- Fontana, Claudio, Zorana Grbac, and Thorsten Schmidt. 2024. Term structure modeling with overnight rates beyond stochastic continuity. Mathematical Finance 34: 151–89. [Google Scholar] [CrossRef]
- Fukasawa, M. 2011. Asymptotic analysis for stochastic volatility: Martingale expansion. Finance and Stochastics 15: 635–54. [Google Scholar] [CrossRef]
- Gellert, Karol, and Erik Schloegl. 2021. Short Rate Dynamics: A Fed Funds and SOFR Perspective. Available online: https://ssrn.com/abstract=3763589 (accessed on 28 December 2023).
- Genaro, Alan De, and Marco Avellaneda. 2018. Pricing interest rate derivatives under monetary policy changes. International Journal of Theoretical and Applied Finance 21: 1850037. [Google Scholar] [CrossRef]
- Glasserman, P. 2004. Applications of mathematics: Stochastic modelling and applied probability. In Monte Carlo Methods in Financial Engineering. New York: Springer. [Google Scholar]
- Glasserman, Paul, and Steven Kou. 2003. The term structure of simple forward rates with jump risk. Mathematical Finance 13: 383–410. [Google Scholar] [CrossRef]
- Heidari, Massoud, and Liuren Wu. 2009. Market Anticipation of Fed Policy Changes and the Term Structure of Interest Rates. Review of Finance 14: 313–42. [Google Scholar] [CrossRef]
- Johannes, Michael S. 2004. The statistical and economic role of jumps in continuous-time interest rate models. Journal of Finance 59: 227–60. [Google Scholar] [CrossRef]
- Johnson, N. L., A. W. Kemp, and S. Kotz. 2006. Univariate Discrete Distributions, 3rd ed. Wiley Series in Probability and Statistics. New York: Wiley. [Google Scholar]
- Kienitz, Joerg, and Daniel Wetterau. 2012. Financial Modelling: Theory, Implementation and Practice with MATLAB Source. The Wiley Finance Series; New York: Wiley. [Google Scholar]
- Kim, Don H., and Jonathan H. Wright. 2014. Jumps in Bond Yields at Known Times. Finance and economics discussion series; Cambridge: National Bureau of Economic Research. [Google Scholar]
- Kuncoro, Haryo. 2020. Central bank communication and policy interest rate. International Journal of Financial Research. [Google Scholar] [CrossRef]
- Lin, Shih-Kuei, Shin-Yun Wang, Carl R. Chen, and Lian-Wen Xu. 2017. Pricing range accrual interest rate swap employing libor market models with jump risks. The North American Journal of Economics and Finance 42: 359–73. [Google Scholar] [CrossRef][Green Version]
- Liu, Shican, Yanli Zhou, Yonghong Wu, and Xiangyu Ge. 2019. Option pricing under the jump diffusion and multifactor stochastic processes. Journal of Function Spaces 2019: 1–12. [Google Scholar] [CrossRef]
- Oosterlee, Cornelis W., and Lech A. Grzelak. 2019. Mathematical Modeling and Computation in Finance. Singapore: World Scientific. [Google Scholar]
- Piazzesi, Monika. 2005. Bond yields and the federal reserve. Journal of Political Economy 113: 311–44. [Google Scholar] [CrossRef]
- Schloegl, Erik, Jacob Bjerre Skov, and David Skovmand. 2023. Term structure modeling of sofr: Evaluating the importance of scheduled jumps. Available online: https://ssrn.com/abstract=4431839 (accessed on 28 December 2023).
- Shaibu, I., and E. E. Enofe. 2021. Monetary policy instruments and economic growth in nigeria: An empirical evaluation. International Journal of Academic Research in Business and Social Sciences 11: 864–80. [Google Scholar] [CrossRef] [PubMed]
- Topper, J. 2005. Financial Engineering with Finite Elements. The Wiley Finance Series; New York: Wiley. [Google Scholar]
- Valentim, José. 2022. Renda Fixa Aplicada ao Mercado Brasileiro. Rio de Janeiro: IMPA. [Google Scholar]
- Vasicek, Oldrich. 1977. An equilibrium characterization of the term structure. Journal of Financial Economics 5: 177–88. [Google Scholar] [CrossRef]
- Wilmott, Paul. 2006. Paul Wilmott on Quantitative Finance, 2nd ed. Chichester: John Wiley & Sons. [Google Scholar]
- Xu, Mingyang. 2021. Sofr Derivative Pricing Using a Short Rate Model. Available online: https://ssrn.com/abstract=4007604 (accessed on 28 December 2023).
- Yang, Gongyan, and Hongzhong Liu. 2016. Financial development, interest rate liberalization, and macroeconomic volatility. Emerging Markets Finance and Trade 52: 1001–991. [Google Scholar] [CrossRef]

| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | |
| 0.10 | 0.09 | 0.07 | 0.08 | 0.104 | 0.11 | 0.102 | 0.08 | 0.093 | 0.09 | 0.11 | 0.09 | 0.11 | 0.11 | |
| 0.27 | 0.20 | 0.37 | 0.26 | 0.23 | 0.20 | 0.29 | 0.41 | 0.78 | 0.91 | 1.05 | 0.40 | 0.37 | 0.40 | |
| 1.3 × | 3 × | 4.9 × | 3.4 × | 2.1 × | 2.7 × | 0.002 | 0.000 | 0.099 | 0 | 9.4 × | 1.1 × | 1.6 × | 2.8 × | |
| 0.059 | 0.055 | 0.050 | 0.040 | 0.026 | 0.016 | 0.008 | 0.010 | 0.019 | 0.043 | 0.062 | 0.116 | 0.129 | 0.134 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | |
| 2.65 | 2.65 | 2.74 | 2.76 | 2.79 | 2.90 | 2.99 | 0.24 | 0.17 | 0.13 | 0.14 | 0.28 | 0.24 | 0.25 | |
| 0.004 | 0.002 | 0.003 | 0.005 | 0.006 | 0.008 | 0.009 | 0.127 | 0.355 | 0.685 | 0.743 | 1.69 | 1.56 | 2.00 | |
| 5.0 × | 4.5 × | 9.2 × | 8.6 × | 4.6 × | 0.003 | 0.032 | 0.074 | 0.145 | 0.165 | 0.176 | 1.00 | 0.763 | 1.00 | |
| 0.059 | 0.056 | 0.047 | 0.039 | 0.029 | 0.014 | 0.012 | 0.012 | 0.022 | 0.038 | 0.061 | 0.055 | 0.094 | 0.102 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
da Silva, A.J.; Baczynski, J. Discretely Distributed Scheduled Jumps and Interest Rate Derivatives: Pricing in the Context of Central Bank Actions. Economies 2024, 12, 73. https://doi.org/10.3390/economies12030073
da Silva AJ, Baczynski J. Discretely Distributed Scheduled Jumps and Interest Rate Derivatives: Pricing in the Context of Central Bank Actions. Economies. 2024; 12(3):73. https://doi.org/10.3390/economies12030073
Chicago/Turabian Styleda Silva, Allan Jonathan, and Jack Baczynski. 2024. "Discretely Distributed Scheduled Jumps and Interest Rate Derivatives: Pricing in the Context of Central Bank Actions" Economies 12, no. 3: 73. https://doi.org/10.3390/economies12030073
APA Styleda Silva, A. J., & Baczynski, J. (2024). Discretely Distributed Scheduled Jumps and Interest Rate Derivatives: Pricing in the Context of Central Bank Actions. Economies, 12(3), 73. https://doi.org/10.3390/economies12030073






