Strategic Learning Alliances and Cooperation: A Game Theory Perspective on Organizational Collaboration

Abstract

This study explores the dynamics of international strategic learning alliances through the lens of game theory, incorporating complexity and cooperative game theories to develop a model of organizational evolution. Using simulations and network resources, we examine 1200 cases to assess the costs and benefits of inter-organizational cooperation, with a focus on mutual payoffs and strategic decision-making. Our research addresses key gaps in the literature by analyzing how game-theoretic structures impact the success of alliances, providing actionable insights for firms aiming to enhance strategic partnerships. The findings offer valuable guidance for international partners involved in learning alliances, emphasizing the importance of aligning institutional responses with perceived risks and opportunities. By identifying the motivations and success factors behind strategic alliances, organizations can better formulate optimal strategies for collaboration. This paper contributes to the discourse on inter-firm cooperation by highlighting the complexities of strategic learning alliances and offering new perspectives for future research.

1. Introduction

The objective of this paper is to explore the factors essential for establishing successful strategic learning alliances in international contexts, using game theory as the primary analytical framework. This approach provides a detailed examination of how different strategic behaviors influence net payoffs for stakeholders, enabling a nuanced understanding of alliance success. Through the application of theoretical models and empirical simulations, this study contributes to the understanding of inter-firm cooperation dynamics and demonstrates how alliances can be structured to enhance collaboration while mitigating risks, such as opportunistic behavior.

This research stems from a comprehensive investigation into learning dynamics within strategic alliances, integrating both theoretical and empirical elements. While theoretical frameworks provide the foundation, the empirical component, including simulations, plays a significant role in the latter part of the paper. Game theory is employed to examine learning processes in alliances, recognizing that these dynamics may involve both one-time and repeated interactions between partners.

This study focuses on identifying the key drivers of successful strategic learning alliances in international collaborations. Specifically, it aims to (a) examine the motivations and determinants that contribute to alliance success and (b) evaluate partners’ perceptions of the net payoffs from their strategic relationships, which include both costs and benefits. In addition, this research seeks to define optimal behavioral strategies that align with the unique dynamics of learning alliances.

The decision to focus on international alliances stems from the unique challenges and dynamics that these alliances present, which are often less prevalent in purely domestic collaborations or other forms of partnerships. International strategic alliances introduce additional layers of complexity, including cultural, regulatory, and economic differences, that directly impact the strategic decisions and cooperative behaviors of the involved organizations. These factors make international alliances a particularly relevant context for applying game theory to understand how entities navigate and manage such complexities to achieve successful collaboration.

By concentrating on international alliances, this study aims to provide insights into strategies that are specifically tailored to the complexities of cross-border partnerships. This targeted approach allows us to explore the distinct motivations, risks, and success factors that international organizations face, thereby contributing more precise and actionable guidance for entities engaged in these types of alliances.

Several factors motivated the choice of this topic. First, alliances play a crucial role in fostering inter-firm cooperation, as highlighted by scholars such as Hamel (1991), Majdalawieh et al. (2017), Olk and Elvira (2001), Tlemsani and Matthews (2021), Day (1995), Tlemsani et al. (2024), and Mintzberg et al. (1998), who emphasize their significance in shaping corporate strategies and global economic development. Second, alliances serve as mechanisms for exchanging information (Mohamed Hashim et al. 2024), disseminating knowledge, and facilitating learning, as discussed by Mohamed Hashim et al. (2022b), Child and Faulkner (1998). These scholars argue that alliances should be designed to maximize their potential for organizational learning.

This research addresses the following key questions:

• What net payoffs do stakeholders derive from their collaborative efforts in alliances?
• What factors contribute to the success of international organizations in realizing the benefits of strategic learning alliances?
• What cooperative strategies are most effective in fostering successful learning alliances?

The structure of the paper is outlined as follows: Section 2 offers a review of the existing literature on strategic alliances, discussing the driving factors behind alliance formation, as well as the associated advantages and disadvantages, factors contributing to success or failure, and the role of networks in alliance dynamics. Section 3 outlines the research methodology, describing both secondary and primary data collection methods, as well as the simulations conducted (Mohamed Hashim et al. 2021). The Section also explains the models employed in the analysis, examples include models based on predefined assumptions employing ergodic search techniques, the a priori model incorporating logical constraints, and the Random Landscape Model used for simulation purposes.

In Section 4, the analysis of the results is presented, including a new taxonomy of games that explores the dynamics of cooperation and defection among coalition members. The benefit and cost structure of cooperation is examined, with an emphasis on the importance of joint efforts and reputation in shaping outcomes. Section 5 discusses the empirical findings, considering their broader implications for strategic alliances. Finally, Section 6 offers conclusions based on the research findings and discusses potential directions for future research.

2. Literature Review

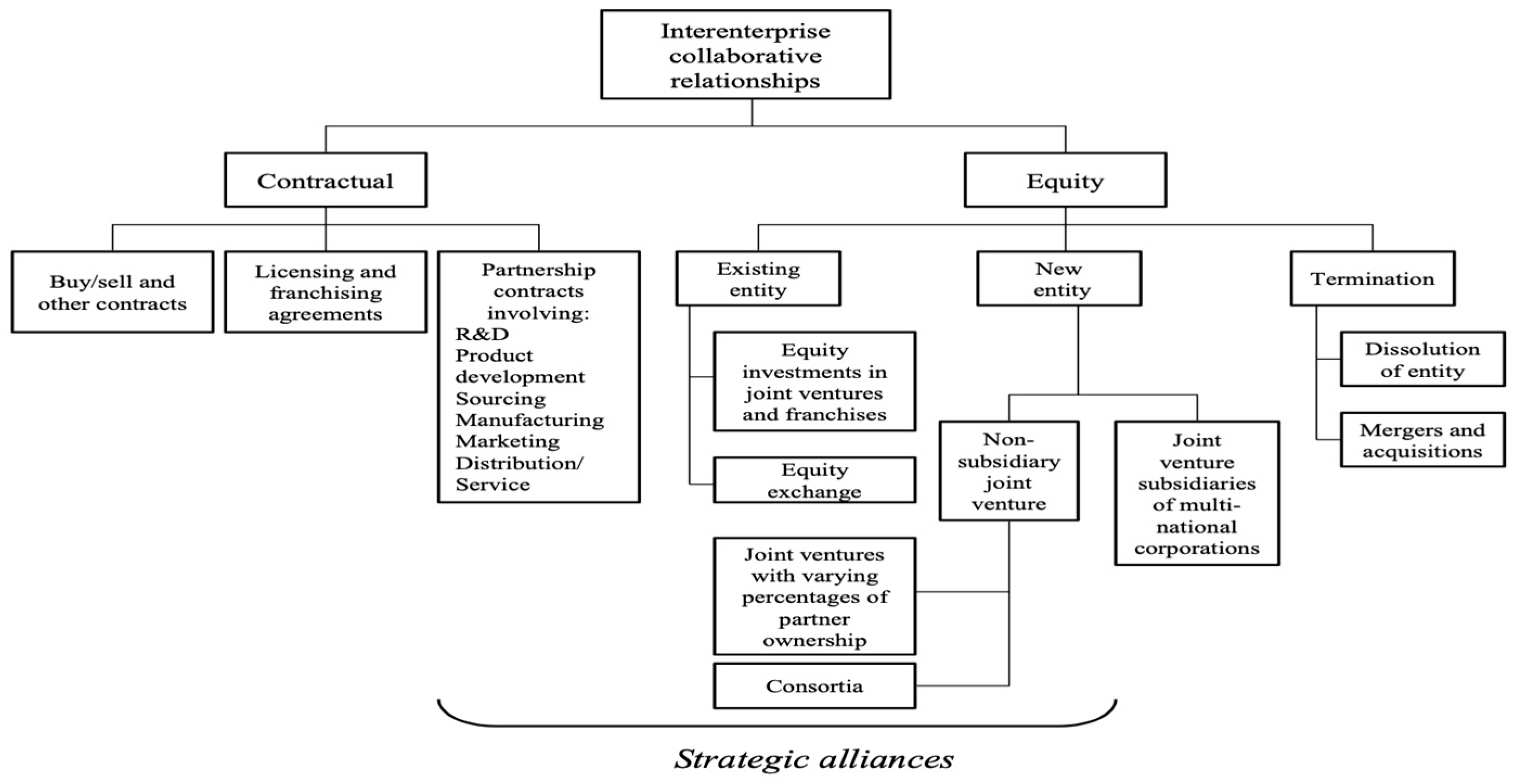
2.1. Strategic Alliances

The study of strategic alliances spans a broad spectrum of perspectives, focusing on their formation, evolution, and underlying dynamics. Key scholars, such as Gulati (1998), Gulati et al. (2000), Mockler (2000), Tlemsani (2010), and Parkhe (2017), have delved into the conceptual foundations of strategic alliances, emphasizing their strategic importance in modern business environments. These alliances are recognized as critical tools for organizations to achieve long-term objectives and competitive advantage.

A growing body of research, including works by Nevaer and Deck (1990), Stafford (1994), Tlemsani (2022), Mohamed Hashim et al. (2024), Varadarajan and Cunningham (1995), and Rule and Keown (1998), highlights the increasing adoption of strategic alliances across various industries. These studies reveal how alliances have become integral to the evolving landscape of business relationships, facilitating the attainment of strategic goals and the realization of competitive advantages (Figure 1).

The efficacy of partnership relations as a method for maintaining or enhancing competitive positioning is supported by Porter and Fuller (1986). Lorange and Roos (1992) further expand on this by distinguishing alliances based on hierarchical versus free-market relationships, underscoring the varied nature of strategic partnerships. Harbison and Pekar (1998) also highlight the importance of strategic alliances, noting their role in shared distribution, collaborative marketing, and the broader strategic objectives of firms.

Strategic alliances are often employed to expand market reach, improve competitive positioning, and acquire technical expertise. While alliances are powerful tools for growth, scholars like Tlemsani (2020), Faems et al. (2012), and Dodge and Salahuddin (1998) also argue for alternative strategies, such as internal growth or mergers and acquisitions, when appropriate. The notion of co-specialization, as explored by Haberberg and Rieple (2001), emphasizes how alliances leverage complementary skills, making them key contributors to organizational success.

Risk mitigation is another major motivation for forming alliances, as argued by Jarillo (1993) and Inkpen (1998). Alliances allow firms to share risks and gain access to each other’s resources, enhancing overall strategic capabilities. Moreover, studies by Hoogeboom and Wilderom (2019), Tlemsani et al. (2023b), and Contractor and Lorange (1988) point to the role of alliances in achieving economies of scale and competitive positioning. Bidault and Cummings (1996) reinforce this, suggesting that alliances are primarily formed to exchange resources and competencies.

Empirical studies also support the growing relevance of strategic alliances in corporate strategy. Harbison and Pekar (1998) document a significant increase in revenue generated through alliances among leading U.S. firms, with alliance-oriented companies consistently outperforming others in terms of returns on investment. Mockler (2000) highlights a global trend in alliance formation, with U.S. companies increasingly collaborating with international partners, and a majority of CEOs acknowledging the success of such collaborations.

Key insights from the literature include the following:

Collaboration maximizes total realized payoffs (Σ$a_{xy}$ actual): Successful alliances depend on collaboration to achieve mutual benefits. Maximizing collective payoffs requires aligning individual payoffs for all partners over time.

• Short-term strategies can undermine long-term cooperation: Strategies focused on immediate gains, such as defection in one-shot prisoner’s dilemma games, can damage trust and destabilize alliances.
• Joint and reputation benefits are crucial for sustainable alliances: Cooperative strategies that emphasize shared and reputation-based benefits, as seen in games 1, foster long-term collaboration.
• Sophisticated cooperative strategies build trust: Approaches like “Firm-but-Fair”, supported by communication, are more effective than retaliatory strategies like Tit-for-Tat. These strategies foster collaboration and strengthen trust within alliances.

2.2. Game Theory

Game theory offers a systematic approach to examining strategic decision-making within markets, helping in understanding competitor and partner behaviors under various conditions Tlemsani et al. (2023a), and Dixit and Nalebuff (1991). Rather than recommending optimal strategies, it clarifies potential outcomes when rules or strategies change, enhancing business competitiveness and guiding policy development (Nalebuff and Brandenburger 1996). This approach is valuable for studying competitive and cooperative behaviors, offering strategic insights into complex social and economic systems.

This study categorizes alliances into specific game types, such as the prisoner’s dilemma, Chicken Game, and Dominant Cooperative Games, each with defined Nash equilibria. These classifications aim to analyze distinct strategic choices in structured scenarios. However, real-world alliances often involve evolving, dynamic interactions, especially in repeated engagements where past outcomes influence future decisions.

In zero-sum games, one player’s gain is the other’s loss, making maximum strategy (selecting the best of the worst outcomes) rational. In non-zero-sum games, cooperative elements often emerge, allowing players to benefit from coordination, a more common dynamic in real-world scenarios.

The Nash equilibrium represents a stable state where no player benefits from unilaterally changing their strategy. This stability assumes common knowledge rationality (CKR) and consistently aligned beliefs (CABs), where players share rational expectations and conclusions (Harsanyi 1966).

(a)

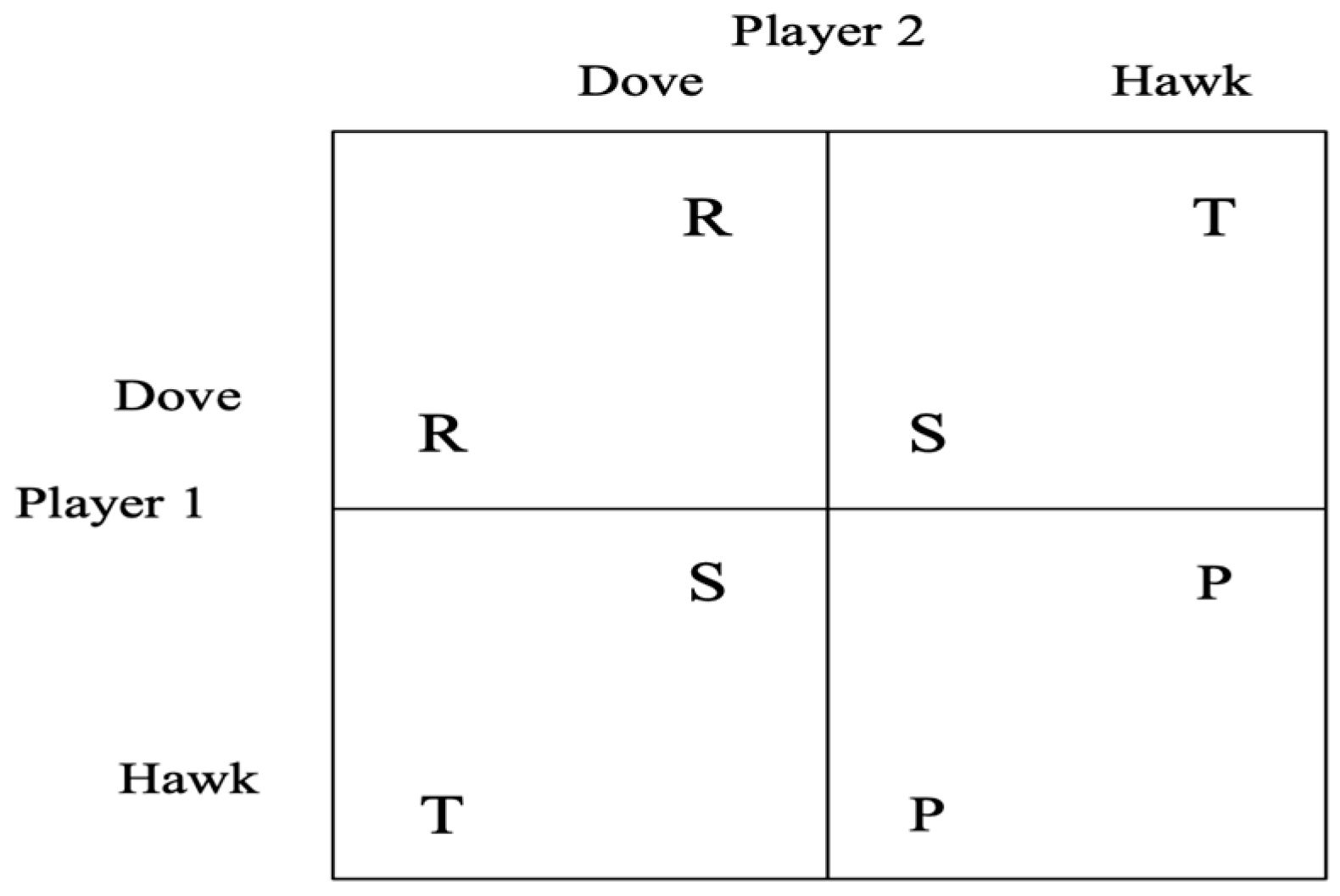
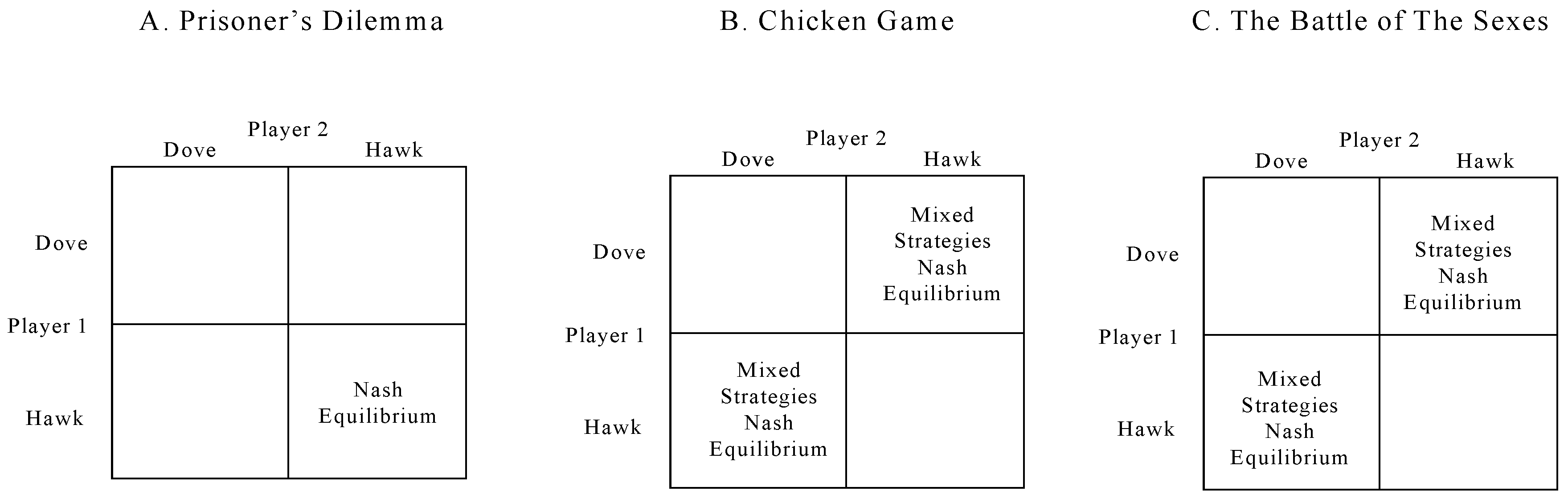
The Prisoner’s Dilemma: This well-known scenario illustrates a situation where two participants must choose between cooperating or acting in their own self-interest by defecting. While the optimal choice for each individual is to defect, resulting in a suboptimal outcome for both, cooperation would actually lead to a more favorable result for both parties. This results in a suboptimal outcome for both, highlighting the challenges of strategic decision-making in alliances. The game represents Games 2 scenario in game theory, illustrating the conflict between individual rationality and collective benefit.

(b)

Chicken Game: The Chicken Game derives from a contest where two drivers head toward each other, with the first to swerve being labeled the “chicken”. If neither swerve, both lose, and if both swerve, the result is mutual avoidance. This game, classified as a Games 3, highlights the risks associated with aggressive competitive strategies in alliances. Strategic decisions in such contexts depend heavily on the willingness of each party to compromise.

(c)

Dominant Cooperative Strategy Games: In these games, cooperative behavior is the most advantageous outcome for all players. The payoff structure incentivizes cooperation, making it the dominant strategy. Such games are classified as Games 1, where alliances succeed through mutual collaboration and trust-building.

(d)

The Gender Dynamics Debate: This coordination game, classified as Game 4, features two players attempting to align their actions, even though they have different preferences. The challenge lies in balancing individual desires with the need for mutual coordination. Strategies like commitment or hierarchical decision-making can help overcome this coordination dilemma and lead to optimal outcomes.

(e)

The Cost/Benefit Structure of a ‘One-Shot Game’: In one-shot games, players’ perceptions of payoffs play a crucial role in shaping their decisions. Rapoport and Chammah (1965) explored the distribution of payoffs in two-player positive-sum games, underscoring the significance of players’ perceptions in driving game outcomes.

In the prisoner’s dilemma, the preference order typically follows T > R > P > S, while in Chicken, the order is T > R > S > P. This differentiation clarifies how varying payoff structures influence strategic decision-making.

Figure 2 illustrates the payoffs for two-player positive-sum games, such as the prisoner’s dilemma or Chicken. These games encompass both collaborative and competitive elements. For instance, players can choose between hawkish (H) or dove-like (D) strategies in a simultaneous move game. If both players adopt dove-like strategies, they share the value V. Conversely, if both players behave hawkishly, they destroy the value, resulting in each player receiving W, where W = ½ (V − C), with C representing the cost of conflict (Vega-Redondo 1996).

Avoiding aggressive, hawkish strategies in favor of cooperation benefits both parties, suggesting that alliances perform better when partners avoid direct conflict. When the value of cooperation exceeds the cost, the game aligns with the prisoner’s dilemma. However, when costs are higher, the game mirrors Chicken, where the risks of defection are significant.

Rational strategies and Nash equilibria differ across games, as illustrated by Figure 3. In one-shot Chicken Games, for example, the Nash equilibria include both pure strategies, such as (H, D) and (D, H), and a mixed-strategy Nash equilibrium (MSNE), where each player adopts a probabilistic strategy based on the payoff structure: V/C.

3. Research Methodology

Our approach utilizes a multi-step methodology that incorporates a comprehensive literature review, the collection of both qualitative and quantitative primary data, and the application of sophisticated simulation models. The a priori model with ergodic search and Random Landscape Model are employed to systematically evaluate various payoff scenarios within alliances, allowing for an in-depth assessment of cooperative versus competitive outcomes. Key assumptions include the symmetry of payoffs and the impact of external variables on alliance stability. The Delphi technique is used to refine hypotheses, while survey data are analyzed to validate the models’ predictive accuracy regarding alliance performance across different strategic contexts.

This study employs static game models to focus on one-time interactions between alliance partners. This approach prioritizes immediate payoff structures without factoring in temporal elements like a discount factor, which are essential in dynamic or repeated game models. The omission of a discount factor means that the simulations do not explicitly account for the value of future cooperation versus immediate gains, as would typically be conducted in models that consider ongoing interactions and evolving strategies over time.

We acknowledge that incorporating a discount factor could enhance the model’s ability to reflect realistic alliance dynamics by allowing for the evaluation of long-term cooperation potential. Future iterations of this research could introduce a repeated-game framework with a discount factor to represent the diminishing present value of future payoffs, thereby providing a more comprehensive analysis of sustained cooperative behavior in alliances. This addition would allow the model to explore how the value of cooperation might shift over time, encouraging strategies that favor long-term collaboration over short-term gains.

3.1. Simulation

The choice to utilize simulated cases rather than actual real-world data was primarily driven by the complexity and variability of real-world alliances, which can introduce numerous uncontrollable external factors. The simulation model enables a systematic exploration of alliance dynamics across a wide range of scenarios and controlled variables, allowing for a more focused analysis of strategic decision-making patterns and cooperative behaviors in international alliances. By standardizing the variables, the simulations facilitate a clearer understanding of the impact of game-theoretic structures on alliance outcomes.

Moreover, the lack of comprehensive, detailed, and comparable real-world data on strategic alliances across diverse international contexts presents a significant limitation in conducting empirical studies (Mohamed Hashim et al. 2022a). Simulations provide a viable alternative to explore theoretical frameworks and to generate insights that can later be tested empirically if such data become available.

• Model A: An ergodic search method was utilized to explore all possible configurations of payoff perceptions from the perspective of Player 1, a member of the coalition. Initially, 24 payoff combinations were generated. By considering all permutations of positive and negative payoffs, this number expanded to 120 potential outcomes. A comprehensive search was then conducted to pinpoint games that met the predefined criteria of the model.
• Model B: This model built on the outcomes of Model A by introducing logical constraints to refine the search parameters. These constraints were designed to exclude combinations that were logically inconsistent with the results of the first model. This refinement process narrowed the focus to more feasible game scenarios, enabling a more targeted analysis.
• Model C: Stochastic Landscape Simulation in Computing: This approach was chosen for several critical reasons, such as the limited availability of empirical data, the necessity to analyze extensive datasets, and the objective of evaluating random variations in coalition benefits and costs in comparison to the outcomes predicted by the a priori models. The randomly selected values in this simulation were assigned to the cost and benefit variables (as outlined in

  Table 1. Outlines the ranges for the benefit and cost variables.

  Benefit/Cost	Description	Range
  Benefits of transfer	Agent X’s benefit as part of a coalition with Agent Y	r ∈ (0, 1)
  Transfer costs	Expenses incurred by agent x for making a transfer	c ∈ (0, 1)
  Benefits of Joint	The payoffs agents receive through collaborative efforts	b∈ (0, 1)
  Reputation benefits	Net gained by coalition members from their association	d ∈ (0, 1)
  Exit costs	Penalties or costs associated with leaving the coalition	h ∈ (−1, 1)

  ), and various payoff matrices (A, B, C, and D) were calculated for 1200 cases. The analysis of this dataset allowed for the identification and examination of diverse categories of games based on the delivery of outcomes.

3.2. Research Model

This study employs a static game approach to analyze strategic decision-making within international alliances, focusing primarily on immediate interactions rather than long-term benefit distribution mechanisms that are typically explored in cooperative game theory. The static game models were chosen to examine how partners in international alliances make one-time strategic choices under fixed conditions, reflecting scenarios where immediate payoffs are critical.

In this paper, the focus remains on understanding how different strategic behaviors influence net payoffs within these alliances rather than on determining payoff distribution among coalition members. While cooperative game theory elements, such as Shapley value and coalition formation, provide valuable insights into long-term payoff allocation and shared benefits, these were beyond the scope of the current analysis.

However, recognizing the importance of cooperative game theory in understanding coalition benefits and payoff allocation, future works could expand the model to incorporate these elements. Integrating Shapley values or coalition formation benefits would allow for a deeper exploration of equitable payoff distribution and enhance the model’s capacity to analyze sustained cooperative strategies within alliances.

The research model developed by Matthews (1999, 2002) incorporates essential concepts from complexity theory, cooperative game theory, and network resource theory. The model incorporates several crucial components, which are detailed below:

• As noted by Matthews (1999, 2002), within an alliance, two entities, referred to as stakeholders x and y, engage in a partnership that generates two types of payoffs: potential payoffs and realized payoffs. The potential payoffs are denoted by $a_{xy}$, and the sum of these potential payoffs for all members of the alliance is calculated using the formula:

  $${\mathrm{S}}_{\mathrm{potential}}=\mathsf{\Sigma }{a}_{xy}$$

  (1)
• The potential payoffs in an alliance are determined by deducting the costs (β_ij) from the benefits (α_ij). This relationship is expressed by the following equation

  a_xy = (α_ij − β_ij).

  (2)
• The realization of payoffs is contingent upon the degree of cooperation between partners x and y, who are identified as agents or stakeholders. Payoffs remain in their potential state until they are activated by the stakeholders. The cooperative variables are denoted as Θ_x and Θ_y; which represents the level of collaboration between the two stakeholders. The decision-making process is binary, involving an all-or-nothing approach (Θ ∈ 0, 1) and the realizing payoffs requires both identifying the potential payoffs $a_{xy}$ and taking steps to activating them.
• Thus, the model suggests that the realized payoffs from an alliance depend on balancing potential benefits and costs, along with the level of cooperation between partners.
  Or, briefly,

  a_ij ~ Θ_xΘ_y

  (3)

  S_actual = Σ_xΣ_y a_xy. Θ_xΘ_y

  (4)
• Matthews (1999) examines coalitions through the framework of cooperative games and introduces a model for understanding cooperation. He describes several key variables involved in alliances:
  • Transfer benefits (r) are those transferred from one agent (i) to another agent (j), while transfer costs (c) are the expenses incurred by the agent making the transfer, thus, if Θ_x = 1 then r_xy ≥ 0 and c_xy ≤ 0.
  • Joint benefits (b) represent the net outcomes that all agents receive from collaborating, thus, bxy ≥ 0 if and only if both Θ_x ≥ 0 and Θ_y ≥ 0.
  • Reputation benefits refer to the net advantages (d) gained by individuals simply through their association with the coalition, thus, d_xy ≥ 0 if Θ_x ≥ 0 or Θ_y ≥ 0 or both.
  • Exit costs (h) represent the costs of leaving the coalition, thus, h_x ≤ 0 and h_y ≤ 0 if Θ_x = 0 or Θ_y = 0.
• The actual payoff is summarized as follows:

  S_actual = Σ_xΣ_y (r_xy + b_xy + d_xy – c_xy + h_xy) Θ_xΘ_y

  (5)

The model operates under assumptions including the equal distribution of payoffs among coalition members and the characterization of the coalition as a binary framework.

Assuming symmetry, the payoff for any individual player is represented as S_(player):

S_(player)x = r + b + d − c  if  Θx = Θy = 1
S_(player)x = d − c   if  Θx = 1 and Θy = 0
S_(player)x = r + d   if  Θy = 1 and Θx = 0
S_(player)x = h       otherwise

(6)

• The benefits and costs arising from the coalition are distributed randomly, with values between zero and one. However, exit costs are unique, ranging from negative-one to one (indicating that exit costs may be either positive or negative, leading to distinct games 2 and 3).
  The random distribution of benefits and costs in the simulation model was employed to capture a broad spectrum of potential scenarios that coalition members might encounter in strategic alliances. This approach enables an exploration of player behavior across diverse payoff structures without predefining specific conditions, thereby reflecting the uncertainty and variability often present in real-world alliances.
  To analyze player behavior under these varying conditions, the model evaluates each scenario by calculating payoffs based on different combinations of cooperative and competitive strategies. By doing so, it identifies patterns in decision-making and determines the conditions under which cooperation becomes a dominant strategy or when defection is more likely. The model allows for an examination of how players adapt their strategies in response to different benefit–cost distributions, thereby providing insights into strategic behavior across a range of alliance dynamics.
• Alliances seek to explore different combinations of potential outcomes, which are influenced by how each participant values the benefits and costs associated with the alliance. Equations (1) through (7) offer a comprehensive visual representation of the research model.

  Transfer benefits      r ∈ (0, 1)
  Transfer costs       c ∈ (0, 1)
  Joint benefits       b ∈ (0, 1)
  Reputation benefits    d ∈ (0, 1)
  Exit costs         h ∈ (−1, 1)
  

  (7)

• Model A Rational Possibilities I

Three distinct outcomes arise in the initial iteration based on Equations (1) to (6).

• Game 1: When A > C and B > D, joint benefits surpass transfer costs, making cooperation the optimal strategy. The Nash equilibrium in this scenario is (1, 1).
• Game 2: If A < C, B < D, and D ≥ 0, then the shared benefits are insufficient to cover the costs of transfers, with these costs outweighing reputation benefits. This situation presents two possible games:

  (a)

  A one-time (prisoner’s dilemma) game where the Nash equilibrium is (0, 0).

  (b)

  A repeated interaction game where the Nash equilibrium shifts to (1, 1).

• Game 3: If A < C and B < D, and D < 0, the game takes on characteristics of a “chicken” scenario, presenting three Nash equilibria: (0, 1), (1, 0), and a mixed-strategy equilibrium.

• Model B Rational Possibilities II

A second iteration, using Equations (1) to (7) refines the classification of these games. The methodology outlined above serves as the foundation for the research approach.

4. Findings

4.1. Simulation

Model A—Ergodic Search: Considering diverse rankings of game payoff perceptions among coalition members, there emerge 24 potential variants of payoff perceptions.

In each scenario, payoffs can either be positive or negative, resulting in a notably higher variety of possible outcomes. For example, if the initial decision, referred to as A in Variant 1, has a negative payoff, then the subsequent decisions (B, C, D) will also yield negative payoffs. Despite this, the total number of possible outcomes is considerably smaller than in cases where positive and negative payoffs are assigned randomly. Figure 4 below provides an illustration of how these positive and negative payoffs can be distributed across different outcomes. For each variant (e.g., Variant 1) there are 5 possible outcomes (Figure 4).

If A results in a negative outcome, then B, C, and D will also produce negative outcomes. On the other hand, if A is positive, the outcomes for B, C, and D may be either positive or negative. As a result, the total number of possible combinations across the 24 variations is calculated as 24 × 5 = 120.

Our simulation includes all 120 potential combinations. Out of these, each of the 24 variants consists of six instances for game 1, game 2, and game 3. Furthermore, among the total 120 potential payoff outcomes, there are 30 games in game 1, 20 games in game 2, and 10 games in game 3.

Model B—Restricted Search: Some outcomes may not be practically achievable due to logical constraints. To handle this, it is essential to evaluate different payoffs and apply specific restrictions to ensure consistency in the results. The relationships and dependencies between variables are summarized in 3 steps.

Step 1: focusing on the viewpoint of one player (such as Player 1), the payoffs can be assessed by examining the relationship between costs and benefits (

Table 2. Logical constraints. Step 1.

Compared Payoffs			Compared Benefits and Costs
A	B	A–B	= (r + b + d − c) − (d − c) = r + b > 0	A > B	Possible	A < B	Impossible
A	C	A–C	= (r + b + d − c) − (d − c) = b − c > or < 0	A > C	Possible	A < C	Possible
A	D	A–D	= (r + b + d − c) − h > or < 0	A > D	Possible	A < D	Possible
B	C	B–C	= (d − c) − (r + d) = −r – c = −(r + c) < 0	B > C	Impossible	B < C	Possible
B	D	B–D	= (d − c) − h > or < 0	B > D	Possible	B < D	Possible
C	D	C–D	= (r + d) − h > or < 0	C > D	Possible	C < D	Possible

r, b and c are positive, therefore (r + b) > 0 and (r + c) < 0 that is logically consistent: B is often called as “sucker’s payoff” and should be avoided.

).

As a result of Step 1, two key logical constraints have been established: (i) A cannot be smaller than B (A < B—not possible), and (ii) B cannot exceed C (C < B—not possible).

Step 2: Further evaluation indicates that D will not be the initial option for every coalition, as it suggests non-cooperative actions from both parties, ultimately leading to the breakup of the coalition. Therefore, (iii) D cannot surpass A, B, or C (D > A, B, C—not possible).

Step 3: After reviewing the payoffs for A, B, C, and D, and taking into account their cost–benefit relationships, it becomes clear that C is composed of r and d, meaning it cannot have a negative value. Thus, (iv) C cannot be less than zero (C < 0—not possible)

By applying the four steps (i) through (iv) to the set of all possible outcomes, 100 out of the 120 games are excluded. This approach narrows the distribution of games through a constrained search method. The resulting 20 games are organized within a newly created, comprehensive taxonomy that encompasses all potential game types.

4.2. New Games Taxonomy

Out of the original 120 possible outcomes, 20 games meet the logical constraints. These games are divided into four distinct types, with each type further categorized into several subtypes.

• Model 3—Random Landscape

Each run produces unique combinations of coalition benefit and cost variables, leading to entirely different payoff rankings and game distribution combinations. However, despite the variation in results, the number of games and their proportions tend to remain consistent.

The intervals chosen for the Random Landscape Model were designed to reflect a wide range of potential alliance outcomes, capturing both cooperative and competitive dynamics commonly seen in strategic alliances. These ranges were selected based on theoretical principles of game theory and strategic management, representing various scenarios from highly collaborative to more adversarial interactions.

• Representation of Cooperative Scenarios: In strategic alliances, partners often aim to maximize joint benefits while sharing resources and risks. To reflect this, the model includes intervals that favor positive payoffs for both parties, simulating scenarios where trust and alignment lead to high mutual benefits. These intervals capture alliance settings where cooperation is incentivized, allowing us to analyze how alliances perform under optimal collaborative conditions.
• Competitive and Mixed-Motive Scenarios: Recognizing that not all alliances are purely cooperative, some intervals are set to capture competitive or mixed-motive dynamics. These ranges simulate situations where organizations may face conflicts of interest or where individual incentives diverge from collective goals. For instance, payoff intervals that include lower or negative values represent potential risks or costs each partner might incur, allowing the model to reflect scenarios similar to the prisoner’s dilemma, where individual gains can undermine collective benefits.
• Exploration of Alliance Evolution: The chosen intervals are designed with the understanding that alliances often evolve over time, influenced by feedback, learning, and changing external conditions. Although the Random Landscape Model in its current form uses static intervals, these ranges provide a foundation for future research that might incorporate dynamic or adaptive payoff structures to reflect shifting alliance contexts more accurately.

5. Analysis and Discussion

Results reveal that alliances thrive under cooperative strategies that prioritize joint and reputation benefits. Visual analyses, including heatmaps and comparative charts, underscore the differential impact of cooperative versus non-cooperative behaviors on alliance longevity and success. The analysis identifies specific game types where cooperation yields Pareto-optimal outcomes, aligning with theoretical expectations of cooperative game models. These findings are contextualized within the broader literature on strategic alliances, confirming and extending existing theories on the benefits of cooperative strategies. Our discussion elaborates on how strategic decisions, influenced by perceived costs and benefits, shape the evolutionary paths of alliances, offering a refined framework for predicting alliance outcomes.

5.1. Strategic Alliances and Games New Classification

The classification of games into different types is based on the order of payoffs and is determined by the cost and benefit structure specific to each game.

i. 

Games 1

• Game 1.1 is a fully cooperative scenario where “A” serves as both the Pareto optimal outcome and the Nash equilibrium. In this game, cooperation emerges as the most favorable strategy for all participants.
• Games 1.2 and 1.3 also have “A” as the Pareto optimum, but each game type includes two Nash equilibria.

In both cases, although “A” is the best option for both players, another option, “D”, also functions as a Nash equilibrium. Players may hesitate to choose “A” because they fear that if they cooperate (play Dove), the other player might defect (play Hawk), resulting in “B”, the sucker’s payoff. This uncertainty creates a temptation for both players to play Hawk.

To overcome this issue and successfully choose “A” in 1.2 and 1.3 games, communication between players is necessary. In these games, shared benefits and reputation, along with the difference between the payoff’s “A” and “D” play a crucial role in maintaining cooperation.

ii. 

Games 2

Game 2 mirrors the structure of the prisoner’s dilemma. In this game, “C” represents the Pareto optimal outcome, whereas “D” functions as the Nash equilibrium in a single-round interaction. However, with repeated interactions, the Nash equilibrium gradually moves toward “A” (

Table 3. Games 2 benefits and costs structure.

Games	Payoff Ordering	Costs and Benefits Structure
Game 2.1	C > A > D > B, D >= 0	r + d > r + b + d − c > h > d − c, h >= 0
Game 2.2	C > D > A > B, D >= 0	r + d > h > r + b + d − c > d − c, h >= 0

).

In this type of game, the relationship between “b” and “c” is key, with a small “b” and a large “c” being characteristic of the game dynamics.

iii. 

Games 3

Games 3 correspond to the Chicken game. Similar to games 2, “C” represents the Pareto optimal outcome; however, in this case, “D” is negative. This scenario gives rise to multiple Nash equilibria, including (0, 1), (1, 0), and a mixed-strategy equilibrium. In the mixed strategy, each player chooses to play hawk with a probability determined by the balance between the reward for winning and the cost of the conflict (

Table 4. Games 3 benefits and costs structure.

Games	Payoff Ordering	Costs and Benefits Structure
Game 3.1	C > A > D > B, D < 0	r + d > r + b + d − c > h > d − c, h < 0
Game 3.2	C > D > A > B, D < 0	r + d > h > r + b + d − c > d − c, h < 0

).

iv. 

Games 4

Games 4 represent a new category introduced in this game classification framework, where “C” continues to act as the Pareto optimal outcome.

• Game 4.1 represents the classic "hawk-dove" scenario. The inclusion of a negative payoff, D, leads to the existence of multiple equilibria, akin to the strategic dynamics observed in the Chicken game. In this context, each player chooses the hawk strategy with a probability influenced by the payoff structure, striking a balance between the potential rewards of victory and the associated costs of conflict.
• Game 4.2, in contrast, feature a positive “D” making them resemble the “Battle of the Sexes” game. In these games, each player prefers to participate in an activity they like with their partner, such as Player 1 going to a football game (play 0, 1) or Player 2 attending a theater performance (play 1, 0). However, if neither option is possible, they would each prefer to go alone to their favorite activity (play 0, 0) (

  Table 5. Games 4 benefits and Costs structure.

  Games	Payoff Ordering	Costs and Benefits Structure
  Game 4.1	C > A > B > D, D < 0	r + d > r + b + d − c > d − c > h, h < 0
  Game 4.2	C > A > B > D, D >= 0	r + d > h > r + b + d − c > d − c > h, h >= 0

  ).

5.2. New Taxonomy and Strategic Alliances

The newly developed taxonomy of games offers a framework for analyzing and predicting cooperative outcomes in strategic alliances. By assessing potential outcomes for prospective alliance members and categorizing them into one of four game types, we can make informed predictions about the likelihood of alliance success.

• Game 1.1 games present the most favorable conditions for alliance formation, as cooperation is the dominant strategy. These situations typically lead to successful alliances, as both parties are incentivized to collaborate. In contrast, Game 1.2 and Game 1.3 games require effective communication to ensure that both partners adopt cooperative behavior, as the possibility of defection exists without adequate coordination.
• In games 2, partners are more likely to avoid forming an alliance, as the payoff structure is less attractive. Potential partners would be better off seeking alternative coalitions that offer more favorable payoff combinations. However, if an alliance is deemed necessary or desirable, factors such as repetition, reputation benefits, and the difference between payoffs (A and D) will significantly influence its success.
• Game 3 and Game 4.1 games are highly competitive, making long-term coalition formation unlikely. In these scenarios, prospective partners may seek to avoid cooperation unless they have a critical need that can only be met through the alliance. In such cases, the success of cooperation will largely depend on the magnitude of payoff D and the associated conflict costs.
• Game 4.2 games represent unique situations where partners may prioritize participation in a coalition over actual cooperation and individual payoffs. In these instances, partners are more likely to adopt asymmetric strategies, such as (0, 1) and (1, 0), or pursue a mixed-strategy Nash equilibrium, rather than striving for mutual cooperation (1, 1).

5.3. Comparison: Priori Model vs. Random Landscape

The distribution of games by the Random Landscape Model shows notable differences compared to the results from the a priori model. These variations can be explained by several factors:

(a) 

Difference Between Classified Games and Total Cases

The inconsistency arises between the overall number of cases (1,200) and the categorized games stems from differing criteria in the two models. In the a priori model, scenarios where D is the dominant choice (D > A, B, C) are excluded due to step 3. Conversely, in the Random Landscape Model, where the parameters r, d, c, and h are assigned randomly, there are situations where D surpasses A, B, and C. These “D-dominated games” are included in the count of classified games, resulting in a higher number of games compared to the total cases (

Table 6. Game distribution— Models (A, B, C) vs. the Random Landscape.

A Priori (Restricted)
	Game1				Game2			Game3			Game4			Total
	1.1	1.2	1.3	1	2.1	2.2	2	3.1	3.2	3	4.1	4.2	4
# of games	3	3	2	8	2	3	5	2	1	3	3	1	4	20
% of games #	15	15	10	40	10	15	25	10	5	15	15	5	20	100
Random Landscape
	Game 1				Game 2			Game 3			Game 4			Total
	1.1	1.2	1.3	1	2.1	2.2	2	3.1	3.2	3	4.1	4.2	4
# of games	292	180	30	502	147	55	202	59	2	61	170	20	188	955
% of games #	29.2	18	3	50.2	14.7	5.5	20.2	5.9	0.2	6.1	17	2.0	18.8	95.5
Total number of cases 1200

).

(b) 

Discrepancy in Game Distribution Between a priori and Random Landscape Models.

The variation in the distribution of games between the a priori model and the Random Landscape Model (for example, games 1 account for 40% in a priori but 52.3% in Random Landscape, while games 3 make up 15% in a priori compared to 6.7% in Random Landscape) stems from the differing ways these models predict outcomes. The a priori model uses predefined probabilities and expected payoffs, influenced by cooperation-related variables. In contrast, the Random Landscape Model produces outcomes based on randomly assigned expected values, offering a more realistic reflection of how games are distributed in practice.

Table 7. Anticipated values of cooperation cost variables and benefit across various cooperation outcomes. Source, the authors built upon their previous work, Tlemsani et al. (2023a).

Benefit and Cost Variables and Cooperation Outcomes	Intervals (for Benefit and Cost Variables) and Formulas for Cooperation Outcomes	Expected Values
Transfer benefits (r)	(0, 1)	0.5
Transfer costs (c)	(0, 1)	0.5
Joint benefits (b)	(0, 1)	0.5
Reputation benefits (j)	(0, 1)	0.5
Exit costs (h)—for all h	(−1, 1)	0
Exit costs (h)—for positive h	(0, 1)	0.5
Exit costs (h)—for negative h	(−1, 0)	−0.5
A	A = r + b + d − c	1
B	B = d − c	0
C	C = r + d	1
D—for all h	D = h	0
D—for positive h	D = h	0.5
D—for negative h	D = h	−0.5

presents the anticipated values for the cooperation benefit and cost variables, along with the different cooperation outcomes forecasted by the a priori model.

Within the Random Landscape Model, the values are calculated by taking the average across all cases. Some cells display the anticipated values for both the positive and negative ranges of h. These values, generated by the Random Landscape Model, can be directly contrasted with the predicted outcomes from the a priori model, demonstrating a significant level of similarity between the two. Table 7 illustrates how expected values impact the structure of payoffs and, consequently, the distribution of games.

This clarifies why 1.1 and 1.2 games, characterized by payoff sequences of A > C > B > D and A > C > D > B, respectively, tend to occur more frequently and hold a larger proportion within the game distribution. Conversely, game 1.3, which follow the payoff order A > D > C > B, are comparatively less frequent and occupy a smaller proportion in the Random Landscape Model when contrasted with the a priori model.

Another possible explanation for the difference between the logical model and the simulation-based distribution of games is the limited number of cases in the simulation (1000). While this sample size is relatively large, it may still be insufficient to fully reflect the distribution predicted by the logical model.

6. Empirical Results

All participants in the interviews highlighted the importance of joint and reputation benefits, which are key features of games 1. The majority of respondents rated reputation and mutual benefits highly, with average scores of 4.1 and 3.85 out of 5, respectively. In comparison, the net transfer benefits (r − c) were rated much lower, with an average score of only 0.61 out of 5.

The a priori model underscores the significant role of joint and reputation benefits in games 1, which are the most cooperative within the game taxonomy. According to this model, games 1 account for 8 out of the 20 possible games, representing 40% of the overall game distribution. Similarly, the Random Landscape Model, which simulates potential cooperation outcomes within coalitions, supports these findings by showing that games 1 are even more likely, constituting around 50% of the game distribution.

The integration of empirical data with the payoff dynamics of games 1 strongly suggests that joint and reputation benefits serve as the key motivators for cooperation, making it the predominant strategy within coalitions. This study underscores the critical role these benefits play in fostering successful collaboration, shaping corporate behavior in strategic partnerships. Respondents consistently emphasized the importance of cooperation and shared benefits (joint and reputation gains) over competitive strategies, particularly in alliances centered on learning, where partners aim to acquire knowledge while protecting their own interests—a dynamic often referred to as the “learning race”. Consequently, it is unsurprising that the questionnaire responses reflect the cooperation-driven benefits and associated costs that define the typical payoff structures of games 1: A > C > B > D. The empirical data for payoff distribution is presented as follows:

A = r + b + d − c = 8.57; B = d − c = 0.95; C = r + d = 7.91; D = −h − 3.2.

The empirical data for cooperation payoffs highlights the outcomes based on the cooperative states of the players. When both Player 1 and Player 2 are cooperative (Θ₁₂ = 1 and Θ₂₁ = 1), the payoff is A = 8.57. If Player 1 is cooperative (Θ₁₂ = 1) while Player 2 is not (Θ₂₁ = 0), the payoff drops to B = 0.9. Conversely, when Player 1 is non-cooperative (Θ₁₂ = 0) and Player 2 remains cooperative (Θ₂₁ = 1), the payoff becomes C = 7.91. Finally, if neither Player 1 nor Player 2 is cooperative (Θ₁₂ = 0 and Θ₂₁ = 0), the resulting payoff is D = −3.2. These values illustrate the varying outcomes of cooperation and non-cooperation between the two players.

This indicates that both current and potential alliance members view the balance of benefits and costs associated with cooperation as central to shaping the collaborative behavior of companies within coalitions. The success of learning in alliances is ultimately influenced by the cooperative actions of the partners involved.

7. Conclusions

This study contributes to strategic management by identifying conditions where cooperation becomes the dominant strategy in alliances, highlighting the roles of communication, trust, and shared benefits in sustaining long-term partnerships. The findings offer practical guidelines for managers to foster effective inter-firm collaboration. Additionally, future research could examine external influences, such as regulatory environments and technological advances, on alliance dynamics. Investigating cultural dimensions may also shed light on how diverse organizational contexts shape cooperative behavior.

The proposed taxonomy provides a structured approach for identifying cooperative strategies in alliances, enabling partners to evaluate whether a coalition is well-suited or if an alternative with a more favorable payoff structure would be better.

Games 1, identified as particularly conducive to cooperation, emphasize joint and reputation benefits. Among these, three games naturally promote cooperation, while the remaining require strong communication to reach optimal outcomes. These insights are valuable for enhancing learning and knowledge exchange in strategic alliances.

While learning alliances focus on mutual knowledge gain, cooperative strategies especially in games 1 help partners avoid opportunistic behaviors, where one party might gain while withholding resources. These high mutual-gain scenarios make cooperation the preferred approach for alliances aiming for shared benefits, a conclusion supported by primary research and simulations.

Based on simulations, Game 1 emerges as the most common scenario in both the a priori and Random Landscape models, representing 40% of all potential games and nearly 50% of observed instances. Data collected through interviews and questionnaires also highlight the significance of joint benefits and reputation, reinforcing the cooperative dynamics characteristic of Game 1.

The main limitation of this research is its reliance on simulated models, which, while useful, may not fully capture the complexity of real-world alliances. Models like a priori and Random Landscape assume fixed payoff structures and static cooperation variables, potentially oversimplifying dynamic alliance behaviors. Additionally, data from interviews and questionnaires may contain respondent bias, affecting the findings. Future studies should include longitudinal case studies and real-time data from diverse industries to enhance generalizability.

Another limitation is the model’s static nature, which restricts its ability to depict evolving alliance dynamics, where strategies adapt based on changing circumstances, feedback, and external pressures. For instance, alliances might start as a prisoner’s dilemma but shift toward cooperation as trust builds over time.

For future research, we suggest incorporating repeated-game frameworks or evolutionary game theory to capture strategy evolution across interactions, reflecting learning and adaptation. Evolutionary game theory could model gradual strategy shifts, potentially leading to stable cooperative equilibria as organizations adjust to internal and external changes.

In conclusion, organizations in strategic alliances should prioritize open communication and trust-building to maximize joint and reputation benefits, especially in high-stakes partnerships like learning alliances. Using game-theoretic models to assess potential outcomes and select partners whose goals align for mutual gain is recommended. Future research should also consider external factors such as regulatory impacts and cultural differences to better understand how they shape cooperative strategies in global partnerships.