Productivity and Wages in South Africa
Abstract
1. Introduction
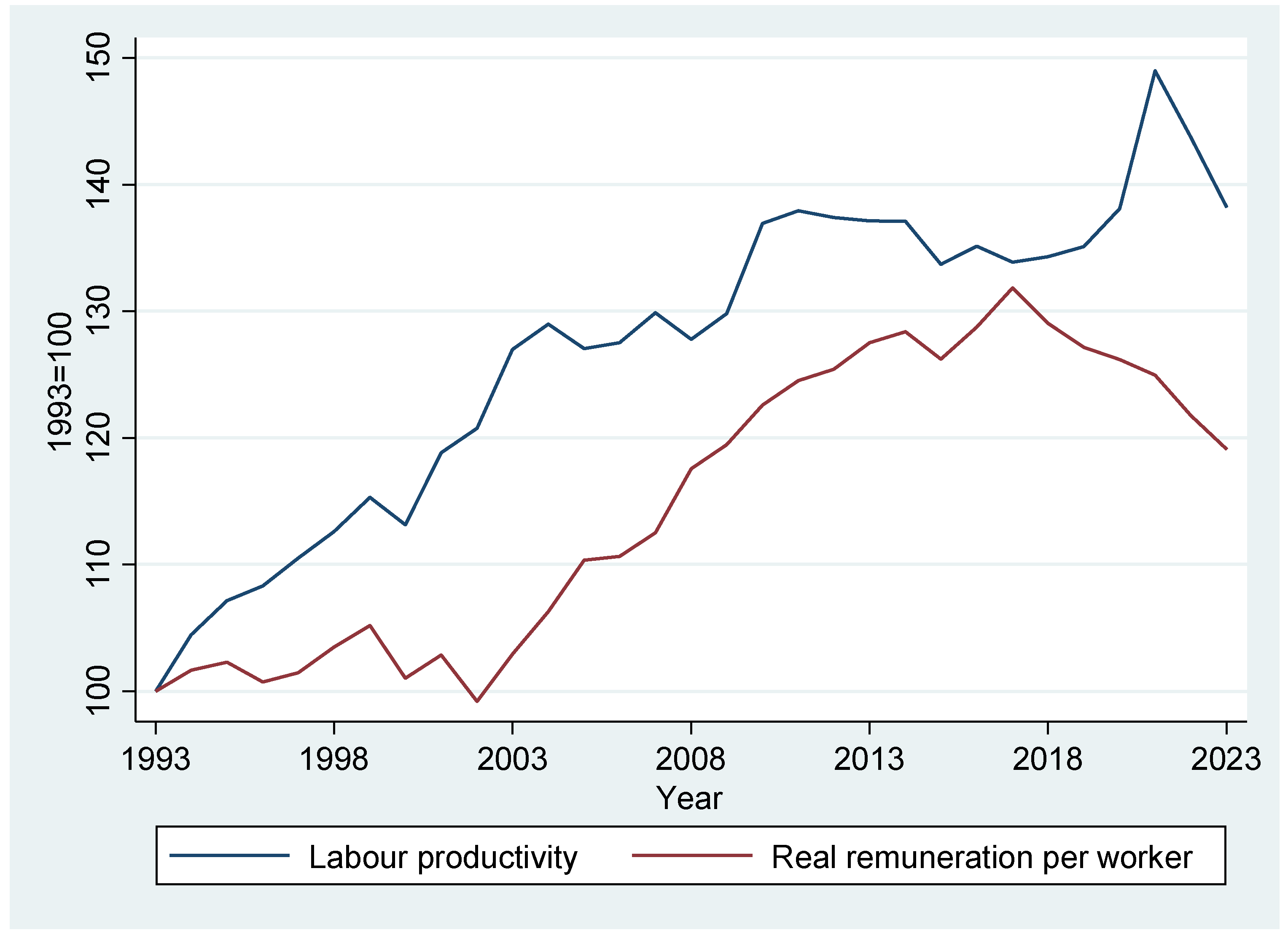
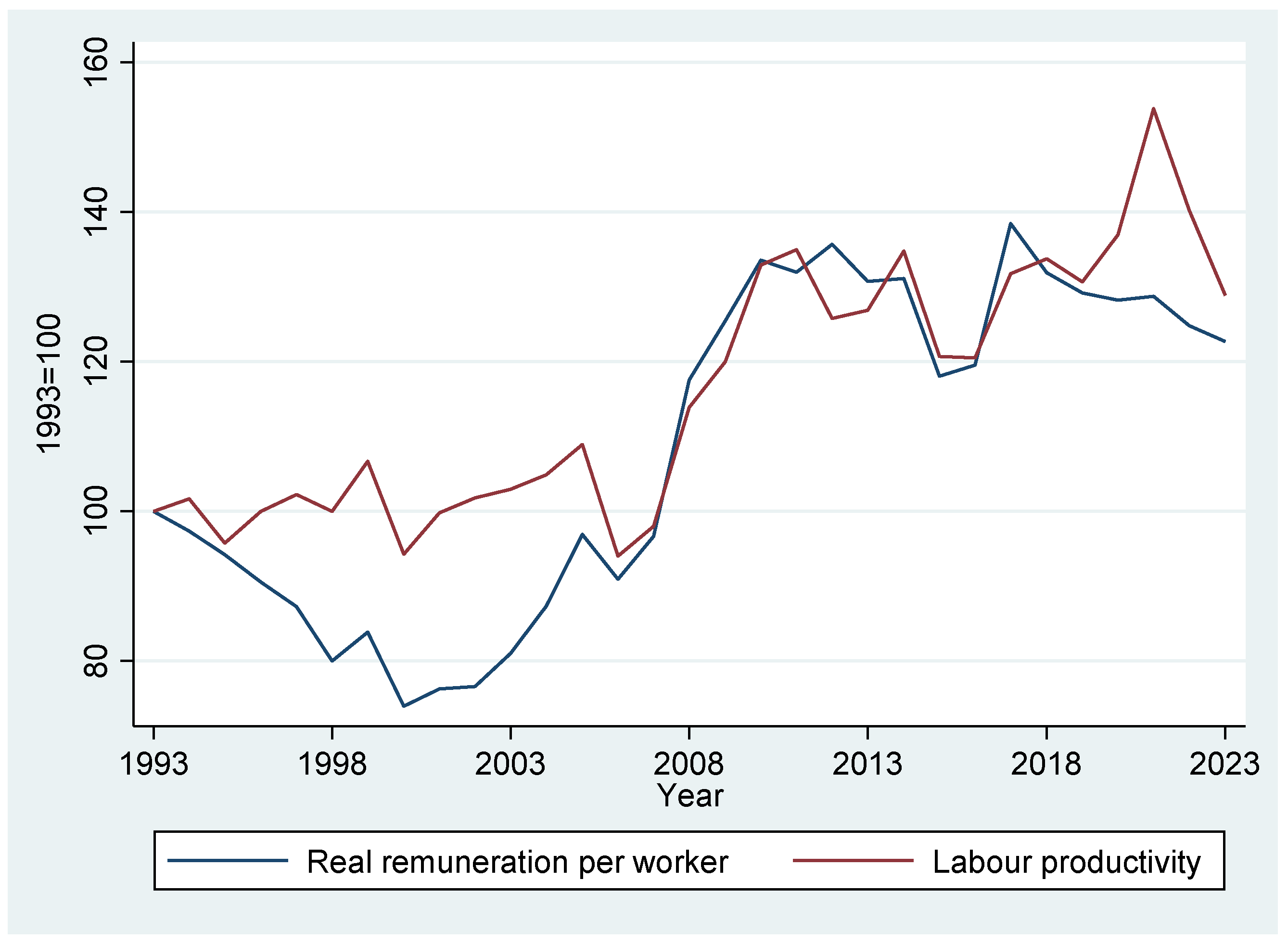
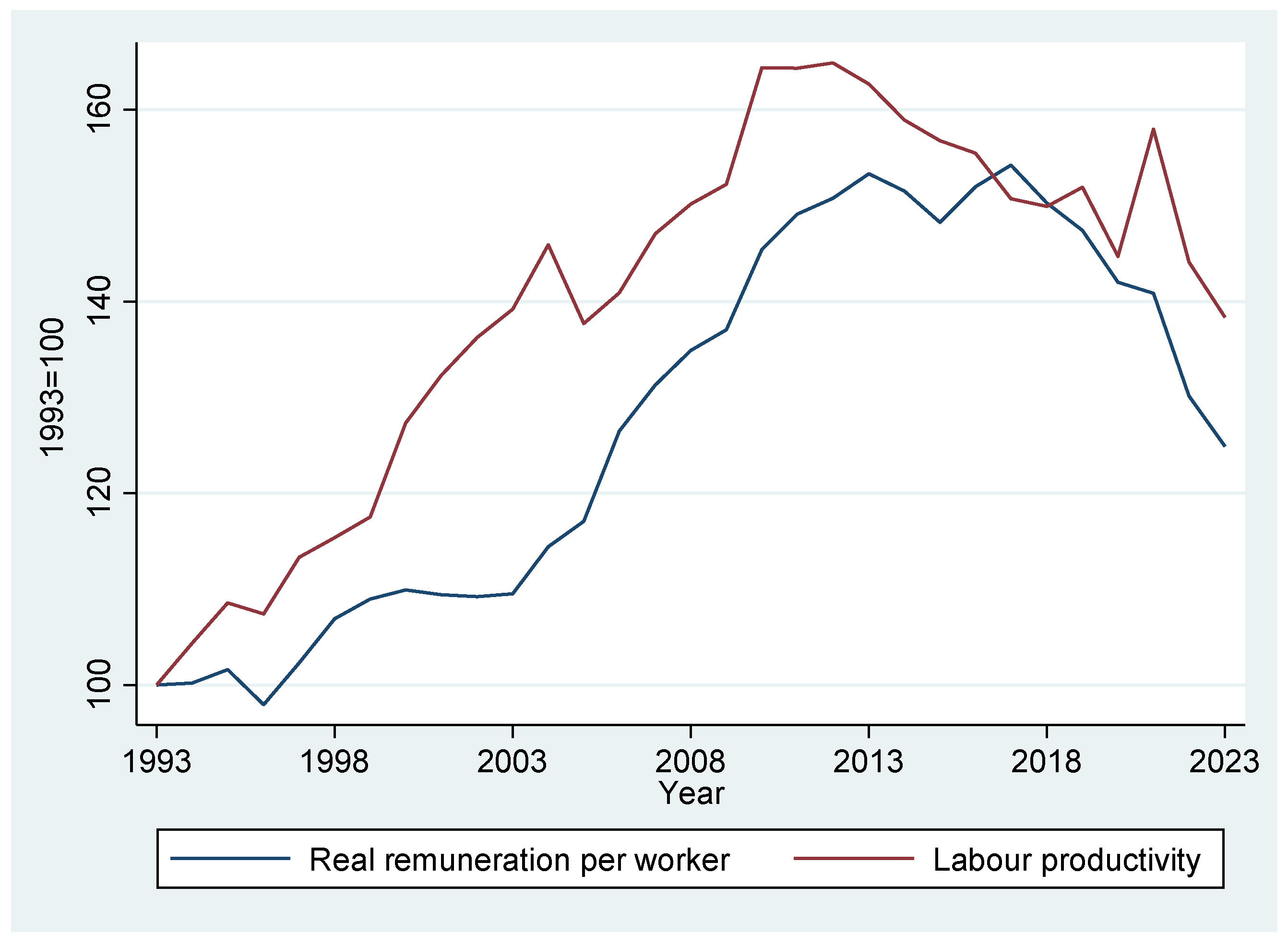
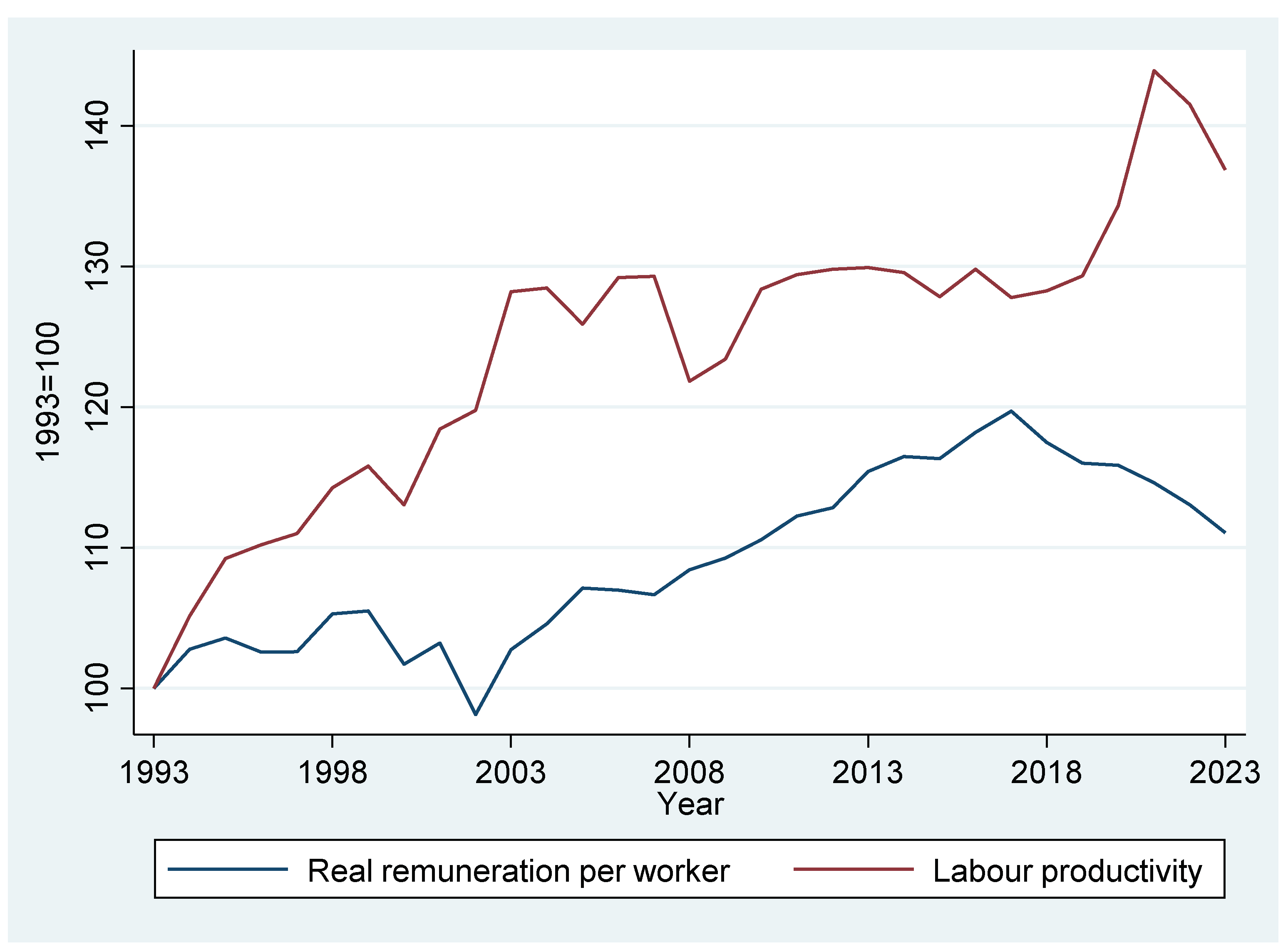
2. The Decoupling of Productivity and Remuneration in South Africa: Stylised Facts
Literature Review
3. Materials and Methods
3.1. Data and Variables
3.2. Estimation Strategy
3.3. Empirical Model
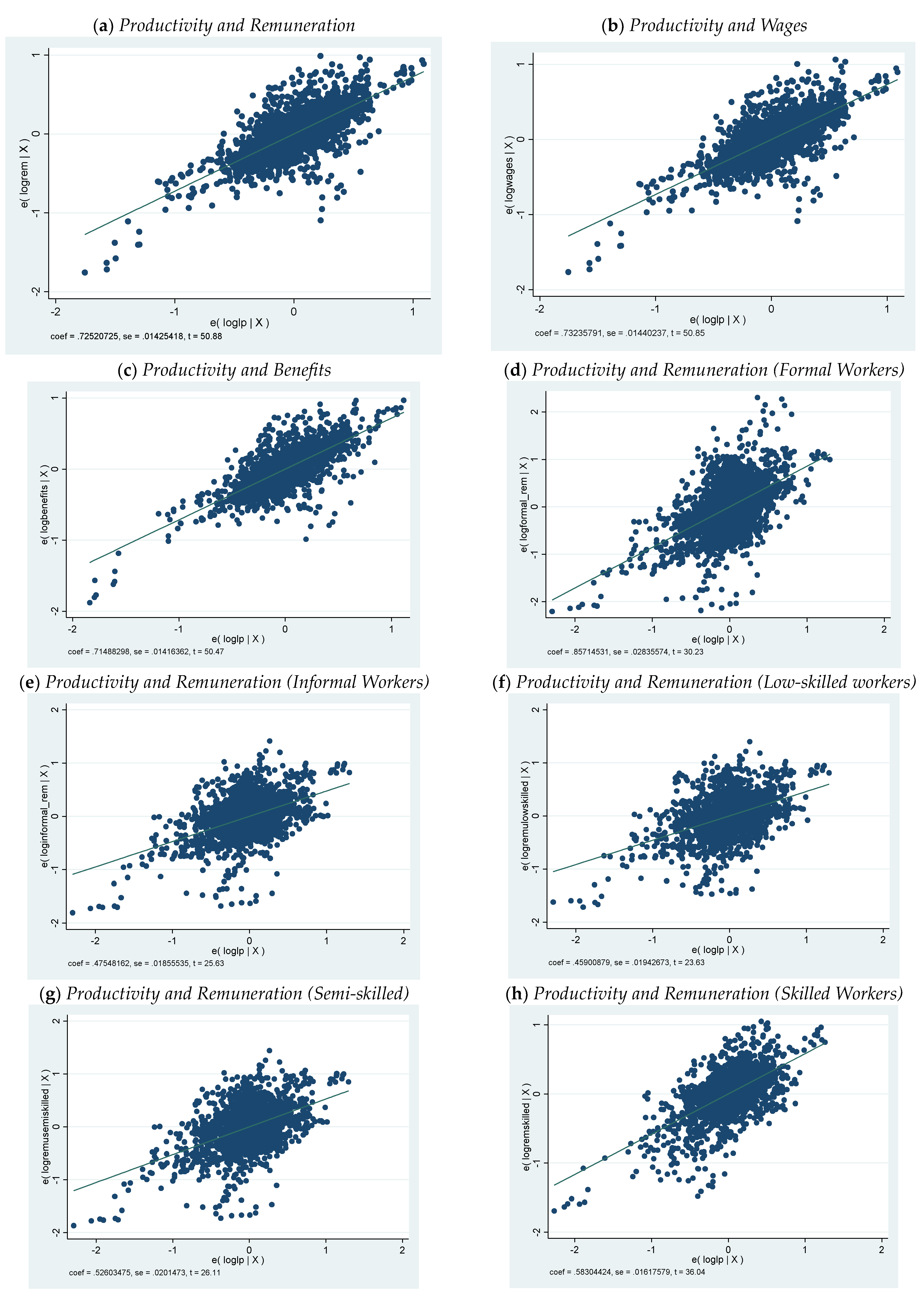
4. Empirical Results
4.1. Pre-Estimation Tests—Unit Roots and Cointegration
4.2. Productivity and Real Remuneration Between Formal and Informal Workers
4.3. Productivity and Real Remuneration Between Low-Skilled, Semi-Skilled, and Skilled Workers
4.4. Productivity, Wages, and Benefits
4.5. Robustness Exercises
4.6. Discussion
5. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Baltagi, Badi Hani, and Chihwa Kao. 2001. Nonstationary panels, cointegration in panels and dynamic panels: A survey. In Nonstationary Panels, Panel Cointegration, and Dynamic Panels. Bingley: Emerald Publishing, pp. 7–51. [Google Scholar]
- Blackburne, Edward F., III, and Mark W. Frank. 2007. Estimation of nonstationary heterogeneous panels. The Stata Journal 7: 197–208. [Google Scholar] [CrossRef]
- Bosworth, Barry, George L. Perry, and Matthew D. Shapiro. 1994. Productivity and real wages: Is there a puzzle? Brookings Papers on Economic Activity 1994: 317–44. [Google Scholar] [CrossRef]
- Breitung, Jorg, and Samarjit Das. 2005. Panel unit root tests under cross-sectional dependence. Statistica Neerlandica 59: 414–33. [Google Scholar] [CrossRef]
- Cashell, Brian W. 2004. Productivity and Wages. Congressional Research Service Report for Congress. Denton: Congressional Research Service. [Google Scholar]
- Chudik, Alexander, and M. Hashem Pesaran. 2015. Common correlated effects estimation of heterogeneous dynamic panel data models with weakly exogenous regressors. Journal of Econometrics 188: 393–420. [Google Scholar] [CrossRef]
- Cirillo, Valeria, and Andrea Ricci. 2022. Heterogeneity matters: Temporary employment, productivity and wages in Italian firms. Economia Politica 39: 567–93. [Google Scholar] [CrossRef]
- Conti, Gabriella. 2005. Training, productivity and wages in Italy. Labour Economics 12: 557–76. [Google Scholar] [CrossRef]
- Cruz, Manuel David. 2023. Labor productivity, real wages, and employment in OECD economies. Structural Change and Economic Dynamics 66: 367–82. [Google Scholar] [CrossRef]
- Davis, John C., and Thomas K. Hitch. 1949. Wages and productivity. The Review of Economics and Statistics 31: 292–98. [Google Scholar] [CrossRef]
- Dostie, B. 2011. Wages, productivity and aging. De Economist 159: 139–58. [Google Scholar] [CrossRef]
- Faggio, Giulia, Kjell G. Salvanes, and John Van Reenen. 2010. The evolution of inequality in productivity and wages: Panel data evidence. Industrial and Corporate Change 19: 1919–51. [Google Scholar] [CrossRef]
- Feldstein, Martin S. 2008. Did wages reflect growth in productivity? Journal of Policy Modeling 30: 591–94. [Google Scholar] [CrossRef]
- Geyer, H.S., Jr. 2023. Precarious and non-precarious work in the informal sector: Evidence from South Africa. Urban Studies 60: 1915–31. [Google Scholar] [CrossRef]
- Habanabakize, Thomas, Daniel Francois Meyer, and Judit Oláh. 2019. The impact of productivity, investment and real wages on employment absorption rate in South Africa. Social Sciences 8: 330. [Google Scholar] [CrossRef]
- Harris, Richard, and Robert Sollis. 2003. Applied Time Series Modelling and Forecasting. Durham: Wiley. [Google Scholar]
- Herman, Emilia. 2020. Labour productivity and wages in the Romanian manufacturing sector. Procedia Manufacturing 46: 313–21. [Google Scholar] [CrossRef]
- Im, Kyung So, M. Hashem Pesaran, and Yongcheol Shin. 2003. Testing for unit roots in heterogeneous panels. Journal of Econometrics 115: 53–74. [Google Scholar] [CrossRef]
- Jenkins, Rhys. 2008. Trade, technology and employment in South Africa. The Journal of Development Studies 44: 60–79. [Google Scholar] [CrossRef]
- Kao, Chihwa. 1999. Spurious regression and residual-based tests for cointegration in panel data. Journal of Econometrics 90: 1–44. [Google Scholar]
- Katz, Lawrence F. 1986. Efficiency wage theories: A partial evaluation. NBER Macroeconomics Annual 1: 235–76. [Google Scholar]
- Konings, Jozef, and Luco Marcolin. 2014. Do wages reflect labor productivity? The case of Belgian regions. IZA Journal of European Labor Studies 3: 1–21. [Google Scholar]
- Leibenstein, Harvey. 1957. The theory of underemployment in backward economies. Journal of Political Economy 65: 91–103. [Google Scholar] [CrossRef]
- Levin, Andrew, and Chien Fu Lin. 1993. Unit Root Tests in Panel Data: New Results. Economics Working Paper Series. La Jolla: University of California at San Diego. [Google Scholar]
- Mahlberg, Bernhard, Inga Freund, Jesus C. Prskawetz, and Alexia Cuaresma. 2013. Ageing, productivity and wages in Austria. Labour Economics 22: 5–15. [Google Scholar] [CrossRef]
- Mawejje, Joseph, and Ibrahim Mike Okumu. 2018. Wages and labour productivity in African manufacturing. African Development Review 30: 386–98. [Google Scholar] [CrossRef]
- Mishel, Lawrence. 2012. The wedges between productivity and median compensation growth. Issue Brief 330: 1–7. [Google Scholar]
- Pedroni, Peter. 2001. Purchasing power parity tests in cointegrated panels. Review of Economics and Statistics 83: 727–31. [Google Scholar] [CrossRef]
- Pedroni, Peter. 2004. Panel cointegration: Asymptotic and finite sample properties of pooled time series tests with an application to the PPP hypothesis. Econometric Theory 20: 597–625. [Google Scholar] [CrossRef]
- Pesaran, M. Hashem, and Ron Smith. 1995. The role of theory in econometrics. Journal of Econometrics 67: 61–79. [Google Scholar] [CrossRef]
- Pesaran, M. Hashem, Yongcheol Shin, and Ron P. Smith. 1999. Pooled mean group estimation of dynamic heterogeneous panels. Journal of the American Statistical Association 94: 621–34. [Google Scholar] [CrossRef]
- Phillips, Peter C. 1994. Some exact distribution theory for maximum likelihood estimators of cointegrating coefficients in error correction models. Econometrica: Journal of the Econometric Society 62: 73–93. [Google Scholar] [CrossRef]
- Phillips, Peter C., and Hyungsik R. Moon. 2000. Nonstationary panel data analysis: An overview of some recent developments. Econometric Reviews 19: 263–86. [Google Scholar] [CrossRef]
- Rodrik, Dani. 2008. Understanding South Africa’s economic puzzles. Economics of Transition 16: 769–97. [Google Scholar] [CrossRef]
- Schultz, T. Paul, and Germano Mwabu. 1998. Labor unions and the distribution of wages and employment in South Africa. ILR Review 51: 680–703. [Google Scholar] [CrossRef]
- Schwellnus, Cyrille, Andreas Kappeler, and Pierre-Alain Pionnier. 2017. The decoupling of median wages from productivity in OECD countries. International Productivity Monitor 32: 44–60. [Google Scholar]
- Shapiro, Carl, and Joseph E. Stiglitz. 1984. Equilibrium unemployment as a worker discipline device. The American Economic Review 74: 433–44. [Google Scholar]
- Stansbury, Anna M., and Lawrence H. Summers. 2018. Productivity and Pay: Is the Link broken? Working Paper 24165. Cambridge: National Bureau of Economic Research. Available online: http://www.nber.org/papers/w24165 (accessed on 5 October 2024).
- Strauss, Jack, and Mark E. Wohar. 2004. The linkage between prices, wages, and labor productivity: A panel study of manufacturing industries. Southern Economic Journal 70: 920–41. [Google Scholar]
- Tsoku, Johannes Tshepiso, and Florance Matarise. 2014. An analysis of the relationship between remuneration (real wage) and labour productivity in South Africa. Journal of Educational and Social Research 4: 1–10. [Google Scholar] [CrossRef]
- Valodia, Imran, and Arabo K. Ewinyu. 2023. The Economics of Discrimination and Affirmative Action in South Africa. In Handbook on Economics of Discrimination and Affirmative Action. Berlin/Heidelberg: Springer, pp. 481–98. [Google Scholar]
- Van Biesebroeck, Johannes. 2003. Productivity dynamics with technology choice: An application to automobile assembly. The Review of Economic Studies 70: 167–98. [Google Scholar] [CrossRef]
- Wakeford, Jeremy. 2004. The productivity–wage relationship in South Africa: An empirical investigation. Development Southern Africa 21: 109–32. [Google Scholar] [CrossRef]
- Webster, Eddie. 1991. Taking labour seriously: Sociology and labour in South Africa. South African Sociological Review 4: 50–72. [Google Scholar]
- Wolpe, Harold. 2023. Capitalism and cheap labour-power in South Africa: From segregation to apartheid 1. In The Articulation of Modes of Production. Abingdon-on-Thames: Routledge, pp. 289–320. [Google Scholar]
- Wu, Joseph S., and Chi Pui Ho. 2012. Towards a more complete efficiency wage theory. Pacific Economic Review 17: 660–76. [Google Scholar] [CrossRef]
| Variable | Test | Levels | First Difference | Order of Integration |
|---|---|---|---|---|
| Log remuneration per worker (formal and informal) | IPS | 3.08040 | −15.9840 *** | I(1) |
| LLC | 0.40850 | −13.4722 *** | I(1) | |
| Breitung | 3.32021 | −11.6504 *** | I(1) | |
| Loglabour productivity | IPS | 3.12740 | −16.9281 *** | I(1) |
| LLC | 0.18352 | −10.8071 *** | I(1) | |
| Breitung | 3.18375 | −7.77637 *** | I(1) | |
| Export intensity | IPS | −3.57098 *** | I(0) | |
| LLC | −2.64192 *** | I(0) | ||
| Breitung | −0.39777 | −7.43588 *** | I(1) | |
| Import penetration | IPS | −3.03335 *** | I(0) | |
| LLC | −2.66237 *** | I(0) | ||
| Breitung | −1.37007 * | −12.2021 *** | I(1) | |
| Unemployment | IPS | 0.49277 | −4.58095 *** | I(1) |
| LLC | 3.24511 | −10.5830 *** | I(1) | |
| Breitung | −10.3456 *** | I(0) |
| Variable | Test | Levels | First Difference | Order of Integration |
|---|---|---|---|---|
| Log remuneration per worker (formal) | IPS | 3.05361 | −15.7811 *** | I(1) |
| LLC | 0.19360 | −12.5626 *** | I(1) | |
| Breitung | 3.06485 | −12.1811 *** | I(1) | |
| Log remuneration per worker (informal) | IPS | −0.40414 | −14.6803 *** | I(1) |
| LLC | 0.03839 | −10.6244 *** | I(1) | |
| Breitung | −3.80570 *** | I(0) | ||
| Log remuneration per worker (low-skilled workers) | IPS | 3.09796 | −14.4360 *** | I(1) |
| LLC | 1.24781 | −11.5560 *** | I(1) | |
| Breitung | 2.67308 | −11.0325 *** | I(1) | |
| Log remuneration per worker (semi-skilled workers) | IPS | 3.16854 | −15.3179 *** | I(1) |
| LLC | 0.99817 | −12.2892 *** | I(1) | |
| Breitung | 3.39130 | −11.5972 *** | I(1) | |
| Log remuneration per worker (skilled workers) | IPS | 2.61938 | −16.6027 *** | I(1) |
| LLC | −0.95911 | −13.5041 *** | I(1) | |
| Breitung | 2.81033 | −13.3606 *** | I(1) |
| Variable | Test | Levels | First Difference | Order of Integration |
|---|---|---|---|---|
| Wages per worker (formal and informal) | IPS | 0.34452 | −15.7344 *** | I(1) |
| LLC | −0.68803 | −12.5431 *** | I(1) | |
| Breitung | 1.19109 | −6.51086 *** | I(1) | |
| Benefits per worker (formal and informal) | IPS | 1.73343 | −15.2179 *** | I(1) |
| LLC | 0.50484 | −12.0791 *** | I(1) | |
| Breitung | 2.21157 | −8.89573 *** | I(1) |
| Dependent Variable | Pedroni | Kao | |
|---|---|---|---|
| Group ADF-Statistic | Panel ADF-Statistic | ADF Statistic | |
| Log remuneration per worker (both formal and informal) | −2.315 ** | 0.866 | −6.487 *** |
| Log remuneration per worker (formal) | −1.341 * | 1.117 | −6.063 *** |
| Log remuneration per worker (informal) | −0.121 | 0.615 | −2.425 *** |
| Log remuneration per worker (low skilled) | −6.371 *** | −4.688 *** | −5.417 *** |
| Log remuneration per worker (semi-skilled) | −5.837 *** | −4.208 *** | −6.041 *** |
| Log remuneration per worker (skilled) | −5.441 *** | −3.902 *** | −6.539 *** |
| Log wage per worker | −6.689 *** | −4.285 *** | −6.077 *** |
| Log benefits per worker | −6.981 *** | −4.625 *** | −6.487 *** |
| Variant | (1) | (2) | (3) | (4) | (5) |
|---|---|---|---|---|---|
| Hausman statistic | 2.84 | 3.10 | 6.51 | 3.78 | 1.05 |
| Prob > chi2 | 0.4172 | 0.3764 | 0.1640 | 0.1513 | 0.5961 |
| Dependent Variable: Log Remuneration per Worker | Formal and Informal | Formal | Informal | Formal and Informal |
|---|---|---|---|---|
| ARDL (1, 1, 1, 1, 1) | ARDL (2, 1, 1, 1, 1) | ARDL (2, 2, 2, 2, 2) | ARDL (2, 2, 2, 2, 2) | |
| LogLP | 0.760 *** (0.018) | 0.619 *** (0.019) | 0.469 *** (0.052) | 0.964 *** (0.024) |
| Export | −0.005 *** (0.001) | 0.005 *** (0.001) | 0.001 (0.002) | −0.005 *** (0.001) |
| Import | 0.002 *** (0.0005) | 0.001 (0.001) | 0.004** (0.002) | 0.012 *** (0.001) |
| Unem | −0.009 *** (0.001) | −0.011 *** (0.001) | −0.050 *** (0.004) | −0.005 *** (0.001) |
| GM | −0.010 *** (0.001) | |||
| COINTEQ01 | −0.295 *** (0.025) | −0.338 *** (0.029) | −0.226 *** (0.015) | −0.238 *** (0.025) |
| log remuneration per worker (−1) | ---- | 0.103 *** (0.020) | −0.112 *** (0.024) | 0.067 *** (0.031) |
| logLP | 0.361 *** (0.018) | 0.314 *** (0.033) | 0.591 *** (0.053) | 1.187 *** (0.047) |
| logLP (−1) | ---- | ---- | −0.012 (0.052) | 0.044 (0.045) |
| Export | 0.002 (0.002) | 0.004 (0.004) | −0.020 ** (0.009) | −0.006 ** (0.003) |
| Export (−1) | ---- | ---- | −0.031 ** (0.014) | 0.017 (0.001) |
| Import | −0.005 (0.004) | −0.006 (0.004) | −0.030 ** (0.013) | 0.007 (0.004) |
| Import (−1) | ---- | ---- | 0.046 ** (0.022) | −0.002 (0.004) |
| Unem | −0.005 *** (0.001) | −0.003 *** (0.001) | 0.041 *** (0.002) | 0.0001 (0.001) |
| Unem (−1) | ---- | ---- | 0.031 *** (0.002) | −0.001 (0.001) |
| GM | −0.024 *** (0.001) | |||
| GM (−1) | −0.001 (0.001) | |||
| C | 2.601 (0.219) | −1.445 (0.178) | −1.145 (0.040) | −0.738 (0.104) |
| @Trend | 0.003 *** (0.001) | 0.004 *** (0.001) | 0.015 *** (0.001) | 0.001 *** (0.0001) |
| Observations | 2144 | 2070 | 2069 | 2069 |
| C (1) = 1 | 169.38 *** | 409.68 *** | 105.45 *** | 2.16 |
| Dependent Variable: Log Remuneration per Worker | Low-Skilled | Semi-Skilled | Skilled | |
|---|---|---|---|---|
| ARDL (2, 1, 1, 1, 1) | ARDL (2, 1, 1, 1, 1) | ARDL (1, 1, 1, 1, 1) | ARDL (1, 1, 1, 1, 1) | |
| LogLP | 0.621 *** (0.017) | 0.761 *** (0.016) | 0.619 *** (0.022) | 0.734 *** (0.034) |
| Export | −0.004 *** (0.001) | 0.004 *** (0.001) | −0.006 *** (0.001) | −0.0027 ** (0.001) |
| Import | 0.004 (0.0005) | 0.0018 *** (0.0005) | 0.0011 * (0.0006) | −0.004 *** (0.001) |
| Unem | −0.015 *** (0.001) | −0.011 *** (0.001) | −0.001 (0.001) | −0.025 *** (0.002) |
| COINTEQ01 | −0.362 *** (0.030) | −0.325 *** (0.028) | −0.273 *** (0.027) | −0.136 *** (0.014) |
| log remuneration per worker (−1) | 0.118 *** (0.021) | 0.091 *** (0.022) | ---- | ---- |
| logLP | 0.299 *** (0.030) | 0.294 *** (0.034) | 0.354 *** (0.030) | 0.417 *** (0.028) |
| Export | 0.004 (0.004) | 0.003 (0.004) | 0.0054 * (0.003) | 0.001 (0.002) |
| Import | −0.005 (0.004) | −0.005 (0.004) | −0.0087 * (0.0049) | −0.002 (0.002) |
| Unem | −0.004 (0.003) | −0.004 *** (0.001) | −0.0063 *** (0.001) | −0.004 *** (0.001) |
| C | −1.709 (0.135) | −1.706 (0.152) | −0.980 (0.102) | −0.466 (0.047) |
| @Trend | 0.006 *** (0.001) | 0.005 *** (0.001) | −0.0003 (0.001) | ---- |
| C (1) = 1 | 490 *** | 219 *** | 290 *** | 60 *** |
| Observations | 2070 | 2070 | 2144 | 2144 |
| Dependent Variable: Log Real Wages or Benefits per Worker | Wages | Benefits |
|---|---|---|
| ARDL (1, 1, 1, 1, 1) | ARDL (1, 1, 1, 1, 1) | |
| LogLP | 0.691 *** (0.018) | 0.760 *** (0.018) |
| Export | −0.006 *** (0.001) | −0.005 *** (0.001) |
| Import | 0.002 *** (0.001) | 0.002 *** (0.001) |
| Unem | −0.004 *** (0.001) | −0.008 *** (0.001) |
| COINTEQ01 | −0.306 *** (0.026) | −0.295 *** (0.026) |
| logLP | 0.402 *** (0.021) | 0.361 *** (0.021) |
| Export | 0.0004 (0.003) | 0.0004 (0.003) |
| Import | −0.008 * (0.005) | −0.006 (0.004) |
| Unem | 0.0003 (0.001) | −0.005 *** (0.001) |
| C | 0.411 (0.049) | 2.600 (0.218) |
| @Trend | 0.003 *** (0.001) | 0.003 *** (0.001) |
| Observations | 2144 | 2144 |
| C (1) = 1 | 309 *** | 169 *** |
| Dependent Variable: Log Remuneration per Worker | Formal and Informal | Formal | Informal | Formal and Informal |
|---|---|---|---|---|
| LogLP | 0.576 *** (0.042) | 0.606 *** (0.040) | 0.453 *** (0.075) | 0.956 *** (0.029) |
| Export | 0.049 *** (0.009) | 0.049 *** (0.009) | −0.007 (0.017) | 0.029 *** (0.008) |
| Import | −0.006 (0.007) | −0.006 (0.007) | 0.074 *** (0.025) | −0.015 *** (0.004) |
| Unem | −0.015 *** (0.002) | −0.013 *** (0.002) | 0.019 *** (0.004) | −0.015 *** (0.001) |
| GM | −0.022 *** (0.001) | |||
| Observations | 2018 | 2024 | 2006 | 2003 |
| C (1) = 1 | 101.99 *** | 94.35 *** | 51.91 *** | 2.365725 |
| Dependent Variable: Log Remuneration per Worker | Formal and Informal | Formal | Informal | Formal and Informal |
|---|---|---|---|---|
| LogLP | 0.627 *** (0.017) | 0.622 *** (0.017) | 0.385 *** (0.031) | 0.953 *** (0.009) |
| Export | 0.015 *** (0.002) | 0.015 *** (0.002) | −0.016 ** (0.006) | 0.002 (0.002) |
| Import | 0.001 (0.002) | −0.0003 (0.002) | 0.021 * (0.012) | 0.011 *** (0.001) |
| Unem | −0.009 *** (0.001) | −0.010 *** (0.001) | 0.028 *** (0.001) | −0.011 *** (0.0004) |
| GM | −0.021 *** (0.0003) | |||
| Observations | 2144 | 2144 | 2144 | 2144 |
| C (1) = 1 | 472.75 *** | 468.75 *** | 377.10 *** | 0.03 |
| Dependent Variable: Log | (1) | (2) | (3) | (4) |
|---|---|---|---|---|
| Remuneration per Worker | Both | Both | Informal | Formal |
| L. . log remuneration | 0.053 * | 0.022 | 0.0595 * | −0.008 |
| (0.029) | (0.016) | (0.0309) | (0.031) | |
| . LogLP | 0.227 *** | 0.553 *** | 0.203 *** | 0.300 *** |
| (0.031) | (0.025) | (0.033) | (0.048) | |
| . Import | −0.010 ** | −0.009 | −0.0102 ** | −0.040 |
| (0.005) | (0.007) | (0.005) | (0.028) | |
| . Export | 0.009 | 0.003 | 0.009 | 0.001 |
| (0.007) | (0.004) | (0.007) | (0.008) | |
| . GM | −0.015 *** | |||
| (0.001) | ||||
| COINTEQ01 | −0.520 *** | −0.415 *** | −0.529 *** | −0.408 *** |
| (0.191) | (0.133) | (0.166) | (0.101) | |
| LogLP | 0.626 *** | 0.938 *** | 0.610 *** | 0.779 ** |
| (0.195) | (0.232) | (0.187) | (0.381) | |
| Import | 0.0003 | 0.003 | 0.001 | −0.001 |
| (0.009) | (0.016) | (0.006) | (0.034) | |
| Export | 0.0004 | −0.001 | 0.0004 | 0.001 |
| (0.005) | (0.008) | (0.009) | (0.016) | |
| GM | −0.014 * | |||
| (0.008) | ||||
| Constant | −0.023 | −0.897 | −0.400 | −0.122 |
| (0.754) | (0.709) | (0.767) | (0.264) | |
| Observations | 2070 | 2070 | 2070 | 2070 |
| R-squared | 0.661 | 0.909 | 0.656 | 0.633 |
| Number of groups | 74 | 74 | 74 | 74 |
| CD-statistic | −0.67 | −0.83 | −1.08 | −0.73 |
| CD-statistic (p-value) | 0.5052 | 0.4089 | 0.2809 | 0.4625 |
| Dependent Variable: Log Remuneration per Worker | Industrial Cluster | Sectoral Cluster | ||
|---|---|---|---|---|
| (1) Without Controls | (2) With Controls | (3) Without Controls | (4) With Controls | |
| LogLP | 0.659 *** (0.124) | 0.618 *** (0.143) | 1.157 *** (0.280) | 1.1900 *** (0.264) |
| Export | 0.003 (0.009) | 6.890 *** (1.368) | 0.0082 *** (0.001) | |
| Import | −0.00086 * (0.0004) | −0.0032 *** (0.0005) | ||
| Unem | −0.011 *** (0.004) | −0.0157 *** (0.004) | ||
| Year | 0.012 *** (0.003) | 0.0099 *** (0.009) | ||
| Constant | 8.869 (0.651) | −15.848 (6.249) | −12.931 (7.644) | |
| Random effects parameters | ||||
| Var(loglp) | 0.047 * (0.039) | 0.067 * (0.050) | 0.227 * (0.1993) | 0.200 *** (0.0178) |
| Var(cons) | 1.402 *** (1.197) | 0.952 (0.776) | 5.435 * (4.736) | 5.093 * (4.469) |
| Cov (loglP, cons) | 0.138 *** (0.002) | 0.131 *** (0.003) | 1.110 (1.972) | 1.010 * (0.893) |
| Prob > chi2 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| LR test vs. linear model | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| ICC | 0.786 *** (0.143) | 0.716 *** (0.166) | 0.903 (0,076) | 0.901 *** (0.078) |
| Chi2(1) b = 1 | 7.50 *** | 7.04 *** | 0.32 | 0.52 |
| Number of groups | 4 | 4 | 3 | 3 |
| Observations | 2219 | 2219 | 2219 | 2219 |
| Dependent Variable: Log Remuneration per Worker | Industrial Cluster | Sectoral Cluster | ||
|---|---|---|---|---|
| With Socio-Economic Controls | With Racial Controls | With Socio-Economic Controls | With Racial Controls | |
| LogLP | 0.6171 *** (0.143) | 0.6175 *** (0.137) | 1.197 *** (0.406) | 1.143 *** (0.291) |
| Export | 0.00031 (0.0009) | 0.008 (0.012) | ||
| Import | −0.000852 * (0.005) | −0.0031 (0.003) | ||
| Unem | −0.0133 0.009) | −0.011 (0.006) | ||
| Female literacy rate | 0.042 (0.130) | 0.017 (0.053) | ||
| Male literacy rate | 0.043 (0.141) | −0.010 (0.046) | ||
| Log bottom 10% income | 0.0155 (0.998) | 0.197 (0.296) | ||
| Log top 2.5% income | 0.0522 (1.125) | 0.111 (0409) | ||
| Black African literacy rate | 0.019 (0.066) | 0.045 (0.081) | ||
| Coloured literacy rate | 0.0125 (0.198) | 0.074 (0.244) | ||
| Indian literacy rate | 0.0044 (0.019) | 0.022 (0.135) | ||
| Year | 0.0182 (0.042) | 0.032 (0.013) | 0.009 (0.021) | 0.003 (0.016) |
| Constant | −26.423 (78.392) | 15.436 (25.823) | −11.709 (39.353) | 14.063 (31.894) |
| Random effects parameters | ||||
| Var(loglp) | 0.0672 * (0.050) | 0.0602 * (0.052) | 0.199 *** (0.0108) | 0.245 ** (0.114) |
| Var(cons) | 1.402 * (1.197) | 1.101 * (0.909) | 5.059 *** (2.667) | 5.093 * (4.469) |
| Cov (loglP, cons) | 0.9541 * (0.779) | 0.133 (0.160) | 1.002 ** (0.538) | 1.194 * (1.041) |
| Prob > chi2 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| LR test vs. linear model | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| ICC | 0.71603 *** (0.085) | 0.743 *** (0.157) | 0.899 *** (0.079) | 0.910 *** (0.071) |
| Chi2(1) b = 1 | 6.17 ** | 7.77 *** | 0.56 | 0.24 |
| Number of groups | 4 | 4 | 3 | 3 |
| Observations | 2219 | 2219 | 2219 | 2219 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mazorodze, B.T. Productivity and Wages in South Africa. Economies 2024, 12, 330. https://doi.org/10.3390/economies12120330
Mazorodze BT. Productivity and Wages in South Africa. Economies. 2024; 12(12):330. https://doi.org/10.3390/economies12120330
Chicago/Turabian StyleMazorodze, Brian Tavonga. 2024. "Productivity and Wages in South Africa" Economies 12, no. 12: 330. https://doi.org/10.3390/economies12120330
APA StyleMazorodze, B. T. (2024). Productivity and Wages in South Africa. Economies, 12(12), 330. https://doi.org/10.3390/economies12120330






