Parallel Currencies under Free Floating Exchange Rates: A Model Setting Out the Conditions for Stable Currency Competition

Abstract

We use a theoretical model to set up the conditions for a country to attain monetary stability by allowing for two freely tradable currencies to circulate in parallel. For this parallel system to function properly, confidence in the good behavior of the monetary authorities in charge of the two currencies is key. Our model shows how a floating exchange rate between the two can keep the issuers of the local currency in check. The results from our model show the conditions under which a parallel currency system disciplines the issuers of the currencies and thus maintains their purchasing power. In non-volatile economies, it also discourages governments (or private issuers) from inflating one of the currencies as a means to raise seigniorage, as this policy results in the displacement of the currency from the market. When foreign payments shortfall—such as in Greece and Cyprus during the ‘euro crisis’ in the mid-2010s, or intractable hyperinflation—leave the country without a medium of exchange, our model shows how currency choice can restore monetary circulation and offer a path to achieving and maintaining monetary stability.

1. Introduction: When Parallel Currency Systems Emerge: A Bottom-Up System to Achieve Monetary Stability

There are many historical and recent examples of failure by monetary authorities to achieve monetary stability and price stability. These examples abound particularly in times of great crisis, when the lack of money in the market forces governments to explore alternatives to be able to make payments, such as the introduction of a new currency in the economy. We consider two scenarios where this occurs: On the one hand, in economies in times of a major crisis within a monetary union, such as in Greece and Cyprus in the aftermath of the ‘euro crisis’ in the mid-2010s, academics and policy makers considered the possibility to reintroduce the old national currency (or a new one) to offset the lack of medium of exchange for the government to make payments. We will show that, once the crisis is over currency competition would help to keep the amount of money in circulation at levels compatible with price stability. On the other hand, the two-currency system solution has also arisen after an episode of high inflation—let alone hyperinflation—when money users do not trust the national (devalued) currency any longer and opt for another more credible currency, effectively creating a two-currency system. In these circumstances, governments and central banks are forced to introduce (or simply allow for) greater monetary competition.

The coexistence of multiple currencies in the market has been very well documented in monetary history (see the compilation made in Amato and Fantacci 2020, and the seminal work by Selgin 2011). But it is also present today in several economies, either de jure or de facto.

In Peru, after the stabilization shock of President Fujimori in August 1990, the way was open to ‘dollarize’ the economy and make the US dollar the national currency. The positive side was that hyperinflation would just disappear overnight and that the hands of present and future populist governments would be tied; the negative was that the Treasury would lose seigniorage income and that the Peruvian economy would be open to shocks coming from changes in US monetary policy. The Peruvian authorities opted for a managed float. However, this system produced volatile inflation, until a new exchange regime was institutionalized under central bank president Velarde in 2006. This was to manage the exchange rate between the national currency (sol) and the US dollar so that it moved within tight margins. Any excesses in the issue of the new sols would soon reflect in the price of the national currency against the dollar and thus function as an indicator and a warning of future inflation.

In other words, the system in Peru is one of monetary competition. By law, Peruvians can and do use two currencies, the sol and the US dollar. Due to its large mineral and guano exports, Peru has a constant supply of dollars to settle taxes and wages, and Peruvian residents and foreign companies can open, hold, and use deposits in dollars. The sol is used for smaller local transactions and the payment of taxes, which is a source of seigniorage revenue. The Central Reserve Bank of Peru (CRBP) has set an inflation objective between 1% and 3% annually and has been able to maintain the lowest inflation rate in Latin America in recent years. The CRBP uses the exchange rate as warning signal and takes the adequate monetary and credit measures to achieve its inflation target. Every day at 11:00 in the morning, the Directorate of the Bank, in view of market conditions, quotes its buy and sell prices of the sol in terms of dollars.1 This managed floating system imposes the discipline on the CRBP to keep the purchasing power of the currency. As a result, confidence in the local currency is well anchored in Peru, especially because residents and foreigners can move to the US dollar in case of shocks, as has marginally happened during the COVID-19 crisis.2

In addition, particularly in times of great crisis, governments and other economic agents operate under a de facto parallel currency system. There are many examples of this scenario in economies that have suffered from persistent high inflation and economic instability, such as in Argentina in the early 2000s, Zimbabwe in the late 2000s, Venezuela since 2018, or other economies under a balance of payments crisis within a monetary union, thus lacking in liquidity to make payments (such as Cyprus and Greece in the mid-2010s).

We shall see how a regime of parallel currencies would work, especially for failing economies that are part of a monetary union and those with a record of high inflation. We will use a two-currency system model to detail the conditions under which greater monetary competition contributes to monetary and price stability.

In Section 2 and Section 3, we describe a parallel currency system and its functioning under the ‘inverse Gresham law’. In Section 4, we set up a model of currency competition, with two currencies running under floating exchange rates. In Section 5, we discuss the results of the equilibrium of the model and show under which conditions a system of parallel currencies can function stably and contribute to keeping inflation in check in both currencies. In Section 6, we interpret the results of the model in two different policy scenarios, one corresponding to macroeconomic stability and another to extreme fluctuation in prices, either hyperinflation or hyperdeflation. Section 7 concludes by spelling out policy implications.

2. Parallel Currency Regimes

A parallel currencies system was proposed at the time of the discussion of European Monetary Union (EMU)3 by prominent academics (see Vaubel 1978) and as an official proposal by the British government in the early 1990s (see Dowd 1991; Phelan 2015)4. These proposals were made in the context of the discussion of how to proceed further with the process of monetary integration in Europe but were disregarded in the so-called ‘Delors Report’. Vaubel (1990) focused on the ‘exit’ and ‘voice’ mechanisms by which currency competition would lower the rate of inflation in the economy. The former refers to the fall in the demand of the inflationary currency and the latter to the ability of voters to penalize the running of inflationary policies, particularly under flexible exchange rates. In the absence of currency competition, Vaubel (1990) advocated for a parallel currency system (with no legal tender) to achieve monetary integration in Europe with low inflation. The argument in favor of currency competition as a means to achieve lower rates of inflation is not new, as seminally put in (Hayek 1976). Mafi-Kreft (2003) shows that those periods where money holders had the ability to use different currencies were associated with lower inflation, as compared to those dominated by a single currency issued by the national central bank. Monetary competition is considered as an effective factor in imposing discipline on the national central banks in the issue of money. Fernandez-Villaverde and Sanches (2019) highlight one of the major policy outcomes of currency competition in imposing credible market discipline for the national central bank to produce a stable currency. Specifically, the adoption of a policy rule that preserves the value of the national currency leads to an equilibrium with stable prices, where the national currency expels any other private money from the economy.

It is in the context of the discussion of EMU in the 1990s where (Dowd and Greenway 1993) discussed how realistic it would be to have a monetary system with two currencies in competition. Their model is based on the comparison of the utility functions resulting from the use of each currency, which (crucially) depend on the network effects and switching costs. Contrary to our results, (Dowd and Greenway 1993) explain why currency competition or the introduction of a new (parallel) currency do not usually prevail in the economy and why it is optimal to have a single currency in the economy. Switching costs and inertia in the use of the (incumbent) currency are the major drivers of a single currency solution, and both factors have been at the core of the discussion in the literature on currency competition since then.5

Lotz and Rocheteau (2002) also stress the high inertia of users of the old (incumbent) currency. They develop a search model of money to analyze ways to successfully launch a new fiat currency in a parallel currency scenario. Inertia would require specific policy actions from the government to encourage and even enforce the transition to the new currency. Selgin (2003a) uses a different approach with adaptive learning models to show how determinant network effects are in explaining the predominance of the government favored (fiat) currency. Following Selgin’s (2003a) argument, even if it renders higher expected holding costs, the government can use different means to increase the market of its own currency, thus making it preferable by the public to a potentially more stable currency. The inertia in the use of the incumbent currency, even when it shows a consistently inferior value than the alternatives, as well as the role of governments in supporting the transition to the stronger currency, can also be found in (Luther 2016), where he examines the prospects of Bitcoin as a successful alternative to government money. In a broader study, (Klein and Selgin 2000) assess how money emerges in the first place, from an evolutionary perspective that stresses the effects of limited information in agents’ decisions.

Parallel currency systems have also been discussed in times of monetary crisis and lack of trust in the national currency6, indeed in the context of hyperinflation, when the launch of a new currency is considered as a policy option. Colacelli and Blackburn (2009) studied the determinants of the launch of a second currency in the context of a crisis, when the supply of the national currency is low. We have examples of this discussion in many economies in different parts of the world. For example, (Gomez and Helmsing 2008) discuss the stabilizing benefits resulting from the adoption of new local currency systems in Argentina in the 1990s, at the time of the collapse of the value of the Argentinian peso. In the same vein, (Hanke et al. 1993) discuss this possibility for the post-soviet Russian economy.

The resurgence of the debate on parallel currencies in Europe in the aftermath of the Global Financial Crisis underlines the heavy adjustment costs undertaken by those economies most affected by the crisis (see Economides et al. 2021, on Greece). Théret et al. (2015) argued for the introduction of a new national currency during and in the aftermath of the ‘Euro crisis’ years (2010–2013), so that national governments find it easier to make payments in the new currency. Similarly, (Amato et al. 2016) advocated for the introduction of a parallel currency system ‘as a way to restore fiscal space in peripheral countries’.7 More recently, in the aftermath of the COVID-19 crisis, (Mayer and Schnabl 2020) made the case for the introduction of a parallel currency system in the eurozone; in particular, they suggested the introduction of this system in those less competitive economies so they can benefit from the depreciation of their currencies in real terms. Also, (Lippi 2021) models an economy with two currencies though under a fixed exchange rate.

We follow up on Dowd and Greenway’s (1993) model by considering switching costs in our model, and we also share the assumption that monetary competition—or the introduction of a parallel currency system—is frequently proposed when the incumbent currency has been very poorly managed for a long time. This is in line with (Dowd 1991) where, in the presence of meaningful switching costs, the demand for another currency only exists when inflation rates are significantly high. We examine the transition to the new currency system as mainly driven by economic rather than political reasons. So, however important political considerations are in the economic integration literature, we do not set up our model in the context of the discussion on how to achieve monetary integration, but in that of a country with a national (legal tender) currency that has decided to add another one in competition with it (equally legal tender). However, unlike Dowd and Greenway’s (1993), our model is not based on the running of parallel currencies under a fixed exchange rate. Critically, we assume that the two currencies float against each other and show the equilibrium conditions determining the market share of each currency. We set up a model with two currencies running in parallel under a floating rate system.

3. Parallel Currencies under Floating Exchange Rates: The Operation of the ‘Inverse Gresham’s Law’

Following (Mundell 1998), there are two versions of Gresham’s Law, direct and inverse, depending on whether fixed or flexible exchange rates are in place: the direct is expressed in the traditional statement that ‘bad money displaces good’ (when the rate of exchange is fixed, or legal tender laws are enforced to defend the bad currency); the inverse is expressed in the statement that ‘good money displaces bad’ (when the exchanges are free at the market rate). Bernholz (1989) documents several historical episodes with the application of both the Gresham law and the inverse Gresham law (or Thiers law) under two exchange rate regimes, the former under fixed rates and the latter under floating rates. Bernholz (1989) uses a four-period model with two currencies (the domestic versus the international currency), one being used by the government to finance the deficit, which ultimately leads to an inflated currency. In this model, currency substitution operates when the inflated (domestic) currency lowers its demand in real terms. This result explains the application of Thiers’ law in the context of currency competition and an inflated national currency, under flexible exchange rates. In the same vein, (Selgin 1996, 2003b) show how the Gresham law works under fixed exchange rates in the absence of rules (e.g., legal tender status) forcing agents to accept the ‘bad’ money at par. And also under flexible exchange rates, as both currencies can coexist stably when they float and capital moves freely, if the central banks in charge of each currency focus on maintaining the purchasing power of the currency. And they will tend to do so, for the very depreciation of the more inflationary currency will be an incentive to avoid over-issue: the inflationary currency would be less and less demanded in the market and thus its issuer would suffer a loss in seigniorage revenues. This is what we will examine with our model, which can be applied to an economy under a severe crisis that is running out of the supply of the local currency, and also to an economy with a record of monetary instability and high inflation.

As applied to the Eurozone or a multi-country monetary system, such a parallel currency arrangement could be introduced in times of a crisis affecting Member States disproportionally or a crisis resulting from the unsustainable finances of a Member State. Also, the Member State in crisis would find it easier to correct its course by having temporary recourse to its national currency (see Schwartz et al. 2013; Théret et al. 2015). Further, the experience of Greece during the Eurozone crisis has shown that there is the danger that a euro Member State will run out of cash, since it cannot ‘print’ its own money and its only source of means of payment is a positive balance of payments.8 With a parallel currency system, a failing Member State could temporarily have recourse to the local currency if they ran out of the common currency due to persistent balance of payment deficits, while the flexible exchange rates between the common currency and the national currency would discipline Member States’ central banks and treasuries.

As applied to an economy with a poor inflation record and lack of trust in the government on the issue of a stable currency, the national authorities usually have no choice but to allow for payments in another (more stable) currency, thus effectively running a two-currency system. We have plenty of evidence of this phenomenon in economies like Argentina in the early 2000s, Zimbabwe in the late 2000s, or more recently in Venezuela (2018–2022).

What our model provides is a framework to explain how such a parallel currency system would run de jure, under a floating rates system, and the conditions for both currencies to circulate in the economy.

4. A Formal Model of Parallel Currencies

Our flexible exchange rate model gives conditions under which two currencies (being both legal tender), $i$ and $j$, can coexist in parallel: (a) low price-level elasticity of the demand for either currency, (b) comparable switching costs from one currency to the other, and (c) monetary discipline from the central bank in both currencies. We will assume that the share of each currency is determined by the exchange rate of both currencies and switching costs. Our model focuses on the long-term equilibrium conditions and thus does not include interest rates as determinants of the currencies’ respective market shares.9 As our model shows, the long-term equilibrium is conditional on all the conditions above, in particular (a). The implicit assumption is that such stickiness reflects confidence in the proper behavior of the respective central banks.

4.1. Definitions

4.1.1. Flexible Exchange Rate between the Two Currencies

Let $X_{i,j}$ denote the exchange rate between the two currencies; that is, how many units of currency $j$ [the national currency] can be bought with one unit of currency $i$ [the common or external currency].10 An increase in the value of $X_{i,j}$ means that one unit of currency $i$ buys more units of currency $j$ and thus represents an appreciation of currency $i$. Let the price level of currency $i$ be denoted by $P_i$ and the one for currency $j$ by $P_j$. A high value of $P_i$ in relation to $P_j$ means that currency $i$ has a lower purchasing power than currency $j$ and thus is less valued in the market (in other words, $X_{i,j}$ is small). The exchange rate is fully determined by price differentials in both currencies: an increasing price level for currency $i$, i.e., decreasing purchasing power of currency $i$, will decrease the exchange rate as one unit of currency $i$is worth fewer units of currency $j$. Similarly, an increase in the price level for currency $j$ will increase the exchange rate. With $a$ being the sensitivity of the exchange rate to the ratio of price levels in both currencies, we have the following equation for the exchange rate between the two currencies:

$$X_{i,j}={\left({\displaystyle \frac{P_j}{P_i}}\right)}^a$$

(1)

Due to rigidities caused by determinants other than the price levels in both currencies, which we omit here for simplicity and our focus on the long term, the value of the exchange rate will be less than proportional to the ratio of the price levels in both currencies; thus, we expect a $\le 1$.

Parameter $a$ will be typically lower than 1, at least in our ‘normal’ or stable macroeconomic scenario—one in which money holders do not likely experience major changes in their purchasing power in either currency—therefore, there is no need to change currencies often. This would explain the relative stability in the exchange rate despite (minor or moderate) changes in inflation differentials. This is also explained by the high degree of inertia money holders show under stable macroeconomic conditions (additionally, gathering information to assess changes in the expected purchasing power of the currencies is costly too). However, under a very volatile macroeconomic scenario, the reaction of the exchange rate to (exceptionally high) changes in inflation differentials will likely be much greater and more than proportional to changes in price differentials (i.e., with the possibility of $a$ being higher than 1). This will become more obvious in a hyperinflation scenario, where the expectation of further increases in inflation quickly translates into the depreciation of that currency.11

Let the exchange rate $X_{j,i}$ measure the number of units of $i$ that can be bought with one unit of currency $j$. Modelling the exchange rate as in (1) ensures the necessary condition that the two exchange rates $X_{i,j}$ and $X_{j,i}$ are inverses of each other, i.e.:

$$X_{i,j}=X_{j,i}^{-1}$$

4.1.2. Switching Costs

We denote the cost of switching from currency $j$ to $i$ by $s_i$ and the cost of switching from currency $i$to $j$ by $s_j$. A high value of $s_i$ means high costs to switch from $j$ to $i$. We assume that, other things equal, when it becomes more costly to switch from currency $j$ to $i$ than from $i$ to $j$ (i.e., if ${\displaystyle \frac{s_i}{s_j}}>1$), then agents will want to keep more currency $i$. Therefore, the higher the ratio of the switching costs ${\displaystyle \frac{s_i}{s_j}}$, the higher the share of currency $i$, ceteris paribus. Let us denote the ratio of the switching costs as $s_{i,j}={\displaystyle \frac{s_i}{s_j}}$. The reciprocal will be denoted as $s_{j,i}$.

Switching costs are more relevant in those economies where the national government forces the population to pay taxes in their national currency. In fact, this puts a barrier in the market and impedes an effective competition between the two currencies. In this context, switching costs become more relevant, as the population must keep a large fraction of their income in the national currency to pay taxes. Also, we can distinguish the relevance of switching costs in the two macroeconomic scenarios studied in this paper: if in a stable macroeconomic scenario, there would not be the need to switch currency often. However, if an in unstable macroeconomic scenario, switching currencies will be much more frequent and, to some extent, regardless of the value of switching costs.

4.1.3. Market Share of a Currency

Below in (2), we denote by ${\theta }_i$ and ${\theta }_j$ the shares of currencies $i$and $j$, respectively; that is, ${\theta }_i$ of the economic transactions are made in currency $i$ and ${\theta }_j$ are made in currency $j$. Consequently, in an economy with only two currencies available for market transactions, we have the following necessary requirements for ${\theta }_i$ and ${\theta }_j$:

$$\begin{gathered} {\theta }_i,{\theta }_j\in \left[\mathrm{0,1}\right] \\ {\theta }_i+{\theta }_j=1 \end{gathered}$$

(2)

The aggregate share of the two currencies in the market must be one, as each transaction must be made in one of the two currencies available.

In our model the shares of the currencies will depend on the exchange rate and the ratio of switching costs between the two currencies. Specifically, the influence of the exchange rate $X_{i,j}$ on the share of currency $i$ is positive as agents would prefer a currency with a higher purchasing power, and would also want to keep more of the currency to which it is more costly to swap. We adopt Equations (3) and (4) below to describe the dependence of the share of currencies $i$ and $j$ on their respective the exchange rate and switching costs (see the Appendix A for a verification that this functional form respects the conditions in (2)):

$${\theta }_i={\displaystyle \frac{1}{1+X_{i,j}^{-\nu }·s_{i,j}^{-\mu }}}$$

(3)

$${\theta }_j={\displaystyle \frac{1}{1+X_{j,i}^{-\nu }·s_{j,i}^{-\mu }}}$$

(4)

Here $\nu ,\mu >0$ measure how sensitive the currency share is to changes in $X_{i,j}$ and $s_{i,j}$, respectively. The higher their value the more sensitive the share of currency $i$ reacts to changes in the exchange rate and switching costs. For instance, for a very high value of $\nu$ an exchange rate $X_{i,j}$ just above one might lead to near full displacement of currency $j$ from the market, whereas if $\nu$ is very small, the share of currency $i$ does not react much to changes in the exchange rate. Again, since there are certain rigidities (inertia)12 in the use of the currency that our model does not account for, we expect that $\nu$ and $\mu$ would not be very high and therefore the shares of the currencies would not be overly sensitive to changes in either the exchange rate or switching costs. We will discuss this in more detail in Section 5 and Section 6 below.

4.2. Market Share Determinants

We will determine the factors affecting the exchange rates and thus the market share of a currency. Since we focus on the long-term relation between exchange rates and prices, we will explain the major determinants of the price level according to the standard equation of the quantity theory of money:

$$M·V=P·Y$$

(5)

where $M$ is the amount of money, $V$ the income velocity of money, $Y$ the real income of the economy, and $P$ the price level.13 In our model with two currencies, we have the following equations for each currency:

$$\begin{gathered} M_i·V_i=P_i·{\theta }_{i}Y \\ {M}_j·V_j=P_j·{\theta }_{j}Y \end{gathered}$$

(6)

where $V_i$ is the velocity of currency $i$ and $M_i$ the amount of currency $i$, similarly for $j$. For simplicity, we will assume that both velocities are equal $V_i=V_j$ and constant—in particular, not influenced by the amount of money or other variables in the model (thus, we will denote it by $V$). In (6), we use the share of the income exchanged in the respective currency, and thus we have ${\theta }_{i}Y$ and ${\theta }_{j}Y$. We will treat the level of income $Y$ as a constant as well, since our interest is in the shares of the parallel currencies. We can interpret the predictions for ${\theta }_i$ as the share of currency $i$ that allows for Equation (6) to be in equilibrium.

Rearranging (6) we reach the following expressions for the price levels in both currencies:

$$\begin{gathered} P_i={\displaystyle \frac{M_i·V}{{\theta }_{i}Y}} \\ {P}_j={\displaystyle \frac{M_j·V}{{\theta }_{j}Y}} \end{gathered}$$

(7)

According to Equation (6) above the amount of money has an influence on the market share of each currency. Since both money velocity and the level of income are fixed,14 the effects of changes in the amount of each currency on their respective market share is explained by two different channels that move in opposite directions: on the one hand, a positive effect by which the increase in the amount of currency i, $M_i$, is followed by an increase in its market share ${\theta }_i$. On the other hand, another option for (6) to remain balanced is that the increase in the amount of currency i leads to an increase in the price level in that currency (i.e., $P_i$ increases) via (7). As a result of the increase in $P_i$, the exchange rate $X_{i,j}$ would decrease as currency $i$ becomes less valuable, resulting in a decrease in the market share of currency $i$. We can see that the effect of an increase in $M_i$ is ambiguous, so we need to assess which prevails: (a) If the influence of $P_i$ on ${\theta }_i$ is so strong that an increase in $P_i$ decreases the product $P_i·{\theta }_i$, then the positive effect of $M_i$ on ${\theta }_i$ will prevail. (b) For a weak influence of $P_i$ on ${\theta }_i$, a higher level of $M_i$ could be accounted for by an increase in $P_i$. The higher price level will be less than offset by its effect on ${\theta }_i$, so that the right-hand side of Equation (6) for currency $i$rises. We can suggest an economic interpretation for these two scenarios: (a) corresponds to a scenario where prices are rather sticky and the increase in the amount of the currency is not readily followed by an increase in prices in that currency; whereas scenario (b) occurs when prices are flexible enough to reflect changes in the amount of the currency.

A similar pattern explains the expected effects of changes in switching costs on the currencies’ market share. We argued above that increased costs for switching from currency $j$ to $i$ should increase the share of currency $i$. We verify this in Appendix A by assuming that the exchange rate remains constant. But this assumption is not realistic: if the share of currency $i$ increases, then the price level $P_i$ and the exchange rate will also be affected (see Equation (7) above). The higher exchange rate $X_{ij}$ in turn will have a negative effect on the share of currency $i.$ We gauge these effects in Section 4.3 below.

In order to see whether both currencies can coexist, we derive an expression of ${\theta }_i$ in terms of $M_i$, $M_j$, and $s_{i,j}$ (see Appendix A for details):

$${\theta }_i={\displaystyle \frac{1}{1+X_{i,j}^{-\nu }·s_{i,j}^{-\mu }}}={\displaystyle \frac{1}{1+{\left(\frac{M_j}{M_i}·\frac{{\theta }_i}{1-{\theta }_i}\right)}^{-a\nu }·s_{i,j}^{-\mu }}}$$

(8)

This equation implicitly links the equilibrium share of currency $i$ to the amount of money in both currencies and the switching costs. Since the amount of money can be seen as a variable at the discretion of the respective central banks (an exogenous variable in our model determined by the monetary authorities), we next examine how changes in the amount of money influence the equilibrium share of currency $i$. In addition, we also assess the net effect of a change in the switching costs. To achieve this, we will solve (8) for ${\theta }_i$.

4.3. Market Share Equilibrium

Two trivial solutions for Equation (8) can easily be identified, namely, ${\theta }_i=1$ and ${\theta }_i=0$, which correspond to the situation in which only currency $i$ or only currency $j$ runs in the market. This is the usual central bank monopolist situation of a single currency under legal tender. We will now see whether both currencies can coexist. In order to address this question, we have to discard the two obvious solutions (see Appendix A):

$${\theta }_i={\displaystyle \frac{1}{1+{\left(\frac{M_i}{M_j}\right)}^{\frac{-a\nu }{a\nu -1}}·s_{i,j}^{\frac{\mu }{a\nu -1}}}}$$

(9)

Equation (9) above states the equilibrium share of currency $i$ as a function of the amount of money in both currencies and the switching costs. It is clear that (9) is a solution strictly between zero and one if the amounts of money $M_i$ and $M_j$ are non-zero, so it describes a situation where both currencies coexist.

We can also use (9) for ${\theta }_i$ to establish an explicit description of the price levels in both currencies in terms of the amount of currencies i and j and the switching costs. To do so, we insert (9), which determines the currency share ${\theta }_i$, into Equation (7) as follows:

$$P_i={\displaystyle \frac{V}{Y}}·\left(M_i+M_i^{{\displaystyle \frac{-1}{a\nu -1}}}·M_j^{{\displaystyle \frac{a\nu }{a\nu -1}}}·s_{i,j}^{{\displaystyle \frac{\mu }{a\nu -1}}}\right)$$

(10)

$$P_j={\displaystyle \frac{V}{Y}}·\left(M_j+M_j^{{\displaystyle \frac{-1}{a\nu -1}}}·M_i^{{\displaystyle \frac{a\nu }{a\nu -1}}}·s_{i,j}^{{\displaystyle \frac{-\mu }{a\nu -1}}}\right)$$

(11)

$${\displaystyle \frac{P_j}{P_i}}={\displaystyle \frac{\frac{M_j·V}{{\theta }_{j}Y}}{\frac{M_i·V}{{\theta }_{i}Y}}}={\displaystyle \frac{M_j}{M_i}}·{\displaystyle \frac{{\theta }_i}{1-{\theta }_i}}={\displaystyle \frac{M_j}{M_i}}·{\left({\displaystyle \frac{M_i}{M_j}}\right)}^{{\displaystyle \frac{a\nu }{a\nu -1}}}·s_{i,j}^{{\displaystyle \frac{-\mu }{a\nu -1}}}=M_i^{{\displaystyle \frac{1}{a\nu -1}}}·M_j^{{\displaystyle \frac{-1}{a\nu -1}}}·s_{i,j}^{{\displaystyle \frac{-\mu }{a\nu -1}}}$$

(12)

For the expression of $P_j$ in (11) above we impose symmetry and exchange the currencies with respect to (10). For the ratio of price levels in (12), we insert (9), which determines the share of currency $i$ as a function of the amount of money in both currencies and the switching costs.

Now that we have an explicit expression for ${\theta }_i$ in terms of $M_i$, $M_j$, and $s_{i,j}$, we can assess the net effects of changes in these variables on ${\theta }_i$ and thus resolve the ambiguities mentioned in the section above. We will discuss the effects of $M_i$ and $s_{i,j}$ on ${\theta }_i$.15 To see how $M_i$ influences ${\theta }_i$, we calculate the derivative of ${\theta }_i$ by $M_i$:

$${\displaystyle \frac{\partial {\theta }_i}{\partial M_i}}={\displaystyle \frac{a\nu }{a\nu -1}}·{\displaystyle \frac{s_{i,j}^{\frac{\mu }{a\nu -1}}·M_j^{\frac{-a\nu }{a\nu -1}}·M_i^{\frac{-2a\nu +1}{a\nu -1}}}{{\left(1+{\left(\frac{M_i}{M_j}\right)}^{\frac{-a\nu }{a\nu -1}}·s_{i,j}^{\frac{\mu }{a\nu -1}}\right)}^2}}$$

(13)

Given that the sign of the last fraction in (13) is positive, the sign of the derivative will be determined by ${\displaystyle \frac{a\nu }{a\nu -1}}$, i.e., the effect of changes in the amount of currency $i$ on its market share will be negative if $a\nu <1$ and positive if $a\nu >1$.

Since the price levels affect the share of the currencies, it is worth assessing the reaction of prices to the amount of money directly. Differentiating (10), (11), and (12) by $M_i$, we arrive at the following expressions:

$${\displaystyle \frac{\partial P_i}{\partial M_i}}={\displaystyle \frac{V}{Y}}·\left(1-{\displaystyle \frac{1}{a\nu -1}}·M_i^{{\displaystyle \frac{a\nu }{a\nu -1}}}·M_j^{{\displaystyle \frac{a\nu }{a\nu -1}}}·s_{i,j}^{{\displaystyle \frac{\mu }{a\nu -1}}}\right)$$

(14)

$${\displaystyle \frac{\partial P_j}{\partial M_i}}={\displaystyle \frac{a\nu }{a\nu -1}}·{\displaystyle \frac{V}{Y}}·{\left({\displaystyle \frac{M_i}{M_j}}\right)}^{{\displaystyle \frac{1}{a\nu -1}}}·s_{i,j}^{{\displaystyle \frac{-\mu }{a\nu -1}}}$$

(15)

$${\displaystyle \frac{\partial \left(\frac{P_j}{P_i}\right)}{\partial M_i}}={\displaystyle \frac{1}{a\nu -1}}·s_{i,j}^{{\displaystyle \frac{-\mu }{a\nu -1}}}·M_j^{{\displaystyle \frac{-1}{a\nu -1}}}·M_i^{{\displaystyle \frac{2-a\nu }{a\nu -1}}}$$

(16)

As with (13), the sign of $a\nu -1$ will be key to determine the sign of the relation between prices and money in (14): if $a\nu <1$, the derivative of the price level$P_i$ by $M_i$ will be positive, whereas the derivative of the price level $P_j$ by $M_i$, and thus the derivative of the ratio of price levels by $M_i$, is negative. This result shows that increases in the amount of a currency will end up raising prices in that currency. However, if $av>1$, then the sign of the derivative of $P_i$ by $M_i$ will depend specifically on the amount of money in each currency in the economy and the switching costs. Regarding (15) and (16), the signs of the derivative of $P_j$ by $M_i$ and the derivative of the ratio of price levels by $M_i$ are positive.

Before we interpret these results, we will also calculate the derivative of ${\theta }_i$ with respect to $s_{i,j}$:

$${\displaystyle \frac{\partial {\theta }_i}{\partial s_{i,j}}}={\displaystyle \frac{-\mu }{a\nu -1}}·{\displaystyle \frac{{\left(\frac{M_i}{M_j}\right)}^{\frac{-a\nu }{a\nu -1}}·s_{i,j}^{\frac{\mu -a\nu +1}{a\nu -1}}}{{\left(1+{\left(\frac{M_i}{M_j}\right)}^{\frac{-a\nu }{a\nu -1}}·s_{i,j}^{\frac{\mu }{a\nu -1}}\right)}^2}}$$

(17)

The last fraction in (17) is positive; therefore, the sign is determined by ${\displaystyle \frac{-\mu }{a\nu -1}}$: the derivative of ${\theta }_i$ by $s_{i,j}$ will be positive if $a\nu <1$ and negative if $a\nu >1$.

Finally, we calculate the derivative of the price levels with respect to the switching costs:

$${\displaystyle \frac{\partial P_i}{\partial s_{i,j}}}={\displaystyle \frac{\mu }{a\nu -1}}·{\displaystyle \frac{V}{Y}}·M_i^{{\displaystyle \frac{-1}{a\nu -1}}}·M_j^{{\displaystyle \frac{a\nu }{a\nu -1}}}·s_{i,j}^{{\displaystyle \frac{\mu -a\nu +1}{a\nu -1}}}$$

(18)

$${\displaystyle \frac{\partial P_j}{\partial s_{i,j}}}={\displaystyle \frac{-\mu }{a\nu -1}}·{\displaystyle \frac{V}{Y}}·M_i^{{\displaystyle \frac{a\nu }{a\nu -1}}}·M_j^{{\displaystyle \frac{-1}{a\nu -1}}}·s_{i,j}^{{\displaystyle \frac{-\mu -a\nu +1}{a\nu -1}}}$$

(19)

$${\displaystyle \frac{\partial \left(\frac{P_j}{P_i}\right)}{\partial s_{i,j}}}={\displaystyle \frac{-\mu }{a\nu -1}}·{\left({\displaystyle \frac{M_i}{M_j}}\right)}^{{\displaystyle \frac{1}{a\nu -1}}}·s_{i,j}^{{\displaystyle \frac{-\mu -a\nu +1}{a\nu -1}}}$$

(20)

If $a\nu <1$, then the derivative of $P_i$ by the switching costs is negative, the derivative of $P_j$ by $s_{i,j}$ is positive as well is the derivative of the ratio of price levels by the ratio of switching costs. In the case of $a\nu >1$ the derivatives have the opposite sign, so ${\displaystyle \frac{\partial P_i}{\partial s_{i,j}}}>0$, whereas both ${\displaystyle \frac{\partial P_j}{\partial s_{i,j}}}$ and the derivative of the ratio of price levels by the switching costs are negative. The major assumption of our model concerns the value of $a\nu$, as extensively discussed in Section 4.3 and Section 5. If this value is below one, our model predicts that two currencies can coexist. If it is above one, maintaining stability and the circulation of both currencies will be very difficult.

4.4. Statistical Inference

In order to make quantitative predictions and gain quantitative insights into the sensitivities $a·\nu$ and $\mu$, we need to fit our model to data. While the analysis of real data is left for future work (which will require assigning numerical values to the switching costs), we provide an outline and a synthetic example of how the parameters of the model can be inferred from data.

The dependent variable ${\theta }_i$ is the market currency share, and therefore lies between $0$ and $1$, making normal linear regression a poor model choice. We consider two suitable alternatives. First, our model admits a treatment as a generalized linear model in the explanatory variables $\log \left({\displaystyle \frac{M_i}{M_j}}\right)$ and $\mathrm{l}\mathrm{o}\mathrm{g}\left(s_{ij}\right)$ as follows:

$${\theta }_i={\displaystyle \frac{1}{1+{\left(\frac{M_i}{M_j}\right)}^{\frac{-a\nu }{a\nu -1}}·s_{i,j}^{\frac{\mu }{a\nu -1}}}}={\displaystyle \frac{1}{1+\exp \left(-\left(\frac{a\nu }{a\nu -1}\log \left(\frac{M_i}{M_j}\right)-\frac{\mu }{a\nu -1}\log \left(s_{ij}\right)\right)\right)}}=f\left({\psi }_0\log \left({\displaystyle \frac{M_i}{M_j}}\right)+{\psi }_1\log \left(s_{ij}\right)\right)$$

(21)

where $f\left(x\right)={\displaystyle \frac{1}{1+\exp (-x)}}$ is the logistic function and ${\psi }_0={\displaystyle \frac{a\nu }{a\nu -1}}$ and ${\psi }_1={\displaystyle \frac{-\mu }{a\nu -1}}$. Note that we can recover $a·\nu$ and $\mu$ from ${\psi }_0$ and ${\psi }_1$. This suggests a treatment as a generalized linear model with a logit link function ($f^{-1}$):

$$\begin{gathered} f^{-1}\left({\theta }_i\right)~\mathcal{N}\left(m,{\sigma }^2\right) \\ m={\psi }_0\log \left({\displaystyle \frac{M_i}{M_j}}\right)+{\psi }_1\log \left(s_{ij}\right) \end{gathered}$$

(22)

This approach has the disadvantage that the mean and variance of ${\theta }_i$ are not given in closed form because the noise model is in the logit-transformed space.

Instead, we favor a beta-regression (Ferrari and Cribari-Neto 2004), as it is precisely designed for data in the $(0,1)$ range and offers an easier interpretation (Geissinger et al. 2022). The probabilistic model becomes:

$$\begin{gathered} {\theta }_i~Beta\left(m,\varphi \right) \\ m=f\left({\psi }_0\log \left({\displaystyle \frac{M_i}{M_j}}\right)+{\psi }_1\log \left(s_{ij}\right)\right). \end{gathered}$$

(23)

We use the mean and precision parametrization of the beta distribution:

$$Beta\left(x;m,\varphi \right)={\displaystyle \frac{\mathsf{\Gamma }\left(\varphi \right)}{\mathsf{\Gamma }\left(m\varphi \right)\mathsf{\Gamma }\left(\left(1-m\right)\varphi \right)}}{x}^{m\varphi -1}{(1-x)}^{\left(1-m\right)\varphi -1},0<x<1$$

(24)

The mean is directly given by $m$ while the variance is mean-dependent: $Var\left(m,\varphi \right)={\displaystyle \frac{m(1-m)}{1+\varphi }}$. This accommodates the typical heteroscedastic setting of lower variance for data close to the boundaries of the interval $\left[0,1\right]$ (Geissinger et al. 2022).

Assume we have $n$ data points ${\left({\log \left({\displaystyle \frac{M_i}{M_j}}\right)}_t,{\log \left(s_{ij}\right)}_t,{{(\theta }_i)}_t\right)}_{t=1,\dots ,n}$. Then, we fit the parameters ${\psi }_0,{\psi }_1,\varphi$ by maximising the log likelihood function:

$$\begin{gathered} l\left({\psi }_0,{\psi }_1,\varphi \right)={\sum }_{t=1}^n{l}_t\left(m_t,{\psi }_0,{\psi }_1,\varphi \right) \\ {l}_t\left(m_t,{\psi }_0,{\psi }_1,\varphi \right)=\log \mathsf{\Gamma }\left(\varphi \right)-\log \mathsf{\Gamma }\left(m_t\varphi \right)-\log \mathsf{\Gamma }\left(\left(1-m_t\right)\varphi \right) \\ +\left(m_t\varphi -1\right){\log ({\theta }_i)}_t+\left(\left(1-m_t\right)\varphi -1\right)\log \left(1-{\left({\theta }_i\right)}_t\right), \end{gathered}$$

(25)

where $m_t$ is the mean for the $t^{th}$ data sample.

We illustrate the beta regression on a suite of synthetic experiments. For these, we generated explanatory variables by sampling $n$ times:

$$\begin{gathered} \log \left({\displaystyle \frac{M_i}{M_j}}\right)~\mathcal{N}\left(0,{0.4}^2\right) \\ \log \left(s_{ij}\right)~\mathcal{N}\left(0,{0.2}^2\right). \end{gathered}$$

(26)

For each such data point, we computed $m$ with ground truth parameters $a·\nu =0.8$ and $\mu =0.7$ before sampling the noisy currency share:

$${\theta }_i~Beta\left(m,10\right).$$

(27)

Then, we estimated $\widehat{a·nu},\widehat{\mu },\widehat{\varphi }$ via a beta regression. We explored seven different sample sizes $n\in [10,10000]$ and sampled with five random seeds for each dataset size.

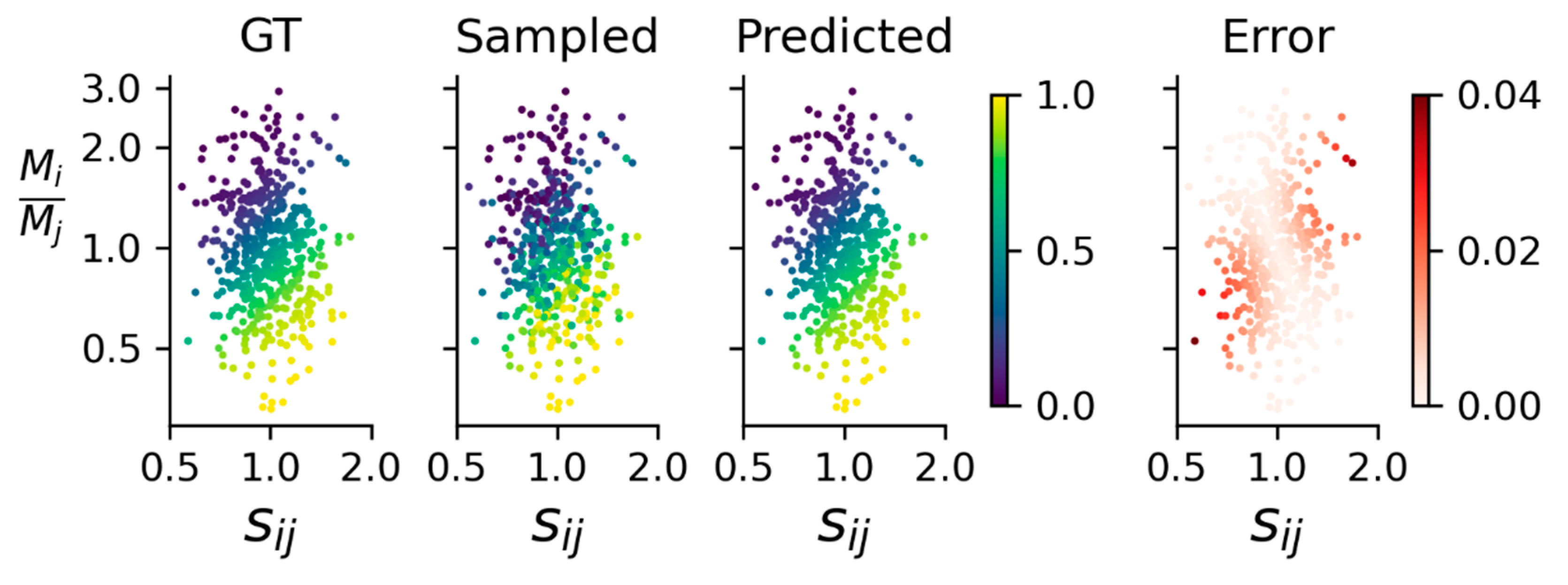
We illustrate one setting for $n=1000$ in Figure 1, which shows that (a) the precision level $\varphi =10$ is low, making the sampled data quite noisy. Despite this challenging setting, we recover the currency shares with very little absolute error. The most difficult setting is when the ratio of the amounts of money and the ratio of the switching costs are both low or both high.

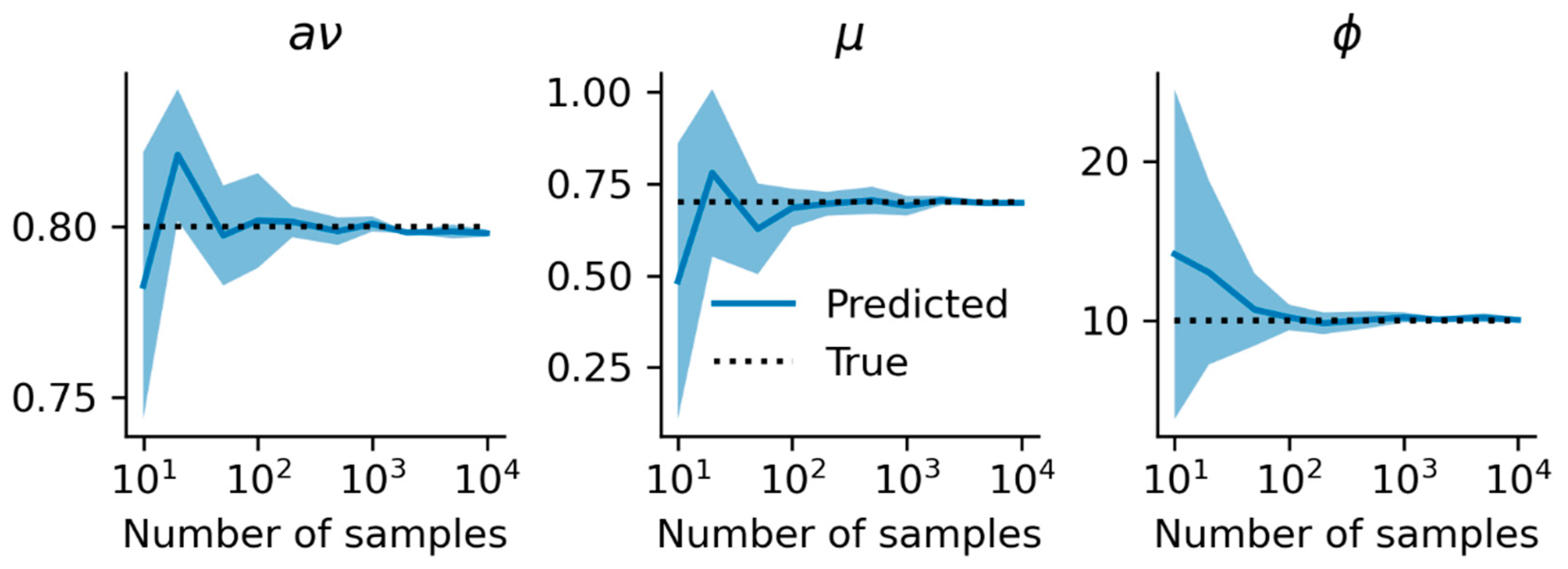
In Figure 2, we see that the beta regression successfully recovers the correct parameter values from about $n\ge 100$data points onward.

The built-in heteroscedasticity of $Beta\left(m,\varphi \right)$-distributed data can be extended by making the precision $\varphi$ a function of the explanatory variables as well (Simas et al. 2010). Misspecification tests for beta regression are described, for instance, by (Cribari-Neto et al. 2024).

5. Interpretation of the Results under Different Macroeconomic Scenarios

In the section above, we showed that whether $a\nu$ is greater or smaller than 1 is crucial in the interpretation of our results. $a$ is the sensitivity of the exchange rate with respect to changes in the price levels, so that a high value of $a$ means that a small change in the ratio of price levels has a great impact on the exchange rate. $\nu$ is the sensitivity of the currency shares with respect to the exchange rate, so that a high value of $\nu$ means that ${\theta }_i$ reacts very strongly to a change in the exchange rate. Therefore, the combined value of $a\nu$ is the sensitivity of the share of currency $i$ with respect to the ratio of price levels: the higher it is, the stronger ${\theta }_i$ decreases if ${\displaystyle \frac{P_j}{P_i}}$ decreases.

Our model links prices, currency shares, and the amount of money in each currency through Equation (6). Therefore, our model predicts how currency shares and price levels need to react to changes in the amount of money and switching cost so that the Equation (6) remains in equilibrium.

5.1. Currency Share and Money Supply

In Section 4 above, we anticipated that a change in the amount of money $M_i$ has a positive effect on ${\theta }_i$directly through Equation (6) and a negative effect indirectly through the increased price level, and computed which effect prevails in which situation. We will now assess the economic plausibility of these predictions.

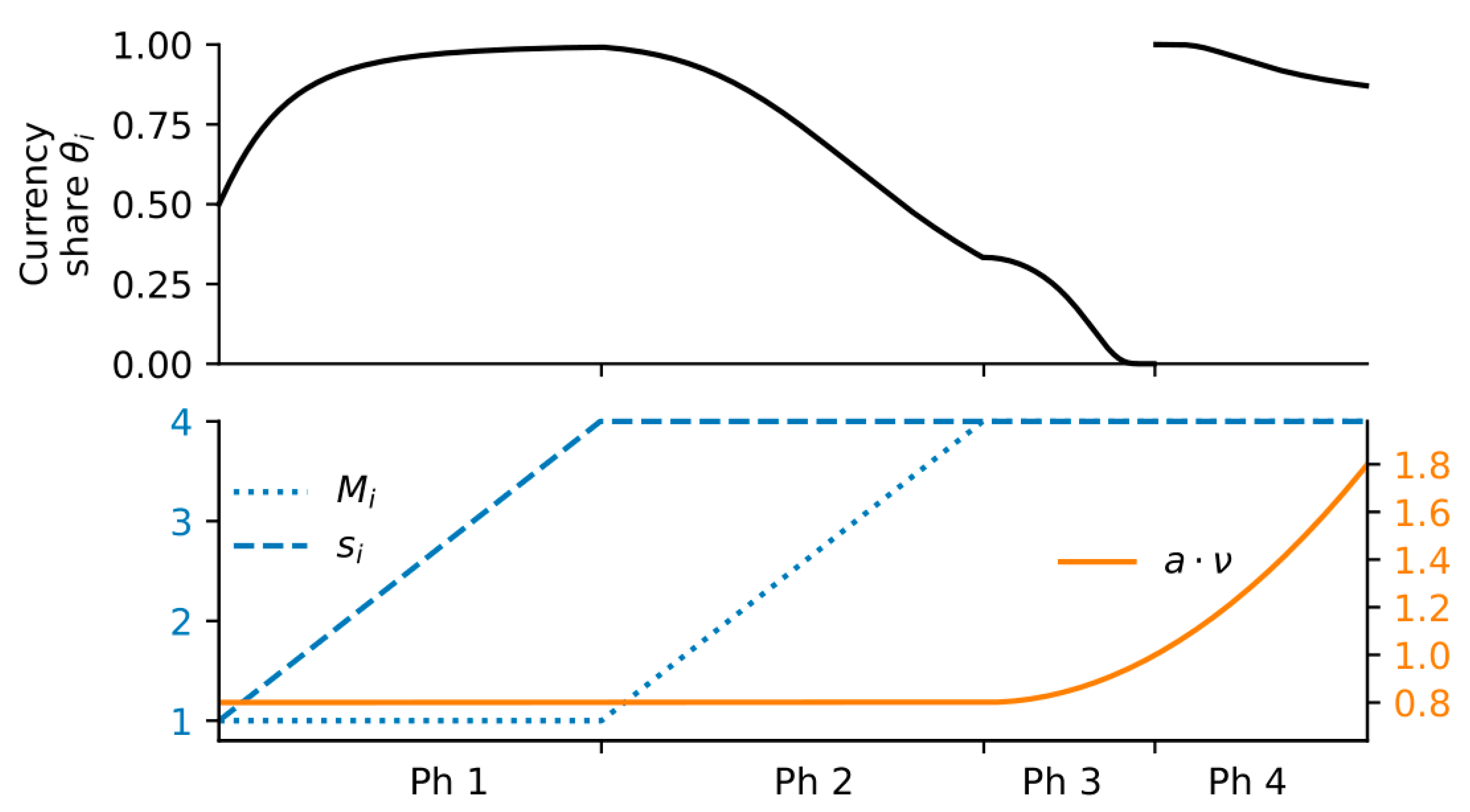
Let us assume that we are in a scenario with low price-sensitivity, i.e., $a\nu <1$, corresponding to a relatively stable economy, one in which the amount of money in each currency does not vary drastically. In this regime, our model requires that an increase in the amount of money $M_i$ raises prices $P_i$ according to (14) and that this also decreases $P_j$, and thus the ratio ${\displaystyle \frac{P_j}{P_i}}$ (via (15) and (16)). Similarly, the market share of the more inflationary currency (${\theta }_i$) should decrease as well according to the model, and consequently that of the more stable currency (${\theta }_j$) should increase. Both conditions are realistic and expected in a scenario of a more inflationary currency (i). As a result, the quantity equation for currency $i$ balances with an increased amount of currency $i$, which is offset by a substantial increase in $P_i$ and a relatively small decrease in ${\theta }_i$. The quantity equation for $j$ remains balanced on the same level as before; in this case, the decrease in $P_j$ is counteracted by the increase in ${\theta }_j$. Thus, under low price-sensitivity, we expect that both currencies coexist in the long run. Of course, were the central bank to significantly increase the amount of currency $i$, its share might still become very small.

Next, we consider the less likely case of high price-sensitivity, i.e., $a\nu >1$. In such a highly price-sensitive situation, one would assume extreme behavior in the economy should the determinants of prices and exchange rates vary. Such extreme effects can be explained along the lines of our model. However, we will see that such an explanation would prevent us from reaching equilibrium in Equation (6), as the reactions that the model shows needed to balance Equation (6) are opposed to the economically plausible ones. If $a\nu >1$, we expect that one of the two currencies is prone to completely displacing the other from the market. The value of our model’s at first sight surprising results is to caution us against this highly volatile scenario and can at the same time be understood as the policy description of what the monetary authorities would need to do in order to maintain a stable two currency economy, even when price sensitivity is high, so that we can avoid hyperinflation in either currency. We will discuss these monetary policy prescriptions in Section 7.

Let us first describe intuitively what would happen if $a\nu >1$ and the amount of money in currency $i$ increases. In this scenario we would expect the price level $P_i$ to increase too, similar to what happened in the case of low price-sensitivity described above. But since ${\theta }_i$ is now very price-sensitive, the result of such an increase in $P_i$ would be a sharp drop in the share of currency $i$. Overall, the right-hand side of Equation (6) for currency $i$ would decrease. Since there is more currency $i$ in the market than needed for the share of the output that is traded in currency $i$, prices in currency $P_i$ would rise even further. Now we enter a process leading to greater and greater inflation, and we cannot reach equilibrium anymore, and as a result, ${\theta }_i$ would fall continuously. In fact, we are under a hyperinflation spiral in currency i: eventually, currency $i$ would nearly disappear, while prices in currency $i$ become arbitrarily large. This means that ${\theta }_j$ would get close to 1 (and thus becomes the virtual monopolist currency in the market) and that $P_j$ would fall, which again would make ${\theta }_i$ decrease further. Note that this analysis prevents Equation (6) from ever becoming balanced again with positive shares in both currencies. In the real world, where arbitrarily small shares of currency $i$ are not possible, currency $i$ will eventually disappear entirely. This corresponds to the more standard situation of a single currency in the market.

We now turn to our model to see how to regain balance after increasing the amount of currency in this highly price-sensitive situation. By Equation (13), the share of the currency would have to increase for a new equilibrium at the higher amount of money and prices in the other currency would have to rise. As outlined above, these are not effects that will happen automatically. Rather, policy makers would have to take decisive actions to achieve this outcome, and hence a new equilibrium with a greater amount of money and both currencies still coexisting.

5.2. Currency Share and Switching Costs

Under a scenario with low price-sensitivity of the currency share ($a\nu <1$), we turn now our focus to the effect of changes in the switching costs on each currency’s market share. It is important to note that switching costs affect the currency share directly. In contrast to what happened as a result of changes in the amount of money, now, changes in the price levels do not play a role in the explanation of the change in the shares of the currencies but are rather a consequence of it.

When the ratio of switching costs increases, i.e., $s_{i,j}$ rises, the share of currency $i$ will be higher for all ratios of price levels, as Equation (A4) in Appendix A shows. Since more goods are now traded in currency $i$, while the amount of currency $i$ stays the same, the price level $P_i$ decreases. In this case, the increased use of currency $i$ and the supply of currency $i$ being steady will increase its purchasing power. Applying a similar argument to the equation for $j$, we see that the price level $P_j$ rises as there is an excess of currency $j$, and it thus loses purchasing power. Consequently, the ratio of price levels increases (see (20)), which has an additional positive effect on the market share of currency$i$. However, due to the low price-sensitivity assumed in this scenario, this positive effect is small and the resulting increase in the ratio of price levels has an even smaller positive effect on ${\theta }_i$. As before, the predicted outcome aligns with our expectation and shows that in case of low price-sensitivity of the currency shares, these are feasible conditions for the running of two competing currencies in parallel.

Under a scenario with high price-sensitivity, i.e., $a\nu >1$, when the ratio of switching costs increases, $s_{i,j},$ following Equation (A4), at each ratio of price levels, the share of currency ${\theta }_i$ will be higher. As described above, this leads to hyperdeflation in currency $i$, eventually leading to a currency monopoly (currency $j$ will disappear from circulation). In contrast to this analysis, our model requires a decreased share of currency $i$ to achieve a new equilibrium at the higher ratio of switching costs, making the coexistence of the two currencies difficult. Nevertheless, the model indicates how it could still be achieved: policy makers would need to make it possible to decrease the share of currency $i$ if the ratio of switching costs $s_{i,j}$were to be increased. One such possibility might be to combine an increase in the amount of currency $i$ with an increase in the ratio of switching costs, so that the necessary changes on the currency shares—which the model predicts—cancel out and the economy remains at equilibrium.

We illustrate how the currency share changes with respect to the amounts of money, the switching costs, and sensitivities in Figure 3.

6. Monetary Policy under Extreme Macroeconomic Conditions

According to our analysis above, under a high price-sensitivity scenario, changes in the amount of money or in the switching costs may well lead to the collapse of the two-currency system, ending in a currency monopoly with either hyperinflation or hyperdeflation in one of the currencies. The issuers of the currency would have to be very careful in order to maintain a stable two-currency system in this very volatile economy.

Our model, however, makes counter-intuitive predictions in the high price-sensitivity scenario. As discussed above, this is to be expected, since the model is built on the assumption that both equations in (6) hold and both currencies coexist. As the intuitive arguments in Section 4 show, this is not plausible in a high price-sensitivity scenario (one currency completely displaces the other, which would allow for the equations in (6) to be balanced). This might suggest that our model is not suitable for this scenario.

But the predictions of our model are not without value in this high price-sensitivity scenario. We can interpret them as a policy prescription of what would need to happen for both currencies to keep their value and coexist even in a high price-sensitivity setting. In a high price-sensitivity scenario, a continuous increase in the supply of local currency $M_i$ or a forced decrease in the ratio of switching costs $s_{i,j}$, rather than defending the local currency, will lead to local users fleeing the local currency and have an accelerating inflation effect. This is in line with Dowd (1991)’s analysis of Hard-ECU proposal as a competing currency with the national currency; given that switching costs and network effects are very prominent, the demand for such a parallel currency system would only exist if the local currency were significantly inflated.16 We can see an extreme version of this in Venezuela and also in Argentina in recent years.

The indirect effects that guarantee a stable two-currency economy in the case of high price-sensitivity are plausible though more difficult to achieve in real-world scenarios (though examples exist of a successful running of two currencies). The more intuitive scenario of hyperinflation or hyperdeflation in one currency seems more likely. However, our model gives an indication of potential mechanisms available for policy makers to avoid this collapse to one currency and maintain a parallel currency system, even under a volatile scenario with high price-sensitivity.

7. Policy Conclusions

The analysis of our two-currency model shows that there is an equilibrium in the market for the coexistence of both currencies. However, this equilibrium can only be maintained under what we have called a stable macroeconomic scenario; one in which the sensitivity of the market share of the currencies to changes in prices in both currencies is not high (as we presume changes in inflation in both currencies will be rather small). In this scenario, changes in the market share of one currency will be ultimately determined by the relative changes in the amount of that currency and thus in relative changes in prices in one currency relative to the other. Therefore, the less inflationary currency will gain market share over the other currency. This would allow for the members of a monetary union to keep a sound national currency along with the common currency—a monetary system that offers the incentives to keep the purchasing power of both currencies stable. Such a monetary system would offer more policy options for Member States suffering a liquidity crisis, as they could use their own currency for temporary relief. The flexible exchange rate would give timely warnings when this temporary remedy was being abused.

The model can also be applied to an economy with a record of high inflation, where money users had eventually opted for using a more credible currency, thus creating (de facto or de jure) a parallel currency system. In this scenario, the model explains the conditions for the national currency to run in parallel with the (external) currency. In addition, the model also explains under which conditions the two-currency economy would collapse into a single currency as the failed currency would suffer from hyperinflation. Crucially, the full expulsion of one currency by the other would likely happen in a highly volatile macroeconomic scenario, where agents’ demand of each currency is very sensitive to changes in relative prices in both currencies. In this highly price-sensitive scenario, an increase in switching costs to favor the use of one of the currencies (i.e., the government’s preferred currency) would only lead to inflation in that favored currency and very quickly to its expulsion from the market. In order to keep both currencies running, our model requires that the share of a currency increases when the amount of money in this currency is increased and or when switching costs are changed to its apparent disadvantage. Therefore, only a very careful policy combination of both a change in switching costs and the amount of money would contribute to preserving both currencies in circulation.

The results from our model show the conditions under which a parallel currency system will discipline the issuers of the currencies and thus maintain their purchasing power. In non-volatile economies, it also discourages governments (or private issuers) from inflating one of the currencies as a means to raise seigniorage, as this policy quickly results in the displacement of the currency from the market. In addition, any efforts by the issuer of the inflated currency to force agents to use their currency (i.e., by increasing the costs of switching to the other, more stable currency) would also accelerate inflation in that currency and thus its expulsion from the market.