Abstract
The COVID-19 pandemic has introduced significant uncertainty across various economic sectors, most notably in the industrial sector due to the high volatility in copper futures markets. These markets play a crucial role in the construction, electrical networks, electronic products, and industrial machinery industries. Therefore, the aim of this study is to evaluate the impact of the COVID-19 pandemic on the volatility of copper futures returns from 2 January 2018 to 30 December 2022 using an extended ARMA(m,n)–GARCH(p,q) framework. According to the results, the occurrence of the pandemic nearly doubled the long-run equilibrium volatility of returns compared to the values obtained in the pre-pandemic period. Hence, we conclude that the COVID-19 pandemic has a significant influence on the volatility in the copper futures market.
1. Introduction
At the beginning of the COVID-19 pandemic, most countries had imposed multiple restrictions and health protocols due to the rapid spread of the coronavirus, such as social distancing, limitations on gatherings, international travel controls, etc. However, around the middle of 2020, these measures caused a global economic recession and an interruption in the proper functioning of the financial and commodity markets (Al-Awadhi et al. 2020; Bai et al. 2021). Although the greatest panic caused by the COVID-19 pandemic was observed at the end of the first quarter of 2020, the lack of knowledge regarding the virus’s evolution caused a delay in the development of the COVID-19 vaccine, and its economic consequences continued to be highly uncertain (Umar et al. 2021). Hence, due to the high economic uncertainty, investors, portfolio managers, entrepreneurs, and policymakers have mainly focused on comprehending the volatile behavior of commodity futures markets (Bentes 2022; Rizvi and Itani 2022; Xu et al. 2022) since it is a key input in hedging, asset pricing, portfolio allocation, derivatives and options trading, and regulation (Liu and Guo 2022).
In particular, we highlight the importance of understanding the price and return fluctuations in the copper futures market since copper is one of the main metals used in the industrial sector in a variety of manufacturing processes, infrastructure, electrical and electronic products, transportation, wiring and plumbing (Elshkaki et al. 2016). Copper production is concentrated in a few countries, with the four largest producers (Chile, Peru, Congo, and China) generating more than 50% of the world’s mined copper production, although China consumes more than half of the world’s production (United States Geological Survey 2023; Wood Mackenzie 2023). Hence, this implies that copper futures prices may become vulnerable to an event caused by the consequences of the coronavirus in those countries.
Furthermore, despite the importance of assessing the volatility of the copper futures market during the COVID-19 pandemic in the economic system, specifically in the industrial sector, there are few studies that have comprehensively investigated the impact of this pandemic on the volatility in this market (Zhang and Wang 2022; Zhou et al. 2022).
Regarding the consequences of the coronavirus, preliminarily, Figure 1 shows that the copper futures price series began to have a highly volatile behavior during the COVID-19 era, in contrast to the relative stability experienced in the pre-COVID-19 phase.
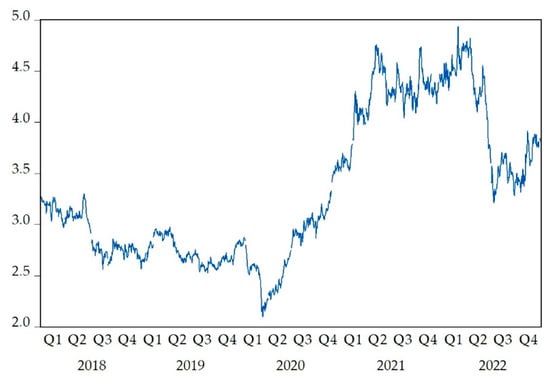
Figure 1.
Copper futures daily prices in U.S. dollars per pound during 2018–2022.
This unstable behavior of prices during the COVID-19 pandemic may have been due to certain news and events that generated fluctuations resulting in both peaks and valleys in the copper futures price series. Some of the relevant news and its dates related to high fluctuations in copper futures prices are:
- 18 March 2020; the world’s top metal producers (Chile, Peru, Canada, and others) began limiting their operations as governments took steps to contain coronavirus contagion, dimming the supply outlook (Mining.com 2020).
- 23 March 2020; regarding the prospects for the price of the metal in the short term, the Chilean Copper Commission pointed to a pessimistic scenario as a result of the severe contraction in industrial activity due to the COVID-19 pandemic (Reporte Minero 2020).
- 26 February 2021; suspension of new and pending projects of the Peruvian refinery Southern Copper Corp. Together with the high demand from China and restricted supply due to the COVID-19 pandemic, which boosted the price of copper (Reuters 2021a).
- 26 July 2021; copper prices began recovering due to the economic reopening in the supplying countries, which was driven by high demand from China (Reuters 2021b).
- 26 November 2021; copper prices fell on fears that a new coronavirus variant, possibly resistant to vaccines, could derail global economic growth and undermine demand, adversely affecting the market risk (Reuters 2021c).
- 5 July 2022; copper continued to plummet to a 17-month low due to several factors such as aggressive interest rate hikes, an uptick in COVID-19 cases in China, potential recession, and rising inventories weighing on investor sentiment (Arab News 2022).
- 4 November 2022; copper prices experienced a 2% uptick, with sentiment lifted by hopes of easing COVID-19 curbs in China, the world’s leading consumer of metals. Nonetheless, fears over constrained supply persisted due to persistently lean inventories and new production disruptions in Peru, the world’s second-largest copper producer, due to the consequences of the COVID-19 pandemic (MarketScreener 2022).
- 11 November 2022; although China’s strict COVID-19 measures had hit its industrial activities and dragged down copper futures demand, the copper prices climbed to a five-month high due to the Fed having a slower pace of rate hikes (Reuters 2022).
The news indicated that many of the distortions in the copper futures prices during the COVID-19 pandemic may have been generated by several labor, operational, and logistical restrictions in the production supply chain of the main producing countries. According to the aforementioned news, one of the main causes of the price’s volatile behavior was COVID-19 restrictions in China, the main buyer of this commodity, generating a reduction in copper imports.
The primary objective of this study is to empirically investigate the impact of the COVID-19 pandemic on the copper futures market from 2 January 2018 to 30 December 2022. In addition, our research contributes to the recent but insufficient body of literature detailing the copper futures market’s response to the COVID-19 crisis. Moreover, our findings are relevant for industrial sector agents, investors, and portfolio managers in their attempts to understand and forecast the behavior of copper futures prices during periods of global economic and financial recession.
2. Literature Review
Prior to the appearance of the COVID-19 pandemic, some authors had proposed to empirically investigate the influence of several economic and non-economic factors on the volatility in commodity prices. The GARCH model and its variations are widely used to analyze the volatility in commodities markets.
In relation to the macroeconomic impact, Vivian and Wohar (2012) examined 28 different commodities from 1985 to 2010 in a GARCH model and found that the volatility remained very persistent in the short term for many commodities and returns even after structural breaks were accounted and where supply and demand factors were important determinants of volatility. Karali and Power (2013) analyzed numerous agricultural, energy, and metal futures prices using a spline-GARCH model, concluding for most commodities, the volatility was affected by factors such as alterations in inflation, industrial output, inventory levels, and the long-term and short-term interest rate spread. In addition, Li et al. (2013) investigated the oil future prices during the period 1983–2012 in an asset pricing model and found that there was a significant intertemporal relationship between the diffusion information and the volatility price of oil futures, generating predictability in price dynamics. Gevorkyan (2017) comparatively examined the volatilities between the renewable and nonrenewable commodities during the period 1996–2013 and found that futures prices for certain renewable resources exhibit a higher degree of variability compared to those of the benchmark crude oil due to the uncertainty about supply factors. Furthermore, Gruber and Vigfusson (2018) evaluated the impact of the interest rates on the volatility of commodities futures prices between 1992 and 2012 in a panel GARCH model. Their results showed that the volatility of the prices falls as the real interest rate declines for crude oil and metals futures.
In the same line, Mo et al. (2018) examined the commodity futures prices from two emerging commodity markets (China and India) using a GARCH-MIDAS model and found that both domestic and international macroeconomic variables significantly determined the long-run volatility of the Chinese and Indian commodity futures markets. Ayele et al. (2020) conducted a study in which they examined the dynamics of silver price volatility on the Ethiopian market from 1998 to 2014. They employed an EGARCH model and determined that unexpected changes in price, saving rates, interest rates, and general inflation exhibited statistical significance in relation to silver’s price volatility. Liu et al. (2021) investigated the impact of geopolitical uncertainty on energy commodities futures volatility (for crude oil, heating oil, and natural gas); their results showed that geopolitical uncertainty, financial market stress, and economic policy uncertainty had a significant impact on the volatility prices of energy futures. Ye et al. (2021) investigated 15 Chinese commodities futures prices and found that the volatility of commodity futures was impacted more strongly by macroeconomic forecasts than by concurrent economic conditions. Su et al. (2022) analyzed three commodities futures (corn, soybean, and wheat) from 1990 to 2021, and found that El Niño-Southern Oscillation (ENSO) played a significantly important role in grain futures price volatility. Zhao (2022) examined crude oil prices from 2000 to 2020, and found that crude oil inventory, US dollar exchange rate, and geopolitical risk had a significant influence on oil price volatility.
Regarding the impact of financial variables, Olowe (2011) investigated the day-of-the-week effect on UK Brent crude oil prices over the period 1997–2008 using GARCH models. The results indicated that there were significant positive Thursday effects in volatility returns in the oil market. Sharma and Malhotra (2015) examined the guard seed futures return series from April 2004 to November 2011 in an augmented GARCH model and found that if the level of futures trading volume increases unexpectedly, then the volatility increases and has a destabilizing impact on futures trading. In the same way, Boonvorachote and Lakmas (2016) examined the impact of the trading activity on price volatility in Asian futures exchanges from 2006 to 2012 using a GARCH (1,1) model and found that expected and unexpected trading volumes and open interests had, respectively, a positive and negative impact on volatility. Then, Qadan (2019) contrasted the hypothesis that the investor’s risk appetite and the prices of precious metals are tightly linked by applying GJR-GARCH and causality models. The results showed that the variance risk premium, which proxies for investors’ appetite for risk, drove the price movements of precious metals (returns and volatility), affirming the hypothesis that was initially raised. In addition, Ismailova (2019) examined lumber futures prices from 2000 to 2017 and found that when the level of inventory was low, positive housing starts news had the largest effect on lumber volatility. Next, Sobti (2019) evaluated whether the ban on futures trading had an impact on price volatility for five agriculture commodities (wheat, sugar, refined soya oil, rubber, and chickpeas) by applying an augmented EGARCH model. The author found that a ban on futures trading destabilized the spot markets by increasing spot volatility. In addition, Boyd et al. (2020) examined how risk premium affects the volatility in crude oil futures. Their results indicated that there was a significant positive relation between volatility and futures risk premium before May 2005 but a significant negative relation after that date.
Regarding the effect of speculation on volatility, Algieri (2016) used data from four commodities (maize, soybean, rice, and wheat) during the period 1995–2012, and the results indicated that excessive speculation leads to conditional price volatility. Next, Brümmer et al. (2016) investigated oilseed and oil vegetable commodities from May 1990 to July 2012 using VAR and GARCH models and found that financialization and speculation had no significant effects on the commodities price volatility. Along the same line, Bohl et al. (2018) investigated agriculture commodities in the Chinese futures markets by applying GARCH and VAR models and found that speculation activity, proxied by speculation and hedging ratios, had a positive influence on returns volatility for most of the commodities examined. Then, Bohl and Sulewski (2019) investigated five agricultural commodities (corn, soybean, sugar, coffee, and wheat) over the period 2006–2017 and found that long/short speculators have a calming or stabilizing effect on conditional volatility regardless of the underlying speculation measure and market liquidity. In addition, Yuan et al. (2020) analyzed the volatility among different agricultural commodity markets (corn, wheat, soybean, soya oil, cotton, and oat) from 2000 to 2019, applying a copula-GARCH model; their evidence indicated that potential speculation effects on one agricultural market could be contagious to another commodity market and results in an increase in volatility in agricultural product markets. Furthermore, Staugaitis and Vaznonis (2022) examined the returns on milling wheat, corn, and soybean futures between 2003 and 2021 and found that financial speculation, in most cases, has no effect or reduces the volatility of the underlying futures prices.
Regarding the impact of policy announcements on the volatility of commodities, Papadamou and Sogiakas (2018) examined unconventional monetary policies and their effects on the price volatility of silver and gold futures during the period 2009–2015. The evidence indicated that the Japanese Central Bank policies strengthened precious metal returns by causing stabilization effects in contrast to the European Central Bank (ECB) policies that had an opposite impact. Then, Farida and Singagerda (2020) analyzed several food commodities (rice, wheat, corn, and soybean) from 1960 to 2018 and found that the price of food commodities was more volatile after the adoption of the Renewable Fuel Standard 2 (RFS) policy in 2007. Hence, the development of biofuels generated higher price volatility in these commodities. In addition, Scarcioffolo and Etienne (2021) examined oil and natural gas prices from 1994 to 2019, applying a Markov-switching GARCH model and found that economic policy uncertainty had a significant impact on the volatility of both commodities, increasing the probability of agitated market conditions of both markets. Next, Goyal and Adjemian (2021) evaluated corn and soybean options during the period 1995–2019 and concluded that the news about policy announcements increased the implied volatility in both commodity markets. Along the same line, Mei and Xie (2022) investigated the impact of trade policy uncertainty (TPU) on the volatility of future prices under the GARCH-MIDAS framework and found that the TPU and other indicators of economic and financial uncertainty had a positive impact on the price volatility of the grain futures market.
Recently, the emergence of COVID-19 has affected many aspects of the worldwide economy, especially commodity futures markets, due to the disruption risk of global supply chains. Therefore, many researchers have made efforts to explain the impact of the coronavirus pandemic on the volatility of commodities prices. For instance, Bouazizi et al. (2020) examined oil prices during the period 2019–2020 using an EGARCH model and found that, during the times of the coronavirus crisis, oil prices exhibited higher volatility spikes. Then, Bentes (2022) investigated the stylized facts associated with the volatility of precious metals (gold, silver, platinum, and palladium) before and during the coronavirus pandemic using several GARCH models. The results supported the hypothesis that the pandemic impacted precious metals’ volatility. Moreover, Lin et al. (2022) analyzed numerous commodities futures from 1971 to 2020 in a GARCH framework and found that the price volatility in natural resources was higher during the COVID-19 pandemic, so price sensitivity increased during this term. Furthermore, Rizvi and Itani (2022) comparatively analyzed volatility spams in the oil market during the COVID-19 pandemic, the 2008 Global Financial Crisis (GFC), and the SARS outbreak of 2002–2004 (SARS) applying several GARCH models. The authors concluded that all of the crisis periods affected the volatility of oil prices, but the COVID-19 period caused more uncertainty and pessimism compared to either the GFC or SARS periods.
Szczygielski et al. (2022) investigated the magnitude of the impact of COVID-19-related uncertainty on returns and volatility for 20 national energy indices and a global energy index using ARCH and GARCH models. The evidence indicated that the energy sectors of countries further west from the outbreak of the virus in China were impacted to a greater extent by COVID-19-related uncertainty. Then, Zhang et al. (2022) investigated the influence of the COVID-19 pandemic on the volatility in three commodities futures (palladium, platinum, and silver) during the period 2012–2020. The authors found that platinum and silver prices were more sensitive to negative shocks due to coronavirus, while positive shocks played a more influential role in palladium price volatility. In addition, Xu et al. (2022) examined the gold futures prices using GARCH models and found that the COVID-19 pandemic period had a greater impact on gold price volatility than during the period of the 2008 GFC due to the uncertainty felt by the general public and the immediate closure of economic and financial activities. In the same way, (Zhang and Wang 2022) examined the pandemic effect on both short-term and long-run volatilities of futures for four commodities over the 2019–2021 period. They found that the COVID-19 pandemic heightened the long-run volatilities for all four commodities futures, with the impact descending in the following order: copper, soybean, oil, and gold. Finally, Zhou et al. (2022) examined the copper and crude oil prices from January 2019 to October 2021 using EGARCH and TGARCH models and found that both commodities showed volatility during the COVID-19 pandemic. However, the negative shocks due to coronavirus had a more pronounced effect on crude oil prices, making them more volatile compared to copper prices.
3. Methodology
3.1. Data and Variables
We consider the daily closing price for COMEX’s copper from 2 January 2018 to 30 December 2022, which was extracted from the Nasdaq1. Copper represents one of the highest futures trading volume commodities (CME 2022), and it has a long trading history in futures exchanges to avoid the excessive price volatility problem for a low trading frequency (CME 2020).
The daily return is defined as , where and are the closing prices at day t and t − 1, respectively. According to (WHO 2020), 11 March 2020 was the first day the global COVID-19 outbreak was considered a pandemic. Therefore, we define the dummy variable D = 0 before this date and D = 1 after that.
3.2. Econometric Strategy
In order to analyze whether COVID-19 had an effect on the volatility of copper futures daily returns, we extended the ARMA(m,n)–GARCH(p,q) model proposed by Bollerslev (1987) to include a dummy indicating the days that were affected by the coronavirus. In the model, GARCH(p,q) describes the variance equation for futures returns with the dummy variable included and the mean equation under the ARMA(m,n) framework. However, before estimating the model, we needed to make some previous procedures to ensure that the model satisfied some requirements.
The model has to use a stationary time series to avoid autocorrelation problems, so we use the breaking point unit root test by Perron (1989) to evaluate the stationarity considering that the structural breaks in the series time, in our case, appear when the quarantine started due to the worldwide consequences of COVID-19 (see Figure 1). Other tests, such as augmented Dicker Fuller (ADF) or Phillip Perron, are not employed since the unit root test will be biased towards the non-rejection of the null hypothesis in the presence of structural breaks (Nelson and Plosser 1982).
The (m,n) order of the mean equation was selected by using the Akaike information criterion (AIC), Schwarz criterion (SC), and the Hannan–Quinn criterion (HQC). After fitting the ARMA(m,n) component, the serial correlation Lagrange multiplier test by Godfrey (1996) was used to evaluate if there is autocorrelation in the residuals of the mean equation. Then, we evaluated whether the time series exhibits conditional heteroskedasticity using the ARCH test by Engle (1982) to detect the presence of volatility, where its null hypothesis is that the series of residuals are homoscedastic. Hence, if we reject it, it would mean that we must use an additional component that captures the volatility; thus, we justify the presence of the variance equation in the model.
In the same way as in the mean equation, the p and q values of the ARMA(m,n)–GARCH(p,q) model were chosen using the AIC, SC, and HQC. After fitting the mean and variance equation, we establish the model to determine whether coronavirus can affect the variance of the returns after we control for the volatility, which is defined as:
where is the futures returns at time t is the residual of the mean Equation (1) at the time t is the volatility at time t; is the standard normal white noise with , and , and measure the impact of the COVID-19 event in the long-run equilibrium variance.
The variance Equation (3) decomposes the variance of the residual at time t into three elements: the long-run equilibrium variance during the COVID-19 period , the impact of past variance information and the effect of squared lag errors .
After joining the model together with the dummy variable, we used the AIC, SC, and HQC to select the error distribution density that best fits the copper futures daily returns data since these data may not fit a normal distribution (Limpert and Stahel 2011). Then, we used the ARCH test to detect if the residuals of the final model are homoscedastic since the model must capture the volatility to avoid inaccuracies.
4. Results
Based on the empirical findings, we classified the results into three parts: descriptive statistics and stationarity, mean equation selection, and GARCH estimation.
4.1. Descriptive Statistics and Stationarity
Table 1 provides the statistical information for each price and return series of the copper futures. These data show that the mean value for the price and return series are 3.340397 and 0.000114, respectively. In addition, the median value for the return series (0.000109) is closer to its mean value than the median of the price series (3.085750). In addition, there is a small difference between the range values of both time series, with their minimum values occurring just a few days after the beginning of the pandemic. Additionally, the standard deviation of the price series is 0.720676, whereas the return series value is 0.014432. Therefore, the price series could have more volatility than the return series.

Table 1.
Descriptive statistics.
With respect to the asymmetric coefficient, the time series of the price and return have positive and negative skewness, respectively. In addition, the price series has a platykurtic distribution due to its kurtosis value being less than three, whereas the return series has a leptokurtic distribution because its kurtosis value is more than three. Additionally, the Jaque–Bera normality test was used to verify whether the time series fits a normal distribution, but their p-values indicate that both time series do not have normal distributions; which is consistent with their respective skewness and kurtosis coefficients.
As mentioned in the methodology section, the breaking point unit root test was used to assess the stationarity of both time series considering the structural breaks in the time period. Table 2 provides the estimated results of the breaking point unit root test.

Table 2.
Breaking unit root test in level.
From the empirical results, the price series do not reject the null hypothesis, which means that there is a presence of a unit root. Along with the unit root, the test indicates that 1 October 2020, is the day when the structural break happened. In addition, this breakpoint occurred when there was a deep reduction in copper production in Chile, the world’s largest copper producer, since a work shutdown occurred due to measures designed to curb the spread of COVID-19 (Woodall 2020).
Meanwhile, the returns series have an ADF value significant at 1%, so it follows a stationary process. The test showed that 18 March 2020 is the day when the breaking point is observed. This breakpoint happened one week after the WHO officially declared the start of the pandemic. Therefore, it could be inferred that the COVID-19 pandemic had a significant impact on the price and return series due to its breaking points occurring in the COVID-19 period.
After comparing both results, we decided to use the returns instead of the prices in the econometric model since the stationarity of the time series is a necessary condition for the subsequent model building.
4.2. Mean Equation’s Selection
We establish the (m,n) order for the mean equation using the AIC, SC, and HQC to determine the best-fitted model. In Table 3, after comparing multiple ARMA(m,n) equations, we find that the best-fitted mean equation is the ARMA(0,1) because its AIC, SC, and HQC statistics are the smallest among the five mean equations. In addition, an estimation of the MA(1) model is provided in Table 4, in which the coefficient value is negative (−0.048210 with a 5% significance level). However, the intercept value is statistically insignificant at the 1%, 5%, and 10% levels. Next, the mean equation for copper futures is given by:

Table 3.
Comparison of AIC, SC, and HQC statistics for ARMA models for copper futures daily returns.

Table 4.
Results of the ARMA(0,1) model for copper futures daily returns.
In which the mean equation did not have to satisfy the condition of stationarity of the return series since we did not have an autoregressive component; hence, the ARMA(0,1) is a consistent component.
Table 5 shows that the residuals of the ARMA(0,1) are not autocorrelated, so the mean equation is consistent and unbiased. Regarding the presence of ARCH effects in the ARMA(0,1), the estimated values of the ARCH(1) effects are provided in Table 6, in which both the intercept and coefficient values are found to be positive with a 1% significance level. It means that its squared residuals (RSD2) are autocorrelated to its lagged values, i.e., RSD2 (−1). In addition, the value of the Obs*R-squared parameter is 10.08858, with a Chi2(1) probability value of 0.0015; which rejects the null hypothesis that the residuals are homoscedastic; therefore, the mean equation presents heteroskedasticity.

Table 5.
Serial correlation LM test for residual of ARMA(0,1) model for copper returns.

Table 6.
Testing for ARCH(1) effects on ARMA(0,1) model for copper returns.
Then, as discussed earlier in the methodology section, an additional equation must be included to capture the ARCH effects. Thus, the inclusion of a variance equation in the model is justified due to the high volatility of the copper futures returns that can be observed in Figure 2, which shows that the variance in returns has an unstable movement across the time period. Furthermore, this variance component will be explained in detail in the next subsection.
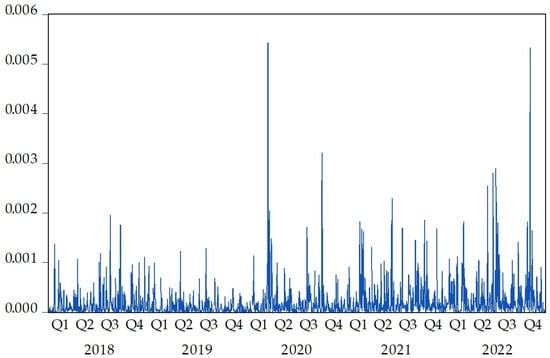
Figure 2.
Variance of the copper futures daily returns during 2018–2022.
4.3. GARCH Estimation
Once the order(m,n) has been determined, the best GARCH(p,q) equation was selected using the AIC, SC, and HQC to have a good fit measurement for modeling variance. In Table 7, after comparing the information criteria of multiple GARCH (m,n) equations, the GARCH(1,1) model was selected since it has the lowest SC and HQC values. Thus, considering both the mean and variance equation, the ARMA(0,1)–GARCH(1,1) model presents the m, n, p, and q values that best fit the copper futures returns market. Then, from Table 8, we find that the residuals of the model do not have ARCH effects, as both p-values for F (0.4495) and Chi2 (0.4491) statistics exceed the 10% level significance, so it means that the model correctly represents the volatile behavior of the returns.

Table 7.
Comparison of AIC, SC, and HQC statistics for GARCH models for copper futures daily returns.

Table 8.
Testing for ARCH(1) effects on ARMA(0,1)–GARCH(1,1) model for copper returns.
However, as we mentioned in the methodology, the error distribution density must be chosen that best fits the copper futures returns since the model may not fit a normal distribution. In Table 9, we compare the select model with a different error distribution using the AIC, SC, and HQC values, finding that the best error distribution for the ARMA(0,1)–GARCH(1,1) is the t-student distributions for the normal and generalized error distributions. The result is consistent with the kurtosis, skewness, and Jaque–Bera coefficients of the returns series (see Table 1), since, preliminarily, we know that the returns do not have a normal distribution.

Table 9.
Comparison of AIC, SC, and HQC statistics of the distribution of the ARMA(0,1)–GARCH(1,1) models for copper futures daily returns.
Table 10 shows the results of the ARMA(0,1)–GARCH(1,1) model with the COVID-19 dummy and t-student distribution. Regarding the mean equation, the moving-average component MA(1) has a negative value (−0.078656) with a 1% significance level. However, the intercept value is statistically insignificant at the 1%, 5%, and 10% levels.

Table 10.
Fitting results of the ARMA(0,1)–GARCH(1,1) model with the “COVID” dummy variable and t-student distribution for copper futures daily returns.
Meanwhile, the variance equation indicates that ARCH(1) and GARCH(1) components are positive and significant at the 5% and 1% levels, respectively. Furthermore, the constant value is positively significant at the 10% level.
In relation to the COVID-19 dummy, the coefficient for the dummy variable D was found to be positive and significant at 10%, indicating that the coronavirus increased the long-run equilibrium variance of the copper futures market. Since the coefficient of the dummy is added to the initial value of the constant, it increases the long-run equilibrium variance from 0.0000254 to 0.0000476, which means that it has approximately doubled its initial value. In this way, the pandemic has generated considerable uncertainty in the copper futures market in the long term, due to the fact that the closures of productive activities led to scenarios of insufficient supply with excessive demand, generating increases in price volatility. Likewise, it is worth noting that copper is an industrial metal, and its production is concentrated in a few countries (Chile, Peru, Congo DRC, and China). Thus, this context made the copper supply chain more vulnerable to an event caused by the consequences of the coronavirus in those countries, generating volatility in copper futures prices.
Next, the ARMA (0,1)–GARCH (1,1) model with the “COVID” dummy variable and the t-student distribution for copper futures is given by:
where , in which are data regarding the returns, and represents that the errors have t-student distribution with 1260 degrees of freedom (DF) since the DFs are calculated by subtracting one from the total number of observations (n − 1).
In the same line, the variance equation satisfies three necessary conditions to be a well-specified and efficient model. First, the ARCH and the GARCH components are positive since the variance is required to be positive and finite and have a non-negative conditional variance, respectively. Next, the sum of the ARCH and GARCH coefficients is between 0 and 1 because the variance cannot grow to infinity, and the constant term is positive. Hence, given that in the previous subsection, we already defined that the mean equation fulfills all its conditions, we can guarantee that the model, which integrates Equations (5)–(7), is efficient and consistent. In addition, the squared lag errors take on greater importance in the variance equation. This is illustrated in Table 3, which shows that the time series of copper futures returns follow an MA(1) process.
Finally, in Table 11, the presence of ARCH effects is tested in the above model, resulting in the rejection of the null hypothesis due to both p-values for F (0.4442) and Chi2 (0.4438) statistics exceeding the 10% level significance, which means that the model fits the volatility of the copper futures returns.

Table 11.
Testing for ARCH(1) effects on ARMA(0,1)–GARCH(1,1) model with the “COVID” dummy variable and t-student distribution for copper futures daily returns.
5. Discussion and Conclusions
The recent crisis unleashed by the COVID-19 pandemic has affected different economic sectors, especially the metal industry, because the coronavirus quarantine generated many logistical and operational restrictions in the supply production chain, generating a shortage of supply and high metal futures price fluctuations. In particular, this context caused a high uncertainty in the industrial sector as a consequence of the volatile behavior of the copper futures price, which is one of the main metals used in this sector. Therefore, this study investigates the impact of the COVID-19 pandemic on the volatility of copper futures prices employing an extended ARMA(m,n)–GARCH(p,q) model to incorporate a coronavirus influence variable during the period from 2 January 2018 to 30 December 2022.
The results indicate that the model that best fits the returns volatility is the ARMA(0,1)–GARCH(1,1) model with a t-student error distribution, in which we included a dummy variable that synthesizes the effect of the coronavirus. In addition, this study concludes that the COVID-19 pandemic has a significant influence on the volatility of the copper futures returns due to the impact of the coronavirus causing long-run equilibrium volatility to be more than double compared to the period before 11 March 2020, which is the day that COVID-19 was officially declared a pandemic. In general, our findings are in the same line with the empirical results of Bouazizi et al. (2020), Bentes (2022), Rizvi and Itani (2022), Zhang et al. (2022), and Xu et al. (2022) that demonstrate the existence of an influence of the COVID-19 pandemic on the volatility of commodities prices and returns using the GARCH framework.
Specifically, with regard to previous studies in the copper futures market, Zhang and Wang (2022); and Zhou et al. (2022) obtained the same conclusions as in our study since the pandemic event has increased the volatility in the copper futures prices and returns. However, from a methodological perspective, we use the copper returns rather than the prices in the ARMA(m,n)–GARCH(p,q) model, similar to the work of Zhang and Wang (2022), since stationary time series must be used in these kinds of models. This study is unlike the research of Zhou et al. (2022) in which, despite the breaking point unit root test results indicating that the copper prices did not follow a stationary process, the authors still decided to use the GARCH model.
While the empirical findings of this study hold considerable significance, there are several limitations that must be acknowledged. For instance, our research only examines the impact of the COVID-19 pandemic on copper futures returns by applying a traditional GARCH model, despite its known deficiencies and drawbacks. Additionally, these findings could help educate investors and policymakers about the risks of investing in highly volatile markets, especially during short-term shocks. This could involve public awareness campaigns and investor education programs.
Future studies would benefit from evaluating the impact of the coronavirus along with other variables such as financial indices, speculative activities, macroeconomic indicators, policy announcements, and more. The goal would be to assess whether the effect of COVID-19 remains as significant when these other factors are taken into account. We recommend the use of a GARCH model that considers the asymmetry of shocks, given that negative shocks may not have the same impact as positive shocks on the volatility of copper futures returns.
Author Contributions
Conceptualization, O.M.-V.-A. and B.C.-L.; methodology, O.M.-V.-A. and B.C.-L.; software, O.M.-V.-A. and B.C.-L.; validation, O.M.-V.-A. and B.C.-L.; formal analysis, O.M.-V.-A. and B.C.-L.; investigation, O.M.-V.-A. and B.C.-L.; resources, O.M.-V.-A. and B.C.-L.; data curation, O.M.-V.-A. and B.C.-L.; writing—original draft preparation, O.M.-V.-A. and B.C.-L.; writing—review and editing, O.M.-V.-A. and B.C.-L.; visualization, O.M.-V.-A. and B.C.-L.; supervision, O.M.-V.-A. and B.C.-L.; project administration, O.M.-V.-A. and B.C.-L.; funding acquisition, O.M.-V.-A. and B.C.-L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Instituto de Investigación Científica (IDIC) at the Universidad de Lima, grant number AC.06.045.2023.
Informed Consent Statement
Not applicable.
Data Availability Statement
Filtered and cured data at https://doi.org/10.17632/fm6y2szjhv.1 (accessed on 12 June 2023).
Acknowledgments
We express our sincere gratitude for the valuable comments provided by Guillermo Boitano, Director of the Economics Program at the Universidad de Lima.
Conflicts of Interest
The authors declare no conflict of interest.
Note
| 1 | https://www.nasdaq.com/market-activity/commodities/hg:cmx/historical (accessed on 17 March 2023). |
References
- Al-Awadhi, Abdullah M., Khaled Alsaifi, Ahmad Al-Awadhi, and Salah Alhammadi. 2020. Death and Contagious Infectious Diseases: Impact of the COVID-19 Virus on Stock Market Returns. Journal of Behavioral and Experimental Finance 27: 100326. [Google Scholar] [CrossRef] [PubMed]
- Algieri, Bernardina. 2016. Conditional Price Volatility, Speculation, and Excessive Speculation in Commodity Markets: Sheep or Shepherd Behaviour? International Review of Applied Economics 30: 210–37. [Google Scholar] [CrossRef]
- Arab News. 2022. Commodities Update—Gold Edges up; Copper Falls; Russian Wheat Prices Down. Arab News, July 5. [Google Scholar]
- Ayele, Amare Wubishet, Emmanuel Gabreyohannes, and Hayimro Edmealem. 2020. Generalized Autoregressive Conditional Heteroskedastic Model to Examine Silver Price Volatility and Its Macroeconomic Determinant in Ethiopia Market. Journal of Probability and Statistics 2020: 5095181. [Google Scholar] [CrossRef]
- Bai, Lan, Yu Wei, Guiwu Wei, Xiafei Li, and Songyun Zhang. 2021. Infectious Disease Pandemic and Permanent Volatility of International Stock Markets: A Long-Term Perspective. Finance Research Letters 40: 101709. [Google Scholar] [CrossRef]
- Bentes, Sónia R. 2022. On the Stylized Facts of Precious Metals’ Volatility: A Comparative Analysis of Pre- and during COVID-19 Crisis. Physica A: Statistical Mechanics and Its Applications 600: 127528. [Google Scholar] [CrossRef]
- Bohl, Martin T., and Christoph Sulewski. 2019. The Impact of Long-Short Speculators on the Volatility of Agricultural Commodity Futures Prices. Journal of Commodity Markets 16: 100085. [Google Scholar] [CrossRef]
- Bohl, Martin T., Pierre L. Siklos, and Claudia Wellenreuther. 2018. Speculative Activity and Returns Volatility of Chinese Agricultural Commodity Futures. Journal of Asian Economics 54: 69–91. [Google Scholar] [CrossRef]
- Bollerslev, Tim. 1987. A Conditionally Heteroskedastic Time Series Model for Speculative Prices and Rates of Return. The Review of Economics and Statistics 69: 542. [Google Scholar] [CrossRef]
- Boonvorachote, Tanachote, and Kritika Lakmas. 2016. Price Volatility, Trading Volume, and Market Depth in Asian Commodity Futures Exchanges. Kasetsart Journal of Social Sciences 37: 53–58. [Google Scholar] [CrossRef]
- Bouazizi, Tarek, Mongi Lassoued, and Zouhaier Hadhek. 2020. Oil price volatility models during coronavirus crisis: Testing with appropriate models using further univariate GARCH and Monte Carlo Simulation Models. International Journal of Energy Economics and Policy 11: 281–92. [Google Scholar] [CrossRef]
- Boyd, Naomi E., Bingxin Li, and Rui Liu. 2020. Risk Premia in the Term Structure of Crude Oil Futures: Long-Run and Short-Run Volatility Components. SSRN Electronic Journal 58: 1505–33. [Google Scholar] [CrossRef]
- Brümmer, Bernhard, Olaf Korn, Kristina Schlüßler, and Tinoush Jamali Jaghdani. 2016. Volatility in Oilseeds and Vegetable Oils Markets: Drivers and Spillovers. Journal of Agricultural Economics 67: 685–705. [Google Scholar] [CrossRef]
- CME. 2020. Metal Options Liquidity during London Market Hours. March 4. Available online: https://www.cmegroup.com/education/articles-and-reports/metal-options-liquidity-during-london-market-hours.html (accessed on 19 April 2023).
- CME. 2022. Copper Insights: November 2022. November 23. Available online: https://www.cmegroup.com/trading/metals/base/copper-insights/comex-copper-insights-november-2022.html (accessed on 20 April 2023).
- Elshkaki, Ayman, T. E. Graedel, Luca Ciacci, and Barbara K. Reck. 2016. Copper Demand, Supply, and Associated Energy Use to 2050. Global Environmental Change 39: 305–15. [Google Scholar] [CrossRef]
- Engle, Robert F. 1982. Autoregressive Conditional Heteroscedasticity with Estimates of the Variance of United Kingdom Inflation. Econometrica 50: 987–1007. [Google Scholar] [CrossRef]
- Farida, Ida, and Faurani Santi Singagerda. 2020. Volatility of world food commodity prices and renewable fuel standard policy. International Journal of Energy Economics and Policy 11: 516–27. [Google Scholar] [CrossRef]
- Gevorkyan, Arkady. 2017. Renewable versus Nonrenewable Resources: An Analysis of Volatility in Futures Prices. Australian Journal of Agricultural and Resource Economics 61: 19–35. [Google Scholar] [CrossRef]
- Godfrey, Leslie G. 1996. Misspecification Tests and Their Uses in Econometrics. Journal of Statistical Planning and Inference 49: 241–60. [Google Scholar] [CrossRef]
- Goyal, Raghav, and Michael K. Adjemian. 2021. The 2019 Government Shutdown Increased Uncertainty in Major Agricultural Commodity Markets. Food Policy 102: 102064. [Google Scholar] [CrossRef]
- Gruber, Joseph W., and Robert J. Vigfusson. 2018. Interest Rates and the Volatility and Correlation of Commodity Prices. Macroeconomic Dynamics 22: 600–19. [Google Scholar] [CrossRef]
- Ismailova, Zarina Mamadalievna. 2019. Quantifying the Announcement Effects in the U.S. Lumber Market. Morgantown: West Virginia University Libraries. [Google Scholar] [CrossRef]
- Karali, Berna, and Gabriel J. Power. 2013. Short- and Long-Run Determinants of Commodity Price Volatility. American Journal of Agricultural Economics 95: 724–38. [Google Scholar] [CrossRef]
- Limpert, Eckhard, and Werner A. Stahel. 2011. Problems with Using the Normal Distribution—And Ways to Improve Quality and Efficiency of Data Analysis. PLoS ONE 6: e21403. [Google Scholar] [CrossRef] [PubMed]
- Lin, Shiwei, Yanan Wang, Xiaojian Niu, and Hazar Dördüncü. 2022. Revisiting Volatility in Global Natural Resources Commodities? Evidence from Global Data. Resources Policy 77: 102759. [Google Scholar] [CrossRef]
- Liu, Guangqiang, and Xiaozhu Guo. 2022. Forecasting Stock Market Volatility Using Commodity Futures Volatility Information. Resources Policy 75: 102481. [Google Scholar] [CrossRef]
- Liu, Yang, Liyan Han, and Yang Xu. 2021. The Impact of Geopolitical Uncertainty on Energy Volatility. International Review of Financial Analysis 75: 101743. [Google Scholar] [CrossRef]
- Li, Ziran, Jiajing Sun, and Shouyang Wang. 2013. An Information Diffusion-Based Model of Oil Futures Price. Energy Economics 36: 518–25. [Google Scholar] [CrossRef]
- MarketScreener. 2022. Copper Prices Jump on China Reopening Hopes, Global Supply Woes. MarketScreener, November 4. [Google Scholar]
- Mei, Dexiang, and Yutang Xie. 2022. U.S. Grain Commodity Futures Price Volatility: Does Trade Policy Uncertainty Matter? Finance Research Letters 48: 103028. [Google Scholar] [CrossRef]
- Mining.com. 2020. Top Metal Miners Curb Operations as Governments Fight Virus. Mining.com, March 18. [Google Scholar]
- Mo, Di, Rakesh Gupta, Bin Li, and Tarlok Singh. 2018. The Macroeconomic Determinants of Commodity Futures Volatility: Evidence from Chinese and Indian Markets. Economic Modelling 70: 543–60. [Google Scholar] [CrossRef]
- Nelson, Charles R., and Charles R. Plosser. 1982. Trends and Random Walks in Macroeconmic Time Series: Some Evidence and Implications. Journal of Monetary Economics 10: 139–62. [Google Scholar] [CrossRef]
- Olowe, Rufus Ayodeji. 2011. Oil Price Volatility, the Global Financial Crisis, and the Day-of-the-Week Effect. Journal of African Business 12: 178–97. [Google Scholar] [CrossRef]
- Papadamou, Stephanos, and Vasilios Sogiakas. 2018. The Informational Content of Unconventional Monetary Policy on Precious Metal Markets. Journal of Forecasting 37: 16–36. [Google Scholar] [CrossRef]
- Perron, Pierre. 1989. The Great Crash, the Oil Price Shock, and the Unit Root Hypothesis. Econometrica 57: 1361–401. [Google Scholar] [CrossRef]
- Qadan, Mahmoud. 2019. Risk Appetite and the Prices of Precious Metals. Resources Policy 62: 136–53. [Google Scholar] [CrossRef]
- Reporte Minero. 2020. Inventarios de Cobre En Bolsas de Metales Crecen Más de 100% Por COVID-19. Reporte Minero, March 23. [Google Scholar]
- Reuters. 2021a. METALS-Copper Set for Best Monthly Gain since 2016 on Tight Supply, Demand Outlook. Reuters, February 25. [Google Scholar]
- Reuters. 2021b. METALS-Copper Hits near 6-Week Peak on China Floods, Equities Rout. Reuters, July 26. [Google Scholar]
- Reuters. 2021c. Industrial Metals Slide on New Coronavirus Variant Jitters. Reuters, November 26. [Google Scholar]
- Reuters. 2022. METALS-Copper Hits near 5-Month High on Demand Hopes, Dollar Weakness. Reuters, November 11. [Google Scholar]
- Rizvi, Syed Kumail Abbas, and Rania Itani. 2022. Oil Market Volatility: Comparison of COVID-19 Crisis with the SARS Outbreak of 2002 and the Global Financial Crisis of 2008. Economic Research-Ekonomska Istraživanja 35: 1935–49. [Google Scholar] [CrossRef]
- Scarcioffolo, Alexandre R., and Xiaoli L. Etienne. 2021. Regime-Switching Energy Price Volatility: The Role of Economic Policy Uncertainty. International Review of Economics & Finance 76: 336–56. [Google Scholar] [CrossRef]
- Sharma, Dinesh Kumar, and Meenakshi Malhotra. 2015. Impact of Futures Trading on Volatility of Spot Market—A Case of Guar Seed. Agricultural Finance Review 75: 416–31. [Google Scholar] [CrossRef]
- Sobti, Neharika. 2019. Does Ban on Futures Trading (de)Stabilise Spot Volatility? South Asian Journal of Business Studies 9: 145–66. [Google Scholar] [CrossRef]
- Staugaitis, Algirdas Justinas, and Bernardas Vaznonis. 2022. Short-Term Speculation Effects on Agricultural Commodity Returns and Volatility in the European Market Prior to and during the Pandemic. Agriculture 12: 623. [Google Scholar] [CrossRef]
- Su, Yuandong, Chao Liang, Li Zhang, and Qing Zeng. 2022. Uncover the Response of the U.S Grain Commodity Market on El Niño–Southern Oscillation. International Review of Economics & Finance 81: 98–112. [Google Scholar] [CrossRef]
- Szczygielski, Jan Jakub, Janusz Brzeszczyński, Ailie Charteris, and Princess Rutendo Bwanya. 2022. The COVID-19 Storm and the Energy Sector: The Impact and Role of Uncertainty. Energy Economics 109: 105258. [Google Scholar] [CrossRef]
- Umar, Zaghum, Mariya Gubareva, and Tamara Teplova. 2021. The Impact of COVID-19 on Commodity Markets Volatility: Analyzing Time-Frequency Relations between Commodity Prices and Coronavirus Panic Levels. Resources Policy 73: 102164. [Google Scholar] [CrossRef] [PubMed]
- United States Geological Survey. 2023. Mineral Commodity Summaries 2023. Available online: https://pubs.usgs.gov/periodicals/mcs2023/mcs2023.pdf (accessed on 15 April 2023).
- Vivian, Andrew, and Mark E. Wohar. 2012. Commodity Volatility Breaks. Journal of International Financial Markets, Institutions and Money 22: 395–422. [Google Scholar] [CrossRef]
- WHO. 2020. WHO Director-General’s Opening Remarks at the Media Briefing on COVID-19—11 March 2020. World Health Organization, March 12. Available online: https://www.who.int/director-general/speeches/detail/who-director-general-s-opening-remarks-at-the-media-briefing-on-covid-19---11-march-2020 (accessed on 10 March 2023).
- Woodall, Toby. 2020. Copper Supply Faces Struggle to Keep up with Growing Demand. S&P Global Market Intelligence, October 1. [Google Scholar]
- Wood Mackenzie. 2023. Global Copper Short-Term Outlook February 2023. Available online: https://www.woodmac.com/reports/metals-global-copper-short-term-outlook-february-2023-150104015/ (accessed on 20 April 2023).
- Xu, Qingqing, Tianci Meng, Yue Sha, and Xia Jiang. 2022. Volatility in Metallic Resources Prices in COVID-19 and Financial Crises-2008: Evidence from Global Market. Resources Policy 78: 102927. [Google Scholar] [CrossRef]
- Ye, Wuyi, Ranran Guo, Bruno Deschamps, Ying Jiang, and Xiaoquan Liu. 2021. Macroeconomic Forecasts and Commodity Futures Volatility. Economic Modelling 94: 981–94. [Google Scholar] [CrossRef]
- Yuan, Xinyu, Jiechen Tang, Wing-Keung Wong, and Songsak Sriboonchitta. 2020. Modeling Co-Movement among Different Agricultural Commodity Markets: A Copula-GARCH Approach. Sustainability 12: 393. [Google Scholar] [CrossRef]
- Zhang, Yanyan, Hsuling Chang, Chafic Saliba, and Amir Hasnaoui. 2022. Metallic Natural Resources Commodity Prices Volatility in the Pandemic: Evidence for Silver, Platinum, and Palladium. Resources Policy 78: 102924. [Google Scholar] [CrossRef]
- Zhang, Yongmin, and Ruizhi Wang. 2022. COVID-19 Impact on Commodity Futures Volatilities. Finance Research Letters 47: 102624. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Jing. 2022. Exploring the Influence of the Main Factors on the Crude Oil Price Volatility: An Analysis Based on GARCH-MIDAS Model with Lasso Approach. Resources Policy 79: 103031. [Google Scholar] [CrossRef]
- Zhou, Yang, Xiaoxiao Wang, Rebecca Kechen Dong, Ruihui Pu, and Xiao-Guang Yue. 2022. Natural Resources Commodity Prices Volatility: Evidence from COVID-19 for the US Economy. Resources Policy 78: 102895. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).