The Twin Impacts of Income Inequality and Unemployment on Murder Crime in African Emerging Economies: A Mixed Models Approach
Abstract
:1. Introduction
2. Theoretical Framework
2.1. Theoretical Channels of Income Inequality, Unemployment, and Crime
2.2. Empirical Literature
3. Research Methods and Data Used for the Study
3.1. Random Forest Model
3.1.1. Feature Importance
3.1.2. Gini Importance
3.2. Panel Vector Auto Regression (PVAR) Approach
3.3. Generalized Method of Moments and Fixed-Effect Models
4. Analysis of Results and Data Analysis
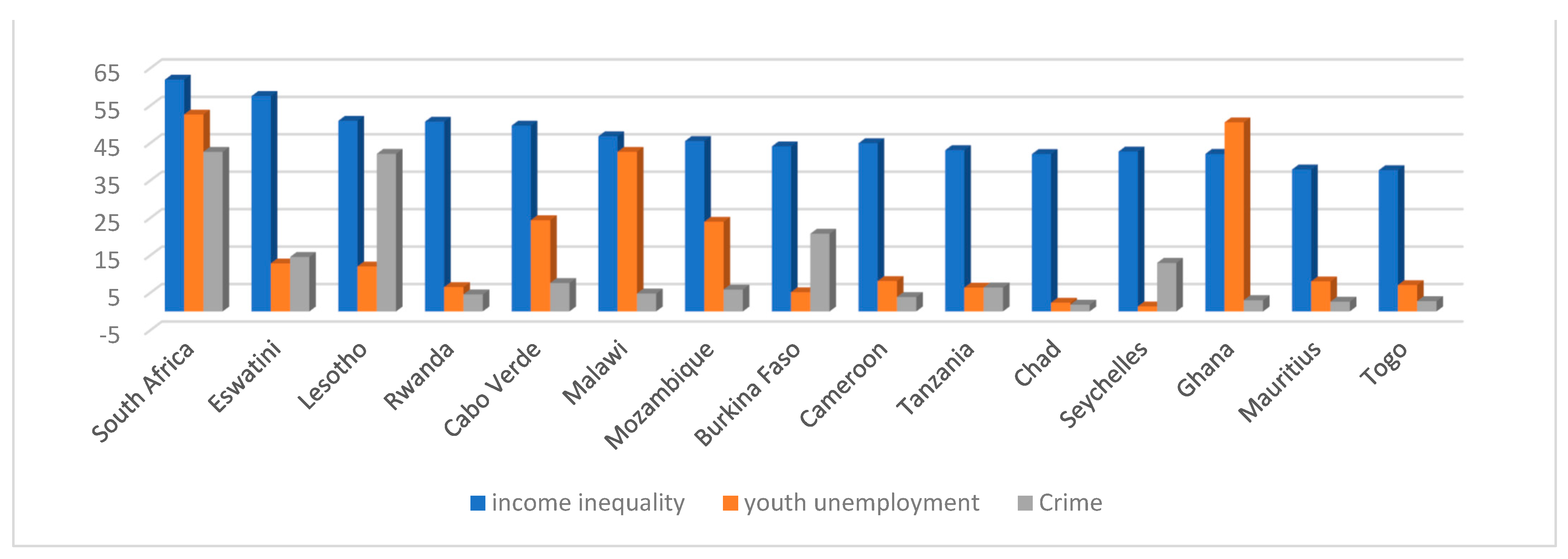
4.1. Data Analysis
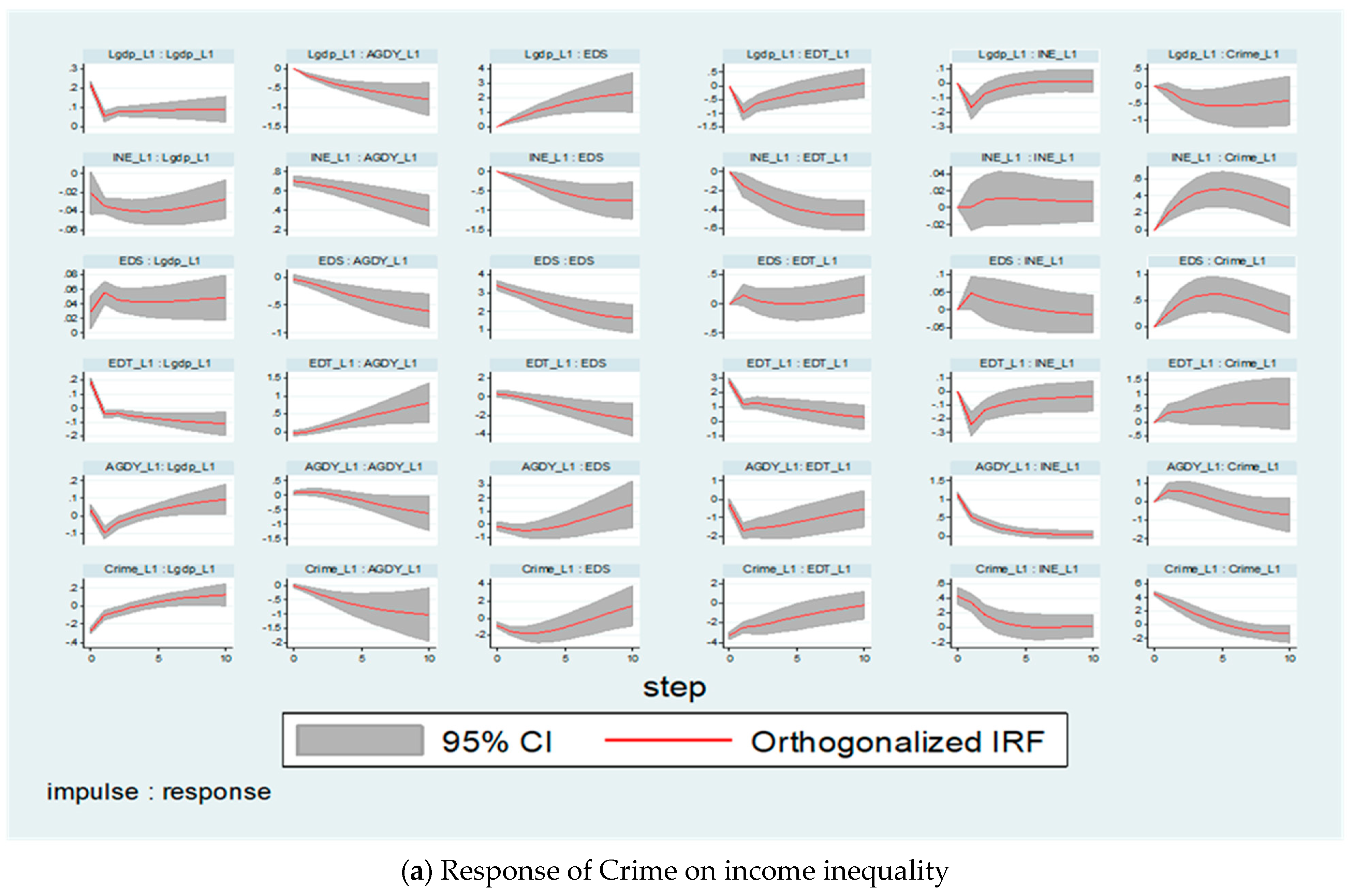
4.2. The Model Instability, Results, and PVAR Interpretations
4.3. Empirical Results of the Robustness and Sensitivity Analysis Using the GMM and FE Models
| Variables | Model III: Income Inequality-Crime | Model IV: Unemployment-Crime | ||
|---|---|---|---|---|
| S-GMM | FE | S-GMM | FE | |
| Pre-tax National Income (TOP10) | 5.80 ** (1.30) | 3.30 *** (0.99) | ||
| Male Unemployment (MUN) | 2.98 *** (0.10) | 2.00 *** (0.10) | ||
| GDP per Capita (GDPp) | −4.93 ** (2.10) | −2.45 ** (1.00) | −3.02 ** (1.98) | −2.00 ** (0.87) |
| School Enrolment, Secondary (EDS) | −2.30 ** (1.02) | −3.57 *** (0.06) | −1.80 ** (0.70) | −2.90 *** (0.09) |
| Age Dependency (AGDY) | 2.90 ** (0.80) | 1.50 ** (0.70) | 3.69 ** (1.40) | 0.98 ** (0.25) |
| Population Growth (EDT) | 1.90 *** (0.04) | 2.00 ** (1.00) | 0.80 *** (0.07) | 1.43 ** (0.60) |
| AR(1): p-value | 0.008 | 0.005 | ||
| AR(2): p-value | 0.180 | 0.139 | ||
| Hansen: p-value | 0.698 | 0.598 | ||
| 0.598 | 0.608 | |||
| # of obs. | 210 | 390 | 210 | 390 |
| # of countries | 15 | |||
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| t-Statistic | CRIME | INE | Top10 | YOU | MUN | EDS | EDT | AGDY | LGDP |
|---|---|---|---|---|---|---|---|---|---|
| CRIME | 1.00 | ||||||||
| INE | 0.64 (16.42) | 1.00 | |||||||
| TOP10 | 0.60 (10.55) | 0.78 (20.55) | 1.00 | ||||||
| YOU | 0.22 (4.48) | 0.15 (3.01) | 0.30 (2.00) | 1.00 | |||||
| MUN | 0.30 (2.66) | 0.45 (4.78) | 0.55 (4.61) | 0.14 (3.01) | 1.00 | ||||
| EDS | 0.24 (5.05) | 0.24 (4.99) | 0.28 (6.54) | 0.48 (10.94) | 0.30 (2.70) | 1.00 | |||
| EDT | −0.37 (−2.55) | −0.27 (3.56) | −0.57 (5.00) | 0.35 (7.43) | −0.50 (6.90) | 0.72 (20.68) | 1.00 | ||
| AGDY | 0.33 (7.04) | −0.37 (7.85) | −0.38 (4.75) | −0.37 (7.84) | −0.44 (8.00) | −0.86 (33.75) | −0.69 (18.84) | 1.00 | |
| LGDP | −0.26 (5.44) | 0.41 (8.95) | −0.50 (7.34) | 0.41 (9.11) | −0.56 (7.21) | 0.88 (37.94) | 0.65 (16.85) | −0.84 (30.72) | 1.00 |
| Lag | CD | J | J-P.v | MBIC | MAIC | MQIC |
|---|---|---|---|---|---|---|
| 1 | 0.99 | 190.22 | 0.30 | −633.07 | −114.90 | −310.33 |
| 2 | 0.99 | 101.34 | 0.35 | −658.40 | −83.05 | −230.20 |
| 3 | 0.99 | 50.20 | 0.45 | −356.62 | −61.51 | −110.40 |
| 4 | 0.99 | 20.70 | 0.50 | −135.09 | −40.10 | −80.91 |
| 5 | 0.99 | 10.22 | 0.20 | −100.91 | −15.10 | −59.40 |
| 6 | 0.99 | ….. | … | … | … | … |

References
- Abrigo, Michael, and Inessa Love. 2016. Estimation of panel vector autoregression in Stata. The Stata Journal 16: 778–804. [Google Scholar] [CrossRef]
- Anser, Muhammad Khalid, Yousaf Zahid, Nassani Abdelmohsen, Alotaibi Saad, Kabbani Ahmad, and Zaman Khalid. 2020. Dynamic linkages between poverty, inequality, crime, and social expenditures in a panel of 16 countries: Two-step GMM estimates. Economic Structures 9: 43. [Google Scholar] [CrossRef]
- Anwar, Awais, Noman Arshed, and Sofia Anwar. 2017. Socio-economic determinants of crime: An empirical study of Pakistan. International Journal of Economics and Financial Issues 7: 312–22. [Google Scholar]
- Arellano, Manuel, and Stephen Bond. 1991. Some tests of specification for panel data: Monte Carlo evidence and an application to employment. Review of Economic Studies Limited 58: 277–97. [Google Scholar] [CrossRef]
- Asteriou, Dimitris, and Stephen Hall. 2007. Applied Econometrics: A Modern Approach. New York: Palgrave Macmillan. [Google Scholar]
- Ayhan, Fatih, and Nurbanu Bursa. 2019. Unemployment and crime nexus in european union countries: A panel data analysis. Journal of Administrative Sciences 17: 465–84. [Google Scholar] [CrossRef]
- Becker, Gary. 1968. Crime and punishment: An economic approach. Journal of Political Economy 76: 169–217. [Google Scholar] [CrossRef]
- Bell, Brian, Costa Rui, and Machin Stephen. 2022. Why Does Education Reduce Crime? Journal of Political Economy 130: 1. [Google Scholar] [CrossRef]
- Biau, Gerard, Devroye Luc, and Lugosi Gabor. 2008. Consistency of random forests and other averaging classifiers. Journal of Machine Learning Research 9: 2015–33. [Google Scholar]
- Biau, Gerard. 2012. Analysis of a Random Forests Model. Journal of Machine Learning Research 13: 1063–95. [Google Scholar]
- Blundell, Richard, and Stephen Bond. 1998. Initial conditions and moment restrictions in dynamic panel data models. Journal of Econometrics 87: 115–43. [Google Scholar] [CrossRef]
- Breiman, Leo. 2001. Random forests. Machine Learning 45: 5–32. [Google Scholar] [CrossRef]
- Breiman, Leo. 2004. Consistency for a Simple Model of Random Forests. Technical Report 670. Berkeley: University of California. [Google Scholar]
- Cantor, David, and Kenneth Land. 1985. Unemployment and crime rates in the post-World War II United States: A theoretical and empirical analysis. American Sociological Review 50: 317–32. [Google Scholar] [CrossRef]
- Cantor, David, and Kenneth Land. 2001. Unemployment and crime rate fluctuations: A comment on Greenberg. Journal of Quantitative Criminology 17: 329–42. [Google Scholar] [CrossRef]
- Chang, Yu Sang, Sung Sup Choi, Jinsoo Lee, and Jin Won Chang. 2018. Population size vs. number of crime–Is the relationship super-linear? International Journal of Information and Decision Science 9: 26–39. [Google Scholar] [CrossRef]
- Charemza, Wojaciech, and Derek Deadman. 1992. New Directions in Econometric Practice: General to Specific Modelling, Cointegration, and Vector Autoregression. Edited by Edward Elgar. Berkeley: The University of California, p. 370. [Google Scholar]
- Chen, Xi, and Hua Zhong. 2020. Development and crime drop: A time-series analysis of crime rates in Hong Kong in the last three decades. International Journal of Offender Therapy and Comparative Criminology, 1–25. [Google Scholar] [CrossRef]
- Costantini, Mauro, Meco Iris, and Paradiso Antonion. 2018. Do inequality, unemployment and deterrence affect crime over the long run? Regional Studies 52: 558–71. [Google Scholar] [CrossRef]
- Edmark, Karin. 2005. Unemployment and crime: Is there a connection? Scandinavian Journal of Economics 107: 353–73. [Google Scholar] [CrossRef]
- Ehrlich, Isaac. 1975. The deterrent effect of capital punishment: A question of life and death. American Economic Review 65: 397–417. [Google Scholar]
- Fajnzylber, Pablo, Ledeman Daniel, and Loayza Nnrman. 2002. What causes violent crime? European Economic Review 46: 1323–57. [Google Scholar] [CrossRef]
- Faryad, Parhiz, Zarrabi Asghar, and Meshkini Abolfazl. 2017. Analyzing the Relationship between Crime and Population Intensity (12th Municipality Area of Tehran as a Case Study). European Online Journal of Natural and Social Sciences 6: 1. Available online: www.european-science.com (accessed on 3 February 2022).
- Felson, Marcus, and Lawrence Cohen. 1980. Human ecology and crime: A routine activity approach. Human Ecology 8: 389–406. [Google Scholar] [CrossRef]
- Freeman, Richard. 1999. The economics of crime. Handbook of Labor Economics 3: 3529–71. [Google Scholar] [CrossRef]
- Frees, Edward. 1995. Assessing cross-sectional correlation in panel data. Journal of Econometrics 69: 393–414. [Google Scholar] [CrossRef]
- Friedman, Milton. 1937. The use of ranks to avoid the assumption of normality implicit in the analysis of variance. Journal of the American Statistical Association 32: 675–701. [Google Scholar] [CrossRef]
- Galbraith, James. 1998. Created Unequal: The Crisis in American Pay. New York: Free Press. [Google Scholar]
- Geurts, Pierre, Ernst Damien, and Wehenkel Louis. 2006. Extremely randomized trees. Machine Learning 63: 3–42. [Google Scholar] [CrossRef]
- Goh, Lim Thye, and Siong Hook Law. 2021. The crime rate and income inequality in Brazil: A nonlinear ARDL approach. International Journal of Economic Policy in Emerging Economies 15: 1. Available online: https://www.inderscienceonline.com/doi/pdf/10.1504/IJEPEE.2022.120063 (accessed on 3 January 2022). [CrossRef]
- Grogger, John. 2006. An economic model of recent trends in violence. In The Crime Drop in America, 2nd ed. Edited by A. Blumstein and J. Wallman. Cambridge: Cambridge University Press, pp. 266–87. [Google Scholar]
- Harris, Richard, and Elias Tzavalis. 1999. Inference for unit roots in dynamic panels where the time dimension is fixed. Journal of Econometrics 91: 201–26. [Google Scholar] [CrossRef]
- Im, Kyung, So Pesaran, M. Hashem, and Shin Yongcheol. 2003. Testing for unit roots in heterogeneous panels. Journal of Econometrics 115: 53–74. [Google Scholar] [CrossRef]
- Kelly, Morgan. 2000. Inequality and crime. The Review of Economics and Statistics 82: 530–39. [Google Scholar] [CrossRef]
- Kujala, Pietari, Kallio Johanna, and Niemelä Mikko. 2019. Income inequality, poverty, and fear of crime in Europe. SAGE Publications 53: 163–85. [Google Scholar] [CrossRef]
- Lobonţ, Oana-Ramona, Nicolescu Ana-Cristina, Moldovan Nicoleta-Claudia, and Kuloğlu Ayhan. 2017. The effect of socioeconomic factors on crime rates in Romania: A macro-level analysis. Economic Research-Ekonomska Istraživanja 30: 91–111. [Google Scholar] [CrossRef]
- Lochner, Lance. 2020. Education and crime. In The Economics of Education, 2nd ed. A Comprehensive Overview. chap. 9. Amsterdam: ScienceDirect, pp. 109–17. [Google Scholar] [CrossRef]
- Maddah, Majid. 2013. The effect of unemployment and income inequality on crimes, a time series analysis. International Journal of Economics Research 2: 37–42. [Google Scholar]
- Mazorodze, Brain Tavonga. 2020. Youth unemployment and murder crimes in KwaZulu-Natal, South Africa. Cogent Economics & Finance 8: 1799480. [Google Scholar] [CrossRef]
- Meinshausen, Nicolai. 2006. Quantile regression forests. Journal of Machine Learning Research 7: 983–99. [Google Scholar]
- Merton, Robert. 1938. Social structure and anomie. American Sociological Review 3: 672–82. [Google Scholar] [CrossRef]
- Ngozi, Adeleye, and Jamal Abdul. 2020. Dynamic analysis of violent crime and income inequality in Africa. International Journal of Economics, Commerce and Management. VIII, p. 2. Available online: http://ijecm.co.uk/ (accessed on 19 January 2022).
- Nilsson, Anna. 2004. Income Inequality and Crime: The Case of Sweden. Working Paper. Uppsala: Institute of Labour Market Policy Evaluation, p. 6. [Google Scholar]
- Pesaran, Hashen. 2004. General Diagnostic Tests for Cross-Sectional Dependence in Panels. Cambridge Working Papers in Economics No. 0435. Cambridge: Faculty of Economics, The University of Cambridge. [Google Scholar] [CrossRef]
- Quetelet, Adolphe. 1984. Research on the Propensity for Crime at Different Ages. Translated by S. Sylvester. Cincinnati: Anderson. First published 1831. [Google Scholar]
- Siwach, Garima. 2018. Unemployment shocks for individuals on the margin: Exploring recidivism effects. Labour Economics 52: 231–44. [Google Scholar] [CrossRef]
- Solt, Frederick. 2020. The standardized world Income-inequality database. Social Science Quarterly 90: 231–42. [Google Scholar] [CrossRef]
- United Nations Office on Drugs Crime UNODC. 2019. Global Study on Homicide. Vienna. Available online: https://www.unodc.org/gsh/ (accessed on 3 January 2022).
- Witt, Robert, Clarke Alan, and Fielding Nigel. 1998. Crime, earnings inequality and unemployment in England and Wales. Applied Economics Letters 5: 265–67. [Google Scholar] [CrossRef]
- World Development Indicators WDI. 2022. World Bank. Washington, DC. Available online: http://data.worldbank.org/data-catalog/world-development-indicators (accessed on 3 January 2022).
- Zaman, Khalid. 2018. Crime-poverty nexus: An intellectual survey. Forensic Res Criminol International Journal 6: 327–29. [Google Scholar] [CrossRef]

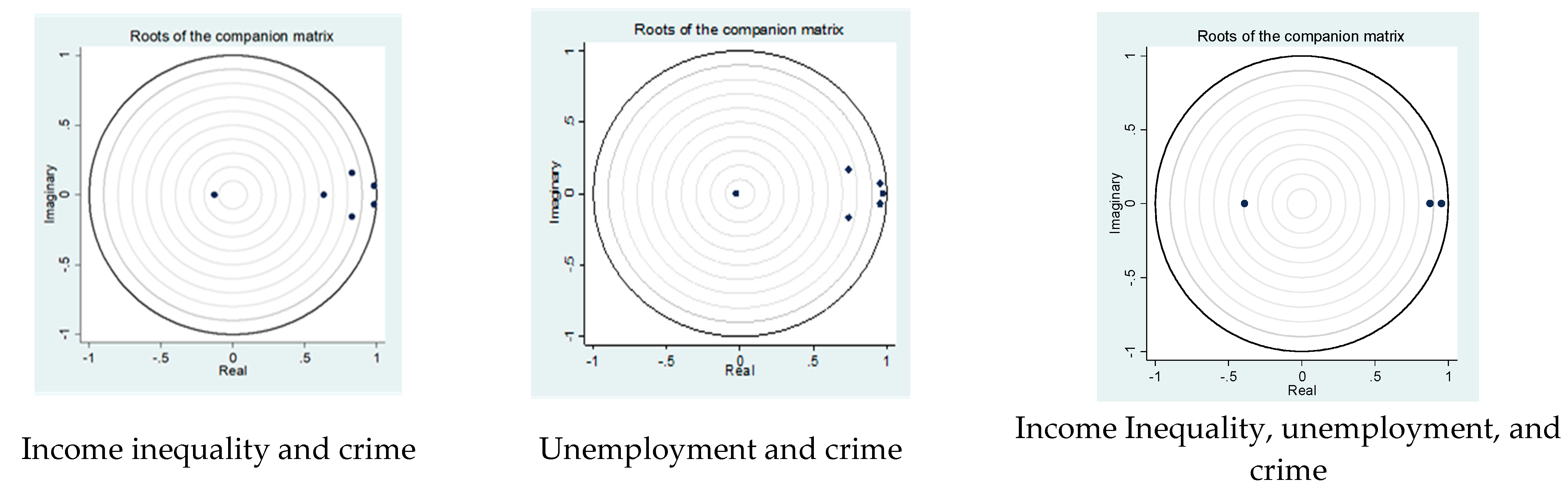

| Descriptive Statistics | Im–Pesaran–Shin | Harris–Tzavalis | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Variables | Mea | Std.d | Min | Max | SKW | KUR | JB-ST | JB-P | Level | 1st | Inte | Level | 1st | Inte |
| Crime | 10.29 | 13.68 | 6.52 | 60.84 | −0.05 | 2.77 | 93.20 | 0.00 | 1.20 | −5.19 *** | I(1) | 2.11 | −6.10 *** | I(1) |
| INE | 46.48 | 6.58 | 10.30 | 63.00 | −0.67 | 2.89 | 55.11 | 0.00 | 1.09 | −3.92 *** | I(1) | 4.20 | −8.80 *** | I(1) |
| Top10 | 48.20 | 10.40 | 12.10 | 64.30 | −0.40 | 3.44 | 14.00 | 0.00 | 2.11 | −5.21 *** | I(1) | 3.19 | −10.83 *** | I(1) |
| YOU | 17.17 | 6.04 | 5.39 | 60.83 | −0.53 | 2.93 | 19.24 | 0.00 | −8.87 *** | I(0) | −4.33 *** | I(0) | ||
| MUN | 19.71 | 8.09 | 0.60 | 59.99 | −0.50 | 2.89 | 22.43 | 0.00 | 0.88 | −5.40 *** | I(1) | 3.22 | −4.99 ** | I(1) |
| EDT | 70.23 | 19.98 | 8.20 | 115.95 | −0.10 | 3.19 | 14.92 | 0.00 | 1.90 | −4.10 ** | I(1) | 1.28 | 14.20 ** | I(1) |
| EDS | 48.03 | 6.20 | 5.95 | 41.59 | −0.44 | 2.27 | 18.81 | 0.00 | −8.10 *** | I(0) | −9.17 *** | I(0) | ||
| AGDY | 72.16 | 19.63 | 25.15 | 102.44 | −0.11 | 2.11 | 15.88 | 0.00 | 2.09 | −9.15 *** | I(1) | 0.30 | −15.13 *** | I(1) |
| LGDP | 7.04 | 1.18 | 4.79 | 9.68 | −0.41 | 2.87 | 78.29 | 0.00 | 1.89 | −6.30 *** | I(1) | 1.20 | −8.30 *** | I(1) |
| Pedroni Tests for Cointegration | Tests for Cross-Sectional Independence | ||||
|---|---|---|---|---|---|
| Augmented Dickey–Fuller t | 7.87 | Pr = 0.00 | Friedman’s test | 140.43 | Pr = 0.00 |
| Modified Phillips–Perron t | 3.92 | Pr = 0.03 | Frees’ test | 0.78 | Pr = 0.00 |
| Phillips Perron t | 5.19 | Pr = 0.000 | Pesaran’s test | 10.30 | Pr = 0.00 |
| Region/Countries | Author (S) | Income Inequality-Crime | Unemployment-Crime |
|---|---|---|---|
| African emerging economies | Our results | 5.80 ** (1.30) | 2.98 *** (0.10) |
| Brazil | Goh and Law (2021) | 9.48 ** | |
| Africa | Ngozi and Abdul (2020) | 7.58 *** (2.90) | |
| Panel of 16 countries | Anser et al. (2020) | 0.818 ** | 0.425 ** |
| Southern African provinces | Mazorodze (2020) | 0.510 *** (0.191) | |
| United State of America | Costantini et al. (2018) | 2.98 ** (0.24) | 0.62 *** (0.04) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zungu, L.T.; Mtshengu, T.R. The Twin Impacts of Income Inequality and Unemployment on Murder Crime in African Emerging Economies: A Mixed Models Approach. Economies 2023, 11, 58. https://doi.org/10.3390/economies11020058
Zungu LT, Mtshengu TR. The Twin Impacts of Income Inequality and Unemployment on Murder Crime in African Emerging Economies: A Mixed Models Approach. Economies. 2023; 11(2):58. https://doi.org/10.3390/economies11020058
Chicago/Turabian StyleZungu, Lindokuhle Talent, and Thamsanqa Reginald Mtshengu. 2023. "The Twin Impacts of Income Inequality and Unemployment on Murder Crime in African Emerging Economies: A Mixed Models Approach" Economies 11, no. 2: 58. https://doi.org/10.3390/economies11020058
APA StyleZungu, L. T., & Mtshengu, T. R. (2023). The Twin Impacts of Income Inequality and Unemployment on Murder Crime in African Emerging Economies: A Mixed Models Approach. Economies, 11(2), 58. https://doi.org/10.3390/economies11020058






